A new metaheuristic for continuous structural optimization: water evaporation optimization

Abstract

The paper proposes a novel physically inspired population-based metaheuristic algorithm for continuous structural optimization called as Water Evaporation Optimization (WEO). WEO mimics the evaporation of a tiny amount of water molecules adhered on a solid surface with different wettability which can be studied by molecular dynamics simulations. A set of six truss design problems from the small to normal scale are considered for evaluating the WEO. The most effective available state-of-the-art metaheuristic optimization methods are used as basis of comparison. The optimization results demonstrate the efficiency and robustness of the WEO and its competitive performance to other algorithms for continuous structural optimization problems.

1 Introduction

The aim of structural optimization is to generate automated procedures for finding the best possible design with respect to at least one criterion (the objective), satisfying a set of constraints (Davarynejad et al. 2012). Structural optimization is an important area related to both optimization and structural engineering. From the optimization point of view, efficient and fast stochastic optimization algorithms (metaheuristic algorithms) are developed to overcome the difficulties of traditional optimization solvers (Gradient-based optimization algorithms) and gained increasing popularity because of their ability to deliver satisfactory solutions in a reasonable time. Performance assessment of a metaheuristic algorithm may be used by solution quality, computational effort, and robustness (Talbi 2009), directly affected by its two contradictory criteria: exploration of the search space (diversification) and exploitation of the best solutions found (intensification). To alleviate these two features over the last three decades various kinds of population based metaheuristic algorithms have been developed and modified, and applied successfully to structural optimization. From these approaches for example one can refer to Genetic Algorithms (GA) (Rajeev and Krishnamoorthy 1992), Simulated Annealing (SA) (Lamberti 2008), Ant Colony Optimization (ACO) (Camp and Bichon 2004), Particle Swarm Optimization (PSO) (Kaveh and Talatahari 2009a), Harmony Search (HS) (Degertekin 2012; Lee and Geem 2004), Big Bang-Big Crunch (BB-BC) (Camp 2007), Charged System Search (CSS) (Kaveh and Talatahari 2010b), Imperialist Competitive Algorithm (ICA) (Kaveh and Talatahari 2010c), Cuckoo Search algorithm (CS) (Yang and Deb 2010), Teaching Learning Based Optimization algorithm (TLBO) (Degertekin and Hayalioglu 2013), Mine Blast Algorithm (MBA) (Sadollah et al. 2012), Dolphin echolocation optimization (DEO) (Kaveh and Farhoudi 2013), Ray Optimization algorithm (RO) (Kaveh and Khayatazad 2012) and Colliding Bodies Optimization (CBO) (Kaveh and Mahdavi 2014).

Very recently the authors developed a novel and efficient physically inspired multiple population based metaheuristic algorithm for real parameter optimization called as Water Evaporation Optimization (WEO). WEO mimics the evaporation of a tiny amount of water molecules adhered on a solid surface with different wettability which can be studied by molecular dynamics simulations.

Structural optimization problems can have discrete, continuous and/or mixed continuous and discrete design variables. Although it is often desirable to have discrete or mixed discrete and continuous design variables for structural optimization problems it is common to develop the optimization algorithms for continuous engineering optimization in the aspect of theory and practice. In this regard our aim is to assess the efficiency of implementing WEO on continuous structural optimization problems.

Many structural test functions exist in the literature, but there is no standard list one has to follow. In this regard Gandomi and Yang (2011) have categorized structural optimization problems into two groups, truss and non-truss design problems. Truss design problems are highly non-linear, involving many different design variables under complex and nonlinear constraints which can be classified as small scale, normal scale, large scale and very large scale problems. Truss optimization is a challenging area of structural optimization, and many researchers have tried to minimize the weight (or volume) of truss structures using different algorithms as it is reviewed in the first paragraph of this section. In this regard six truss design problems (planar 10-bar truss, spatial 22-bar truss, spatial 25-bar truss, spatial 72-bar truss, 120-bar truss dome, and planar 200-bar truss) are used here as small and normal scale benchmarks for evaluating the search behavior of WEO utilizing three metrics: solution quality, computational effort and robustness. The most effective available state-of-the-art metaheuristic optimization methods based on our knowledge are used here as the basis of comparison. The optimization results demonstrate the efficiency and competitive performance of the WEO algorithm in terms of the solution quality and robustness.

The structure of the paper is as follows. Section 2 develops the novel proposed WEO algorithm in detail. Section 3 presents mathematical model of structural optimization with continuous design variables, and investigates parameter setting and the search behavior of WEO in depth, and experimentally validates the WEO and compares it with most efficient metaheuristics. At the end conclusions are derived in Section 4.

2 Water evaporation optimization (WEO)

The evaporation of water is very important in biological and environmental science. The water evaporation from bulk surface such as a lake or a river is different from evaporation of water restricted to the surface of solid materials. The second type of evaporation is the inspiration basis of WEO. This type of water evaporation is essential in the macroscopic world such as the water loss through the surface of soil (Zarei et al. 2010). Wang et al. (Wang et al. 2012) presented Molecular Dynamics (MD) simulations on the evaporation of water from a solid substrate with different surface wettability. In the following, first their simulation result is outlined which is considered as an effective essence to develop the present WEO algorithm. Then the analogy between this type of evaporation and a population-based metaheuristic algorithm is established. This analogy leads us to the mechanisms of the WEO. At the end, the proposed WEO is presented.

2.1 MD simulations for water evaporation from a solid surface

MD simulations were carried out in a neutral substrate which is chargeable between q = 0e to q = 0.7e, where e stands for an elementary charge with a measured value of approximately 1.6 × 10⁻¹⁹ coulombs. By changing the value of charge (q), a substrate with tunable surface wettability can be obtained.

Initially, the fixed number of water molecules was piled upon the substrate in a water cube form as shown in Fig. 1a. In the simulation, q is sampled from 0-0.7e with an increment of 0.1e. The simulations show that the water spreads smoothly on the substrate when q ≥ 0.4e (Fig. 1c). When q <0.4e, the water shrinks gradually into a sessile droplet like a spherical cap with the contact angle (θ) to the substrate as q decreased (Fig. 1b). In this phase, the contact angle between droplet and substrate can be affected by the amount of aqueous (Gelderblom et al. 2011), nearby liquid molecules (Hong-Kai and Hai-Ping 2005), and the surface wettability. However the contact angle (θ) can be used only as a phenomenology criterion of surface wettability and it can be consistent to the experimental results of relatively small amount of water.

Fig. 1

(a) Side view of the initial system; (b) Snapshot of water on the substrate with low wettability (q = 0 e); (c) Snapshot of water on the substrate with high wettability (q = 0.7 e) (Wang et al. 2012)

The evaporation speed of the water layer can be described by the evaporation flux which is defined as the average number of the water molecules entering the accelerating region (the upward arrow denoted in Fig. 1a) from the substrate per nanosecond. Counter to intuition, the evaporation flux does not decrease monotonically as q increases. Actually the evaporation flux first increases as q increases when q < 0.4e; then the evaporation flux reaches its maximum around q = 0.4e; when q ≥ 0.4e, the evaporation flux decreases as q increases.

To analyze this unusual variation of the evaporation flux, Wang et al. (Wang et al. 2012) assumed that the evaporation flux J(q) can be considered as a product of the aggregation probability of a water molecule in the interfacial liquid–gas surface and the escape probability of such surficial water molecule:

$$ J(q)\propto {P}_{geo}\left(\theta (q)\right){P}_{ener}(E) $$

(1)

where P _geo (θ) is the probability for a water molecule on the liquid–gas surface, which is a geometry related factor. With respect to molecular dynamics simulation, P _geo (θ) is defined as the ratio of the number of surficial water molecules to the total number of all condensed water molecules, and it is calculated as:

$$ {P}_{geo}\left(\theta \right)={P}_o{\left(\frac{2}{3}+\frac{{ \cos}^3\theta }{3}- \cos \theta \right)}^{-2/3}\left(1- \cos \theta \right) $$

(2)

where P ₀ is a constant function of water molecule diameter and total volume of molecules. It should be noted that this probability is obtained for q < 0.4e in which the water molecules shrink gradually into a sessile droplet like a spherical cap with contact angle θ to the substrate. For more detail, the reader can refer to MD simulations conducted by Wang et al. (Wang et al. 2012). P _ener (E) is the escape probability of a surficial water molecule. E = E _WW  + E _sub (q) is the average interaction energy exerted on the surficial water molecules, E _ww is the energy provided by the neighboring water molecules; E _sub (q) represents the interaction energy from the substrate, mainly provided by the electrical charge q assigned on the substrate.

The relationship between the assigned charge q and the contact angle of the water droplet is shown in Fig. 2a. The contact angle of the water droplet θ decreases as q increases and reaches 0° when q = 0.4 e. When q < 0.4 e, most of the surficial water molecules are relatively far from the substrate. According to Fig. 2b, the energy E _sub provided by the substrate does not change much, and its variation is negligible if compared to the E _sub of q ≥ 0.4e. At the same time, the E _ww provided by the neighboring water molecules almost keeps constant in simulation. Hence, for q < 0.4e, the escape probability of a surficial water molecule (P _ener (E)) is nearly a constant. Therefore the evaporation flux (1) will be updated as follows in which J ₀ is constant equal to 1.24 ns⁻¹.

Fig. 2

(a) The contact angle θ of the water droplet with different assigned charge q; (b) The interaction energy exerted on the outermost-layer water by the substrate (E _sub ) with different assigned charge q (Wang et al. 2012)

$$ J\left(\theta \right)={J}_o{P}_{geo}\left(\theta \right),\;q<0.4 $$

(3)

For q ≥ 0.4e, the adhered water forms a flat single-layer molecule sheet with only a few water molecules overlapping upon it, and the shape of the tiny water aggregation does not change much with different q. According to the definition of P _geo (θ), all the water molecules are on the surface layer now, therefore P _geo (θ) = 1. According to the thermal dynamics, for the system under the NVT ensemble (NVT ensemble indicates a canonical ensemble representing possible states of a mechanical system in thermal equilibrium), the probability for a free molecule to gain kinetic energy more than E ₀ is proportional to $\exp \left(-\frac{E_o}{K_BT}\right)$ (Bond and Struchtrup 2004). Based on the MD simulations the evaporation flux decreases almost exponentially with respect to E _sub . Therefore the evaporation flux (1) will be updated as follows in which T is the room temperature and K _B is the Boltzman constant (Bond and Struchtrup 2004).

$$ J(q)= \exp \left(-\frac{E_{sub}}{K_BT}\right),\;q\ge 0.4e $$

(4)

2.2 Inspiration of the WEO algorithm

Based on the previous subsection one can see a fine analogy between this type of water evaporation phenomena and a population based metaheuristic algorithm, if he/she notes their MD simulations results from end to the beginning. It should be noted that this analogy is stated for a minimization problem. Water molecules can be considered as algorithm individuals. Solid surface or substrate with variable wettability is reflected as the search space. Decreasing the surface wettability (substrate changed from hydrophility to hydrophobicity) reforms the water aggregation from a monolayer to a sessile droplet. Such a behavior is in coincidence with how the layout of the algorithm individuals changes to each other as the algorithm progresses. Furthermore, decreasing wettability of the surface (decreasing q from 0.7 e to 0.0e) can represent the reduction of the objective function for a minimization optimization problem as the algorithm progresses. Evaporation flux variation of the water molecules can be considered as the most appropriate measure for updating the individuals which is in a good agreement with the local and global search ability of the algorithm, and can help us to develop the WEO with significantly good convergence behavior and simple algorithmic structure.

The evaporation flux is considered as a measure for determining the probability of updating the individuals of the algorithm that reaches its maximum around q = 0.4e. This situation is considered until the algorithm reaches the middle of the optimization process. In other words, WEO updates the individuals with the probability based on (4) (this probability is named Monolayer Evaporation Probability or MEP) until it reaches to half of the number of objective function evaluations. This first phase provides the global search ability of the algorithm. After this phase, individuals update with the probability based on (3), which is named as Droplet Evaporation Probability or DEP. This phase provides the local search ability of the algorithm. These two phases are introduced extensively in the following, and then the updating mechanism of individuals is introduced.

2.2.1 Monolayer evaporation phase

In the monolayer evaporation phase we can estimate the (4) with a simple exponential function of the substrate interaction energy, i.e., exp(E _sub ). As mentioned before, in this phase (q > 0.4e), as q increases, the substrate will have more energy and as a result less evaporation will occur. Let us consider the maximum (E _max ) and minimum (E _min ) values of E _sub , as -0.5 and -3.5, respectively, for the tth iteration of the algorithm until half the number of algorithm iterations. These values are based on Fig. 2b. The monolayer evaporation probability for different values of substrate energy between -3.5 and -0.5 is shown in Fig. 3.

Fig. 3

Monolayer evaporation flux with different substrate energy for the WEO

In each iteration, the objective function of individuals Fit _i ^t is scaled to the interval [-3.5, -0.5] representing the corresponding E _sub (i)^t inserted to each individual (substrate energy vector), via the following scaling function:

$$ {E}_{sub}{(i)}^t=\frac{\left({E}_{\max }-{E}_{\min}\right)\times \left(Fi{t}_i^t-Min(Fit)\right)}{\left( Max(Fit)-Min(Fit)\right)}+{E}_{\min } $$

(5)

where Min and Max are the minimum and maximum functions, respectively. After generating the substrate energy vector, the Monolayer Evaporation Probability matrix (MEP) is constructed by the following equation:

$$ ME{P}_{ij}^t=\left\{\begin{array}{c}\hfill 1\kern0.36em if\; ran{d}_{ij}< \exp \left({E}_{sub}{(i)}^t\right)\hfill \\ {}\hfill 0\kern0.36em if\; ran{d}_{ij}\ge \exp \left({E}_{sub}{(i)}^t\right)\hfill \end{array}\right. $$

(6)

where MEP ^t _ij is the updating probability for the jth variable of the ith individual or water molecule in the tth iteration of the algorithm. In this way an individual with better objective function (considering the minimization problem) is more likely to remain unchanged in the search space. In detail we can say that in each iteration the best and worst candidate solutions will be updated by the probability equal to exp(-3.5) = 0.03 and exp(-0.5) = 0.6, respectively. In other words we can consider these values as minimum (MEP _min ) and maximum (MEP _max ) values of monolayer evaporation probability. Our simulation results show that considering MEP _min  = 0.03 and MEP _max  = 0.6 based on the simulation results (Fig. 2b) is logical. However, these values can be considered as the first two parameters of the algorithm.

2.2.2 Droplet evaporation phase

In the droplet evaporation phase, using (2 and 3) the evaporation flux is as:

$$ J\left(\theta \right)={J}_o{P}_o{\left(\frac{2}{3}+\frac{{ \cos}^3\theta }{3}- \cos \theta \right)}^{-2/3}\left(1- \cos \theta \right) $$

(7)

where J ₀ and P ₀ are constant values. As it was mentioned before, in this phase (q < 0.4e), since q is smaller, the contact angle is greater and as a result we will have less evaporation. According to Fig. 2a the maximum and minimum values of contact angle are 50° and 0°, respectively. Based on the MD simulations results, the variation of the evaporation flux perfectly fitted to the experimental results in the range 20° < θ < 50°. It can be interpreted that for θ < 20° the water droplet is no longer observed like a perfect sessile spherical cap. Figures 4a and b illustrate this evaporation flux functions neglecting the constant values J ₀ and P ₀ for various contact angles between 0° < θ < 50° and 20° < θ < 50°, respectively.

Fig. 4

Droplet evaporation flux based on the MD simulations

Our simulation results show that considering contact angle between 20° < θ < 50° is quite suitable for WEO. Based on Fig. 4b, the maximum value for droplet evaporation probability is 2.6. Considering J ₀  × P ₀ equal to $\frac{1}{2.6}$ for limiting the upper bound of droplet evaporation probability to 1, and considering -20 and -50 as the maximum (θ _max ) and minimum (θ _min ) values of contact angle, the droplet evaporation probability for various contact angles between -50° < θ < -20° are shown in Fig. 5. For all iterations in the second half of the algorithm, the objective function of individuals Fit _i ^t is scaled to the interval [-50°, -20°] via the following scaling function which represents the corresponding contact angle θ(i)^t (contact angle vector):

$$ \theta {(i)}^t=\frac{\left({\theta}_{\max }-{\theta}_{\min}\right)\times \left(Fi{t}_i^t-Min(Fit)\right)}{\left( \max (Fit)-Min(Fit)\right)}+{\theta}_{\min } $$

(8)

where the Min and Max are the minimum and maximum functions. Such an assumption is consistent with MD simulations as depicted in Fig. 2a and results in a good performance of the WEO. Negative values have no effect on computations (cosine is an even function). In this way, the best and worst individuals have the smaller and bigger updating probability like the evaporation speed of a droplet on a substrate with less (q = 0.0e) and more (q = 0.4 e) wettability, respectively. In other words we can have the droplet evaporation probability matrix with minimum (DEP _min ) and maximum (DEP _max ) values of droplet evaporation probability equal to 0.6 and 1, respectively as shown in Fig. 5. Our algorithm performance evaluation results show that these values are suitable. However these parameters can be considered as the next two parameters of the algorithm.

Fig. 5

Droplet evaporation flux with different contact angles considered for the WEO

After generating contact angle vector θ(i)^t, the Droplet Evaporation Probability matrix (DEP) is constructed by the following equation:

$$ DE{F}_{ij}^t=\left\{\begin{array}{c}\hfill 1\kern0.48em if\; ran{d}_{ij}<J\left({\theta}_i^{(t)}\right)\hfill \\ {}\hfill 0\kern0.48em if\; ran{d}_{ij}\ge J\left({\theta}_i^{(t)}\right)\hfill \end{array}\right. $$

(9)

where DEP ^t _ij is the updating probability for the jth variable of the ith individual or water molecule in the tth iteration of the algorithm.

2.2.3 Updating water molecules

In the MD simulations, the number of evaporated water molecules in the entire simulation process is considered negligible compared to the total number of the water molecules resulting in a constant total number of molecules. In the WEO also the number of algorithm individuals or number of the water molecules (nWM) is considered as constant, in all tth algorithm iterations. nWM is the algorithm parameter like other population based algorithms. t is the number of the current iteration. Considering a maximum value for algorithm iterations (t _max ) is essential for WEO to determine the evaporation phase of the algorithm, and also use as the stopping criterion. Such stopping criterion is utilized in many of optimization algorithms. When a water molecule is evaporated it should be renewed. Updating or evaporation of the current water molecules is made with the aim of improving objective function. The best strategy for regenerating the evaporated water molecules is using the current set of water molecules (WM ^(t)). In this way a random permutation based step size can be considered for possible modification of the individuals as:

$$ S= rand.\left(W{M}^{(t)}\left[ permute1(i)(j)\right]-W{M}^{(t)}\left[ permute2(i)(j)\right]\right) $$

(10)

where rand is a random number in [0, 1] range, permute1 and permute2 are different rows permutation functions. i is the number of water molecule, j is the number of dimensions of the problem at hand. The next set of molecules (WM ^(t+1)) is generated by adding this random permutation based step size multiplied by the corresponding updating probability (monolayer evaporation and droplet evaporation probability) and can be stated mathematically as:

$$ W{M}^{\left(t+1\right)}=W{M}^{(t)}+S\times \left\{\begin{array}{c}\hfill ME{P}^{(t)}\kern0.36em t\le {t}_{\max }/2\hfill \\ {}\hfill DE{P}^{(t)}\kern0.36em t>{t}_{\max }/2\hfill \end{array}\right. $$

(11)

Each water molecule is compared and replaced by the corresponding renewed molecule based on the objective function. It should be noted that random permutation based step size can help us in two aspects. In the first phase, water molecules are more far from each other than in the second phase. In this way the generated permutation based step size will guarantee global and local search capability in each phase. The random part guarantees the algorithm to be sufficiently dynamic. It should also be noted that these two aspects are guaranteed with more emphasis by considering two specific evaporation probability mechanisms for each phase. As it is clear from Figs. 3 and 5, best water molecules are renewed locally (with less evaporation probability) while bad quality molecules are renewed globally (with more evaporation probability).

2.3 The proposed WEO algorithm

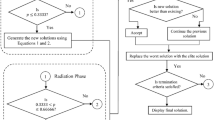
In this section, the proposed WEO algorithm is presented. The flowchart of WEO is illustrated in Fig. 6 and the steps involved are as follows:

Fig. 6

Flowchart of the WEO algorithm

• Step 1 Initialization

Algorithm parameters are determined in the first step. These parameters are the number of water molecules (nWM), maximum number of algorithm iterations (t _max ), minimum (MEP _min ) and maximum (MEP _max ) values of monolayer evaporation probability, minimum (DEP _min ) and maximum (DEP _max ) values of droplet evaporation probability. As mentioned before, evaporation probability parameters are determined efficiently for WEO based on the MD simulations results. The initial positions of all water molecules are generated randomly within the n-dimensional search space (WM ⁽⁰⁾), and are evaluated based on the objective function of the problem at hand.

• Step 2 Generating water evaporation matrix

Every water molecule follows the evaporation probability rules specified for each phase of the algorithm based on the (6 and 9). For t ≤ t _max /2, water molecules are globally evaporated based on the monolayer evaporation probability (MEP) rule (6); for t > t _max /2, evaporation occurs based on the droplet evaporation probability (DEP) rule (9). It should be noted that for generating monolayer and droplet evaporation probability matrices, it is necessary to generate the correspondent substrate energy vector (5) and contact angle vector (8), respectively.

• Step 3 Generating random permutation based step size matrix

A random permutation based step size matrix is generated according to (10).

• Step 4 Generating evaporated water molecules and updating the matrix of water molecules.

The evaporated set of water molecules WM ^(t+1) is generated by adding the product of step size matrix and evaporation probability matrix to the current set of molecules WM ^(t) according to (11). These molecules are evaluated based on the objective function. For the molecule i (i = 1, 2, …, nWM) if the newly generated molecule is better than the current one, the latter should be replaced. Return the best water molecule as the output of the algorithm.

• Step 5 Terminating condition check

If the number of iteration of the algorithm (t) becomes larger than the maximum number of iterations (t _max ), the algorithm terminates. Otherwise goes to Step 2.

3 Test problems and optimization results

The WEO algorithm developed in this research is tested in six continuous weight minimization problems consisting of a planar 10-bar truss, a spatial 22-bar truss, a spatial 25-bar transmission tower, a spatial 72-bar truss, a 120-bar dome shaped truss and a planar 200-bar truss. These problems include 10, 7, 8, 16, 7 and 29 continuous sizing variables, respectively. The most effective available state-of-the-art metaheuristic optimization methods based on the author’s knowledge are used here for comparison. Since the search process is governed by random rules, each test problem is solved by carrying out 50 independent optimization runs to obtain statistically significant results. During each run, the maximum number of structural analyses (NSA) of 2 × 10⁴ is used. The maximum number of algorithm iterations (t _max ) is equal to the result of dividing the maximum number of structural analysis to the number of water molecules (nWM). The performance assessment of the algorithm is carried out based on three metrics, namely, accuracy, reliability and convergence speed. The WEO is coded in the MATLAB software environment. Structural analyses entailed by the optimization process are performed by means of the direct stiffness method (Kaveh 1997).

3.1 Statement of the truss weight minimization problem

The weight minimization problem of a truss structure can be stated as follows:

$$ \begin{array}{c}\hfill F\operatorname{in}d\ \left\{X\right\}=\left[{x}_1,{x}_2,\cdots, {x}_{ng}\right],\;{x}_i\in D\hfill \\ {}\hfill to\; \min imize\ W\left(\left\{X\right\}\right)={\displaystyle \sum_{i=1}^{ng}{X}_i{\displaystyle \sum_{j=1}^{nm(i)}{p}_{j{L}_j}}}\hfill \\ {}\hfill Subject\;to:\ gk\left(\left\{X\right\}\right)\le 0\;K=1,2,\cdots, n\hfill \end{array} $$

(12)

where {X} is the set of design variables; ng is the number of member groups (i.e., the number of optimization variables) defined according to structural symmetry; D represents the design space including the cross-sectional areas of truss elements that can take discrete or continuous values; W({X}) is the weight of the structure; nm(i) is the number of members included in the ith group; ρ _i and L _j are respectively the material density and the length of the jth member included in the ith group; g _k ({X}) denote the n optimization constraints.

In order to handle optimization constraints, a penalty approach is utilized in this study by introducing the following pseudo-cost function:

$$ {f}_{\cos t}\left(\left\{X\right\}\right)={\left(1+{\varepsilon}_1\cdot v\right)}^{\varepsilon_2}\times W\left(\left\{X\right\}\right),\kern0.36em v={\displaystyle \sum_{k=1}^n \max \left[0,{g}_k\left(\left\{X\right\}\right)\right]} $$

(13)

where υ is the total constraint violation. Constants ε ₁ and ε ₂ must be selected considering the exploration and the exploitation rates of the search space. In this study, ε ₁ is set equal to one while ε ₂ is selected so as to decrease the total penalty yet reducing cross-sectional areas. Thus, ε ₂ is increased from the value of 1.5 set in the first steps of the search process to the value of 3 set toward the end of the optimization process.

Stress limits on truss members are imposed according to ASD-AISC (Manual of steel construction–allowable stress design 1989) provisions

$$ \left\{\begin{array}{c}\hfill {\sigma}_i^{+}=0.6{F}_y\kern0.36em for\;{\sigma}_i\ge 0\hfill \\ {}\hfill {\sigma}_i^{-}\kern3.9em for\;{\sigma}_i<0\hfill \end{array}\right. $$

(14)

$$ {\sigma}_i^{-}=\left\{\begin{array}{c}\hfill \left[\left(1-\frac{\lambda_i^2}{2{C}_c^2}\right){F}_y\right]/\left(\frac{5}{3}+\frac{3{\lambda}_i}{8{C}_c}+\frac{\lambda_i^3}{8{C}_c^3}\right)\kern0.36em for{\lambda}_i\ge {C}_c\hfill \\ {}\hfill \frac{12{\pi}^2E}{23{\lambda}_I^2}\kern6.72em for{\lambda}_i<{C}_c\hfill \end{array}\right. $$

(15)

where E is the modulus of elasticity; F _y is the yield stress; λ _i is the slenderness ratio (λ _I  = kl _i /r _i ); C _c is the slenderness ratio separating elastic and inelastic buckling regions $\left({C}_c=\sqrt{2{\pi}^2E/{F}_y}\right)$; k is the effective length factor; l _i is the length and r _i the corresponding radius of gyration of the ith element. The radius of gyration can be related to cross-sectional areas as (r _i  = aA ^b _i ) where constants a and b depend on the type of element cross section (for example, pipes, angles, and tees). In this study, pipe sections (a = 0.4993 and b = 0.6777) are adopted for bars (Lee and Geem 2004).

Optimization constraints on nodal displacements are set as follows which should be checked for all translational degrees of freedom:

$$ {\delta}_i-{\delta}_i^u\le 0\;i-1,2,\cdots, nn $$

(16)

where δ _i is the displacement of the ith node of the truss, δ _i ^u is the corresponding allowable displacement, and nn is the number of nodes.

3.2 Sensitivity analysis on WEO search behavior

In this section, the search behavior of WEO is studied. The effects of each evaporation phase, the number of water molecules (nWM), minimum and maximum values of monolayer (MEP _min and MEP _max ) and droplet (DEP _min and DEP _max ) evaporation probabilities will be analyzed in detail. In particular the suitability of minimum and maximum value of monolayer and droplet evaporation probability based on the molecular dynamic simulation results (MEP _min  = 0.03 and MEP _max  = 0.6; DEP _min  = 0.6 and DEP _max  = 1) will be sought.

The search behavior of WEO is investigated using the planar spatial 25-bar transmission tower, the spatial 72-bar truss, and the 120-bar dome shaped truss.

For a better study of the performance of the monolayer and droplet evaporation phases, Fig. 7 depicts the average convergence curves resulted by 10 independent runs of WEO for these trusses. Each truss is solved two more series of 10 independent runs considering monolayer and droplet evaporation updating mechanisms alone for all t _max algorithm iterations which are reported as WEO-MEP and WEO–DEP, respectively. It should be noted that nWM is considered as 10. For a more precise monitoring of the results, the weight minimization convergence histories are divided into two parts by taking four hundredths iteration as the separating point. Based on these values, it is clear that considering two phases in the content of WEO is inevitable to guarantee a good balance between global and local search ability and keep the dynamicity of the algorithm and preserves it from premature convergence. The most interesting observed result is the way WEO matches WEO-MEP in the first half of the iterations and then tries to coincide with the WEO-DEP.

Fig. 7

Sensitivity analysis on convergence behavior of the WEO for: (a) 25-bar tower, (b) 72-bar truss, (c) 120-bar dome truss

Table 1 presents the statistical results of 10 independent runs for these three trusses considering variable number of water molecules: 5, 10, 15, 20, 30, 50 and 100, in which Mean, Best, Worst and SD stand for average, best observed, worst observed, standard deviation of optimum designs resulted by 10 independent runs, respectively. NSA stands for the number of structural analyses. For clarity, the best observed results for each performance metric are marked in boldface. Considering nWM between 10 and 20, results in better performance of the algorithm. nWM will be considered 10 for all trusses. Increasing the number of water molecules results in poor performance of the algorithm in the aspect of accuracy.

Table 1 Statistical results of sensitivity analysis with respect to the nWM parameter for the 25-bar and 120-bar truss problems

To study the suitability of monolayer and droplet evaporation probability values (MEP _min  = 0.03 and MEP _max  = 0.6; DEP _min  = 0.6 and DEP _max  = 1) legislated based on the MD simulations results, the algorithm is employed for these three trusses several times and it is found that these values lead to efficient performance of the WEO. Let us consider [-3.5, -3, -2.5, -2, -1.5, -1] as minimum values of E _sub which result in MEP _min between [0.03, 0.6]. For each MEP _min different values are considered for MEP _max and 10 independent runs of algorithm (only monolayer evaporation phase) is conducted. For example, considering E _sub equal to -3.5 (MEP _min  = 0.03) different values of MEP _max will be obtained considering [-3, -2.5, -2, -1.5, -1, -0.5, -0.3, -0.1] as maximum values for E _sub . The obtained mean weight of 10 independent runs for different sets of monolayer evaporation probabilities for the 25-bar truss and 120-bar dome are depicted in the Fig. 8. Figure 9 shows the penalized weight convergence curves of a single trial run monitored for 25-bar truss with MEP _min  = 0.03 and different values of MEP _max . For further clarity, the Y axis is in the logarithmic scale. As it is clear considering maximum value of substrate energy equal to -0.5 which is equivalent to MEP _max  = 0.6 provides better performance of the algorithm. It can be seen from Fig. 8 that the performance of the WEO algorithm is rather insensitive to the value of MEP _min. Furthermore, Fig. 9 shows that considering MEP _max = 0.6 ensures dynamicity and good convergence behavior of the search process. Sensitivity analysis also indicates that DEP _min and DEP _max are suitable values.

Fig. 8

Mean penalized weight of 10 independent runs for different values of MEP _min and MEP _max: (a) 25-bar tower and (b) 120-bar dome truss

Fig. 9

Variation of convergence behavior of the WEO for MEP _min  = 0.03 and different values of MEP _max in the 25-bar truss problem

3.3 Continuous truss design problems

3.3.1 Planar 10-bar truss

This test case is frequently used in structural design optimization to test optimization algorithms. The optimization problem formulation is described in detail in (Kaveh and Talatahari 2009b). Truss geometry including node and element numbering, loading conditions (there may be two variants) and kinematic constraints are shown in Fig. 10.

Fig. 10

Schematic of the planar 10-bar truss

Table 2 presents the best optimized designs found by WEO for the two problem variants and the corresponding number of structural analyses. The present algorithm is compared with PSO variants (Multi-stage Particle Swarm Optimization (MSPSO) (Talatahari et al. 2013), Hybrid Particle Swallow Swarm Optimization (HPSSO) (Kaveh et al. 2014)), a hybrid scheme of Particle Swarm Optimizer, Ant Colony Strategy and Harmony Search (HPSACO) (Kaveh and Talatahari 2009b), Artificial Bee Colony algorithm with an adaptive penalty function approach (ABC-AP) (Sonmez 2011), a Self Adaptive Harmony Search algorithm (SAHS) as an advanced version of Harmony Search algorithm presented by Degertekin (Degertekin 2012), and Teaching Learning Based Otimization algorithm (TLBO) (Degertekin and Hayalioglu 2013). In both loading cases, WEO is competitive with other algorithms from accuracy point of view and leads to optimum design obtained by HPSSO as the best available result. It should be noted that the lightest design obtained by HPSACO slightly violates the design constraints. The present algorithm used all of its predefined number of iterations for converging to the optimum design and shows low convergence speed in comparison to the other algorithms. Table 3 presents the statistical results obtained for 50 independent runs carried out from different initial populations randomly generated. It is clear that WEO is competitive with other algorithms.

Table 2 Comparison of optimization results obtained by WEO and some other metaheuristic algorithmss for the 10-bar truss problem

Table 3 Comparison of robustness and reliability of the WEO and other metaheuristic algorithms for the 10-bar truss problem

3.3.2 Spatial 22-bar truss

The second structural optimization problem solved in this study is the optimal design of the spatial 22-bar truss shown in Fig. 11. This test case, described in detail in (Lee and Geem 2004), was previously studied by Lee and Geem (Lee and Geem 2004) using Harmony Search (HS) algorithm, Talatahari et al. (Talatahari et al. 2013) using multi-stage particle swarm optimization (MSPSO) algorithm, and Kaveh et al. (Kaveh et al. 2014)) using Hybrid Particle Swallow Swarm Optimization (HPSSO) algorithm. The optimized designs found by different algorithms are compared in Table 4 showing that the WEO is capable to find slightly lighter design than those obtained by HPSSO, and MSPSO which were practically identical. WEO again required more structural analyses than others and used all of its predefined number of iterations. Statistical results of independent optimization runs are presented in Table 5. WEO is much more robust than other algorithms.

Fig. 11

Schematic of the spatial 22-bar truss

Table 4 Comparison of optimization results obtained by the WEO and some other metaheuristic algorithms for the 22-bar truss problem

Table 5 Comparison of robustness and reliability of the WEO and other metaheuristic methods for the 22-bar truss problem

3.3.3 Spatial 25-bar tower

The third structural optimization problem solved in this research is the weight minimization of the spatial 25-bar truss schematized in Fig. 12. This is a very well-known test problem and described in detail in (Kaveh and Bakhshpoori 2013). Table 6 compares the optimized design found by WEO with those found by HPSACO (Kaveh and Talatahari 2009b), hybrid Big-Bang Big-Crunch algorithm (HBB-BC) (Kaveh and Talatahari 2009c), SAHS (Degertekin 2012), TLBO (Degertekin and Hayalioglu 2013), MSPSO (Talatahari et al. 2013) and HPSSO (Kaveh et al. 2014). The lightest design is obtained by TLBO algorithm which is 0.076 lb lighter than that found by WEO. SAHS is overall the most efficient optimizer considering both convergence speed and structural weight. WEO again uses all of its defined number of FEs. Statistical results of 50 independent runs are compared in Table 7. The present WEO is the most robust algorithm.

Fig. 12

Schematic of the spatial 25-bar truss

Table 6 Comparison of optimization results obtained by WEO and some other metaheuristic algorithms for the 25-bar tower problem

Table 7 Comparison of robustness and reliability of WEO and some other metaheuristic algorithms for the 25-bar tower problem

Figure 13a compares the convergence curves obtained for WEO, HPSACO (Kaveh and Talatahari 2009b), HBB-BC (Kaveh and Talatahari 2009c), SAHS (Degertekin 2012), TLBO (Degertekin and Hayalioglu 2013), MSPSO (Talatahari et al. 2013) and HPSSO (Kaveh et al. 2014). Each curve is relative to the best optimization run amongst the independent runs carried out from different initial populations randomly generated. It can be seen that the present algorithm converges more slowly than the other metaheuristic optimizers. HPSACO is the fastest algorithm and requires about half of the structural analyses of WEO.

Fig. 13

Convergence curves recorded for the spatial 25-bar truss: a) Comparison of convergence rate for the algorithms; b) Comparison of the best and worst molecules and average of all molecules for the WEO

Convergence curves reported for HPSACO (Kaveh and Talatahari 2009b), HBB-BC (Kaveh and Talatahari 2009c), SAHS (Degertekin 2012), TLBO (Degertekin and Hayalioglu 2013), PSO and MSPSO (Talatahari et al. 2013) and HPSSO (Kaveh et al. 2014) as the best optimization observed run for independently runs starting from a different population randomly generated beside the obtained one based on the WEO are compared in Fig. 13a. WEO shows the slower convergence rate in comparison to the other algorithms. The best converging rate is obtained by HPSACO: in particular WEO needs the number of structural analyses as big as twice the ones needed by HPSACO. In order to further evaluate algorithm performance, Fig. 13b shows the penalized weight optimized histories for a trial run seen for the best water molecule, average of all molecules, and worst one. The most notable fact is that optimization histories converge to the same point.

3.3.4 Spatial 72-bar truss

Figure 14 shows the schematic of the spatial 72-bar truss (numbering of nodes and elements and element grouping are indicated in the figure). Detailed information on this test problem are given in (Kaveh and Talatahari 2009b). Table 8 compares optimization results of the WEO with those of MSPSO (Talatahari et al. 2013), HPSSO (Kaveh et al. 2014), ABC-AP (Sonmez 2011), SAHS (Degertekin 2012) and TLBO (Degertekin and Hayalioglu 2013). It can be seen that the lightest design is obtained by TLBO which is 0.1417 lb lighter than that obtained by WEO. The present algorithm is competitive with other algorithms but requires 7000 structural analyses more than the fastest algorithm, SAHS. It should be noted that WEO used all of predefined number of iterations for reaching the optimum design. Statistical results of 50 independent runs for HPSSO, SAHS, TLBO, MSPSO and WEO are presented in Table 9. WEO is competitive with other algorithms from the robustness point of view.

Fig. 14

Schematic of the spatial 72-bar truss

Table 8 Comparison of optimization results obtained by HPSSO and some other metaheuristic algorithms for the 72-bar truss problem

Table 9 Comparison of the robustness and reliability of HPSSO and other metaheuristic algorithms for the 72-bar truss problem

Figure 15a compares the convergence curves obtained for WEO, SAHS (Degertekin 2012), TLBO (Degertekin and Hayalioglu 2013), MSPSO (Talatahari et al. 2013) and HPSSO (Kaveh et al. 2014). Each curve is relative to the best optimization run amongst the independent runs carried out from different initial populations randomly generated. The present algorithm converges to the optimum design more slowly than the other metaheuristic optimizers: in particular, it is 50% slower than SAHS.

Fig. 15

Convergence curves recorded for the spatial 72-bar truss: a) Comparison of convergence rate for the algorithms; b) Comparison of the best and worst particles and average of all particles for the WEO

3.3.5 120-bar dome truss

The 120-bar dome truss optimized in this study is schematized in Fig. 16. For the sake of clarity, not all the element groups are numbered in the figure. Because of structural symmetry, the 120 members are divided into seven groups. Stress constraints are defined by (14) and (15), and displacement limitations are imposed on all nodes in x, y and z coordinate directions. Further details on this optimization problem can be found in (Kaveh and Bakhshpoori 2013). The structure was previously optimized by HPSACO (Kaveh and Talatahari 2009b), Charged system Search algorithm (CSS) (Kaveh and Talatahari 2010a), Imperialist Competitive Algorithm (ICA) (Kaveh and Talatahari 2010c), Cuckoo Search algorithm (CS) (Kaveh and Bakhshpoori 2013), standard PSO (Talatahari et al. 2013), MSPSO (Talatahari et al. 2013), and HPSSO (Kaveh et al. 2014).

Fig. 16

Schematic of the 120-bar dome truss

Table 10 compares the optimization results of the WEO algorithm with those found by other methods. The statistical results of 50 independent runs are provided in Table 11 for HPSSO, MSPSO and WEO. It can be seen that the present algorithm is competitive with the other metaheuristic methods except for the slow convergence rate: in fact, WEO required three times more structural analyses than the fastest optimizer.

Table 10 Comparison of optimization results obtained by WEO and some other metaheuristic algorithms for the 120-bar dome problem

Table 11 Comparison of robustness and reliability of the WEO and some other metaheuristic algorithms for the 120-bar dome problem

3.3.6 Planar 200-bar truss

The planar 200-bar truss optimized as the last test problem is shown in Fig. 17. The elastic modulus of the material is 30,000 ksi while density is 0.283 lb/in³. The allowable stress for all members is 10 ksi (the same in tension and compression). No displacement constraints are included in the optimization process. The structure is divided into 29 groups of elements. The minimum cross-sectional area of all design variables is taken as 0.1 in². This truss is subjected to three independent loading conditions. Further details on this optimization problem can be found in (Degertekin and Hayalioglu 2013). Table 12 presents the optimum designs obtained by WEO, HPSACO (Kaveh and Talatahari 2009b), a Corrected Multi-Level and Multi-Point Simulated Annealing algorithm (CMLPSA) (Lamberti 2008), SAHS (Degertekin 2012), TLBO (Degertekin and Hayalioglu 2013), and HPSSO (Kaveh et al. 2014). CMPLSA, TLBO and SAHS designed the lightest structures amongst feasible or almost feasible optimized designs: the corresponding optimized weights are 25445.63, 25488.15 and 25491.9 lb. The scaled weight of CMPLSA to recover the 0.071% violation on stress constraints is 25463.7 lb. The design optimized by WEO weigh 25674.83 lbs, hence it is only 0.71%, 0.73% and 0.83% heavier than those optimized by SAHS, TLBO and CMPLSA, respectively. WEO again needs all of its predefined number of iterations to reach the optimum design. While WEO needs less structural analyses than SAHS and TLBO, it requires more than twice the structural analyses of CMPLSA. However, CMPLSA adopted a hybrid formulation, tailored to sizing optimization of truss structures, utilizing explicit gradient information on cost function. A more logical comparison should have entailed the use of the same information also for WEO.

Fig. 17

Schematic of the planar 200-bar truss

Table 12 Comparison of optimization results obtained by WEO and other metaheuristic algorithms for the 200-bar truss problem

3.4 Diversity assessment of WEO

In order to further asses the performance of the algorithm, a diversity index defined by Kaveh and Zolghadr (Kaveh and Zolghadr 2014) is utilized in this study. Diversity Index (DI) reflects the ratio of the portion of the search space covered by the population to the entire search space at each step, and it is defined as:

$$ DI=\frac{1}{nWM}{\displaystyle \sum_{j=1}^{nWM}\sqrt{{\displaystyle {\sum}_{i=1}^{ng}{\left(\frac{GB(i)-W{M}_j(i)}{x_{i, \max }-{x}_{i, \min }}\right)}^2}}} $$

(17)

where WM _i (j) is the value of the ith variable of the jth molecule; x _i,min and x _i,max are the minimum and maximum values of the ith design variable, respectively; ng is the number of design variables and nWM is the number of water molecules. In fact the diversity index represents the distribution of the solution candidates around the best solution of the current iteration. Figure 18 depicts the variation of the diversity index for a single run of the WEO for all test problems with respect to the iteration number. Desirable trend of variation of the diversity index is obtained by WEO. Up down step like movements of the DI convergence history in the early stages of the optimization process shows how WEO covers numerous promising points of the search space. High values of diversity are provided in the early stages of the optimization process. As the optimization process continues, the water molecules focus on more promising regions of the search space in order to perform local search and diversity index values gradually decrease.

Fig. 18

Values of diversity index recorded in the optimization history for a single run of different test problems

4 Conclusions

A novel physically inspired population based metaheuristic for continuous structural optimization called as Water Evaporation Optimization (WEO) is proposed in this paper. WEO mimics the evaporation of a tiny amount of water molecules adhered on a solid surface with different wettability which can be studied by molecular dynamics simulations. A set of six truss design problems from small to normal scale are considered for evaluating the WEO. The most effective available state-of-the-art metaheuristic optimization methods are used as basis of comparison. The optimization results demonstrate its competitive performance for continuous structural optimization problems in terms of solution quality and robustness. At this stage the only weak point of the algorithm is its low convergence speed.