Abstract
A generalized sensitivity formulation described in a curvilinear coordinate system is proposed. Utilizing it, the continuum-based isogeometric shape sensitivity analysis method for the shell components is developed in the curvilinear coordinates derived from the given NURBS geometry. In isogeometric approach, the designs are embedded into the NURBS basis functions and the control points so that geometrically exact shell models can be incorporated in both response and sensitivity analyses. The precise shape sensitivities can be obtained by considering accurate and continuous normal and curvatures in the boundary integrals of the boundary resultants of the shell and their material derivatives. Through numerical examples, the developed isogeometric shape sensitivity is verified to demonstrate excellent agreements with finite difference sensitivity. Also, the importance of higher order geometric information in the sensitivity expressions is identified. For the shape optimization problem of the shell, the proposed method works well with boundary resultants accompanying severe curvature changes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Geometric modeling in CAD (computer-aided design) systems is usually described by the NURBS (non-uniform rational B-Splines) basis functions. In finite element based shape sensitivity analysis and optimization, however, the finite element meshes are approximated from the given CAD geometry while designs are directly embedded in CAD systems. The geometric approximations have been usually accomplished by piecewise linear (or quadratic) polynomials, which leads accuracy problems in response analysis and more unfavorably in shape sensitivity analysis. The finite element based shape optimization changing boundary shapes could be converged to an undesirable local optimum of selected finite element nodes representing boundary shapes (Haftka and Grandhi 1986). For smooth and continuous design parametrization, NURBS parameterization has been employed in which the spatial positions of the control points of a design model are parametrized by design variables (Ansola et al. 2002; Espath et al. 2011; Hassani et al. 2013). The structural responses and shape sensitivities are, however, computed in an additional finite element analysis model. This causes degeneration of accuracy of solutions and sensitivities of complex geometries. Moreover, mesh constructions and further refinements during iterations of design optimization require repetitive communication with the CAD system.
In order to deal with the geometric disparity between analysis and design models, the isogeometric analysis based on NURBS was developed by Hughes et al. (2005) and Cottrell et al. (2006). In the isogeometric approach, the analysis model employs the same basis functions in the CAD systems rather than uses the shape functions for the finite element meshes. The geometric flexibility of the NURBS basis is further capable to exactly represent the CAD geometry and makes the subsequent refinements greatly simplified due to no need of additional communications with the CAD systems (Cottrell et al. 2007). Recently, the complete integration of design and analysis models has been accomplished in the isogeometric framework for a two-dimensional elasticity problem (Cho and Ha 2009). They derived a continuum-based isogeometric shape sensitivity analysis method and performed the shape optimization with the adjoint sensitivity analysis. Due to the higher continuity of the NURBS functions, it is capable to enhance the accuracy of shape sensitivities of complex geometries including higher order geometric effects, such as normal, curvature, etc. Utilizing the NURBS basis functions both in the response and sensitivity analyses, design modifications during optimization process can be performed conveniently with adjusting control points that represent the geometric model (Cho and Ha 2009). A mathematical foundation for shape optimization problem based on continuum-based isogeometric shape sensitivity can be found in Fuβeder et al. (2015) in which control points and weights are simultaneously optimized. Qian (2010) also provided analytical sensitivity with respect to both control points and weights in discrete isogeometric systems.
In many engineering applications on a wide scale, curved geometries represented by shell components have been employed from microscale graphene to cars, airplanes, ships, etc. The degenerated solid approach has been widely used for finite element shell analysis ever since Ahmad et al. (1970). Alternatively, Simo and Fox (1989) introduced the geometrically exact shell formulation based on the classical shell theory. Although the degenerated solid approach and classical shell theory share the same hypothesis for shell structures, the resultant formulation is typically derived numerically in the former, and analytically in the latter. Avoiding the mathematical complexities associated with classical shell theory, the degenerated solid approach would be better for the numerical implementation. On the other hand, the geometrically exact formulation describes the mathematical model of a shell naturally by curvilinear coordinates (Roh and Cho 2003). Employing the degenerated solid approach, Benson et al. (2010) and Hosseini et al. (2014) have developed the isogeometric shell analysis in the rectangular Cartesian coordinate system: a set of orthogonal unit base vectors has been employed as the basis for representation of vectors and tensors. Bouclier et al. (2013) have proposed the locking free isogeometric degenerated solid model with mixed formulation. Indeed, the parametric knot representations of the NURBS geometries are rather suited to describe curved geometries in curvilinear coordinate systems: arbitrary bases, with base vectors not necessarily orthogonal nor of unit length, are considered. Thus the isogeometric analysis of the geometrically exact shell models has been formulated in curvilinear coordinate systems (Kiendl et al. 2009; Echter et al. 2013; Nagy et al. 2013).
In the finite element based shape optimization of shell structures, some early works can be found in Hinton and Rao (1993), Bletzinger and Ramm (2001), Bletzinger et al. (2010) and Espath et al. (2011). Additionally, Ansola et al. (2002) and Hassani et al. (2013) have studied on an integrated approach for shape and topology optimization of shell structures. For the isogeometric shape optimization of shell structures, the sensitivities are evaluated in the system of discrete matrix equations (Nagy et al. 2010, 2013; Kiendl et al. 2014). In those works, however, the continuum-based sensitivity analysis method was not provided. Moreover, the boundary resultants that are typical loading components for shells and design gradients of them were missing. Although the continuum-based isogeometric sensitivity analysis has been formulated in the two-dimensional Cartesian coordinate system (Cho and Ha 2009), it would not be directly applicable to the general curved shells described in the curvilinear coordinate systems.
In this study, the continuum-based shape sensitivity analysis using the isogeometric approach is derived in the curvilinear coordinate systems for arbitrary surface shapes. Note that the curvilinear coordinates compose the “generalized” coordinate systems from which orthogonal and Cartesian systems are reduced with geometric restrictions. The generalized formulations are applied to the shape sensitivity analysis of the geometrically exact shell model in which the curvilinear coordinates are directly formed on the given NURBS geometries. The precise sensitivity can be obtained by complete formulations of boundary integrals for the shell boundary resultants and their material derivatives. Incorporating structural response and generalized shape sensitivity analyses in the isogeometric framework into the shape optimization problem, moreover, a complete integration of CAD, CAE, and design optimization for the general curved geometries is accomplished. For the shape optimization of the shell, the shape design velocity that is the rate of shape perturbation is capable to represent the configuration design change without considering additional geometric constraints that is required in the typical configuration design velocity field. Through the demonstrative numerical examples, it is verified that the precise sensitivity computations including normal and curvatures are critical and important in the design optimization. A design optimization problem subjected to the boundary resultant shows that the original geometry of the shell component can be perturbed into an arbitrary shape and configuration with severe curvature variation and then a reasonable optimal shape can be obtained.
The paper is organized as follows. In Section 2, a shape design sensitivity analysis is derived in the curvilinear coordinate systems. A brief review of the curvilinear coordinate systems is given and then material derivative formulas in the curvilinear systems are derived. Note that the derivations provide a generalized version of design sensitivity analysis since the typical sensitivity expressions described in the Cartesian coordinate system can be readily reduced from the generalized forms. In Section 3, the generalized formulations are applied to the shear deformable shell model (Naghdi 1963). The curvilinear coordinates are formed adaptively from the given NURBS geometry and then the geometrically exact response and sensitivity formulations are derived. In order to deal with the boundary resultants of the shell, the boundary integrals and corresponding shape sensitivities are considered incorporating the NURBS functions of higher order continuity. In Section 4, the isogeometric shape optimization problem of geometrically exact shell is then formulated utilizing the derived adjoint sensitivity expressions. Design parameterization with sensitivity analysis and the multilevel design formulation are also discussed. Numerical examples are then presented in Section 5. The accuracy of the isogeometric sensitivity is compared to the finite difference solution. Also, the applicability of isogeometric shape optimization for shell structures is demonstrated. Finally, conclusions are given in Section 6.
2 Generalized shape sensitivity analysis in curvilinear coordinate system
2.1 Curvilinear coordinate system
A position vector x = x 1 e 1 + x 2 e 2 + x 3 e 3 in the Cartesian coordinate system with the fixed base vectors e 1, e 2, e 3 and the coordinates (x 1, x 2, x 3) can be expressed in terms of curvilinear coordinates (θ 1, θ 2, θ 3) as
Covariant base vectors at x are given as
where g i emanate from x and are directed towards the site of increasing coordinate θ i. The covariant base vectors are not necessarily orthonormal to each other and contravariant base vectors g i are introduced to satisfy the relationship between reciprocal pairs of general bases: g i ⋅ g j = δ i j . Then, the dot products of a covariant/contravariant base vector with another base vector define the useful metric coefficients, such as
Obviously, their determinants relate to the square of the determinants of the Jacobian matrix J≡[∂x i/dθ j]:
Differentiation in curvilinear coordinates is more involved than that in Cartesian coordinates because the base vectors are no longer constant and their derivatives need to be taken into account. Introducing the second-kind Christoffel symbols to represent the partial derivatives of base vectors as
we have the covariant derivative of the vector as:
Consider the surface area dΓ 1 of a face of the differential parallelepiped on which θ 1 is constant. On dΓ 1 the tangential curves are aligned with the coordinate curves θ 2 and θ 3 while θ 1 is constant, and thus g 1 is normal to the surface dΓ 1. Similarly on the other surfaces, g 2 and g 3 are normal, respectively. The surface area dΓ 1 is then calculated as
and similarly for the other surfaces. The volume dΩ of the parallelepiped is
Note that an orthonormal Cartesian coordinate system can be obtained with the following conditions g i = g i = e i , g ij = δ ij , |g ij | = 1, Γ k ij = 0.
2.2 Material derivatives in curvilinear coordinate system
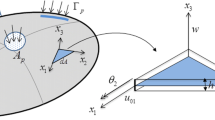
If we consider the variation of the structural domain as shown schematically in Fig. 1. The initial structural geometry Ω is changed to the perturbed geometry Ω τ by using a mapping or transformation T. A scalar parameter τ denotes the amount of shape change in the design variable direction. The mapping T : x → x τ , x ∈ Ω is given by:
and
A design velocity field that is equivalent to a mapping rate can be defined as
Suppose z τ (x τ ) is a smooth, classical solution to the variational equation on the perturbed domain Ω τ :
where Z τ ⊂ H m(Ω τ ) is the space of kinetically admissible displacements. If the point-wise material derivative exists at x ∈ Ω, then it is defined as
where V(x)≡V(x, 0). z ′ and ∇z are the partial derivative and gradient of z, respectively.
Since the parametric coordinate is independent of design perturbation, the order of differentiation between the material derivative and parametric derivative can be interchanged. However, since the Jacobian matrix J≡[∂x i/dθ j] relates the physical coordinate to the parametric coordinate, it depends on the design. The material derivative of the Jacobian matrix becomes the Jacobian matrix of the shape design velocity as
and the material derivative of its inverse can also be obtained, by using the fact of JJ −1 = I, as
Finally, the material derivative of the determinant of the Jacobian matrix can be obtained from direct calculation with Jacobi’s formula as
Using the fact that dΩ τ = |J τ |dθ 1 dθ 2 dθ 3 from (8), the variation of the infinitesimal volume of domain Ω τ can be obtained as
From (7), the variation of the infinitesimal surface area of a face of domain Ω τ on which θ 1 is constant (to which g 1 τ is normal) can be calculated as
According to Theorem 3.5.3 in (Haug et al. 1986), only the normal component of the velocity field V need be considered. When V = V 1 g 1 on Γ 1, (18) can be rewritten as
and similarly for the other surfaces.
Consider the performance measures in domain and boundary integral forms:
and
where i, j, k are different to each other and repeated indices are not summed. The first order variations with respect to the shape design parameter are, respectively, derived as:
and
where i, j, k are different to each other and the quantities with the repeated index i are not summed.
Note that the generalized derivations on the curvilinear coordinate system can be reduced to the expressions for the Cartesian coordinate system introduced in (Haug et al. 1986). In the Cartesian system, we consider V = V n n on Γ and then we have
Since n in this case is a unit normal vector, the following relation holds:
Finally, (23) is rewritten as
which is the material derivative of boundary functional for the Cartesian coordinate system given in (Haug et al. 1986).
3 Isogeometric shape sensitivity analysis of geometrically exact shell
The geometric modeling in the CAD system can be generated by the NURBS basis functions and control points. In this section, we firstly introduce the generalized curvilinear coordinate system based on NURBS representations. In the isogeometric framework, the geometrically exact shell model is then formulated in the derived curvilinear coordinate system. In the isogeometric analysis, the solution space is represented in terms of the same basis functions to represent the NURBS geometry in the CAD systems. Due to the use of NURBS, the isogeometric analysis has advantages in terms of geometric exactness and simple refinements over the conventional finite element analysis. Besides, the isogeometric shape design sensitivity analysis of the geometrically exact shell model is derived based on the generalized shape sensitivity introduced in Section 2.
3.1 Curvilinear coordinate system based on NURBS representation
Consider a knot vector in one dimensional space, which is the set of coordinates θ i in a parametric space:
where p and m are the order and the number of basis functions, respectively. It is called a uniform knot vector if knots are equally spaced in the parametric space and a non-uniform knot vector, otherwise. The knots are named as repeated when they are repeated at the same coordinates, and open when the end knots are repeated (p + 1) times. The B-spline basis functions are defined, recursively, as
and
Note that the denominators involving knot differences can become zero (in the case of repeated knots); the quotient is defined to be zero in this case. The B-spline has the following desirable properties as a basis function:
-
(A)
∑ m i = 1 ϕ i,p (θ) = 1 (partition of unity)
-
(B)
ϕ i,p is contained in the interval \( \left[\begin{array}{cc}\hfill {\theta}_i,\hfill & \hfill {\theta}_{i+p+1}\hfill \end{array}\right] \) (compactness)
-
(C)
ϕ i,p (θ) ≥ 0 (non-negativity)
NURBS curves are obtained from the linear combination of rational basis functions ϕ i,p and the corresponding control points P i = P i (x). For the given m pairs of p-th order B-spline basis function ϕ i,p and the corresponding (projective) control points, the NURBS curve in d-dimensional space is defined at a single parametric coordinate θ 1, such as
where
and
For a point P i = (x 1 i , x 2 i , x 3 i ) in three-dimensional Euclidean space (d = 3), for instance, the homogeneous coordinates in four-dimensional space are defined as P ω i = (ω i x 1 i , ω i x 2 i , ω i x 3 i , ω i ) where ω i ≠ 0. If an equal weight ω i is used, the NURBS curve becomes the B-spline curve. Using a tensor product of coordinates, NURBS surfaces can be defined:
For brevity of expressions, (34) is rewritten as:
with CP = m ⋅ n. Besides the properties as a basis function mentioned previously, the constructed NURBS basis functions possess the property of affine covariance and are (p - 1) continuously differentiable. If the knots or control points are repeated k-times, the continuity decreases k-times as well. Note that the NURBS basis functions are not interpolatory. The detail of NURBS geometry can be found in the following references, Piegl and Tiller (1997), Rogers (2001), and Farin (2002).
(35) implies that any point on a NURBS geometry can be expressed in terms of a set of parametric coordinates (θ 1, θ 2, θ 3). Note that the knot parameters are independent to each other and then the corresponding covariant base vectors can be obtained from (2):
The derivative of the NURBS basis function can be explicitly obtained from the well known recursive formula for the n-th order derivative of B-spline basis function as
The metric coefficients g ij and other geometric quantities can be explicitly computed with NURBS basis functions.
3.2 Geometrically exact isogeometric shell analysis
In this section, we employ the NURBS representation of the curvilinear coordinates to derive geometrically exact shell formulations in isogeometric framework. In what follows, for brevity of expressions, (•),i will denote partial differentiation with respect to the curvilinear coordinates θ i. Moreover, in the index notation, Greek letters such as α, β take values 1 and 2 while Latin italic letters take values from 1 to 3.
Consider a three-dimensional solid structure in domain Ω ⊂ R 3 bounded by a closed boundary Γ. A material point x in domain Ω is transformed to the curvilinear coordinates (θ 1, θ 2, θ 3). If one takes θ 3 as a parameter defined as − 0.5h ≤ θ 3 ≤ 0.5h with h as the shell thickness, a neutral surface (θ 3 = 0) of the shell component can be represented by a surface geometry as shown in Fig. 2. For the shell surface, the boundary Γ can be decomposed into Γ 1 and Γ 2. On the edge of Γ 1, the tangential curve is aligned with the coordinate curve θ 2 while θ 1 is constant, and thus an outward normal vector n to the boundary is parallel to g 1. Similarly on Γ 2, g 2 is perpendicular to the tangential coordinate curve θ 1. In terms of boundary conditions, the boundary is composed of a prescribed displacement boundary Γ D and a prescribed traction boundary Γ N and mutually disjointed as
The traction boundary Γ N is subjected to the boundary resultants q while the distributed load intensities p is imposed on Ω.
In Fig. 2, the position vector x is a material point in the undeformed configuration of the shell. The position vector n x denotes the point to the neutral surface of the shell. Let a 3 be a unit normal vector to the given surface. The position vector x is then given as
and the corresponding covariant base vectors are
where a α ≡n x ,α and b β α are the tangent base vector to the surface coordinate curve and the mixed curvature tensor, respectively. The covariant components of the surface metric tensor is given as
Using the facts that a α3 = a α3 = 0 and a 33 = a 33 = 1, the determinant of metric coefficients is
We consider the shear deformable shell model (Naghdi 1963) in which the shell is deformed linearly by transverse shearing. The displacement is then assumed as
where u α = u α (θ 1, θ 2), w = w(θ 1, θ 2), and ψ α = ψ α (θ 1, θ 2) are response coefficients of in-surface displacement, out-of-surface displacement, and rotational angle measure, respectively. Notice that the dependence on the parametric coordinates will not be appeared unless necessary for brevity. For the further derivations, the vector of response coefficients is useful, such as
Thus strain tensors in the shell tangent plane are given as, in terms of the response coefficients,
where
and
in which (•) α ‖ β ≡(•) α,β − (•) μ Γ μ αβ means covariant differentiation in the shell surface. Similarly, the transverse shear strain can be found as
Using the principle of virtual work, an equilibrium equation is expressed as
where \( \overline{Z} \) is a variational space defined by:
The bilinear strain energy form can be written as
Note that the coupled terms of ε αβ and ω αβ vanish since they are odd functions of θ 3. For homogeneous linear elastic isotropic materials, material tensors are
where E is Young’s modulus and ν is Poisson’s ratio. For a conservative system, the external load is independent of deformation and then the linear load form can be composed of the virtual works of distributed load intensities and boundary resultants. According to the response coefficient vector d, the distributed load intensity vector p and the boundary resultant vector q can be defined as:
where p α and p 3 are, respectively, in-surface distributed load intensities and an out-of-surface distributed load intensity. N α and Q are in-surface stretching resultants and a shear resultant, respectively. M α are moment resultants. All of force quantities are presumed to be applied on the neutral surface (θ 3 = 0) and its traction boundary Γ N. Depending on the directions of edge rotations on Γ N1 , M 1 = − M B , M 2 = M T where M B and M T are the bending and twisting moment resultants, respectively. Similarly, M 1 = M T , M 2 = − M B on Γ N2 . For \( \overline{\mathbf{d}}={\left[\begin{array}{ccccc}\hfill {\overline{u}}_1\hfill & \hfill {\overline{u}}_2\hfill & \hfill \overline{w}\hfill & \hfill {\overline{\psi}}_1\hfill & \hfill {\overline{\psi}}_2\hfill \end{array}\right]}^{\mathrm{T}} \), the linear load form is written as
Using (35), the material point on the neutral surface can be expressed in terms of NURBS basis functions and coefficients at control points, such as
Then, the covariant base vectors are obtained as
Using an isoparametric mapping, the response coefficient vector (44) can be expressed as:
where \( {\mathbf{y}}_I=\mathbf{y}\left(\mathbf{x}\right)={\left[\begin{array}{ccccc}\hfill {u}_{1I}\hfill & \hfill {u}_{2I}\hfill & \hfill {w}_I\hfill & \hfill {\psi}_{1I}\hfill & \hfill {\psi}_{2I}\hfill \end{array}\right]}^{\mathrm{T}} \) are the response coefficients at control points. Then (49) can be rewritten as:
where the bilinear strain energy form of
in which the subscripts m, b, and s are the indications for membrane, bending, and transverse shear, respectively. In the strain measures, the differential operators B m , B b and B s include not only partial derivatives with respect to θ 1 and θ 2 but also the second-kind Christoffel symbols. To help the comprehension, membrane, bending and shear measures are given in the matrix form in detail as follows.
and
The linear load form is written as
where \( {\tilde{W}}_I \) is the modified NURBS basis function for the boundary integral.
3.3 Material derivatives for shell structural domain
The variation of the structural domain of the shell component can be described as shown in Fig. 3. The design dependence on the thickness coordinate θ 3 of the shell is neglected. Applying (39) into (9), we have
A design velocity field of the shell component is then given as
where \( \mathbf{V}\left({}^n\mathbf{x}\right)\equiv {\left.{\scriptscriptstyle \frac{d{}^n\mathbf{x}_{\tau }}{d\tau }}\right|}_{\tau =0} \) and ∇a 3 is the gradient of a 3. Note that the design velocity field does not have to satisfy the geometric constraint that is required in the typical configuration design velocity field. Therefore, in this formulation, the original geometry of the shell component can be perturbed into any configurations with arbitrary curvatures.
We recall the point-wise material derivative of the displacement z at x ∈ Ω, such as:
For the shell component, the partial derivative of z is given as
and the convective term is calculated as
For shell analysis, every variables is represented on the neutral surface and thus the superscript n can be omitted without confusion: e.g., V = V(n x) in (66). The details for the gradient computations can be found in Appendix.
A performance measure for the shell structure is usually defined on the neutral surface and written in integral form as
The first order variation with respect to the shape design parameter is derived as
where, considering (16) on the neutral surface, the material derivative of the determinant of the Jacobian matrix is obtained as
3.4 Isogeometric shape sensitivity analysis—direct differentiation method
Taking the first order variation of the bilinear strain energy form and linear load form with respect to shape design parameter τ, we have the followings:
and
where \( \mathbf{d}^{\prime}\equiv {\left[\begin{array}{ccccc}\hfill {u}_1^{\prime}\hfill & \hfill {u}_2^{\prime}\hfill & \hfill w\prime \hfill & \hfill {\psi}_1^{\prime}\hfill & \hfill {\psi}_2^{\prime}\hfill \end{array}\right]}^{\mathrm{T}} \). \( a^{\prime}\left(\mathbf{d},\overline{\mathbf{d}}\right) \) and \( \ell^{\prime}\left(\overline{\mathbf{d}}\right) \) denote the explicit variation terms with the dependence of their arguments on the shape design parameter suppressed. Using the fact that \( a\left(\mathbf{d},\overline{\mathbf{d}}^{\prime}\right)=\ell \left(\overline{\mathbf{d}}^{\prime}\right),\kern1em \forall \overline{\mathbf{d}}^{\prime}\in \overline{Z} \), the shape sensitivity equation is obtained as
where
and
For conservative loads, the variation of the load linear form (76) has no implicit dependence terms. If the concentrated, constant load is only considered, (76) vanishes. Besides, ż is recovered by (66) after calculating d ′ from (74).
The explicit expression of \( a^{\prime}\left(\mathbf{d},\overline{\mathbf{d}}\right) \) depends on the shell formulation, which will be derived as follows. The first order variation of the membrane strain tensor with respect to shape design parameter can be obtained from (46), such as
ε ′ αβ (d) represents the explicitly dependent part computed from both the structural response and the design velocity. Similarly, the first order variation of the bending and shear strain tensors (47–48) become
and
Finally, the explicitly dependent term of the bilinear strain energy form \( a^{\prime}\left(\mathbf{z},\overline{\mathbf{z}}\right) \) can be calculated as
In Appendix, the gradient computations with respect to the design velocity V in (77–80) are expressed in detail.
Using isogeometric discretization, (74) can be written as:
where
and
in which the quantities having the additional subscript V include the gradient computations with respect to the design velocity V referring to (77–80). To help the comprehension, explicit dependences of membrane, bending and shear measures are given in the matrix form in detail as follows:
and
3.5 Isogeometric shape sensitivity analysis—adjoint variable method
To derive an adjoint equation for the adjoint sensitivity analysis, consider a general performance functional in integral forms, such as
Taking the Fréchet derivative 〈 •, • 〉 with respect to the response coefficient vector d in the direction of \( \overline{\mathbf{d}} \) leads to
Define a Lagrangian as
where λ is the solution (coefficients) of an adjoint system. Taking the Fréchet derivative 〈 •, • 〉 of (90) with respect to d in the direction of kinematically admissible \( \overline{\boldsymbol{\uplambda}} \), using a stationary condition, the adjoint equation can be derived as
Using (51) and the symmetry of bilinear form, the followings yield
Also, using (54) we have
Substituting (92–93) into (91), the following adjoint equations can be obtained as
Differentiating the Lagrangian (90) with respect to design we have the followings:
where the explicitly dependent terms on the design are expressed, respectively,
and
a ′ (d, λ) is the same as in (80) by substituting \( \overline{\mathbf{d}} \) into λ. Using the fact that \( a\left(\mathbf{d},\boldsymbol{\uplambda}^{\prime}\right)=\ell \left(\boldsymbol{\uplambda}^{\prime}\right),\kern0.36em \forall \boldsymbol{\uplambda}^{\prime}\in \overline{Z} \) and \( a\left(\mathbf{d}^{\prime },\boldsymbol{\uplambda} \right)=\varPhi \left(\mathbf{d}^{\prime}\right)\equiv \ell \left(\mathbf{d}^{\prime}\right),\kern0.36em \forall \mathbf{d}^{\prime}\in \overline{Z} \), the adjoint shape sensitivity equation is derived as
For brevity of the problem, the external loads are assumed independent of shape variations and the integrand of performance functional is assumed linear to the response coefficients, i.e., F(y) = y T f and G(y) = y T g. (98) can be written, using isogeometric discretization, as:
where
and
4 Isogeometric shape optimization
4.1 Optimization formulations
In the isogeometric shape optimization, the control points P play the role of design variables. The objective of isogeometric shape optimization is to determine the design variables P that minimize the objective function Φ(P, z) of system under the prescribed loadings while satisfying the constraint functions g i (P, z). The structural shape optimization problem can be expressed as:
where the side constraint for the admissible displacement field is given by
To solve the nonlinear mathematical programming problem of (103–105), a gradient-based optimization algorithm (MMFD; modified method of feasible direction) and the gradients of objective and constraint functions, \( \overset{\cdot }{\varPhi}\left(\mathbf{P},\mathbf{z},\overset{\cdot }{\mathbf{z}},\mathbf{V}\right) \) and \( \overset{\cdot }{g}\left(\mathbf{P},\mathbf{z},\overset{\cdot }{\mathbf{z}},\mathbf{V}\right) \), are used. The necessary design velocity field can be obtained, by the material derivative of (55), directly from the NURBS basis function as:
4.2 Multilevel design parameterization
In design parameterization, the structural shape is controlled by a set of design variables. The design control net is only as dense as necessary for defining the boundary shape. Excessive number of design variables could lead to wriggly optimal shapes. Although the isogeometric analysis can be performed with the CAD model without further FE discretization, the fine analysis model is still required for the accurate analysis. It is more essential for the accurate analytical sensitivity analysis and thus for successful gradient-based shape optimization. In this study, the resolutions of the design and analysis models are different: the analysis model is obtained through h-refinement of the design model keeping the polynomial degree constant. The basic concept of the multilevel design parameterization has been presented as sensitivity propagation concept in (Qian 2010). It is worthwhile to present the brief procedure of multilevel design parameterization for a NURBS curve and updating the shape design velocity during the isogeometric shape optimization. Note that in this study the control points are design variables while the weights not.
The basic procedure for h-refinement is accomplished by multiple applications of the knot insertion. Inserting a new knot \( \overline{\theta}\in \left[{\theta}_k,{\theta}_{k+1}\right) \) into the given knot vector (27), the NURBS curve has a representation on the new knot vector of the form
where \( \left\{{\overline{W}}_I\left(\theta \right)\right\} \) are the NURBS basis functions on the new knot space. The knot insertion does not change the curve either geometrically or parametrically, but it is just a change of vector space basis. Solving a system of linear equations as
we obtain the formula for computing Q I , that is
where
For the isogeometric shape optimization, two sets of control points {P I } and {Q I } compose the design and analysis models, respectively. Let the knot space be independent of the design space, the definition of the design velocity (106) is valid through the knot refinement, such as
Once a control point P M of the design model is perturbed (thus, only δ P M ≠ 0), corresponding control points in the analysis model is perturbed with the following relation,
and
Then the design velocity in the analysis model is calculated accordingly. By repeating the above knot insertion procedure and the design velocity update to the bivariate knot space and corresponding control points, the multilevel design parameterization can thus be applied to a NURBS surface.
5 Numerical examples
5.1 Verification of isogeometric shape sensitivity of the hemispherical shell
The purpose of this example is to verify the generalized shape sensitivity analysis by comparing with the numerical sensitivity analysis using finite difference method. The verification model shown in Fig. 4a is a quarter model of a pinched hemispherical shell along its equator. The hemisphere has a radius of 10 and an 18° hole at its top. As shown in Fig. 4a, the symmetry boundary conditions are applied along the cutting edges and other two are free. There are two point loads (F = 1.0) alternating sign at 90° intervals along the equator. The thickness of the shell is 0.4. A linear elastic material with E = 6.825 × 107 and ν = 0.3 is used.
For the verification of isogeometric sensitivity for the geometrically exact shell model, the derived generalized isogeometric shape sensitivity formulation is employed. The surface is represented by the quadratic NURBS basis function and 529 control points. The control points of the model are perturbed by 0.1 % in radial direction to obtain the finite difference sensitivity. The perturbed domain in Fig. 4b is drawn by 200 times exaggerated design velocities for illustration purposes. The isogeometric shape sensitivity of response coefficients at the selected positions 1–4 as shown in Fig. 4b is compared with the central finite difference sensitivity using the isogeometric analysis. Table 1 shows the finite difference sensitivity, the analytical isogeometric sensitivity, and their percent agreements for response coefficients at the selected coordinates 1–4. Excellent agreements are observed at all the degrees of freedom of the control points as shown in the last column.
5.2 Higher order geometric effects of isogeometric sensitivity
In this example, the higher order geometric effects implemented on isogeometric shape sensitivity are examined by comparing with finite difference sensitivity. The verification model shown in Fig. 5a is a cantilevered planar shell with a curved edge. The model is subjected to a uniform twisting moment resultant M T = 50 along the curved edge and then the deformation appears in Fig. 5a. A linear elastic material with E = 1.0 × 107 and ν = 0.3 is considered and the shell thickness is 0.05. The geometrically exact isogeometric formulation for the shear deformable shell model and its generalized isogeometric shape sensitivity formulation are used with the quadratic NURBS basis function and 91 control points. To obtain the finite difference sensitivity using the isogeometric analysis, the control points along the curved edge are perturbed by a simple quadratic function of y(x) = τ(1 − x 2). Note that τ = 0.001 to obtain the accurate finite difference sensitivity while the perturbed design in Fig. 5b is drawn by 500 times exaggerated design velocities for illustration purposes.
Recalling the isogeometric shape sensitivity (83), normal vectors and their derivatives are found in the boundary integral forms where the problem has boundary resultants. In this example, the curved edge Γ N2 is subjected to the twisting moment resultant M T and thus the variation of the linear load form (83) can be rewritten as
The higher order geometric components, such as a 2, ∇a 2 and div a 2, can be exactly obtained from the NURBS basis function and the well known recursive formula for the n-th order derivative of B-spline basis function (37).
The isogeometric shape sensitivity of displacements at the selected positions 1–5 as shown in Fig. 5b is compared with the central finite difference sensitivity using the isogeometric analysis. To examine the higher order effects of geometry, the sensitivities including the higher order (HO) terms of ∇a 2, div a 2 in (114) are compared to the sensitivity analysis results artificially excluding those HO terms. During the implementation of conventional finite element based shape sensitivity, the higher order geometric effects are generally missing or inaccurate due to the use of linear elements (Cho and Ha 2009). Table 2 shows the finite difference sensitivity, the isogeometric sensitivity excluding HO terms (case A), the isogeometric sensitivity including HO terms (case B), and their percent agreements for the displacements at the selected coordinates in Fig. 5b. As expected, the results of case A show very bad agreements whereas those of case B excellent ones as shown in the last column. The sensitivity distributions of displacements of cases A and B are, respectively, illustrated in Figs. 6 and 7. Not only the sensitivity values shown in Table 2, but overall distributions are also quite different between two distinct cases. For the two-dimensional isogeometric model developed in the Cartesian coordinate system, Cho and Ha (2009) also examined the importance of the higher order geometric components in the shape sensitivity for the traction loads applied along the curved boundary. Comparing with their shape sensitivity expressions in Cartesian coordinate system, there are not only the curvature div a 2 but also the gradient of the normal vector ∇a 2 involved due to the representation in the curvilinear coordinate system. Since the shell boundary could be typically curved and subjected to various boundary resultants, moreover, it would be more required the use of the isogeometric shape sensitivity analysis providing better gradient information than the conventional finite element sensitivity for the precise shape optimization of the shell geometry.
5.3 Isogeometric shape optimization: cantilever shell under edge moments
Accurate sensitivity analysis is important in the shape design optimization since the shape sensitivity provides the search direction in gradient based optimization. Using the derived isogeometric shape sensitivity, shape design optimization problems of shell structures are solved for minimal compliance with a material volume constraint. The structural shape optimization problem is then stated, using the adjoint sensitivity analysis method, as:
where M max and λ are the allowable material volume and the response of adjoint system, respectively. P is a control point as a design variable whose lower and upper bounds are P lower and P upper , respectively. Using the fact that d = λ for the compliance performance measure and (95–97), the shape variation of (115) is obtained as:
Also, the shape variation of (116) can be obtained by:
Consider a square shell model with the thickness of 0.1 and the width of 12. As shown in Fig. 8, the shell model is clamped along an edge and subjected to a uniform bending moment resultant M B = 1 along the other side. The material properties are E = 10 × 106 and ν = 0.3. The design model is composed of 49 control points to represent arbitrary curved surfaces as shown in Fig. 9. Besides, the control points or design variables are parameterized into 24 sets according to the locations where the symmetry of the model is considered: the control points (dv1-dv18) in the solid square are capable to translate in x, y, and z directions while (dv19-dv24) in the circles are only able to move in z direction. The control points in the dotted square are symmetric pairs of the solid square and then they have to move symmetrically to those in the solid square with respect to the symmetry line. Control points along the fixed edge are excluded from the design parameterization. For all design variables, the translations on the xy plane are allowed from −1.5 to 1.5 while the movement along z direction is allowed from −6 to 6. Notice that the initial shell model is an almost flat and shallow arch: along the y-directional edges the z coordinate is 0 but it is smoothly increasing toward 0.01 on the symmetry line.
Although the resolution of the design model, 49 control points, would be sufficient to represent curved surfaces, the analysis model shall be refined from the design model to have 729 control points for accurate response and sensitivity analyses. The multilevel design parameterization obtained through h-refinement was explained in the Section 4.2. In order to prevent the locking phenomenon during the analysis, the reduced integration scheme is selectively employed for membrane and transverse shear stiffness matrices. The optimum shell shape is found in Fig. 10 to minimize the compliance for the given boundary conditions while keeping the same material volume or m = M max. The control points or design variables are determined by the mathematical programming algorithm, based on the shape sensitivities in (118–119). After the shape optimization, the loaded edge winds roundly to reduce the deformation against bending as shown in Fig. 10a. The optimum design demonstrates the well-known fact that an open circular cylindrical shell supports the bending moments not only by means of the bending but also by straining the surface while a flat plate resists the applied moment by means of bending only. Consequently, the maximum value of the deflection in the optimum design is only 0.04 % of 1.33759 in the initial design and it appears only at the local part of the rounded edge as shown in Fig. 10b. As shown in Fig. 8, whilst, the initial model suffers large and global deformation. Figure 11 shows the optimization history that the compliance is smoothly minimized with nine sensitivity evaluations. Under the condition of same material volume or m = M max, the compliance of the optimum design can be decreased by 0.12 % of the one of the initial design ([L(d, λ)] optimum = 6.635E − 02, [L(d, λ)] initial = 5.636E + 01). Note that the allowable movement along z direction of design variables is sufficiently large so that, in the optimum design, the largest value is less than 1.5 while the translation on the xy plane is restricted to prevent entangling control nets. One could use the initial design with opposite arch: along the y-directional edges the z coordinate changes from 0 to −0.01 on the symmetry line. The optimized shape configuration from this initial design appears perfectly overturned the optimum design shown in Fig. 10. However, the optimization histories of performance measures are exactly same for both problems.
The higher order geometric components are incorporated into the boundary integrals in (118). In order to investigate the impact of the higher order geometric components on the design optimization, the optimum design is found through the exactly same conditions of the previous optimization problem using inaccurate sensitivity expression of (118) excluding the higher order geometric components. The optimization result is illustrated in Fig. 12. Comparing with Fig. 10a, this inaccurate shell shape in Fig. 12 is more uniformly rounded and much smoother around the corners of the loading boundary. This test implies that the influence of higher order geometric components on the optimum shape is not trivial.
6 Conclusions
A generalized formulation of a continuum-based shape sensitivity analysis is derived in curvilinear coordinate systems. Note that the curvilinear coordinates compose the generalized coordinate systems from which orthogonal and Cartesian systems are readily reduced with geometric restrictions. Utilizing the generalized formulation in the isogeometric framework, both of the response and sensitivity analysis methods for the geometrically exact shear deformable shell are developed in the curvilinear coordinates. The curvilinear coordinate system can be directly and adaptively derived from the given NURBS surface geometry. By the fully analytical derivations, the boundary integrals for the boundary resultants that would be important in many engineering applications, and their material derivatives are precisely incorporated. In the sensitivity computations of the boundary integrals, furthermore, the higher order geometric effects, such as normal and curvatures, are encountered. The NURBS basis functions have the higher order continuity from the recursive differentiability of B-spline functions, and thus the higher order geometric information can be accurately calculated and enhance the accuracy of sensitivities. Through numerical examples, the developed isogeometric sensitivity analysis method is verified to provide very accurate design gradients comparing with finite difference sensitivities. The importance of existing higher order geometric effects for the sensitivity analysis is also confirmed through ostensive comparisons of isogeometric sensitivity results including or excluding the higher order terms. Moreover, the NURBS basis functions conveniently provide the smooth and non-local design velocity field whose computation is essential but not easy in the finite element based shape optimization. For the shape optimization of the cantilevered shell subjected to the boundary resultants, the derived adjoint variable sensitivity analysis method is incorporated with the gradient-based numerical optimization method. As a result, the applicability of the isogeometric shape optimization for the shell is demonstrated.
At the present time only spatial positions of control points are considered as design variables, although the weights also alter NURBS geometry. Examples provided are single patch surface models in a linear elastic material, while many practical industrial problems could be represented with several patches and behaved nonlinearly. Considering those issues, the generalized shape sensitivity analysis and optimization systems proposed in this work could be further extended in the future.
References
Ahmad S, Orons BM, Zienkiewicz OC (1970) Analysis of thick and thin shell structures by curved finite elements. Int J Numer Meth Eng 2:419–451
Ansola R, Canales J, Tárrago JA, Rasmussen J (2002) An integrated approach for shape and topology optimization of shell structures. Comput Methods Appl Mech Eng 80:447–458
Benson DJ, Bazilevs Y, Hsu MC, Hughes TJR (2010) Isogeometric shell analysis: the Reissner-Mindlin shell. Comput Methods Appl Mech Eng 199:276–289
Bletzinger KU, Ramm E (2001) Structural optimization and form finding of light weight structures. Comput Struct 79:2053–2062
Bletzinger KU, Firl M, Linhard J, Wüchner R (2010) Optimal shapes of mechanically motivated surfaces. Comput Methods Appl Mech Eng 199:324–333
Bouclier R, Elguedj T, Combescure A (2013) Efficient isogeometric NURBS-based solid-shell elements: mixed formulation and B-method. Comput Methods Appl Mech Eng 267:86–110
Cho S, Ha SH (2009) Isogeometric shape design optimization: exact geometry and enhanced sensitivity. Struct Multidiscip Optim 38:53–70
Cottrell JA, Reali A, Bazilevs Y, Hughes TJR (2006) Isogeometric analysis of structural vibrations. Comput Methods Appl Mech Eng 195:5257–5296
Cottrell JA, Hughes TJR, Reali A (2007) Studies of refinement and continuity in isogeometric structural analysis. Comput Methods Appl Mech Eng 196:264–275
Echter R, Oesterle B, Bischoff M (2013) A hierarchic family of isogeometric shell finite elements. Comput Methods Appl Mech Eng 254:170–180
Espath LFR, Linn RV, Awruch AM (2011) Shape optimization of shell structures based on NURBS description using automatic differentiation. Int J Numer Methods Eng 88:613–636
Farin G (2002) Curves and surfaces for CAGD: a practical guide. Academic, New York
Fuβeder D, Simeon B, Vuong AV (2015) Fundamental aspects of shape optimization in the context of isogeometric analysis. Comput Methods Appl Mech Eng 286:313–331
Haftka RT, Grandhi RV (1986) Structural shape optimization—a survey. Comput Methods Appl Mech Eng 57:91–106
Hassani B, Tavakkoli SM, Ghasemnejad H (2013) Simultaneous shape and topology optimization of shell structures. Struct Multidiscip Optim 48:221–233
Haug EJ, Choi KK, Komkov V (1986) Design sensitivity analysis of structural systems. Academic, New York
Hinton E, Rao NVR (1993) Structural shape optimization of shells and folded plates using two-noded finite strips. Comput Struct 46(6):1055–1071
Hosseini S, Remmers JJC, Verhoosel CV, Borst R (2014) An isogeometric continuum shell element for non-linear analysis. Comput Methods Appl Mech Eng 271:1–22
Hughes TJR, Cottrell JA, Bazilevs Y (2005) Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Methods Appl Mech Eng 194:4135–4195
Kiendl J, Bletzinger KU, Linhard J, Wüchner R (2009) Isogeometric shell analysis with Kirchhoff-Love element. Comput Methods Appl Mech Eng 198:3902–3914
Kiendl J, Schmidt R, Wüchner R, Bletzinger KU (2014) Isogeometric shape optimization of shells using semi-analytical sensitivity analysis and sensitivity weighting. Comput Methods Appl Mech Eng 274:148–167
Naghdi PM (1963) Foundations of elastic shell theory. In: Sneddon IN (ed) Progress in solid mechanics, vol 4. North-Holland, Amsterdam
Nagy AP, Abdalla MM, Gürdal Z (2010) Isogeometric sizing and shape optimisation of beam structures. Comput Methods Appl Mech Eng 199:1216–1230
Nagy AP, Ijsselmuiden ST, Abdalla MM (2013) Isogeometric design of anisotropic shells: optimal form and material distribution. Comput Methods Appl Mech Eng 264:145–162
Piegl L, Tiller W (1997) The NURBS book (monographs in visual communication), 2nd edn. Springer, New York
Qian X (2010) Full analytical sensitivities in NURBS based isogeometric shape optimization. Comput Methods Appl Mech Eng 199:2059–2071
Rogers DF (2001) An introduction to NURBS with historical perspective. Academic, San Diego
Roh HY, Cho M (2003) Development of geometrically exact new shell elements based on general curvilinear coordinates. Comput Methods Appl Mech Eng 56(1):81–115
Simo JC, Fox DD (1989) On a stress resultant geometrically exact shell model. Part I: formulation and optimal parametrization. Comput Methods Appl Mech Eng 72:267–304
Acknowledgments
This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (NRF-2012R1A1A1040019). The support is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Appendix. Gradient computations for design sensitivity analysis
Appendix. Gradient computations for design sensitivity analysis
The unit normal vector a 3 to the other base vectors can be calculated as
Its gradient computation shown in (68) with respect to the shape parameter is given by
where
Obviously, V = V(n x) in all equations in this appendix. Also in (68), the following yields
Using a αλ a λμ = δ α μ , we have
The gradient computations shown in (77) are given by
and
Also in (79), we have
Moreover, the gradient computations of the material tensors in (80) can be given from (52),
and
Rights and permissions
About this article
Cite this article
Ha, Y.D. Generalized isogeometric shape sensitivity analysis in curvilinear coordinate system and shape optimization of shell structures. Struct Multidisc Optim 52, 1069–1088 (2015). https://doi.org/10.1007/s00158-015-1297-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-015-1297-x