Abstract
Preliminary aircraft design studies use structural weight models that are calibrated with data from existing aircraft. Computing weights with these models is a fast procedure that provides reliable weight estimates when the candidate designs lie within the domain of the data used for calibration. However, this limitation is too restrictive when we wish to assess the relative benefits of new structural technologies and new aircraft configurations early in the design process. To address this limitation, we present a computationally efficient aerostructural design framework for initial aircraft design studies that uses a full finite-element model of key structural components to better assess the potential benefits of new technologies. We use a three-dimensional panel method to predict the aerodynamic forces and couple the lifting surface deflections to compute the deformed aerodynamic flying shape. To be used early in the design cycle, the aerostructural computations must be fast, robust, and allow for significant design flexibility. To address these requirements, we develop a geometry parametrization technique that enables large geometric modifications, we implement a parallel Newton–Krylov approach that is robust and computationally efficient to solve the aeroelastic system, and we develop an adjoint-based derivative evaluation method to compute the derivatives of functions of interest for design optimization. To demonstrate the capabilities of the framework, we present a design optimization of a large transport aircraft wing that includes a detailed structural design parametrization. The results demonstrate that the proposed framework can be used to make detailed structural design decisions to meet overall aircraft mission requirements.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The rapid assessment of candidate technologies is an essential aspect of preliminary aircraft design. Within the context of aircraft structural design, advanced lightweight materials and novel structural layouts should be considered during the early stages of the design process. At this stage, aircraft weight estimates are usually obtained using simplified structural weight models that are calibrated with weight data from existing aircraft (Ning and Kroo 2010). They are usually correlations that are combined with simple strength-of-materials structural models (Hajela and Chen 1988). These models have the advantages that they are computationally inexpensive and provide sufficiently accurate weight predictions. However, these correlation-based weight predictions are valid only within the design space for which data exists; they are not applicable when the impact of new weight reduction technologies is being assessed. In this paper, we address this issue by developing techniques that are fast enough to be suitable for initial design studies, while providing a more reliable aircraft structural weight prediction. We achieve this through a multidisciplinary analysis and optimization framework that includes a full structural finite-element model of the structure.
Advanced materials with greater strength and stiffness may enable the use of slender, higher-aspect ratio wings that are aerodynamically favorable, but exhibit greater flexibility than conventional wings. Therefore, even at an early stage of the design process, it is important to model the effects of wing flexibility using aeroelastic analysis. While dynamic aeroelastic phenomena are often critical in the design of wings, especially in the transonic regime, we focus on static aeroelastic analysis, which we call aerostructural analysis. In this work, we use a design parametrization that includes geometric, aerodynamic, and structural design variables. Since we use low-fidelity aerodynamics, we usually restrict the geometric design variables so that only planform modifications are possible, and we do not design the section profile shapes. This reduces the number of geometric and aerodynamic design variables involved in the design problem. However, we do utilize detailed structural models that can be used to accurately size the structure for strength and buckling constraints, to predict structural weight, and to compute aerostructural deflections. These detailed structural models often include sophisticated structural design parametrizations for advanced materials. As a result, the full aerostructural design space may have thousands of design variables. To handle these large design problems in an efficient manner, we use gradient-based design optimization methods with an efficient coupled adjoint implementation that can be used to evaluate the derivative with respect to thousands of design variables in a reasonable computational time (Martins and Hwang 2013).
Since rapid analysis and design capabilities are essential for preliminary design optimization, we focus on improving the turn-around time required for an optimization by making the most efficient use of parallel high-performance computing resources. Within our aerostructural framework, we use three levels of parallelism to achieve computational efficiency: optimization-level, aerostructural-level, and discipline-level. The optimization-level parallelism consists of concurrently analyzing multiple flight conditions on different groups of processors. This level is embarrassingly parallel and requires only communication at the beginning and at the end of each analysis or gradient evaluation. Parallelism at the aerostructural level is achieved by dividing processors assigned to the aerodynamics and structural analysis into nonoverlapping groups within each optimization-level subgroup. This second level of parallelism involves coordination of the discipline-level analyses to perform an aerostructural solution or gradient calculation. The last level of parallelism is at the discipline-level, where efficient single-discipline aerodynamic and structural analyses run on independent process groups within each aerostructural group. We use these three levels to achieve efficient parallel multidisciplinary analysis and optimization.
Many authors have performed design optimization studies that take into account wing flexibility. In one of the earliest examples of aerostructural optimization, Haftka (1977) performed a static aeroelastic optimization of composite and aluminum fighter aircraft undergoing a pull-up maneuver. The aeroelastic model included a small finite-element model of the wing and a lifting line model of the aerodynamics. Later, Grossman et al. (1988) compared aerostructural design optimization using a sequential approach, in which the aerodynamic and structural variables were optimized in sequence, to an integrated approach, in which all design variables were optimized at once. They found that the integrated approach produced better designs in terms of both aerodynamic and structural performance, and that the integrated designs exhibited more favorable aeroelastic interactions. In an application to transport aircraft wings, Grossman et al. (1990) performed an aerostructural optimization of a wing for minimum structural weight subject to a fixed range requirement. Jansen et al. (2010) performed a series of aerostructural optimization studies for nonplanar lifting configurations with a lifting line theory coupled to a beam model of the wing. They utilized a gradient-free method (Jansen and Perez 2011) to obtain optimal designs considering a sequence of aerodynamic modeling assumptions. Ning and Kroo (2010) performed a series of optimizations of wings with various wing-tip devices. They used a weight model that included a historical weight correlation and an integrated bending moment over wing thickness to predict the relative changes in weight of different designs. These studies demonstrate that important conclusions can be drawn from simple analytical models. However, in almost all cases, the scope of the studies was limited by the use of either statistical weight correlations or simplified finite-element models.
High-fidelity aerostructural design optimization methods that couple computational fluid dynamics (CFD) models with finite-element structural models can be used to reduce the impact of the modeling limitations inherent in low-fidelity analysis. Maute et al. (2001) were the first to perform high-fidelity aerostructural design optimization, coupling a linear finite-element solver to an Euler CFD solver. However, this work was limited to applications with small numbers of design variables since the authors employed the direct method, which scales well with the number of functions of interest but poorly with the number of design variables. Later, Martins et al. (2001) proposed the application of the adjoint method to high-fidelity aerostructural design optimization, which in contrast to the direct method, scales well with the number of design variables but poorly with the number of functions of interest. As a result, the coupled adjoint method enables the efficient evaluation of the derivatives required for high-fidelity aerostructural optimization with a computational cost that is nearly independent of the dimensionality of the design space (Martins et al. 2005). Martins et al. (2004) applied the coupled adjoint method to the design optimization of a supersonic business jet. Maute et al. (2003) also developed a coupled adjoint implementation for high-fidelity static aeroelastic simulations. To develop more robust aerostructural solution strategies, Barcelos et al. (2006) proposed a Newton–Krylov–Schur method to solve coupled aerostructural problems. Later, Barcelos and Maute (2008) developed a coupled adjoint method for the turbulent Reynolds averaged Navier–Stokes equations. More recently, Kenway et al. (2014) developed a more scalable coupled adjoint for high-fidelity aerostructural optimization using the ADjoint approach (Mader et al. 2008). This framework has since been applied to the design of large transport aircraft (Kenway and Martins 2014; Liem et al. 2012).
Given these developments, it may seem that high-fidelity aerostructural design optimization can now be used routinely earlier in the design cycle. However, there remain limitations that are difficult to overcome. Most of these limitations are due to the fact that CFD methods require volume meshes, which are time-consuming to generate. In addition, mesh movement strategies are required for design optimization with large-scale geometry modifications. This requirement substantially increases the complexity of the implementation of the aerostructural analysis and coupled adjoint method. Finally, mesh movement strategies cannot handle drastic changes in the aircraft shape, thus restricting the design space. While these high-fidelity aerostructural optimization tools are extremely useful for design refinement, they may not have the flexibility required for the early stages of the aircraft design process. Therefore, we regard the present work as a practical middle ground in which we use high-fidelity structures coupled to a lower-fidelity aerodynamic analysis to enable greater design flexibility and a faster turnaround time in the design cycle.
One of the primary tasks in aerostructural analysis is to develop a scheme to couple the aerodynamic and structural disciplines into a single, integrated analysis. To integrate the structures and aerodynamics, it is necessary to extrapolate the displacements from the structure to the aerodynamic surface and to transfer forces from the aerodynamic surface back to the structure. Numerous authors have developed load and displacement transfer methods (Smith et al. 2000). Displacement extrapolation can be extremely difficult when there are large gaps between the aerodynamic and structural models. These gaps arise when the secondary structure is on the wetted aerodynamic surface, but it is not included in the model used for structural sizing. As a result, the aerodynamic and structural surface meshes may not be coincident everywhere, and thus displacement extrapolation is required. Load transfer schemes must also handle noncoincident surfaces. There are two types of load transfer methods: methods that transfer the aerodynamic loads to the structure directly, and methods that integrate the force contribution on either the aerodynamic surface or an intermediate surface such as the outer mold line. In the first approach, we must ensure that the loads transferred to the structure are consistent with the original aerodynamic forces, i.e., we must ensure that the work done on the aerodynamic mesh is equal to the work done on the structure. In the second approach, this consistency and conservativeness property is nearly automatic if the scheme is derived using the method of virtual work and the forces are integrated with sufficient accuracy.
Maman and Farhat (1995) developed a method for matching aerodynamic and structural meshes for the direct transfer of loads and displacements in a parallel computing environment. In their scheme, pressure and shear stresses from the fluid solver are transferred to Gauss points on the structural mesh, and displacements are transferred back to the aerodynamic nodes. Their method employs a fast matching algorithm that quickly determines pairs of adjacent aerodynamic and structural points. Farhat et al. (1998) devised two methods for load and displacement transfer for transient problems. The first is a method based on consistent interpolation between coincident surfaces, and the second, more general, method is based on displacement and load transfer between discrete surfaces. Brown (1997) focused on the development of load and displacement transfer schemes where the structural and fluid models are nonconforming, where large gaps may exist between the structural and aerodynamic meshes. Brown used displacement interpolation functions that are either a continuous extension of the finite-element shape functions, or a rigid attachment to the nodal degrees of freedom. The load transfer was derived based on the principle of virtual work.
One common issue with the load and displacement transfer schemes described above is that they are not able to handle the different mesh resolution requirements of the aerodynamics surface panel mesh and finite-element structural model. To address this, we develop an adaptive refinement scheme tailored to coupling low- or medium-fidelity aerodynamic analysis to more refined structural finite-element models. Following Brown (1997), we extrapolate the displacements to the aerodynamic surface and use the method of virtual work to derive the consistent force vector. In a departure from Brown (1997) and Farhat et al. (1998), we use an adaptive refinement approach to integrate the aerodynamic force contribution.
In the remainder of this paper, we describe a parallel gradient-based aerostructural analysis and design optimization framework for initial aircraft design studies. The key components of this framework include a panel method that predicts the induced drag and estimates profile and wave drag contributions using an empirical model; a full finite-element model of the flexible lifting surfaces for the estimation of a portion of the structural weight; and an accurate and robust load and displacement transfer technique for transferring loads and displacements between disciplines. The discipline-level analyses, the load and displacement transfer technique, and the overall aerostructural solution method are implemented efficiently in parallel. The key contributions of the analysis framework are the load and displacement transfer technique, tailored for coupling coarse aerodynamic models to refined structural finite-element models, and the novel approximation strategies used in the Newton–Krylov solution method that enable rapid parallel aerostructural analysis. To enable design optimization, we present a novel flexible geometric parametrization technique that can be used to perform large geometry modifications that are consistent with preliminary design studies. Since we utilize gradient-based design optimization methods, we present an efficient coupled adjoint method for the aerostructural system that is implemented efficiently in parallel. We verify the accuracy of the gradient evaluation technique using the complex-step method (Squire and Trapp 1998; Martins et al. 2003). As a demonstration of the framework, we present an optimization of a large transport aircraft.
2 Aerostructural analysis components
In this section, we outline the key components of our aerostructural analysis framework. These components include the aerodynamic analysis, load and displacement transfer scheme, structural analysis, and geometric parametrization.
2.1 Aerodynamic analysis
Panel methods are a mature aerodynamic analysis tool that can be used for the prediction of aerodynamic forces on aircraft in subsonic and supersonic conditions (Erickson 1990). Since panel methods require only a surface discretization, they have much less demanding mesh requirements than CFD methods, which rely on a volume discretization. As a result, panel methods can be employed to rapidly analyze a variety of aerodynamic shapes. In this work, we use an unstructured three-dimensional panel code that can determine the aerodynamic characteristics of inviscid, external lifting flows governed by the Prandtl–Glauert equation (Erickson 1990). The panel method uses constant source and doublet singularity elements distributed over the surface of a body discretized with quadrilateral and triangular panels that form a closed, watertight surface (Katz and Plotkin 1991; Hess and Smith 1967). Based on an early version of the code, which handled only triangular discretizations, we call this panel code TriPan. In TriPan, the induced drag is computed using a Trefftz plane integration scheme with a stream-wise wake (Smith 1996). We add profile and wave drag corrections using an empirical model (Wakayama and Kroo 1995; Kennedy and Martins 2012). The remaining aerodynamic forces and moments are calculated using surface pressure integration. The discretized set of boundary conditions governing the doublet strengths is represented by the following vector of aerodynamic residuals:
where x A are the aerodynamic design variables, X A are the surface mesh nodal locations, x G are the geometric design variables, and w represents a vector of the doublet strengths. In addition, A is the dense aerodynamic-influence coefficient matrix and b is the vector of boundary conditions, where for simplicity, we omit the dependence on the design variables and the nodal locations. We solve the linear system (1) using the parallel linear algebra routines in PETSc (Balay et al. 1997; Balay et al. 2004). We use a dense matrix storage format to store the full aerodynamic-influence coefficient matrix, which is distributed across the group of aerodynamic processors by row. Each processor is assigned a group of contiguous panels that corresponds to a range of rows in the aerodynamic-influence coefficient matrix. The panels are assigned to each processor based on a domain decomposition of the dual graph of the surface mesh computed using METIS (Karypis and Kumar 1998). The mesh is reordered to ensure that all panels within each domain are ordered contiguously.
Within PETSc, we solve the system of linear equations (1) using GMRES(60) (Saad and Schultz 1986) with a block–Jacobi preconditioner. Each block in the preconditioner corresponds to the group of panels assigned to a processor. The preconditioner on each block is an incomplete LU decomposition with a level of fill of zero (ILU(0)) (Saad 2003). Instead of using all the entries from the dense matrix in the preconditioner, we use a subset of entries selected based on the initial surface mesh. For each row in the block preconditioner we include the column entry only if the centroids of the two corresponding panels are within a prescribed radius of one another. We construct the nonzero pattern for the preconditioner at initialization and keep it fixed regardless of subsequent geometric modifications during the optimization. The rationale for this construction is that the largest influence coefficients should be contributed by the panels that are closest to each other. We note that a similar effect to a higher ILU fill level can be achieved by selecting a larger inclusion radius.
A key component of TriPan that is required for aerostructural gradient-based evaluation is its discrete adjoint implementation, which enables the rapid evaluation of gradients for design optimization. To the best of our knowledge, no other panel method of this type has a discrete adjoint implementation. Within TriPan, the design variables are split into two distinct groups: aerodynamic-only design variables and geometric design variables, which we write as x A and x G , respectively. Given an aerodynamic function of interest, f(x,w), where \(\mathbf {x}^{T} = \left [\mathbf {x}_{A}^{T}, \mathbf {x}_{G}^{T} \right ]\), the total derivative can be evaluated as follows:
The derivative of the aerodynamic residuals with respect to the geometric design variables requires special consideration. For this computation, we use the product rule and compute the following product:
where X A is a vector containing all the aerodynamic surface nodes. In this implementation, we evaluate the dense matrix ∂ R A /∂ X A using a hand-coded implementation of the derivatives, and we store it in a distributed format in an analogous manner to the aerodynamic-influence coefficient matrix. Computing this dense matrix exactly requires 10 to 20 times the computational cost of the aerodynamic-influence coefficient matrix evaluation. This high computational cost is due to the complex expressions that are evaluated to determine the derivative of the aerodynamic-influence coefficients with respect to the 9 to 12 surface mesh coordinates for each panel. Like the aerodynamic-influence coefficient matrix, this computation does not require any parallel communication and exhibits excellent parallel performance. While the set-up cost of this term is high, it can be reused to evaluate the total derivative for multiple functions of interest.
Many panel methods implement a far-field approximation in which exact but computationally expensive influence coefficients are calculated for points in close proximity to the panel, while approximate expressions are used for points far from the panel (Smith 1996). These approximations introduce a conditional switch into the aerodynamic-influence coefficient calculations that can reduce computational times considerably. We found that while these far-field approximations do not have a significant impact on the function values within engineering precision, they can produce gradient errors that lead to slow convergence and failure during the optimization. As a result, we do not use far-field approximations.
Figure 1 shows a comparison of the computational times of several operations performed by TriPan on 4, 8, 16, 24, and 32 processors for a mesh with 8000 surface panels. The solution time is the time to form the aerodynamic-influence coefficient matrix, factor the preconditioner, and solve the linear system (1). We also show the time to compute ∂ R A /∂ X A , and the time to solve the adjoint system and evaluate the total derivative (2) for lift, with respect to 100 design variables. Both the solution time and the computation of ∂ R A /∂ X A exhibit excellent scalability with the number of processors. The time to compute the adjoint and evaluate the derivative is less than the solution time, once ∂ R A /∂ X A is assembled. All subsequent derivatives would scale with the adjoint time shown here, and therefore the computation of ∂ R A /∂ X A can be amortized when multiple derivatives are required for the same analysis condition.
2.1.1 Verification of TriPan
Since TriPan is a new panel-method implementation, we present the results of a verification study for the ONERA M6 wing. In this study, we compare the pressure distribution on the wing at Mach numbers of 0.5, 0.7, and 0.8395, respectively, for an angle of attack of 3.06∘. These Mach numbers span from the subsonic regime well into the transonic regime. At all Mach numbers compressibility effects are significant, so this study tests the accuracy of the compressibility correction used in TriPan. For this study, we compare the results against SUmb (van der Weide et al. 2006), a finite-volume structured multi-block code that we use here to solve the Euler equations. The surface panel mesh consists of 160 chord-wise panels and 50 span-wise panels for a total of 8000 surface panels. The CFD volume mesh, for SUmb, contains 3.15 million cells, with 32 768 cells lying on the wing surface. Figure 2 shows the chord-wise C p distributions at 20% and 80% of the semi-span of the ONERA M6 wing. For M=0.5, the agreement between TriPan and SUmb is excellent with small discrepancies of the peak C p at the leading edge. For M=0.7, there is a greater discrepancy at the leading edge and on the upper surface. For M=0.8395, TriPan cannot capture the transonic shocks and the solutions clearly diverge, as expected. This case demonstrates the range of applicability of the TriPan aerodynamic model.
Verification results for a comparison between SUmb (van der Weide et al. 2006) and TriPan for the ONERA M6 wing at a Mach numbers of 0.5, 0.7, and 0.8395. The TriPan surface mesh has 8000 surface panels. The SUmb mesh has 3.15 million volume cells, including 32 768 wing surface cells
2.2 Structural analysis
Within the present framework, the structural analysis is performed using the Toolkit for the Analysis of Composite Structures (TACS), a parallel finite-element code designed specifically for the design optimization of stiffened, thin-walled composite structures using either linear or geometrically nonlinear strain relationships (Kennedy and Martins 2014). We typically use third-order elements for structural design optimization problems, since these elements are a good trade-off between solution accuracy and gradient evaluation cost (Kennedy and Martins 2014). Within this paper, we focus on aerostructural design optimization using linear structural analysis. We view this as a necessary first step before the inclusion of either geometric or material nonlinearities in the design optimization problem.
The residuals of the structural governing equations, without aerodynamic forces, can be written as follows:
where X S are the structural nodal locations, u is the finite-element state vector, K is the linear stiffness matrix, and F I are the inertial forces on the structure. We split the design variables into two groups: material design variables, denoted x M , and geometric design variables, denoted x G . The geometric variables are shared between the aerodynamics and the structures. The distinction between the material and geometric design variables arises at the element level, where the material design variables modify the constitutive relationships, while the geometric design variables modify only the finite-element nodal locations. The force vector F I consists of two main contributions: the inertial self-weight and the inertial fuel loads. The self-weight is evaluated based solely on the density per unit area of each component of the structure. The fuel loads are applied as a distributed force per unit area of the surface. These forces are calculated based on the amount of fuel stored locally with the rib-bay formed by the adjacent spars and ribs.
To ensure the safe operation of the aircraft within the flight envelope, we impose both failure and buckling constraints at a number of off-design conditions, such as 2.5 g or −1 g maneuver cases. To reduce the number of constraints in the design problem to a practical number for adjoint-based gradient evaluation, we use a Kreisselmeier–Steinhauser (KS) aggregation technique, which provides a conservative estimate of the feasible domain of the disaggregated constraint set (Akgun et al. 2001; Poon and Martins 2007; Kennedy and Martins 2014). For both the strength and buckling constraints we compute a local constraint envelope at each Gauss point within each element of the finite-element model. Instead of grouping all envelopes together into a single constraint, we group the aggregation domains by structural design condition, major structural component, and constraint type. For instance, we often aggregate all the failure constraints for the 2.5-g maneuver condition for the upper skin into a single constraint. This aggregation approach has two advantages: it simplifies the interpretation of the results and, based on our experience, it typically leads to optimization problems that require fewer optimization iterations to solve.
2.3 Load and displacement transfer
In this section, we present the load and displacement transfer schemes that link the structural displacement to the aerodynamic surface and transfer the loads from the aerodynamic surface to the structure. We develop these schemes in a general manner to link any structural analysis method to an aerodynamic analysis that utilizes a full surface discretization. For instance, the following scheme could be used to link a panel or CFD analysis to a beam model, but it could not be used to link lifting line methods to a full three-dimensional finite-element model.
The surface discretizations employed by panel methods often use high-aspect-ratio cells that are stretched span-wise. These stretched surface meshes are designed to capture the rapid chord-wise variation of the pressure distribution without over-resolving the more gradual span-wise variation of the solution. On the other hand, finite-element meshes used for structural analysis tend to have near-uniform resolution with elements that have approximately a unit aspect ratio. Depending on the relative resolution of the surface discretizations, this can lead to an issue with the load transfer scheme, where a single aerodynamic panel may stretch over several finite-elements. Under these conditions, certain load transfer schemes apply loads to a small fraction of the surface elements in the structural mesh, which leads to a nonsmooth stress distribution. While many of these schemes are consistent and conservative, the introduction of nonsmoothness makes the design optimization problem more challenging, due to the introduction of local stress concentrations. In this work, we develop a load transfer scheme that alleviates this issue by matching the discretization level used to perform the surface pressure integration. Our proposed approach produces a smoother load transfer, even when high-aspect-ratio cells are present.
To present the load and displacement transfer schemes concisely, we introduce a new notation for the aerodynamic and structural surfaces. In our approach, we treat the aerodynamic and structural geometry not as discrete meshes, but as a representation of the underlying geometry. For the structure, we represent this geometry using the finite-element shape functions, while for the aerodynamics, we introduce an interpolation consistent with the aerodynamic discretization. The structural surface is defined as follows:
where \(\mathbf {d}_{S}^{(e)}\) is the position vector at parametric point ξ within finite-element e, and \(\mathbf {N}^{(e)}_{s} \in \mathbb {R}^{3 \times n_{s}}\) are the finite-element shape functions defined parametrically over the domain \(\boldsymbol {\xi } \in \mathcal {D}_{S} \subset \mathbb {R}^{2}\). We also define a displacement and rotation interpolation in which we first restrict the full vector of displacements and rotations, u, to a vector containing either the nodal displacements or nodal rotations, and then interpolate these using the finite-element shape functions. We write these operations as follows:
where \(\mathbf {u}_{S}^{(e)}\) and \(\boldsymbol {\theta }_{S}^{(e)}\) are the displacement and rotation interpolated within finite-element e, and D u and D 𝜃 are the displacement and rotation restriction operators, respectively. We also define the aerodynamic surface using the following interpolation:
where \(\mathbf {X}_{A}^{0}\) are the undeformed aerodynamic mesh locations, \(\mathbf {d}_{A}^{(c)}\) is the position within cell c at the parametric point η, and \(\mathbf {N}_{A}^{(c)} \in \mathbb {R}^{3 \times n_{a}}\) are the shape functions, which are also defined over the domain \(\boldsymbol {\eta } \in \mathcal {D}_{A} \subset \mathbb {R}^{2}\). Note that we write these formulae in terms of the full displacement and nodal vectors, but in the implementation we exploit the sparsity structure of the interpolation to improve the computational performance of the approach.
Our load and displacement transfer scheme is based on the work of Brown (1997). In Brown’s approach, the displacement extrapolation and load transfer utilize so-called rigid links, which are vectors that originate on the structural surface and extend to the aerodynamic surface. The displacements at the aerodynamic surface nodes are extrapolated based on the displacements and rotation at the origin of the rigid link as follows:
where we have omitted the parametric points for ease of presentation. Here \(\mathbf {u}_{A}^{(c)}\) is the displacement extrapolated to the aerodynamic surface in cell c, from finite-element e on the structural surface. Note that the rigid link \(\mathbf{r} = {\mathbf{d}}_{A}^{(c)} - {\mathbf{d}}_{S}^{(e)}\) is evaluated based on the distance between the undeformed geometries. Omitting the second rotational term from the displacement extrapolation (7) produces unrealistic deformed aerodynamic surfaces in areas where there are gaps between the aerodynamic and structural surfaces, e.g., at the leading edge, trailing edge, or wing tip. Throughout this work, we restrict the discussion to small-angle approximations, but the displacement extrapolation (7) could also be extended to large rotations using the following expression:
where C is a rotation matrix and I is the identity matrix.
The information required to compute a rigid link (7) includes the aerodynamic cell index c, the parametric point within the aerodynamic cell η, the finite-element index e, and the parametric point within the finite-element ξ. We introduce the following notation for the information required to compute a rigid link: \((c,\, \boldsymbol {\eta },\, e,\, \boldsymbol {\xi }) \in \mathcal {R}\). We compute the rigid links by fixing a cell index and parametric location on the aerodynamic surface and then searching for the closest point within any finite-element on the structural surface. This can be expressed as follows:
We compute each rigid link based on the initial geometry, and then we fix each \(\mathcal {R}\) for all subsequent geometry modifications. As a result, the rigid link changes and may no longer be the closest point to the aerodynamic surface. It is possible to construct the rigid links with a different norm. For instance, we have experimented with the following formulation:
where \(\mathbf {r} = \mathbf {d}^{(e)}_{S}(\boldsymbol {\xi }) - \mathbf {d}^{(c)}_{A}(\boldsymbol {\eta })\), and n is a unit normal vector perpendicular to the symmetry plane. Note that the first term |n T r| adds the perpendicular distance to the norm to remove the nonuniqueness of the symmetry-plane distance alone. This modified norm produces rigid links that are predominantly aligned with the symmetry plane.
Using the above definitions, we can now describe the displacement extrapolation scheme. First, we determine the rigid links for each aerodynamic surface node based on the initial aerodynamic and structural geometry. For each rigid link, we then compute the displacement extrapolation (7). These aerodynamic surface displacements are added to the undeformed aerodynamic surface nodal locations. Therefore, the result of the structural deformation can be transferred to the aerodynamic surface nodes as follows:
where \(\mathbf {X}_{A}^{0}\) and X A are the initial and deformed aerodynamic surface nodal locations and T A u represents the extrapolation of the structural deformation to the aerodynamic surface nodes through (7). Figure 3a shows the rigid links for the displacement extrapolation and the deformed structural and aerodynamic surface meshes. The displacements are computed at each aerodynamic node via the closest point search (8), but are interpolated from parametric locations within each element on the structural mesh.
Next, we present the load transfer scheme based on the rigid-link approach. To derive this scheme, we use the method of virtual work in conjunction with the displacementextrapolation (7) to determine the aerodynamic force vector to apply to the finite-element structural model. The virtual work done by the pressure loads acting through the virtual displacement and rotation from the rigid-link extrapolation is
where q is the dynamic pressure, C p (η,w) is the surface pressure coefficient, and \(\hat {\mathbf {n}}\) is the normal defined on the deformed aerodynamic surface. Note that the pressure coefficient depends on the aerodynamic state variables w and may also vary spatially over the aerodynamic cell as a function of η depending on the spatial reconstruction of C p . The deformed aerodynamic surface normal \(\hat {\mathbf {n}}\) from (10) is computed as follows:
where \(\mathbf {N}^{(c)}_{A,\eta _{1}}\) and \(\mathbf {N}^{(c)}_{A,\eta _{2}}\) are the derivatives of the shape functions along the first and second coordinate directions. Note that the integration in the method of virtual work (10) is performed over the deformed aerodynamic surface rather than the undeformed surface. This leads to a nonconservative following force that produces nonsymmetric components in the structural Jacobian.
Based on (10), the expression for the consistent forces due to the application of aerodynamic loads can be written as
This formulation produces both forces and moments exerted on the structural model. The first term within the integrand in (11) represents the forces acting on the structure, and the second term contributes the moments. The one remaining task is to approximate the integral in (11) over each surface panel. We evaluate this integral using a two-part numerical quadrature rule. First, we split quadrilateral cells based on a specified characteristic length scale into a series of subquadrilaterals. The characteristic length scale is selected to match the length scale of the average finite-element within the structural model. If any side of the quadrilateral exceeds the characteristic length scale, we split the cell along that edge into multiple subcells. Next, on each subcell we use a Gauss quadrature scheme that matches the order of accuracy required by the underlying finite-elements. For each quadrature point within each subcell, we compute a rigid link using (8). In an analogous manner to the displacement transfer scheme, we evaluate the rigid links based on the initial geometry and keep them fixed throughout the optimization. We have found that this two-level quadrature rule is effective at smoothly transferring loads to the finite-element mesh even in the presence of high-aspect-ratio surface cells. Figure 3b illustrates the load transfer scheme including the subcell refinement step.
Figure 4 shows the impact of the subcell refinement on the von Mises stress distribution in the structure. In this example, the loads from the coarse aerodynamic mesh and a refined aerodynamic submesh are transferred to the same underlying structural discretization. The initial aerodynamic surface panel mesh is shown in Fig. 4a. The subcell refinement process, illustrated in Fig. 4b, produces a significant number of subcells within each cell of the initial aerodynamic surface mesh. The difference between the aerodynamic surface pressure integration using (11) over the initial and the refined meshes is reflected in the von Mises stress distributions in the underlying structure. The resulting von Mises stress distributions are shown for the coarse and refined aerodynamic integration in Figs. 4c and 4d, respectively. The underlying third-order structural mesh is shown in Fig. 4e. With subcell refinement, the von Mises stress distribution is smooth, while without subcell refinement there are significant stress concentrations at some locations within the finite-element mesh. These stress concentrations are due to large point loads applied by the unrefined load transfer scheme.
Initial and refined meshes used for the load transfer quadrature and the resulting stress distributions. The refinement-based approach (d) produces a smoother stress distribution. (a) Initial aerodynamic mesh. (b) Refined aerodynamic submesh. (c) Initial von Mises. (d) Refined von Mises. (e) Third-order structural mesh
2.4 Geometry parametrization
The selection of the geometric parametrization technique impacts both the aerodynamic and structural disciplines. Any proposed geometric parametrization must handle both disciplines in a consistent manner to ensure compatibility of the resulting geometry. Within the context of gradient-based aerostructural optimization, we also require a geometry parametrization that is sufficiently smooth and yet able to handle the large geometric modifications that are required in the preliminary design context. Finally, the approach must be computationally efficient for both geometry manipulation and derivative computation.
In this work, we address these requirements by utilizing a geometry parametrization based on free-form deformation (FFD) volumes (Sederberg and Parry 1986) to define a design-dependent modification of the initial aerodynamic and structural surfaces. Using the FFD approach, we embed the structural and aerodynamic meshes inside a B-spline volume and perform design-dependent modifications of the B-spline volume control points to manipulate the embedded aerodynamic and structural meshes. One of the main advantages of the FFD approach is that it produces smooth and differentiable geometry modifications. Furthermore, the derivatives of the embedded points with respect to the design variables can be computed efficiently. The disadvantage of the FFD approach is that the initial source geometry representation and the final geometry representation are not the same. However, the FFD approach is flexible, and it can be applied to any mesh without knowledge of the source geometric representation.
In the following section, we outline a systematic way to manipulate the B-spline control points that define the FFD volume to obtain geometry changes consistent with planform variables appropriate for preliminary aircraft design studies. In particular, we include changes to the local twist angle, span, chord, thickness-to-chord ratio, dihedral, and sweep. In the proposed scheme, geometric modifications are applied to the initial set of B-spline control points, \(\mathbf {p}_{ijk} \in \mathbb {R}^{3}\), to obtain the final set of control points, \(\mathbf {p}_{ijk} \in \mathbb {R}^{3}\), where all coordinates are given in a global Cartesian reference frame. The chord, span, and thickness-to-chord ratio are modified through an anisotropic scaling of the geometry along different directions, while the twist, dihedral, and sweep changes are applied in a consistent manner that avoids self-intersecting surfaces for large changes to sweep and dihedral and moderate changes to twist.
To apply these changes in a consistent manner, we employ a series of unit vectors that define a span-wise direction, t s , a chord-wise direction, t c , and a vertical direction, t v . In addition, we also employ a series of reference points, \(\mathbf {r}_{n} \in \mathbb {R}^{3}\), for n=1,…,N, connected by line segments. The geometry modification is divided into two steps: first, the geometry changes are applied to the reference points; second, the locations of the initial B-spline points, p i j k , relative to the initial reference line segments are used to determine the final position of the B-spline control points. The geometric variables are split into two groups: those given for each span-wise segment, and those given at each span-wise station. The geometric variables given for each segment consist of the scaling along the span-wise direction, s n , dihedral, Γ n , and sweep, Λ n , while the geometric variables given for each span-wise station consist of the twist, 𝜃 n , chord-wise scaling, c n , and vertical scaling, v n .
The following rotation matrix is used extensively in the proposed FFD manipulation scheme:
where \(\mathbf {a} \in \mathbb {R}^{3}\) is a unit vector such that a T a=1, and φ is the angle of about the unit vector a (Hughes 2004). This rotation matrix is defined such that the components of the the transformed vector are expressed in the transformed reference frame.
In the proposed scheme, the geometric modifications are applied to the reference line segments. The reference line segment is modified in the following manner: we first apply the dihedral, then a sweep modification, and finally a span scaling operation. These operations can be written as follows:
where b=C(t c ,Γ n )T t v is the vertical direction vector rotated through the dihedral angle and the differencebetween adjacent reference line points is a n =r n+1−r n . The final reference point locations, R n , are determined by applying the update
with R 1=r 1, for n=1,…,N−1.
The twist axis, t 𝜃 , which defines the axis about which the twist rotation is applied, is determined by projecting the segment direction, A k , onto the plane defined by the span axis, t s , and vertical axis, t v , as follows:
To obtain the final geometry, the vertical axis and the chord axis are scaled and rotated based on the values of the twist, dihedral, chord, and vertical scaling. In the final geometry, the modified vertical and chord axes are denoted v n and c n , respectively. These vectors are defined for each segment as follows:
where \(\tilde {\Gamma }_{n} = {1}/{2}\left ({\Gamma }_{n} + {\Gamma }_{n+1}\right )\), \(\tilde {\Gamma }_{N} = {\Gamma }_{N}\).
After the final reference line locations and the transformed chord and vertical axes, c n and v n , have been calculated, the final FFD control point locations are determined based on the values of the following projections:
where u s is the projection onto the span direction, u c is the projection onto the chord direction, and u v is the projection onto the vertical direction. If 0≤u s <1, then the following update is applied:
If u s <0 or u s ≥1, then P i j k is not modified by the segment.
To demonstrate the flexibility of this geometry parametrization, we take a simple straight wing and modify it into a swept C-wing with taper and a crank. The result is shown in Fig. 5, which also shows the FFD volume points, reference points, and line segments.
3 Aerostructural analysis
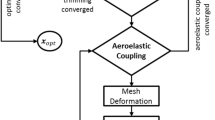
In the following section, we present a robust parallel Newton–Krylov method for the solution of the coupled aerostructural system of equations and demonstrate the scalability of the approach with respect to the number of processors. This Newton–Krylov solution strategy utilizes novel approximation techniques that make use of the nature of the three-dimensional panel method to reduce the computational time required to solve the coupled system. The aerostructural system of equations is formed by evaluating the aerodynamic residuals (1) on the deformed mesh (9), and by adding the aerodynamic forces (11) to the original system of structural governing equarions (3). This coupled system of equations is written as follows:
where q T=[w T u T] are the aerodynamic and structural state variables, \(\mathbf {x}^{T} = \left [ \mathbf {x}_{A}^{T}\;\; \mathbf {x}_{M}^{T}\;\; \mathbf {x}_{G}^{T} \right ]\) are the aerodynamic, material, and geometric design variables, and \(\mathbf {X}_{A} = \mathbf {X}_{A}^{0} + \mathbf {T}_{A}\mathbf {u}\) are the deformed aerodynamic surface nodal locations. Note that we have suppressed the dependence of the aerodynamic and structural nodal locations on the geometric design variables x G for ease of presentation.
While the individual aerodynamic and structural disciplines are linear, the coupled aerostructural system (15) is nonlinear. This nonlinearity is due both to the aerodynamic forces and the nonlinear relationship between the aerodynamic surface nodal locations and the aerodynamic residuals. Linearity of the system is recovered when the displacements are zero, u=0, or when the dynamic pressure is zero, q=0.
3.1 A Newton–Krylov method
During the solution procedure, we accept a point as converged when the relative tolerances of both the aerodynamic and structural residuals are reduced below a given threshold. As a result, our stopping criterion does not depend on the relative scaling of the structural and aerodynamic governing equations and can be written as follows:
To solve the coupled aerostructural (15) we use an approximate and inexact Newton method where the update at each iteration, Δq (n), is computed from the following linear system:
where we apply the update q (n+1)=q (n)+Δq (n). We select J≈∂ R/∂ q to be a computationally convenient approximation of the exact Jacobian. Instead of solving the approximate Newton update (17) exactly, we use inexact solutions with the following stopping criterion:
While we have experimented with more sophisticated methods for selecting 𝜖 n k , we have found that an effective approach is to fix this parameter to 𝜖 n k =10−3 for all iterations.
At each iteration, we solve the linear system (18) inexactly using a preconditioned Krylov subspace method. We use inexact solutions (18) that make sufficient progress toward the solution but require less computational time than exact solutions (Eisenstat and Walker 1996). The preconditioner consists of a single iteration of block–Jacobi where each block consists of the discipline-level solvers. We use a full factorization of the stiffness matrix for the structural block and preconditioned GMRES(5) for the aerodynamic block. We have found that this selection approximately balances the workload between disciplines for a wide range of problem sizes. Since the aerodynamic discipline solver is also a Krylov subspace method, we use FGMRES(15), a flexible variant of GMRES (Saad 1993), to solve (17).
It is often necessary to employ globalization strategies in Newton’s method to converge from starting points far from the solution (Kelley and Keyes 1997). In our experience, however, globalization is not required for the aerostructural system (15). We attribute this to the mild nonlinearity of the coupled system, where the nonlinearities arise entirely from the coupling, rather than the individual disciplines. We also note that many authors have used Jacobian-free Newton–Krylov methods where the matrix-vector products are calculated using finite differences (Knoll and Keyes 2004). However, Jacobian-free methods are not competitive for this coupled system, since it is as costly to evaluate the residual as it is to evaluate the full aerodynamic-influence coefficient matrix. Therefore, we compute and store most components of the aerostructural Jacobian.
3.2 Approximate Jacobian
At each iteration of the Newton method, we solve the linear system (18) using the following approximate Jacobian that is less computationally expensive to compute than the exact Jacobian:
where the off-diagonal terms J A S and J S A represent the coupling between the aerodynamics and structures. Note that the approximate Jacobian is formed by omitting the contribution to the structural block from the Jacobian of the aerodynamic forces, −∂ F A /∂ u. Since we use Krylov subspace methods to solve (18), in practice only matrix-vector products are required with the Jacobian (19). This poses no problem for the diagonal blocks, since they are stored explicitly. For the off-diagonal blocks, we compute the matrix-vector product
for the aerodynamic input v, using an exact expression for ∂ F A /∂ w. For the other off-diagonal term, we compute the following matrix-vector product:
where we form J X such that it approximates the exact term J X ≈∂ R A /∂ X A . We compute the matrix-vector product (21) by first transferring the input s from the structural processors to the aerodynamic processors, using the operator T A , and then evaluating the matrix-vector product with J X . In this implementation, we compute and store J X on the aerodynamic processors in the same dense matrix used to store ∂ R A /∂ X A . We have experimented with both an exact linearization and an approximate linearization for the term J X . In the exact approach, we use J X =∂ R A /∂ X A . However, as discussed in Section 2.1, computing this term is 10 to 20 times more computationally expensive than evaluating the aerodynamic-influence coefficient matrix. A second approach, which we have found effective, is to construct an approximation by computing the contributions to ∂ R A /∂ x A from the panels that are within the nonzero pattern of the preconditioner. This typically makes the computational cost of computing J X approximately equal to the cost of computing the aerodynamic residuals. As a final approximation strategy within the Newton method, we do not re-evaluate J X at every iteration, but instead update it only every m iterations. Typically we choose m=10, so that J X is recomputed only if the aerostructural system is relatively difficult to solve. This high value of m is chosen since we have found that approximations of J X are effective, even in subsequent iterations.
3.3 Aerostructural solution scalability
To demonstrate the scalability of the aerostructural solution methods, we examine the parallel scalability of the Newton–Krylov solution method presented above for a large aerostructural model. The aerodynamic model consists of a mesh with 13 250 quadrilateral surface panels. The structural finite-element model consists of 39 134 third-order MITC9 shell finite-elements (Bucalem and Bathe 1993) with 151 107 nodes and roughly 906 000 degrees of freedom. We use a characteristic length of 0.1 m for the load transfer refinement, which results in a nearly 15-fold increase in the number of integration cells used in the load transfer scheme.
Figure 6 shows the solution time of two variants of the Newton–Krylov method on 16, 24, 32, 64, and 96 processors. The method labeled “NK” updates the exact derivative ∂ R A /∂ x A every 10 iterations, while the method labeled “ANK” forms the approximate J X every 10 iterations. Both methods achieve excellent parallel scalability. The first Newton–Krylov variant requires 522 seconds on 16 processors and only 90 seconds on 96 processors, while the second Newton–Krylov variant takes 237 seconds on 16 processors and 47 seconds on 96. The nearly two-fold difference between the computational time required by the two methods is due to the additional time required to compute ∂ R A /∂ x A exactly, rather than the approximation J X used in the second variant.
4 Coupled aerostructural adjoint implementation
Gradient-based design optimization methods require accurate derivatives of the objective and constraints within the design problem. In many aerostructural design optimization problems there are fewer objective and constraint functions than there are design variables. Therefore, an adjoint implementation is more efficient than a direct method (Martins and Hwang 2013). Following Martins et al. (2005) and Kenway et al. (2014), who developed coupled adjoint methods using CFD, we develop a coupled adjoint method for the aerostructural system (15). Our implementation is based entirely on hand-coded analytic derivatives that produce highly accurate gradients at a low computational cost compared to finite-difference or complex-step calculations. Similar accuracy and computational efficiency could also be achieved using selective automatic differentiation (Mader et al. 2008).
The aerostructural adjoint equations can be written in the following form:
where f(x,q) is a function of interest, and \(\boldsymbol {\psi }^{T} = \left [ \boldsymbol {\psi }_{A}^{T} \;\; \boldsymbol {\psi }_{S}^{T} \right ]\) are the aerodynamic and structural adjoint variables. After the adjoint variables have been obtained, the total derivative is evaluated using the additional computation,
We implement the adjoint equation (22) and the total derivative equation (23) for a number of aerodynamic and structural functions of interest, including induced drag, lift, and moments, as well as the KS aggregation function for both stress and buckling constraints (Poon and Martins 2007; Kennedy and Martins 2014).
In our adjoint implementation, we solve the linear system (22) using a coupled Krylov approach, with a block–Jacobi preconditioner formed from the adjoint solvers for each discipline. We use the aerodynamic adjoint implementation from (2) with GMRES(5) as a preconditioner for the aerodynamic block, and the stiffness matrix as the preconditioner for the structural block. The coupled linear system is solved using the flexible variant of GMRES(60) since the discipline-level aerodynamic preconditioner is nonstationary. Unlike the solution phase, the adjoint system/equation (22) must be solved with the exact transpose matrix-vector products, without any approximation. These exact products are required to obtain accurate values of the adjoint variables ψ and, in turn, accurate gradients. The exact transpose of the Jacobian is
where we note that in contrast to the Newton–Krylov approach, ∂ R A /∂ X A is computed exactly, and the following force term ∂ F A /∂ X A is included in the Jacobian.
To compute the adjoint variables, it is also necessary to evaluate the right-hand side, ∂ f/∂ q, in the adjoint (22). This derivative is handled differently for aerodynamic and structural functions of interest. For an aerodynamic function of interest, f A (x,q), we have
Note that the aerodynamic function depends on the structural state variables because of the displacement transfer that modifies the aerodynamic surface nodes. Structural functions, on the other hand, typically depend only on the structural state variables, f S (x,u), and as a result, the derivative of the function with respect to the aerodynamic state variables, ∂ f S /∂ w, is zero.
Once the adjoint variables have been determined by solving the adjoint equation (22) with the exact linearization (24), the total derivative must be evaluated using (23). The derivatives with respect to the geometric design variables are the most complex to evaluate. For the geometric variables, the contribution from the product of the adjoint vector with the derivative of the residuals can be written as follows:
where the derivatives with respect to the deformed and the undeformed aerodynamic surface nodal locations arise because of the load and displacement transfer. These terms must be evaluated with care to ensure that the resulting derivative is correct. The derivative of the deformed aerodynamic surface nodal locations with respect to the geometric design variables contains two contributions:
where the transfer matrix T A depends on the geometry of the aerodynamic and structural surfaces due to the rigid-link terms. Omitting the contribution from these derivative terms results in gradient errors that can lead to poor optimizer performance.
4.1 Derivative accuracy study
In this section, we present a verification of the derivatives for aerodynamic and structural functions of interest using the complex-step method (Squire and Trapp 1998; Martins et al. 2003) as the benchmark. In this approach, the total derivative is calculated using complex arithmetic as follows:
where \(j = \sqrt {-1}\) and the entire code must perform all arithmetic operations using complex numbers. The step size h in the complex-step derivative approximation (26) is a complex perturbation of the i th design variable, where e i is the i th Cartesian basis vector. The advantage of the complex step method is that it does not suffer from subtractive cancellation (Squire and Trapp 1998; Martins et al. 2003). As a result, very small step sizes—\(\mathcal {O}(10^{-20})\) and smaller—may be used, yielding extremely accurate gradient approximations that can be used for conclusive gradient verification, which is not possible with finite-difference methods (Martins et al. 2003).
To verify our adjoint implementation, we compare the derivatives computed using the complex-step and coupled adjoint methods for a small aerostructural problem with 566 surface panels and 1956 structural degrees of freedom. A small case is chosen to allow rapid testing of all aerodynamic and structural functions. The design variables consist of five geometric twists, eight structural thicknesses, and one angle of attack. Figure 7 shows the relative error of the lift, normalized by the dynamic pressure, and the KS failure function. The results demonstrate that the relative error of any gradient component is less than 10−7.
4.2 Coupled adjoint scalability
In this section, we demonstrate the scalability of the adjoint-based gradient evaluation method with the number of processors for the large aerostructural model presented in Section 3.3. Figure 8 shows the computational times for 16, 24, 32, 64, and 96 processors. The computational time is divided between the time to evaluate and store the exact Jacobian of the aerostructural system, and the time to solve the adjoint system and evaluate the total derivative. The exact linearization can be reused when multiple adjoint solutions are required at the same operating condition. Both the computational time to evaluate the exact Jacobian and the time to solve the adjoint and evaluate the total derivatives of the structural and aerodynamic functions of interest scale well with the number of processors. The computational time to compute ∂ R A /∂ x A scales from 360 seconds on 16 processors to 61 seconds on 96 processors. The time to solve the adjoint equations and compute the total derivative is 10 to 20 times less than the time to compute ∂ R A /∂ x A for the lift and KS functions, respectively. The times for the lift and KS functions scale from 29 and 15 seconds on 16 processors to 6.4 and 3.0 seconds on 96 processors, respectively. Note that the discrepancy between the time required for the aerodynamic and structural gradients is due to the additional iterations required in the coupled adjoint solution for the lift adjoint variables.
5 Aerostructural optimization of an aircraft wing
In this section, we present an aerostructural optimization study of a large transport aircraft wing using the framework presented above. The geometry of the configuration has roughly the same dimensions as a Boeing 777-200ER, so we utilize secondary weight and geometric data from this aircraft. In this study, we compare the results of takeoff gross weight minimization and a composite objective consisting of the mission fuel consumption added to the takeoff gross weight for a single long-range, high-payload mission.
5.1 Quasi-CRM geometry
For this study we use what we call the quasi-CRM (QCRM) geometry. The QCRM is a wing-tail geometry, without a fuselage, with a planform that is roughly the same as that of the common research model (CRM) used in the DPW 4 and 5 workshops (Vassberg et al. 2008; Vassberg 2011) but is not derived from the CRM geometry directly. The QCRM wing is untwisted and has a root chord of 12 m, a tip chord of 2.75 m, a semi-span of 30 m, and a quarter-chord sweep of 35∘. The leading edge of the wing is straight, while the trailing edge of the wing is quadratically interpolated between the root trailing edge and the tip. The trailing edge is determined using a quadratic spline where a control point is added at a span-wise location of 10.5 m, with a chord of 6.5 m. The curved trailing edge mimics a wing crank in a smooth manner. The wing geometry is constructed using a set of lofted super-critical NASA airfoil sections. The first two sections are NASA SC(2)-0414 sections, while the tip section is a NASA SC(2)-0610 airfoil. While the initial aerodynamic performance of the QCRM wing is poor because of the initial twist distribution, we do not use its initial performance as a baseline and instead compare only optimized designs.
The geometry of the wing and the internal wing structure is shown in Fig. 9. The wing box structure consists of two structural spars and 44 ribs, as well as top and bottom wing skins. Within the wing box, the first 3 ribs in the structure are parallel to the symmetry plane. This section of the wing box lies within the fuselage and is designed to model the center wing-box. The leading- and trailing-edge spars lie at 15% and 65% of the root chord, respectively.
To model the structure of the QCRM, we use a finite-element mesh with 28 778 third-order MITC9 shell elements, with 110 395 nodes, resulting in just over 662 000 degrees of freedom. For the aerodynamic model, we use a surface mesh for both the wing and tail with 2300 quadrilateral panels. We set the characteristic length scale for the load transfer scheme to 0.1 m, which results in roughly 15 times more quadrilateral subcells for the load transfer integration.
5.2 Aircraft design problem
To demonstrate the capabilities of our framework, we present a design formulation where we minimize either the takeoff gross weight (TOGW) or the mission fuel burn (FB) added to the TOGW of the aircraft for a long-range, high-payload mission. We label these objectives TOGW and FB + TOGW, respectively. The TOGW consists of a measure of both the structural and aerodynamic performance of the aircraft. The structural performance enters through the empty weight contribution to TOGW, while the aerodynamic performance enters through the mission fuel weight component of TOGW. The FB + TOGW objective places additional importance on the aerodynamic performance of the aircraft relative to the structural weight. The TOGW and FB + TOGW objectives are equivalently the zero fuel weight plus fuel burn and the zero fuel weight plus twice the fuel burn, respectively.
We estimate the mission fuel requirements using the Breguet range equation. The fuel consumption over the entire mission can be predicted from the Breguet range equation based on a single value of L/D. In aerostructural analysis, however, L/D depends on the actual aircraft weight through the structural deflection. Therefore, a more accurate fuel burn estimate could be obtained by integrating the rate of fuel consumption over the entire mission taking this L/D variation into account (Liem et al. 2012). To simplify the design problem, however, we analyze only the performance of the aircraft at the mid-fuel weight point. Note that this is not the same as the mid-mission point. Using the Breguet range equation, we can calculate the mission fuel burn as follows:
where W m is the half-fuel mass of the aircraft and β is defined as follows:
where R is the mission range, TSFC is the thrust-specific fuel consumption, and L/D is the lift to drag ratio. The takeoff gross weight of the aircraft can then be calculated as
To simplify the design formulation, we add the mission fuel mass and the takeoff gross weight as design variables and add (27) and (28) as compatibility constraints within the design optimization problem. The use of these compatibility variables also simplifies the application of preliminary weight estimates of secondary aircraft components that play an important role in weight estimation and balance computations.
In the design problem, we analyze three flight conditions: the mid-fuel cruise condition and 2.5-g and −1-g maneuver condition at the takeoff gross weight. We trim the cruise and maneuver flight conditions using a fully moving tail. We set the payload for the mission to 55 000 kg and use a range of 6000 nautical miles. Since this is a high-payload, long-range mission, we analyze the cruise flight condition at an altitude of 33 000 ft and a Mach number of 0.85 to obtain a reasonable cruise C L . For both the 2.5-g and −1-g maneuver conditions, we perform the analysis at 20 000 ft, and we use a Mach number of 0.9 to simulate a dive condition.
5.3 Aircraft weight estimation and balance
We perform a detailed breakdown of the weight of the aircraft using a combination of preliminary weight estimation techniques based on statistical correlations (Shevell 1989; Kroo 2013) and weight predicted using the finite-element model of the wing and horizontal tail. Instead of using the weight directly from the finite-element models, we compute the weight as follows:
where \(W^{(\text {FE})}_{\text {wing}}\) is the finite-element mass of the full wing, and S wing is the projected area of the wing in square meters. The mark-up factor of 1.5 is designed to account for additional fastener weight and component weight not captured in the finite-element model, while the area-dependent factor is designed to capture secondary weight contributions from the leading- and trailing-edge structure. We place this additional mass contribution at the same center of mass as that for the finite-element wing model and use an analogous expression for the horizontal tail weight.
5.4 Structural parametrization
In this work, we use an approach for preliminary structural wing-box sizing using an analysis based on smeared-stiffener calculations. In this approach, the effect of discrete stiffeners is included by modeling the impact of the stiffeners on the average panel stiffness, rather than including discrete stiffeners directly in the finite-element model. This smeared-stiffness approach works well when the ratio of the panel side-length to stiffener pitch is high, meaning that there is a high density of stiffeners (Stroud and Agranoff 1976).
In this design problem, we use a blade-stiffened panel model with the design variables shown in Fig. 10. We model all components using aluminum 7075-T6 with a Young’s modulus of 70 GPa, a Poisson’s ratio of 0.33, and a maximum design stress of 420 MPa. Only the upper and lower wing skins are modeled using this approach, while the remainder of the structure is modeled using a single thickness variable. The design variables in the smeared-stiffness formulation include the panel thickness t p , the stiffener height h s , the stiffener width t w , and the stiffener pitch s p .
To size the stiffener dimensions and skin thicknesses, we consider both strength and local buckling requirements. Including both strength and buckling criteria leads to a more realistic sizing problem that produces a more reliable wing-box weight estimate than considering strength requirements alone. For both the strength and buckling constraints, we use the KS constraint aggregation technique, applying a point-wise strength or buckling envelope at each Gauss point within the aggregation domain. For the strength constraints, we apply a von Mises criterion and utilize three aggregation domains: one for the upper skins, a second for the lower skins, and a third for the spars and ribs. For the buckling constraints, we apply the methodology proposed by Stroud and Agranoff (1976) to compute a buckling envelope. Within the analysis, the critical buckling loads are calculated based on the panels formed by the spar and rib intersections in the finite-element model. We use two buckling constraint aggregation domains: one for the top skins and another for the bottom skins.
To calculate the buckling envelope for each panel, we consider several independent buckling modes and construct an envelope based on an assumed interaction between modes. These independent modes include buckling of the skin between stiffeners, buckling of the stiffeners themselves, and overall panel buckling. The details of this method can be found in Stroud and Agranoff (1976) and (Kennedy et al. 2014). This approach to local buckling does not require the computation of a global buckling eigenvalue problem and can be easily and inexpensively incorporated within the aerostructural framework presented above.
5.5 Design problem summary
There are 577 design variables in the design parametrization for both the TOGW and FB + TOGW optimization problems. The design parametrization is summarized in Table 1. We add 121 compatibility variables to simplify the problem formulation. These include the TOGW, the fuel mass, the reference area of the wing and tail, the mean aerodynamic chord of the wing and tail, the panel length variables, and the fuel traction variables. A corresponding constraint is added for each compatibility variable, which reduces the size of the effective design space.
Table 2 summarizes the constraint parametrization used in the design problem. The constraints can be divided into two categories: constraints whose gradient must be computed using a total derivative, and sparse constraints that do not depend on the aerostructural state variables and therefore do not require a total derivative. In total there are 18 constraints in the first category and 604 sparse linear and nonlinear constraints in the second category. To evaluate the 18 constraints in the first category, we use 20 evaluations of more basic structural and aerodynamic functions that can be computed directly from the aerostructural solution including the lift, moment, and normal force for all three flight conditions, as well as the drag for the cruise condition, and 5 KS functions for each of the maneuver conditions.
When evaluating the objective and constraint gradients, we compute the gradient of these 20 more basic functions using the adjoint method outlined above. Next, we evaluate the gradient with respect to the fuel burn, TOGW, and trim constraints using the derivatives of the basic functions. The computational cost could be reduced by implementing the adjoint for these constraints directly and eliminating the two additional adjoint solutions. However, this would complicate the implementation and make it more difficult to modify the optimization problem formulation. For this problem, the elimination of these two additional adjoint calculations would save roughly 20 seconds per gradient evaluation.
5.6 Results
To solve the TOGW and FB + TOGW design optimization problems, we use the sparse gradient-based optimizer SNOPT (Gill et al. 2005) with the feasibility and optimality tolerance set to 10−5. We use the interface to SNOPT from the Python-based package pyOpt (Perez et al. 2012). Before starting the aerostructural optimization, we perform a structural-only optimization with fixed aerodynamic loads. We then start the aerostructural optimization with the values obtained from the optimized structural-only solution. We run all flight conditions on a single aerostructural-level group of 24 processors split between 16 structural processors and 8 aerodynamic processors. In this configuration, each evaluation of the objective and constraints requires approximately 2 minutes and 10 seconds of computational time. Note that this is the time to solve three aerostructural cases and evaluate the functions of interest. The gradient evaluation requires 3 minutes and 20 seconds of computational time per evaluation to compute the total derivative for 20 functions of interest.
The TOGW optimization requires 1033 objective and constraint evaluations, and 456 gradient evaluations, while the FB + TOGW design requires 769 objective and constraint evaluations, and 370 gradient evaluations. Optimization results that are within engineering precision of the solution are produce after roughly two-thirds of the total optimization iterations. Based on our experience, larger span designs require more design iterations to converge to a given optimization tolerance. In addition, these two optimization examples are typical in terms of function and gradient-evaluation count. To further reduce the computational time we could have run the tests using three independent aerostructural-level groups. This would result in an objective evaluation time of roughly 45 seconds and a gradient evaluation time of 70 seconds, but it would require 72 processors.
A summary of the optimized TOGW and FB + TOGW designs is presented in Table 3, where the relative differences are calculated with respect to the TOGW design. The results show that the FB + TOGW design has a 0.46% higher TOGW, due to a 15% increase in the wing mass, but it achieves a 2.9% fuel-burn advantage over the TOGW design. This lower fuel burn is achieved through a 5.2 m wing-span extension that leads to a 14% reduction in the induced drag. The 21% higher wing mass is due to a combination of thicker wing skins that are required to support the span increase and a 5.7% increase in the reference area.
Figure 11 shows the twist and lift distributions for the TOGW and FB + TOGW wings. The twist is shown at the jig, cruise, and 2.5 g conditions. In Fig. 11, the lift distribution is normalized by dynamic pressure and is shown at the cruise and at the 2.5-g maneuver condition. Both designs exhibit considerable aerostructural twist resulting in significant load alleviation at the 2.5-g maneuver condition. The TOGW design has 7.3∘ of aerostructural washout at the tip relative to the jig condition, and 4.3∘ of aerostructural washout relative to the cruise condition. The FB + TOGW design exhibits even larger aerostructural twist at the tip, with 8.6∘ of additional aerostructural washout relative to the jig condition, and 5∘ relative to the cruise condition. The normalized lift distributions for the TOGW design are larger because of the higher wing loading relative to the FB + TOGW design.
Figure 12 shows the structural deflection at the −1 g, cruise, and 2.5 g conditions, as well as the planform of the designs, and the C p distribution on the top surface of the wing. Note that the chord of the FB + TOGW design is smaller than that of the TOGW design, but the reference area is higher. The FB + TOGW design is more flexible than the TOGW design because of the larger wing span. At the 2.5-g maneuver condition, the TOGW and FB + TOGW designs exhibit 3.7 m and 4.6 m wingtip deflections, respectively.
Figure 13 shows the panel thickness and stiffener height distributions for the optimized TOGW and FB + TOGW designs for the upper and lower wing skins. In both the TOGW and FB + TOGW designs the lower skin thickness is higher than the upper skin thickness, while the lower stiffener height is smaller than the upper-skin stiffener height. The relative sizes are due to the buckling constraints, which have a greater impact on the sizing of the upper-skin panel at the 2.5-g maneuver condition. The lower skin is subject to compression only at the −1-g maneuver condition, where the loads are considerably smaller. In addition, the thicknesses and stiffener heights of the FB + TOGW designs are larger than those of the TOGW designs because of both the higher TOGW and the larger wing span.
6 Conclusion
We developed a fast, robust, and flexible aerostructural analysis and design optimization framework for initial aircraft design studies. This framework utilizes a full finite-element model of the structure, and a panel method to predict the aerodynamic forces on the wing, with added empirical corrections for profile and wave drag.
We developed a new load and displacement transfer technique designed for both parallel solution methods and load transfer between a coarse surface panel model and refined structural finite-element models. To handle large-scale geometric design changes, we developed a flexible geometric parametrization technique based on free-form deformation volumes.
To create a rapid design tool that is suitable for preliminary design optimization studies, we used parallel high-performance computing techniques to solve the coupled aerostructural system and evaluate the total derivative using the adjoint method. We demonstrated the performance of the approximate and inexact Newton–Krylov solution method and the adjoint-based coupled Krylov method for aerostructural gradient evaluation for a large aerostructural problem with 13 250 surface panels and 906 000 structural degrees of freedom. The Newton–Krylov solution strategy achieves excellent scalability between 16 and 96 processors, with a solution time of 47 seconds on 96 processors. The coupled Krylov method also exhibits good scalability on between 16 and 96 processors. For 96 processors, the adjoint method requires 61 seconds of set-up and 3.0 and 6.4 seconds for each additional structural and aerodynamic function of interest, respectively. Furthermore, we verified that our implementation of the coupled adjoint method achieves an accuracy of at least 10−7 for all the derivative components.
To demonstrate the capabilities of our framework, we performed a design optimization study for a large transport aircraft wing. Since we optimized the aerodynamic shape and structural sizing simultaneously, we obtained a wing design with optimal static aeroelastic tailoring that takes advantage of flexibility to obtain optimal performance at the cruise condition, while unloading the outboard of the wing at the maneuver condition.
This wing design optimization included a detailed structural parametrization of a metallic stiffened structure. The results show that the proposed framework can be used to make detailed design decisions in the structure in order to meet overall aircraft mission requirements. This flexible framework will be valuable in future aircraft design studies that compare the impact of new structural technologies.
References
Akgun MA, Haftka RT, Wu KC, Walsh JL, Garcelon JH (2001) Efficient structural optimization for multiple load cases using adjoint sensitivities. AIAA J 39(3):511–516. doi:10.2514/2.1336
Balay S, Buschelman K, Eijkhout V, Gropp WD, Kaushik D, Knepley MG, McInnes LC, Smith BF, Zhang H (2004) PETSc users manual. Technical Report ANL-95/11 - Revision 2.1.5, Argonne National Laboratory
Balay S, Gropp WD, McInnes LC, Smith BF (1997) Efficient management of parallelism in object oriented numerical software libraries. In: Arge E, Bruaset A M, Langtangen H P (eds) Modern Software Tools in Scientific Computing. Birkhäuser Press, pp 163– 202
Barcelos M, Bavestrello H, Maute K (2006) A Schur-Newton-Krylov solver for steady-state aeroelastic analysis and design sensitivity analysis. Comput Methods Appl Mech Eng 195(17-18):2050–2069. doi:10.1016/j.cma.2004.09.013
Barcelos M, Maute K (2008) Aeroelastic design optimization for laminar and turbulent flows. Comput Methods Appl Mech Eng 197(19-20):1813–1832. doi:10.1016/j.cma.2007.03.009
Brown S A (1997) Displacement extrapolation for CFD+CSM aeroelastic analysis. AIAA Paper: 97–1090
Bucalem ML, Bathe K-J (1993) Higher-order MITC general shell elements. Int J Numer Methods Eng 36:3729–3754. doi:10.1002/nme.1620362109
Eisenstat S, Walker H (1996) Choosing the forcing terms in an inexact newton method. SIAM J Sci Comput 17(1):16–32. doi:10.1137/0917003
Erickson LL (1990) Panel methods:An introduction. Technical Report NASA TP-2995, NASA Ames Research Center. Moffett Field, California
Farhat C, Lesoinne M, Tallec PL (1998) Load and motion transfer algorithms for fluid/structure interaction problems with non-matching discrete interfaces:Momentum and energy conservation, optimal discretization and application to aeroelasticity. Comput Methods Appl Mech Eng 157(1–2):95–114. doi:10.1016/S0045-7825(97)00216-8
Gill PE, Murray W, MA Saunders. (2005) SNOPT:An SQP algorithm for large-scale constrained optimization. SIAM Rev 47(1):99–131. doi:10.1137/S0036144504446096
Grossman B, Gurdal Z, Haftka RT, Strauch GJ, Eppard WM (1988) Integrated aerodynamic/structural design of a sailplane wing. J Aircr 25(9):855–860. doi:10.2514/3.45980. 2013/09/28
Grossman B, Haftka RT, Sobieszczanski-Sobieski J, Kao PJ, Polen DM, Rais-Rohani M (1990) Integrated aerodynamic-structural design of a transport wing. J Aircr 27(12):1050–1056. doi:10.2514/3.45980
Haftka RT (1977) Optimization of flexible wing structures subject to strength and induced drag constraints. AIAA J 15(8):1101–1106. doi:10.2514/3.7400
Hajela P, Chen JL (1988) Preliminary weight estimation of conventional and joined wings using equivalent beam models. J Aircr 25(6):574–576. doi:10.2514/3.45625
Hess J, Smith A (1967) Calculation of potential flow about arbitrary bodies. Prog Aerosp Sci 8:1–138
Hughes PC (2004) Spacecraft attitude dynamics. Dover books on engineering. Dover Publications
Jansen P, Perez R (2011) Constrained structural design optimization via a parallel augmented Lagrangian particle swarm optimization approach. Comput Struct 89(14):1352–1366. doi:10.1016/j.compstruc.2011.03.011
Jansen P, Perez RE, Martins JRRA (2010) Aerostructural optimization of nonplanar lifting surfaces. J Aircr 47(5):1491–1503. doi:10.2514/1.44727
Karypis G, Kumar V (1998) A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J Sci Comput 20(1):359–392
Katz J, Plotkin A (1991) Low–Speed Aerodynamics. McGraw–Hill Inc.
Kelley CT, Keyes DE (1997) Convergence analysis of pseudo-transient continuation. SIAM J Num Anal 35:508–523
Kennedy GJ, Kenway GKW, Martins JRRA (2014) High aspect ratio wing design: Optimal aerostructural tradeoffs for the next generation of materials. In 52nd Aerospace Sciences Meeting, National Harbor, Maryland. AIAA 2014-0596
Kennedy GJ, Martins JRRA (2012) A comparison of metallic and composite aircraft wings using aerostructural design optimization. In 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Indianapolis, IN
Kennedy GJ, Martins JRRA (2014) A parallel finite element framework for large-scale gradient-based design optimization of high-performance structures. Finite Elem Anal Des. doi:10.1016/j.finel.2014.04.011. In press
Kenway GKW, Kennedy GJ, Martins JRRA (2014) A scalable parallel approach for high-fidelity steady-state aeroelastic analysis and adjoint derivative computations. AIAA Journal 52(5):935–951. doi:10.2514/1.J052255
Kenway GKW, Martins JRRA (2014) Multi-point high-fidelity aerostructural optimization of a transport aircraft configuration. J Aircr 51(1):144–160. doi:10.2514/1.C032150
Knoll D, Keyes D (2004) Jacobian-free Newton–Krylov methods:a survey of approaches and applications. J Comput Phys 193(2):357–397. doi:10.1016/j.jcp.2003.08.010
Kroo I (2013) Aircraft design:Synthesis and analysis. http://adg.stanford.edu/aa241/AircraftDesign.html
Liem RP, Kenway GKW, Martins JRRA (2014) Multi-mission aircraft fuel burn minimization via multi-point aerostructural optimization. AIAA J. (Accepted)
Mader CA, Martins JRRA, Alonso JJ, van der Weide E (2008) ADjoint:An approach for the rapid development of discrete adjoint solvers. AIAA J 46(4):863–873. doi:10.2514/1.29123
Maman N, Farhat C (1995) Matching fluid and structure meshes for aeroelastic computations:A parallel approach. Comput Struct 54(4):779–785. doi:10.1016/0045-7949(94)00359-B
Martins JRRA, Alonso JJ, Reuther JJ (2001) Aero-structural wing design optimization using high-fidelity sensitivity analysis. In Proceedings of the CEAS Conference on Multidisciplinary Aircraft Design and Optimization
Martins JRRA, Alonso JJ, Reuther JJ (2004) High-fidelity aerostructural design optimization of a supersonic business jet. J Aircr 41(3):523–530. doi:10.2514/1.11478
Martins JRRA, Alonso JJ, Reuther JJ (2005) A coupled–adjoint sensitivity analysis method for high–fidelity aero–structural design. Optim Eng 6:33–62. doi:10.1023/B:OPTE.0000048536.47956.62
Martins JRRA, Hwang JT (2013) Review and unification of methods for computing derivatives of multidisciplinary computational models. AIAA J 51(11):2582–2599. doi:10.2514/1.J052184
Martins JRRA, Sturdza P, Alonso JJ (2003) The complex-step derivative approximationx. AIAA J 29(3):245–262. doi:10.1145/838250.838251
Maute K, Nikbay M, Farhat C (2001) Coupled analytical sensitivity analysis and optimization of three-dimensional nonlinear aeroelastic systems. AIAA J 39(11):2051–2061. doi:10.2514/2.1227
Maute K, Nikbay M, Farhat C (2003) Sensitivity analysis and design optimization of three-dimensional non-linear aeroelastic systems by the adjoint method. Int J Numer Methods Eng 56(6):911–933. doi:10.1002/nme.599
Ning SA, Kroo I (2010) Multidisciplinary considerations in the design of wings and wing tip devices. J Aircr 47(2):534–543. doi:10.2514/1.41833
Perez RE, Jansen PW, Martins JRRA (2012) pyOpt:a Python-based object-oriented framework for nonlinear constrained optimization. Struct Multidiscip Optim 45(1):101–118. doi:10.1007/s00158-011-0666-3
Poon N, Martins JRRA (2007) An adaptive approach to constraint aggregation using adjoint sensitivity analysis. Struct Multidiscip Optim 34:61–73. doi:10.1007/s00158-006-0061-7
Saad Y (1993) A fexible inner-outer preconditioned GMRES algorithm. SIAM J Sci Comput 14(2):461–469. doi:10.1137/0914028
Saad Y (2003) Iterative Methods for Sparse Linear Systems. PWS Pub. Co. 2nd edn
Saad Y, Schultz MH (1986) GMRES:A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J Sci Stat Comput 7(3):856–869. doi:10.1137/0907058
Sederberg TW, Parry SR (1986) Free-form deformation of solid geometric models. SIGGRAPH Comput Graph 20(4):151–160. acm.org/10.1145/15886.15903
Shevell RS (1989) Fundamentals of Flight. Prentice Hall PTR
Smith MJ, Hodges DH, Cesnik CES (2000) Evaluation of computational algorithms suitable for fluid-structure interactions. J Aircr 37(2):282–294. doi:10.2514/2.2592
Smith S (1996) A computational and experimental study of nonlinear aspects of induced drag. Tech. Rep. NASA TP 3598, National Aeronautics and Space Administration, Ames Research Center, Moffett Field, CA
Squire W, Trapp G (1998) Using complex variables to estimate derivatives of real functions. SIAM Rev 40(1):110–112. doi:10.1137/S003614459631241X
Stroud WJ, Agranoff N (1976) Minimum mass design of filamentary composite panels under combined loads. Design procedure based on simplified buckling equations. Technical report, NASA Langley Research Center, Hampton, VA
van der Weide E, Kalitzin G, Schluter J, Alonso JJ (2006) Unsteady turbomachinery computations using massively parallel platforms. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV. AIAA 2006-0421
Vassberg J, DeHaan M, Rivers S, Wahls R (2008) Development of a common research model for applied CFD validation studies. AIAA 2008-6919
Vassberg JC (2011) A unified baseline grid about the Common Research Model wing-body for the fifth AIAA CFD drag prediction workshop. In 29th Applied Aerodynamics Conference, Honolulu, Hawaii. AIAA 2011-3508
Wakayama S, Kroo I (1995) Subsonic wing planform design using multidisciplinary optimization 32(4):746–753. doi:10.2514/3.46786
Acknowledgments
This work was partially funded by NASA under grant number NNX11AI19A. The authors would like to acknowledge Gaetan Kenway for his assistance with the verification cases presented in this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kennedy, G.J., Martins, J.R.R.A. A parallel aerostructural optimization framework for aircraft design studies. Struct Multidisc Optim 50, 1079–1101 (2014). https://doi.org/10.1007/s00158-014-1108-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-014-1108-9