1 Introduction

Structure designers often consider rigidity as one of the important design requirements. However, a flexible structural member may bring in additional functionalities. A compliant mechanism is one of the best examples. The main characteristic of compliant mechanisms is to transform force, motion, or energy using their flexible structural members. Compliant mechanisms replace hinges used in the rigid body mechanisms for lower manufacturing and assembly cost while achieving similar performance. They also can be miniaturized and used in MEMS or embedded structures (Ananthasuresh and Kota 1996; Sigmund 2001; Frecker 2003; Ananthasuresh and Howell 2005). The most popular design method for compliant mechanisms is the energy based topology optimization (Howell and Midha 1993; Ananthasuresh et al. 1994a, 1994b; Sigmund 1997). Variousapplications for compliant mechanism designs using the energy based topology optimization have been reported in literature (Larsen et al. 1997; Kikuchi et al. 1998; Yin and Ananthasuresh 2002; Luo et al. 2005, 2008).

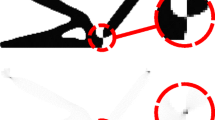
Since a compliant mechanism works as both a mechanism as well as a structure, two contradictory functionalities – flexibility and rigidity – must be considered simultaneously. For the flexibility design objective, maximizing a selected nodal displacement (mutual potential energy) is employed; for the rigidity design objective, minimizing the mean compliance strain energy) is commonly used. To accommodate both design objectives, the solution requires a multi-objective optimization formulation. Various formulations which combine these two design objectives have been proposed and many successful examples have been presented (Frecker et al. 1997; Nishiwaki et al. 1998; Saxena and Ananthasuresh 2000; Pedersen et al. 2001; Jung and Gea 2004) However, configurations of many optimized compliant mechanisms are very similar to the rigid link mechanisms just replacing joins connector with compliant members (Pedersen et al. 2001) as shown in Fig. 1. It is obvious that these compliant members will endure large strain under applied force in order to perform the specified motions. The large strain in particular areas are very undesirable in compliant mechanism design since it could cause structural failure. Moreover, there are always problems on the solution convergence although various forms have been used in combining both flexibility and rigidity such as weighted sum and ratios.

Fig. 1
figure 1

Energy based compliant mechanism design: compliant gripper I (Yin and Ananthasuresh 2001: a). displacement inverter (Jung and Gea 2004: b). compliant gripper II (Lin et al. 2010: c)

Full size image

In this paper, a strain based topology optimization method is proposed to produce optimal compliant mechanism. Minimizing a global effective strain function is implemented for the rigidity design objective. Furthermore, the physical programming method (Messac 1996; Messac and Ismail-Yahaya 2002; Lin et al. 2010) is adopted to accommodate both flexibility and rigidity design objectives.

The remainder of this paper is organized as follows: first the energy based topology optimization for compliant mechanisms is reviewed followed by the problems associated with this formulation. In Section 3, the proposed strain based topology optimization method is presented and the implementation of physical programming in the multi-objective optimization problem is described. Then, solution procedures including sensitivity analysis is derived. Finally, comparisons of design examples from both the energy based topology optimization and the strain based method are presented and discussed.

2 Energy based topology optimization for compliant mechanism

Consider a topology optimization problem setting for a compliant mechanism design, the applied force F i n to the design domain Ω will drive the output node producing a disireable displacement in the direction of U o u t as shown in Fig. 2, where. Ω represents entire design domain, Ω s denotes solid areas and Ω v is areas without material.

Fig. 2
figure 2

Schematic representation of a topology optimization formulation for compliant mechanism

Full size image

To consider the flexibility of the compliant mechanism, the displacement at output point can be formulated as the mutual potential energy (MPE):

$$ MPE=U^{T}\Phi $$
(1)

where U is the displacement vector and Φ is a unit vector that can be viewed as a dummy load. At the same time, the rigidity of the design is evaluated by the strain energy (SE) which can be expressed as:

$$ SE=\frac{1}{2}U^{T}KU $$
(2)

where K is a global stiffness matrix of the design.

Since both flexibility and rigidity should be accommodated for the complaint mechanism design, two objective functions, maximizing mutual strain energy and minimizing strain energy, are needed. However, the compliant mechanism may also have localized large strain at compliant joints, if the traditional minimizing strain energy formulation is used. To perform the desired function as a mechanism, these compliant joints will suffer from localized large strain when external forces are applied. We will discuss the causes of this localized large strain in the next section. Then, our proposed solutions will be presented in Section 3.

To find the optimized solution in topology optimization, the Solid Isotropic Microstructure with Penalty (SIMP) (Bensøe 1989) material model is usually implemented. In the SIMP model, Young’s modulus E is defined as a function of artificial material density. It is formulated as

$$ E( x )=f(x)E_{0} ,\,\,f(x)=x^{p},\,\,P>1 $$
(3)

where x is the artificial material density of each element and has a range as 0 ≤ x ≤ 1. p is a penalty coefficient of material, which is greater than 1 to provide penalty on the stiffness of the material, E 0 is Young’s modulus of the base material, and f(x)is the penalty function. Graphs of penalty function are plotted under different penalty coefficient values in Fig. 3.

Fig. 3
figure 3

Penalty function in SIMP model

Full size image

Since Young’s modulus of SIMP model represents material properties of each element, the total strain energy can be formulated as a summation of element strain energy. From (3), the element stiffness matrix can be defined as a function of material density since \(k_{i} =f( {x_{i} } )k_{i}^{0} \), where \(k_{i}^{0} \) is the element stiffness matrix with base material. Then, then element strain energy can be described as a function of material density as shown in (4)

$$ SE=\frac{1}{2}U^{T}KU=\frac{1}{2}\sum {u_{i}^{T} k_{i} u_{i} } =\frac{1}{2}\sum {f( {x_{i} } )u_{i}^{T} k_{i}^{0} u_{i} } $$
(4)

where u e represents the element displacement vector and k e is the element stiffness matrix.Although minimizing the strain energy can improve the structural rigidity, the strain energy in (4) actually reveals a major defect on local strain because strain energy is determined by not only strain but also material density. Considering an element with very large strain but relatively low artificial material density such as in red line range in Fig. 3, the impact of the large strain will be washed out significantly by the penalty function f(x) if p is larger than 1. Therefore, the optimizer will not try to reduce the large strain, and the material density of that element will be reduced to zero even though it has large strain. As a result, the strain will be transferred to the neighbor elements, and the neighbor elements will have higher strain than before. Hence, the optimal solution could be a high rigidity but localized large strain.

3 Strain based topology optimization method for compliant mechanism

To overcome the drawbacks of the energy based topology optimization formulation for compliant mechanism design, a strain based topology optimization method is presented in this section. The problem formulation of the proposed method will be discussed first and then the sensitivity is derived. Finally, the implementation of the physical programming method for multi-objective optimization formulation for compliant mechanisms is presented.

3.1 Problem formulation

As we discussed in the previous section, the penalty function in (4) will distort the solution by discounting the localized large strain if the artificial material density is relatively small in the same element. In order to accurately account for the local strain we propose the effective strain as an objective function for structure rigidity since the effective strain allows any three dimensional stain state to be represented as a single positive strain value. The effective strain can be decomposed with displacement with stiffness matrix as shown in (5).

$$ \,\overline \varepsilon^{2}=\varepsilon^{T}D_{0} \varepsilon^{T}=u_{i}^{T} Cu_{i} =\frac{u_{i}^{T} k_{i}^{0} u_{i} }{E_{0} } $$
(5)

where C is a positive definite dimensionless matrix, and D 0 is a strain stress relation matrix without Young’s modulus. Composition of displacement vectors and C matrix can be used to define the effective strain as \(\overline \varepsilon \) (Jung and Gea 2004). The equation shows that the effective strain does not include penalty function in the form. Therefore, the effective strain is a direct indicator of strain, the rigidity design objective of the compliant mechanism can be replaced by a minimized global effective strain. The formulation of compliant mechanism design is described with effective strain term in (6).

$$ \begin{array}{l} \mbox{Minimize:}\,\,\sum\limits_{i=1}^{n} {\overline \varepsilon^{2}_{i} } ,\,\,\,\,\,\,\mbox{Maximize:}\,U^{T}\Phi \,\,\,\,\,\,\,\,\,\,\,\,\, \\ \mbox{Subject}\,\mbox{to}\,\,\,\,\,\,KU=F \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,V(X)=\sum\limits_{i=1}^{N} {x_{i} v_{i} \le \overline V_{0} } \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\hspace*{17pt}X=\left\{ {x_{1} ,x_{2} ,\cdots ,x_{N} } \right\},\,\,\,\,{x}\le x_{i} \le \bar{{x}} \\ \end{array} $$
(6)

3.2 Physical programming

Considering both flexibility and rigidity simultaneously requires multi-objective optimization formulations and both of the weighted-sum and the fraction formulations experiences numerical and convergence problems. A physical programming (Messac 1996) framework is implemented in this study. One of the advantages of physical programming is that it can incorporate designers’ preference by specifying desirability ranges. This is particularly important in the compliant mechanism design because the flexibility function and the rigidity function have completely different numerical orders and different sensitivity with respect to design variables. The physical programming method can remove the problems by defining proper class functions with suitable desirability.

Based on the effective strain energy formulation and the physical programming method, the strain based topology optimization problem can be defined as a summation of functions of the effective strain and the mutual potential energy as follows:

$$ \begin{array}{l} \mbox{Minimize}\,\,\,\,\,F_{1} \left( {\sum\limits_{i=1}^{n} {\overline \varepsilon^{2}_{i} } } \right)+F_{2} \left( {U^{T}\Phi } \right)\,\,\,\,\,\,\,\,\,\,\,\,\, \\ \mbox{Subject}\,\mbox{to}\,\,\,\,\,\,KU=F \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,V(X)=\sum\limits_{i=1}^{N} {x_{i} v_{i} \le \overline V_{0} } \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\hspace*{1pt} X=\left\{ {x_{1} ,x_{2} ,\cdots ,x_{N} } \right\},\,\,\,\,{x}\le x_{i} \le \overline x \\ \end{array} $$
(7)

where F 1 and F 2 are two class functions in the physical programming method. In our study, F 1 is a preference function representing the benefits of the smaller value of global effective strain, and F 2 representing the benefits of larger value of output displacement. Both class functions are shown in Fig. 4. The choices of ranges between f 0 and f ∗ on both class functions are pre-defined by the designer. In this way, optimization algorithm can process both of the flexibility and rigidity at the equal levels and provide satisfactory solutions.

Fig. 4
figure 4

Class function: class 1 (the rigidity function) and class 2 (the flexibility function)

Full size image

3.3 Sensitivity analysis

One of the most important tasks in topology optimization is evaluating the sensitivity of functions with respect to design variables. In this paper, two class functions are used to design the compliant mechanism. The first one is a function of the global effective strain, and the second one is the mutual potential energy. The sensitivity of the mutual potential energy has been studied by many researchers. In this section, our focus is on the sensitivity analysis of the global effective strain function.

From (5), the sensitivity of F 1 can be expanded as the following:

$$ \frac{d}{dx_{i} }\left( {\sum\limits_{i=1}^{n} {\bar{{\varepsilon }}_{i}^{2}} } \right)=\frac{d}{dx_{i} }\left( {\sum\limits_{i=1}^{n} {u_{i}^{T} Cu_{i} } } \right) $$
(8)

Since u i is difficult to differentiate and the gradient of C is zero, the sensitivity of the effective strain cannot be derived directly. To derive the sensitivity of the effective strain, we introduce the virtual stiffness matrix \(k_{i}^{1}\) which is filled with the material density of one. By using the linear relations of \(k_{i}^{1\thinspace }=E_{0}C\), the (8) can be converted as

$$\begin{array}{lll} \frac{d}{dx_{i} }\left( {\sum\limits_{i=1}^{n} {u_{i}^{T} Cu_{i} } } \right)&=&\frac{d}{dx_{i} }\left( {\sum\limits_{i=1}^{n} {\frac{u_{i}^{T} k_{i}^{1} u_{i} }{E_{0} }} } \right)=\frac{d}{dx_{i} }\left( {\frac{U^{T}K^{1}U}{E_{0} }} \right) \\ &=&\frac{1}{\mbox{E}_{\mbox{0}} }\frac{dU^{T}}{dx_{i} }K^{1}U \end{array} $$
(9)

The derivative of K 1 is zero since the material density of K 1 is constant. The K 1 U is actually the loading vector generated by the imposed displacement field in the new system. If we applied this loading vector as the applied force to the original system, we will have a system governing equation as KV = K 1 U. Substituting the KV into (9) and applying the derivative results of the original system, K ″ U + KU’ = 0, we arrive at the following expression:

$$ \frac{d}{dx_{i} }\left( {\sum {\bar{{\varepsilon }}_{e}^{2}} } \right)=\frac{1}{\mbox{E}_{\mbox{0}} }\frac{dU^{T}}{dx_{i} }K^{1}U=-\frac{1}{\mbox{E}_{\mbox{0}} }U^{T}\frac{dK}{dx_{i} }V\, $$
(10)

Since the sensitivity of effective strain is derived in (10), the sensitivity of objective function in (7) can simply derived using chain rule. Once the sensitivity is obtained, a gradient based optimization method such as the Generalized Convex Approximation (Chickermane and Gea 1996) can be used to generate the optimal configures.

The flowchart of the strain based topology optimization method for compliant mechanism design is described in Fig. 5. Firstly, a FEM analysis (KU = F) is performed. Based on the resulting displacement field ( U), the adjoint force ( K 1 U) is used to evaluate the adjoint displacement vector, V . Then, the sensitivity of F 1can be obtained using (10). Furthermore, the sensitivity evaluation of F 2 can be easily obtained by applying dummy load (Φ) to the system. Once the sensitivity evaluation is completed, the material distribution is updated using a gradient based optimization algorithm. This iterative process is repeated until the design is converged.

Fig. 5
figure 5

Flowchart for strain based topology optimization for compliant mechanism design

Full size image

4 Design example

In this section, the design examples of the strain based topology optimization for complaint mechanism are presented. First, the optimal designs of the strain energy based formulation and the strain based formulation are compared and discussed using a compliant gripper example. Then, two additional examples are presented to demonstrate the proposed method. In all examples, the material properties are Young’s modulus E 0 = 100Pa, Poisson’s ratio υ = 0. 3.

4.1 Compliant gripper I

In this example, complaint gripper design problem is studied. The device is fixed at the bottom and external force is applied downward at the upper left corner as shown in Fig. 6. The design objective is to generate a compliant gripper that produces a downward motion at the lower right corner. Both the strain energy based and the strain based formulations are used, and their solutions are presented in Fig. 7. The main difference of these two solutions is on the left side of the designs. The strain energy based formulation produces a straight member below the force and the strain based formulation generates a curved member.

Fig. 6
figure 6

Design domain and boundary condition for compliant gripper I

Full size image
Fig. 7
figure 7

Optimal design: the strain energy based formulation (top), and the strain based formulation (bottom)

Full size image

To examine the impact of these two different designs, strain energy distributions of both solutions are plotted in Fig. 8. One can easily find that some localized high strain regions are found in the straight member but the strain energy is greatly reduced for the curved member. This result matches with our derivations very well.

Fig. 8
figure 8

Strain energy comparison: the strain energy based formulation (top), and the strain based formulation (bottom)

Full size image

In addition to the lower strain energy, the output displacement of the solution from the strain based method is 22 % larger than that from the strain energy based method. It is because the solution from the strain based method has larger leverage on the right side of the structure. The full gripper designs are shown in Fig. 9 again for comparison.

Fig. 9
figure 9

Full gripper design: the strain energy based formulation (left), and the strain based formulation (right)

Full size image

4.2 Compliant gripper II

The second example is another gripper design. The design domain is very similar to that of the first gripper but boundary conditions are very different as shown in Fig. 10.

Fig. 10
figure 10

Design domain and boundary condition for compliant gripper II

Full size image

The upper left corner is fixed and the bottom is only constrained in the y-direction due to the symmetric condition. The force is applied at the lower left corner toward right and the desired output displacement is a downward motion at the lower right corner.

The optimal topology configuration of the gripper problem and its deformed shape is shown in Fig. 11. The deformation configuration obviously shows that the optimal design of gripper provides proper mechanism according to the problem specifications. Strain energy of each element are also plotted to demonstrate that the strain energy is well distributed. The full gripper design is illustrated in Fig. 12.

Fig. 11
figure 11

Compliant gripper II: the optimized design (top), the deformed shape (middle), and the strain energy distribution (bottom)

Full size image
Fig. 12
figure 12

The full gripper design of example 2

Full size image

4.3 Displacement inverter

In the third example, a displacement inverter is studied. Because of the symmetric conditions, only half of the design domain is modeled. The force is applied at the upper left corner and the displacement is expected to be produced at the lower right corner towards left as shown in Fig. 13.

Fig. 13
figure 13

Design domain and boundary condition for displacement inverter

Full size image

The optimized design and its deformed shape with strain energy distribution are illustrated in Fig. 14. Once again, the strain is well distributed as we expected. From the deformation figure, it is clear that the deformation of the optimal design can afford displacement inversion motion when force is applied to downward direction at left top corner. The strain energy distribution plot also shows that the optimal design using strain based formulation does not have high concentrated strain energy. The full inverter is shown in Fig. 15.

Fig. 14
figure 14

Displacement inverter: the optimized design (top), the deformed shape (middle), and the strain energy distribution (bottom)

Full size image
Fig. 15
figure 15

Displacement inverter optimization design for full design domain

Full size image

5 Conclusion

In this paper, the strain based topology optimization method for compliant mechanism is presented. Instead of the strain energy used in common topology optimization formulation, a global effective strain functional is implemented for maximizing the rigidity of compliant mechanism design. This new formulation can reduce localized high strain in compliant joints generated by the strain energy based formulation. Drawbacks from the weighted sum and the fraction methods are eliminated by the implementations of the physical programming method. Numerical examples further demonstrated the advantages of the proposed method for compliant mechanism design.