1 Introduction

At present, the reduction factor of uplift pressure at the drainage curtain is adopted in the design to reflect the effect of the curtain grouting on seepage pressure on the foundation plane (Qi 1997). By means of this empirical factor, only the whole effect of curtain grouting and drainage curtain is reflected comprehensively (Mao 2003). The quantitative effect of permeability coefficient, thickness and depth of the curtain grouting on seepage pressure on foundation plane is not taken into account (Chai et al. 2005a). Based on the one-dimensional seepage theory, the effect of curtain grouting on seepage pressure on foundation will be analyzed in this paper and the theory of the optimum thickness of curtain grouting is proposed from the viewpoint of the minimum seepage pressure resultant and proved by the two-dimensional seepage model and the finite element method, which includes two cases of homogenous foundation and layered foundation.

Most optimization problems can be formulated as a formal mathematical problem of the form min f(x) subject to g(x) < 0 (Piermatei Filho and Leontiev 2009; Akbari et al. 2010; Fuchs and Shemesh 2004; Zhang et al. 2008). But in this paper, we propose the optimum thickness of curtain grouting on dam foundation from the viewpoint of the minimum seepage pressure resultant (min f(x)) by equating the first derivative to zero, the constraint conditions g(x) < 0 (various parameters of curtain grouting) will be meet by engineering experiences.

2 Effect of the curtain grouting on seepage pressure on the foundation plane

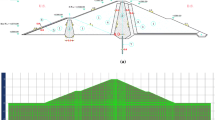
The sketch of a dam foundation with a complete curtain grouting is shown as Fig. 1a, and the symbols and notations are given in Table 1.

Fig. 1
figure 1

Complete curtain grouting. a Complete curtain grouting. b Hydrostatic seepage pressure distribution on foundation plane

Full size image
Table 1 The symbols and notations
Full size table

The flow in differential depth dz, which is close to the foundation plane, is assumed to be one-dimensional in order to obtain the seepage velocity and unit discharge directly by Darcy’s law.

The unit seepage discharge q 1 through AB is

$$ \label{eq1} q_{^1} =\emph{v}_{^1} \cdot dz=kJ_1 dz=k\frac{H-H_1 }{a_1 }dz $$
(1)

where \(\emph{v}_{1}\) and J 1 are the seepage velocity and hydraulic gradient of AB, respectively.

We can obtain the unit discharge q 2 and q 3 through BC and CD, respectively, by the same theory as follows,

$$ q_2 = \emph{v}_2 \cdot dz=k_g J_2 dz=k_g \frac{H_1 -H_2 }{t}dz \label{eq2} $$
(2)
$$ \label{eq3} q_3 = \emph{v}_3 \cdot dz=kJ_3 dz=k\frac{H_2 }{a_2 }dz $$
(3)

where \(\emph{v}_{2}\) and J 2 are the seepage velocity and hydraulic gradient of BC, respectively; \(\emph{v}_{3}\) and J 3 are the seepage velocity and hydraulic gradient of CD, respectively.

From the continuity of fluid flow we have

$$ \label{eq4} q_1 =q_2 =q_3 $$
(4)

From (1–3) and (4), we have the following equations

$$ \label{eq5} \left\{ {\begin{array}{l} k\dfrac{H-H_1 }{a_1 }dz=k_g \dfrac{H_1 -H_2 }{t}dz \\[12pt] k_g \dfrac{H_1 -H_2 }{t}dz=k\dfrac{H_2 }{a_2 }dz \\ \end{array}} \right. $$
(5)

Since H 1 and H 2 are unknown, the equations may be solved as follows.

$$ \label{eq6} \left\{ {\begin{array}{l} H_1 =\dfrac{\frac{k}{k_g }t+a_2 }{\frac{k}{k_g }t+a_1 +a_2 }H \\[12pt] H_2 =\dfrac{a_2 }{\frac{k}{k_g }t+a_1 +a_2 }H \\ \end{array}} \right. $$
(6)

which quantitatively reflects the effect of the thickness of curtain grouting t and permeability coefficient k g of curtain on head distribution of the foundation plane. From (6), the equivalent seepage travel length of curtain is approximately equal to \(\frac{k}{k_g }\) times the actual thickness of curtain t via similar triangles.

The total head h at any point in the seepage field is composed of the pressure head \(( {\frac{p}{\gamma }})\), elevation head z and velocity head \(( {\frac{a\emph{v}^2}{2g}} )\), that is (Chai et al. 1996),

$$ \label{eq7} h=\frac{p}{\gamma }+z+\frac{a\emph{v}^2}{2g} $$
(7)

where p is the seepage pressure, γ is the gravity density of water, z is the vertical ordinate, \(\emph{v}\) is the seepage velocity, a is the velocity head modification coefficient, and g is the gravity acceleration.

In general, the seepage velocity \(\emph{v}\) is very small and \(\frac{a\emph{v}^2}{2g}\) is so much smaller that it can be neglected. On the foundation plane the elevation head z = 0. So, the seepage pressure on foundation plane p can be expressed as follows.

$$ \label{eq8} p=\gamma h $$
(8)

Therefore the seepage pressure distribution in the case of the complete curtain grouting can be obtained as shown in Fig. 1b. The seepage pressure p 1 and p 2 at the upstream and downstream curtain face can be expressed as follows.

$$ \label{eq9} \left\{ {\begin{array}{l} p_1 =\dfrac{\frac{k}{k_g }t+a_2 }{\frac{k}{k_g }t+a_1 +a_2 }H\gamma =\dfrac{L+\left[ {\frac{k}{k_g }-1} \right]t-a_1 }{L+\left[ {\frac{k}{k_g }-1} \right]t}H\gamma \\[20pt] p_2 =\dfrac{a_2 }{\frac{k}{k_g }t+a_1 +a_2 }H\gamma =\dfrac{L-a_1 -t}{L+\left[ {\frac{k}{k_g }-1} \right]t}H\gamma \\ \end{array}} \right. $$
(9)

We can see that p 1 increases and approaches to Hγ and p 2 reduces and approaches to zero when \(\frac{k}{k_g}\) increases gradually or the permeability coefficient k g of curtain grouting decreases gradually.

According to (9) and Fig. 1b, we can get the resultant force P (the area of the map 1(b)) of seepage pressure within unit width of dam foundation as follows.

$$ \begin{array}{rll} \label{eq10} P&=&\frac{a_1 }{2}\left( {\gamma H+p_1 } \right)+\frac{t}{2}\left( {p_1 +p_2 } \right)+\frac{a_2 }{2}p_2\\ &=&\frac{\gamma H}{2}\cdot \frac{t^2+2a_1 t+\beta L^2}{t+\beta L} \end{array} $$
(10)

in which

$$ \label{eq11} \beta =\left[ {\frac{k}{k_g }-1} \right]^{-1} $$
(11)

Now we analyze the effect of a 1, k g and t on P, respectively.

  1. (1)

    From (10), P will increase correspondingly while a 1 increases. When a 1 = 0, the value of P is minimum. But in engineering practice, the curtain grouting cannot begin from heel due to the limits of the construction conditions and so on. So it is better to make a 1 as small as possible in order to reduce the seepage pressure resultant P.

  2. (2)

    Taking P differentiating with respect to β, we have

    $$ \label{eq12} \frac{\partial P}{\partial \beta }=\frac{\gamma H}{2}\cdot \frac{Lt\left( {L-t-2a_1 } \right)}{\left( {t+\beta L} \right)^2}=\frac{\gamma H}{2}\cdot \frac{Lt\left( {a_2 -a_1 } \right)}{\left( {t+\beta L} \right)^2} $$
    (12)

Generally, a 2 > a 1, so \(\frac{\partial P}{\partial \beta }>0\) and P reduces if β reduces. That is to say, β and total seepage pressure resultant P reduces while k g reduces and the value of \(\frac{k}{k_g }\) increases.

  1. (3)

    Taking P differentiating with respect to t, we have

$$ \label{eq13} \frac{\partial P}{\partial t}=\frac{\gamma H}{2}\cdot \frac{t^2+2\beta Lt+\left( {2\beta La_1 -\beta L^2} \right)}{\left( {t+\beta L} \right)^2} $$
(13)

We can see from the above equation that when \(t<\left[ {\sqrt {\beta^{_2 }+\beta -2\beta \frac{a_1 }{L}} -\beta } \right]L\), \(\frac{\partial P}{\partial t}<0\), so the seepage pressure resultant P decreases with the thickness of curtain grouting t increasing. But \(\frac{\partial P}{\partial t}>0\) in the case of \(t>\left[ {\sqrt {\beta^{_2 }+\beta -2\beta \frac{a_1 }{L}} -\beta } \right]L\), so the seepage pressure resultant P increases with the thickness of curtain grouting t increasing. Therefore, the thickness of grouting can not be increased infinitely. In theory, the optimum thickness of grouting t opt can be given as follows.

$$ \label{eq14} t_{opt} =\left[ {\sqrt {\beta^{_2 }+\beta -2\beta \frac{a_1 }{L}} -\beta } \right]L $$
(14)

The corresponding minimum seepage pressure resultant \(P_{\rm min}\) is

$$ \begin{array}{rll} \label{eq15} P_{\min } &=&\gamma HL\left[ {\sqrt {\beta^{_2 }+\beta -2\beta \frac{a_1 }{L}} +\frac{a_1 }{L}-\beta } \right]\nonumber\\&=&\gamma Ht_{opt} +\gamma Ha_1 \end{array} $$
(15)

The optimum thickness of curtain grouting t opt and the corresponding minimum seepage pressure resultant P min are calculated and listed in Table 2 for several cases.

Table 2 The optimum thickness of curtain grouting
Full size table

3 Example and validation

The two-dimensional computational model for calculation example is shown as Fig. 2. In the case of complete curtain grouting, the above model is calculated by two-dimensional finite element method. The dam foundation (seepage area) is divided into 20×20 = 400 elements and 21×21 = 441 nodes. The one-dimensional seepage model theory is verified by two-dimensional finite element method (Chai and Deng 2004; Chai and Li 2004; Chai et al. 2004, 2005b; Piermatei Filho and Leontiev 2009; Akbari et al. 2010; Fuchs and Shemesh 2004; Zhang et al. 2008). The solutions of seepage pressure distribution and the resultant force by two methods are listed in Table 3 under four different cases with different k/k g and t.

Fig. 2
figure 2

The computation model and FE mesh of the example

Full size image
Table 3 The seepage pressure distribution and the resultant force on homogenous foundation
Full size table

It can be seen from Table 3 that the result has a small error and the same law of seepage pressure distribution and resultant force, comparing one-dimensional seepage model with two-dimensional finite element method. Comparing case 1 with case 2, we can see that the seepage pressure resultant P reduces when the thickness of curtain t increases from 0.1L to 0.2L, which is because the optimum thickness t opt is 0.207L under these two cases, P reduces with t arising when t < t opt. Comparing case 3 with case 4, P increases when t increases from 0.1L to 0.2L, which is because t opt is 0.080L under these two cases, P increases with t arising when t > t opt. This indicates the rationality of the optimum thickness theory of curtain grouting from the viewpoint of the minimum seepage pressure resultant.

In addition, comparing case 1 with case 3, and comparing case 2 with case 4, we can know that the total seepage pressure P reduces with k/k g increasing, which also supports the above conclusion.

4 Discussions about the layered foundation

The above discussions are all about simple and homogeneous foundations, but in reality most foundations are layered. The theory of OPTIMUM thickness of curtain grouting based on the one-dimensional theory for a homogeneous case could not apply directly to the multi-layer scenario. Here we show the error and effectivity of the theory of OPTIMUM thickness of curtain grouting in case of the multi-layer scenario. Now we assume that the foundation of the computation model (in Fig. 2) is divided into four layers averagely, and that k 1, k 2, k 3, k 4 are the permeability coefficients of four layers, respectively, from up to down. By the one-dimensional theory and two-dimensional finite element method, we can get the calculating results as Table 4.

Table 4 Seepage pressure distribution and resultant force on layered foundation
Full size table

We can see from Table 4 that the permeability of layered foundation has certain effect on seepage pressure. The seepage pressure mainly depends upon the permeability of the top layer. Comparing case 1 with case 3, and case 2 with case 4, it can be seen that the theory of the optimum thickness of curtain grouting on dam foundation is also effective from the viewpoint of the minimum seepage pressure resultant.

5 Conclusions

In this paper we analyze the seepage pressure on the foundation plane with curtain grouting by the one-dimensional theory and propose the optimum thickness of curtain grouting from the viewpoint of the minimum seepage pressure resultant and proved by the two-dimensional seepage model and the finite element method, which includes two cases of homogenous foundation and layered foundation. In engineering practice, it is better to make the distance from curtain grouting to the heel of dam as near as possible (to make a 1 minimum), to make the highest quality of the curtain grouting (to make k g minimum), and to make the thickness of curtain grouting near the optimum thickness t opt, so that the seepage pressure resultant can be minimized. The conclusions have an important value for engineering design of the curtain grouting on dam foundation.