Analytical and numerical solutions for a reliability-based benchmark example

Abstract

The aim of this elementary reliability-based truss topology example is to serve as a benchmark for checking on the validity, accuracy and convergence of FE-based numerical topology optimization methods. The above problem has been solved analytically by using an extension of the optimal layout theory (Prager and Rozvany) and the solution has been verified numerically by a first order reliability approach (FORM) combined with a material distribution method (SIMP).

1 Introduction

It is well known that the optimal topology of perforated plates in plane stress and bending, respectively, tends to that of trusses and grillages, if the volume fraction of the plates approaches zero (e. g. Rozvany et al. 1985, 1987; Bendsoe and Haber 1993; Allaire and Kohn 1993). This property is often used for verifying the validity, accuracy and convergence of numerical topology optimization methods by a comparison with reliable benchmarks in the form of exact analytical truss or grillage solutions.

A good truss benchmark example may involve a relatively simple layout, although the corresponding numerical perforated plate model is usually much more complicated, involving many thousand elements. The goal of this paper is to derive a reliable, analytical benchmark problem for probabilistic or also called reliability-based topology optimization (RBTO) where the geometry, material, and material properties are uncertain and can be described via a probabilistic stochastic model. Benchmark problems for this class of topology optimization are particularly important, because for this problem class exact solutions have not existed to the authors’ knowledge and the necessary approximations used in numerical methods may lead to large errors.

Whilst the present example is very simple, involving only one probabilistic variable, extensions to more challenging problems will be attempted in the future.

The problem studied in this paper was solved analytically by the first author already in 2007, and the results briefly presented at two international conferences (Rozvany 2008a, b). The first author has shown that the proposed symmetric two-bar topology is optimal considering all possible topologies. In this paper we show that the same results are obtained by first order reliability method (FORM) assuming a priori a two-bar truss topology. Furthermore we demonstrate that integrating FORM into material-based topology optimization (Maute and Frangopol 2003) leads to numerical results with layout and geometry (i. e. bar orientations) similar to that derived analytically. Comparable results have been obtained numerically by Silva et al. (2010).

2 Problem statement

The general form of the considered problem class is as follows.

$$ \min V=\sum\limits_i {A_i L_i } , $$

(1)

subject to

$$ \Pr \left[ {C\le K} \right]\ge R, $$

(2)

$$ C=\sum\limits_i {\frac{F_i^2 L_i }{A_i E_i }} , $$

(3)

where V = truss volume, A _i = cross-sectional area of member i, L _i = length of member i, Pr = probability, C = total compliance, K = limiting value of total compliance, R = limiting value of probability, F _i = force in member i and E _i = Young’s modulus of member i. We may add that a compliance constraint may not be very meaningful in terms of real world design requirements, but it is useful in benchmark problems for checking on various methods.

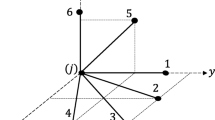
The particular example considered in this paper is shown in Fig. 1a. The topology of a truss is to be optimized within the design domain ABDG with potential supports along AB, subject to a non-random vertical load of V = 300 and a random horizontal load H, with a mean of zero and a normal distribution having a standard deviation of σ = 100. The truss volume is to be minimized for the conditions in (1)–(3). It will be shown that the solution for the considered problem is a symmetric two bar truss (as shown in Fig. 1b). For simplicity, we assign a unit value to Young’s modulus.

Fig. 1

Elementary benchmark example

3 Analytical derivation of the optimal topology by means of the optimal layout theory

It is important to note that the proposed procedure, based on an extension (Rozvany 1992) of the optimal layout theory (Prager and Rozvany 1977), selects the optimal one out of an infinite number of possible topologies, using sufficient conditions for optimality. It does not assume a priori that the optimal topology is a two-bar system.

We can use this truss layout for checking on a perforated plate solution from a numerical, FE-based method (e. g. SIMP, Bendsoe 1989; Zhou and Rozvany 1991). In the latter the topology will appear with jagged boundaries (see checkered part of Fig. 1b), which require postprocessing.

3.1 Reformulation of the problem for the optimal layout theory

Since this problem is symmetric in the only random variable (H), condition (2) is fulfilled if we consider the range of values for the random variable:

$$ -H_0 \le H\le H_0 , $$

(4)

where the value H ₀ can be calculated from the inverse normal distribution cumulative probability function (also called “quantile” or “probit”) function Φ^− 1 and R in (2):

$$ H_0 /\sigma =\Phi ^{-1}\left( {\frac{1+R}{2}} \right). $$

(5)

In (5), (1 + R)/2 is used, since the failure may occur at both ends of the interval of (4). This implies (see Fig. 2)

$$ \begin{array}{rll} R&=&\Phi (\mu +H_0 /\sigma )-\Phi (\mu -H_0 /\sigma )\\ &=&\Phi (\mu +H_0 /\sigma )-(1-\Phi (\mu +H_0 /\sigma ))\\ &=&2\Phi (\mu +H_0 /\sigma )-1 \end{array} $$

(6)

from which with μ = 0 follows (5).

Fig. 2

Reason for relations (5) and (6)

For example, if we require a probability of R = 0.9999 (failure probability of PF = 10^− 4), then we have Φ^− 1((1 + 0.9999)/2) = 3.89 and hence

$$ H_0 =3.89\sigma =389 $$

(7)

in (4). This means that we can now consider an infinite number of alternative loading cases for the range of H-values in (4) in deterministic design, and for that problem optimality criteria are available in extended versions (e. g. Rozvany 1992) of the Prager-Rozvany optimal layout theory (Prager and Rozvany 1977).

3.2 Proof that only the load condition |H| = H ₀ can be active in the reformulated problem

Considering the loads and member directions in Fig. 1, we have from equilibrium

$$ \begin{array}{rll} \sum_i F_i^2 &=&\left( \frac{V}{2\cos \alpha }+\frac{H}{2\sin \alpha } \right)^{2} +\left( \frac{V}{2\cos \alpha }-\frac{H}{2\sin \alpha } \right)^2\\ &=&\frac{V^2}{2\cos ^2\alpha }+\frac{H^2}{2\sin ^{2}\alpha }. \end{array} $$

(8)

This implies that for a given truss layout an increase in the absolute value of H always causes an increase in the value of the compliance C in (3). Hence only the load conditions with

$$ H=\pm H_0 $$

(9)

can be active for the worst compliance case.

3.3 Derivation of global optimal topology on the basis of the Prager and Rozvany (1977) layout theory

For a globally optimal volume and any number of load conditions with a compliance constraint, sufficient conditions in the paper by Rozvany (1992) reduce to the following static-kinematic optimality criteria (see also Rozvany et al. 1993).

The “real” strains for members with non-zero cross section are given by

$$ \varepsilon _{ik} =\frac{F_{ik} }{A_i E_i }, $$

(10)

where k denotes a load condition.

For global optimality, these real strains along truss members must be embedded over the design domain in a plane strain fields termed “adjoint” strain fields, such that

$$ \begin{array}{rll} (\mbox{for}\;A_i >0)\;E_i \sum\limits_i \upsilon _k \varepsilon _{ik}^2 &=&1,\\ (\mbox{for}\;A_i =0)\;E_i \sum\limits_k \upsilon _k \varepsilon _{ik}^2 &\le& 1 . \end{array} $$

(11)

Moreover, the Lagrange multiplier υ _k must be zero,

$$ \upsilon _k =0 $$

(12)

for any inactive load condition (for which the compliance is smaller than its limiting value). This means that the Lagrange multiplier is nonzero only for the two biggest loads with H = ±H ₀. The second condition under (11) refers to any line element in the design domain, along which there is no truss member.

It is shown in the paper by Rozvany et al. (1993), that the above global optimality conditions are fulfilled for the considered skew symmetric problem by a two-bar truss with the bar orientation

$$ \alpha _{opt} =\arctan \sqrt {\left( {\sqrt {\tan ^4\beta +8\tan ^2\beta } -\tan ^2\beta } \right)\Big/4} , $$

(13)

where β is the angle between the vertical and the resultant of H and V (see Fig. 1a). The relation in (13) is shown graphically in Fig. 3.

Fig. 3

The relation between the angle of the critical load (β) and the optimal bar angle (α)

The optimal volume of the truss is given by (Rozvany et al. 1993)

$$ V_{opt} =\frac{L^2P^2}{CE\cos ^2\alpha }\left( {\frac{\cos ^2\beta }{\cos ^2\alpha }+\frac{\sin ^2\beta }{\sin ^2\alpha }} \right), $$

(14)

where L is the distance of the load H from the horizontal support and P is the magnitude of the resultant of H and V.

3.4 Check on optimality by other methods

In addition to global proof via layout theory, in this rather remarkable paper (Rozvany et al. 1993) optimality of the solutions was also checked by the co-authors (Zhou and Birker) numerically by using a dense grid of potential truss members and by optimizing a perforated plate by means of SIMP (Bendsoe 1989, Zhou and Rozvany 1991). Also, for the given topology (two-bar truss), the optimal angle was derived from the Kuhn-Tucker condition. All solutions derived by three different authors have shown a complete agreement. For this reason, “reliability” of the above analytical solutions is fairly high.

3.5 Example

Let us assume a probability value of R = 0.9973. Then, as in Section 2, we have by (5)

$$ \Phi ^{-1}((1+0.9973)/2)=H_0 /\sigma =3.0. $$

(15)

For this case we have V = H = H ₀ = 300 and then for β = 45° the relation (12) gives α = 35.264° and a non-dimensional volume of 3.375. Both can be used for verifying results by FE-based numerical probabilistic topology optimization methods.

3.6 Extensions to nonzero mean values

For the time being, this will be illustrated only by a trivially simple example. Consider again the problem in Fig. 1a, but with H = 0, and a random vertical force V with normal distribution having a mean value of μ = 200 and a standard deviation of σ = 100. Let us calculate the probability value associated with a maximum vertical load of V = 300 = μ + σ.

Firstly, the optimal topology for the considered vertical load is extremely simple, (see Fig. 4), it is actually a special case of the one in Fig. 1, for β = 0. Since in this example the mean value is nonzero, we do not have both failures at the same distance from the center of the probability distribution (as in Section 6). For an upward load we reach the same compliance at V = − 300 = μ − 5σ. The corresponding probability is:

$$ \begin{array}{rll} R&=&\Phi (1)-\Phi (-5)=0.841344745-0.000000287 \\&=&0.841344458. \end{array} $$

(16)

It will be seen that the critical upward load has very little effect on the probability (only in the seventh digit).

Fig. 4

Simple topology optimization problem with non-zero mean value for the load

For the above problem with the probability in (16), the vertical load V = 300 and a given compliance (C), we get the cross sectional area

$$ A=\frac{9L}{EC} $$

(17)

A general expression for calculating the probability for any limit V ₀ on the vertical load

$$ R=\Phi ((V_0 -\mu )/\sigma )-\Phi (-(V_0 +\mu )/\sigma )), $$

(18)

which gives the result in (16). If we neglect the often very small second term in (18), then we get

$$ V_0 =(\Phi ^{-1}(R)+\mu )\sigma . $$

(19)

4 Analytical reliability-based optimization considering a priori a two-bar truss topology

Here we solve the layout problem of Fig. 1 by integrating the probabilistic compliance constraint via the first order reliability method. This approach leads to the identical result as the layout theory presented above but it assumes a priori that the solution is a two-bar truss of unknown inclination α. While less general than the layout theory, we present this approach as it is based on the same formulation as the majority of numerical methods for solving probabilistic topology optimization problem (see Section 5). Further we note that for the present problem with only one random variable FORM predicts exactly the probability of failure (Fig. 5).

Fig. 5

Contour lines of objective (thin colored lines) and constraint F = 0 (bold black line) for varying $\bar {K}$ (first row) for $\bar {\mu }=0$ and $\bar {\sigma }=1/3$, and varying $\bar {\sigma }$ (second row) for $\bar {K}=20$ and $\bar {\mu }=0$

We restate the optimization problem (1)–(3) for a two-bar truss topology as follows:

$$ \begin{array}{lll} &&\mathop {\min }\limits_{\lambda ,\alpha } \;\frac{2\;L\;A_{\max } \;\lambda }{\cos (\alpha )} \\ &&s.t.\;\;P(C\le K)\ge R \\ &&\quad \;\;0\le \lambda \le 1\;;\quad 0<\alpha <\frac{\pi }{2} \end{array} $$

(20)

where the cross-sectional area is defined as: A = A _max λ. Note the length the truss is L/cos(α). For a two-bar truss the compliance C is:

$$ C=\frac{L}{2\;E\;A_{\max } \;\lambda \;\cos (\alpha )}\left( {\frac{V^2}{\cos ^2(\alpha )}+\frac{H^2}{\sin ^2(\alpha )}} \right) $$

(21)

where the vertical load V is deterministic and the horizontal load H is Gaussian, i.e. H = N(μ,σ).

The optimization problem can be re-written as follows:

$$ \begin{array}{lll} &&\mathop {\min }\limits_{\lambda ,\alpha } \;\frac{\lambda }{\cos (\alpha )} \\ &&s.t.\;\;P(F\le 0)\le 1-R \\ &&\quad \;\;0\le \lambda \le 1\;;\;0<\alpha <\frac{\pi }{2} \end{array} $$

(22)

where the failure criterion F is defined as:

$$ \begin{array}{rll} F&=&K-C=\underbrace {\frac{2\;E\;K\;A_{\max } }{V^2L}}_{\bar {K}}\\&&-\,\frac{1}{\lambda \;\cos (\alpha )}\left( {\frac{1}{\cos ^2(\alpha )}+\frac{\left( {H/V} \right)^2}{\sin ^2(\alpha )}} \right) \\ &=&\bar {K}-\frac{1}{\lambda \;\cos (\alpha )}\left( {\frac{1}{\cos ^2(\alpha )}+\frac{\bar {H}^2}{\sin ^2(\alpha )}} \right) \end{array} $$

(23)

with $\bar {H}=H/V=N(\bar {\mu },\bar {\sigma })$ with $\bar {\mu }=\mu /V,\;\bar {\sigma }=\sigma /V$. $\bar {K}$ is a non-dimensional maximum compliance and $\bar {H}$ is a non-dimensional horizontal load.

4.1 Numerical study

The nature of the problem can be studied numerically evaluating the probability of failure by Monte Carlo Simulation (MCS). Figures 6 and 7 show the contour lines of objective and constraint for R = 0.9999. The angle α is plotted on the horizontal axis and the cross-sectional area factor λ on the vertical axis. The results are based on MSC with 10⁵ samples. The plots show that the feasible domain shrinks as $\bar {K}$ decreases and the standard deviation $\bar {\mu }$ increases. The plots further suggest that the optimum angle is not affected by the value of $\bar {K}$ but by $\bar {\mu }$.

Fig. 6

Comparison of MCS and analytical evaluation of probability of failure: constraint contour for R = 0.9999 (the two curves are so close that they are indistinguishable in this plot)

Fig. 7

Contour plot of objective and constraint with optimum solution marked by red square

4.2 Analytical evaluation of probability of failure

The probability of failure P(F ≤ 0) can be evaluated analytically by determining the most probable point (MPP) of failure in the standard normal space u:

$$ \bar {H}=\bar {\mu }+\bar {\sigma }u $$

(24)

where the MPP is defined by: F(u ^∗) = 0. The failure probability is then

$$ P(F\le 0)=2\;\Phi (-u^\ast ) $$

(25)

where Φ is the cumulative distribution function of the standard normal distribution. The factor 2 in the above equations is due to the symmetry of the problem.

The MPP u ^∗ is the solution of the following problem:

$$ F=\bar {K}-\frac{1}{\lambda \;\cos (\alpha )}\left( {\frac{1}{\cos ^2(\alpha )}+\frac{\left( {\bar {\mu }+\bar {\sigma }u^\ast } \right)^2}{\sin ^2(\alpha )}} \right)=0 $$

(26)

$$ u^\ast =\frac{1}{\bar {\sigma }}\left[ {\sin (\alpha )\sqrt {\bar {K}\;\lambda \;\cos (\alpha )-\frac{1}{\cos ^2(\alpha )}} -\bar {\mu }} \right] $$

(27)

The analytical and MSC results for $\bar {\mu }=0$, $\bar {\sigma }=1/3$, and $\bar {K}=20$ are compared in Fig. 6. Note the excellent agreement between MSC and analytical prediction of the failure probability.

4.3 Analytical solution of optimization problem

The analytical solution of the MPP problem allows re-writing the optimization problem as follows:

$$ \begin{array}{lll} &&\mathop {\min }\limits_{\lambda ,\alpha } \;\frac{\lambda }{\cos (\alpha )} \\ &&s.t.\quad u^\ast \ge \Phi ^{-1}\left( {\frac{1-R}{2}} \right) \\ &&\qquad 0\le \lambda \le 1\;;\;0<\alpha <\frac{\pi }{2} \end{array} $$

(28)

Note that $\Phi ^{-1}( {\frac{1-R}{2}})=\Phi ^{-1}( {\frac{1+R}{2}} )$ (see (5)). The associated Lagrange function is:

$$ \begin{array}{rll} L(\lambda ,\alpha ,\gamma )&=&\frac{\lambda }{\cos (\alpha )}+\gamma \left[ {\Phi ^{-1}\left( {\frac{1-R}{2}} \right)-u^\ast } \right]\\ 0&\le& \lambda \le 1\;;\;\;0<\alpha <\frac{\pi }{2};\;\;0\le \gamma \end{array} $$

(29)

Substituting the expression (22) for u ^∗, the Lagrange function is:

$$ \begin{array}{rll} L(\lambda ,\alpha ,\gamma )&==&\frac{\lambda }{\cos (\alpha )}\\&&+\,\gamma \left\{ {\Omega -\sin (\alpha )\sqrt {\bar {K}\;\lambda \;\cos (\alpha )-\frac{1}{\cos ^2(\alpha )}} } \right\}\\ \end{array} $$

(30)

where Ω is defined as $\Omega =\bar {\sigma }\;\Phi ^{-1}( {\frac{1-R}{2}} )+\bar {\mu }$ and is identical to tan β (see Fig. 1 and Section 3.3).

Assuming that the constraint is active at the optimum, the optimality conditions yield the following equations:

$$ \frac{\partial L}{\partial \lambda }=0\to \gamma =\frac{2}{\bar {K}\cos ^2(\alpha )\sin (\alpha )}\sqrt {\bar {K}\lambda \;\cos (\alpha )-\frac{1}{\cos ^2(\alpha )}} $$

(31)

$$ \frac{\partial L}{\partial \alpha }=0\to \lambda =\frac{1}{\bar {K}\;\cos ^3(\alpha )\left( {\cos ^2(\alpha )-\sin ^2(\alpha )} \right)} $$

(32)

and with $\mbox{u}^\ast =\Phi ^{-1}\left( {\frac{1-R}{2}} \right)$ and (27)

$$ \lambda =\frac{1}{\bar {K}\;\cos (\alpha )}\left( {\frac{\Omega ^2}{\sin ^2(\alpha )}+\frac{1}{\cos ^2(\alpha )}} \right) $$

(33)

Combining (32) and (33) yields:

$$ \alpha =\cos ^{-1}\left( {\sqrt \vartheta } \right) $$

(34)

where ϑ is the solution of

$$ 2\left( {\Omega ^2-1} \right)\vartheta ^2+\left( {4-\Omega ^2} \right)\vartheta -2=0 $$

(35)

The solution of interest of the above equation is

$$ \vartheta =\frac{\beta ^2-4+\beta \sqrt {\beta ^2+8} }{4\left( {\beta ^2-1} \right)} $$

(36)

Accounting for the identity Ω = tanβ, one can easily show that this result is identical to the solution in (13). Also note the analytical result is in agreement with the observations made earlier in Fig. 5: the optimum angle is not a function of the allowable compliance $\bar {K}$; only the optimum cross-section depends on $\bar {K}$. The optimum angle depends on the stochastic parameters of the horizontal load and the required reliability level.

In Fig. 7 we plot the contours of the mass and mark the solution of the optimization problem for R = 0.9999, $\bar {K}=20$, $\bar {\mu }=0$ and $\bar {\sigma }=1/3$. In Figure 8 we show how the optimum angle varies with R for and $\bar {\sigma }=1/3$. Figure 11 presents the optimization results for varying the standard deviation of the horizontal load for R = 0.9999.

Fig. 8

Optimum angle in dependence of required reliability level

5 Material distribution (SIMP) based topology optimization

In this approach, the geometry of the structure is described by its material distribution in the design domain. To allow for a smooth transition between solid and void states we interpolate the material properties by SIMP. To mitigate the mesh dependency of the optimization results and checkerboarding the material distribution is parameterized via nodal densities and smoothed by a Sigmund-type filter (Sigmund and Petersson 1998).

The probabilistic design constraint is integrated into the formulation of the optimization problem via the Performance Measure approach (PMA). The reader is referred to Lee and Kwak (1987), and Tu et al. (1999), for details about PMA, and Maute and Frangopol (2003), for its integration into material-based topology optimization. Note that for the present benchmark problem with only one random variable the PMA sub-problem can be solved analytically. The topology optimization problem is solved by the Method of Moving Asymptotes (MMA) (Svanberg 1987).

The computational design domain is a 5 × 1 rectangle discretized by 240 × 48 bi-linear plane stress elements of thickness t = 1. The load is applied at the center of the upper edge; the lower edge is clamped. The Young’s modulus of the bulk material is set to E ₀ = 1, the Poisson ratio to ν = 0, and the density to ρ ₀ = 1. The vertical load is V = 100. Below we present results for a mean value of the horizontal load of $\bar {\mu }=0$ and a standard deviation of $\bar {\sigma }=1/3$. The maximum compliance is set to K = 10⁶. The optimization process is initialized with a uniform density distribution of ρ = 1/3 (Fig. 9).

Fig. 9

Optimum angle in dependence of standard deviation of horizontal load

Numerical optimization results for a range of required maximum failure probabilities PF are shown in Fig. 10 and compared with the analytical results in Fig. 11 and Table 1. In agreement with the layout theory presented in Section 3 the optimized density distributions describe a two-bar truss. The inclination angle of the bars also agrees well with the analytical results. The small differences between numerical and analytical results can be contributed to differences between the bar model and the finite element approximation of the plane stress model.

Fig. 10

Optimum material distribution for varying probabilities of failure

Fig. 11

Comparison of analytical and numerical optimization results; solid line—analytical solution; circles—material-distribution based topology optimization

Table 1 Comparison of analytical and numerical optimization results

6 Conclusions

We have introduced and analyzed a simple benchmark problem for reliability based topology optimization. The problem was solved analytically by optimal layout theory. The solution was confirmed by reliability based optimization assuming a two-bar truss topology. The analytical results were closely matched by material distribution (SIMP) based topology optimization results.