Metamodel-Based Multi-Objective Reliable Optimization for Front Structure of Electric Vehicle

Abstract

In this paper, a multi-objective reliable optimization (MORO) procedure for the front body of an electric vehicle is proposed and compared with determinate multi-objective optimization (DMOO). The energy absorption and peak crash force of the simplified vehicle model under the full-lap frontal impact condition are used as the design objectives, with the weighted sum of the basic frequency, the first-order torsional and bending frequencies of the full-size vehicle model, and the weight of the front body taken as the constraints. The thicknesses of nine components on the front body are defined as design variables, and their geometric tolerances determine the uncertainty factor. The most accurate metamodel using the polynomial response surface, kriging, and a radial basis function is selected to model four design criteria during optimization, allowing the efficiency improvement to be computed. Monte Carlo simulations are adopted to handle the probability constraints, and multi-objective particle swarm optimization is employed as the solver. The MORO results indicate reliability levels of $R = 100$%, demonstrating the significant enhancement in reliability of the front body over that given by DMOO, and reliable design schemes and proposals are provided for further study.

1 Introduction

Similar to conventional-fuel automobiles, poor body designs of electric vehicles will lead to many severe problems [1]. Consequently, structural design optimization at the body-in-white (BIW) stage is a major concern in the electric automotive industry. Of all the structural properties of the vehicle body, frontal crashworthiness has attracted the most research interest in terms of the safety consideration [2]. There are many practical metrics for evaluating a vehicle’s crashworthiness, such as the energy absorption, maximum acceleration, and maximum intrusion, although many of these conflict with one another. Therefore, to acquire the optimal crashworthiness, a multi-objective optimization (MOO) problem must be explored.

Numerous finite element method (FEM) simulations are required to evaluate the objectives and constraints in MOO problems, and these can be extremely time-consuming when using either gradient-based or evolutionary-based optimization techniques. To enhance the optimization efficiency, the widely used metamodel technique uses a set of samples determined by the design of experiment (DOE) during the FEM optimization [3]. The polynomial response surface (PRS), kriging (KRG), and radial basis function (RBF) are popular models in MOO for vehicle bodies. For instance, Liao et al. employed the PRS-based non-dominated sorting genetic algorithm II (NSGA-II) algorithm to perform MOO for vehicle body, using the weight, full-lap crashworthiness, and 40% offset frontal impact as design criteria [4]. By combining a sequential RBF-based metamodeling technique with a micro-multi-objective genetic algorithm, Chen et al. used MOO to simultaneously reduce the peak impact force in the event of a roof crash and decrease the weight of the car [5]. To maximize the absorbed energy of a bus frame under the rollover condition while ensuring as light a weight as possible, Fan et al. conducted MOO using NSGA-II [6]. Note that the types of metamodels used for structural mechanics depend greatly on the specific research objectives. Consequently, it is necessary to study the most accurate and appropriate metamodel for predicting multi-discipline response in vehicle BIW optimization.

The above-mentioned studies did not consider uncertainty factors such as the manufacturing tolerance, materials, loading conditions, or environment, resulting in considerable limitations in practical applications. In deterministic optimization, designs are often pushed to the limit, and small variations in design variables or parameters could cause the design to violate some crucial constraints. To take various uncertainties into consideration, reliable design optimization (RDO) has received increasing attention in automotive structure optimization. For example, a comparative study of multi-objective, deterministic, reliable, and robust design optimization for the crashworthiness improvement of a car’s B-pillar assembly was presented by Shetty et al. [7]. Fang et al. [8] explored multi-objective reliable optimization (MORO) for a vehicle door using Monte Carlo simulations (MCS) based on the probabilistic sufficiency factor method, metamodel technique, and multi-objective particle swarm optimization (MOPSO) algorithm. Song et al. [9] implemented RDO for an automotive knuckle component under different working conditions, where a constraint-feasible moving least-square method was adopted to model the functional inequality constraint. Shi et al. [10] developed a stochastic sensitivity analysis method to compute the sensitivities of the probabilistic response using a metamodel with MCS, where the metamodel is determined by a Bayesian metric with data uncertainty. Rais-Rohani et al. [11] optimized the shape and size of vehicle structures by examining the effects of different constraints and their associated uncertainties on the reliability and efficiency of the optimum designs for 100% or offset frontal crashes. Nevertheless, RDO for the front body structure of an electric vehicle considering multiple performance requirements and uncertainty factors has received limited attention in the literature.

In this paper, a MORO procedure for an electric vehicle’s front body structure is presented, and the effects of uncertainties in the geometric parameters of components are examined. After constructing and implementing FEM for the baseline design of an electric vehicle body structure, there is still a relatively large optimization design space in its frontal part. The crashworthiness with full-lap frontal impact of this front structure, and the effect on the basic modal frequency and lightweight property of the whole body, is investigated using deterministic multi-objective optimization (DMOO) and the corresponding MORO, with the thicknesses of nine key components taken as the design variables. MCS is employed to address the probabilistic constraints in MORO, and different metamodels are screened to select the most suitable substitute for the costly FEM. The MOPSO algorithm is adopted to generate well-distributed Pareto solutions in both DMOO and MORO.

2 Theory and Methodology

2.1 Deterministic Multi-objective Optimization

To optimize the trade-off performance in engineering, the mathematical model of DMOO is generally established as

$$\begin{aligned} \left\{ {\begin{array}{lll} \hbox {Min}&{} f(\mathbf{x})=(f_1 (\mathbf{x}),f_2 (\mathbf{x}),\ldots ,f_i (\mathbf{x})) \\ \hbox {s. t.}&{} g_j (\mathbf{x})\le 0 \\ &{}\mathbf{x}^{L}\le \mathbf{x}\le \mathbf{x}^{U} \\ &{}i=1,2,\ldots ,m \\ &{}j=1,2,\ldots ,n \\ \end{array}} \right. \end{aligned}$$

(1)

where $f_{i}(\mathbf{x})$ and $g_{j}(\mathbf{x})$ are the ith objective function and the jth constraint, respectively; x represents the vector of design variables, with superscripts L and U denoting its lower and upper bounds.

2.2 Multi-objective Reliable Optimization

Different from DMOO, MORO considers uncertainties in input parameters, i.e., optimum schemes subject to probabilistic bounds on the constraints. The resulting mathematical expression is

$$\begin{aligned} \left\{ {\begin{array}{lll} \hbox {Min}&{} f(\mathbf{x})=(f_1 (\mathbf{x}),f_2 (\mathbf{x}),\ldots ,f_i (\mathbf{x})) \\ \hbox {s. t.} &{} P(g_j (\mathbf{x})\le \hbox {0) }\ge R_j \\ &{}\mathbf{x}^{L}\le \mathbf{x}\le \mathbf{x}^{U} \\ &{}i=1,2,\ldots ,m \\ &{}j=1,2,\ldots ,n \\ \end{array}} \right. \end{aligned}$$

(2)

where P(.) is the probability evaluated for some safe region defined by $g_j (\mathbf{x})\le 0$ and $R_{j}$ is the desired reliability satisfying the functional constraint. The two main phases of MORO are reliability analysis and optimization.

2.3 Monte Carlo Simulation

As stated in Eq. (2), probabilistic constraints should be repeatedly evaluated in MORO. MCS has been widely applied in approximating the probability of a series of random process output events by randomly sampling for uncertain variables [9, 11,12,13]. The MCS procedure is composed of the following steps: (1) generating the sample set of random variables based on the probability density function; (2) constructing the mathematical model of the limit state function to ensure the failure probability of known sample points for random variables; (3) calculating the probabilistic characteristics of the structural system response after simulating for the sampling points of the random variables.

For a random process problem, several key parameters are of most concern, including the mean ($\mu )$, standard deviation ($\sigma )$, and coefficient of variation (COV). These can be calculated as

$$\begin{aligned} \left\{ \begin{array}{l} \mu =\frac{1}{N_\mathrm{t} }\sum \nolimits _{i=1}^n x _i \\ \sigma =\left[ \frac{1}{N_\mathrm{t} -1}\sum \nolimits _{i=1}^n {(x} _i -\mu )^{2}\right] ^{\frac{1}{2}} \\ CoV=\mu /\sigma \end{array}\right. \end{aligned}$$

(3)

where $x_i$ is the ith random variable and $N_\mathrm{t}$ is the total number of sampling points.

Based on the law of large numbers in statistics, the probability in Eq. (2) can be simply estimated by

$$\begin{aligned} P(g_j \hbox {(x)}\le 0)=\frac{N_\mathrm{s} }{N_\mathrm{t} } \end{aligned}$$

(4)

where $N_\mathrm{s}$ is the number of sampling points satisfying the constraint $g_j \hbox {(x)}\le 0$. Additionally, it is recommended that $N_\mathrm{t}$ should be no less than $10/[1-P(g_j (\mathbf{x})\le 0)]$ to guarantee the accuracy of the probability calculation [12]. If the failure probability is very small, $N_\mathrm{t}$ becomes very large, indicating that many simulations are needed. However, this could be infeasible for MORO, as the FEM runs can be extremely expensive. Therefore, instead of simulations based on the time-consuming true model, a metamodel could be used in the MCS technique.

2.4 Metamodel Technique

In general, direct structural optimization based on a simulation model might be inefficient or even infeasible, as iterative nonlinear FEM runs for objectives and constraints evaluation usually have an extremely high computational burden. As a model of models, a metamodel can be constructed from the relationship between the inputs, i.e., the set of design variables generated by DOE, and the outputs, i.e., the corresponding system responses, and this metamodel can be conveniently used to predict the response at other points within the design space. The metamodel technique has been widely adopted in DMOO and MORO [13]. In this paper, three types of metamodels are studied, namely PRS, KRG, and RBF.

2.4.1 PRS

The classic PRS model is the original and probably the most widely used form of metamodel in engineering design [14]. Its mathematical expression from the first to the fourth order can be formulated as

$$\begin{aligned} \left\{ {\begin{array}{l} {\tilde{y}}=\alpha +\mathop {\sum }\nolimits _{i=1}^t {\beta x_i } \\ {\tilde{y}}=\alpha +\mathop {\sum }\nolimits _{i=1}^t {\beta x_i } +\mathop {\sum }\nolimits _{i=1}^t {\gamma x_i^2 +} \mathop {\sum }\nolimits _{i=1}^t {\mathop {\sum }\nolimits _{i<j}^t {\omega x_i x_j } } \\ {\tilde{y}}=\alpha +\mathop {\sum }\nolimits _{i=1}^t {\beta x_i } +\mathop {\sum }\nolimits _{i=1}^t {\gamma x_i^2 +} \mathop {\sum }\nolimits _{i=1}^t {\mathop {\sum }\nolimits _{i<j}^t {\omega x_i x_j } } \\ \quad +\mathop {\sum }\nolimits _{i=1}^t {\varepsilon x_i^3 } \\ {\tilde{y}}=\alpha +\mathop {\sum }\nolimits _{i=1}^t {\beta x_i } +\mathop {\sum }\nolimits _{i=1}^t {\gamma x_i^2 +} \mathop {\sum }\nolimits _{i=1}^t {\mathop {\sum }\nolimits _{i<j}^t {\omega x_i x_j } } \\ \quad +\mathop {\sum }\nolimits _{i=1}^t {\varepsilon x_i^3 +\mathop {\sum }\nolimits _{i=1}^t {\theta x_i^4 } } \\ \end{array}} \right. \end{aligned}$$

(5)

where $x_{i} (i = 1, 2, {\ldots }, t)$ and ${\tilde{y}}$ represent the t-dimensional design variable vector and the approximate response, respectively; the estimated regression coefficients $\alpha$, $\beta$, $\gamma$, $\omega$, $\varepsilon$, and $\theta$ can be computed on the basis of the least-squares method. The interactions among the design variables involved in PRS are signified by $x_{i} x_{j}$, and the nonlinear characteristics of PRS are explained by their higher-order terms. PRS above the fourth order is not recommended as the enhanced accuracy is outweighed by the reduced efficiency.

2.4.2 KRG

The fundamental basis of KRG is the assumption that the model can be simulated as a realization of a Gaussian stochastic process [15, 16]. A KRG model contains a known fixed global model $f_j (\mathbf{x})$ and a local departure $Z(\mathbf{x})$ in the form

$$\begin{aligned} {\tilde{y}}=\mathop {\sum }\nolimits _{j=1}^s {\eta _j } f_j (\mathbf{x})+Z(\mathbf{x}) \end{aligned}$$

(6)

where $Z(\mathbf{x})$ is assumed to be a realization of a stochastic process with a mean of zero and a spatial correlation function expressed by

$$\begin{aligned} \hbox {cov}\left[ {Z(x_i ),Z(x_j )} \right] =\sigma ^{2}{} \mathbf{R}(x_i ,x_j ) \end{aligned}$$

(7)

where $\sigma ^{2}$ is the process variance. The correlation matrix $\mathbf{R}$ is defined by

$$\begin{aligned} \mathbf{R}(x_i ,x_j )=\hbox {exp}\left[ {-\mathop {\sum }\nolimits _{k=1}^n {\chi _k \left| {x_i^k -x_j^k } \right| ^{2}} } \right] \end{aligned}$$

(8)

where $\chi _k$ is the unknown correlation parameter used to fit KRG.

2.4.3 RBF

RBF was developed to approximate multivariate functions with highly nonlinear features [17]. There are two parts to the RBF model, namely, the m radial basis functions and n polynomial terms with weighted coefficients. The model is written as

$$\begin{aligned} {\tilde{y}}=\mathop {\sum }\nolimits _{i=1}^m {\lambda _i } \varphi (\left\| {\mathbf{x}-\mu ^{i}} \right\| )+\mathop {\sum }\nolimits _{j=1}^n {C_j } \phi _j (\mathbf{x}) \end{aligned}$$

(9)

where $\left\| {\mathbf{x}-\mu ^{i}} \right\|$ represents the Euclidean distance between the design point x and the observed input $\mu ^{i}$; $\varphi$ is the basis function; $\lambda$ is the unknown weighting factor; and $\phi _j (\mathbf{x})$ denotes the polynomial term with coefficient C.

2.4.4 Accuracy Evaluation Metrics for Metamodels

The accuracy of the results given by metamodel-based optimization is greatly affected by the model constructed. To evaluate the accuracy, the global metric of $R^{2}$ and the local metric of the relative average absolute error (RAAE) are used. These can be expressed as

$$\begin{aligned} R^{2}=1-\frac{\sum _{i=1}^q {(y_i -{\tilde{y}}_i )^{2}} }{\sum _{i=1}^q {(y_i -\bar{{y}})^{2}} },\hbox { }\hbox {RAAE}=\frac{\sum _{i=1}^q {\left| {y_i -{\tilde{y}}_i } \right| } }{\sum _{i=1}^q {\left| {y_i -\bar{{y}}} \right| } } \end{aligned}$$

(10)

where $y_{i}$ and $\tilde{y}_{i}$ are the true values and the approximated values of the ith known sampling point, respectively; $\bar{{y}}$ is the mean of $y_i$; and q is the number of samples. Generally, it is preferable for the metamodel to have a larger value of $R^{2}$ and a smaller value of RAAE.

2.5 Multi-objective Particle Swarm Optimization Algorithm

The MOPSO algorithm is an extension of conventional PSO, which has gained considerable attention for its fast convergence and well-distributed Pareto frontier [17]. MOPSO uses an external archive to save the non-dominated solutions during the search procedure, and clips these non-dominated solutions through a crowded degree algorithm. Elite individuals are finally selected from sparse regions in the external archive as the global optimal solution. The main steps in MOPSO can be summarized as:

• Step 1. Set the number of iterations as t = 0, initialize the position ($\mathbf{x}_i )$ and velocity ($\mathbf{v}_i )$ of each particle, compute the objective vector corresponding to each particle, extract the non-dominated solutions, and place them in an external archive ($\hbox {A}_i )$;

• Step 2. Determine the optimal positions of each particle ($\mathbf{p}_i )$ and the whole particle swarm ($\mathbf{p}_g )$;

• Step 3. Under the condition of ensuring the particles move about the search space, update $\mathbf{x}_i$ and $\mathbf{v}_i$ according to

  $$\begin{aligned} \left\{ \begin{array}{l} \mathbf{v}_i (t+1)=\mathbf{v}_i (t)+r_1 c_1 \left[ {\mathbf{p}_i (t)-\mathbf{x}_i (t)} \right] \\ \qquad \qquad \qquad +\,r_2 c_2 \left[ {\mathbf{p}_g (t)-\mathbf{x}_i (t)} \right] \\ \mathbf{x}_i (t+1)=\mathbf{x}_i (t)+\mathbf{v}_i (t+1) \\ \end{array}\right. \end{aligned}$$

  (11)

• Step 4. Update $\hbox {A}_i$ and $\mathbf{p}_g$ based on the newly derived non-dominated solutions;

• Step 5. Terminate the algorithm if the convergence condition is satisfied; if not, return to step 3.

3 FEM of Electric Vehicle Body-In-White

3.1 FEM Simulation for Free Modal Analysis

The baseline design for an electric vehicle’s BIW is modeled by 2D shell elements, where the material is mainly steel with linear elastic isotropic characteristics. Testing shows that 8-mm and 18-mm elements are adequate to capture the converged responses and acquire acceptable computational efficiency for parts with smaller curvature radius and more geometric features, such as front longitudinal members, and those with larger curvature radius, such as the roof. Components are assembled by the co-node technique or as 1D rigid elements. The BIW shown in Fig. 1 has 252289 2D shell elements and 3114 1D elements, giving a total weight of 196.5 kg.

Fig. 1

FEM model of the electric vehicle BIW

As an important factor in the noise, vibration, and harshness (NVH) of a vehicle, the modal features of this BIW are investigated in this study. Based on the FEM model, the natural frequencies and corresponding modal shapes are determined using the Lanczos method. Note that the first-order (basic) modal frequency of the BIW receives considerable attention, as higher values prevent any increase in internal noise, fatigue damage of structural members, and discomfort to passengers by staggering the resonance frequency with external excitations and other vehicle-mounted components. In addition, the first-order torsional and bending frequencies of BIW are often considered [2]. In this BIW baseline, the three relevant frequencies are summarized in Table 1 and their corresponding modal shapes are shown in Fig. 2. Note that the front body is sensitive to these three modalities.

Table 1 Three natural frequencies of the BIW

Fig. 2

Three modal shapes of the BIW. a Basic modal shape. b First-order torsional modal shape. c First-order bending modal shape

3.2 FEM Simulation for Crashworthiness with Full-Lap Frontal Impact

As one of the most dangerous extreme working conditions of passenger vehicles, this paper examines the 100%-overlap frontal crashworthiness. In this case, structural deformations mainly occur at the front end of the vehicle to absorb kinetic energy and reduce the force passing into the passenger compartment. A single simulation of the crash process using a detailed FEM model of the entire vehicle requires enormous computational effort and has a high risk of divergence. In view of this, only the FEM model of the front body structure is used, and other parts of the vehicle are substituted and represented by a board with a uniformly distributed mass rigidly attached to the front body [18, 19]. Thus, Blytskho–Tsay shell elements and piecewise linear plasticity material models are arranged here. The FEM model of this vehicle for 100%-overlap frontal crashworthiness analysis involves 90267 elements (see Fig. 3). An initial velocity of 50 km/h is considered, and the crash process occurs within 25 ms.

Figure 4 shows the energy variation curves in the simulation of the baseline design for this vehicle. These results demonstrate the accuracy and reliability of the simplified FEM model, because the hourglass energy to the total energy is found to be less than 5%. The simulation indicates that the total energy absorption and the maximum impact force on the rigid wall are 16.18 kJ and 421.93 kN, respectively. The deformation form of the entire front body is illustrated in Fig. 5. Note that the maximum impact force is relatively high, and there is the potential risk that the peak acceleration of the passenger compartment during a crash would be excessive. To handle this problem, the design of the front body must be optimized.

Fig. 3

FEM model of the vehicle for 100%-overlap frontal crashworthiness analysis

Fig. 4

Energy variation curves during crash

4 Optimization Design for the Front BIW

Fig. 5

Deformation form of the entire front body after crash

Fig. 6

Illustration of design variables

Table 2 Detailed information on nine design variables

Owing to its specific contribution to the comprehensive mechanical performance of the whole vehicle body, the front structure is now optimized. In the frontal crash study, it would be preferable for a higher amount of energy absorption and a lower peak impact force. In the dynamic investigation, the basic frequency ($f_\mathrm{B} )$,first-order torsional frequency ($f_\mathrm{t} )$, and first-order bending frequency ($f_\mathrm{b} )$ should be systematically improved to enhance the NVH characteristics. Consequently, the weighted sum of these three frequencies ($f_\mathrm{w} )$ is selected as a design criterion. This is calculated as

$$\begin{aligned} \begin{array}{l} f_\mathrm{w} =\omega _1 f_\mathrm{B} +\omega _2 f_\mathrm{t} +\omega _3 f_\mathrm{b} \\ \omega _1 =\omega _2 =\omega _3 =1/3 \\ \end{array} \end{aligned}$$

(12)

where $\omega _i$ denotes the weight value. Furthermore, the front body should be as light as possible to increase the mileage range. The thicknesses of nine key components on the front body are selected as design variables, and their variations are considered to be normally distributed with COV = 1%. Detailed information on these design variables is presented in Fig. 6 and Table 2.

Fig. 7

Flowchart of the proposed optimization procedure

Table 3 Accuracy assessment for different metamodels

To achieve a design scheme that satisfies the above-mentioned design criteria, the following DMOO problem is established:

$$\begin{aligned} \left\{ {\begin{array}{lll} \hbox {Min}&{}F(\mathbf{x})=(-E(\mathbf{x}),\,F_{\mathrm{max}} (\mathbf{x})) \\ \hbox {s. t. }&{}M(\mathbf{x}) \le 18.03\hbox {Kg }\\ &{}f_\mathrm{w} (\mathbf{x})\ge 30.74\hbox {Hz} \\ &{}\mathbf{x}^{L}\le \mathbf{x}\le \mathbf{x}^{U}\\ \end{array}} \right. \end{aligned}$$

(13)

where E and $F_{\mathrm{max}}$ are the energy absorption and maximum crash force, respectively; M is the total mass of this front body, and its initial value is 18.03 kg; $f_\mathrm{w}$ is the weighted-sum frequency of the entire vehicle body, as defined in Eq. (12).

By setting the reliability level of the two constraints in Eq. (13) to be 99% and introducing the uncertainties of the design variables, the mathematical MORO model for this front body can be formulated as

$$\begin{aligned} \left\{ \begin{array}{lll} \hbox {Min}&{} F(\mathbf{x})=(-E(\mathbf{x}),\,F_{\mathrm{max}} (\mathbf{x})) \\ \hbox {s.t }&{}P(M(\mathbf{x})\le 18.03\hbox {Kg})\ge 99\% \\ &{}P(f_\mathrm{w} (\mathbf{x})\ge 30.74\hbox {Hz})\ge 99\% \\ &{}\mathbf{x}^{L}\le \mathbf{x}\le \mathbf{x}^{U}\\ \end{array} \right. \end{aligned}$$

(14)

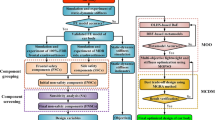
To improve the optimization efficiency, the metamodeling technique is applied using PRS, KRG, and RBF. Among these metamodels, the most accurate one will be used to predict $E(\mathbf{x})$, $F_{\mathrm{max}} (\mathbf{x})$, $M(\mathbf{x})$, and $f_\mathrm{w} (\mathbf{x})$ in the DMOO and to conduct MCS in MORO. To construct a high-accuracy metamodel, optimal Latin hypercube sampling (OLHS) is used to generate uniform training points in the design space. To capture the modal frequency and crashworthiness property with nonlinear characteristics, 50 training points are initially generated. If the accuracy of the metamodels constructed by these initial samples is unacceptable, the optimization procedure should return to the DOE step and more sampling points be generated by a max–min distance criterion. These can then be added to the sample pool to update the metamodels [20]. The MOPSO algorithm is employed as the solver for the DMOO and MORO problems. For clarification, the proposed optimization procedure is summarized as a flowchart in Fig. 7.

Fig. 8

POF of DMOO with different iterations and Knee point

Table 4 Comparison between the baseline and the knee-point plan in DMOO

5 Results and Analysis

5.1 Selection and Analysis of Metamodels

As the weight of the front structure of this BIW has a linear relationship with the thicknesses of its components, the first-order PRS is selected to model M. To evaluate the accuracy of the different metamodels, 10 extra validation points are generated at random over the whole design space by OLHS. The computational results are compared in Table 3.

From Table 3, it is clear that the third-order PRS, second-order PRS, and fourth-order PRS are the most accurate and appropriate metamodels for predicting $F_{\mathrm{max}}$, E, and $f_\mathrm{w}$, respectively, as they give the highest $R^{2}$ values in conjunction with the lowest RAAE values for each design criterion.

5.2 Results and Analysis of DMOO

The non-dominated solutions of the DMOO defined in Eq. (13) are achieved by MOPSO. Figure 8 shows the Pareto frontier (POF) obtained in the 40th, 80th, and 100th iterations of MOPSO. The results indicate that the 100th iteration provides sufficient convergence, and its POF can thus be taken as the final optimization result. Composed of 100 well-distributed solutions, the final POF is convex, signifying that there is a contradiction between the optimal E and the optimal $F_{\mathrm{max}}$. All 100 solutions on the final POF can be selected as design schemes for further decision making by engineers. Note that if better energy absorption is preferred, the schemes on the left of the final POF should be selected; if a reduction in peak crash force is more important, schemes on the right part can be used as alternatives. In this study, the knee-point scheme is used, as this gives the best trade-off among the solutions [8, 14].

Fig. 9

Comparison of POFs from MORO and DMOO

Table 5 Comparison of results from MORO and DMOO

Table 4 compares the mechanical responses of the vehicle body regarding the design criteria for the baseline design and the knee- point plan in the DMOO. Note that the optimization effect is enormous, as the relevant $F_{\mathrm{max}}$ is decreased by 37.5%, although E is degraded by $\sim$23.3%. Additionally, M and $f_\mathrm{w}$ are reduced by 14.8% and improved by 0.6%, respectively, over the baseline design. This analysis validates the accuracy of the knee-point plan, because the differences between the four design criteria and the corresponding FEM results are all within 5%. However, the knee-point plan in DMOO does not give a suitable value of $f_\mathrm{w}$: the reliability computed by MCS is only 55%, which means $f_\mathrm{w}$ has a 45% chance of being less than its baseline value (30.74 Hz). In view of this, MORO is required for this front body.

5.3 Results and Analysis of MORO

In consideration of the uncertainty from the manufacturing tolerances of the components corresponding to the nine design variables, this section considers the application of MORO for the front body. The probability evaluation for the constraints in Eq. (14) is performed by metamodel-based MCS with a MOPSO optimizer. The final POF given by MORO is contrasted with that from DMOO in Fig. 9. The POF of MORO is located to the right of the DMOO POF, demonstrating that conservative optimum results are obtained by MORO. Furthermore, these two POFs are becoming closer toward the lower right corner, which indicates a relative sacrifice in E rather than $F_{\mathrm{max}}$ to accommodate the randomness of the design variables in MORO. Therefore, Pareto solutions placed on the left half of the POF represent alternative design schemes for designers.

The optimally balanced knee-point plan is also extracted as the optimum design scheme for MORO. This is compared with that from DMOO in Table 5. To account for the uncertainty factor, E in the conservative MORO knee-point plan is further reduced to 10.58 kJ. $F_{\mathrm{max}}$ is decreased to 241.86 kN, lowering the safety risk for this vehicle in a frontal crash. After MORO, M has increased to 17.39 kg, which still has a clear margin from the boundary value of 18.03 kg. The larger values of design variables $x_{1}$ and $x_{2}$ contribute most to the increased weight of the front body, as their corresponding components are the two largest in the front assembly. Compared with the results given by DMOO, $f_\mathrm{w}$ is obviously ameliorated to 31.61 Hz, away from the design criterion of 30.74 Hz. Therefore, both M and $f_\mathrm{w}$ have reliability values in excess of the 99% target, indicating the effectiveness of the knee-point design scheme in MORO.

6 Conclusions

In this study, MORO has been applied to the front structure of an electric vehicle. An optimization model was constructed to obtain the optimal trade-off between the energy absorption and maximum impact force under full-lap frontal impact, subject to the vehicle weight and the influence of the weighted-sum frequency composed of the basic frequency, first-order torsional frequency, and first-order bending frequency of the whole BIW. The thicknesses of nine key components were taken as the design variables, with uncertainties given by geometric tolerances. The metamodel technique was used to model these design criteria during optimization, and MCS was employed to address the probabilistic constraints. The MORO problem was solved by the MOPSO algorithm. From the results, the following conclusions can be stated:

• (1) The second-order PRS, third-order PRS, and fourth-order PRS are the most appropriate metamodels for the energy absorption, maximum crash force, and weighted-sum frequency of the entire body, respectively.

• (2) The reliability of the weighted-sum frequency in the knee-point design scheme from DMOO is 55%, which is much less than the 99% design requirement.

• (3) The knee-point scheme from MORO is much more reliable and achieves an acceptable sacrifice of the overall performance of the vehicle body.