From Cryptomania to Obfustopia Through Secret-Key Functional Encryption

Abstract

Functional encryption lies at the frontiers of the current research in cryptography; some variants have been shown sufficiently powerful to yield indistinguishability obfuscation (IO), while other variants have been constructed from standard assumptions such as LWE. Indeed, most variants have been classified as belonging to either the former or the latter category. However, one mystery that has remained is the case of secret-key functional encryption with an unbounded number of keys and ciphertexts. On the one hand, this primitive is not known to imply anything outside of minicrypt, the land of secret-key cryptography, but, on the other hand, we do no know how to construct it without the heavy hammers in obfustopia. In this work, we show that (subexponentially secure) secret-key functional encryption is powerful enough to construct indistinguishability obfuscation if we additionally assume the existence of (subexponentially secure) plain public-key encryption. In other words, secret-key functional encryption provides a bridge from cryptomania to obfustopia. On the technical side, our result relies on two main components. As our first contribution, we show how to use secret-key functional encryption to get “exponentially efficient indistinguishability obfuscation” (XIO), a notion recently introduced by Lin et al. (PKC’16) as a relaxation of IO. Lin et al. show how to use XIO and the LWE assumption to build IO. As our second contribution, we improve on this result by replacing its reliance on the LWE assumption with any plain public-key encryption scheme. Lastly, we ask whether secret-key functional encryption can be used to construct public-key encryption itself and therefore take us all the way from minicrypt to obfustopia. A result of Asharov and Segev (FOCS’15) shows that this is not the case under black-box constructions, even for exponentially secure functional encryption. We show, through a non-black-box construction, that subexponentially secure-key functional encryption indeed leads to public-key encryption. The resulting public-key encryption scheme, however, is at most quasi-polynomially secure, which is insufficient to take us to obfustopia.

1 Introduction

The concept of functional encryption [21, 55] extends that of traditional encryption by allowing the distribution of functional decryption keys that reveal specified functions of encrypted messages, but nothing beyond. This concept is one of the main frontiers in cryptography today. It offers tremendous flexibility in controlling and computing on encrypted data, is strongly connected to the holy grail of program obfuscation [3, 22, 52], and for many problems, may give superior solutions to obfuscation-based ones [34, 35]. Accordingly, recent years have seen outstanding progress in the study of functional encryption, both in constructing functional encryption schemes and in exploring different notions, their power, and the relationship among them (see, for instance, [1, 2, 4, 5, 9, 12, 16, 18,19,20, 26,27,28,29, 32, 33, 37, 38, 47, 48, 58, 60] and many more).

One striking question that has yet to be solved is the gap between public-key and secret-key functional encryption schemes. In particular, does any secret-key scheme imply a public-key one?

The answer to this question is nuanced and seems to depend on certain features of functional encryption schemes, such as the number of functional decryption keys and number of ciphertexts that can be released. For functional encryption schemes that only allow the release of an a priori bounded number of functional keys (often referred to as bounded collusion), we know that the above gap is essentially the same as the gap between plain (rather than functional) secret-key encryption and public-key encryption, and should thus be as hard to bridge. Specifically, in the secret-key setting, such schemes supporting an unbounded number of ciphertexts can be constructed assuming low-depth pseudorandom generators (or just one-way functions in the single-key case) [37, 58]. These secret-key constructions are then converted to public-key ones, relying on (plain) public-key encryption (and this is done quite directly by replacing invocations of a secret-key encryption scheme with invocations of a public-key one). The same state of affairs holds when reversing the roles and considering a bounded number of ciphertexts and an unbounded number of keys [37, 58]. In other words, in the terminology of Impagliazzo’s complexity worlds [40], if the number of keys or ciphertexts is a priori bounded, then symmetric-key functional encryption lies in minicrypt, the world of one-way functions, and public-key functional encryption lies in cryptomania, the world of public-key encryption.

For functional encryption schemes supporting an unbounded (polynomial) number of keys and unbounded number of ciphertexts, which will be the default notion throughout the rest of the paper, the question is far less understood (we will often refer to such schemes as multi-key and multi-ciphertext, respectively). In the public-key setting, such functional encryption schemes with subexponential security are known to imply indistinguishability obfuscation [3, 4, 22]. In contrast, Bitansky and Vaikuntanathan [22] show that their construction of indistinguishability obfuscation using functional encryption may be insecure when instantiated with a secret-key functional encryption scheme. In fact, secret-key functional encryption schemes (even exponentially secure ones) are not known to imply any cryptographic primitive beyond those that follow from one-way functions. As far as we know, the two notions of functional encryption may correspond to opposite extremes of the complexity spectrum: on one side, public-key schemes correspond to obfustopia, the world where indistinguishability obfuscation exists, and on the other side secret-key schemes may lie in minicrypt where there is even no (plain) public-key encryption.

One piece of evidence that may support such a view of the world is given by Asharov and Segev [6] who show that there do not exist fully black-box constructions of plain public-key encryption from secret-key functional encryption, even if the latter is exponentially secure. Still, while we may hope that secret-key functional encryption schemes could be constructed from significantly weaker assumptions than needed for public-key schemes, so far no such construction has been exhibited—all known constructions live in obfustopia.

1.1 Our Contributions

In this work, we shed new light on the question of secret-key vs public-key functional encryption (in the multi-key, multi-ciphertext setting). Our main result bridges the two notions based on (plain) public-key encryption.

Theorem 1.1

(Informal) Assuming secret-key functional encryption and plain public-key encryption that are both subexponentially secure, there exists indistinguishability obfuscation, and in particular, also public-key functional encryption.

In the terminology of Impagliazzo’s complexity worlds: secret-key functional encryption would turn cryptomania, the land of public-key encryption, into obfustopia. This puts in new perspective the question of constructing such secret-key schemes from standard assumptions—any such construction would lead to indistinguishability obfuscation from standard assumptions.

The above result still does not settle the question of whether secret-key functional encryption on its own implies (plain) public-key encryption. Here, we show that assuming subexponentially secure secret-key functional encryption and (almost) exponentially secure one-way functions, there exists (polynomially secure) public-key encryption.

Theorem 1.2

(Informal) Assuming subexponentially secure secret-key functional encryption and $2^{n/\log \log n}$-secure one-way functions, there exists (polynomially secure) public-key encryption.

The resulting public-key encryption is not strong enough to take us to obfustopia. Concretely, the constructed scheme is not subexponentially secure as required by our first theorem—it can be quasi-polynomially broken. Nevertheless, the result does show that the black-box barrier shown by Asharov and Segev [6], which applies even if the underlying secret-key functional encryption scheme and one-way functions are exponentially secure, can be circumvented. Indeed, our construction uses the functional encryption scheme in a non-black-box way (see further details in A Technical Overview section below).

1.2 A Technical Overview

We now provide an overview of the main steps and ideas leading to our results.

Key observation: from SKFE to (strong) exponentially efficient IO Our first observation is that secret-key functional encryption (or SKFE in short) implies a weak form of indistinguishability obfuscators termed by Lin et al. [51] exponentially efficient indistinguishability obfuscation (XIO). Like IO, this notion preserves the functionality of obfuscated circuits and guarantees that obfuscations of circuits of the same size and functionality are indistinguishable. However, in terms of efficiency the XIO notion only requires that an obfuscation $\widetilde{C}$ of a circuit $C:\{0,1\}^{n}\rightarrow \{0,1\}^{m}$ is just mildly smaller than its truth table, namely $|\widetilde{C}|\le 2^{\gamma n}\cdot \mathrm {poly}(|C|)$, for some compression factor $\gamma < 1$, and a fixed polynomial $\mathrm {poly}$, rather than the usual requirement that the time to obfuscate, and in particular the size of $\widetilde{C}$, are polynomial in |C|. We show that SKFE implies a slightly stronger notion than XIO where the time to obfuscate C is bounded by $2^{\gamma n}\cdot \mathrm {poly}(|C|)$. We call this notion strong exponentially efficient indistinguishability obfuscation (SXIO). (We note that, for either XIO or SXIO, we shall typically be interested in circuits over some polynomial-size domain, which could be much larger than the circuit itself, e.g., $\{0,1\}^n$ where $n = 100\log |C|$.)

Proposition 1.1

(Informal)

• 1. For any constant $\gamma <1$, there exists a transformation from SKFE to SXIO with compression factor $\gamma$ (and polynomial security loss).

• 2. For some subconstant $\gamma =o(1)$, there exists a transformation from subexponentially secure SKFE to polynomially secure SXIO with compression factor $\gamma$.

We add more technical details regarding the proof of the above $\text {SXIO}$ proposition later on. Both of our theorems stated above rely on the constructed SXIO as a main tool. We next explain, still at a high-level, how the first theorem is obtained. We then dive into further technical details about the proof of this theorem as well as the proof of the second theorem.

From SXIO to IO through public-key encryption Subexponentially secure $\text {SXIO}$ (or even $\text {XIO}$) schemes with a constant compression factor (as in Proposition 1.1) are already shown to be quite strong in [51]—assuming subexponential hardness of learning with errors (LWE) [56], they imply IO.

Corollary 1.1

(of Proposition 1.1 and [51]) Assuming SKFE and LWE, both subexponentially secure, there exists IO.

We go beyond the above corollary, showing that LWE can be replaced with a generic assumption—the existence of (plain) public-key encryption schemes. The transformation of [51] from LWE and XIO to IOessentially relies on LWE to obtain a specific type of public-key functional encryption (PKFE) with certain succinctness properties. We show how to construct such PKFE from public-key encryption and SXIO. More details follow.

Concretely, the notion considered is of PKFE schemes that support a single decryption key. Furthermore, the time complexity of encryption is bounded by roughly $s^{\beta }\cdot d^{O(1)}$, where s and d are the size and depth of the circuit computing the function, and $\beta <1$ is some compression factor. We call such schemes weakly succinct PKFE schemes. A weakly succinct PKFE for boolean functions (i.e., functions with a single output bit) is constructed by Goldwasser et al. [33] from (subexponentially hard) $\text {LWE}$; in fact, the Goldwasser et al. construction has no dependence at all on the circuit size s (namely, $\beta =0$).

Lin et al. [51] then show a transformation, relying on $\text {XIO}$, that extends the class of functions also to functions with a long output, rather than just boolean ones (their transformation is stated for the case that $\beta =0$ assuming any constant XIO compression factor $\gamma <1$, but can be extended to also work for any sufficiently small constant compression factor $\beta$ for the $\text {PKFE}$). Such weakly succinct PKFE schemes can then be plugged in to the transformations of [3, 22, 52] to obtain full-fledged IO.¹

We follow a similar blueprint. We first construct weakly succinct PKFE for functions with a single output bit based on SXIO and PKE, rather than $\text {LWE}$ (much of the technical effort in this work lies in this construction). We then bootstrap the construction to deal with multi-bit functions using (a slightly augmented version of) the transformation from [51].

Proposition 1.2

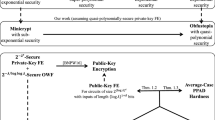
(Informal) For any $\beta =\Omega (1)$, assuming PKE and SXIO with a small enough constant compression factor $\gamma$, there exists a single-key weakly succinct PKFE scheme with compression factor $\beta$ (for functions with long output). We summarize how to construct IO from SKFE and PKE in Fig 1.

Fig. 1

An illustration of our result on IO. Dashed lines denote known results. White backgrounds denote our ingredients or goal. Primitives in rounded rectangles are subexponentially secure. t-SKFE denotes t-input SKFE. $\gamma$-SXIO denotes SXIO with compression factor $\gamma$, which is an arbitrary constant less than 1

1.3 A Closer Look into the Techniques

We now provide further details regarding the proofs of Propositions 1.1 and 1.2 as well as the proof of Theorem 1.2.

SKFE to SXIO: the basic idea To convey the basic idea behind the transformation, we first describe a construction of $\text {SXIO}$ with compression $\gamma = 1/2$. We then explain how to extend it to obtain the more general form of Proposition 1.1.

Recall that in an SKFE scheme, first a master secret key ${\textsf {MSK} }$ is generated, and can then be used to:

• encrypt (any number of) plaintext messages,

• derive (any number of) functional keys.

The constructed obfuscator $\textsf {sxi} \mathcal {O}$ is given a circuit C defined on domain $\{0,1\}^{n}$, where we shall assume for simplicity that the input length is even (this is not essential), and works as follows:

• For every $x\in \{0,1\}^{n/2}$, computes a ciphertext ${\textsf {CT} }_x$ encrypting the circuit $C_x(\cdot )$ that given input $y\in \{0,1\}^{n/2}$, returns C(x, y).

• For every $y\in \{0,1\}^{n/2}$, derives a functional decryption key ${\textsf {SK} }_y$ for the function $U_y(\cdot )$ that given as input a circuit D of size at most $\max _{x}|C_x|$, returns D(y).

• Outputs $\widetilde{C}=\left( \left\{ {\textsf {CT} }_x\right\} _{x\in \{0,1\}^{n/2}},\left\{ {\textsf {SK} }_y\right\} _{y\in \{0,1\}^{n/2}}\right)$ as the obfuscation.

To evaluate $\widetilde{C}$ on input $(x,y)\in \{0,1\}^{n}$, simply decrypt

$$\begin{aligned} {\textsf {Dec} }({\textsf {SK} }_y,{\textsf {CT} }_x) = U_y(C_x) = C_x(y) = C(x,y). \end{aligned}$$

Indeed, the required compression factor $\gamma =1/2$ is achieved. Generating each ciphertext is proportional to the size of the message $|C_x|= \tilde{O}(|C|)$ and some fixed polynomial in the security parameter $\lambda$. Similarly, the time to generate each functional key is proportional to the size of the circuit $|U_y|=\tilde{O}(|C|)$ and some fixed polynomial in the security parameter $\lambda$. Thus overall, the time to generate $\widetilde{C}$ is bounded by $2^{n/2} \cdot \mathrm {poly}(|C|,\lambda )$.

The indistinguishability guarantee follows easily from that of the underlying $\text {SKFE}$. Indeed, $\text {SKFE}$ guarantees that for any two sequences $\mathbf {m}=\left\{ m_i\right\}$ and $\mathbf {m}' = \left\{ m'_i\right\}$ of messages to be encrypted and any sequence of functions $\left\{ f_i\right\}$ for which keys are derived, encryptions of the $\mathbf {m}$ are indistinguishable from encryptions of the $\mathbf {m}'$, provided that the messages are not “separated by the functions,” i.e., $f_j(m_i) = f_j(m'_i)$ for every (i, j). In particular, any two circuits C and $C'$ that have equal size and functionality will correspond to such two sequences of messages $\left\{ C_x\right\} _{x\in \{0,1\}^{n/2}}$ and $\left\{ C'_x\right\} _{x\in \{0,1\}^{n/2}}$, whereas $\left\{ U_y\right\} _{y\in \{0,1\}^n}$ are indeed functions such that $U_y(C_x) =C(x,y)=C'(x,y) = U_y(C'_x)$ for all (x, y). (The above argument works even given a very weak selective security definition where all messages and functions are chosen by the attacker ahead of time.)

As said, the above transformation achieves compression factor $\gamma =1/2$. While such compression is sufficient, for example, to obtain IO based on LWE, it will not suffice for our two Theorems 1.1 and 1.2 (for the first we will need $\gamma$ to be a smaller constant, and for the second we will need it to even be slightly subconstant). To prove Proposition 1.1 in its more general form, we rely on a result by Brakerski et al. [16] that shows how to convert any $\text {SKFE}$ into a t-input $\text {SKFE}$. A t-input scheme allows to encrypt a tuple of messages $(m_1,\dots ,m_t)$ each independently and derive keys for t-input functions $f(m_1,\dots ,m_t)$. In their transformation, starting from a multi-key $\text {SKFE}$ results in a multi-key t-input $\text {SKFE}$.

The general transformation then follows naturally. Rather than arranging the input space in a 2-dimensional cube $\{0,1\}^{n/2}\times \{0,1\}^{n/2}$ as we did before with a 1-input scheme, given a t-input scheme we can arrange it in a $(t+1)$-dimensional cube $\{0,1\}^{n/(t+1)}\times \cdots \times \{0,1\}^{n/(t+1)}$, and we will accordingly get compression $\gamma =1/(t+1)$. The only caveat is that the BKS transformation incurs a security loss and blowup in the size of the scheme that can grow doubly exponentially in t. As long as t is constant, the security loss and blowup are fixed polynomials. The transformation can also be invoked for slightly super-constant t (double logarithmic) assuming subexponential security of the underlying 1-input SKFE (giving rise to the second part of Proposition 1.1).

We remark that previously Goldwasser et al. [27] showed that t-input SKFE for polynomial t directly gives full-fledged IO. We demonstrate that even when t is small (even constant), t-input SKFE implies a meaningful obfuscation notion such as $\text {SXIO}$.

From SXIO and PKE to weakly succinct PKFE: main ideas We now describe the main ideas behind our construction of a single-key weakly succinct PKFE. We shall focus on the main step of obtaining such a scheme for functions with a single output bit.²

Our starting point is the single-key PKFE scheme of Sahai and Seyalioglu [58] based on Yao’s garbled circuit method [61]. Their scheme basically works as follows (we assume basic familiarity with the garbled circuit method):

• The master public key $\textsf {MPK}$ consists of $L$ pairs of public keys $\left\{ \textsf {PK} _i^0,\textsf {PK} _i^1\right\} _{i\in L}$ for a (plain) public-key encryption scheme.

• A functional decryption key ${\textsf {SK} }_f$ for a function (circuit) f of size $L$ consists of the secret decryption keys $\{{\textsf {SK} }_i^{f_i}\}_{i\in L}$ corresponding to the above public keys, according to the bits of f’s description.

• To encrypt a message m, the encryptor generates a garbled circuit $\widehat{U}_m$ for the universal circuit $U_m$ that given f, returns f(m). It then encrypts the corresponding input labels $\{k_i^0,k_i^1\}_{i\in L}$ under the corresponding public keys.

• The decryptor in possession of ${\textsf {SK} }_f$ can then decrypt to obtain the labels $\{k_i^{f_i}\}_{i\in L}$ and decode the garbled circuit to obtain $U_m(f) = f(m)$.

Selective security of this scheme (where the function f and all messages are chosen ahead of time) follows from the semantic security of PKE and the garbled circuit guarantee which says that $\widehat{U}_m,\{k_i^{f_i}\}_{i\in L}$ can be simulated from f(m).

The scheme is indeed not succinct in any way. The complexity of encryption and even the size of the ciphertext grows with the complexity of f. Nevertheless, it does seem that the encryption process has a much more succinct representation. In particular, computing a garbled circuit is a decomposable process—each garbled gate in $\widehat{U}_m$ depends on a single gate in the original circuit ${U}_m$ and a small amount of randomness (for computing the labels corresponding to its wires). Furthermore, the universal circuit $U_m$ itself is also decomposable—there exists a small (say, $\mathrm {poly}(\left| m\right| ,\log L)$-sized) circuit that given i can output the i-th gate in $U_m$ along with its neighbors. The derivation of randomness itself can also be made decomposable using a pseudorandom function. All in all, there exists a small ($\mathrm {poly}(\left| m\right| ,\log L,\lambda )$-size, for security parameter $\lambda$), decomposition circuit$U_{m,K}^{\textsf {de} }$ associated with a key $K\in \{0,1\}^\lambda$ for a pseudorandom function that can produce the ith garbled gate/input-label given input i.

Yet, the second part of the encryption process, where the input labels $\{k_i^0,k_i^1\}_{i\in L}$ are encrypted under the corresponding public keys $\left\{ \textsf {PK} _i^0,\textsf {PK} _i^1\right\} _{i\in L}$, may not be decomposable at all. Indeed, in general, it is not clear how to even compress the representation of these 2L public keys. In this high-level exposition, let us make the simplifying assumption that we have at our disposal a succinct identity-based-encryption (IBE) scheme. Such a scheme has a single public-key $\textsf {PK}$ that allows to encrypt a message to an identity $\textsf {id} \in \mathcal {ID}$ taken from an identity space $\mathcal {ID}$. Those in possession of a corresponding secret key ${\textsf {SK} }_\textsf {id}$ can decrypt and others learn nothing. Succinctness means that the complexity of encryption may only grow mildly in the size of the identity space. Concretely, by a factor of $|\mathcal {ID}|^\gamma$ for some small constant $\gamma <1$. In the body, we show that such a scheme can be constructed from (plain) public-key encryption and SXIO. (The construction relies on standard “puncturing techniques” and is pretty natural, see Sect. 5.1 for more details.)

Equipped with such an IBE scheme, we can now augment the Sahai–Seyalioglu scheme to make sure that the entire encryption procedure is decomposable. Concretely, we will consider the identity space $\mathcal {ID}= [L]\times \{0,1\}$, augment the public key to only include the IBE’s public key $\textsf {PK}$, and provide the decryptor with the identity keys $\{{\textsf {SK} }_{(i,f_i)}\}_{i\in L}$. Encrypting the input labels $\{k_i^0,k_i^1\}_{i\in L}$ will now be done by simply encrypting to the corresponding identities $\{(i,0),(i,1)\}_{i\in L}$. This part of the encryption can now also be described by a small (say $L^{\gamma }\cdot \mathrm {poly}(\lambda ,\log L)$-size) decomposition circuit $E^{\textsf {de} }_{K,K',\textsf {PK} }$ that has the PRF key K to derive input labels, the IBE public key $\textsf {PK}$, and another PRF key $K'$ to derive randomness for encryption. Given an identity (i, b), it generates the corresponding encrypted input label.

At this point, a natural direction is to have the encryptor send a compressed version of the Sahai–Seyalioglu encryption, by first using $\text {SXIO}$ to shield the two decomposition circuits $E^{\textsf {de} }_{K,K',\textsf {PK} },U_{m,K}^{\textsf {de} }$ and then sending the two obfuscations. Indeed, decryption can be done just as before by first reconstructing the expanded garbled circuit and input labels and then proceeding as before. Also, in terms of encryption complexity, provided that the IBE compression factor $\gamma$ is a small enough constant, the entire encryption time will scale only sublinearly in the function’s size $|f|=L$ (i.e., with $L^{\beta }$ for some constant $\beta <1$).

The only question is of course security. It is not too hard to see that if the decomposition circuits $E^{\textsf {de} }_{K,K',\textsf {PK} },U_{m,K}^{\textsf {de} }$ are given as black boxes, then security is guaranteed just as before. The challenge is to prove security relying only on the indistinguishability guarantee of SXIO. A somewhat similar challenge is encountered in the work of Bitansky et al. [8, 13] when constructing succinct randomized encodings. In their setting, they obfuscate (using standard IO rather than SXIO) a decomposition circuit $C^{\textsf {de} }_{x,K}$ (analogous to our $U^{\textsf {de} }_{m,K}$) that computes the garbled gates of some succinctly represented long computation.

As already demonstrated in [8, 13], proving the security of such a construction is rather delicate. As in the standard setting of garbled circuits, the goal is to gradually transition through a sequence of hybrids, from a real garbled circuit (that depends on the actual computation) to a simulated garbled circuit that depends just on the result of the computation. However, unlike the standard setting of garbled circuits, here each of these hybrids should be generated by a hybrid obfuscated decomposition circuit and the attacker should not be able to tell the hybrid circuits apart.

A feature of the hybrid strategy which is crucial in this context is the amount of information that hybrid decomposition circuits need to maintain about the actual computation. Indeed, as the amount of this information grows so will the size of these decomposition circuits as will the size of the decomposition circuits in the actual construction (that will have to be equally padded to preserve indistinguishability). Accordingly, this feature affects the succinctness of the entire construction.

Bitansky et al. [8, 13] show a hybrid strategy where the amount of information scales with the space of the computation (or circuit width). Whereas in their context this is meaningful (as the aim is to save comparing to the time of the computation), in our context this is clearly insufficient. Indeed, in our case the space of the computation given by the universal circuit $U_m$ and the function f can be as large as f’s description. Instead, we invoke a different hybrid strategy by Hemenway et al. [39] that scales only with the circuit depth. Indeed, this is the cause for the polynomial dependence on depth in our single-key PKFE construction. Below, we further elaborate on the Hemenway et al. hybrid strategy and how it is imported into our setting.

Decomposable Garbling and Pebbling The work of Hemenway et al. [39] provided a useful abstraction for proving the security of Yao’s garbled circuits via a sequence of hybrid games. The goal is to transition from a “real” garbled circuit, where each garbled gate is in “$\textsf {RealGate}$” mode consisting of four ciphertexts encrypting the two labels $k_c^0,k_c^1$ of the output wire c under the labels of the input wires, to a “simulated” garbled circuit where each garbled gate is in $\textsf {SimGate}$ mode consisting of four ciphertexts that all encrypt the same dummy label $k_c^0$. As an intermediate step, we can also create a garbled gate in $\textsf {CompDepSimGate}$ mode consisting of four ciphertexts encrypting the same label $k_c^{v(c)}$ where v(c) is the value going over wire c during the computation C(x) and therefore depends on the actual computation.

The transition from a real garbled circuit to a simulated garbled circuit proceeds via a sequence of hybrids where in each subsequent hybrid we can change one gate at a time from $\textsf {RealGate}$ to $\textsf {CompDepSimGate}$ (and vice versa) if all of its predecessors are in $\textsf {CompDepSimGate}$ mode or it is an input gate, or change a gate from $\textsf {CompDepSimGate}$ mode to $\textsf {SimGate}$ mode (and vice versa) if all of its successors are in $\textsf {CompDepSimGate}$ or $\textsf {SimGate}$ modes. The goal of Hemenway et al. was to give a strategy using the least number of gates in $\textsf {CompDepSimGate}$ mode as possible.³ They abstracted this problem as a pebbling game and show that for circuits of depth d there exists a sequence of $2^{O(d)}$ hybrids with at most O(d) gates in $\textsf {CompDepSimGate}$ mode in any single hybrid.

In our case, we can give a decomposable circuit for each such hybrid game consisting of gates in $\textsf {RealGate} ,\textsf {SimGate} ,\textsf {CompDepSimGate}$ modes. In particular, the decomposable circuit takes as input a gate index and outputs the garbled gate in the correct mode. We only need to remember which gate is in which mode, and for all gates in $\textsf {CompDepSimGate}$ mode we need to remember the bit v(c) going over the wire c during the computation C(x). It turns out that the configuration of which mode each gate is in can be represented succinctly, and therefore the number of bits we need to remember is roughly proportional to the number of gates in $\textsf {CompDepSimGate}$ mode in any given hybrid. Therefore, for circuits of depth d, the decomposable circuit is of size O(d) and the number of hybrid steps is $2^{O(d)}$.

To ensure that the obfuscations of decomposable circuits corresponding to neighboring hybrids are indistinguishable, we also need to rely on standard puncturing techniques. In particular, the gates are garbled using a punctured PRF and we show that in any transition between neighboring hybrids we can even give the adversary the PRF key punctured only on the surrounding of the gate whose mode is changed.

On the Security Loss We note that our transformation from SXIO and PKE to weakly succinct PKFE only incurs a polynomial security loss when considering logarithmic depth circuits. Subexponential security of SXIO and PKE in Theorem 1.1 is required in order to use the known transformations from PKFE to IO, which require subexponential security [3, 22].

From SKFE to PKE: the basic idea We end our technical exposition by explaining the basic idea behind the construction of public-key encryption (PKE) from SKFE. The construction is rather natural. Using subexponentially secure SKFE and the second part of Proposition 1.1, we can obtain a $\mathrm {poly}(\lambda )$-secure $\text {SXIO}$ with a subconstant compression factor $\gamma =o(1)$; concretely, it can be, for example, $O(1/ \log \log \lambda )$. We can now think about this obfuscator as a plain (efficient) indistinguishability obfuscator for circuits with input length at most $\log \lambda \cdot \log \log \lambda$.

Then, we take a construction of public-key encryption from IO and one-way functions where the input size of obfuscated circuits can be scaled down at the expense of strengthening the one-way functions. For instance, following the basic witness encryption paradigm in [31], the public key can be a pseudorandom string $\textsf {PK} ={\textsf {PRG} }(s)$ for a $2^{n/\log \log n}$-secure length-doubling pseudorandom generator with seed length $n=\log \lambda \cdot \log \log \lambda$. Here, the obfuscator is only invoked for a circuit with inputs in $\{0,1\}^n$. An encryption of m is simply an obfuscation of a circuit that has $\textsf {PK}$ hardwired, and releases m only given a seed s such that $\textsf {PK} ={\textsf {PRG} }(s)$. Security follows essentially as in [31]. Note that in this construction, we cannot expect more than $2^n$ security, which is quasi-polynomial in the security parameter $\lambda$.

How does the construction circumvent the Asharov-Segev barrier? As noted earlier, Asharov and Segev [6] show that even exponentially secure $\text {SKFE}$ cannot lead to public-key encryption through a fully black-box construction (see their paper for details about the exact model). The reason that our construction does not fall under their criteria lies in the transformation from $\text {SKFE}$ to $\text {SXIO}$ with subconstant compression, and concretely in the Brakerski–Komargodski–Segev [16] transformation from $\text {SKFE}$ to t-input $\text {SKFE}$ that makes non-black-box use in the algorithms of the underlying $\text {SKFE}$ scheme.

1.4 Subsequent Works

We now mention several follow-up works, including ones that have relied on our work for new application and ones that have extended our work.

• New Transformations Several works gave different improved transformations from SKFE to IO. Komargodski and Segev [46] improved the known transformation [16] from single-input SKFE to multi-input SKFE. Via the improved transformation, they can improve the direct IO construction we described above, which avoids the reliance on public-key encryption. Starting from quasi-polynomially SKFE, they obtain IO for circuits of sub-polynomial size and inputs of polylogarithmic.

  Kitagawa et al. [44] present a simpler transformation from SKFE and public-key encryption to PKFE (and IO) than the one presented here. Then, in a follow-up work, the same set of authors [42, 43] removed the reliance on public-key encryption altogether. That is, they transform any subexponentially secure multi-key SKFE to IO for all circuits (without a restriction on their size or input length). In another follow-up work, the same set of authors [41, 43] replace multi-key SKFE with single-key weakly succinct SKFE in the transformation above by showing a transformation from any single-key weakly succinct SKFE to multi-key (succint) SKFE.

• IO from SKFE A progression of works [7, 48, 49, 53, 54] has shown how to reduce the degree of multi-linear maps required for constructing IO. In these constructions, the core ingredient is a construction of FE for low-degree polynomials, which is then bootstrapped to full-fledged FE and IO. Relying on our work, it is sufficient to construct such schemes in the secret-key setting, which allows reducing the required degree to three in the state of the art (assuming also appropriate pseudorandom generators) [49].

• Non-Trivial null XIO from Standard Assumptions Brakerski et al. [15] show that our key technique can actually be applied to existing constructions of attribute-based, or predicate, encryption. This yields non-trivial notions of exponential witness encryption (XWE) and null XIO for $\text {NC}^1$, based on standard assumptions like learning with errors.

• FE with Ideal Multi-Linear Maps Bitansky, Lin, and Paneth [17] prove that any construction of FE schemes that are succinct enough that uses constant degree multi-linear maps in a black-box way, can be transformed into a scheme based on bilinear maps. For this, they use XIO as a main component and crucially rely on the fact that our XIO construction from FE uses the underlying FE as a black box.

Organization In Sect. 2, we provide preliminaries and basic definitions used throughout the paper. In Sect. 3, we introduce the definition of SXIO and present our construction based on SKFE schemes. In Sect. 4, we review Yao’s garbled circuits and introduce a notion of decomposable garbling. In Sect. 5, we present our construction of $\text {IO}$ from PKE and SXIO. In Sect. 6, we present a polynomially secure PKE scheme from SKFE schemes.

2 Preliminaries

We review basic concepts and definitions used throughout the paper.

2.1 Standard Computational Concepts

We rely on the standard notions of Turing machines and Boolean circuits.

• We say that a (uniform) Turing machine is $\text {PPT}$ if it is probabilistic and runs in polynomial time.

• A polynomial-size (or just polysize) circuit family ${\mathcal {C}}$ is a sequence of circuits ${\mathcal {C}}=\left\{ C_\lambda \right\} _{\lambda \in \mathbb {N}}$, such that each circuit $C_\lambda$ is of polynomial size $\lambda ^{O(1)}$ and has $\lambda ^{O(1)}$ input and output bits.

• We follow the standard habit of modeling any efficient adversary strategy as a family of polynomial-size circuits. For an adversary $\mathcal {A}$ corresponding to a family of polysize circuits $\left\{ \mathcal {A}_\lambda \right\} _{\lambda \in \mathbb {N}}$, we often omit the subscript $\lambda$, when it is clear from the context.

• We say that a function $f:\mathbb {N}\rightarrow \mathbb {R}$ is negligible if for all constants $c > 0$, there exists $N \in \mathbb {N}$ such that for all $n > N$, $f(n) < n^{-c}$.

• If $\mathcal {X}^{(b)}=\{X^{(b)}_{\lambda }\}_{\lambda \in \mathbb {N}}$ for $b \in \{0,1\}$ are two ensembles of random variables indexed by $\lambda \in \mathbb {N}$, we say that $\mathcal {X}^{(0)}$ and $\mathcal {X}^{(1)}$ are computationally indistinguishable if for all polysize distinguishers $\mathcal {D}$, there exists a negligible function $\nu$ such that for all $\lambda$,

  $$\begin{aligned} \Delta&=\left| \Pr [\mathcal {D}(X^{(0)}_\lambda )=1] - \Pr [\mathcal {D}(X^{(1)}_\lambda )=1] \right| \le \nu (\lambda ). \end{aligned}$$

• We write $\mathcal {X}^{(0)} \approx _{\delta } \mathcal {X}^{(1)}$ to denote that the advantage $\Delta$ is bounded by $\delta$.

2.2 Functional Encryption

In this section, we define the different notions of functional encryption (FE) considered in this work.

Definition 2.1

(Multi-input secret-key functional encryption) Let $t(\lambda )$ be a function, $\overline{{\mathcal {M}}}=\{\overline{{\mathcal {M}}}_\lambda ={\mathcal {M}}^{(1)}_\lambda \times \cdots \times {\mathcal {M}}^{(t(\lambda ))}_\lambda \}_{\lambda \in \mathbb {N}}$ be a product message domain, ${\mathcal {Y}}=\left\{ {\mathcal {Y}}_\lambda \right\} _{\lambda \in \mathbb {N}}$ a range, and ${\mathcal {F}}=\left\{ {\mathcal {F}}_\lambda \right\} _{\lambda \in \mathbb {N}}$ a class of t-input functions $f:\overline{{\mathcal {M}}}_\lambda \rightarrow {\mathcal {Y}}_\lambda$. A t-input secret-key functional encryption (t-SKFE) scheme for ${\mathcal {M}},{\mathcal {Y}},{\mathcal {F}}$ is a tuple of algorithms $\textsf {SKFE} _t = ({\textsf {Setup} },{\textsf {KeyGen} },{\textsf {Enc} },{\textsf {Dec} })$ where:

•  ${\textsf {Setup} }(1^\lambda )$ takes as input the security parameter and outputs a master secret key ${\textsf {MSK} }$.

•  ${\textsf {KeyGen} }({\textsf {MSK} },f)$ takes as input the master secret ${\textsf {MSK} }$ and a function $f\in {\mathcal {F}}$. It outputs a secret key ${\textsf {SK} }_f$ for f.

•  ${\textsf {Enc} }({\textsf {MSK} },m,i)$ takes as input the master secret key ${\textsf {MSK} }$, a message $m\in {\mathcal {M}}^{(i)}_\lambda$, and an index $i \in [t(\lambda )]$, and outputs a ciphertext ${\textsf {CT} }_i$.

•  ${\textsf {Dec} }({\textsf {SK} }_f,{\textsf {CT} }_1,\ldots ,{\textsf {CT} }_t)$ takes as input the secret key ${\textsf {SK} }_f$ for a function $f\in {\mathcal {F}}$ and ciphertexts ${\textsf {CT} }_1,\ldots ,{\textsf {CT} }_t$, and outputs some $y\in {\mathcal {Y}}$, or $\bot$.

We also require the following property: Correctness: For all tuples $\mathbf {m} = (m_1,\ldots ,m_t)\in \overline{{\mathcal {M}}}_\lambda$ and any function $f\in {\mathcal {F}}_\lambda$, we have that

$$\begin{aligned} \Pr \left[ {\textsf {Dec} }({\textsf {SK} }_f,{\textsf {CT} }_1,\ldots ,{\textsf {CT} }_t)=f(\mathbf {m}): \begin{array}{l} {\textsf {MSK} }\leftarrow {\textsf {Setup} }(1^\lambda ),\\ {\textsf {SK} }_f\leftarrow {\textsf {KeyGen} }({\textsf {MSK} },f),\\ \forall i\ {\textsf {CT} }_i\leftarrow {\textsf {Enc} }({\textsf {MSK} },m,i) \end{array} \right] =1 \end{aligned}$$

Definition 2.2

(Selectively secure multi-key t-SKFE) We say that a tuple of algorithms $\textsf {SKFE} _t = ({\textsf {Setup} }, {\textsf {KeyGen} },{\textsf {Enc} },{\textsf {Dec} })$ is a selectively securet-input secret-key functional encryption scheme for $\overline{{\mathcal {M}}},{\mathcal {Y}},{\mathcal {F}}$, if it satisfies the following requirement, formalized by the experiment $\mathsf {Expt}^{\mathsf {SKFE_{t}}}_{{\mathcal {A}}}(1^{\lambda },b)$ between an adversary ${\mathcal {A}}$ and a challenger:

• 1. The adversary submits challenge message tuples $\left\{ (m_{i,1}^0,m_{i,1}^1,i)\right\} _{i\in [t]},\ldots ,\left\{ (m_{i,q}^0,m_{i,q}^1,i)\right\} _{i\in [t]}$ for all $i \in [t]$ to the challenger where q is an arbitrary polynomial in $\lambda$.

• 2. The challenger runs ${\textsf {MSK} }\leftarrow {\textsf {Setup} }(1^\lambda )$

• 3. The challenger generates ciphertexts ${\textsf {CT} }_{i,j}\leftarrow {\textsf {Enc} }({\textsf {MSK} },m_{i,j}^b,i)$ for all $i\in [t]$ and $j\in [q]$, and gives $\{{\textsf {CT} }_{i,j}\}_{i\in [t],j\in [q]}$ to ${\mathcal {A}}$.

• 4. ${\mathcal {A}}$ is allowed to make q function queries, where it sends a function $f_{j}\in {\mathcal {F}}$ to the challenger for $j\in [q]$ and q is an arbitrary polynomial in $\lambda$. The challenger responds with ${\textsf {SK} }_{f_j}\leftarrow {\textsf {KeyGen} }({\textsf {MSK} },f_j)$.

• 5. ${\mathcal {A}}$ outputs a guess $b'$ for b.

• 6. The output of the experiment is $b'$ if the adversary’s queries are valid:

  $$\begin{aligned} f_j(m_{1,j_1}^0,\dots ,m_{t,j_t}^0) = f_j(m_{1,j_1}^1,\dots ,m_{t,j_t}^1) \text { for all } j_1,\dots ,j_t,j \in [q]. \end{aligned}$$

  Otherwise, the output of the experiment is set to be $\bot$.

We say that the functional encryption scheme is selectively secure if, for all polysize adversaries ${\mathcal {A}}$, there exists a negligible function $\mu (\lambda )$, such that

$$\begin{aligned} \mathsf {Adv}^{\mathsf {SKFE_{t}}}_{{\mathcal {A}}} =\left| \Pr \left[ \mathsf {Expt}^{\mathsf {SKFE_{t}}}_{{\mathcal {A}}}(1^\lambda ,0)=1\right] - \Pr \left[ \mathsf {Expt}^{\mathsf {SKFE_{\text {{ t}}}}}_{{\mathcal {A}}}(1^\lambda ,1)=1\right] \right| \le \mu (\lambda ). \end{aligned}$$

We further say that $\textsf {SKFE} _t$ is $\delta$-selectively secure, for some concrete negligible function $\delta (\cdot )$, if the above indistinguishability gap $\mu (\lambda )$ is smaller than $\delta (\lambda )^{\Omega (1)}$.

We recall the following theorem by Brakerski, Komargodski, and Segev, which states that one can build selectively secure t-SKFE from any selectively secure 1-SKFE. The transformation induces a significant blowup and security loss in the number of inputs t. This loss is polynomial as long as t is constant, but in general grows doubly exponentially in t.

Theorem 2.1

([16])

• 1. For $t=O(1)$, if there exists $\delta$-selectively secure single-input SKFE for $\textsf {P} /\textsf {poly}$, then there exists $\delta$-selectively secure t-input SKFE for $\textsf {P} /\textsf {poly}$.

• 2. There exists a constant $\varepsilon <1$, such that for $t(\lambda )=\varepsilon \cdot \log \log (\lambda )$, $\tilde{\lambda } = 2^{(\log \lambda )^{\varepsilon }}$, $\delta (\tilde{\lambda }) = 2^{-\tilde{\lambda }^\varepsilon }$, if there exists $\delta$-selectively secure single-input SKFE for $\textsf {P} /\textsf {poly}$, then there exists polynomially secure selectively secure t-input SKFE for functions of size at most $2^{O((\log \lambda )^{\varepsilon })}$. (Here, $\tilde{\lambda }$ is the single-input $\text {SKFE}$ security parameter and $\lambda$ is the t-input $\text {SKFE}$ security parameter.)

Remark 2.1

(Dependence on circuit size in [16]) The [16] transformation incurs a $(s\cdot \tilde{\lambda })^{2^{O(t)}}$ blowup in parameters, where s is the size of maximal circuit size of supported functions and $\tilde{\lambda }$ is the security parameter used in the underlying single-input SKFE. In the main setting of parameters considered there, $t=O(1)$, the security parameter $\lambda$ of the t-SKFE scheme can be identified with $\tilde{\lambda }$ and s can be any polynomial in this security parameter. (Accordingly, the dependence on s is implicit there, and the blowup they address is $\lambda ^{2^{O(t)}}$.)

For the second part of the theorem, to avoid superpolynomial blowup in $\lambda$, the security parameter $\tilde{\lambda }$ for the underlying SKFE and the maximal circuit size s should be set to $2^{O((\log \lambda )^{\varepsilon })}$.

Definition 2.3

(Public-key functional encryption) Let ${\mathcal {M}}=\left\{ {\mathcal {M}}_\lambda \right\} _{\lambda \in \mathbb {N}}$ be a message domain, ${\mathcal {Y}}=\left\{ {\mathcal {Y}}_\lambda \right\} _{\lambda \in \mathbb {N}}$ a range, and ${\mathcal {F}}=\left\{ {\mathcal {F}}_\lambda \right\} _{\lambda \in \mathbb {N}}$ a class of functions $f:{\mathcal {M}}\rightarrow {\mathcal {Y}}$. A public-key functional encryption (PKFE) scheme for ${\mathcal {M}},{\mathcal {Y}},{\mathcal {F}}$ is a tuple of algorithms $\textsf {PKFE} = ({\textsf {Setup} },{\textsf {KeyGen} },{\textsf {Enc} },{\textsf {Dec} })$ where:

•  ${\textsf {Setup} }(1^\lambda )$ takes as input the security parameter and outputs a master secret key ${\textsf {MSK} }$ and master public key ${{\textsf {MPK}}}$.

•  ${\textsf {KeyGen} }({\textsf {MSK} },f)$ takes as input the master secret ${\textsf {MSK} }$ and a function $f\in {\mathcal {F}}$. It outputs a secret key ${\textsf {SK} }_f$ for f.

•  ${\textsf {Enc} }({{\textsf {MPK}}},m)$ takes as input the master public key ${{\textsf {MPK}}}$ and a message $m\in {\mathcal {M}}$, and outputs a ciphertext c.

•  ${\textsf {Dec} }({\textsf {SK} }_f,c)$ takes as input the secret key ${\textsf {SK} }_f$ for a function $f\in {\mathcal {F}}$ and a ciphertext c, and outputs some $y\in {\mathcal {Y}}$, or $\bot$.

We also require the following property: Correctness: For any message $m\in {\mathcal {M}}$ and function $f\in {\mathcal {F}}$, we have that

$$\begin{aligned} \Pr \left[ {\textsf {Dec} }({\textsf {SK} }_f,c)=f(m): \begin{array}{l} ({\textsf {MSK} },{{\textsf {MPK}}})\leftarrow {\textsf {Setup} }(1^\lambda ),\\ {\textsf {SK} }_f\leftarrow {\textsf {KeyGen} }({\textsf {MSK} },f),\\ c\leftarrow {\textsf {Enc} }({{\textsf {MPK}}},m) \end{array} \right] =1 \end{aligned}$$

Definition 2.4

(Selectively secure single-key PKFE) We say that a tuple of algorithm $\textsf {PKFE} = ({\textsf {Setup} },{\textsf {KeyGen} },{\textsf {Enc} },{\textsf {Dec} })$ is a selectively secure single-key public-key functional encryption scheme for ${\mathcal {M}},{\mathcal {Y}},{\mathcal {F}}$, if it satisfies the following requirement, formalized by the experiment $\mathsf {Expt}^{\mathsf {PKFE}}_{{\mathcal {A}}}(1^\lambda ,b)$ between an adversary ${\mathcal {A}}$ and a challenger:

• 1. ${\mathcal {A}}$ submits the message pair $m_0^*,m_1^* \in {\mathcal {M}}$ and a function f to the challenger.

• 2. The challenger runs $({\textsf {MSK} },{{\textsf {MPK}}})\leftarrow {\textsf {Setup} }(1^\lambda )$, generates ciphertext ${\textsf {CT} }^*\leftarrow {\textsf {Enc} }({{\textsf {MPK}}},m_b^*)$ and a secret key ${\textsf {SK} }_f \leftarrow {\textsf {KeyGen} }({\textsf {MSK} },f)$. The challenger gives $({{\textsf {MPK}}},{\textsf {CT} }^*,sk_f)$ to ${\mathcal {A}}$.

• 3. ${\mathcal {A}}$ outputs a guess $b'$ for b.

• 4. The output of the experiment is $b'$ if $f(m_0^*) = f(m_1^*)$ and $\bot$ otherwise.

We say that the public-key functional encryption scheme is selectively secure if, for all PPT adversaries ${\mathcal {A}}$, there exists a negligible function $\mu (\lambda )$, such that

$$\begin{aligned} \mathsf {Adv}^{\mathsf {PKFE}}_{{\mathcal {A}}} =\left| \Pr \left[ \mathsf {Expt}^{\mathsf {PKFE}}_{{\mathcal {A}}}(1^\lambda ,0)=1\right] - \Pr \left[ \mathsf {Expt}^{\mathsf {PKFE}}_{{\mathcal {A}}}(1^\lambda ,1)=1\right] \right| \le \mu (\lambda ). \end{aligned}$$

We further say that $\textsf {PKFE}$ is $\delta$-selectively secure, for some concrete negligible function $\delta (\cdot )$, if for all polysize distinguishers the above indistinguishability gap $\mu (\lambda )$ is smaller than $\delta (\lambda )^{\Omega (1)}$.

We now further define a notion of succinctness for functional encryption schemes as above. To do this, we define functional encryption for collections of classes $\varvec{\mathcal {F}} =\{\mathcal {F}= \{\mathcal {F}_\lambda \}\}$, such as $\textsf {P} /\textsf {poly}$ or $\text {NC}^1$.

Definition 2.5

(Functional Encryption for a Collection of Functions [17]) In a functional encryption scheme $\textsf {FE} = ({\textsf {Setup} },{\textsf {KeyGen} },{\textsf {Enc} },{\textsf {Dec} })$ for a collection of function classes $\varvec{\mathcal {F}} = \{\mathcal {F}= \{\mathcal {F}_\lambda \}\}$, the setup algorithm ${\textsf {Setup} }(1^\lambda ,n,s)$ takes the security parameter $1^\lambda$ and two parameters $(n(\lambda ),s(\lambda ))$ representing bounds on input length and circuit size.

For any class $\mathcal {F}= \{\mathcal {F}_\lambda \}\in \varvec{\mathcal {F}}$ with maximum input length $n(\lambda )$ and maximum circuit size $s(\lambda )$, $\textsf {FE} _\mathcal {F}= ({\textsf {Setup} }(\cdot ,n(\cdot ),s(\cdot )),{\textsf {KeyGen} },{\textsf {Enc} },{\textsf {Dec} })$ satisfies the correctness and security requirement defined above for general functional encryption schemes.

Definition 2.6

(Weakly Succinct functional encryption [17, 22]) A functional encryption scheme for a collection of function classes $\varvec{\mathcal {F}} =\{\mathcal {F}= \{\mathcal {F}_\lambda \}\}$ is weakly succinct if there exists a constant $\gamma <1$, and a fixed polynomial $\mathrm {poly}(\cdot )$, depending only on $\varvec{\mathcal {F}}$ (but not on any specific $\mathcal {F}\in \varvec{\mathcal {F}}$), such that for any class ${\mathcal {F}}= \left\{ {\mathcal {F}}_\lambda \right\} \in \varvec{\mathcal {F}}$ with

• maximum input length $n(\lambda )$,

• maximum circuit size $s(\lambda )$, and

• maximum circuit depth $d(\lambda )$,

in $\textsf {FE} _{\mathcal {F}}$, the size of the encryption circuit is bounded by $s^{\gamma }\cdot \mathrm {poly}(n,\lambda ,d)$. We call $\gamma$ the compression factor.

The following result from [22, Sections 3.1 and 3.2] states that one can construct an indistinguishability obfuscator from any single-key weakly succinct public-key functional encryption scheme.

Theorem 2.2

([22]) If there exists a subexponentially secure single-key weakly succinct PKFE scheme for $\textsf {P} /\textsf {poly}$, then there exists an indistinguishability obfuscator for $\textsf {P} /\textsf {poly}$.

2.3 Indistinguishability Obfuscation

We recall the notion of indistinguishability obfuscation (IO) [10].

Definition 2.7

(Indistinguishability obfuscator (IO)) A PPT machine $\textsf {i} \mathcal {O}$ is an indistinguishability obfuscator for a circuit class $\{\mathcal {C}_\lambda \}_{\lambda \in \mathbb {N}}$ if the following conditions are satisfied:

• Functionality for all security parameters $\lambda \in \mathbb {N}$, for all $C \in \mathcal {C}_\lambda$, for all inputs x, we have that

  $$\begin{aligned} \Pr [C'(x)=C(x) : C' \leftarrow \textsf {i} \mathcal {O}(C)] = 1. \end{aligned}$$

• Indistinguishability for any polysize distinguisher $\mathcal {D}$, there exists a negligible function $\mu (\cdot )$ such that the following holds: for all security parameters $\lambda \in \mathbb {N}$, for all pairs of circuits $C_0, C_1 \in \mathcal {C}_\lambda$ of the same size and such that $C_0(x) = C_1(x)$ for all inputs x, then

  $$\begin{aligned} \left| \Pr \big [\mathcal {D}(\textsf {i} \mathcal {O}(C_0))= 1\big ] - \Pr \big [\mathcal {D}(\textsf {i} \mathcal {O}(C_1))= 1\big ] \right| \le \mu (\lambda ). \end{aligned}$$

  We further say that $\textsf {i} \mathcal {O}$ is $\delta$-secure, for some concrete negligible function $\delta (\cdot )$, if for all polysize distinguishers the above indistinguishability gap $\mu (\lambda )$ is smaller than $\delta (\lambda )^{\Omega (1)}$.

2.4 Puncturable Pseudorandom Functions

Puncturable PRFs, defined by Sahai and Waters [59], are PRFs with a key-puncturing procedure that produces keys that allow evaluation of the PRF on all inputs, except for a designated polynomial-size set.

Definition 2.8

(Puncturable pseudorandom function) For sets $\mathcal {D},\mathcal {R}$, a puncturable pseudorandom function (PPRF) consists of a tuple of algorithms $\mathcal {PPRF}= ({\textsf {PRF.Gen} }, {\textsf {PRF.Ev} },{\textsf {PRF.Punc} })$ that satisfy the following two conditions.

• Functionality preserving under puncturing: For all polynomial-size set $S \subseteq \mathcal {D}$ and for all $x\in \mathcal {D}\setminus S$, it holds that

  $$\begin{aligned}&\Pr [{\textsf {PRF.Ev} }_{K}(x) = {\textsf {PRF.Ev} }_{K\{S\}}(x) : K \leftarrow {\textsf {PRF.Gen} }(1^{\lambda }), \\&\quad K{\{S\}} \leftarrow {\textsf {PRF.Punc} }(K,S)]=1. \end{aligned}$$

• Pseudorandom at punctured points: For all polynomial size set $S \subseteq \mathcal {D}$ with $S = \{x_1,\ldots ,x_{k(\lambda )}\}$ and any polysize distinguisher ${\mathcal {A}}$, there exists a negligible function $\mu$, such that:

  $$\begin{aligned}&\vert \Pr [{\mathcal {A}}({\textsf {PRF.Ev} }_{K\{S\}},\{{\textsf {PRF.Ev} }_{K}(x_i)\}_{i\in [k]}) = 1] \\&\quad -\Pr [{\mathcal {A}}({\textsf {PRF.Ev} }_{K\{S\}}, U^{k}) = 1] \vert \le \mu (\lambda ) \end{aligned}$$

  where $K\leftarrow {\textsf {PRF.Gen} }(1^{\lambda })$, $K{\{S\}} \leftarrow {\textsf {PRF.Punc} }(K,S)$ and U denotes the uniform distribution over $\mathcal {R}$. We further say that $\mathcal {PPRF}$ is $\delta$-secure, for some concrete negligible function $\delta (\cdot )$, if for all polysize distinguishers the above indistinguishability gap $\mu (\lambda )$ is smaller than $\delta (\lambda )^{\Omega (1)}$.

The GGM tree-based construction of PRFs [30] from one-way functions is easily seen to yield puncturable PRFs where the size of the punctured key grows polynomially with the size of the set S being punctured, as recently observed by [11, 23, 45]. Thus, we have:

Theorem 2.3

([11, 23, 30, 45]) If one-way functions exist, then for all efficiently computable functions $n(\lambda )$ and $m(\lambda )$, there exists a puncturable pseudorandom function that maps $n(\lambda )$ bits to $m(\lambda )$ bits (i.e., $\mathcal {D}=\{0,1\}^{n(\lambda )}$ and $\mathcal {R}=\{0,1\}^{m(\lambda )}$).

2.5 Public-Key Encryption

We recall the notion of plain public-key encryption (PKE).

Definition 2.9

(Plain public-key encryption) Let ${\mathcal {M}}$ be some message space. A public-key encryption (PKE) scheme for ${\mathcal {M}}$ is a tuple of algorithms $({\textsf {KeyGen} },{\textsf {Enc} },{\textsf {Dec} })$ where:

•  ${\textsf {KeyGen} }(1^\lambda )$ takes as input the security parameter and outputs a public key $\textsf {PK}$ and a secret key ${\textsf {SK} }$.

•  ${\textsf {Enc} }(\textsf {PK} ,m)$ takes as input the public key $\textsf {PK}$ and a message $m\in {\mathcal {M}}$ and outputs a ciphertext ${\textsf {CT} }$.

•  ${\textsf {Dec} }({\textsf {SK} },{\textsf {CT} })$ takes as input the secret key ${\textsf {SK} }$ and a ciphertext ${\textsf {CT} }$, and outputs some $m \in {\mathcal {M}}$, or $\bot$.

We also require the following property:

Correctness For any message $m\in {\mathcal {M}}$, we have that

$$\begin{aligned} \Pr \left[ {\textsf {Dec} }({\textsf {SK} },c)=m: \begin{array}{l} ({\textsf {SK} },\textsf {PK} )\leftarrow {\textsf {KeyGen} }(1^\lambda ),\\ {\textsf {CT} }\leftarrow {\textsf {Enc} }(\textsf {PK} ,m) \end{array} \right] =1 \end{aligned}$$

We also recall the standard notion of security.

Definition 2.10

(Secure public-key encryption) A tuple of algorithms $PKE= ({\textsf {KeyGen} },{\textsf {Enc} },{\textsf {Dec} })$ is a secure PKE for ${\mathcal {M}}$ if it satisfies the following requirement, formalized by the experiment $\mathsf {Expt}^{\mathsf {PKE}}_{{\mathcal {A}}}(1^\lambda ,b)$ between an adversary ${\mathcal {A}}$ and a challenger:

• 1. The challenger runs $({\textsf {SK} },\textsf {PK} )\leftarrow {\textsf {KeyGen} }(1^\lambda )$, and gives $\textsf {PK}$ to ${\mathcal {A}}$.

• 2. At some point, ${\mathcal {A}}$ sends two messages $m_0^*,m_1^*$ as the challenge messages to the challenger.

• 3. The challenger generates ciphertext ${\textsf {CT} }^*\leftarrow {\textsf {Enc} }(\textsf {PK} ,m_b^*)$ and sends ${\textsf {CT} }^*$ to ${\mathcal {A}}$.

• 4. ${\mathcal {A}}$ outputs a guess $b'$ for b. The experiment outputs 1 if $b'=b$, 0 otherwise.

We say the PKE scheme is secure if, for all PPT adversaries ${\mathcal {A}}$, there exists a negligible function $\mu (\lambda )$, it holds:

$$\begin{aligned} \mathsf {Adv}^{\mathsf {PKE}}_{{\mathcal {A}}} =\left| \Pr [\mathsf {Expt}^{\mathsf {PKE}}_{{\mathcal {A}}}(1^\lambda ,0)=1] - \Pr [\mathsf {Expt}^{\mathsf {PKE}}_{{\mathcal {A}}}(1^\lambda ,1)=1]\right| \le \mu (\lambda ). \end{aligned}$$

We further say that $PKE$ is $\delta$-secure, for some concrete negligible function $\delta (\cdot )$, if for all polysize distinguishers the above indistinguishability gap $\mu (\lambda )$ is smaller than $\delta (\lambda )^{\Omega (1)}$.

2.6 Succinct Identity-Based Encryption

We define identity-based encryption (IBE) [57] with a succinctness properties.

Definition 2.11

(Succinct IBE with$\gamma$-compression) Let ${\mathcal {M}}$ be some message space and $\mathcal {ID}$ be an identity space. A succint IBE scheme with$\gamma$-compression for ${\mathcal {M}},\mathcal {ID}$ is a tuple of algorithms $({\textsf {Setup} },{\textsf {KeyGen} },{\textsf {Enc} },{\textsf {Dec} })$ where:

•  ${\textsf {Setup} }(1^\lambda )$ takes as input the security parameter and outputs a master secret key ${\textsf {MSK} }$ and a master public key ${{\textsf {MPK}}}$.

•  ${\textsf {KeyGen} }({\textsf {MSK} },\textsf {id} )$ takes as input the master secret ${\textsf {MSK} }$ and an identity $\textsf {id} \in \mathcal {ID}$. It outputs a secret key ${\textsf {SK} }_\textsf {id}$ for $\textsf {id}$.

•  ${\textsf {Enc} }({{\textsf {MPK}}},\textsf {id} ,m)$ takes as input the public-parameter ${{\textsf {MPK}}}$, an identity $\textsf {id} \in \mathcal {ID}$, and a message $m\in {\mathcal {M}}$, and outputs a ciphertext c.

•  ${\textsf {Dec} }({\textsf {SK} }_\textsf {id} ,c)$ takes as input the secret key ${\textsf {SK} }_\textsf {id}$ for an identity $\textsf {id} \in \mathcal {ID}$ and a ciphertext c, and outputs some $m \in {\mathcal {M}}$, or $\bot$.

We require the following properties:

Correctness For any message $m\in {\mathcal {M}}$ and identity $\textsf {id} \in \mathcal {ID}$, we have that

$$\begin{aligned} \Pr \left[ {\textsf {Dec} }({\textsf {SK} }_\textsf {id} ,c)=m: \begin{array}{l} ({\textsf {MSK} },{{\textsf {MPK}}})\leftarrow {\textsf {Setup} }(1^\lambda ),\\ {\textsf {SK} }_\textsf {id} \leftarrow {\textsf {KeyGen} }({\textsf {MSK} },\textsf {id} ),\\ c\leftarrow {\textsf {Enc} }({{\textsf {MPK}}},\textsf {id} ,m) \end{array} \right] =1 \end{aligned}$$

Succinctness: For any security parameter $\lambda \in \mathbb {N}$, identity space $\mathcal {ID}$, the size of the encryption circuit ${\textsf {Enc} }$, for messages of size $\ell$, is at most $|\mathcal {ID}|^{\gamma }\cdot \mathrm {poly}(\lambda ,\ell )$.

In this work, we shall consider the following selective security.

Definition 2.12

(Selectively secure IBE) A tuple of algorithms ${\textsf {IBE} }= ({\textsf {Setup} },{\textsf {KeyGen} },{\textsf {Enc} },{\textsf {Dec} })$ is a selectively secure IBE scheme for ${\mathcal {M}},\mathcal {ID}$ if it satisfies the following requirement, formalized by the experiment $\mathsf {Expt}^{\mathsf {IBE}}_{{\mathcal {A}}}(1^\lambda ,b)$ between an adversary ${\mathcal {A}}$ and a challenger:

• 1. ${\mathcal {A}}$ submits the challenge identity $\textsf {id} ^* \in \mathcal {ID}$ and the challenge messages $(m_0^*,m_1^*)$ to the challenger.

• 2. The challenger runs $({\textsf {MSK} },{{\textsf {MPK}}})\leftarrow {\textsf {Setup} }(1^\lambda )$, generates ciphertext ${\textsf {CT} }^*\leftarrow {\textsf {Enc} }({{\textsf {MPK}}},m_b^*)$, and gives $({{\textsf {MPK}}},{\textsf {CT} }^*)$ to ${\mathcal {A}}$.

• 3. ${\mathcal {A}}$ is allowed to query (polynomially many) identities $\textsf {id} \in \mathcal {ID}$ such that $\textsf {id} \ne \textsf {id} ^*$. The challenger gives ${\textsf {SK} }_\textsf {id} \leftarrow {\textsf {KeyGen} }(1^\lambda ,{\textsf {MSK} },\textsf {id} )$ to the adversary.

• 4. ${\mathcal {A}}$ outputs a guess $b'$ for b. The experiment outputs 1 if $b'=b$, 0 otherwise.

We say the IBE scheme is selectively secure if, for all PPT adversaries ${\mathcal {A}}$, there exists a negligible function $\mu (\lambda )$, it holds

$$\begin{aligned} \mathsf {Adv}^{\mathsf {IBE}}_{{\mathcal {A}}} =\left| \Pr [\mathsf {Expt}^{\mathsf {IBE}}_{{\mathcal {A}}}(1^\lambda ,0)=1] - \Pr [\mathsf {Expt}^{\mathsf {IBE}}_{{\mathcal {A}}}(1^\lambda ,1)=1]\right| \le \mu (\lambda ). \end{aligned}$$

We further say that ${\textsf {IBE} }$ is $\delta$-selectively secure, for some concrete negligible function $\delta (\cdot )$, if for all polysize distinguishers the above indistinguishability gap $\mu (\lambda )$ is smaller than $\delta (\lambda )^{\Omega (1)}$.

3 Strong Exponentially Efficient Indistinguishability Obfuscation

Lin et al. [51] propose a variant of IO that has a weak (yet non-trivial) efficiency, which they call exponentially efficient IO (XIO). All that this notion requires in terms of efficiency is that the size of an obfuscated circuit is sublinear in the size of the corresponding truth table. They also refer to a stronger notion that requires that also the time to obfuscate a given circuit is sublinear in the size of the truth table. This notion, which we call strong exponentially efficient IO (SXIO), serves as one of the main abstractions in our work.

Definition 3.1

(Strong exponentially efficient indistinguishability obfuscation (SXIO) [51]) For a constant $\gamma < 1$, a machine $\textsf {sxi} \mathcal {O}$ is a $\gamma$-compressing strong exponentially efficient indistinguishability obfuscator (SXIO) for a collection of circuit classes $\varvec{\mathcal {C}} =\{\mathcal {C}_\lambda \}_{\lambda \in \mathbb {N}}$ if it satisfies the functionality and indistinguishability in Definition 2.7 and the following efficiency requirements:

Non-trivial time efficiency there exists a constant $\gamma <1$ and a fixed polynomial $\mathrm {poly}(\cdot )$, depending on the collection $\varvec{C}$ (but not on any specific class $\mathcal {C}\in \varvec{C}$), such that for any class $\mathcal {C}\in \varvec{C}$, security parameter $\lambda \in \mathbb {N}$, and circuit $C \in \{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}$ with input length n, the running time of $\textsf {sxi} \mathcal {O}$ on input $(1^\lambda ,C)$ is at most $2^{n\gamma }\cdot \mathrm {poly}(\lambda ,|C|)$.

3.1 SXIO from Single-Input SKFE

In this section, we show that we can construct SXIO from any selectively secure t-input SKFE scheme. We recall that such a t-SKFE scheme can be constructed from any selectively secure 1-SKFE scheme, as stated in Theorem 2.1.

Theorem 3.1

For any function $t(\lambda )$, if there exists $\delta$-selectively secure t-SKFE for $\textsf {P} /\textsf {poly}$, then there exists $\frac{1}{t+1}$-compressing $\delta$-secure SXIO for $\textsf {P} /\textsf {poly}$.

The idea of the construction of SXIO from SKFE is explained in Introduction.

We immediately obtain the following corollary from Theorems 2.1 and 3.1.

Corollary 3.1

• 1. If there exists $\delta$-selectively secure single-input SKFE for $\textsf {P} /\textsf {poly}$, then there exists $\gamma$-compressing $\delta$-secure SXIO for $\textsf {P} /\textsf {poly}$ where $\gamma <1$ is an arbitrary constant.

• 2. Let $\varepsilon <1$ be a constant and $\tilde{\lambda } = 2^{(\log \lambda )^{\varepsilon }}$. If there exists $2^{-\tilde{\lambda }^{\Omega (1)}}$-selectively secure single-input SKFE for $\textsf {P} /\textsf {poly}$, then there exists polynomially secure SXIO with compression factor $\gamma (\lambda ) = O(1/\log \log \lambda )$ for circuits of size at most $2^{O((\log \lambda )^{\varepsilon })}$. (Here, $\tilde{\lambda }$ is the single-input $\text {SKFE}$ security parameter and $\lambda$ is the $\text {SXIO}$ security parameter.)

3.2 The Construction of SXIO

We start by describing the SXIO construction and next argue its security. In what follows, given a circuit C, we identify its input space with $[N] =\left\{ 1,\dots ,N\right\}$ (so in particular, $N= 2^n$ if C takes n-bit strings as input). Let $\textsf {SKFE} _t = ({\textsf {Setup} },{\textsf {KeyGen} },{\textsf {Enc} },{\textsf {Dec} })$ be a selectively secure t-input secret-key functional encryption scheme.

Construction We construct an SXIO scheme $\textsf {sxi} \mathcal {O}$ as follows.

•  $\textsf {sxi} \mathcal {O}(1^\lambda ,C)$: For every $j \in [N^{1/(t+1)}]$:

  • let $U_{j}$ be the t-input universal circuit that given $j_1,\ldots ,j_{t-1} \in [N^{1/(t+1)}]$ and a t-input circuit D, returns $D(j_1,\ldots , j_{t-1},j)$.

  • let $C_{j}$ be the t-input circuit that given $j_1,\ldots ,j_{t}\in [N^{1/(t+1)}]$ returns $C(j_1,\ldots , j_{t},j)$.

  • 1. Generate ${\textsf {MSK} }\leftarrow {\textsf {Setup} }(1^\lambda )$.

  • 2. Generate ${\textsf {CT} }_{t,j} \leftarrow {\textsf {Enc} }({\textsf {MSK} },C_j,t)$ for $j\in [N^{1/(t+1)}]$.

  • 3. Generate ${\textsf {CT} }_{i,j} \leftarrow {\textsf {Enc} }({\textsf {MSK} },j,i)$ for $i\in [t-1]$ and $j\in [N^{1/(t+1)}]$.

  • 4. Generate ${\textsf {SK} }_{U_j} \leftarrow {\textsf {KeyGen} }({\textsf {MSK} },U_j)$ for $j\in [N^{1/(t+1)}]$

  • 5. $\textsf {sxi} \mathcal {O}(C) =(\{{\textsf {CT} }_{i,j}\}_{i\in [t],j\in [N^{1/(t+1)}]},\{{\textsf {SK} }_{U_j}\}_{j\in [N^{1/(t+1)}]})$

•  $\textsf {Eval} (\textsf {sxi} \mathcal {O},x)$: To evaluate the obfuscated circuit, convert $x \in [N]$ into $(j_1,\ldots , j_t,j_{t+1}) \in [N^{1/(t+1)}]^{(t+1)}$ and output ${\textsf {Dec} }({\textsf {SK} }_{U_{j_{t+1}}},{\textsf {CT} }_{1,j_1},\ldots ,{\textsf {CT} }_{t,j_t}).$

Proof of Theorem 3.1

We first note that $\textsf {sxi} \mathcal {O}$ indeed satisfies the non-trivial time efficiency requirement. The obfuscated circuit consists of $t\cdot N^{1/(t+1)}$ ciphertexts, each computable in time $\mathrm {poly}(|C|,\lambda )$, and $N^{1/(t+1)}$ secret keys of $\textsf {SKFE} _t$, each computable in time $\mathrm {poly}(|C|,\lambda )$. Thus, for $t\le \lambda$, the overall running time of the obfuscator is bounded by $N^{1/(t+1)}\cdot \mathrm {poly}(|C|,\lambda )$, as required.

Security We show that if there exists a distinguisher $\mathcal {D}$ against $\textsf {sxi} \mathcal {O}$, then there exists an adversary ${\mathcal {A}}$ that breaks the security of the underlying scheme $\textsf {SKFE} _t$. (It even breaks a weaker security notion than the one from Definition 2.2, where function queries are also fixed in advance.)

The reduction is straightforward. If $\mathcal {D}$ distinguishes $\textsf {sxi} \mathcal {O}$ obfuscations of circuits $C,C'$ (of same size and functionality), then ${\mathcal {A}}$ can invoke $\mathcal {D}$ to distinguish

$$\begin{aligned} \left\{ (j_1,\dots ,j_{t-1},C_{j_t}):j_i\in [N^{{1}/{(t+1)}}]\right\} \hbox { and } \left\{ (j_1,\dots ,j_{t-1}, C'_{j_t}): j_i\in [N^{{1}/{(t+1)}}]\right\} , \end{aligned}$$

given secret keys for all functions $\left\{ U_{j_{t+1}}:j_{t+1}\in [N^{{1}/{(t+1)}}]\right\}$. Since the two circuits are functionally equivalent, all these queries are valid queries, since $U_{j_{t+1}}(j_1,\dots ,j_{t-1},C_{j_t}) = C(j_1,\dots ,j_t,j_{t+1}) = C(j_1,\dots ,j_t,j_{t+1}) = U_{j_{t+1}}(j_1,\dots ,j_{t-1},C'_{j_t})$.

This completes the proof of Theorem 3.1. $\square$

Remark 3.1

(SXIO from succinct single-key SKFE) To get t-input SKFE as required above from 1-input SKFE, via the [16] transformation, the original SKFE indeed has to support an unbounded polynomial number of functional keys. We note that a similar SXIO construction is possible from a 1-input SKFE that supports a functional key for a single function f, but is succinct in the sense that encryption only grows mildly with the complexity of f, namely with $|f|^\beta$ for some constant $\beta <1$.

In more detail, assume a (1-input) single-key SKFE with succinctness as above, where the time to derive a key for a function f is bounded by $|f|^c\cdot \mathrm {poly}(\lambda )$ for some constant $c \ge 1$. The SXIO will consist of a single key for the function f that given as input $C_j$, as defined above, returns $C_j(1),\dots ,C_j(N^{\frac{1}{c+1-\beta }})$, and encryptions of $C_1,\dots ,C_{N^{c-\beta /c+1-\beta }}$. Accordingly, we still get $\text {SXIO}$ with compression factor $\gamma = 1-\frac{1-\beta }{c+1-\beta }$. This does not lead to arbitrary constant compression (in contrast with the theorem above), since $\frac{1}{2} \le \gamma < 1$. Yet, it already suffices to obtain IO, when combined with LWE (as in Corollary 1.1).

4 Yao’s Garbled Circuits are Decomposable

In this section, we define the notion of decomposable garbled circuits and prove that the classical Yao’s garbled circuit construction satisfies our definition of decomposability (in some parameter regime). We use a decomposable garbling scheme as a building block to construct a PKFE scheme in Sect. 5.2.

4.1 Decomposable Garbling

Circuit garbling schemes [14, 61] typically consist of algorithms $(\textsf {Gar.CirEn} ,\textsf {Gar.InpEn} ,\textsf {Gar.De} )$. $\textsf {Gar.CirEn} (C,K)$ is a circuit garbling algorithm that given a circuit $C$ and secret key K produces a garbled circuit $\widehat{C}$. $\textsf {Gar.InpEn} (x,K)$ is an input garbling algorithm that takes an input $x$ and the same secret key K, and produces a garbled input $\widehat{x}$. $\textsf {Gar.De} (\widehat{C},\widehat{x})$ is a decoder that given the garbled circuit and input decodes the result y.

In this work, we shall particularly be interested in garbling decomposable circuits. A decomposable circuit $C$ can be represented by a smaller circuit $C_\mathsf{de}$ that can generate each of the gates in the circuit $C$ (along with pointers to their neighbors). When garbling such circuits, we shall require that the garbling process will also be decomposable and will admit certain decomposable security properties. We next formally define the notion of decomposable circuits and decomposable garbling schemes.

Definition 4.1

(Decomposable Circuit) Let $C:\{0,1\}^n\rightarrow \{0,1\}$ be a boolean circuit with $L$ binary gates and W wires. Each gate $g \in [L]$ has an associated tuple $(f, w_{a}, w_{b}, w_{c})$ where $f~:~ \{0,1\}^2 \rightarrow \{0,1\}$ is the binary function computed by the gate, $w_{a}, w_{b} \in [W]$ are the incoming wires, and $w_{c} \in [W]$ is the outgoing wire. A wire $w_c$ can be the outgoing wire of at most a single gate, but can be used as an incoming wire to several different gates and therefore this models a circuit with fan-in 2 and unbounded fan-out. We define the predecessor gates of g to be the gates whose outgoing wires are $w_a,w_b$ (at most 2 of them). We define the successor gates of g to be the gates that have $w_c$ as an incoming wire. The gates are topologically ordered and labeled by $1,\dots ,L$ so that if j is a successor of i, then $i<j$. A wire w is an input wire if it is not the outgoing wire of any gate. We assume that the wires $1,\ldots ,n$ are the input wires. There is a unique output wirew which is not an incoming wire to any gate.

We say that $C$ is decomposable if there exists a smaller circuit $C_\mathsf{de}$, called the decomposition circuit, that given a gate label $g\in [L]$ as input, outputs the associated tuple $C_\mathsf{de}(g) = (f, w_{a}, w_{b}, w_{c})$.

Definition 4.2

(Decomposable Garbling) A decomposable garbling scheme consists of a tuple of three deterministic polynomial-time algorithms $(\textsf {Gar.CirEn} ,\textsf {Gar.InpEn} ,\textsf {Gar.De} )$ that work as follows:

•  $\widehat{b}_i \leftarrow \textsf {Gar.InpEn} (i,b;K)$: takes as an input label $i \in [n]$, a bit $b\in \{0,1\}$, and secret key $K\in \{0,1\}^\lambda$, and outputs a garbled input bit $\widehat{b}_i$.

•  $\widehat{G}_g \leftarrow \textsf {Gar.CirEn} (C_\mathsf{de},g;K)$: takes as input a decomposition circuit $C_\mathsf{de}:\{0,1\}^L\rightarrow \{0,1\}^*$, a gate label $g\in [L]$, and secret key $K\in \{0,1\}^\lambda$, and outputs a garbled gate $\widehat{G}_g$.

•  $y\leftarrow \textsf {Gar.De} (\widehat{C},\widehat{b})$: takes as input garbled gates $\widehat{C}= \left\{ \widehat{G}_g\right\} _{g\in [L]}$, and garbled input bits $\widehat{b}= \left\{ \widehat{b}_i\right\} _{i\in [n]}$, and outputs $y\in \{0,1\}^m$.

The scheme should satisfy the following requirements:

• 1. Correctness: for every decomposable circuit $C$ with decomposition circuit $C_\mathsf{de}$ and any input $b_1,\dots ,b_n\in \{0,1\}^{n}$, the decoding procedure $\textsf {Gar.De}$ produces the correct output $y=C(b_1,\dots ,b_n)$.

• 2. $(\sigma ,\tau ,\delta )$-Decomposable Indistinguishability: There are functions $\sigma (\Phi ,s,\lambda ),\tau (\Phi ) \in \mathbb {N}$, $\delta (\lambda ) \le 1$ such that for any security parameter $\lambda$, any input $x\in \{0,1\}^n$, and any two circuits $(C,C')$ that:

  • have the same topology $\Phi$, and in particular the same size $L$ and input-output lengths $(n,m)$,

  • have decomposition circuits $(C_\mathsf{de},C_\mathsf{de}')$ of the same size s

  • and agree on $x$: $C(x)=C'(x)$,

  there exist hybrid circuits $\left\{ \textsf {Gar.HInpEn} ^{(t)},\textsf {Gar.HCirEn} ^{(t)}\; \big \vert \;t\in [\tau ]\right\}$, each being of size at most $\sigma$, as well as (possibly inefficient) hybrid functions $\left\{ \textsf {Gar.HPunc} ^{(t)}\; \big \vert \;t\in [\tau ]\right\}$ with the following syntax:

  •  $(K_{\textsf {pun} }^{(t)},g_{\textsf {pun} }^{(t)},i_{\textsf {pun} }^{(t)})\leftarrow \textsf {Gar.HPunc} ^{(t)}(K)$, given a key $K\in \{0,1\}^\lambda$ and an index $t\in [\tau ]$, outputs a punctured key$K_{\textsf {pun} }^{(t)}$, a gate label $g_{\textsf {pun} }^{(t)}\in [L]$, and an input label $i_{\textsf {pun} }^{(t)}\in [n]$.

  •  $\widehat{G}_g\leftarrow \textsf {Gar.HCirEn} ^{(t)}(g;K)$, given a gate label $g\in [L]$, and a (possibly punctured) key $K$, outputs a fake garbled gate$\widehat{G}_{g}$.

  •  $\widehat{b}_i \leftarrow \textsf {Gar.HInpEn} ^{(t)}(i,b;K)$, given an input label $i\in [n]$, and a (possibly punctured) key $K$, outputs a fake garbled input bit$\widehat{b}_{i}$.

  We require that the following properties hold:

  • (a) The hybrids transition fromCto$C'$: For any $K\in \{0,1\}^\lambda$, $g\in [L]$, $i\in [n]$, $b\in \{0,1\}$,

    $$\begin{aligned} \textsf {Gar.CirEn} (C_\mathsf{de},g;K)&= \textsf {Gar.HCirEn} ^{(1)}(g;K), \\ \textsf {Gar.InpEn} (i,b;K)&= \textsf {Gar.HInpEn} ^{(1)}(i,b;K),\\ \textsf {Gar.CirEn} (C_\mathsf{de}',g;K)&= \textsf {Gar.HCirEn} ^{(\tau )}(g;K), \\ \textsf {Gar.InpEn} (i,b;K)&= \textsf {Gar.HInpEn} ^{(\tau )}(i,b;K). \end{aligned}$$

  • (b) Punctured keys preserve functionality: For any $K\in \{0,1\}^\lambda$, and $t\in [\tau -1]$, and letting $(K_{\textsf {pun} }^{(t)},g_{\textsf {pun} }^{(t)},i_{\textsf {pun} }^{(t)}) =\textsf {Gar.HPunc} ^{(t)}(K)$, it holds that:

    • For any $g \ne g_{\textsf {pun} }^{(t)}$, we have

      $$\begin{aligned} \textsf {Gar.HCirEn} ^{(t)}(g;K)&= \textsf {Gar.HCirEn} ^{(t)}(g;K_{\textsf {pun} }^{(t)}) \\&= \textsf {Gar.HCirEn} ^{(t+1)}(g,K). \end{aligned}$$

    • For any $i \ne i_{\textsf {pun} }^{(t)}$ and $b\in \{0,1\}$, we have

      $$\begin{aligned} \textsf {Gar.HInpEn} ^{(t)}(i,b;K)&= \textsf {Gar.HInpEn} ^{(t)}(i,b;K_{\textsf {pun} }^{(t)}) \\&=\textsf {Gar.HInpEn} ^{(t+1)}(i,b,K). \end{aligned}$$

  • (c) Indistinguishability on punctured inputs: For any polysize distinguisher $\mathcal {D}$, security parameter $\lambda \in \mathbb {N}$, and circuits $(C,C')$ as above,

    $$\begin{aligned}&\Big |\Pr \left[ \mathcal {D}\left( \hat{g}_{\textsf {pun} }^{(t)},\hat{i}_{\textsf {pun} }^{(t)}, \textsf {Gar.HPunc} ^{(t)}(K)\right) =1\right] \\&\quad -\Pr \left[ \mathcal {D}\left( \hat{g}_{\textsf {pun} }^{(t+1)},\hat{i}_{\textsf {pun} }^{(t+1)}, \textsf {Gar.HPunc} ^{(t)}(K)\right) =1\right] \Big | \le \delta (\lambda ), \end{aligned}$$

    where, for $t \ge 0$ we denote by $\hat{g}_{\textsf {pun} }^{(t)}$ the value $\textsf {Gar.HCirEn} ^{(t)}(g_{\textsf {pun} }^{(t)};K)$ and by $\hat{i}_{\textsf {pun} }^{(t)}$ the value $\textsf {Gar.HInpEn} ^{(t)}(i_{\textsf {pun} }^{(t)},x_{i_{\textsf {pun} }^{(t)}};K)$, with $x$ being the input on which the two circuits $C$ and $C'$ agree on. The probability is over $K\leftarrow \{0,1\}^\lambda$, and $(K_{\textsf {pun} }^{(t)},g_{\textsf {pun} }^{(t)},i_{\textsf {pun} }^{(t)}) =\textsf {Gar.HPunc} ^{(t)}(K)$.

We show that Yao’s garbled circuit scheme, in fact, gives rise to a decomposable garbling scheme where the security loss and size of the hybrid circuits scale with the depth of the garbled circuits.

Theorem 4.1

Let $\mathcal {C}= \left\{ \mathcal {C}_{\lambda }\right\} _{\lambda \in \mathbb {N}}$ be a class of boolean circuits where each $C\in \mathcal {C}_\lambda$ has circuit size at most $L(\lambda )$, input size at most $n(\lambda )$, depth at most $d(\lambda )$, fan-out at most $\varphi (\lambda )$, and decomposition circuit of size at most $\Delta (\lambda )$. Then, assuming the existence of $\delta$-secure one-way functions, $\mathcal {C}$ has a decomposable garbling scheme with $(\sigma ,\tau ,\delta )$-decomposable indistinguishability where the bound on the size of hybrid circuits is $\sigma = \mathrm {poly}(\lambda , d, \log L, \varphi , \Delta )$, the number of hybrids is $\tau = L \cdot 2^{O(d)}$, and the indistinguishability gap is $\delta ^{\Omega (1)}$.

The proof of the above theorem spans the rest of this section. We rely heavily on the ideas of Hemenway et al. [39] which considered an orthogonal question of adaptively secure garbling schemes but (for entirely different reasons) developed ideas that are useful for decomposable garbling.

4.2 Yao’s Garbled Circuits: Construction

Let $(\textsf {SEnc} ,\textsf {SDec} )$ be a CPA-secure symmetric-key encryption scheme with key space $\{0,1\}^\lambda$. Furthermore, assume it satisfies special correctness so that for all messages m we have:

$$\begin{aligned} \Pr [ \textsf {SDec} _{k}(\textsf {SEnc} _{k'}(m)) \ne \bot ~:~ k,k' \leftarrow \{0,1\}^\lambda ] = \mathrm {negl}(\lambda ). \end{aligned}$$

Such encryption schemes can be based on one-way functions.

Let $\mathcal {PPRF}= ({\textsf {PRF.Gen} }, {\textsf {PRF.Ev} },{\textsf {PRF.Punc} })$ be a PPRF with:

• domain $\mathcal {D}= ([W] \times \{0,1\}) \cup [L]$, where [W] is the set of wires and [L] is the set of gates

• range $\mathcal {R}= \{0,1\}^{\lambda }$

and furthermore assume that the keys output by ${\textsf {PRF.Gen} }$ are just random values $K \in \{0,1\}^\lambda$. Such PPRFs can be constructed based on one-way functions.

Yao’s Garbled Circuit Construction The key K of the garbling scheme is just a key for the PPRF. We define the two functions $\textsf {Gar.InpEn} , \textsf {Gar.CirEn}$ as follows.

•  $\widehat{b}_i \leftarrow \textsf {Gar.InpEn} (i,b;K)$: Output $\widehat{b}_i = {\textsf {PRF.Ev} }_{K}((i, b))$.

•  $\widehat{G}_g \leftarrow \textsf {Gar.CirEn} (C_\mathsf{de},g;K)$: Let $C_\mathsf{de}(g)= (f, w_a, w_b, w_c)$. Compute the 6 wire labels $k_\alpha ^\beta = {\textsf {PRF.Ev} }_K(w_\alpha , \beta )$ for $\alpha \in \{a,b,c\}$ and $\beta \in \{0,1\}$, unless $w_c$ is an output wire in which case set $k_c^0 = 0$, $k_c^1 = 1$. Compute 4 ciphertexts:

  •  $c_{0,0}\leftarrow \textsf {SEnc} _{k^0_{a}}(\textsf {SEnc} _{k^0_{b}}(k^{f(0,0)}_{c}))$

  •  $c_{0,1}\leftarrow \textsf {SEnc} _{k^0_{a}}(\textsf {SEnc} _{k^1_{b}}(k^{f(0,1)}_{c}))$

  •  $c_{1,0}\leftarrow \textsf {SEnc} _{k^1_{a}}(\textsf {SEnc} _{k^0_{b}}(k^{f(1,0)}_{c}))$

  •  $c_{1,1}\leftarrow \textsf {SEnc} _{k^1_{a}}(\textsf {SEnc} _{k^0_{b}}(k^{f(1,1)}_{c}))$

  where the encryption randomness is derived using ${\textsf {PRF.Ev} }_K(g)$. Set $\widehat{G}_g = [c_1, c_2, c_3, c_4]$ to be a lexicographic ordering of the above ciphertexts.

•  $y\leftarrow \textsf {Gar.De} (\widehat{C},\widehat{b})$: On input garbled gates $\widehat{C}= \left\{ \widehat{G}_g\right\} _{g\in [L]}$ and garbled input bits $\widehat{b}= \left\{ \widehat{b}_i\right\} _{i\in [n]}$, iteratively compute a wire label for every wire in the circuit.

  For the input wires, the labels these are given by $\widehat{b}$. For any gate g with incoming wires $w_a,w_b$ and outgoing wire $w_c$ such that the labels $k_a,k_b$ of $w_a,w_b$ have already been computed, derive the label $k_c$ of $w_c$ as follows. Parse $\widehat{G}_g = [c_1, c_2, c_3, c_4]$ and set $k_c = \textsf {SDec} _{k_b}(\textsf {SDec} _{k_a}(c_i))$ for the first one of $i=1,2,3,4$ for which the outcome is not $\bot$.

  Finally, output the value $y$ which is the wire label of the output wire.

The correctness of this construction follows by inspection and from the special correctness of the symmetric-key encryption scheme.

4.3 Hybrid Circuits and Pebbling

We now show that Yao’s construction is decomposable by defining the hybrid functions as in Definition 4.2.

Half-Sequence We now define the sequence of hybrid functions

$$\begin{aligned} \left\{ \textsf {Gar.HInpEn} ^{(t)},\textsf {Gar.HCirEn} ^{(t)}, \textsf {Gar.HPunc} ^{(t)} \; \big \vert \;t\in [\tau ]\right\} . \end{aligned}$$

We will actually only define a half-sequence which ensures that:

•  $\textsf {Gar.CirEn} (C_\mathsf{de},g;K) = \textsf {Gar.HCirEn} ^{(1)}(g;K), \textsf {Gar.InpEn} (i,b;K) = \textsf {Gar.HInpEn} ^{(1)}(i,b;K) = \textsf {Gar.HInpEn} ^{(\tau )}(i,b;K)$,

•  $\textsf {Gar.HCirEn} ^{(\tau )}(g;K)$ does not depend on $C_\mathsf{de}$ but only on its topology $\Phi$ and the output bit $C(x) = C'(x)$.

By adding a symmetric sequence of additional hybrid functions

$$\begin{aligned} \left\{ \textsf {Gar.HInpEn} ^{(t)},\textsf {Gar.HCirEn} ^{(t)}, \textsf {Gar.HPunc} ^{(t)} \; \big \vert \;t\in \{\tau +1,\ldots ,2\tau -1\}\right\} \end{aligned}$$

where we define the functions with $t= \tau +i$ the same way as those with $t = \tau -i$ but with $C_\mathsf{de}'$ instead of $C_\mathsf{de}$ we then get the full hybrid sequence satisfying the definition.

Pebbling We define the following pebbling game over a circuit with some topology $\Phi$. Each gate of the circuit can either have no pebble, a black pebble, or a gray pebble. The rules of the game are as follows:

• I. We can place or remove a black pebble on a gate as long as both predecessors of that gate have black pebbles on them (or the gate is an input gate).

• II. We can replace a black pebble with a gray pebble on any non-output gate as long as all successors of that gate have black or gray pebbles on them.

A pebbling of the topology $\Phi$ is a sequence of steps where we start with no pebbles on any gate and sequentially apply rules I and II so as to end up with a gray pebble on every non-output gate and a black pebble on the output. Let us assume that the topology $\Phi$ admits a pebbling consisting of steps $\textsf {pstep} _1,\ldots ,\textsf {pstep} _{\tau '}$.

Pebbling and Circuit Configurations We will define the hybrids, each of which being parametrized by a circuit configuration $\textsf {conf}$. For every gate g, the configuration $\textsf {conf}$ specifies if the gate is in one of four possible modes

$$\begin{aligned} \{\textsf {RealGate} , \textsf {SimGate} , \textsf {CompDepSimGate} , \frac{1}{2}\textsf {CompDepSimGate} \}. \end{aligned}$$

Furthermore, for every wire w which is an incoming or outgoing wire of some gate in mode $\textsf {CompDepSimGate}$ or $\frac{1}{2}\textsf {CompDepSimGate}$, the configuration specifies a bit v(w).

Assume we are given an input x and a circuit C having topology $\Phi$ that admits a pebbling consisting of steps $\textsf {pstep} _1,\ldots ,\textsf {pstep} _{\tau '}$. We first define a sequence of configurations $\textsf {conf} '_1,\ldots ,\textsf {conf} '_{\tau '}$ where every configuration $\textsf {conf} '_i$ corresponds to the pebble placement after step i of the pebbling: every gate that has no pebble is in $\textsf {RealGate}$ mode, every gate that has a black pebble is in $\textsf {CompDepSimGate}$ mode, every gate that has a gray pebble is in $\textsf {SimGate}$ mode. Furthermore, for every wire w which is an incoming or outgoing wire of some gate in mode $\textsf {CompDepSimGate}$ we set v(w) to be the bit going over the wire w during the computation C(x). Next we add several intermediate configurations as follows: if the transition from $\textsf {conf} '_i, \textsf {conf} '_{i+1}$ corresponds to an application of rule I in the pebbling, meaning that we either add or remove a black pebble on some gate g, then we add an intermediate configuration in between these, which is identical to $\textsf {conf} '_i, \textsf {conf} '_{i+1}$ except that the gate g is in $\frac{1}{2}\textsf {CompDepSimGate}$ mode. This results in a sequence $\textsf {conf} _1,\ldots ,\textsf {conf} _{\tau }$ where $\tau \le 2\tau '$.

Configurations and Hybrids We now define the hybrid functions

$$\begin{aligned} \left\{ \textsf {Gar.HInpEn} ^{(t)},\textsf {Gar.HCirEn} ^{(t)}, \textsf {Gar.HPunc} ^{(t)} \; \big \vert \;t\in [\tau ]\right\} . \end{aligned}$$

First, for a configuration $\textsf {conf}$ we define the functions $\textsf {Gar.HInpEn} ^{(\textsf {conf} )}$ and $\textsf {Gar.HCirEn} ^{(\textsf {conf} )}$ parameterized by $\textsf {conf}$. For every $t \in [\tau ]$, we then define $\textsf {Gar.HInpEn} ^{(t)} = \textsf {Gar.HInpEn} ^{(\textsf {conf} _t)}$ and $\textsf {Gar.HCirEn} ^{(t)} = \textsf {Gar.HCirEn} ^{(\textsf {conf} _t)}$ where $\textsf {conf} _1,\ldots ,\textsf {conf} _{\tau }$ is the sequence of configuration given by the pebbling game as above.

•  $\widehat{G}_g\leftarrow \textsf {Gar.HCirEn} ^{(\textsf {conf} )}(g;K)$: Let $C_\mathsf{de}(g)= (f, w_a, w_b, w_c)$.

  If the key K is a standard PPRF key, then proceed as follows. Compute the 6 wire labels $k_\alpha ^\beta = {\textsf {PRF.Ev} }_K(w_\alpha , \beta )$ for $\alpha \in \{a,b,c\}$ and $\beta \in \{0,1\}$, unless $w_c$ is an output wire in which case set $k_c^0 = 0$, $k_c^1 = 1$. Compute 4 ciphertexts $c_{0,0}$, $c_{0,1}$, $c_{1,0}$, $c_{1,1}$ as in Fig. 2 depending on the mode of g, where the encryption randomness is derived from ${\textsf {PRF.Ev} }_K(g)$. Let $\widehat{G}_g = [c_1, c_2, c_3, c_4]$ to be a lexicographic ordering of the above ciphertexts.

  If the key K is not a standard PPRF key, then parse $K = (K\{S\}, H)$. If there is a tuple of the form $(g, \widehat{G}_g)$ in H then output $\widehat{G}_g$. Else attempt to compute $\widehat{G}_g$ as above using the punctured PPRF key $K\{S\}$ and output $\bot$ if this is not possible.

•  $\textsf {Gar.HInpEn} ^{(\textsf {conf} )}(i,b;K)$: If the key K is a standard PPRF key, then output $\widehat{b}_i = {\textsf {PRF.Ev} }_{K}((i, b))$. Else parse $K = (K\{S\},H)$ and output $\widehat{b}_i = {\textsf {PRF.Ev} }_{K\{S\}}((i, b))$ or $\bot$ if this computation fails.

Fig. 2

Garbling Gate modes: $\textsf {RealGate}$, $\textsf {SimGate}$, $\textsf {CompDepSimGate}$, $\frac{1}{2}\textsf {CompDepSimGate}$

We define $\textsf {Gar.HPunc} ^{(t)}(K)$ as follows. Assume that the transition from $\textsf {conf} _t$ to $\textsf {conf} _{t+1}$ changes the mode of a gate $g_{\textsf {pun} }^{(t)}$ such that $g_{\textsf {pun} }^{(t)}$ has incoming wires $w_a,w_b$ and outgoing wire $w_c$.

• If the transition changes $g_{\textsf {pun} }^{(t)}$ from $\textsf {RealGate}$ to $\frac{1}{2}\textsf {CompDepSimGate}$ (or vice versa): $\textsf {Gar.HPunc} ^{t}(K) := (K_{\textsf {pun} }^{t} = ((K\{S\},H),g_{\textsf {pun} }^{(t)}, i_a)$ where $S = \{(w_a,1-v(w_a)), g_{\textsf {pun} }^{(t)}\}$, $K\{S\} = {\textsf {PRF.Punc} }(K,S)$, $i_a = \bot$ if $w_a$ is not an input wire, else $i_a$ is the index of input wire $w_a$. For every gate $g \ne g_{\textsf {pun} }^{(t)}$ that has $w_a$ as an input wire compute $\widehat{G}_g \leftarrow \textsf {Gar.HCirEn} ^{(\textsf {conf} _t)}(g;K)$ and add $\widehat{G}_g$ to H.

• If the transition changes $g_{\textsf {pun} }^{(t)}$ from $\frac{1}{2}\textsf {CompDepSimGate}$ to $\textsf {CompDepSimGate}$ (or vice versa): $\textsf {Gar.HPunc} ^{t}(K) := (K_{\textsf {pun} }^{t} = ((K\{S\},H), g_{\textsf {pun} }^{(t)}, i_b)$ where $S = \{(w_b,1-v(w_b)), g_{\textsf {pun} }^{(t)}\}$, $K\{S\} = {\textsf {PRF.Punc} }(K,S)$, $i_b = \bot$ if $w_b$ is not an input wire, else $i_b$ is the index of input wire $w_b$. For every gate $g \ne g_{\textsf {pun} }^{(t)}$ that has $w_b$ as an input wire compute $\widehat{G}_g \leftarrow \textsf {Gar.HCirEn} ^{(\textsf {conf} _t)}(g;K)$ and add $\widehat{G}_g$ to H.

• If the transition changes $g_{\textsf {pun} }^{(t)}$ from $\textsf {CompDepSimGate}$ to $\textsf {SimGate}$ (or vice versa): $\textsf {Gar.HPunc} ^{t}(K) := (K_{\textsf {pun} }^{t} = ((K\{S\},H), g_{\textsf {pun} }^{(t)}, \bot )$ with S being the set $\{(w_c, 0), (w_c, 1), g_{\textsf {pun} }^{(t)}\}$, $K\{S\} = {\textsf {PRF.Punc} }(K,S)$. For every gate $g \ne g_{\textsf {pun} }^{(t)}$ that has $w_c$ as an input wire compute $\widehat{G}_g \leftarrow \textsf {Gar.HCirEn} ^{(\textsf {conf} _t)}(g;K)$ and add $\widehat{G}_g$ to H.

4.4 Proof of Security

We now show that the above hybrid functions satisfy properties (a), (b), (c) of Definition 4.2.

Property (a) Firstly, $\left\{ \textsf {Gar.HInpEn} ^{(t)},\textsf {Gar.HCirEn} ^{(t)}, \textsf {Gar.HPunc} ^{(t)} \; \big \vert \;t\in [\tau ]\right\}$ represents a valid half-sequence, meaning that:

•  $\textsf {Gar.CirEn} (C_\mathsf{de},g;K) = \textsf {Gar.HCirEn} ^{(1)}(g;K), \textsf {Gar.InpEn} (i,b;K) = \textsf {Gar.HInpEn} ^{(1)}(i,b;K) = \textsf {Gar.HInpEn} ^{(\tau )}(i,b;K)$,

•  $\textsf {Gar.HCirEn} ^{(\tau )}(g;K)$ does not depend on $C_\mathsf{de}$ but only on its topology $\Phi$ and the output bit $C_\mathsf{de}(x)$.

In particular, $\textsf {Gar.HCirEn} ^{(\tau )}(g;K) = \textsf {Gar.HCirEn} ^{(\textsf {conf} _\tau )}(g;K)$ corresponds to a configuration where all non-output gates are in $\textsf {SimGate}$ mode and the output gate is in $\textsf {CompDepSimGate}$ mode, meaning that $\textsf {Gar.HCirEn} ^{(\textsf {conf} _\tau )}(g;K)$ does not depend on the boolean function f implemented by any of the gates. Furthermore, the configuration $\textsf {conf} _\tau$ only specifies the output value $v(w_{out}) = C(x)$. Therefore, these functions are a valid half-sequence. As we discussed, by adding a symmetric half-sequence in the reverse direction for the circuit $C_\mathsf{de}'$ we get a sequence that satisfies property (a).

Property (b) This property follows by inspection. In particular,

• For any $g \ne g_{\textsf {pun} }^{(t)}$, we have

  $$\begin{aligned}&\textsf {Gar.HCirEn} ^{(t)}(g;K) = \textsf {Gar.HCirEn} ^{(t)}(g;K_{\textsf {pun} }^{(t)}) = \textsf {Gar.HCirEn} ^{(t+1)}(g,K). \end{aligned}$$

  Since $\textsf {Gar.HCirEn} ^{(t)}(g;K)$ and $\textsf {Gar.HCirEn} ^{(t+1)}(g,K)$ only differ on the mode of the gate $g_{\textsf {pun} }^{(t)}$ and the punctured key $K_{\textsf {pun} }^{(t)}$ hardwires the value of all other gates affected by PRF puncturing to match those of $\textsf {Gar.HCirEn} ^{(t)}(g;K)$

• For any $i \ne i_{\textsf {pun} }^{(t)}$ and $b\in \{0,1\}$, we have $\textsf {Gar.HInpEn} ^{(t)}(i,b;K) = \textsf {Gar.HInpEn} ^{(t)}(i,b;K_{\textsf {pun} }^{(t)}) = \textsf {Gar.HInpEn} ^{(t+1)}(i,b,K)$. Actually, we have $\textsf {Gar.HInpEn} ^{(t)}(i,b;K) = \textsf {Gar.InpEn} (i,b;K)$ as well as $\textsf {Gar.HInpEn} ^{(t)}(i,b;K_{\textsf {pun} }^{(t)}) = \textsf {Gar.InpEn} (i,b;K)$, for all $i \ne i_{\textsf {pun} }^{(t)}$.

Property (c) For property (c), we must show that

$$\begin{aligned}&\left( \textsf {Gar.HCirEn} ^{(t)}(g_{\textsf {pun} }^{(t)};K),\textsf {Gar.HInpEn} ^{(t)}(i_{\textsf {pun} }^{(t)}, x_{i_{\textsf {pun} }^{(t)}};K),K_{\textsf {pun} }^{(t)}\right) \\&\quad \approx \left( \textsf {Gar.HCirEn} ^{(t+1)}(g_{\textsf {pun} }^{(t)};K),\textsf {Gar.HInpEn} ^{(t+1)} (i_{\textsf {pun} }^{(t)},x_{i_{\textsf {pun} }^{(t)}};K),K_{\textsf {pun} }^{(t)}\right) \end{aligned}$$

are computationally indistinguishable, where the probability is over $K\leftarrow \{0,1\}^\lambda$, and $(K_{\textsf {pun} }^{(t)},g_{\textsf {pun} }^{(t)},i_{\textsf {pun} }^{(t)}) =\textsf {Gar.HPunc} ^{(t)}(K)$.

Since in our case $\textsf {Gar.HInpEn} ^{(t)}(i,b;K) = \textsf {Gar.HInpEn} ^{(t+1)}(i,b;K) = \textsf {Gar.InpEn} (i,b;K)$ for all i, b, we can simplify the above to:

$$\begin{aligned}&\left( \textsf {Gar.HCirEn} ^{(t)}(g_{\textsf {pun} }^{(t)};K),\textsf {Gar.InpEn} (i_{\textsf {pun} }^{(t)},x_{i_{\textsf {pun} }^{(t)}}; K),K_{\textsf {pun} }^{(t)}\right) \\&\quad \approx \left( \textsf {Gar.HCirEn} ^{(t+1)}(g_{\textsf {pun} }^{(t)};K),\textsf {Gar.InpEn} (i_{\textsf {pun} }^{(t)}, x_{i_{\textsf {pun} }^{(t)}};K),K_{\textsf {pun} }^{(t)}\right) \end{aligned}$$

We consider several cases. Assume that the transition from $\textsf {conf} _t$ to $\textsf {conf} _{t+1}$ changes the mode of a gate $g_{\textsf {pun} }^{(t)}$ such that $g_{\textsf {pun} }^{(t)}$ has incoming wires $w_a,w_b$ and outgoing wire $w_c$.

Case 1::

If the transition changes $g_{\textsf {pun} }^{(t)}$ from $\textsf {RealGate}$ to $\frac{1}{2}\textsf {CompDepSimGate}$ (or vice versa): The difference between $\textsf {Gar.HCirEn} ^{(t)}(g_{\textsf {pun} }^{(t)};K), \textsf {Gar.HCirEn} ^{(t+1)}(g_{\textsf {pun} }^{(t)};K)$ is only in the value encrypted by the ciphertexts:

$$\begin{aligned}&c_{1-v(w_a),0}\leftarrow \textsf {SEnc} _{k^{1-v(w_a)}_{a}}(\cdots ) \\&c_{1-v(w_a),1}\leftarrow \textsf {SEnc} _{k^{1-v(w_a)}_{a}}(\cdots ) \end{aligned}$$

The key $k^{1-v(w_a)}_a = {\textsf {PRF.Ev} }_K(w_a, 1-v(w_a))$ is computed using a PPRF and the encryption randomness is derived using $r= {\textsf {PRF.Ev} }_K(g_{\textsf {pun} }^{(t)})$. Furthermore, $K_{\textsf {pun} }^{(t)} = (K\{S\}, H)$ where $K\{S\}$ is punctured at $S = \{(w_a,1-v(w_a)), g_{\textsf {pun} }^{(t)}\}$. The set H only contains other ciphertexts created under the key $k^{1-v(w_a)}_a$ but otherwise does not contain any other information related to $k^{1-v(w_a)}_a$ or r. Therefore, we can first rely on punctured PRF security to switch $k^{1-v(w_a)}_a$ and r to random, then on CPA security to switch the value encrypted by the ciphertexts $c_{1-v(w_a),0}, c_{1-v(w_a),1}$ from that of $\textsf {Gar.HCirEn} ^{(t)}(g_{\textsf {pun} }^{(t)};K)$ to that of $\textsf {Gar.HCirEn} ^{(t+1)}(g_{\textsf {pun} }^{(t)};K)$ and then on punctured PRF security again to switch $k^{1-v(w_a)}_a$ and the encryption randomness back to PRF outputs. This proves indistinguishability.

Case 2::

If the transition changes $g_{\textsf {pun} }^{(t)}$ from $\frac{1}{2}\textsf {CompDepSimGate}$ to the mode $\textsf {CompDepSimGate}$ (or vice versa):

This case is identical to the previous one with $w_b$ instead of $w_a$.

Case 3::

If the transition changes $g_{\textsf {pun} }^{(t)}$ from $\textsf {CompDepSimGate}$ to $\textsf {SimGate}$ (or vice versa):

The difference between $\textsf {Gar.HCirEn} ^{(t)}(g_{\textsf {pun} }^{(t)};K), \textsf {Gar.HCirEn} ^{(t+1)}(g_{\textsf {pun} }^{(t)};K)$ is only a switch from $k^{v(w_c)}_{c}$ to $k^{0}_{c}$ in the garbled gate $g_{\textsf {pun} }^{(t)}$.

The keys $k^{0}_{c} = {\textsf {PRF.Ev} }_K(w_c, 0)$, $k^{1}_{c} = {\textsf {PRF.Ev} }_K(w_c, 1)$ are computed using the PPRF. Furthermore, $K_{\textsf {pun} }^{(t)} = (K\{S\}, H)$ where $K\{S\}$ is punctured at $S = \{(w_c,0), (w_c,1) \}$. The keys $k^0_c, k^1_c$ are used to compute some values in H, but they are used in a completely symmetric manner (this is because all successors of $g_{\textsf {pun} }^{(t)}$ are in $\textsf {SimGate} , \textsf {CompDepSimGate}$ modes and therefore the 0 and 1 keys are used identically). Therefore, we first rely on PPRF security to switch $k^0_c,k^1_c$ to random values, then by symmetry we can exchange $k^{v(w_c)}_{c}$ for $k^{0}_{c}$ in the garbled gate $g_{\textsf {pun} }^{(t)}$, and then we rely on PPRF security again to switch them back to PRF outputs.

This completes the proof of property (c).

4.5 Pebble Complexity and Parameters

We now analyze the parameters $\sigma (\Phi ,s,\lambda ),\tau (\Phi ) \in \mathbb {N}$, $\delta (\lambda )$ as defined in Definition 4.2 that our construction achieves. Assume that the topology $\Phi$ has maximum fan-out $\varphi (\Phi )$ and can be pebbled in $\tau '(\Phi )$ steps using at most $p(\Phi )$ black pebbles. Furthermore, assume that the pebbling is succinct meaning that in any step t of the pebbling there is an index $g^{(t)}_{gray} \in [L]$ such that a gate g has a gray pebble on it if and only if g is not the output gate and $g \ge g^{(t)}_{gray}$. Lastly assume that the size of the compact circuits $C_\mathsf{de},C_\mathsf{de}'$ is at most $\Delta$ and that the symmetric-key encryption scheme and the PPRF have security $\delta _{ENC}(\lambda )$ and $\delta _{PPRF}(\lambda )$, respectively, meaning that the advantage of any polynomial-time attacker against these schemes is bounded by $\delta _{ENC}(\lambda )$ and $\delta _{PPRF}(\lambda )$, respectively.

Lemma 4.1

The construction given achieves $\tau (\Phi ) \le 4 \tau '(\Phi )$, $\sigma (\Phi ,s,\lambda ) \le \mathrm {poly}(\lambda , \varphi (\Phi ), p(\Phi ), \log L) + \Delta$, and $\delta (\lambda ) \le O(\delta _{ENC}(\lambda ) + \delta _{PPRF}(\lambda ))$.

Lemma 4.1

It’s easy to see that $\tau (\Phi ) \le 4 \tau '(\Phi )$ since we added at most one intermediate configuration in between any pebbling steps to define the half-sequence of hybrid functions of length at most $2\tau '(\Phi )$, and therefore the length of the full sequence is of length at most $4\tau '(\Phi )$.

We now compute $\sigma (\Phi ,s,\lambda )$ which is a bound on the circuit size of

$$\begin{aligned} \left\{ \textsf {Gar.HInpEn} ^{(t)},\textsf {Gar.HCirEn} ^{(t)}\; \big \vert \;t\in [\tau ]\right\} . \end{aligned}$$

First, we note that the size of the punctured key $K_{\textsf {pun} }^{t}$ is $|K_{\textsf {pun} }^{t}| \le \varphi (\Phi )\mathrm {poly}(\lambda )$ since it hardwires at most $\varphi (\Phi )$ garbled gates. Secondly we note that the size of any configuration $\textsf {conf} _t$ can be described by at most $O(p(\Phi ) \log L)$ bits since it only needs to specify the $p(\Phi )$ gates that are in $\textsf {CompDepSimGate}$ mode and in $\frac{1}{2}\textsf {CompDepSimGate}$ mode, the bits $v(w_c)$ for each outgoing wire $w_c$ of such gates, and the index $g^{(t)}_{gray}$ to be able to decide if a gate is in $\textsf {SimGate}$ or $\textsf {RealGate}$ mode. Lastly, the function $\textsf {Gar.HCirEn} ^{(t)}$ needs to run the circuit $C_\mathsf{de}$ or $C_\mathsf{de}'$ once and then apply some processing on the output. Therefore, by observation, the circuit size is bounded by $\mathrm {poly}(\lambda , \varphi (\Phi ), p(\Phi ), \log L) + \Delta$.

Finally, the bound on $\delta (\lambda )$ follows directly from the security proof. $\square$

In [39] (Section 6, Strategy 2), it is shown that any circuit topology of depth d and circuit size L can be pebbled using $p(\Phi ) \le 2d$ black pebbles and in $\tau '(\Phi ) \le L 4^d$ steps. Furthermore, it is easy to see that this pebbling is succinct.⁴ Therefore, by plugging these parameters into Lemma 4.1 we get the proof of Theorem 4.1.

5 Single-Key Succinct PKFE from SXIO and PKE

This section consists of four subsections. The main part is constructing a weakly succinct PKFE scheme for boolean functions in Sect. 5.2. First, in Sect. 5.1, we construct a succinct IBE scheme with $\gamma$-compression, which we shall use as a building block in Sect. 5.2. In Sect. 5.3, we present a transformation from weakly succinct PKFE schemes for boolean functions into ones for non-boolean functions. Lastly, we explain how the pieces come together to give IO from SKFE in Sect. 5.4.

5.1 A Succinct IBE Scheme

In this section, we construct a succinct IBE scheme from SXIO and PKE. Here by succinct, we mean that the size of the encryption circuit (and then also of the master public key) is sublinear in the size of the identity space (roughly, $\left| \mathcal {ID}\right| ^{\gamma }$, with $\gamma < 1$, see Sect. 2.6 for the complete definition). In the following subsections, we will use the constructed IBE as a building block in our construction of succinct PKFE.

Theorem 5.1

For any $\beta< \gamma < 1$, assuming there exists a $\beta$-compressing SXIO scheme for $\textsf {P} /\textsf {poly}$, a puncturable PRF, and a plain PKE scheme, there exists a succinct IBE scheme with $\gamma$-compression. Moreover, assuming the underlying primitives are $\delta$-secure so is the resulting IBE scheme.

We start by describing the IBE construction and then argue its security. Let $\mathcal {PPRF}= ({\textsf {PRF.Gen} }, {\textsf {PRF.Ev} },{\textsf {PRF.Punc} })$ be a puncturable PRF, $PKE= (\textsf {PKE} .{\textsf {Gen} }, \textsf {PKE} .{\textsf {Enc} }, \textsf {PKE} .{\textsf {Dec} })$ a PKE scheme, and $\textsf {sxi} \mathcal {O}$ a $\beta$-compressing SXIO scheme. Let $[s]$ denote the identity space.

Construction The scheme ${\textsf {IBE} }=({\textsf {Setup} },{\textsf {KeyGen} },{\textsf {Enc} },{\textsf {Dec} })$ for an identity space $\mathcal {ID}=[s]$ is given by the following algorithms.

•  ${\textsf {Setup} }(1^\lambda )$:

  • Choose puncturable PRF key $S\leftarrow {\textsf {PRF.Gen} }(1^\lambda )$.

  • Construct a circuit $\textsf {KG} _{{\textsf {ibe} }}[S]$ as described in Fig. 3 that computes $r_{i} ={\textsf {PRF.Ev} }_{S}(i)$ for an input $i\in [s]$ and generates a pair of keys $(\textsf {PKE} .{\textsf {PK} }_{i},\textsf {PKE} .{\textsf {SK} }_{i}) \leftarrow \textsf {PKE} .{\textsf {Gen} }(1^\lambda ;r_{i})$.

  • Output ${{\textsf {MPK}}} =\textsf {sxi} \mathcal {O}(\textsf {KG} _{{\textsf {ibe} }}[S])$ and ${\textsf {MSK} }=\{\textsf {PKE} .{\textsf {SK} }_{i}\}_{i\in [s]}$.

•  ${\textsf {KeyGen} }({\textsf {MSK} },\textsf {id} )$:

  • Parse ${\textsf {MSK} }= \{\textsf {PKE} .{\textsf {SK} }_{i}\}_{i\in [s]}$.

  • Output ${\textsf {SK} }_{\textsf {id} } =\textsf {PKE} .{\textsf {SK} }_{\textsf {id} }$.

•  ${\textsf {Enc} }({{\textsf {MPK}}},\textsf {id} ,x)$:

  • Compute $\textsf {PKE} .{\textsf {PK} }_{\textsf {id} }$ by running ${{\textsf {MPK}}}(\textsf {id} ) = \textsf {sxi} \mathcal {O}(\textsf {KG} _{{\textsf {ibe} }}[S])(\textsf {id} )$.

  • Output ${\textsf {CT} }\leftarrow \textsf {PKE} .{\textsf {Enc} }(\textsf {PKE} .{\textsf {PK} }_{\textsf {id} },x)$.

•  ${\textsf {Dec} }({\textsf {SK} }_\textsf {id} ,{\textsf {CT} })$:

  • Output $\textsf {PKE} .{\textsf {Dec} }({\textsf {SK} }_\textsf {id} ,{\textsf {CT} })$.

Fig. 3

Circuit $\textsf {KG} _{{\textsf {ibe} }}[S]$

Proof of Theorem 5.1

We now prove Theorem 5.1, starting by analyzing succinctness, and then moving on to the security proof.

5.1.1 Padding Parameter

The proof of security relies on indistinguishability of obfuscations of circuits $\textsf {KG} _{{\textsf {ibe} }}$ and $\textsf {KG} _{{\textsf {ibe} }}^*$ defined in Figs. 3 and 4. Accordingly, we set $\textsf {pad} = \max (\left| \textsf {KG} _{{\textsf {ibe} }}\right| ,\left| \textsf {KG} _{{\textsf {ibe} }}^*\right| )$. The circuits $\textsf {KG} _{{\textsf {ibe} }}$ and $\textsf {KG} _{{\textsf {ibe} }}^*$ compute a puncturable PRF over domain $[s]$, a PKE key pair, and may have punctured PRF keys and public keys hardwired. Thus,

$$\begin{aligned} \textsf {pad} \le \mathrm {poly}(\lambda ,\log (s)). \end{aligned}$$

Fig. 4

Circuit $\textsf {KG} _{{\textsf {ibe} }}^*[S\{\textsf {id} ^*\}]$

5.1.2 Succinctness

The input space for $\textsf {KG} _{{\textsf {ibe} }}$ is $[s]$. Therefore, by the SXIO guarantee, the size of the encryption circuit (dominated by running the obfuscated $\textsf {KG} _{{\textsf {ibe} }}$) is

$$\begin{aligned} s^{\beta } \cdot \mathrm {poly}(\lambda ,\ell ,\log s) \le s^{\gamma } \cdot \mathrm {poly}(\lambda ,\ell ), \end{aligned}$$

where $\ell$ is a bound on the length of encrypted messages.

5.1.3 Security Proof

Let us assume that the underlying primitives are $\delta$-secure. We define a sequence of hybrid games.

•  $\textsf {Hyb} _{0}$: The first game is the original selective security experiment for $b=0$, $\mathsf {Expt}^{\mathsf {IBE}}_{{\mathcal {A}}}(1^\lambda ,0)$. In this game, the adversary first selects the challenge identity $\textsf {id} ^*$ and messages $(m_0^*,m_1^*)$ and then gets an encryption of $m_0^*$ for identity $\textsf {id} ^*$ and the master public key. It can also query polynomially many secret keys for identities different from $\textsf {id} ^*$ (See Definition 2.12 for more details).

•  $\textsf {Hyb} _{1}$: We change $\textsf {KG} _{{\textsf {ibe} }}$ into $\textsf {KG} _{{\textsf {ibe} }}^*$ described in Fig. 4. In this hybrid game, we set $r^* = {\textsf {PRF.Ev} }_{S}(\textsf {id} ^*)$ and $(\textsf {PKE} .{\textsf {PK} }^*,\textsf {PKE} .{\textsf {SK} }^*) \leftarrow \textsf {PKE} .{\textsf {Gen} }(1^\lambda ;r^*)$. Thus, the behaviors of $\textsf {KG} _{{\textsf {ibe} }}$ and $\textsf {KG} _{{\textsf {ibe} }}^*$ are totally the same, and so are their size since we pad circuit $\textsf {KG} _{{\textsf {ibe} }}$ to have the same size as $\textsf {KG} _{{\textsf {ibe} }}^*$. Then, we can use the indistinguishability guarantee of $\textsf {sxi} \mathcal {O}$ and it holds $\textsf {Hyb} _{0}\approx _{\delta }\textsf {Hyb} _{1}$.

•  $\textsf {Hyb} _{2}$: We change $r^* = {\textsf {PRF.Ev} }_{S}(\textsf {id} ^*)$ into uniformly random $r^*$. Due to the pseudorandomness at punctured points, it holds $\textsf {Hyb} _{1}\approx _{\delta }\textsf {Hyb} _{2}$.

•  $\textsf {Hyb} _{3}$: We change ${\textsf {CT} }^*$ from $\textsf {PKE} .{\textsf {Enc} }(\textsf {id} ^*,m_0^*)$ to $\textsf {PKE} .{\textsf {Enc} }(\textsf {id} ^*,m_1^*)$. In $\textsf {Hyb} _{2}$ and $\textsf {Hyb} _{3}$, we do not need randomness used to generate $\textsf {PKE} .{\textsf {PK} }^*$. We just use the hardwired $\textsf {PKE} .{\textsf {PK} }^*$. Therefore, $\textsf {Hyb} _{2} \approx _{\delta } \textsf {Hyb} _{3}$ follows directly from the semantic security of the PKE scheme.

•  $\textsf {Hyb} _{4}$: This is $\mathsf {Expt}^{\mathsf {IBE}}_{{\mathcal {A}}}(1^\lambda ,1)$. We can show the indistinguishability between $\textsf {Hyb} _{3}$ and $\textsf {Hyb} _{4}$ in a reverse manner.

This completes the proof of Theorem 5.1. $\square$

5.2 Weakly Succinct PKFE for Boolean Functions

We now construct a single-key weakly succinct PKFE scheme for the class of boolean functions. The construction is based on succinct IBE, decomposable garbling, and SXIO.

Theorem 5.2

Let $\mathcal {C}= \left\{ \mathcal {C}_\lambda \right\} _{\lambda \in \mathbb {N}}$ be a family of circuits with a single output bit and let $n(\lambda ),s(\lambda ),d(\lambda )$ be bounds on their input length, size, and depth (respectively). For any constants $\beta ,\gamma$ such that $3\beta< \gamma < 1$, assuming a $\delta$-secure, $\beta$-compressing $\text {SXIO}$ for $\textsf {P} /\textsf {poly}$, there exists a constant $\alpha$, such that given any $\delta$-secure, $\alpha$-compressing IBE, and $\delta$-secure one-way functions, there exists a $2^d s \delta$-secure succinct PKFE for $\mathcal {C}$ with compression factor $\gamma$.

Depth preserving universal circuits To prove the above theorem, we recall the existence of depth preserving universal circuits [24]. Concretely, any family of circuits $\mathcal {C}$ as considered in Theorem 5.2 has a uniform family of universal circuits $\left\{ U_\lambda \right\} _{\lambda \in \mathbb {N}}$ with fan-out $\lambda$,⁵ depth O(d), and size $s^3\cdot \mathrm {polylog}(s)$, for some fixed polynomial $\mathrm {poly}$. Each such circuit takes as input a description $(f_1,\dots ,f_s)$ of a function in $\mathcal {C}$ and an input $(x_1,\dots ,x_n)$ and outputs f(x). Furthermore, uniformity here means that each circuit has a decomposition circuit of size $\mathrm {polylog}(s)$.

Ingredients and notation used in the construction

• We denote by $U^{(x)}: \{0,1\}^{s} \rightarrow \{0,1\}$ the universal circuit, with $x \in \{0,1\}^n$ being a hardwired bit string, such that on input $(f_1,\ldots ,f_s)$, the circuit $U^{(x)}$ outputs f(x). This circuit has a decomposition circuit of size $\mathrm {poly}(n,\log (s))$, which we denote by $U^{(x)}_{\textsf {de} }$. We also denote by $L$ the number of gates in the circuit $U^{(x)}$.

• Let $\textsf {sxi} \mathcal {O}$ be a $\delta$-secure, $\beta$-compressing SXIO scheme.

• Let ${\textsf {IBE} }=({\textsf {IBE} }.\textsf {Setup} ,{\textsf {IBE} }.\textsf {KeyGen} ,{\textsf {IBE} }.\textsf {Enc} ,{\textsf {IBE} }.\textsf {Dec} )$ be $\delta$-secure, succinct, IBE scheme with $\alpha$-compression for the identity space being $\mathcal {ID}= [s]\times \{0,1\}$.

• Let $(\textsf {Gar.CirEn} ,\textsf {Gar.InpEn} ,\textsf {Gar.De} )$ be a decomposable garbling scheme with $(\sigma ,\tau ,\delta )$-decomposable indistinguishability where $\tau = s2^{O(d)}$ and $\sigma = \mathrm {poly}(\lambda ,n,d,\log (s))$. Such schemes are implied by $\delta$-secure one-way functions (Theorem 4.1).

• Let $\mathcal {PPRF}= ({\textsf {PRF.Gen} }, {\textsf {PRF.Ev} },{\textsf {PRF.Punc} })$ be a $\delta$-secure puncturable PRF. These are implied by $\delta$-secure one-way functions [11, 23, 30, 45].

Construction The scheme consists of the following algorithms.

•  ${\textsf {PKFE} }.{\textsf {Setup} }(1^\lambda )$:

  • Run $({\textsf {MSK} }_{{\textsf {ibe} }},{{\textsf {MPK}}}_{{\textsf {ibe} }}) \leftarrow {\textsf {IBE} }.\textsf {Setup} (1^\lambda )$.

  • Set ${\textsf {MSK} }= {\textsf {MSK} }_{{\textsf {ibe} }}$, ${{\textsf {MPK}}}= {{\textsf {MPK}}}_{{\textsf {ibe} }}$.

•  ${\textsf {PKFE} }.{\textsf {Key} }({\textsf {MSK} },f)$:

  • Compute ${\textsf {SK} }_{i,f_i} \leftarrow {\textsf {IBE} }.\textsf {KeyGen} ({\textsf {MSK} }_{{\textsf {ibe} }},(i,f_i))$ for $i \in [s]$, where $f = (f_1,\ldots ,f_s)$.

  • Return ${\textsf {SK} }_{f} =\{{\textsf {SK} }_{i,f_i}\}_{i \in [s]}$.

•  ${\textsf {PKFE} }.{\textsf {Enc} }({{\textsf {MPK}}},x)$:

  • Compute $U^{(x)}_{\textsf {de} }$ and pick a garbling key $K\leftarrow \{0,1\}^\lambda$ and a punctured key $S\leftarrow {\textsf {PRF.Gen} }(1^\lambda )$;

  • Generate an obfuscation $\widetilde{\textsf {IGC} }=\textsf {sxi} \mathcal {O}(1^\lambda ,\textsf {IGC} [K,S,{{\textsf {MPK}}}])$ of the input garbling circuit defined in Fig. 5;

  • Generate an obfuscation $\widetilde{\textsf {GGC} }=\textsf {sxi} \mathcal {O}(1^\lambda ,\textsf {GGC} [K,U^{(x)}_{\textsf {de} }])$ of the gate garbling circuit defined in Fig. 6;

  • Return ${\textsf {CT} }_x=(\widetilde{\textsf {IGC} },\widetilde{\textsf {GGC} })$.

•  ${\textsf {PKFE} }.{\textsf {Dec} }({\textsf {SK} }_f,{\textsf {CT} }_x)$:

  • For $i \in [s]$, run $\widetilde{\textsf {IGC} }(i,f_i)$ to obtain an IBE ciphertext, and decrypt the output using ${\textsf {SK} }_{i,f_i}$ to obtain $\hat{f}_i$.

  • For all $g \in [L]$, run $\widetilde{\textsf {GGC} }(g)$, in order to obtain the garbled gate $\widehat{G}_g$.

  • Return $y\leftarrow \textsf {Gar.De} (\widehat{C},\hat{f})$, with $\widehat{C}= \left\{ \widehat{G}_g\right\} _{g\in [L]}$ and $\hat{f}= \left\{ \hat{f}_i\right\} _{i\in [s]}$.

Fig. 5

Circuit $\textsf {IGC} [K,S,{{\textsf {MPK}}}]$

Fig. 6

Circuit $\textsf {GGC} [K,U^{(x)}_{\textsf {de} }]$

Proof of Theorem 5.2

We now prove Theorem 5.2, starting by correctness, continuing to succinctness, and ending with the proof of security. In what follows, let $s$, d, and n be bounds on the size, the depth, and the input length of functions in $\mathcal {C}$.

5.2.1 Correctness

Correctness immediately follows from the correctness of the underlying identity-based encryption and decomposable garbling schemes.

5.2.2 Padding Parameter

The proof of security relies on the indistinguishability guarantee of $\text {SXIO}$ with respect to two hybrid sequences of circuits, one corresponding to input garbling, and the other one corresponding to gate garbling. Thus, we pad every circuit of each sequence to the maximal size of any circuit in the sequence. That is, we consider

$$\begin{aligned}&\mathcal {S}_{\textsf {IGC} } = \{\textsf {IGC} , \textsf {HIGC} _t, \textsf {HIGC} _t^{(j)} \vert 1 \le t \le \tau , 1 \le j \le 5\}\\&\mathcal {S}_{\textsf {GGC} } = \{\textsf {GGC} , \textsf {HGGC} _t, \textsf {HGGC} _t^{(j)} \vert 1 \le t \le \tau , 1 \le j \le 5\}, \end{aligned}$$

and let $\textsf {pad} _{\textsf {IGC} } = \max _{C \in \mathcal {S}_{\textsf {IGC} }} \left| C\right|$ and $\textsf {pad} _{\textsf {GGC} } = \max _{C \in \mathcal {S}_{\textsf {GGC} }} \left| C\right|$.

We bound $\textsf {pad} _{\textsf {IGC} }$ and $\textsf {pad} _{\textsf {GGC} }$ as follows:

• Any circuit in $\mathcal {S}_{\textsf {IGC} }$ consists of the following:

  • – A punctured PRF computation (deriving randomness for IBE encryption) over a domain of size O(s), using keys that may be punctured at at most constant number of points. The contribution to the circuit size is bounded by $\mathrm {poly}(\lambda ,\log (s))$.

  • – Input garbling (possibly via one of the hybrid input garbling circuits). The contribution to the circuit size is bounded by $\sigma = \mathrm {poly}(\lambda ,d,\log (s),n)$.

  • – IBE encryption of garbled inputs, using a hardwired public key and up to a constant number of hardwired ciphertexts. The contribution to the circuit size is bounded by $s^\alpha \cdot \mathrm {poly}(\lambda , \sigma ) = s^\alpha \cdot \mathrm {poly}(\lambda ,d,\log (s),n)$.

  Overall,

  $$\begin{aligned} \textsf {pad} _{\textsf {IGC} } \le s^\alpha \cdot \mathrm {poly}(\lambda ,n,d,\log (s)) . \end{aligned}$$

• Any circuit in $\mathcal {S}_{\textsf {GGC} }$ performs a gate garbling operation (possibly via one of the hybrid gate garbling circuits). The overall contribution to the circuit size is bounded by

  $$\begin{aligned} \textsf {pad} _{\textsf {GGC} } \le \sigma \le \mathrm {poly}(\lambda ,n,d,\log (s)) . \end{aligned}$$

5.2.3 Succinctness

We show that for any $\beta<\gamma <1$ and an appropriate choice of $\alpha <1$, the size of the encryption circuit is bounded by $s^{\gamma }\cdot \mathrm {poly}(\lambda ,n,d)$.

Let $\textsf {sxi} \mathcal {O}$ be $\beta$-compressing. Let e be the size of the obfuscated circuits $\widetilde{\textsf {IGC} }$ and $\widetilde{\textsf {GGC} }$ created during encryption. Since the input spaces of $\textsf {IGC}$ and $\textsf {GGC}$ are, respectively, $[2s]$ and $[L]$, $\text {SXIO}$ guarantees:

$$\begin{aligned} e&\le (2s)^\beta \cdot \mathrm {poly}(\lambda ,\left| \textsf {IGC} \right| ) + L^\beta \cdot \mathrm {poly}(\lambda ,\left| \textsf {GGC} \right| )\\&\le s^\beta \cdot \mathrm {poly}(\lambda ,\textsf {pad} _{\textsf {IGC} }) + L^\beta \cdot \mathrm {poly}(\lambda ,\textsf {pad} _{\textsf {GGC} }) , \end{aligned}$$

where $\mathrm {poly}$ is a fixed polynomial. Then, using the above bounds on $\textsf {pad} _{\textsf {IGC} }$ and $\textsf {pad} _{\textsf {GGC} }$, and denoting by $c = O(1)$ the polynomial blowup in the circuit size incurred in $\textsf {sxi} \mathcal {O}$, we obtain:

$$\begin{aligned} e \le s^{\beta + c \alpha } \cdot \mathrm {poly}(\lambda ,n,d,\log (s)) + L^\beta \cdot \mathrm {poly}(\lambda ,n,d,\log (s)) . \end{aligned}$$

Recalling that $L$ is bounded by $s^3\cdot \mathrm {polylog}(s)$, and that $3\beta < \gamma$, we deduce that

$$\begin{aligned} e \le s^{\gamma } \cdot \mathrm {poly}(\lambda ,n,d), \end{aligned}$$

provided that we choose $\alpha$ such that $\beta +\alpha c < \gamma$ (which is possible since $\beta < \gamma$ and c is a constant).

5.2.4 Security Proof

Let $x_0,x_1 \in \{0,1\}^n$ denote the challenge messages and f denote the function query provided by the adversary, and assume $f(x_0)=f(x_1)$. Let $U^{(x_0)}$ and $U^{(x_1)}$ be the universal circuits defined similarly to $U^{(x)}$ above, and $U^{(x_0)}_{\textsf {de} }$ and $U^{(x_1)}_{\textsf {de} }$ their respective decomposition circuits. Note that $U^{(x_0)}$ and $U^{(x_1)}$ have the same topology (they are the same universal circuit with a different hardwired input of the same size n), and in particular, their decomposition circuits are of the same size. Furthermore, these two circuits also satisfy

$$\begin{aligned} U^{(x_0)}(f) = f(x_0) = f(x_1)=U^{(x_1)}(f) . \end{aligned}$$

$U^{(x_0)}$ and $U^{(x_1)}$ satisfy the properties required by the $(\sigma ,\tau ,\delta )$-decomposable indistinguishability security of the decomposable garbling scheme, and thus, there exist circuits $\left\{ \textsf {Gar.HInpEn} ^{(t)},\textsf {Gar.HCirEn} ^{(t)}\; \big \vert \;t\in [\tau ]\right\}$, whose size is at most $\sigma$, as well as (possibly inefficient) hybrid functions $\left\{ \textsf {Gar.HPunc} ^{(t)}\; \big \vert \;t\in [\tau ]\right\}$ as given by Definition 4.1.

We accordingly consider a sequence of $\tau +2$ hybrid games:

•  $\textsf {Hyb} _{0}$: The first game is $\mathsf {Expt}^{\mathsf {FE}}_{{\mathcal {A}}}(1^\lambda ,0)$, where the adversary hands $x_0,x_1,f$ and gets back from the challenger an encryption of $x_0$.

•  $\textsf {Hyb} _{t}$ ($1 \le t \le \tau$): The t-th game is defined similarly to $\mathsf {Expt}^{\mathsf {FE}}_{{\mathcal {A}}}(1^\lambda ,0)$ except that the challenge ciphertext ${\textsf {CT} }^*$ consists of obfuscations of corresponding hybrid circuits:

  $$\begin{aligned} {\textsf {CT} }^* = (\textsf {sxi} \mathcal {O}(1^\lambda ,\textsf {HIGC} _t[K,S,{{\textsf {MPK}}}]),\textsf {sxi} \mathcal {O}(1^\lambda ,\textsf {HGGC} _t[K])), \end{aligned}$$

  where circuits $\textsf {HIGC} _t[K,{{\textsf {MPK}}}]$ and $\textsf {HGGC} _t[K]$ are defined in Fig. 7 and Fig. 8, respectively, and $K$ is the key used in the decomposable garbling scheme for computing the challenge ciphertext.

•  $\textsf {Hyb} _{\tau +1}$: The last game is $\mathsf {Expt}^{\mathsf {FE}}_{{\mathcal {A}}}(1^\lambda ,1)$, where $x_1$ is encrypted (rather than $x_0$).

Fig. 7

Circuit $\textsf {HIGC} _t[K,S,{{\textsf {MPK}}}]$

Fig. 8

Circuit $\textsf {HGGC} _t[K]$

We first note that $\textsf {Hyb} _{0} \approx _{\delta } \textsf {Hyb} _{1}$ and $\textsf {Hyb} _{\tau } \approx _{\delta } \textsf {Hyb} _{\tau + 1}$. Indeed, by the guarantee of the decomposable garbling scheme (Definition 4.2), the obfuscated circuits in the respective hybrids compute the exact same function (and are padded to the same size). $\delta$-indistinguishability follows by the $\text {SXIO}$ guarantee.

We now argue that hybrids $\textsf {Hyb} _{t}$ and $\textsf {Hyb} _{t+1}$, for $1 \le t \le \tau -1$, are computationally indistinguishable.

Indistinguishability of $\textsf {Hyb} _{t}$ and $\textsf {Hyb} _{t+1}$ $(1\le t\le \tau -1)$

The indistinguishability of each such two hybrid games is proven by a sequence of five intermediate hybrid games $\textsf {Hyb} _{t}^{(1)},\dots ,\textsf {Hyb} _{t}^{(5)}$ as follows. The five hybrid games only differ from $\textsf {Hyb} _{t}$ in the way the challenge ciphertext ${\textsf {CT} }^*$ is computed. For $1 \le j \le 5$, the challenge ciphertext is computed in $\textsf {Hyb} _{t}^{(j)}$ as the obfuscations of the two circuits $\textsf {HIGC} _t^{(j)}$ and $\textsf {HGGC} _t^{(j)}$, described in Figs. 9 and 10, where the role of the hardwired values $K^{(j)},S^{(j)},{\textsf {CT} }_{i^*,f_{i^*}}^{(j)},{\textsf {CT} }_{i^*,1-f_{i^*}}^{(j)}$ and $\widehat{G}_{g^*}^{(j)}$ is described below. We also let $(K^*,g^*,i^*) \leftarrow \textsf {Gar.HPunc} ^{(t)}(K)$. Then, $f_{i^*}$ denotes the $i^*$-th bit of the function queried by the adversary.

Fig. 9

Circuit $\textsf {HIGC} _t^{(j)}[K^{(j)},S^{(j)},{{\textsf {MPK}}},{\textsf {CT} }_{i^*,f_{i^*}}^{(j)},{\textsf {CT} }_{i^*,1-f_{i^*}}^{(j)}]$, $1 \le j \le 5$

Fig. 10

Circuit $\textsf {HGGC} _t^{(j)}[K^{(j)},\widehat{G}_{g^*}^{(j)}]$, $1 \le j \le 5$

We now prove indistinguishability of $\textsf {Hyb} _{t}$ and $\textsf {Hyb} _{t+1}$ as follows:

• $\textsf {Hyb} _{t}$to$\textsf {Hyb} _{t}^{(1)}$: in $\textsf {Hyb} _{t}^{(1)}$, we fix $S^{(1)} \leftarrow {\textsf {PRF.Punc} }(S,\{(i^*,1-f_{i^*})\})$ and $K^{(1)} \leftarrow K^*$. We hardwire the value ${\textsf {CT} }_{i^*,f_{i^*}}^{(1)} \leftarrow {\textsf {IBE} }.\textsf {Enc} ({{\textsf {MPK}}},(i^*,f_{i^*}),\textsf {Gar.HInpEn} ^{(t)}(i^*,f_{i^*};K); {\textsf {PRF.Ev} }_{S^{(1)}}(i^*,f_{i^*}))$, as well as ${\textsf {CT} }_{i^*,1-f_{i^*}}^{(1)} \leftarrow {\textsf {IBE} }.\textsf {Enc} ({{\textsf {MPK}}},(i^*,1-f_{i^*}),\textsf {Gar.HInpEn} ^{(t)}(i^*,1-f_{i^*};K);{\textsf {PRF.Ev} }_{S}(i^*,1-f_{i^*}))$ in the first circuit, and $\widehat{G}_{g^*}^{(1)} \leftarrow \textsf {Gar.HCirEn} ^{(t)}(g^*;K)$ in the second circuit. Therefore, it is immediate that, by definitions, both circuits are functionally equivalent in both games since hardwired values are correctly computed, so the two hybrid games are computationally indistinguishable under the security of $\textsf {sxi} \mathcal {O}$. Hence, we have $\textsf {Hyb} _{t} \approx _{\delta } \textsf {Hyb} _{t}^{(1)}$.

• $\textsf {Hyb} _{t}^{(1)}$to$\textsf {Hyb} _{t}^{(2)}$: The difference between $\textsf {Hyb} _{t}^{(1)}$ and $\textsf {Hyb} _{t}^{(2)}$ is that we now define ${\textsf {CT} }_{i^*,f_{i^*}}^{(2)} \leftarrow {\textsf {IBE} }.\textsf {Enc} ({{\textsf {MPK}}},(i^*,f_{i^*}),\textsf {Gar.HInpEn} ^{(t+1)}(i^*,f_{i^*};K); {\textsf {PRF.Ev} }_{S^{(2)}}(i^*,f_{i^*}))$ in the first circuit, and $\widehat{G}_{g^*}^{(2)} \leftarrow \textsf {Gar.HCirEn} ^{(t+1)}(g^*;K)$. Other values remain the same as before. Thus, these two hybrid games are computationally indistinguishable assuming decomposable indistinguishability of the decomposition garbling scheme, and we have $\textsf {Hyb} _{t}^{(1)} \approx _{\delta } \textsf {Hyb} _{t}^{(2)}$.

• $\textsf {Hyb} _{t}^{(2)}$to$\textsf {Hyb} _{t}^{(3)}$: In the third hybrid game, we only modify the previous game by letting ${\textsf {CT} }_{i^*,1-f_{i^*}}^{(3)} \leftarrow {\textsf {IBE} }.\textsf {Enc} ({{\textsf {MPK}}},(i^*,1-f_{i^*}),\textsf {Gar.HInpEn} ^{(t)}(i^*,1-f_{i^*};K);r)$, with r being a fresh uniformly random value. Other values remain the same as before. Assuming ${\textsf {PRF.Ev} }$ is a $\delta$-secure puncturable pseudorandom function, these two hybrid games are computationally indistinguishable, and we have $\textsf {Hyb} _{t}^{(2)} \approx _{\delta } \textsf {Hyb} _{t}^{(3)}$.

• $\textsf {Hyb} _{t}^{(3)}$to$\textsf {Hyb} _{t}^{(4)}$: In the fourth hybrid game, we define ${\textsf {CT} }_{i^*,1-f_{i^*}}^{(4)} \leftarrow {\textsf {IBE} }.\textsf {Enc} ({{\textsf {MPK}}},(i^*,1-f_{i^*}),\textsf {Gar.HInpEn} ^{(t+1)}(i^*,1-f_{i^*};K);r)$, with r being a fresh uniformly random value. Other values remain the same as before. Assuming the security of the identity-based encryption scheme, these two hybrid games are computationally indistinguishable, and we have $\textsf {Hyb} _{t}^{(3)} \approx _{\delta } \textsf {Hyb} _{t}^{(4)}$. The reduction is immediate but crucially relies on the fact that ${\textsf {CT} }_{i^*,1-f_{i^*}}^{(4)}$ is computed as an encryption for the identity $(i^*,1-f_{i^*})$ and not for the identity $(i^*,f_{i^*})$, since the secret key for identity $(i^*,f_{i^*})$ is revealed to the adversary when giving the functional secret key for f, but not the secret key for identity $(i^*,1-f_{i^*})$.

• $\textsf {Hyb} _{t}^{(4)}$to$\textsf {Hyb} _{t}^{(5)}$: In this fifth hybrid game, we once again use randomness computed with the PPRF by letting ${\textsf {CT} }_{i^*,1-f_{i^*}}^{(5)} \leftarrow {\textsf {IBE} }.\textsf {Enc} ({{\textsf {MPK}}},(i^*,1-f_{i^*}),\textsf {Gar.HInpEn} ^{(t+1)}(i^*,1-f_{i^*};K); {\textsf {PRF.Ev} }_{S}(i^*,1-f_{i^*}))$. Other values remain the same as before. Once again, assuming ${\textsf {PRF.Ev} }$ is a secure puncturable pseudorandom function, we have $\textsf {Hyb} _{t}^{(4)} \approx _{\delta } \textsf {Hyb} _{t}^{(5)}$.

• $\textsf {Hyb} _{t}^{(5)}$to$\textsf {Hyb} _{t+1}$: By definition, it is clear that the two circuits used in $\textsf {Hyb} _{t}^{(5)}$ are functionally equivalent to the two circuits used in $\textsf {Hyb} _{t}^{(5)}$, since $\textsf {Gar.HInpEn} ^{(t)}(i,b;K^{(5)}) = \textsf {Gar.HInpEn} ^{(t+1)}(i,b;K)$ for any (i, b) with that $i \ne i^*$. Therefore, under the security of $\textsf {sxi} \mathcal {O}$, these two hybrid games are computationally indistinguishable, and we have $\textsf {Hyb} _{t}^{(5)} \approx _{\delta } \textsf {Hyb} _{t+1}$.

This concludes the proof of Theorem 5.2. $\square$

5.3 Weakly Succinct PKFE for Non-boolean Functions

In this section, we give a transformation from weakly succinct PKFE schemes for boolean functions into ones for non-boolean functions.

Theorem 5.3

Let $\mathcal {C}= \left\{ \mathcal {C}_\lambda \right\} _{\lambda \in \mathbb {N}}$ be a family of circuits (with multiple output bits) and let $n(\lambda ),s(\lambda ),d(\lambda )$ be bounds on their input length, size, and depth (respectively). For any constants $\beta< \gamma < 1$, assuming a $\beta$-compressing $\text {SXIO}$ for $\textsf {P} /\textsf {poly}$, there exists a constant $\alpha$, such that given any $\alpha$-compressing weakly succinct PKFE for boolean functions of size $s\cdot \mathrm {polylog}(s)$ and depth O(d), and one-way functions, there exists a succinct PKFE for $\mathcal {C}$ with compression factor $\gamma$. If all primitives are $\delta$-secure so is the resulting scheme.

The transformation is essentially the same transformation presented in [51, Section 4], with the following differences:

• They use XIO rather than SXIO, which results in a PKFE scheme where only the size of ciphertexts is compressed, whereas the time to encrypt may be large. They then make an extra step, based on LWE, to make encryption efficient. Using SXIO directly as we do, allows avoiding this step.

• They start from weakly succinct PKFE for boolean functions where the size of ciphertexts is completely independent of the size s of the function class considered. Due to this, they can start from XIO with any compression factor $\beta <1$. In our notion of weakly succinct, there is dependence on $s^\alpha$, for some $\alpha <1$, and we need to make sure that $\beta$ and $\alpha$ are appropriately chosen to account for this.

• As stated, their notion of weak succinctness for PKFE does not explicitly scale with the depth of the function class considered. Eventually, they apply their transformation to function classes in $\text {NC}^1$, assuming puncturable PRFs in $\text {NC}^1$ (which exist under LWE). Our succinctness notion allows polynomial dependence on the depth, which should be roughly preserved through the transformation.

For the sake of completeness, we describe the transformation in full and then analyze the efficiency aspects. The proof of security is identical to the one in [51] and is omitted.

Construction Let $\textsf {BFE} =(\textsf {BFE} .{\textsf {Setup} },\textsf {BFE} .{\textsf {Key} },\textsf {BFE} .{\textsf {Enc} },\textsf {BFE} .{\textsf {Dec} })$ be a weakly succinct single-key public-key FE scheme for boolean functions. Our weakly succinct single-key public-key FE scheme for multi-bit functions is given by the following algorithms.

•  ${\textsf {Setup} }(1^\lambda )$:

  • Compute $(\textsf {BFE} .{{\textsf {MPK}}},\textsf {BFE} .{\textsf {MSK} }) \leftarrow \textsf {BFE} .{\textsf {Setup} }(1^\lambda )$.

  • Output $({{\textsf {MPK}}},{\textsf {MSK} }) =(\textsf {BFE} .{{\textsf {MPK}}},\textsf {BFE} .{\textsf {MSK} })$.

•  ${\textsf {KeyGen} }({\textsf {MSK} },f)$:

  • Run $\textsf {BFE} .{\textsf {SK} }_{C_f} \leftarrow \textsf {BFE} .{\textsf {Key} }(\textsf {BFE} .{\textsf {MSK} },C_f)$ where $C_f:\{0,1\}^n\times \{0,1\}^{\log \ell }$ is a function that takes (x, i) as inputs and outputs the i-th bit (out of $\ell$) of f(x) (this is a boolean function).

•  ${\textsf {Enc} }({{\textsf {MPK}}},x\in \{0,1\}^n)$:

  • Sample a puncturable PRF key $S\leftarrow {\textsf {PRF.Gen} }(1^\lambda )$,

  • Generate $\textsf {sxi} \mathcal {O}(\textsf {SE} [x,S,\textsf {BFE} .{{\textsf {MPK}}}])$ where the circuit $\textsf {SE} [x,S,\textsf {BFE} .{{\textsf {MPK}}}]$ is described in Fig. 11.

  • Output ${\textsf {CT} }= \textsf {sxi} \mathcal {O}(\textsf {SE} [x,S,\textsf {BFE} .{{\textsf {MPK}}}])$.

•  ${\textsf {Dec} }({\textsf {SK} }_f,{\textsf {CT} }_x)$:

  • Compute $\textsf {BFE} .{\textsf {CT} }_i \leftarrow {\textsf {CT} }(i)$, and $y_i \leftarrow \textsf {BFE} .{\textsf {Dec} }(\textsf {BFE} .{\textsf {SK} }_{C_f},\textsf {BFE} .{\textsf {CT} }_i)$ for all $i \in [\ell ]$.

  • Output $y = (y_1, \ldots , y_\ell )$.

Fig. 11

Circuit $\textsf {SE} [x,S,\textsf {BFE} .{{\textsf {MPK}}}]$

Proof of Theorem 5.3

We now prove Theorem 5.3. We focus on succinctness. The proof of security is based on a standard probabilistic IO argument [25], is identical to the one given by Lin et al. [51, Theorem 6], and thus omitted. In what follows, let s, d, n, and $\ell$ be bounds on the size, the depth, input and output lengths of functions in $\mathcal {C}$.

5.3.1 Padding Parameter

In the proof of security [51], the indistinguishability guarantee of $\text {SXIO}$ is invoked for the circuit $\textsf {SE}$ and several hybrid versions of this circuit. All of these circuits compute a puncturable pseudorandom function on an input $i \in [\ell ]$ and an encryption using $\textsf {BFE} .{\textsf {Enc} }$. Therefore, their size is bounded by $\mathrm {poly}(\lambda ,\log (\ell )) + e'$ where $e'$ is the size of the encryption circuit for the class of boolean circuits $\mathcal {C}' = \left\{ C_f\; \big \vert \;f \in \mathcal {C}\right\}$.

To bound $e'$, we note that the size and depth of circuits in $\mathcal {C}'$ are preserved up to polylogarithmic factors (induced by selecting one of $\ell \le s$ output bits):

$$\begin{aligned} s' := \left| C_f\right| \le s\cdot \mathrm {polylog}(s) \quad d' := \textsf {depth} (C_f) \le O(d). \end{aligned}$$

Thus, by the succinctness guarantee of the $\text {PKFE}$ for boolean functions, we know that

$$\begin{aligned} e' \le s'^\alpha \cdot \mathrm {poly}(d',\lambda ,n+\log \ell ) \le s^\alpha \cdot \mathrm {poly}(d,\log (s),\lambda ,n), \end{aligned}$$

where $\alpha$ is the compression factor of the $\text {PKFE}$. Hence, we obtain:

$$\begin{aligned} \textsf {pad} \le s^\alpha \cdot \mathrm {poly}(d,\log (s),\lambda ,n) . \end{aligned}$$

Fig. 12

An illustration of the path from PKE and 1-SKFE to IO. Dashed lines denote known results. White backgrounds denote our ingredients or goal. Primitives in rounded rectangles are subexponentially secure. $\gamma$-SXIO denotes SXIO with compression factor $\gamma$, which is an arbitrary constant less than 1. We ignore puncturable PRF in this figure since it is implied by OWF

5.3.2 Succinctness

We show that for any $\beta<\gamma <1$ and an appropriate choice of $\alpha <1$, the size of the encryption circuit is bounded by $s^{\gamma }\cdot \mathrm {poly}(\lambda ,n,d)$.

Let $\textsf {sxi} \mathcal {O}$ be $\beta$-compressing. Then, by the $\text {SXIO}$ guarantee, the size e of the obfuscated encryption circuit is bounded by

$$\begin{aligned} e \le \ell ^\beta \cdot \mathrm {poly}(\lambda ,\left| \textsf {SE} \right| ) \le s^\beta \cdot \mathrm {poly}(\lambda ,\textsf {pad} ) , \end{aligned}$$

where $\textsf {SE}$ is the obfuscated encryption circuit, and $\mathrm {poly}$ is a fixed polynomial. Then, letting $c = O(1)$ represent the polynomial blowup in circuit size incurred by $\textsf {sxi} \mathcal {O}$, we can bound

$$\begin{aligned} e \le s^\beta \cdot s^{c\cdot \alpha } \cdot \mathrm {poly}(d,n,\lambda ,\log (s)) \le s^{\gamma } \cdot \mathrm {poly}(d,n,\lambda ), \end{aligned}$$

where the last inequality holds provided that we choose the constant $\alpha$ such that $c\alpha + \beta < \gamma$. (Such a constant indeed exist since $\beta <\gamma$ and c is a constant.) $\square$

5.4 Putting It All Together: From SKFE and PKE to IO

We now show how the results proved in this section come together to give our main result. The main implications are also illustrated in Fig. 12.

Theorem 5.4

Let $\mathcal {C}= \left\{ \mathcal {C}_\lambda \right\} _{\lambda \in \mathbb {N}}$ be a family of circuits (with multiple output bits) and let $n(\lambda ),s(\lambda ),d(\lambda )$ be bounds on their input length, size, and depth (respectively). Then, for any constant $\gamma <1$, there exists a constant $\beta$, such that given any $\delta$-secure, $\beta$-compressing $\text {SXIO}$ for $\textsf {P} /\textsf {poly}$, and $\delta$-secure PKE, there exists $2^d s \delta$-secure, $\gamma$-compressing, weakly succinct PKFE for $\mathcal {C}$.

Proof

Fix some constant $\gamma$. The theorem follows from the previous theorems in this section as follows:

• By Theorem 5.3, there exist constants $\beta ',\alpha '$, such that $2^d s \delta$-secure, $\gamma$-compressing, weakly succinct PKFE for $\mathcal {C}$, follows from $2^d s \delta$-secure, $\beta '$-compressing $\text {SXIO}$ and $2^d s \delta$-secure, $\alpha '$-compressing, weakly succinct PKFE for boolean functions of size $s\cdot \mathrm {polylog}(s)$ and depth O(d), and $2^d s \delta$-secure one-way functions.

• By Theorem 5.2, there exist constants $\beta '',\alpha ''$ such that PKFE as required in the previous item follows from $\delta$-secure, $\beta ''$-compressing $\text {SXIO}$ and $\delta$-secure, $\alpha ''$-compressing IBE, and $\delta$-secure one-way functions.

• By Theorem 5.1, there exists a constant $\beta '''$ (in fact any $\beta '''<\alpha ''$), such that IBE as required in the previous item follows from $\delta$-secure, $\beta '''$-compressing $\text {SXIO}$ and $\delta$-secure PKE.

• In all of the above $\delta$-secure one-way functions follow from $\delta$-secure PKE.

Setting $\beta := \min (\beta ',\beta '',\beta ''')$, we derive the theorem. $\square$

Combining the above theorem with the result from Sect. 3, we obtain the following corollary.

Corollary 5.1

If there exist (1-input) SKFE for $\textsf {P} /\textsf {poly}$ and PKE, both subexponentially secure, then there exists IO for $\textsf {P} /\textsf {poly}$.

Proof

Fix any constants $\varepsilon ,\gamma <1$. For $\delta (\lambda )=2^{-\lambda ^{\varepsilon }}$.

• By Theorem 2.2 [22], for any constant $\gamma <1$, IO is implied by $\delta$-secure, $\gamma$-compressing, weakly succinct PKFE.

• By the Theorem 5.4, there exists $\beta$, such that PKFE as required in the previous item follows from $\beta$-compressing, $\delta$-secure $\text {SXIO}$ and $\delta$-secure PKE, when setting the security parameter for the $\text {SXIO}$ and PKE to $\tilde{\lambda }= \lambda \cdot d^{2/\varepsilon }$—this accounts for the $\mathrm {poly}(2^d)$ security loss, and only incurs $\mathrm {poly}(\lambda ,d,\log (s))$ overhead, which satisfies the succinctness requirements of the PKFE.

• By Theorem 3.1, letting $t = \frac{1}{\beta }-1$, SXIO as required in the previous item follows from $\delta$-secure t-input $\text {SKFE}$.

• By Theorem 2.1 [16], the required t-input $\text {SKFE}$ follows from any 1-input, $\delta$-secure SKFE.

The corollary follows. $\square$

Remark 5.1

(The security loss) In order, the known reductions [3, 22] of IO to weakly succinct PKFE incur a subexponential loss. Accordingly, reducing IO to SKFE based on our results incurs a similar loss. However, when restricting attention, to the transformation from SKFE to (weakly succinct) PKFE, then the loss is $\mathrm {poly}(2^d,\lambda )$, for circuits of depth d. In particular, for $\text {NC}^1$, our transformation incurs only polynomial security loss. Such a PKFE for $\text {NC}^1$ can then be bootstrapped to all polynomial-size circuits using the transformation of [1], and assuming also weak PRFs in $\text {NC}^1$.

In concurrent work [36, 50], it is shown that weakly succinct single-key PKFE can then be polynomially reduced to PKFE. In summary, SKFE and PRFs in $\text {NC}^1$ can be polynomially reduced to PKFE for all polynomial-size circuits.

Fig. 13

Circuit $\textsf {WE} [x,\textsf {PK} ]$

6 Polynomially Secure PKE from Secret-Key FE

In this section, we construct PKE from SKFE. Our starting point is Corollary 3.1 that directly follows from Theorems 2.1 and 3.1.

We now show how to construct a PKE scheme from such $\text {SXIO}$.

The construction Let $\left\{ {\textsf {PRG} }:\{0,1\}^n\rightarrow \{0,1\}^{2n}\right\} _{n\in \mathbb {N}}$ be a length-doubling pseudorandom generator that is $2^{-n/\log \log n}$-secure. Let $\textsf {sxi} \mathcal {O}$ be a SXIO with compression factor $\gamma (\lambda )=O(1/\log \log \lambda )$ (and $\mathrm {poly}(\lambda )$ security) for circuits of size at most $2^{O((\log \lambda )^\epsilon )}$.

The scheme $PKE=({\textsf {KeyGen} },{\textsf {Enc} },{\textsf {Dec} })$ is defined as follows:

•  ${\textsf {KeyGen} }(1^\lambda )$:

  • Sample a PRG seed $s \leftarrow \{0,1\}^{\log \lambda /\gamma (\lambda )}$.

  • Output $\textsf {PK} ={\textsf {PRG} }(s)$ and ${\textsf {SK} }=s$.

•  ${\textsf {Enc} }(\textsf {PK} ,x)$:

  • Construct the (witness encryption) circuit $\textsf {WE} [x,\textsf {PK} ]$ described in Fig. 13 that takes $s' \in \{0,1\}^{\log \lambda /\gamma (\lambda )}$ as input and outputs x if and only if $\textsf {PK} = {\textsf {PRG} }(s')$ holds.

  • Output ${\textsf {CT} }= \textsf {sxi} \mathcal {O}(\textsf {WE} [x,\textsf {PK} ])$

•  ${\textsf {Dec} }({\textsf {SK} },{\textsf {CT} })$:

  • Compute $x'= {\textsf {CT} }({\textsf {SK} })$.

Proposition 6.1

$PKE$ is a (polynomially secure) public-key encryption scheme.

Proof sketch

The scheme is clearly correct. We now note that the scheme is efficient; namely, all algorithms run in time $\mathrm {poly}(\lambda )$ in the security parameter $\lambda$. This is clearly the case for ${\textsf {KeyGen} }$ and ${\textsf {Dec} }$. As for ${\textsf {Enc} }$, by the $\text {SXIO}$ compression guarantee, the time required to compute the obfuscation is $2^{\gamma (\lambda )\cdot \log \lambda /\gamma (\lambda )} \cdot \mathrm {poly}(\lambda ,|\textsf {WE} [b,\textsf {PK} ]|)= \mathrm {poly}(\lambda )$. Note that we can apply $\textsf {sxi} \mathcal {O}$ to $\textsf {WE} [b,\textsf {PK} ]$ since $\left| \textsf {WE} [b,\textsf {PK} ]\right|$ is bounded by $\mathrm {poly}(\log \lambda )$ and it is less than $2^{O((\log \lambda )^{\varepsilon })}$. (This bound comes from Corollary 3.1.)

We turn to prove that the scheme is semantically secure. For this purpose, we first consider an alternative encryption scheme where the public key is generated as a truly random string $\textsf {PK} \leftarrow \{0,1\}^{2\log \lambda /\gamma (\lambda )}$. By the security of the PRG, any polysize distinguisher cannot tell apart a real public key from such a fake public key except with advantage

$$\begin{aligned} 2^{-\Omega (n(\lambda )/\log \log n(\lambda ))} = 2^{-\Omega \left( \frac{\log \lambda /\gamma (\lambda )}{\log \log \left( \log \lambda /\gamma (\lambda )\right) }\right) } \le 2^{-\Omega \left( \frac{-\log \lambda \cdot \log \log \lambda }{\log \log \log \lambda }\right) } = 2^{-\omega (\log \lambda )}. \end{aligned}$$

We next note that, by a union bound over all possible seeds, a random $\textsf {PK}$ does not have any preimage under ${\textsf {PRG} }$, except with probability

$$\begin{aligned} 2^{\log \lambda /\gamma (\lambda )}\cdot 2^{-2\log \lambda /\gamma (\lambda )}=2^{-\log \lambda /\gamma (\lambda )}\le 2^{-\omega (\log \lambda )}. \end{aligned}$$

In this case, $\textsf {WE} [b,\textsf {PK} ]$ is functionally equivalent to a circuit $\textsf {WE} [\bot ,\textsf {PK} ]$ that is independent of b and always outputs $\bot$. Security thus follows from the usual $\text {IO}$ guarantee.

$\square$