1 Introduction

Camera calibration is a prerequisite for 3D computer vision because cameras must be calibrated for 3D reconstruction. Calibration aims at determining the intrinsic and extrinsic parameters of cameras or a subset of these parameters. It is generally categorized into four types [1]:

  • Standard calibration

  • Self-calibration

  • Photometric calibration

  • Stereo-setup calibration

Fig. 1
figure 1

Some characteristics and applications of calibration methods

Full size image

Standard calibration methods employ a special calibration object with known dimensions and positions in a certain coordinate system. Self-calibration involves estimating the camera’s parameters using image sequences from multiple perspectives or views and does not require any special calibration pattern. Both methods allow for scene reconstruction up to a certain scaling factor [1].

Conventional calibration techniques are used to calibrate a fixed-parameter lens for 3D reconstruction. With motorized zoom lenses, a stereo camera can adjust itself to objects of different sizes at different distances under various imaging conditions. Moreover, stereo cameras can measure the properties of a scene using information from the dynamics of the camera’s parameters with variable zoom [2]. A motorized zoom lens is inherently more useful than a fixed-parameter lens owing to its applications in active stereo vision [3], 3D reconstruction [4], and visual tracking [5]. Modern zoom lenses are more versatile than manual focus prime lenses and have auto-focus and automatic aperture adjustment capabilities [6]. These lenses use computer-controlled motors, such as servos, to position the lenses to adjust the zoom, focus, and aperture.

Zoom-dependent (or zoom-lens) calibration can be regarded as a combination of static-camera calibrations for a zoom range with a fixed focus [2]. Standard methods require special calibration patterns that are difficult to build because of various imaging conditions in zoom-lens calibration. As a result, some researchers prefer a self-calibration method to calibrate zoom-lens cameras. Given the several types of camera motions involved in self-calibration, users cannot estimate the camera’s parameters precisely, resulting in the degeneracy of a Euclidean reconstruction (also known as a critical motion sequence) [7, 8]. Owing to the susceptibility of self-calibration methods to errors due to inaccurate determination of the conic images [9, 10], hybrid approaches for zoom-lens calibration were proposed by Oh et al. [11] and Sturm [12]. Zoom-lens calibration can be categorized into three approaches: pattern-based calibration [13], self-calibration [14], and hybrid (or semiautomatic) calibration [11]. The challenges in zoom-lens calibration are mainly due to variations in the camera’s zoom parameters and because a simple pinhole camera model cannot represent the entire lens settings [1]. In the present study, we focus on the description and analysis of the three types of calibration methods, namely standard calibration, self-calibration, and hybrid calibration. Owing to the known relationship between single camera and stereo camera calibration in literature, we did not explain the stereo-setup calibration separately. However, the description and analysis of the photometric calibration are outside the scope of the present study. Fig. 1 shows some characteristics and applications for each calibration method. The scope of these characteristics is extended and explained as follows:

  • Standard method These methods require specially prepared calibration objects with known dimensions and position in a certain coordinate system and prominent features of the calibration object, which may be easily and unambiguously localized and measured. Therefore, this method may yield high accuracy [1]. The approaches of zoom-lens calibration based on standard method comprise linear and nonlinear methods. For nonlinear approaches, the initial solution is needed, which is provided by the closed form solution of a least square-based linear approach [15].

  • Hybrid method [11] This method does not require any special 3D calibration object (with known dimension and position). Accurate 3D reconstruction is the characteristic of the hybrid method. Given the prominent features of the calibration object, which may be easily and unambiguously localized and measured, this method may yield high calibration accuracy and accurate 3D reconstruction. The hybrid approach is declared as a balanced approach because it consists of a calibration grid and utilizes self-calibration. Indeed, the hybrid method is better than self-calibration in terms of calibration accuracy; thus, accurate 3D reconstruction may be accomplished.

  • Self-calibration Self-calibration involves estimating the camera’s parameters using images from multiple views and does not require any special calibration target [1]. The attribute of the calibration pattern does not necessarily apply to self-calibration (see Sect. 2). For several types of camera motion involved in self-calibration, the user cannot estimate the camera parameters precisely, resulting in the degeneracy of the Euclidean reconstruction (critical motion) [7, 8]. The conic images are not accurately determined and self-calibration becomes susceptible to errors [9, 10]. Given that the accuracy of the 3D reconstruction is directly proportional to the calibration accuracy, we can conclude that self-calibration methods yield less accurate 3D reconstruction than that of standard and hybrid methods (see Fig. 1). Self-calibration approaches may consist of linear or a combination of linear and nonlinear methods [12, 14, 16,17,18]. In [14, 17], the solution from linear approach was utilized as the initial solution for nonlinear optimization.

This study discusses the three approaches to zoom-camera calibration with a focus on utilizing the relationship between the camera’s parameters and zoom range for 3D reconstruction and augmented reality. Furthermore, the advantages and disadvantages of various zoom-lens calibration approaches are described, and the calibration methods are compared under each approach. The paper is structured as follows: Sect. 2 describes the classification of zoom-lens calibration approaches. The zoom-lens calibration approaches based on the standard method are described in Sect. 3, and those based on self-calibration are described in Sect. 4. Section 5 describes the zoom-lens calibration approach that has the characteristics of a hybrid method. Section 6 provides a discussion and comparative analysis of the above-mentioned approaches, and Sect. 7 concludes the discussion and comparison of these approaches.

Table 1 Classification for different categories of zoom-lens calibration
Full size table
Fig. 2
figure 2

Perspective projection of a camera with different coordinate systems

Full size image

2 Classification

Zoom-lens calibration involves determining the camera’s parameters for different lens settings. Moreover, calibration includes a model for the nonlinear relationship between the camera’s parameters and its lens settings. Ample literature exists on fixed-parameter lens calibration [19,20,21,22,23,24,25,26,27,28,29,30], and surveys are available in [31, 32]. For zoom-lens calibration, specific reviews can be found in [33, 34]; however, these reviews focus exclusively on a comparative analysis of the self-calibration-based methods and techniques used for zoom-lens calibration [35,36,37,38,39]. We have not found any previous survey concurrently comparing all approaches to zoom-lens calibration. Hence, a new classification of the approaches to zoom-lens calibration was generated, as shown in Table 1. The common characteristics in all three categories, including the calibration approach, hardware type, variable parameters, parametric-formulation approach, distortion model for the lens settings, calibration pattern, and system hardware are also shown in Table 1. Given the lack of requirement for any special calibration objects in self-calibration [40], the attribute for the calibration pattern does not necessarily apply to this category. The focus of this study is to investigate the modeling of the intrinsic and extrinsic parameters of a camera and their variation with the zoom or lens settings. The attributes mentioned in Table 1 are described as follows:

  • Approach for calibration: describes the calibration method used for finding the intrinsic and extrinsic parameters, either for single or stereo camera.

  • Hardware type: refers to the hardware of the optical system, and whether it is a single or stereo camera. In Table 1, single cameras are denoted by “1” and stereo cameras (or multiview stereo cameras) are denoted by “2.”

  • Variable parameters: The parameters that display significant variance with a change in the zoom or lens settings.

  • Approach for parametric formulation: depicts the method used for capturing the nonlinear relationship between the camera’s parameters and the lens settings.

  • Distortion model for lens settings: refers to a different set of either radial or tangential-distortion parameters or both of them that are assumed to vary with the lens or zoom settings.

  • Calibration pattern: describes the calibration target used under different zoom-lens approaches. Thus, this attribute does not apply to approaches based on self-calibration.

  • Zooming hardware: refers to system hardware responsible for the zoom lens-i.e., a consumer zoom camera or a camera mounted with an external zoom lens [2].

3 Standard calibration method

To describe and discuss each calibration approach (mentioned in Table 1) in Sect. 6, we present the basic camera model for pattern-based calibration in this section and the self-calibration in Sect. 4, with some common notations and equations.

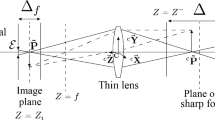
The transformation that deals with the projection of a 3D point on an image plane is called a perspective transformation [41]. Different coordinate systems are depicted in Fig. 2. The relationship between the camera coordinates (\(X_{c},Y_{c},Z_{c})\) and the coordinates of the image (\(u_{i},v_{i})\) is expressed mathematically in matrix “A,” where “s” denotes the scaling factor.

$$\begin{aligned} \left[ {{\begin{array}{l} {su_i } \\ {sv_i } \\ s \\ \end{array} }} \right] =\left[ A \right] \left[ {{\begin{array}{l} {{\begin{array}{l} {X_c } \\ {Y_c } \\ \end{array} }} \\ {Z_c } \\ 1 \\ \end{array} }} \right] \end{aligned}$$
(1)

The matrices “\(M_{e}\)” and “\(M_{i}\)” represent the transformation between the camera coordinates and the world coordinates (\(X_{w}, Y_{w}, Z_{w})\), and the image coordinates and pixel coordinates (\(u_{p}, v_{p})\), respectively. The equations governing these transformations are as follows:

$$\begin{aligned} \left[ {{\begin{array}{l} {\lambda X_c } \\ {\lambda Y_c } \\ {\lambda Z_c } \\ \lambda \\ \end{array} }} \right] =\left[ {M_e } \right] \left[ {{\begin{array}{l} {X_w } \\ {Y_w } \\ {Z_w } \\ 1 \\ \end{array} }} \right] \qquad \left[ {{\begin{array}{l} {su_p } \\ {sv_p } \\ s \\ \end{array} }} \right] =\left[ {M_i } \right] \left[ {{\begin{array}{l} {u_i } \\ {v_i } \\ 1 \\ \end{array} }} \right] \end{aligned}$$
(2)

According to [42], the intrinsic matrix of camera “\(M_{i}\)” can also be defined by Eq. (4). For the 3 \(\times \) 4 camera-projection matrix “H,” the transformation between the world’s coordinates and the pixel coordinates is given as follows:

$$\begin{aligned} H=[M_i ][A][M_e ] \end{aligned}$$
(3)

When skew = 0, we assume that the x and y axes are perpendicular to each other and this is the general case of having no skew in the pixel elements of the CCD [19], which is represented by Eq. (4).

$$\begin{aligned} M_i= & {} \left[ {{\begin{array}{lll} {f_x }&{}\quad 0&{}\quad {c_x } \\ 0&{}\quad {f_y }&{}\quad {c_y } \\ 0&{}\quad 0&{}\quad 1 \\ \end{array} }} \right] A=\left[ {{\begin{array}{l} {{\begin{array}{llll} f&{}\quad 0&{}\quad 0&{}\quad 0 \\ \end{array} }} \\ {{\begin{array}{llll} 0&{}\quad f&{}\quad 0&{}\quad 0 \\ \end{array} }} \\ {{\begin{array}{llll} 0&{}\quad 0&{}\quad 1&{}\quad 0 \\ \end{array} }} \\ \end{array} }} \right] , \quad \nonumber \\ M_e= & {} \left[ {{\begin{array}{cccc} {{\begin{array}{llll} {r_{11} }&{}\quad {r_{12} }&{}\quad {r_{13} }&{}\quad {T_x } \\ \end{array} }} \\ {{\begin{array}{llll} {r_{21} }&{}\quad {r_{22} }&{}\quad {r_{23} }&{}\quad {T_y } \\ \end{array} }} \\ {{\begin{array}{llll} {r_{31} }&{}\quad {r_{32} }&{}\quad {r_{33} }&{}\quad {T_z } \\ \end{array} }} \\ {{\begin{array}{llll} 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ \end{array} }} \\ \end{array} }} \right] \end{aligned}$$
(4)

  • \(f_{x}\) = the image-scaling factor along the x-axis,

  • \(f_{y}\) = the image-scaling factor along the y-axis,

  • (\(C_{x}\), \(C_{y})\) = the coordinates for the principle point,

  • f = focal length,

  • \(({{ T}}_{{{ x}}} ,{{ T}}_{ {{ y}}},{{ T}}_{{{ z}}})\) = translation along x, y, and z axes,

  • \({{r}}_{{ij}}\) = elements of the 3D rotation matrix with \(i = 1\) to 3 (row index), \(j = 1\) to 3 (column index).

To model the distortion, supposing the corrected and the distorted pixel coordinates are denoted by (\(x_{p}, y_{p})\) and (\(x_{d}, y_{d})\), respectively, the first three coefficients of the radial distortion are expressed by \(k_{1}\) to \(k_{3}\), while \(p_{1}\) and \(p_{2}\) correspond to the tangential-distortion coefficients. The pixel coordinates can be undistorted using the following distortion model [42]:

$$\begin{aligned} \left[ {{\begin{array}{l} {x_p } \\ {y_p } \\ \end{array} }} \right]= & {} \left( {1+k_1 r^{2}+k_2 r^{4}} \right) \left[ {{\begin{array}{l} {x_d } \\ {y_d } \\ \end{array} }} \right] \nonumber \\&+\left[ {{\begin{array}{l} {2p_1 x_d y_d +p_2 \left( {r^{2}+2x_d^2 } \right) } \\ {p_1 \left( {r^{2}+2y_d^2 } \right) +2p_2 x_d y_d } \\ \end{array} }} \right] \end{aligned}$$
(5)

Several approaches of pattern-based calibration have been proposed to calibrate zoom-lens cameras. Wilson and Shafer [43, 44] put forward an iterative trial-and-error procedure and modeled the variation of four camera parameters with variable zoom—viz., the focal length f, the coordinates of the principle point (\(C_{x}\), \(C_{y})\), and a translation along the z-axis \(T_{z}\). Their approach was based on the camera model proposed by Tsai [45], which they applied for calibrating a single camera mounted with a zoom lens. They used polynomials of up to five degrees for modeling the parameters with variable zoom and applied a modified Levenberg–Marquardt (LM) algorithm to further refine them. However, they pointed out problems with mechanical hysteresis and difficulty in capturing images under various imaging conditions. They overcame these problems with precise automation, control of the zooming hardware, and the design of the calibration target, which is based on a white plane with circular black dots as control points. They modeled the distortion for the zoom settings with the first coefficient of the radial distortion \(k_{1}\). This approach is based on the translation of a planar pattern along the axis perpendicular to the plane.

Li and Lavest [46] applied a least-squares technique for calibrating a pair of zoom-lens cameras and described some practical and experimental aspects to camera calibration, especially regarding motor-controlled zoom-lens systems. They considered the variation in the image-scaling factors along the x and y axes (\(f_{x}\), \(f_{y})\) with variable zoom and focus. The system hardware consisted of a pair of zoom-lens cameras mounted on a head–eye system. The calibration pattern consisted of 3D cube objects employed under various zoom settings. These objects consisted of three perpendicular surfaces with black background and white horizontal and vertical lines whose intersections yielded control points. They modeled the distortion with a set of the first three radial- and tangential-distortion coefficients.

Zheng et al. [47] presented a perspective-projection-based approach similar to Tsai’s method [45] with a second-order radial lens-distortion model used for the zoom-lens calibration of a single camera. They determined the pan, tilt, and zoom parameters and used these parameters to infer the motion of the image. They considered variations to f, \(C_{x}\), \(C_{y}\), and the first two radial-distortion coefficients (\(k_{1}\), \(k_{2})\), and modeled their relationship with variable zoom and focus using a look-up table. The calibration target consisted of circular disks on a white plane under various imaging conditions.

Chen et al. [48] designed a calibration target based on circles of two different sizes to solve the problem of varying field of views. They determined the intrinsic and extrinsic parameters for a single camera using Weng’s method [49]. They modeled f, \(C_{x}\), \(C_{y}\), \(T_{z}\), and \(k_{1}\) with variable zoom and focus using a look-up table and used bilinear interpolation to acquire the camera’s parameters for lens settings where calibration was not performed. A calibration-on-demand method was applied to the lens settings when the interpolated parameters were found to be inaccurate.

Atienza and Zelinsky [50] proposed a zoom-calibration technique for stereo cameras based on Zhang’s method [51] that employ a chessboard as the calibration object. They considered variations to \(f_{x}\), \(f_{y}\), \(C_{x}\), \(C_{y}\), \(T_{z}\), and the first four radial-distortion coefficients (\(k_{1}\), \(k_{2}\), \(k_{3}\), \(k_{4})\) with variable zoom and focus, and modeled these parameters using a polynomial fitting. They determined the focus setting as a function of the zoom and object distance from the stereo camera, reducing the dimensionality of the data needed to calibrate the zoom lens. Their approach was based on the keypoints that pinhole, and thin lens camera models can be used for each lens setting. The effect of change in camera parameters is negligible with the variation in aperture settings and the intrinsic parameters and translation along the z-axis. \(T_{z}\) is the only parameter that shows significant change in zoom settings [43, 46].

Ahmed and Farag [15] proposed an approach similar to Wilson’s work [43, 44] using an artificial neural network (ANN) for calibrating a trinocular head with an active lightening device for 3D reconstruction under different zoom and focus settings. They assumed variations to \(f_{x}\), \(f_{y}\), \(C_{x}\), \(C_{y}\), and \(T_{z}\) with lens settings and modeled these parameters using a multilayered feed-forward neural network (MLFN). They further suggested a pre-calibration process for certain zoom settings, but they did not provide any mathematical details for the distortion model. They also criticized the parameter-modeling approaches—viz., interpolation, polynomial fitting, and look-up tables.

Xian et al. [52] proposed a perspective-projection-based calibration approach [41] for calibrating the zoom of stereo cameras utilizing a 3D chessboard as a calibration target. They modeled all of the camera’s parameters with variable zoom using polynomial fitting, but they did not consider the radial- and tangential-distortion coefficients. Their study focusses on the 3D modeling and reconstruction with variable zoom. They reported problems related to the nonlinear relationship of the camera’s parameters with variable zoom, the nonlinearity of the lens design, and the residual error from positioning the zoom lens with a driving motor. They criticized the zoom-calibration approach in [50] and pointed out that due to the change in the optical configuration of the vision system, the change in zoom settings results in the variation of the orientation of camera coordinate system.

Figl et al. [53] utilized Wilson’s approach [44] for the zoom-lens calibration of a single camera located behind the eyepiece on a head-mounted display (HMD) in a head-mounted operating microscope and determined the transformation from the world-coordinate system to the camera coordinate system \(T_\mathrm{WC}\). They modeled f, \(C_{x}\), \(C_{y}\), and \(T_{z}\) with variable zoom and focus using polynomial fitting without considering any distortion model for their system, and employed a calibration pattern consisting of black squares on a white plane.

Garcia et al. [54] proposed a novel calibration method known as LED-based calibration. This method is used to calibrate a surgical microscope (i.e., a camera) in terms of focus and zoom settings. They employed an LED-based active optical marker as the calibration object and an LED as the control point. A pinhole camera model was used to determine the camera’s parameters without any distortion parameters. The focal length f,  rotation along the x-axis \(R_{x}\), and translation along the x and z axes (\(T_{x}\), \(T_{z})\) were considered as variable parameters and were modeled using a spline-based model for various zoom and focus settings.

Liu et al. [13] reported Heikkila’s method [55, 56] as a calibration approach for the zoom-lens calibration of a stereo camera and determined the camera’s parameters for the 3D reconstruction under variable zoom. They modeled \(f_{x}\) and \(f_{y}\) with zoom settings using a polynomial fitting. To counteract distortion, they suggested the distortion model from the first two radial- and tangential-distortion coefficients and employed a chessboard as a calibration pattern.

Sarkis et al. [10] applied Tsai’s method [45] for calibrating a single camera under different zoom and focus settings. Their main contribution was the improved modeling of the camera’s parameters using clustered-moving least squares (CMLS). They modeled f, \(C_{x}\), \(C_{y}\), \(T_{z}\), and \(k_{1}\) with variable zoom and focus settings, and they used six scales of the chessboard pattern to overcome the problem of a varying field of view. They modeled the distortion with the first coefficient of radial distortion with various lens settings.

Kim et al. [2] designed a 3D sensing system based on active stereo vision and a zoom-lens control system. This system consisted of a pair of cameras mounted with external zoom lenses and a non-calibrated projector [57, 58]. They determined the intrinsic and extrinsic parameters for each camera using perspective vision [41]. To overcome the problem of a varying field of view, the calibration target consisted of two different-sized circles on a white plane. They designed a zoom-lens control system for the stereo camera based on precise automation using a microcontroller and an image-processing technique. They modeled \(f_{x}\), \(f_{y}\), \(C_{x}\), \(C_{y}\), and \(T_{z}\) for zoom settings using a polynomial fitting, and modeled the distortion throughout the zoom settings with the first two coefficients of radial and tangential distortion. They also assumed that the intrinsic parameters and translation along the z-axis are the only parameters that show significant change in zoom settings [43, 46].

4 Self-calibration

The concept of self-calibration was pioneered by Faugeras et al. [59] for cameras with fixed-parameter lenses. Pollefeys et al. in [60] extended self-calibration to cameras with variable parameters such as the focal length. Self-calibration computes the metric properties of the scene and/or camera using uncalibrated images [19].

Let {\(P^{i}\), \(X_{j}\)}, H and {\(P^{i}\) \(H\), \(H^{-1}\) \(X_{j}\)} be the projective reconstruction, rectifying homography, and metric reconstruction, respectively. We can determine ‘H’ by imposing constraints on the internal parameters of cameras such that metric reconstruction is obtained [19]. Let \({m ,x}^{i}, {X}_{M}, \mathrm{and} {P}_{M}^{i}\) be the number of cameras, image point, 3D point, and the projection matrix for ith views, respectively, where M shows that the world frame is Euclidean and the cameras are calibrated. The relationship between the image point and the 3D point is given as follows:

$$\begin{aligned} P_M^i= & {} K^{i}\left[ {\left. {R^{i}} \right| t^{i}} \right] \nonumber \\ P_M^i= & {} P^{i}H \end{aligned}$$
(6)

where

  • \(I = 1\),..., m, m=no. of cameras or views,

  • \(H =\) unknown \(4\times 4\) homography of 3-space,

  • \(P^{i} =\) projection matrix obtained by projective reconstruction,

  • \({{\varvec{K}}}^{i}\) 612 = calibration matrix for ith view,

  • \(({{\varvec{R}}}^{i},{{\varvec{t}}}^{i}) \) = rotation and translation matrix for ith view.

The expressions \(R^{1} = I\) and \(t^{1} = 0\) for the first camera coincided with the world frame. The Euclidean transformation between the ith camera and the first camera is specified by \(R^{i}\) and \(t^{i}\) and \(P_M^1 =K^{1}\left[ {\left. I \right| 0} \right] \). The homography matrix can be obtained as follows:

$$\begin{aligned} H=\left[ {{\begin{array}{ll} A&{}\quad t \\ {v^{t}}&{}\quad k \\ \end{array} }} \right] \end{aligned}$$

From Eq. 6, we have \(P_M^1 =P^{1}\)H for first camera, and \(A = K^{1}\) and \(t = 0\). Since H is a non-singular matrix, we selected \(k = 1\) to fix the scale of reconstruction. The expression for H is given below.

$$\begin{aligned} H=\left[ {{\begin{array}{ll} {K^{1}}&{}\quad 0 \\ {v^{t}}&{}\quad 1 \\ \end{array} }} \right] \end{aligned}$$

Vector v and \(K^{1}\) were used to specify the plane in the projective reconstruction. The coordinates of the plane at infinity, \({ \varvec{\pi }}_{\infty }\), are as follows:

$$\begin{aligned} {\varvec{\pi }}_{\infty }={{\varvec{H}}}^{-T}\left( \begin{array}{c} \begin{array}{c} \mathbf{0} \\ \mathbf{0} \\ \end{array}\\ \mathbf{0} \\ \mathbf{1} \\ \end{array} \right) = \left( \begin{array}{c} -\left( {{\varvec{K}}}^\mathbf{1} \right) ^{{-T}}{{\varvec{v}}} \\ 1 \\ \end{array}\right) \end{aligned}$$

Let \({\varvec{\pi }}_{\infty }\) \(\mathbf{= }\left( {p^{T},1} \right) ^{T}\), \(K = K^{1}\), and \(p = -\left( {K^{1}} \right) ^{{-T}}v\), then the homography can be defined as follows:

$$\begin{aligned} H=\left[ {{\begin{array}{ll} K&{}\quad 0 \\ {-p^{t}K}&{}\quad 1 \\ \end{array} }} \right] \end{aligned}$$
(7)

The above equation shows the need for the parameters of p and five parameters of \(K^{1}\) to transform projective reconstruction into metric reconstruction. Let the projective cameras be denoted as \(P^{i}=\left[ {\left. {A^{i}} \right| a^{i}} \right] \). Multiplying Eq. 6 by Eq. 7 leads to the following equation.

$$\begin{aligned}&K^{i}R^{i}=\left( {A^{i}-a^{i}p^{T}} \right) K^{1} \nonumber \\&R^{i}=(K^{i})^{-1}\left( {A^{i}-a^{i}p^{T}} \right) K^{1} \end{aligned}$$
(8)

We can eliminate the rotation \(R^{i}\) using RR\(^{T} = I\), with the resulting equation given below:

$$\begin{aligned} K^{i}K^{iT}=\left( {A^{i}-a^{i}p^{T}} \right) K^{1}K^{1T}\left( {A^{i}-a^{i}p^{T}} \right) ^{T} \end{aligned}$$

We know that the dual image of the absolute conic (DIAC), \(\omega ^{*i}=K^{i}K^{iT}\), is obtained as follows:

$$\begin{aligned} \omega ^{*i}= & {} \left( {A^{i}-a^{i}p^{T}} \right) \omega ^{*1}\left( {A^{i}-a^{i}p^{T}} \right) ^{T} \nonumber \\ \omega ^{i}= & {} \left( {A^{i}-a^{i}p^{T}} \right) ^{-T}\omega ^{1}\left( {A^{i}-a^{i}p^{T}} \right) ^{-1} \end{aligned}$$
(9)

where \(\omega ^{i}\) = image of the absolute conic (IAC) for the ith view.

The degenerate dual quadric denoted by 4 \(\times \) 4 homogenous matrix of rank 3 is known as the absolute dual quadric, \(Q_{\infty }^*\) [19]. The importance of this quadric lies in its ability to encode the \(\pi _{\infty }\) and the absolute conic \(\Omega _{\infty }\). The relationship between the DIAC and the absolute dual quadric is given as follows:

$$\begin{aligned} \omega ^{*}=PQ_\infty ^*P^{T} \end{aligned}$$
(10)

The principle of self-calibration is to use an absolute conic as a calibration object [34, 61]. The plane projective transformation between two images induced by \(\pi _{\infty }\) is termed as infinite homography \(H_{\infty }\), whose formula is given below:

$$\begin{aligned} H_\infty ^i =A^{i}-a^{i}p^{T} \end{aligned}$$
(11)

The above equations show that if \(\pi _{\infty }\) and the projective cameras are known, the homography from a camera \(\left[ {\left. I \right| 0} \right] \) to camera \(\left[ {\left. {A^{i}} \right| a^{i}} \right] \), such as \(H_\infty ^i \), can be determined. Substituting the value of \(H_\infty ^i \) from Eq. 11 in Eq. 9 leads to the following equation:

$$\begin{aligned} \omega ^{*i}= & {} H_\infty ^i \omega ^{*1}{H_\infty ^i} ^{T} \nonumber \\ \omega ^{*j}= & {} H_\infty ^i \omega ^{*i}{H_\infty ^i }^{T} \end{aligned}$$
(12)

where

  • \(\omega ^{*1}=\) DIAC for reference view,

  • \(\omega ^{*i}=\) DIAC for ith view,

  • \(\omega ^{*j}=\) DIAC for jth view.

The geometric interpretation of the infinite-homography constraint is depicted in Fig. 3 in terms of the DIAC, which can be transferred from one image to another through the homography of the plane at infinity as depicted in Eq. 12. Let \(\omega ^{*i}\) and \(\omega ^{*j}\) be the DIAC’s of the absolute conic \(\Omega _{\infty }\) on the plane at infinity \(\pi _{\infty }\) in the two views, respectively, while e\(_{a}\) and e\(_{b}\) are the respective epipoles in the two views. The epipolar lines for first view are denoted by l\(_{a}\) and l\(_{b}\), while \(l_a^{\prime } \) and \(l_b^{\prime } \) correspond to the second view. The Kruppa equations show the algebraic representation of the correspondence of the epipolar lines tangent to the conic. The Kruppa equation can be obtained with F being the fundamental matrix as follows [19]:

$$\begin{aligned} \left[ {e_b } \right] _\times \quad \omega ^{*j} \quad \left[ {e_b } \right] _\times \quad =F\omega ^{*i}F^{T} \end{aligned}$$
(13)
Fig. 3
figure 3

Depiction of the conic epipolar matching constraints

Full size image

Agapitos et al. [14] reported both linear and the nonlinear calibration methods (based on the LM algorithm) for self-calibrating rotating and zooming cameras. Their approach was based on the infinite-homography constraint and considered f, \(C_{x}\), \(C_{y}\), and \(k_{1}\) as variable parameters. To increase the accuracy of the camera’s parameters, they utilized a maximum likelihood estimation (MLE) and a maximum a posteriori estimation (MAP). They reported results that are more accurate by keeping the principle point constant. They also analyzed the effects of radial distortion on self-calibration and modeled a variation of the first coefficient of radial distortion using polynomial fitting. A precisely manufactured calibration grid was used to get the ground truth data for evaluation purposes.

Hayman and Murray [18] analyzed the effects of translational misalignment for pure-rotation-based self-calibration approaches [62, 63] when the optic center of a zoom camera does not coincide with the rotation center. They employed a homography-based approach for calibration and utilized homography to relate the intrinsic parameters between the two views. They considered f and \(k_{1}\) as variable parameters and modeled them using polynomial fitting. They performed experiments using simulated data to verify their analysis and concluded that the assumption of pure rotation is valid in cases when noise and radial-distortion effects are more severe and the camera translations are small compared to the distance of the scene.

Sudipta and Pollefeys [16] proposed an automatic method for the calibration of an active pan–tilt–zoom (PTZ) camera without employing any calibration object for generating high-resolution mosaics. They have applied a homography-based calibration approach for the full range of pan, tilt, and zoom. They modeled distortion by considering the first two coefficients of radial distortion. Variations to f, \(C_{x}\), \(C_{y}\), \(k_{1}\), and \(k_{2}\) were modeled with zoom settings using polynomial fitting. They first calculated the intrinsic and distortion parameters for discrete zoom steps between the minimum and maximum zoom, and then used pairwise linear interpolation to estimate these parameters at any zoom step. Their zoom-calibration approach was similar to that of Collins et al. [64] and simpler than the approach of Wilson [44].

Wu and Radke [17] proposed a pure-rotation-based self-calibration technique based on perspective projection [41] for calibrating the PTZ cameras. They used a linear least-squares method to acquire the initial intrinsic parameters that are further refined using the LM algorithm. They considered image-scaling factors (\(f_{x}\), \(f_{y})\) and the first two radial-distortion coefficients (\(k_{1}\), \(k_{2})\) as variable parameters and modeled them using polynomial fitting. They also compared their method with Zhang’s [51] to evaluate the accuracy of their proposal. They used a library of natural features detected during the initial calibration and did not employ a special calibration object. They compared their proposed algorithm with that of Sudipta and Pollefeys [16] in terms of accuracy and required image data for zoom calibration.

5 Hybrid approach

Sturm [12] proposed a self-calibration method for a moving camera based on perspective projection [41] and Kruppa’s equations. First, he proposed an offline pre-calibration of the camera to determine the aspect ratio, skew angle, and principle point coordinates as a function of the image-scaling factor along the y-axis, \(f_{y}\). Then, he expressed the remaining intrinsic parameters for zooming cameras as a function of \(f_{y}\) following the functional relationship determined in the pre-calibration stage. A calibration grid was employed to capture images of different views for self-calibration. No distortion model was considered in this research. Given that this approach is based on the self-calibration method and employs a calibration grid, it can be classified as both self-calibration and hybrid methods.

Oh and Sohn [11] reported a calibration approach for charge-coupled device (CCD) cameras mounted with external zoom lenses. Their approach has the characteristics of both the planar-pattern-based method and the pure-rotation-based self-calibration method. They applied the LM algorithm for calibrating the zoom of a single camera considering f, \(C_{x}\), \(C_{y}\), \(k_{1}\), and \(k_{2}\), and the translation of the projection center ‘t’ as a variable parameter with zoom settings. They used the focal lengths printed on the lens’ zoom ring to initialize the LM algorithm and used the calibration parameters from previous zoom settings as the initial estimates for the calibration of the next zoom setting.

Moreover, they utilized a rotation sensor to overcome the so-called ill-posed problems caused by many parameter dimensions. They employed a chessboard to calibrate the zoom lens and modeled the camera’s parameters using the scattered data interpolation. They determined the first two coefficients of radial distortion to model the distortion for various zoom and focus settings. Their method for calibrating the focus is similar to the zoom-calibration procedure found in [16]. This focus calibration procedure reduces the number of required manual calibrations from \(\mathbf{{P}}^{2}\) to P, saving the user considerable time and effort (P refers to the number of manual calibrations to the zoom and focus). They pointed out the disadvantages to the standard method and self-calibration and justified their novel hybrid approach.

6 Discussion

Table 1 shows two types of zooming hardware for zoom-lens calibration: consumer zoom cameras and cameras mounted with an external zoom lens. Xian et al. [52] pointed out a problem regarding the inaccurate and nonlinear mechanical control in consumer cameras. Therefore, some researchers employed the second category of the zooming hardware—viz., CCD cameras mounted with an external zoom lens. Nonetheless, a possibility of error exists owing to the internal mechanical and optical properties of external zoom lens that can be overcome with precise automation and control of the zooming hardware [43].

Different calibration patterns were used for zoom-lens calibration, as depicted in Table 1. These include a chessboard, an active optical marker, and a target with circles [65, 66] or dots and squares [45, 49]. Several chessboards of various sizes are needed for zoom-lens calibration to cover the whole range of zoom settings [43]. Given the varying field of view and the defocusing problems, the features (centroids, corners, and dots) can be blurred and are thus difficult to measure. To calibrate a zoom lens, a sufficient number of control points should appear in the calibration target, consisting of the features for various zoom settings. However, users will find it difficult to understand the 3D coordinates assumed for the calibration [2]. Thus, Chen et al. [48] and Kim et al. [2] employed a calibration pattern consisting of two different-sized circles.

Researchers [10, 43, 44, 47, 53] have employed Tsai’s method [45] for zoom-lens calibration of a single camera. This method requires different calibration patterns to calibrate a zoom camera at different zoom and focus settings. Modern zoom lenses do not function in the same way as expected in this method [6]. Pattern-based approaches to the zoom-lens calibration of stereo cameras [13, 50] use homography-based calibration methods [51, 55, 56], while calibrating the zoom of a single camera is carried out using homography-based self-calibration in [14, 16, 18]. Oh and Sohn [11] pointed out that homography-based calibration is limited insofar as it can only determine the intrinsic parameters when employed for zoom-lens calibration using planar patterns, and the calibration parameters cannot be accurately estimated for long focal lengths. Ahmed and Farag [15] proposed a calibration approach based on an MLFN, but this method is too complex and requires additional image data, which is not always available [67]. Calibration approaches [2, 52] based on perspective projection [41] were used for zoom-lens calibration, but we cannot assume the perspective projection for all of the zoom settings because on high-zoom settings, the camera more closely resembles an affine than a perspective camera [11].

Different researchers have considered different sets of intrinsic or extrinsic parameters—or a combination of the two—as variable model terms demonstrated in Table 1. They assumed variable camera parameters based on their experimental setup and results. Xian et al. [52] considered all camera parameters as variable model terms and pointed out that the change in the optical configuration of a vision system results in a variation of the extrinsic and intrinsic parameters. Table 1 shows the different distortion models that were presented consisting of radial-distortion coefficients or a combination of radial- and tangential-distortion parameters. In [15, 54], researchers ignored the distortion model for variable zoom. However, they suggested pre-calibration because the distortion can be significant for specific zoom and focus settings, especially at small focal lengths [15]. Alternatively, the distortion can be considered constant [46]. The camera models presented in [52, 53] completely ignored the distortion model, whereas the majority of zoom-lens calibration approaches demonstrate the distortion effect as an inevitability given certain zoom settings (see Table 1).

To find the relationship between the camera’s parameters and its zoom settings, Ahmed and Farag [15] criticized the different techniques mentioned in Table 1-specifically, polynomial fitting, interpolation, and look-up tables. They pointed to both the fitting and interpolation techniques and held them responsible for reducing the overall calibration accuracy. They emphasized the errors resulting from particular parameters when the interactions between all of the camera’s parameters are not considered. They modeled camera parameters using an MLFN for various zoom settings, but their approach requires a considerable amount of data for the artificial neural network to converge [50]. Sarkis et al. [10] applied CMLS to improve the results of Wilson and Shafer [43, 44].

Sturm [12] proposed Kruppa’s equations-based approach for the self-calibration of a moving camera and expressed the intrinsic camera parameters as a function of single parameter. The major drawback to this approach is the time-consuming pre-calibration stage. Moreover, there is an uncertainty to the application of this approach for more complex interdependence models of the intrinsic parameters. A distortion model was not presented in his research; however, the distortion effect cannot be neglected in the self-calibration of a zoom camera because this effect is inversely proportional to the focal length [14, 16].

Several calibration approaches [12, 14, 16,17,18] include linear and nonlinear algorithms for self-calibration. Sturm [12] applied a linear method based on Kruppa’s equations. Oh and Sohn [11] utilized a nonlinear approach to zoom-camera calibration based on the LM algorithm, and the researchers in [14, 17] reported approaches based on both linear and nonlinear algorithms. The LM algorithm requires intrinsic parameters initially and often fails when this requirement is unfulfilled [12, 15]. Hence, the linear method is a high-speed method that is suitable for real-time applications. It does not require initial estimates and has no convergence problem [14]. However, the linear method does not include the necessary constraints on the camera’s parameters, such as the skew, aspect ratio, and principal point [14]. Oh and Sohn [11] used the focal lengths printed on the lens’ zoom ring to initialize the LM algorithm, and the calibration parameters from previous zoom settings were used as the initial estimates for the calibration of the next zoom setting. The self-calibration approaches in [14, 17] utilized the intrinsic parameters estimated from the linear algorithm as the initial postulate for nonlinear optimization.

Sudipta and Pollefeys [16] proposed a pure-rotation-based self-calibration approach using homography to estimate the calibration parameters of a PTZ camera for zoom steps. This approach calibrated only the focal length of the PTZ camera and often involves a number of small but time-consuming steps to reduce noise [17]. A different approach [17] requires relatively fewer images at different zoom settings for calibrating the PTZ camera than the linear-interpolation model reported in [16]. Given the assumption of pure rotation of a PTZ camera in these calibration approaches [16, 17], the effects of translation cannot be neglected except in some practical situations, as mentioned in [18].

Table 2 Advantages and disadvantages of zoom-calibration approaches
Full size table
Table 3 Number of images and uncertainty of zoom-calibration approaches
Full size table

Different self-calibration approaches allow different camera parameters to vary with zoom steps. These approaches [11, 12, 16,17,18] considered the focal length as a variable parameter and tackled the principle point in a different way. Some calibration techniques [17, 18] assumed that the principle point is constant at different zoom settings, while others [11, 12, 14, 16] allowed this parameter to vary throughout the zoom steps. The researchers in [43, 68] reported that the behavior of the principle point while zooming nearly has a translational trajectory. Given the optical and mechanical misalignments in the lens system of the camera, the trajectory of the principle point can be nonlinear, depending on the zoom lens or the consumer camera employed in the experiments [12]. Oh and Sohn [11] observed that the fluctuations in the principle point differ depending on the lens, and that the correlation of the camera’s parameters should be studied to accurately estimate the principle point. The advantages and disadvantages and the optimal number of images and uncertainty found in each approach mentioned in Table  1 were presented in Tables 2 and 3, respectively. The comparison between standard calibration method and self-calibration in term of the number of images suggested shows that the number of images suggested for self-calibration is relatively less than the images for standard method for the suggested lens settings as shown in Table 3.

7 Conclusion

This study investigated three categories of zoom-camera calibration: pattern-based calibration, self-calibration, and hybrid calibration. The relationship between the camera’s parameters and its zoom range is important for applications in the 3D reconstruction and augmented reality [69]. Furthermore, we depicted the characteristics and applications of these calibration methods. We introduced a new classification model based on the approaches applied to the zoom-lens calibration of single and stereo cameras and discussed these approaches under some common attributes. This research described the two categories of zooming hardware and pointed out their inaccuracies and nonlinearities. This study briefly described the different calibration targets used in zoom-lens calibration to overcome various imaging conditions with the zoom and focus. We performed a comparative analysis of zoom-calibration approaches in the above-mentioned categories, pointing out the advantages and disadvantages to each approach. We further compared the linear and nonlinear camera models proposed for zoom calibration with a different set of variable camera parameters based on their experimental results. We explored the different techniques used to model the camera’s parameters with variable zoom and criticized polynomial fitting and interpolation. Finally, this research described the self-calibration methods available for calibrating zoom cameras without using a calibration object.

The approaches [10, 43, 44, 47, 53] employed Tsai’s method [45] for the zoom-lens calibration of a single camera, but modern zoom lenses cannot be modeled using this method [6]. The approach [15] criticized the polynomial fitting, interpolation, and look-up table-based modeling of variable parameters [2, 13, 46,47,48, 50, 52, 54], and emphasized the errors resulting from particular parameters when the interactions between all of the camera’s parameters were not considered. The approaches [12, 15, 52,53,54] ignored the distortion model, whereas the majority of zoom-lens calibration approaches demonstrated the distortion effect as an inevitability given certain zoom settings. The calibration approaches [16, 17] assumed the pure rotation of a PTZ camera and the effects of translation cannot be neglected except in some practical situations, as mentioned in [18]. Similarly, for applications where high calibration accuracy is required, the errors introduced by the translational offset cannot be ignored [37]. Peter Sturm reported the uncertainty to the application of this approach for more complex interdependence models of the intrinsic parameters [12], while the hybrid approach [11] posed the uncertainty in the measurement of focal length at the highest zoom and focus settings. The research [14] addressed the negative effects of radial distortion on the self-calibration of a rotating and zooming camera.

Oh and Sohn [11] criticized the homography-based calibration using planar patterns as they may determine the intrinsic parameters only and may lead to inaccurate measurement of parameters for long focal lengths. We also pointed out advantages and disadvantages of linear and nonlinear methods of self-calibration approaches. The optical and mechanical misalignments in the lens system resulted in a nonlinear trajectory of the principle point depending on the zoom lens [12], and the correlation of the camera parameters should be studied to estimate the principle point accurately [11]. Directions for future work include the study of the behavior of modern zoom lenses with the variation of camera parameters and the study of the correlation of the camera parameters for the accurate estimation of the principle point.