1 Introduction

Cork is a cellular material with an interesting set of properties that is used in a wide range of application areas such as building construction, automobile and space industry, flooring or footwear, and as a sealant (Pereira 2007).

Cork is produced by the cork oak tree (Quercus suber L.) where it is the outer layer in the bark. This material presents a low density with large compressibility and dimensional recovery, insulation properties, very low permeability to liquids and gases, and chemical stability and durability (Rosa and Fortes 1991; Anjos et al. 2008, 2014).

The honeycomb structure of cork with closed cells, of considerable homogeneity, has been well described (Pereira et al. 1987; Pereira 2007). However, it also includes some macroscopic features that impart heterogeneity to the tissue, namely the lenticular channels that cross the cork layers (Pereira 2007) showing an extensive variability in distribution and size in the cork planks and products (Pereira et al. 1996; Oliveira et al. 2012). The porosity of cork induces a high natural variability in cork and in its mechanical properties (Anjos et al. 2008, 2010, 2011a, b, 2014). In general, all previous studies concluded that the mechanical behaviour of cork is related to its structural features and the number and extension of defects.

In all cork applications, its mechanical behaviour is a very important factor for its choice and performance. Cork behaviour is largely determined by the cellular characteristics and the chemical composition of the cell walls (Pereira et al. 1987; Pereira 1988, 2013; Oliveira et al. 2014). In the industry, cork is usually classified into different quality classes depending on its porosity and extension of defects.

One important mechanical property of cork is tension. The situation of cork being submitted to tensile stress is encountered in many uses, namely when a stopper is pulled out of a wine bottle. Rosa and Fortes (1991) described the cell walls’ straightness and alignment in the direction of tension when cork is submitted to tensile stress.

The modelling of the physical and mechanical properties of cork is difficult due to its heterogeneous nature. Several studies (Anjos et al. 2008, 2010, 2011a, b, 2014) found some unknown existing nonlinear relationships related to its higher natural variability. To solve the nonlinear relationship of modelling parameters in other related cellular materials, some optimization algorithms of neural networks have been developed (Esteban et al. 2010; Mansfield et al. 2007).

The aim of this research work was to obtain a predictive model to calculate cork mechanical properties from some measured physical properties. In order to achieve this, artificial neural networks (ANNs) (Haykin 1999) were trained for their use as automated learning tools. They have been applied successfully to a wide variety of environmental problems: for flood forecasting (Leahy et al. 2008); predicting Cu(II) adsorption by sawdust from wastewaters (Prakash et al. 2008); support vector machines (SVM) and multilayer perceptron networks (MLP) have been used for modelling the characteristics of trees for paper manufacture (García Nieto et al. 2012) and for predicting the wood strength of Populus spp (Mansfield et al. 2011) and Douglas-fir wood density (Iliadis et al. 2013); for analysing the optimum parameters of turmeric powder agglomeration process (Dhanalakshmi and Bhattacharya 2014); predicting the turbidity of a river from other parameters measured on site (Iglesias et al. 2014); predicting the mechanical behaviour of steel wires and cord materials (Yilmaz and Ertunc 2007).

2 Materials and methods

2.1 Data

The dataset included measurements of a total of 144 cork specimens which were prepared from raw cork planks collected at an industrial mill, half of them corresponded to samples taken from the tree in the axial direction and the other half to samples taken from the tree in the tangential direction (Fig. 1). Previous studies have already stated the influence of this direction on the mechanical behaviour of cork (Anjos et al. 2010, 2011a).

Fig. 1
figure 1

Explanation of the sampling method (Anjos et al. 2011b)

Full size image

The test specimens were cut from each cork plank as plates with the dimensions of 30 mm × 5 mm × 60 mm with the largest dimension in the tangential and axial directions, respectively.

For each sample, the following parameters were determined:

  • Young’s modulus, E (MPa);

  • Fracture stress, σf (MPa);

  • Fracture strain, εf (%);

  • Porosity, P (%);

  • Number of pores, NP (number/cm2);

  • Density, D (g/cm3);

  • Approximation of the pores to elliptical shape, FE;

  • Approximation of the pores to circular shape, FC;

  • Distance to the nearest pore, ZO (mm).

The porosity and pore number of the specimen plates (reported in % of the area of pores divided by the total area) were determined prior to the tensile tests by image analysis on the two tangential surfaces parallel to the direction of the tensile stress as described by Anjos et al. (2010, 2011a). The specimens were equilibrated in the laboratorial environment to 7 % mean moisture content, weighed, and the density was calculated.

Additionally, the following information was also taken into account regarding the specimens:

  • Cork commercial quality class: good and medium, determined visually by an expert;

  • Radial position: three specimens were obtained from each cork plank, corresponding to the inner part, the middle part and the outer part of the plank. The reason why this was done is because cork properties vary substantially with their radial position in the plank (Pereira 2007);

  • Direction of stress: axial or tangential, depending on the direction of the load application.

A new variable was introduced with the aim of emphasizing the effect of density and porosity in the mechanical properties of the material. Previous studies (Anjos et al. 2008, 2014) showed that density is inversely correlated to porosity, particularly for the better cork quality that has high Young’s modulus, fracture stress and fracture strain. This new variable was a synergistic variable calculated as density/porosity (D/P), and expected to give additional valuable information to the network in order to predict the mechanical behaviour of cork.

The synergy between two or more variables is the interaction that produces a different effect from their individual effects, even greater than that. The joint action of more than one cause has a greater effect than the sum of the individual effects. In a previous research work, the benefits were discussed of including such synergistic variables in the neural networks, resulting in a better prediction of the turbidity of a river basin (Iglesias et al. 2014).

2.2 Artificial neural networks

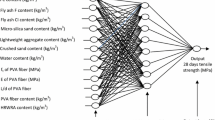
Back in 1943, psychiatrist Warren MacCulloch and mathematician Walter Pitts proposed the first neural network model based on biological neural networks (MacCulloch and Pitts 1943). This neural network model consisted of an input layer, an output layer and a certain number of hidden layers, each of them containing a number of nodes (Fig. 2). Weights connect the nodes of one layer with the nodes of the following layer. The neurons on the input layer contain the input data, while the neurons on the output layer provide the network output.

Fig. 2
figure 2

Architecture of artificial neural networks. The variables wj, wp are the weights of the input layer, while cj and cp are the weights of the hidden layer

Full size image

A neural network defines the function f : X ⊂ ℜd → Y ⊂ ℜc (Shabani and Mazahery 2011) that can be expressed as follows:

$$ {\mathbf{f}}\left( {\mathbf{x}} \right) = \phi \left( {\psi \left( {\mathbf{x}} \right)} \right) $$
(1)
$$ \phi :{\mathbf{X}} \subset \Re^{d} \to {\mathbf{T}} \subset \Re^{p} $$
$$ \psi :{\mathbf{T}} \subset \Re^{p} \to {\mathbf{Y}} \subset \Re^{c} $$

where d is the dimension of input space, p is the number of neurons of the hidden layer, c is the dimension of the output layer, T is the hidden space, ϕ is the activation function of the hidden layer and ψ is the activation function of the input layer.

Multilayer perceptron (MLP) is a particular case of artificial neural network, characterized by its neurons being perceptrons (Bishop 2008) and by a back-propagation process. In the case of MLP, the function is expressed as follows (Bishop 2008; Heaton 2012):

$$ {\mathbf{f}}\left( {\mathbf{x}} \right) = \sum\limits_{j = 1}^{p} {\phi_{j} \left( {c_{j} \psi \left( {{\mathbf{w}}_{j}^{T} {\mathbf{x}} + {\mathbf{w}}_{0} } \right) + c_{0} } \right)} $$
(2)

where w j and w 0 are the weights of the input layer and c j and c 0 are the weights of the hidden layer. Different algorithms are used to adjust the weights of the ANN in a process called learning or training. The neural networks used in this research work implement the Gaussian activation function and the back-propagation algorithm.

The above-mentioned back-propagation process propagates backwards the resulting errors of the neural network training process, thus allowing for the reduction of the errors until the network learns the training data analysed.

2.3 Data processing

The prediction of the mechanical properties of cork was approached in two manners: firstly, a regression problem was considered, thus attempting to obtain the exact numerical value of the predicted variable; secondly, it was studied considering a classification problem, defining a number of intervals for each analysed property and assigning each specimen to a certain class.

The criteria for the determination of the best network were the following:

  • Correlation coefficient in the case of neural networks for solving the regression problem. It is defined as the covariance of the variables divided by the product of their standard deviations;

  • Train error rate and test error rate in the case of neural networks for solving the classification problem. These parameters indicate the proportion of elements incorrectly classified in the train subset and in the test subset, respectively. The lower the error rate the lesser elements are incorrectly classified.

The procedure was the following:

  1. 1.

    The data were prepared in a datasheet with the physical and mechanical parameters in columns, each row corresponding to a different specimen;

  2. 2.

    Then, the neural network was trained and validated through a k-fold validation process. This step was repeated for several numbers of neurons in the hidden layer. Since three mechanical properties were to be predicted, a neural network was trained for each of them setting the Young’s modulus, the fracture stress or the fracture strain as the output. The input data were: porosity (%), number of pores (number/cm2), density (g/cm3), approximation of the pores to elliptical shape, approximation of the pores to circular shape, distance to the nearest pore (mm), quality (good and medium quality), position (inner, mid or outer part), direction (axial and tangential) and the synergetic variable (this last variable was not always considered in the tests);

  3. 3.

    The correlation coefficients and the error rates were calculated;

  4. 4.

    The optimum number of neurons in the hidden layer and the accuracy of the prediction were determined.

For the regression analysis, four different configurations regarding the input variables were considered: A, without quality and D/P; B, with quality and without D/P; C, without quality and with D/P; and D, with quality and D/P.

3 Results and discussion

3.1 Solving the regression problem with neural networks

Predicting the three mechanical properties was approached as a regression problem where the neural networks were trained with the four different configurations (A, B, C and D) and validated with a 20-fold cross validation process (the dataset was divided into 20 subsets, using 19 of them to train the model and the remaining to test it; this process was repeated 20 times).

Since the quality was determined visually by an expert, not analytically, it was analysed whether its inclusion was important or not for the performance of the neural network. Furthermore, the new synergistic variable D/P was also studied in the same manner. Therefore, four different configurations of the neural networks regarding the input variables were considered.

The correlation coefficient was determined and used to evaluate the performance of the network for the four configurations and a different number of neurons in the hidden layer. The results are shown in Table 1. Regarding the prediction of fracture stress, it could be seen that the correlation coefficient was stable when the number of neurons in the hidden layer was greater than 125, not exceeding the value of 0.7 despite the increasing number of neurons. Fracture strain provided poor results, with lower correlation coefficients than that of the other two mechanical properties. Not all the variables and configurations were tested up to the same number of neurons in the hidden layer since no improvement was observed in many cases. Hence, when the correlation coefficients decreased and a maximum value had been reached, no further tests were carried out.

Table 1 Results of the neural networks for the regression problem with the four input variables configurations explained (A, B, C, D)
Full size table

The following could be stated:

  1. 1.

    The weights of the input variables were analysed in order to determine their importance for the network. Each input variable has a weight for each neuron in the hidden layer, so classical descriptive analysis was performed. Their mean and variance were analysed in order to establish the ranges of the weights. In those neural networks that included the synergistic variable in their input data (configurations C and D), the weight of this variable was negligible, of about 10−50 or even lower. It seems that this variable does not give any appreciable information to the net;

  2. 2.

    Despite this fact, the best network for the prediction of Young’s modulus corresponded to configuration D (with quality and the synergistic variable as input variables), with the highest correlation coefficient;

  3. 3.

    The prediction of fracture stress showed better results than the prediction of Young’s modulus;

  4. 4.

    However, in any case, the correlation coefficients exceeded 0.7 despite the high number of neurons in the hidden layer.

In view of the previous studies focused on cork properties (Anjos et al. 2010, 2011a), the Young’s modulus and the fracture stress were expected to be predicted more easily than the fracture strain since they show a greater variation in their values. However, these variables were poorly predicted with the different neural trained networks. This fact induced a change on the approach from a regression problem to a classification problem.

3.2 Solving the classification problem with neural networks

After proving the difficulty in predicting the exact value of the mechanical properties, a new approach was considered consisting of solving a classification problem.

For this purpose, a certain number of intervals were defined for Young’s modulus, fracture stress and fracture strain, bearing in mind that a minimum number of cases was needed for the subsequent validation of the network. In this case, a tenfold cross validation process was performed (the dataset was divided into ten subsets, using nine of them to train the model and the other one to test it; this process was repeated ten times).

The considered intervals (Table 2) take into account the following considerations:

Table 2 Considered intervals of the three parameters to be predicted
Full size table
  1. 1.

    The results of previous studies (Anjos et al. 2010, 2011a), which determined the range of values of the different properties for both commercial qualities in the two tensile directions, and three radial positions;

  2. 2.

    Since a tenfold cross validation was to be performed, a minimum of ten elements in each interval was needed.

Several neural networks were trained with 10, 20, 30, 40 and 50 neurons in the hidden layer, calculating the train error rate and the test error rate. Table 3 shows the results obtained for predicting Young’s modulus, fracture stress and fracture strain. By analysing these results, it can be seen how the performance of the neural network is better as the number of neurons in the hidden layer increases, but once a minimum error rate is achieved, the increase of the number of neurons does not imply a better performance of the network.

Table 3 Performance of the different neural networks trained
Full size table

This circumstance is explained by the overfitting concept in Schittenkopf et al. (1997) and Hagiwara and Fukumizu (2008). Overfitting can be summarised as the fact of having very small training errors due to fitting the noise of the studied data instead of the true function, even with greater test or generalization error than the optimal. In this research work, overfitting was prevented by analysing the results, considering the evolution of the error rates: the optimal number of neurons is the one that provides a low train error rate without incrementing the error rate in test.

While the error rates for predicting Young’s modulus and fracture stress are reasonable (about 15 %), in the case of fracture strain, the error rates are inacceptable (about 50 %). Bearing this in mind, further tests were carried out in order to improve the results. These tests focused on the definition of a different set of intervals for the prediction of fracture strain, and also on the study of the influence of the variables in the network.

Regarding the definition of new intervals for fracture strain variable, Table 4 includes the two additional sets of intervals. Despite these new sets, the error rates in test were higher than that of the previous tests.

Table 4 New sets of intervals for fracture strain variable tested in order to obtain a better prediction
Full size table

In view of the poor prediction performance, the synergistic variable (defined as density/number of pores) was included as an additional input variable with the objective of helping the network to be more accurate. The results obtained with this variable and considering the initial intervals (Table 3) are shown in Table 5. The error rates are very similar to the ones obtained for the neural network without the synergistic variable, and there was no appreciable improvement.

Table 5 Performance of the neural network when the synergistic variable density/number of pores is included in the prediction of fracture strain and Young’s modulus
Full size table

The inclusion of this variable was tested in the prediction of Young’s modulus and fracture strain, but it showed null value for the purpose of this study (specially for fracture strain, the property which has shown as the most difficult one to predict). The error rates of the networks including the synergistic variable (Table 5) are higher than those of the neural networks without the synergistic variable. Thus, this variable was discarded and not tested for the prediction of fracture stress. Once the synergistic variable had proved to be useless for a good prediction of the studied parameters, a different strategy was adopted: the influence of the available input parameters on the behaviour of the network.

At this point, the best performance of the neural networks had an error rate of about 15 % in predicting Young’s modulus and fracture stress, and about 45 % in predicting fracture strain. In an attempt of lowering these rates, the variation of several input variables was analysed in order to find the parameters that influence most the classification process. Those physical properties where values are hardly different for each of the intervals of the predicted variables may hinder the classification, so new neural networks were trained without some of the initial input variables, analysing their performance.

The study of the ranges of the discrete input variables gives information about their influence on the performance of the neural network: the more dissimilar the values of the parameters of each class are, the easier the classification process would probably be. If values of a certain input variable differ little from one interval of the predicted property to another, this input variable is likely to be of limited importance for the prediction process, while those input variables where the variation is higher are expected to be significant.

Among the initial input variables, the discrete ones were analysed calculating their mean value, standard deviation and % variation calculated as (Standard deviation/mean) × 100 (Table 6).

Table 6 Analysis of the discrete input variables
Full size table

While porosity and the number of pores vary considerably (29 and 18 % each), the approximation of the pores to elliptical shape seems to differ little among its 144 measurements. A deeper analysis considered the maximum value, the minimum value and the % variation of each of the classes defined for Young’s modulus (Table 7), fracture stress (Table 8) and fracture strain (Table 9). On this occasion, the % variation is calculated as [(maximum mean − minimum mean)/maximum mean] × 100, only for the class where the mean value is the highest.

Table 7 Analysis of the variation of the discrete input variables considering the six classes defined for Young’s modulus
Full size table
Table 8 Analysis of the variation of the discrete input variables considering the seven classes defined for fracture stress
Full size table
Table 9 Analysis of the variation of the discrete input variables considering the five classes defined for fracture strain
Full size table

Bearing this in mind, the results shown in Tables 6, 7 and 8 for the three mechanical properties to be predicted indicate that the input variables FE (approximation of the pores to elliptical shape) and ZO (distance to the nearest pore) have very similar values for every interval considered. In the three cases, the variation of the mean values of FE regarding the different classes are the lowest (7 % for Young’s modulus, 5 % for fracture stress and 3 % for fracture strain), followed by ZO (7, 9 and 8 %, respectively). Thus, new neural networks were trained without these input variables, obtaining the results shown in Table 10 (without FE variable, without ZO and with neither FE nor ZO).

Table 10 Results of the prediction of E, σ and ε without different parameters among the input variables of the neural network
Full size table

The best prediction of Young’s modulus corresponded to the neural network without FE as input variable, with 35 neurons in the hidden layer and with a test error rate of 10.6 %. The best prediction of fracture stress was achieved with the neural network not including FE nor ZO parameters as input variables, with 35 neurons in the hidden layer and a test error rate of 10.2 %.

Fracture strain was not satisfactorly predicted in any case. This could be due to the fact that fracture strain is more dependent on the specific morphology of the pore type (e.g. cells with thick walls as bordering cells of the lenticular channels) and their position, which may constitute points with higher stress concentration. Furthermore, the point of fracture is very difficult to determine in a material like cork.

4 Conclusion

The study focused on predicting the mechanical behaviour of cork from its physical properties using neural networks to predict tensile Young’s modulus, fracture stress and fracture strain.

As a regression problem, poor results were obtained despite the high number of neurons in the hidden layer. The best correlation coefficient was 0.7 and corresponded to the prediction of fracture stress with 50 neurons in the hidden layer.

The problem was approached as a classification problem, thus defining a number of categories (intervals) for each of the three mechanical properties and training several neural networks. It can be concluded that the prediction of Young’s modulus and fracture stress is possible with neural networks when it is approached as a classification problem, with error rates of about 10 %.

The variable approximation of the pores to elliptical shape (FE) is not needed for the prediction of the Young’s modulus neither for the prediction of fracture stress, for which the distance to the nearest pore is also unnecessary.

Prediction of fracture strain was not satisfactory with the methodologies used in this study. However, neural networks have proved to be a valuable tool for the study of cork properties.