1 Introduction

Modelling of a physical system and its controller design often result in higher-order mathematical representation. The analysis of such higher-order systems is tedious and complicated demanding an appropriate model order reduction technique.

The available methodologies for model reduction in non-interval systems offer well-known algorithm: Routh approximation (RA). The approximation features the advantage of simplicity in mathematical computation and stability retention of the resulting reduced model. Due to the above-mentioned advantages, the researchers have focused their attention on possible extension to other type of systems. The continuous-time RA is applied to discrete-time systems by using an appropriate transformation. Further, the attention of the researchers was drawn to extend the method to interval systems. The viability of RA for interval systems is explored in paper by Choudhary and Nagar [6]. The extension of RA to interval systems does not guarantee the stability of reduced model for a stable high-order interval system. The fundamental reason for limitation is irreversibility of interval arithmetic.

This paper focuses on reduction in discrete-time interval systems which are described by z-domain transfer function. The available techniques in this category are multipoint Pade [20] and Pade approximation allowing dominant pole retention [13]. The other methods of reduction in interval systems include a higher-order integrator approach [10] sampled by a zero-order hold, finite impulse response technique [8], H∞ error performance [25], μ-dependent approach [26], direct truncation [2] and gamma–delta approximation [3]. The reduction in discrete-time interval systems based on co-prime factor approach and linear matrix inequality is proposed by Li [16]. The technique proposed by Gupta and Narain [19] is based on clustering and dominant pole retention. Ruchira [22] proposed an extended methodology from continuous-time domain to discrete-time domain. The technique is essentially a mixed method comprising Mikhailov stability criterion and factor division method. Kumar et al. [14, 21] offered a mixed technique for discrete-time interval systems by using improved bilinear Routh approximation. Sandhya [23] considered particle swarm optimization with fuzzy c-means clustering and Kharitonov theorem. The other techniques are covered in references [1, 9, 15, 27].

Arithmetic rules are vital in the context of interval systems. The various model reduction methods available in the literature for interval systems such as time moments and Markov parameters [5, 11, 12, 24] have fully exploited arithmetic rules. However, the technique of multiplicative operator is not used for interval systems. This is the prime motivation to carry out the present work. The multiplicative operator in conjunction with RA is utilized to derive the simplified model. The novelty of the proposed method is twofold: (a) application of a multiplicative operator and (b) finding an appropriate arrangement from various combinations of µ-(mu) and ν-(nu) (Routh) tables to derive the numerator and denominator polynomials of reduced model of desired order.

The outline of the paper is as follows: The interval systems are described in Sect. 2. The details of the new algorithm are described in Sect. 3. Section 4 provides the illustrative examples. Section 5 discusses the important observations followed by conclusion in Sect. 6.

2 Interval Systems

Basic control theory and its analysis are based on the concept of linear and non-interval systems. The research community in early 1990s encountered an unusual category of problem, i.e. robustness and uncertainty in the system. A brief discussion over such system is mentioned below.

Uncertainty in broad sense is the lack of exact knowledge, regardless of the cause for its existence. Precisely, thorough study of any environmental, management or technical system discovers the various types of uncertainties lying within. It is classified into two categories based on their basic nature: (a) aleatoric uncertainties and (b) epistemic uncertainties. Former is the representative of unknowns that vary each time when the same experiment is performed, i.e. inherent randomness and natural variability. Latter is due to things known in principle but not in practice. It is the result from imperfect knowledge, and linguistic uncertainty, arising from language issues. The first is usually irreducible, whereas the latter can be quantified and reduced.

Uncertainties when considered for deriving mathematical representation of the system offer their best approximation. Uncertainty is not only due to the lack of system knowledge but often subjected to perturbations that change dynamics over time. In physical systems, these uncertainties are the consequence of un-modelled dynamics, sensor noises, disturbances, manual errors, parameter variations, actuator constraints and many others. Presence of these uncertainties alters the coefficients of transfer function from non-interval to interval parameters. Thus, systems having coefficients of unknown nature are known as uncertain systems, and when these systems are bounded by a finite range or boundary, it is designated as Interval Systems. The presence of uncertainties in the systems results in difficulties for the system simulation, design and implementation. Since no adequate method emerged for reducing uncertainty description in systems, research developed towards their order reduction. Few examples of uncertain practical systems are:

Cold rolling mill

$$ H\left( s \right) = \frac{{\left[ {4.2,21} \right]s^{2} + \left[ {3,16} \right]s + \left[ {0.5,2.6} \right]}}{{s^{4} + \left[ {3,8} \right]s^{3} + \left[ {1,2.5} \right]s^{2} + \left[ {0.05,0.15} \right]s}}, $$
(1)
$$ H\left( s \right) = \frac{{\left[ {4.5,24} \right]s^{3} + \left[ {5,29} \right]s^{2} + \left[ {0.9,5} \right]s + \left[ {0.05,0.3} \right]}}{{s^{5} + \left[ {4,9} \right]s^{4} + \left[ {4,9} \right]s^{3} + \left[ {0.7,2} \right]s^{2} + \left[ {0.03,0.08} \right]s}}. $$
(2)

Oblique wing aircraft

$$ H\left( s \right) = \frac{{\left[ {54,74} \right]s + \left[ {90,166} \right]}}{{s^{4} + \left[ {2.8,4.6} \right]s^{3} + \left[ {50.4,80.8} \right]s^{2} + \left[ {30.1,33.9} \right]s + \left[ { - 0.1,0.1} \right]}}. $$
(3)

Electric motors

$$ H\left( s \right) = \frac{{50*10^{ - 3} }}{{\left[ {0.0000096,0.0000336} \right]s^{3} + \left[ {0.0012,0.0028} \right]s^{2} + \left[ {0.002025,0.002475} \right]s}}. $$
(4)
  1. A.

    Interval Arithmetic

Arithmetic rules are essential to study each and every aspect of systems. Similar is the case with interval systems that call for interval arithmetic rules. The brief history of arithmetic rules is:

The idea of Interval Computation pioneered from the monograph by Moore [17]. The literature on interval arithmetic is available at http://www.cs.utep.edu/interval-comp/. Recently, Society for Industrial and Applied Mathematics published a book on Interval Arithmetic [18].

Since the proposed technique in the paper deals with interval systems, their mathematical computation demands interval arithmetic which is very similar to the basic arithmetic rules in mathematics. Only difference is the parameters in the interval arithmetic are of uncertain nature illustrated as follows:

Let [a, b] and [c, d] be two interval parameters where a, c are minimum and b, d are maximum entries in the specific intervals. Analogous to the arithmetic rules of definite numerical, interval arithmetic exists as:

$$ {\text{Addition:}}\;\left[ {a, b} \right] + \left[ {c, d} \right] = \left[ {a + c, b + d} \right], $$
(5)
$$ {\text{Subtraction:}}\;\left[ {a, b} \right] - \left[ {c, d} \right] = \left[ {a - d, b - c} \right], $$
(6)
$$ {\text{Multiplication:}}\;\left[ {a, b} \right] \times \left[ {c, d} \right] = \left[ {{\text{Min}}\left( {ac, ad, bc, bd} \right), {\text{Max}}\left( {ac, ad, bc, bd} \right)} \right], $$
(7)
$$ \begin{aligned} & {\text{Division:}}\;\frac{{\left[ {a,b} \right]}}{{\left[ {c,d} \right]}} = \left[ {a,b} \right] \times \left[ {\frac{1}{d},\frac{1}{c}} \right] \end{aligned} $$
(8)
$$\begin{aligned}&{\text{provided}}\quad \left[ {c, d} \right] \notin \left[ 0 \right]. \end{aligned}$$

These uncertainties significantly affect the stability and performance of the system. Ever since the discovery of uncertainty in system, stability is a major issue. The stability of interval system is checked by Kharitonov theorem [4]. It involves the standard Routh algorithm to check stability. It states that an uncertain family of polynomials is robustly stable if, and only if, the Kharitonov polynomials are stable. The theorem holds true in the discrete domain also [7].

3 Model Order Reduction

This section presents the details of proposed algorithm for higher- and lower-order system representations. Tools for the validation of algorithm are also included.

  1. A.

    Proposed Algorithm

Consider a higher-order z-domain interval system described by

$$ H_{m,n} \left( z \right) = \frac{{X_{m} \left( z \right)}}{{Y_{n} \left( z \right)}} = \frac{{X_{m} z^{m} + X_{m - 1} z^{m - 1} + \cdots + X_{0} }}{{Y_{n} z^{n} + Y_{n - 1} z^{n - 1} + \cdots + Y_{0} }}, $$
(9)

where Xi = [X − i , X + i ], i = 0, 1, 2, …, m, and Yj = [Y − j , Y + j ], j = 0, 1, 2, …, n. Let the system under consideration be a proper system where m ≤ n.

Apply Euler forward differentiation technique, i.e. z = p + 1 to transform the discrete-time system to its corresponding continuous-domain representation. Applying the transformation on (9), one obtains

$$ H\left( p \right) = \frac{{B_{m} \left( p \right)}}{{A_{n} \left( p \right)}} = \frac{{b_{m} p^{m} + b_{m - 1} p^{m - 1} + \cdots + b_{0} }}{{a_{n} p^{n} + a_{n - 1} p^{n - 1} + \cdots + a_{0} }}, $$
(10)

where bi = [b − i , b + i ], i = 0, 1, 2, …, m, and aj = [a − j , a + j ], j = 0, 1, 2, …, n.

In the new method, usage of multiplication between the numerator and denominator polynomials offers a larger polynomial retaining the characteristics of both. We term it as π operator over the numerator and denominator polynomials. It is obtained as:

$$ T_{q} \left( p \right) = B_{m} \left( p \right)A_{n} \left( p \right) = C_{q} p^{q} + C_{q - 1} p^{q - 1} + C_{q - 2} p^{q - 2} + \cdots + C_{1} p + C_{0} , $$
(11)

where Ci = [C − i , C + i ], i = 0, 1, 2, …, q and q = m + n.

Coefficients of the reduced-order transfer function are computed from various combinations of µ- and ν-tables described in Tables 1 and 2, respectively. Entries for the µ-table are from Tq(p)and for the ν-table are from \( \hat{T}_{q} \left( p \right) \). The latter is the inverse of former one defined as

Table 1 µ-Table
Full size table
Table 2 ν-Table
Full size table
$$ \hat{T}_{q} \left( p \right) = \frac{1}{p}T_{q} \left( {\frac{1}{p}} \right) = C_{0} p^{q} + C_{1} p^{q - 1} + C_{2} p^{q - 2} + \cdots + C_{q - 1} p^{1} + C_{q} . $$
(12)

Both the tables (µ- and ν-tables) represent the conventional Routh array and have entries as ci,j = [c − i, j , c + i, j ], i = 0, 1, 2, … and j = 0, 1, 2, ….

Entries from the third row onwards in Tables 1 and 2 are as follows:

$$ c_{i,j} = c_{i - 2,j + 1} - \frac{{\left( {c_{i - 2,0} .c_{i - 1,j + 1} } \right)}}{{c_{i - 1,0} }}, $$
(13)

where ci,j = [c − i, j , c + i, j ], i = 2, 3, 4, …, q − 1,q and j = 0, 1, 2, …, q. The use of RA to interval systems is described in [2] where all the possible arrangement of RA is used for both non-interval and interval systems for continuous- and discrete-time systems.

The two tables (µ- and ν-tables) are considered for obtaining the reduced-order transfer function Rk(p), where k(< q) or k < m ≤ n. k represents the desired order of reduced transfer function. The reduced polynomial coefficients are considered via four cases illustrated in the proposed method. It should be noted that the effects of all the coefficients of the first two rows are taken into consideration while computing the coefficients below the third rows.

Thus, reduced transfer function of order k(< q) or k < m ≤ n is constructed with \( \left( {q + 1} \right){\text{th}} \) and \( \left( {q + 2 - k} \right){\text{th}} \) rows for numerator and \( \left( {q + 1 - k} \right){\text{th}} \) and \( \left( {q + 2 - k} \right){\text{th}} \) rows for denominator coefficients. Accordingly, the generalized transfer function is expressed as:

$$ R_{k} \left( p \right) = \frac{{C_{k} \left( p \right)}}{{D_{k} \left( p \right)}} = \frac{{c_{{\left( {q + 1} \right),0}} p^{k - 1} + c_{{\left( {q + 2 - k} \right),0}} p^{k - 2} + c_{{\left( {q + 1} \right),1}} p^{k - 3} + \cdots }}{{d_{{\left( {q + 1 - k} \right),0}} p^{k} + d_{{\left( {q + 2 - k} \right),0}} p^{k - 1} + d_{{\left( {q + 1 - k} \right),1}} p^{k - 2} + \cdots }}. $$
(14)

The Rk(p)is transformed to desired Rk(z)using transformation p = z − 1 resulting in

$$ R_{k} \left( z \right) = \frac{{C_{k} \left( z \right)}}{{D_{k} \left( z \right)}} = \frac{{c_{k - 1} z^{k - 1} + c_{k - 2} z^{k - 2} + \cdots + c_{0} }}{{d_{k} z^{k} + d_{k - 1} z^{k - 1} + \cdots + d_{0} }}, $$
(15)

where ci = [c − i , c + i ] and di = [d − i , d + i ], i = 0, 1, 2, …, k − 1, k.

The four cases to compute the coefficients of the reduced model numerator and denominator polynomials are as follows:

Case 1

Use only µ-table for both numerator and denominator polynomials.

Case 2

Use only ν-table for both numerator and denominator polynomials.

Case 3

Use µ-table for numerator and ν-table for denominator polynomials.

Case 4

Use ν-table for numerator and µ-table for denominator polynomials.

Once the reduced-order representations are derived using above cases, a comparison is made with each other and the existing techniques. Finally, the case that offer better performance and preserves the stability qualifies for selection of reduced model.

Figure 1 demonstrates the flow chart of the proposed algorithm.

Fig. 1
figure 1

Flow chart for the proposed algorithm

Full size image
  1. B.

    Tools for Validation

For discrete-time systems, weighted error sum over a fixed interval of time is used for performance analysis. It is expressed as:

$$ J = \sum\limits_{k = 0}^{\infty } {\left[ {y_{n} \left( k \right) - y_{k} \left( k \right)} \right]^{2} } $$
(16)

where yn(k) and yk(k) are the step responses of the higher-order system Hm,n(z) and reduced-order model Rk(z), respectively.

Minimum J indicates approximate model of the higher-order representation. Since the system under consideration is of interval structure, two individual transfer functions, namely with lower limits and with upper limits, account for performance check. Thus, the J under two error columns, lower and upper limits, makes the analysis and comparison easy with the proposed techniques.

Graphical version of the approximate tracking of the higher- and lower-order representations of the systems is presented through Bode plot.

4 Illustrative Examples

This section presents three numerical examples to demonstrate procedure and assess the performance of the proposed algorithm.

Example 1

Consider a higher-order system from [2, 3, 20] with its p-domain representation as

$$ H_{2,3} \left( p \right) = \frac{{\left[ {3.25,3.35} \right]p^{2} + \left[ {10,10.35} \right]p + \left[ {9.55,10} \right]}}{{\left[ {5.4,5.5} \right]p^{3} + \left[ {17.2,17.6} \right]p^{2} + \left[ {19.7,20.3} \right]p + \left[ {10,10.35} \right]}}. $$
(17)

Multiplying the two polynomials (numerator and denominator) results T5(p) as:

$$\begin{aligned} T_{5} \left( p \right) = \left( {\left[ {3.25,3.35} \right]p^{2} + \left[ {10,10.35} \right]p + \left[ {9.55,10} \right]} \right)\\ \left( {\left[ {5.4,5.5} \right]p^{3} + \left[ {17.2,17.6} \right]p^{2} + \left[ {19.7,20.3} \right]p + \left[ {10,10.35} \right]} \right),\end{aligned} $$
(18)
$$ T_{5} \left( p \right) = \left[ {17.55,18.42} \right]p^{5} + \left[ {109.9,115.88} \right]p^{4} + \left[ {287.59,305.16} \right]p^{3} { + }\left[ {393.76,420.77} \right]p^{2} + \left[ {288.13,310.12} \right]p + \left[ {95.5,103.5} \right]. $$
(19)

Form Table 3 from the above T5(p).

Table 3 µ-Table
Full size table

Reciprocate T5(p) to obtain \( \hat{T}_{5} \left( p \right) \) to lead to Table 4 as:

Table 4 ν-Table
Full size table
$$ \hat{T}_{5} \left( p \right) = \left[ {95.5,103.5} \right]p^{5} + \left[ {288.13,310.12} \right]p^{4} + \left[ {393.76,420.77} \right]p^{3} { + }\left[ {287.59,305.16} \right]p^{2} + \left[ {109.9,115.88} \right]p + \left[ {17.55,18.42} \right]. $$
(20)

Reduced models allowing the four cases derived in p-domain and z-domain are, respectively:

Case 1

Use only µ-table for both numerator and denominator polynomials

$$ R_{2} \left( p \right) = \frac{{\left[ {163.08,226.47} \right]p + \left[ {95.5,103.5} \right]}}{{\left[ {235.93,299.57} \right]p^{2} + \left[ {163.08,226.47} \right]p + \left[ {95.5,103.5} \right]}}, $$
(21)
$$ R_{2} \left( z \right) = \frac{{\left[ {163.08,226.47} \right]z + \left[ { - 130.97, - 59.58} \right]}}{{\left[ {235.93,299.57} \right]z^{2} + \left[ { - 436.06, - 245.39} \right]z + \left[ {104.96,239.99} \right]}}. $$
(22)

Case 2

Use only ν-table for both numerator and denominator polynomials

$$ R_{2} \left( p \right) = \frac{{\left[ {102.46,110.61} \right]p + \left[ {17.55,18.42} \right]}}{{\left[ { - 2005.71,2733.37} \right]p^{2} + \left[ {102.46,110.61} \right]p + \left[ {17.55,18.42} \right]}}, $$
(23)
$$ R_{2} \left( z \right) = \frac{{\left[ {102.46,110.61} \right]z + \left[ { - 93.06, - 84.04} \right]}}{{\left[ { - 2005.71,2733.37} \right]z^{2} + \left[ { - 5364.2,4122} \right]z + \left[ { - 2098.8,2649.3} \right]}}. $$
(24)

Case 3

Use µ-table for numerator and ν-table for denominator polynomials

$$ R_{2} \left( p \right) = \frac{{\left[ {163.08,226.47} \right]p + \left[ {95.5,103.5} \right]}}{{\left[ { - 2005.71,2733.37} \right]p^{2} + \left[ {102.46,110.61} \right]p + \left[ {17.55,18.42} \right]}}, $$
(25)
$$ R_{2} \left( z \right) = \frac{{\left[ {163.08,226.41} \right]z + \left[ { - 130.97, - 59.58} \right]}}{{\left[ { - 2005.71,2733.37} \right]z^{2} + \left[ { - 5364.2,4122} \right]z + \left[ { - 2098.8,2649.3} \right]}}. $$
(26)

Case 4

Use ν-table for numerator and µ-table for denominator polynomials

$$ R_{2} \left( p \right) = \frac{{\left[ {102.46,110.61} \right]z + \left[ {17.55,18.42} \right]}}{{\left[ {235.93,299.57} \right]z^{2} + \left[ {163.08,226.47} \right]z + \left[ {95.5,103.5} \right]}}, $$
(27)
$$ R_{2} \left( z \right) = \frac{{\left[ {102.46,110.61} \right]z + \left[ { - 93.06, - 84.04} \right]}}{{\left[ {235.93,299.57} \right]z^{2} + \left[ { - 436.06, - 245.39} \right]z + \left[ {104.96,239.99} \right]}}. $$
(28)

Table 5 lists the computed error sum for the above cases and comparison with existing techniques. It presents superiority of Case 4 over other methods. Discussion over the explicit finding is done in next section.

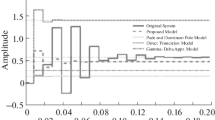
Table 5 Error sum for second-order model for Example 1
Full size table

Figures 2 and 3 present the frequency response for all the cases for lower- and upper-limit transfer functions, respectively. The figures depict an appropriate tracking of the responses.

Fig. 2
figure 2

Frequency response for lower limit (Example 1)

Full size image
Fig. 3
figure 3

Frequency response for upper limit (Example 1)

Full size image

Example 2

Consider higher-order interval system considered in [2, 3, 13]

$$ H_{2,3} \left( z \right) = \frac{{\left[ {1,2} \right]z^{2} + \left[ {3,4} \right]z + \left[ {8,10} \right]}}{{\left[ {6,6} \right]z^{3} + \left[ {9,9.5} \right]z^{2} + \left[ {4.9,5} \right]z + \left[ {0.8,0.85} \right]}}. $$
(29)

Following the proposed procedure, second-order reduced models are obtained as:

Case 1

$$ R_{2} \left( z \right) = \frac{{\left[ {352,1045.04} \right]z + \left[ { - 796.64, - 10.4} \right]}}{{\left[ { - 580.1,737.79} \right]z^{2} + \left[ { - 1123.58,2205.24} \right]z + \left[ { - 1376.74,727.39} \right]}}. $$
(30)

Case 2

$$ R_{2} \left( z \right) = \frac{{\left[ {25.27,564.13} \right]z + \left[ { - 558.13, - 13.27} \right]}}{{\left[ { - 19.33,360.07} \right]z^{2} + \left[ { - 694.87,602.79} \right]z + \left[ { - 577.46,346.8} \right]}}. $$
(31)

Case 3

$$ R_{2} \left( z \right) = \frac{{\left[ {352,1045.04} \right]z + \left[ { - 796.64, - 10.4} \right]}}{{\left[ { - 19.33,360.07} \right]z^{2} + \left[ { - 694.87,602.79} \right]z + \left[ { - 577.46,346.8} \right]}}. $$
(32)

Case 4

$$ R_{2} \left( z \right) = \frac{{\left[ {25.27,564.13} \right]z + \left[ { - 558.13, - 13.27} \right]}}{{\left[ { - 580.1,737.79} \right]z^{2} + \left[ { - 1123.58,2205.24} \right]z + \left[ { - 1376.74,727.39} \right]}}. $$
(33)

The corresponding error sum is given in Table 6. The frequency response plots for lower and upper bounds are shown in Figs. 4 and 5, respectively.

Table 6 Error sum for second-order model for Example 2
Full size table
Fig. 4
figure 4

Frequency response for lower limit (Example 2)

Full size image
Fig. 5
figure 5

Frequency response for upper limit (Example 2)

Full size image

The examples clearly indicate the superiority of Case 4 for computing reduced model.

Example 3

Consider the automatic voltage regulator system shown in Fig. 6. The parameters of system are T1 = 5, T2 = 2, T3 = 0.07, T4 = 0.04, T5 = 0.1, a1 = 2.5, a2 = 3.2, a3 = 6, a4 = 3, a5 = 3 (T1, T2, T3, T4, T5 in s). Due to uncertainties, the system is an interval system described by following z transfer function (T = 0.01 s)

$$ H_{5} \left( z \right) = \frac{\begin{aligned} \left[ {0.95,1.05} \right]z^{4} + \left[ {11.10,12.27} \right]z^{3} + \left[ {11.56,112.78} \right]z^{2} \hfill \\ + \,\left[ {1.76,1.95} \right]z + \left[ {0.031,0.03} \right] \hfill \\ \end{aligned} }{\begin{aligned} \left[ {168.22,185.93} \right]z^{5} + \left[ { - 473.21, - 428.14} \right]z^{4} + \left[ {349.91,386.74} \right]z^{3} \hfill \\ +\, \left[ { - 94.12,85.15} \right]z^{2} + \left[ { - 4.07, - 3.68} \right]z + \left[ { - 1.24, - 1.13} \right] \hfill \\ \end{aligned} }. $$
(34)
Fig. 6
figure 6

Higher-order automatic voltage regulator

Full size image

Reduced model by Case 4 is

$$ R_{2} (z) = \frac{{\left[ { - 3740.8,5834} \right]z + \left[ { - 5674.2,3936} \right]}}{{\left[ { - 41060,45979} \right]z^{2} + \left[ { - 121011,111415} \right]z + \left[ { - 71886,76564} \right]}}. $$
(35)

Table 7 indicates superiority of the second-order reduced model with other techniques. Figures 7 and 8 show frequency response plots for lower and upper limits, respectively.

Table 7 Error sum for second-order model for Example 3
Full size table
Fig. 7
figure 7

Frequency response for lower limit (Example 3)

Full size image
Fig. 8
figure 8

Frequency response for upper limit (Example 3)

Full size image

5 Discussion

It is observed that different techniques proposed in this paper have different error bounds. It will enable us to choose an appropriate model based on accuracy requirement. Some important observations are: in Table 5, proposed Case 1 and gamma–delta approximation offer minimum error; and in Tables 6 and 7, direct truncation presents minimum error. It may be stated that of all the error tables, the Case 4 appears to be the finest, offering minimum error. The prime advantage of Case 4 over the others is the stability retention. This check is performed by Kharitonov theorem for interval systems. Thus, in spite of higher error bounds, Case 4 is superior to the existing techniques.

Further, Figs. 2, 3, 4, 5, 7 and 8 present the frequency responses of reduced-order models and higher-order models. The responses clearly illustrate the validity of higher-order system approximation.

As future work, the reduced-order model may be derived by considering numerator and denominator polynomials separately. The disadvantage of considering separate polynomials is overweighed by lengthy tables and hence more computation.

6 Conclusion

The Routh approximation has been considered here for model reduction in interval system due to its principal advantage of stability retention. The results of the illustrative examples show that proposed method can be a viable alternative for reducing complex system. The focus of the proposed algorithm is the employment of multiplicative operator and the selection of different criterion for deriving the numerator and denominator polynomials of reduced-order representation.