Finite-Time Control of Uncertain Fractional-Order Positive Impulsive Switched Systems with Mode-Dependent Average Dwell Time

Abstract

This paper is concerned with the problem of finite-time control of uncertain fractional-order positive impulsive switched systems (UFOPISS) via mode-dependent average dwell time (MDADT). The uncertainties refer to interval and polytopic uncertainties. Firstly, the proof of the positivity of UFOPISS is given. By constructing linear copositive Lyapunov functions, the finite-time stability (FTS) of autonomous system with MDADT is studied. Then, state feedback controllers are designed to guarantee the FTS of the resulting closed-loop system with interval and polytopic uncertainties, respectively. All presented conditions can be easily solved by linear programming. Finally, a fractional-order circuit model is employed to illustrate the effectiveness of the proposed method.

1 Introduction

During the past decade, positive switched systems with integer order derivative have been paid much attention [8, 17, 20, 30, 36]. By contrast, because fractional differential equations have been proved to be valuable tools in the modeling of many practical dynamics systems, such as fractional PID control [10, 11], fractional electrical networks [3, 16], fractional-order Chuas circuit [13], fractional-order biological system [1] and so on, fractional calculus is more feasible than integer calculations to model the behavior of such systems. Recently, fractional calculus has been introduced to the stability analysis of switched systems [7, 14, 15, 24, 31].

Very recently, a few results about fractional-order positive switched systems (FOPSS) have been presented [2, 19, 34, 35]. [2] considered the controllability of FOPSS for fixed switching sequence. [35] considered the problem of state-dependent switching control of FOPSS. However, these studies mainly focus on the asymptotic stability, which reflects the asymptotic behavior of the system in an infinite time interval. Compared with asymptotic stability, FTS is a more practical concept to study the behavior of the system within a finite interval. For FOPSS, [34] studied the FTS of FOPSS with average dwell time (ADT) approach. [19] considered the guaranteed cost finite-time control of FOPSS with ADT approach. As we know, MDADT approach allows that every subsystem has its own ADT to make the individual properties of each subsystem unneglected, which is more applicable and less conservative compared with ADT. Then, for FOPSS, MDADT must be taken into account in analyzing and implementing finite-time controller scheme.

In addition, affected by the environment and the system itself, the impulse effects always appear at the switching points of switched systems. Moreover, due to the model construction, installation error, and the measurement error of parameters, almost all control systems contain uncertainties. Recently, some results studied the stability and stabilization analysis of fractional-order impulsive switched systems or uncertain fractional-order systems [4, 5, 18, 32]. When the impulsive jumps and uncertainties happen simultaneously in the FOPSS, it will lead to some difficulties for the FTS analysis. To the best of our knowledge, the problem of FTS analysis for fractional-order positive impulsive switched systems with uncertainties is still open.

Motivated by the above discussions, in this paper, the problem of finite-time control of UFOPISS via MDADT is investigated. The main contributions of this paper can be summarized as follows: (i) The proof of the positivity of UFOPISS is given and the definition of finite-time stability is extended to UFOPISS. (ii) By using copositive-type Lyapunov function and MDADT approach, two state feedback controllers are designed. (iii) Some sufficient conditions are obtained to guarantee the corresponding closed-loop systems with interval and polytopic uncertainties are finite-time stable, respectively. Such conditions can be easily solved by linear programming.

The rest of the paper is organized as follows. In Sect. 2, problem formulation and some necessary lemmas are given. In Sect. 3, the issue of finite-time control for UFOPISS with interval and polytopic uncertainties are developed. Section 4 gives a fractional-order circuit model to illustrate the effectiveness of the proposed approach. Section 5 concludes the paper.

Notations Throughout this paper, $A\succ 0$ $(\succeq 0, \prec 0, \preceq 0)$ means that $a_{ij}>0$ $(\ge 0, <0, \le 0)$, which is applicable to a vector. $A\succ B$ $(A\succeq B)$ means that $A- B\succ 0$ $(A-B\succeq 0)$; The symbols R, $R^n$ and $R^{n\times n}$ denote the set of real numbers, the space of the vectors of n-tuples of real numbers and the space of $n\times n$ matrices with real numbers, respectively. $R_+^n$ is the n-dimensional nonnegative (positive) vector space. Matrix $A\in [\underline{\mathrm{A}}, \bar{A}]$ means that $a_{ij}\in [\underline{\mathrm{a}}_{ij}, \bar{a}_{ij}]$. $A^\mathrm{T}$ denotes the transpose of matrix A. $\mathbf {I\mathbf }$ represents the identity matrix. Matrices are assumed to have compatible dimensions for calculating if their dimensions are not explicitly stated.

2 Preliminaries and Problem Statements

2.1 Fractional-Order Calculus

Fractional-order integro-differential operator is the generalization of integer order integro-differential operator. There are different definitions of the fractional-order integral or derivative. Given $0<\alpha <1$, the uniform formula of a fractional integral is defined as

$$\begin{aligned} _{t_0}D_t^{-\alpha }f(t)=\frac{1}{\varGamma (\alpha )}\int _{t_0}^t\frac{f(\tau )}{(t-\tau )^{1-\alpha }}\hbox {d}\tau \end{aligned}$$

(1)

where $\varGamma (\alpha )$ denotes the Gamma function with non-integer arguments. For $0<\alpha <1$, the Riemann–Liouville (RL) definition of fractional derivative is given as

$$\begin{aligned} _{t_0}^\mathrm{RL}D_t^{\alpha }f(t)=\frac{1}{\varGamma (1-\alpha )}\frac{\hbox {d}}{\hbox {d}t}\int _{t_0}^t\frac{f(\tau )}{(t-\tau )^{\alpha }}\hbox {d}\tau , \end{aligned}$$

(2)

and Caputo definition of fractional derivative is given as

$$\begin{aligned} _{t_0}^C D_t^{\alpha }f(t)=\frac{1}{\varGamma (1-\alpha )}\int _{t_0}^t\frac{f'(\tau )}{(t-\tau )^\alpha }\hbox {d}\tau , \end{aligned}$$

(3)

where f(t) is an arbitrary integrable function, $_{t_0}D_t^{-\alpha }$ is the fractional integral of order $\alpha$ on $[t_0, t]$, $\varGamma (\alpha )=\int _0^\infty e^{-t}t^{\alpha -1}\hbox {d}t$. $_{t_0}^\mathrm{RL}D_t^{\alpha }$ and $_{t_0}^\mathrm{RL}D_t^{\alpha }$ represent Riemann–Liouville and Caputo fractional derivatives of order $\alpha$ of f(t) on $[t_0, t]$, respectively. We mainly use these two fractional-order operators in this paper. From the above two definitions, we can obtain the following relation between them:

$$\begin{aligned} _{t_0}^\mathrm{RL}D_t^{\alpha }f(t)=_{t_0}^C D_t^{\alpha }f(t)+\frac{t^{-\alpha }}{\varGamma (1-\alpha )}f(t_0), \end{aligned}$$

(4)

Lemma 1

[17] Let $\alpha \in (0, 1)$, if $f(0)\ge 0$, then $_{t_0}^\mathrm{RL}D_t^{\alpha }f(t)\le {_{t_0}^C}D_t^{\alpha }f(t)$.

2.2 Uncertain Fractional-Order Positive Impulsive Switched Systems

Consider the following UFOPISS:

$$\begin{aligned} \left\{ \begin{array}{l} _{t_0}^C D_t^{\alpha }x(t)=A_{\sigma (t)}{x}(t)+B_{\sigma (t)}u(t), \ t\ne t_k, \ k\in Z^+\\ x(t)=J_{\sigma (t^-)}x(t^-),\ t=t_k, \ k\in Z^+,\ 0<\alpha <1. \end{array} \right. \end{aligned}$$

(5)

where $x(t)\in R^{n}$ is the system state, $u(t)\in R^{m}$ represents the control input. $_{t_0}^C D_t^{\alpha }$ denotes Caputo fractional-order derivative. $x(t_k^-)=\lim _{h\rightarrow 0^-}x(t_k+h)$, $t_k$ denotes the k-th impulsive jump instant, $t_0=0$ is the initial time. $\sigma (t):[0, \infty )\rightarrow \underline{\mathrm{S}}=\{1, 2, \dots , S\}$ is the switching signal, S is the number of subsystems; $\forall p\in \underline{\mathrm{S}}$, $A_p$, $B_p$ and $J_p$ are constant matrices with appropriate dimensions, p denotes the pth systems.

Remark 1

In reality, because of abrupt jumps at certain instants during the switching processes, the states of systems always show impulsive dynamical behaviors, which can be modeled by $x(t)=J_{\sigma (t^-)}x(t^-)$. This model has been reported in temperature process control, induction-motor, biochemical process, transportation and so on (see [6, 21, 28, 29]).

Remark 2

The system model (5) is a more general form. Especially, if $J_p =I$, then the system (5) is turned into fractional-order positive switched systems in [18, 34, 35].

Next, we will present some definitions, lemmas and inequalities for the UFOPISS (5) for our further study.

Definition 1

[34] The system (5) is said to be positive if for any switching signals $\sigma (t)$, any initial conditions $x(t_0)\succeq 0$, the corresponding trajectory satisfies $x(t)\succeq 0$ for all $t\succeq 0$.

Definition 2

[17] A matrix A is called a Metzler matrix if the off-diagonal entries of matrix A are nonnegative.

Lemma 2

[17] A matrix is a Metzler matrix if and only if there exists a positive constant $\varsigma$ such that $A+\varsigma I_n\succeq 0$.

Definition 3

[30] For any switching signal $\sigma (t)$ and any $t_2\ge t_1 \ge 0$, let $N_{\sigma p}(t_1, t_2)$ denote the switching numbers that the pth subsystem is activated over the interval $[t_1, t_2)$ and $T_p(t_1, t_2)$ denote the total running time of the pth subsystem over the interval $[t_1, t_2)$. If there exist $N_{0p}\ge 0$ and $T_{\alpha p}>0$ such that

$$\begin{aligned} N_{\sigma p}(t_1,t_2)\le N_{0p}+\frac{T_p(t_1, t_2)}{T_{\alpha p}}, \ \forall \ t_2\ge t_1 \ge 0,\forall \ p\in \underline{\mathrm{S}} \end{aligned}$$

(6)

then $T_{\alpha p}$ and $N_{0p}$ are called MDADT and mode-dependent chattering bounds, respectively. Generally, we choose $N_{0p}=0.$

Lemma 3

The system (5) is positive if and only if $A_p$, $\forall p\in \underline{\mathrm{S}}$ are Metzler matrices, $B_p\succeq 0$ and $J_p\succeq 0$.

Definition 4

[19] For given time constant $T_f$ and vectors $\delta \succ \varepsilon \succ 0$, the system (5) is said to be finite-time stable with respect to ($\delta$, $\varepsilon$, $T_f$, $\sigma (t)$), if

$$\begin{aligned} x^\mathrm{T}(0)\delta \le 1 \Rightarrow x^\mathrm{T}(t)\varepsilon \le 1, \forall \ t\in [0, T_f]. \end{aligned}$$

(7)

2.3 Some Inequalities

The following inequalities are necessary for our further study.

Lemma 4

(Gronwall–Bellman inequality) Let a(t), b(t) and g(t) be continuous real-valued functions. If a(t) is nonnegative and if g(t) satisfies the integral inequality

$$\begin{aligned} g(t)\le a(t)+\int _0^tb(s)g(s)\hbox {d}s, \end{aligned}$$

then

$$\begin{aligned} g(t)\le a(t)+\int _0^ta(s)b(s)\exp \left( \int _s^tb(r)\hbox {d}r\right) \hbox {d}s. \end{aligned}$$

If, in addition, a(t) is a constant, then

$$\begin{aligned} g(t)\le a(t)\exp (\int _0^tb(s)\hbox {d}s). \end{aligned}$$

Lemma 5

($C_p$ inequality) For $0<a<1$ and any positive real numbers $x_1, x_2, \dots , x_k$,

$$\begin{aligned} \sum _{k=1}^nx_k^a\le n^{1-a}\bigg (\sum _{k=1}^nx_k\bigg )^a. \end{aligned}$$

Lemma 6

(Young’s inequality) If a and b are nonnegative real numbers, p and q are positive real numbers such that $1/p + 1/q = 1$, then

$$\begin{aligned} ab\le \frac{a^p}{p}+\frac{b^q}{q}. \end{aligned}$$

Definition 5

[6] The function $V: R_+\times R^n\rightarrow R_+$ belongs to class $\zeta$ if

(i) the function V is continuous in each of the sets $[t_k, t_{k+1})\times R^n$ and for each $x, y\in R^n$,

$t\in [t_k, t_{k+1})$, $k\in Z^+$, $\lim _{(t,y)\rightarrow (t_k^-,x)}V(t,y)=V(t_k^-, x)$ exists;

(ii) V(t, x(t)) is locally Lipschitzian in all $x\in R^n$, and for all $t\ge t_0$, $V(t, 0)\equiv 0$.

The aim of this paper is to design two state feedback controllers $u(t)=K_{\sigma (t)}x(t)$ and a class of switching signals $\sigma (t)$ for UFOPISS (5) such that the corresponding closed-loop systems with interval and polytopic uncertainties are finite-time stable, respectively.

3 Main Results

3.1 Finite-Time Stability Analysis

In this subsection, we consider the problem of FTS for UFOPISS (5) with $u(t)\equiv 0$. Consider two types of uncertainties: interval and polytopic uncertainties, the following theorems give sufficient conditions of FTS of system (5) via the MDADT approach, respectively.

Firstly, we give the following key lemma.

Lemma 7

Assume $\forall p\in \underline{\mathrm{S}}$, $\underline{\mathrm{A}}_p\preceq A_p\preceq \bar{A}_p$, $0\preceq \underline{\mathrm{B}}_p\preceq B_p\preceq \bar{B}_p$ and $J_p\succeq 0$, where $A_p$ is a Metzler matrix, then system (5) is positive.

Proof

Let $t_1, t_2, \dots , t_k, \dots , t_N$ denote the switching instants on the interval $[t_0, T_f]$. When $t\ne t_k$, similar to Theorem 1 in [23], the positivity of the system can be easily proved. Next, when $t=t_k$, the positivity analysis of the system (5) is given as follows.

Sufficiency: When $t=t_k$, $x(t_k)=J_{\sigma (t_k^-)}x(t_k^-)$, since $x(t_k^-)\succeq 0$, if $J_{\sigma (t_k^-)}\succeq 0$, we have $x(t_k)\succeq 0$.

Necessity: When $t=t_k$, $x(t_k)=J_{\sigma (t_k^-)}x(t_k^-)$. Suppose $J_{\sigma (t_k^-)}$ dissatisfies $J_{\sigma (t_k^-)}\succeq 0$, since $x(t_k^-)\succeq 0$ is any vector, there exists a $x(t_k^-)$ such that $x(t_k)$ dissatisfies $x(t_k)\succeq 0$, it follows that the system (5) is not positive. Therefore, there must be $J_p\succeq 0$, $\forall p\in \underline{\mathrm{S}}$.

From the above, the system (5) is positive under any switching signals if and only if $A_p$ are Metzler matrices, $B_p\succeq 0$ and $J_p\succeq 0$, $\forall p\in \underline{\mathrm{S}}$. $\square$

3.1.1 Interval Uncertainty

In this subsection, we consider the FTS of the system (5) with the interval uncertainties. Consider the following interval uncertainties:

For all $p\in \underline{\mathrm{S}}$, we have $\underline{\mathrm{A}}_p\preceq A_p\preceq \bar{A}_p$ and $0\preceq \underline{\mathrm{B}}_p\preceq B_p\preceq \bar{B}_p$, which can be denoted by $A_p\in [\underline{\mathrm{A}}_p, \bar{A}_p]$ and $B_p\in [\underline{\mathrm{B}}_p, \bar{B}_p]$.

Theorem 1

Assume $A_p\in [\underline{\mathrm{A}}_p, \bar{A}_p]$ for each $p\in \underline{\mathrm{S}}$, where $A_p$ is a Metzler matrix. Consider the system (5) with $u(t)\equiv 0$. Given positive constants $T_f$, $\lambda _p$, vectors $\delta \succ \varepsilon \succ 0$, if there exist positive constants $\xi _1$, $\xi _2$, $\mu _p$, and positive vectors $v_p$, $p\in \underline{\mathrm{S}}$, such that the following inequalities hold:

$$\begin{aligned}&\displaystyle \bar{A}_p^\mathrm{T}v_p\preceq \lambda _p v_p\end{aligned}$$

(8)

$$\begin{aligned}&\displaystyle J_p^\mathrm{T}v_p\preceq \mu _p v_q\end{aligned}$$

(9)

$$\begin{aligned}&\displaystyle \xi _1\varepsilon \prec v_p\prec \xi _2\delta \end{aligned}$$

(10)

$$\begin{aligned}&\displaystyle \frac{\lambda (\alpha T_f-\alpha +1)}{\varGamma (\alpha +1)}<\ln \frac{\xi _1}{\xi _2} \end{aligned}$$

(11)

where $\forall p\in \underline{\mathrm{S}}$, $v_p=[v_{p1}, v_{p2}, \dots , v_{pn}]^\mathrm{T}$, $\lambda =\max _{p\in \underline{\mathrm{S}}}\{\lambda _p\}$, $\mu _p \ge 1$, then under the following MDADT scheme

$$\begin{aligned} T_\alpha >T_\alpha ^*=T_f\bigg (\ln \mu _p+\frac{\lambda (1-\alpha )}{\varGamma (\alpha +1)}\bigg )\big /\bigg (\ln \frac{\xi _1}{\xi _2}-\frac{\lambda (\alpha T_f-\alpha +1)}{\varGamma (\alpha +1)}\bigg ) \end{aligned}$$

(12)

the UFOPISS (5) is finite-time stable with respect to $(\delta , \varepsilon , T_f, \sigma (t))$.

Proof

Constructing the multiple linear-type Lyapunov–Krasovskii functional for the system (5) as follows:

$$\begin{aligned} V_{\sigma (t)}(t,x(t))=x^\mathrm{T} (t)v_{\sigma (t)} \end{aligned}$$

(13)

where $v_p\in R_+^n$, $\forall p \in \underline{\mathrm{S}}$.

Denote $t_0, t_1, \dots$ as the switching instants over the interval $[0, T_f]$. When $t\in (t_k, t_{k+1})$, calculating the upper right-hand derivative of $V_{\sigma (t)}(t)$ along the trajectory of the system (5) with $u(t)\equiv 0$, from (8), we have

$$\begin{aligned} ^C_{t_0}D^\alpha _tV_{\sigma (t)}(t, x(t))=x^\mathrm{T}(t)A^\mathrm{T}_{\sigma (t)} v_{\sigma (t)}\le x^\mathrm{T}(t)\bar{A}^\mathrm{T}_{\sigma (t)} v_{\sigma (t)}\le \lambda _p V_{\sigma (t_k)}(t, x(t)) \end{aligned}$$

(14)

Taking the fractional integral $^C_{t_0}D^{-\alpha }_t$ to both sides of (14) during the period $(t_k, t)$ for $t\in (t_k, t_{k+1})$ leads to

$$\begin{aligned} V_{\sigma (t)}(t, x(t))\le V_{\sigma (t_k)}(t_k, x(t_k))+\frac{\lambda _{\sigma (t_k)}}{\varGamma (\alpha )}\int ^t_{t_k}(t-s)^{\alpha -1}V_{\sigma (t)}(s, x(s))\hbox {d}s \end{aligned}$$

(15)

From Lemma 4 and the properties of Gamma function $\varGamma (\alpha )$, for $t\in (t_k, t_{k+1})$, we have

$$\begin{aligned} V_{\sigma (t)}(t, x(t))\le & {} V_{\sigma (t_k)}(t_k, x(t_k))+\frac{\lambda _{\sigma (t_k)}}{\varGamma (\alpha )}\int ^t_{t_k}(t-s)^{\alpha -1}V_{\sigma (t)}(s, x(s))\hbox {d}s\nonumber \\\le & {} V_{\sigma (t_k)}(t_k, x(t_k))\exp \left\{ \frac{\lambda _{\sigma (t_k)}}{\varGamma (\alpha )}\int _{t_k}^t(t-s)^{\alpha -1}\hbox {d}s\right\} \nonumber \\= & {} V_{\sigma (t_k)}(t_k, x(t_k))\exp \left\{ \frac{\lambda _{\sigma (t_k)}}{\alpha \varGamma (\alpha )}(t-{t_k})^\alpha \right\} \nonumber \\= & {} V_{\sigma (t_k)}(t_k, x(t_k))\exp \left\{ \frac{\lambda _{\sigma (t_k)}}{\varGamma (\alpha +1)}(t-{t_k})^\alpha \right\} \end{aligned}$$

(16)

On the other hand, when $t=t_k$, from (5), (9) and (13), it yields that

$$\begin{aligned} V_{\sigma (t_k)}(t_k)=x^\mathrm{T} (t_k^-)J^\mathrm{T}_{\sigma (t_k^-)}v_{\sigma (t_k)}\le \mu _{\sigma (t)}x^\mathrm{T} (t_k^-)v_{\sigma (t_k^-)}=\mu _pV_{\sigma (t_k^-)}(t_k^-) \end{aligned}$$

(17)

From (16), (17) and $\exp \{\frac{\lambda _{\sigma (t_k)}}{\varGamma (\alpha +1)}(t-t_k)^\alpha \}>0$, we have

$$\begin{aligned} V_{\sigma (t)}(t, x(t))\le \mu _{\sigma (t_k)} V_{\sigma (t_k^-)}(t_k^-, x(t_k^-))\exp \left\{ \frac{\lambda _{\sigma (t_k)}}{\varGamma (\alpha +1)}(t-{t_k})^\alpha \right\} \end{aligned}$$

(18)

Then, from (16) and (18), for $t\in [0, T_f)$, we get

$$\begin{aligned} V_{\sigma (t)}(t, x(t))\le & {} V_{\sigma (t_k)}(t_k, x(t_k))\exp \left\{ \frac{\lambda _{\sigma (t_k)}}{\varGamma (\alpha +1)}(t-{t_k})^\alpha \right\} \nonumber \\\le & {} \mu _{\sigma (t_k)} V_{\sigma (t_k^-)}(t_k^-, x(t_k^-))\exp \left\{ \frac{\lambda _{\sigma (t_k)}}{\varGamma (\alpha +1)}(t-{t_k})^\alpha \right\} \nonumber \\\le & {} \mu _{\sigma (t_{k})} V_{\sigma (t_{k-1})}(t_{k-1}, x(t_{k-1}))\exp \left\{ \left[ \frac{\lambda _{\sigma (t_k)}}{\varGamma (\alpha +1)}(t-{t_k})^\alpha \right. \right. \nonumber \\&\left. \left. +\frac{\lambda _{\sigma (t_{k-1})}}{\varGamma (\alpha +1)}(t_k-t_{k-1})^\alpha \right] \right\} \nonumber \\\le & {} \mu _{\sigma (t_{k})}\mu _{\sigma (t_{k-1})} V_{\sigma (t_{k-1}^-)}(t_{k-1}^-, x(t_{k-1}^-))\exp \left\{ \left[ \frac{\lambda _{\sigma (t_k)}}{\varGamma (\alpha +1)}(t-{t_k})^\alpha \right. \right. \nonumber \\&\left. \left. +\frac{\lambda _{\sigma (t_{k-1})}}{\varGamma (\alpha +1)}(t_k-t_{k-1})^\alpha \right] \right\} \nonumber \\\le & {} \cdots \nonumber \\\le & {} \left( \prod \limits _{i=1}^k\mu _{\sigma (t_{i})}\right) V_{\sigma (0)}(0, x(0))\exp \left\{ \left[ \frac{\lambda _{\sigma (t_k)}}{\varGamma (\alpha +1)}(t-{t_k})^\alpha \right. \right. \nonumber \\&\left. \left. +\frac{\lambda _{\sigma (t_{k-1})}}{\varGamma (\alpha +1)}(t_k-t_{k-1})^\alpha +\cdots + \frac{\lambda _{\sigma (t_0)}}{\varGamma (\alpha +1)}(t_1-t_0)^\alpha \right] \right\} \end{aligned}$$

(19)

Let $\lambda =\max _{p\in \underline{\mathrm{S}}}\{\lambda _p\}$, we have

$$\begin{aligned} V_{\sigma (t)}(t, x(t))\le & {} \left( \prod \limits _{i=1}^k\mu _{\sigma (t_{i})}\right) V_{\sigma (0)}(0, x(0))\exp \left\{ \frac{\lambda }{\varGamma (\alpha +1)}\left[ (t-{t_k})^\alpha \right. \right. \nonumber \\&\left. \left. +(t_k-t_{k-1})^\alpha +\cdots +(t_1-0)^\alpha \right] \right\} \end{aligned}$$

(20)

From Definition 3 and Lemma 5, for $t\in [0, T_f]$, we have

$$\begin{aligned} V_{\sigma (t)}(t, x(t))\le & {} \left( \prod \limits _{p=1}^S\mu _p^{N_{\sigma p}(0, t)}\right) V_{\sigma (0)}(0, x(0))\exp \left\{ \frac{\lambda }{\varGamma (\alpha +1)}[(t-{t_k})^\alpha \right. \nonumber \\&\left. +(t_k-t_{k-1})^\alpha +\cdots +(t_1-0)^\alpha ]\right\} \nonumber \\\le & {} \left( \prod \limits _{p=1}^S\mu _p^{\frac{T_p (0, t)}{T_{\alpha p}}}\right) V_{\sigma (0)}(0, x(0))\exp \left\{ \frac{\lambda }{\varGamma (\alpha +1)}[(t-{t_k})^\alpha \right. \nonumber \\&\left. +(t_k-t_{k-1})^\alpha +\cdots +(t_1-0)^\alpha ]\right\} \nonumber \\\le & {} e^{\sum _{p=1}^S \frac{\ln \mu _p}{T_{\alpha p}}T_p (0, t)}V_{\sigma (0)}(0, x(0))\exp \left\{ \frac{\lambda }{\varGamma (\alpha +1)}[(t-{t_k})^\alpha \right. \nonumber \\&\left. +(t_k-t_{k-1})^\alpha +\cdots +(t_1-0)^\alpha ]\right\} \nonumber \\\le & {} e^{\sum _{p=1}^S \frac{\ln \mu _p}{T_{\alpha p}}T_p (0, T_f)}V_{\sigma (0)}(0, x(0))\exp \left\{ \frac{\lambda }{\varGamma (\alpha +1)}\right. \nonumber \\&\left. \cdot \left[ \left( \frac{T_p (0, T_f)}{T_{\alpha p}}+1\right) ^{1-\alpha } T_f^\alpha \right] \right\} \nonumber \\= & {} V_{\sigma (0)}(0, x(0))\exp \left\{ {\sum \limits _{p=1}^S \frac{\ln \mu _p}{T_{\alpha p}}T_p (0, T_f)}\right. \nonumber \\&\left. + \frac{\lambda }{\varGamma (\alpha +1)}\left[ \left( \frac{T_p (0, T_f)}{T_{\alpha p}}+1\right) ^{1-\alpha } T_f^\alpha \right] \right\} \end{aligned}$$

(21)

According to Lemma 6, (21) can be rewritten as

$$\begin{aligned} V_{\sigma (t)}(t, x(t))\le & {} V_{\sigma (0)}(0, x(0))\exp \left\{ {\sum \limits _{p=1}^S \frac{\ln \mu _p}{T_{\alpha p}}T_p (0, t)}\right. \nonumber \\&\left. + \frac{\lambda }{\varGamma (\alpha +1)}\left[ (1-\alpha )\left( \frac{T_p (0, t)}{T_{\alpha p}}+1\right) +\alpha T_f\right] \right\} \nonumber \\\le & {} V_{\sigma (0)}(0, x(0))\exp \left\{ {\sum \limits _{p=1}^S \frac{\ln \mu _p}{T_{\alpha p}}T_p (0, t)}\right. \nonumber \\&\left. + \frac{\lambda }{\varGamma (\alpha +1)}\left[ (1-\alpha )\left( \frac{\ln \mu _p}{T_{\alpha p}}\cdot \frac{T_p (0, t)}{\ln \mu _p}+1\right) +\alpha T_f\right] \right\} \qquad \end{aligned}$$

(22)

Let $\beta =\max _{p\in \underline{\mathrm{S}}}\{\frac{\ln \mu _p}{T_{\alpha p}}\}$, we have

$$\begin{aligned} V_{\sigma (t)}(t, x(t))\le & {} V_{\sigma (t_0)}(t_0, x(t_0))\exp \left\{ \beta T_f+ \frac{\lambda }{\varGamma (\alpha +1)}\right. \nonumber \\&\left. \left[ (1-\alpha )\left( \beta \frac{T_f}{\ln \mu _p}+1\right) +\alpha T_f\right] \right\} \end{aligned}$$

(23)

From (10), (13) and (23), for $t\in [0, T_f)$, we have

$$\begin{aligned}&V_{\sigma (t)}(t, x(t))\ge \xi _1 x^\mathrm{T}(t)\varepsilon \end{aligned}$$

(24)

$$\begin{aligned}&V_{\sigma (t)}(t, x(t))\le \xi _2x^\mathrm{T}(0)\delta \exp \left\{ \beta T_f+ \frac{\lambda }{\varGamma (\alpha +1)}\left[ (1-\alpha )\left( \beta \frac{T_f}{\ln \mu _p}+1\right) +\alpha T_f\right] \right\} \nonumber \\ \end{aligned}$$

(25)

Combining (24) with (25), we obtain

$$\begin{aligned} x^\mathrm{T}(t)\varepsilon \le \frac{\xi _2}{\xi _1}\{x^\mathrm{T}(0)\delta \} \exp \left\{ \beta T_f+ \frac{\lambda }{\varGamma (\alpha +1)}\left[ (1-\alpha )\left( \beta \frac{T_f}{\ln \mu _p}+1\right) +\alpha T_f\right] \right\} \nonumber \\ \end{aligned}$$

(26)

Substituting (12) into (26), one has

$$\begin{aligned} x^\mathrm{T}(t)\varepsilon <1 \end{aligned}$$

(27)

From Definition 4, we conclude that the system (5) with $u(t)=0$ is finite-time stable with respect to $(\delta , \varepsilon , T_f, \sigma (t))$. Thus, the proof is completed. $\square$

Remark 3

If $\underline{\mathrm{A}}_p=A_p=\bar{A}_p$, then Theorem 1 is still held, where $A_p$ is a Metzler matrix, $p\in \underline{\mathrm{S}}$. One just needs to change (8) into $A_p^\mathrm{T}v_p\preceq \lambda _p v_p$, following the proof line of Theorem 1. The same result can be obtained.

3.1.2 Polytopic Uncertainty

Next, we consider the FTS of the system (5) with the polytopic uncertainties. Consider the following polytopic uncertainties:

$A_p\in co\{A_p^i, i=1, 2, \dots , n.\}$ and $B_p\in co\{B_p^i, i=1, 2, \dots , n.\}$. $\forall p\in \underline{\mathrm{S}}$, where co represents the convex hull of the vertex matrices $A_p^i$(or $B_p^i$). $A_p=\sum _{i=1}^n\gamma _iA_p^i$, where $A_p^i$ is a Metzler matrix, $\gamma _i\in (0, 1)$ and $\sum _{i=1}^n\gamma _i=1$.

Theorem 2

Assume $A_p\in co\{A_p^i, i=1, 2, \dots , n.\}$ for each $p\in \underline{\mathrm{S}}$. Consider the system (5) with $u(t)\equiv 0$. Given positive constants $T_f$, $\lambda _p$, vectors $\delta \succ \varepsilon \succ 0$, if there exist positive constants $\xi _1$, $\xi _2$, $\mu _p$, and positive vectors $v_p$, $p\in \underline{\mathrm{S}}$, such that the following inequalities hold:

$$\begin{aligned}&\displaystyle {A_p^i}^\mathrm{T}v_p\preceq \lambda _p v_p\end{aligned}$$

(28)

$$\begin{aligned}&\displaystyle J_p^\mathrm{T}v_p\preceq \mu _p v_q\end{aligned}$$

(29)

$$\begin{aligned}&\displaystyle \xi _1\varepsilon \prec v_p\prec \xi _2\delta \end{aligned}$$

(30)

$$\begin{aligned}&\displaystyle \frac{\lambda (\alpha T_f-\alpha +1)}{\varGamma (\alpha +1)}<\ln \frac{\xi _1}{\xi _2} \end{aligned}$$

(31)

where $\forall p\in \underline{\mathrm{S}}$, $v_p=[v_{p1}, v_{p2}, \dots , v_{pn}]^\mathrm{T}$, $\lambda =\max _{p\in \underline{\mathrm{S}}}\{\lambda _p\}$, $\mu _p \ge 1$, then under the MDADT scheme (12), the UFOPISS (5) is finite-time stable with respect to $(\delta , \varepsilon , T_f, \sigma (t))$.

Proof

Since $A_p\in co\{A_p^i, i=1, 2, \dots , n.\}$. $A_p=\sum _{i=1}^n\gamma _iA_p^i$, where $\gamma _i\in (0, 1)$ and $\sum _{i=1}^n\gamma _i=1$. Due to (28),

$$\begin{aligned} A_p^\mathrm{T}v_p=\sum _{i=1}^n\gamma _i{A_p^i}^\mathrm{T}v_p\preceq \sum _{i=1}^n\gamma _i\lambda _pv_p=\lambda _pv_p \end{aligned}$$

(32)

i.e., $A_p^\mathrm{T}v_p\preceq \lambda _p v_p$. In Theorem 1, if one chooses $A_p=\bar{A}_p$, Theorem 2 is equivalent to Theorem 1. Thus, the proof is completed.$\square$

Corollary 1

Replace $^C_{t_0}D^\alpha _tx(t)$ by $^\mathrm{RL}_{t_0}D^\alpha _tx(t)$ in Theorem 1. If the conditions in Theorem 1 hold, then the UFOPISS (5) is finite-time stable with respect to $(\delta , \varepsilon , T_f, \sigma (t))$.

Proof

According to (4) and Lemma 1, we can obtain

$$\begin{aligned} ^C_{t_0}D^\alpha _tV_{\sigma (t)}(t, x(t))\le & {} ^\mathrm{RL}_{t_0}D^\alpha _tV_{\sigma (t)}(t, x(t))\nonumber \\\le & {} x^\mathrm{T}(t)A^\mathrm{T}_{\sigma (t)}v_{\sigma (t)}\nonumber \\\le & {} x^\mathrm{T}(t)\bar{A}^\mathrm{T}_{\sigma (t)}v_{\sigma (t)}\nonumber \\\le & {} \lambda _px^\mathrm{T}(t)v_{\sigma (t)}\nonumber \\\le & {} \lambda _p V_{\sigma (t)}(t, x(t)) \end{aligned}$$

(33)

Similar to the proof process of Theorem 1, we can obtain the same results and the proof is omitted.$\square$

Remark 4

Replace $^C_{t_0}D^\alpha _tx(t)$ by $^\mathrm{RL}_{t_0}D^\alpha _tx(t)$ in Theorem 2, if the conditions in Theorem 2 hold, then the UFOPISS (5) is finite-time stable with respect to $(\delta , \varepsilon , T_f, \sigma (t))$. From the proof process of Theorem 2 and Corollary 1, we can obtain the same results easily and the proof is omitted.

3.2 Finite-Time Controller Design

In this section, we focus on the problem of finite-time controller design of the system (5). The state feedback controller will be designed to ensure the corresponding closed-loop system is finite-time stable.

Consider the system (5), under the controller $u(t)=K_{\sigma (t)}x(t)$, the corresponding closed-loop system is given by

$$\begin{aligned} \left\{ \begin{array}{l} _{t_0}^C D_t^{\alpha }x(t)=(A_{\sigma (t)}+B_{\sigma (t)}K_\sigma (t))x(t)\ t\ne t_k, \ k\in Z^+\\ x(t)=J_{\sigma (t^-)}x(t^-),\ t=t_k, \ k\in Z^+,\ 0<\alpha <1 \end{array} \right. \end{aligned}$$

(34)

According to Lemma 2, to guarantee the positivity of the system (34), $A_p + B_p K_p$ should be Metzler matrices, $\forall p \in \underline{\mathrm{S}}$. The following two theorems give some sufficient conditions to guarantee that the closed-loop system (34) with interval or polytopic uncertainties is finite-time stable, respectively.

Theorem 3

Consider the UFOPISS (34) with interval uncertainties. Assume $A_p\in [\underline{\mathrm{A}}_p, \bar{A}_p]$, and $B_p\in [\underline{\mathrm{B}}_p, \bar{B}_p]$ for each $p\in \underline{\mathrm{S}}$. For given constants $T_f$, $\lambda$ and vectors $\delta \succ \varepsilon \succ 0$, if there exist constants $\xi _1$, $\xi _2$, $\mu _p(\mu _p\ge 1)$ and positive vectors $v_p$, $p\in \underline{\mathrm{S}}$, such that the following conditions hold:

$$\begin{aligned}&\begin{array}{lll} \underline{\mathrm{A}}_p+\underline{\mathrm{B}}_p K_{1p}~and~\bar{A}_p+\bar{B}_p K_{1p}~are~Metzler~matrices,~K_{1p}\succeq 0.\end{array}\end{aligned}$$

(35)

$$\begin{aligned}&\bar{A}_p^\mathrm{T}v_p+f_p\preceq \lambda _p v_p\end{aligned}$$

(36)

$$\begin{aligned}&J_p^\mathrm{T}v_p\preceq \mu _p v_q\end{aligned}$$

(37)

$$\begin{aligned}&\xi _1\varepsilon \prec v_p\prec \xi _2\delta \end{aligned}$$

(38)

$$\begin{aligned}&\frac{\lambda (\alpha T_f-\alpha +1)}{\varGamma (\alpha +1)}<\ln \frac{\xi _1}{\xi _2} \end{aligned}$$

(39)

where $f_p=K_{1p}\bar{B}_p v_p$, then under the control law $u(t)=K_{1p}x(t)$, the resulting closed-loop system (34) is finite-time stable with the MDADT scheme (12).

Proof

From (35), we have $\underline{\mathrm{A}}_p+\underline{\mathrm{B}}_p K_{1p}\preceq A_p+B_p K_{1p}\preceq \bar{A}_p+\bar{B}_p K_{1p}$, it means that $A_p+G_p K_{1p}$ are also Metzler matrices for each $p\in \underline{\mathrm{S}}$. Hence, the system (34) is positive by Lemma 3. Replacing $\bar{A}_p$ in (8) with $\bar{A}_p + \bar{B}_p K_{1p}$, letting $f_p =K_{1p}^\mathrm{T} \bar{B}_p^\mathrm{T}v_p$, $\mu (\mu \ge 1)$ satisfies (8), similar to the proof process of Theorem 1, we easily obtain that the resulting closed-loop system (34) is finite-time stable with the MDADT scheme (12).

The proof is completed.$\square$

Remark 5

In Theorem 3, the gain matrix $K_{1p}\succeq 0$, $p\in \underline{\mathrm{S}}$ is used. Naturally, when $K_{1p}\preceq 0$, we only replace (35) by the following condition

$$\begin{aligned} \begin{array}{lll} \underline{\mathrm{A}}_p+\bar{B}_p K_{1p}~and~\bar{A}_p+\underline{\mathrm{B}}_p K_{1p}~are~Metzler~matrices,~K_{1p}\preceq 0. \end{array} \end{aligned}$$

(40)

Following the proof line of Theorem 3, we can also conclude that the resulting closed-loop system (34) is finite-time stale with the MDADT scheme (12).

Next, an algorithm is presented to obtain the feedback gain matrices $K_{1p}$, $p\in \underline{\mathrm{S}}$.

Algorithm 1

• Step 1 Input the matrices $\underline{\mathrm{A}}_p$, $\bar{A}_p$, $\underline{\mathrm{B}}_p$, $\bar{B}_p$, $J_p$, constants $u_p \ge 1$, $p\in \underline{\mathrm{S}}$, and positive vectors $\varepsilon$ and $\delta$.

• Step 2 Choosing the parameters $\lambda _p >0$ and solving (36)–(38) via linear programming, positive vectors $v_p$ and $f_p$ can be obtained.

• Step 3 Substituting $v_p$ and $f_p$ into $f_p =K_{1p}^\mathrm{T} \bar{B}_p^\mathrm{T}v_p$, $K_{1p}$ can be obtained.

• Step 4 The gains $K_{1p}$ are substituted into (35) or (40). If the condition (35) or (40) is satisfied, then $K_{1p}$ are admissible. Otherwise, return to Step 2.

Remark 6

There is not a systemic method to choose the parameters $\lambda _p$; all published papers are involved in the selection of $\lambda _p$ by experience. The solution of Algorithm 1 is an iterative process; for the purpose of adding the feasibility of the Algorithm 1, $\lambda _p$ should be selected small. Otherwise, if $\lambda _p$ are selected largely in equation (36), then it will cause $\xi _1\gg \xi _2$ in equation (39). Thus, for given constants $\varepsilon$ and $\delta$, equation (38) might have no solution. Therefore, in Step 1, $\forall p\in \underline{\mathrm{S}}$, $\lambda _p$ should be small positive numbers.

Remark 7

The feedback gains matrices $K_{1p}$ can be solved by Algorithm 1, which guarantees the system state does not exceed the threshold 1 in a given time interval $T_f$ from Definition 4. Then the system state might not converge to zero in a given time interval. If a smaller threshold is fixed, then the state will become very small.

In the following, we study the FTS problem of system (37) with polytopic uncertainties.

Theorem 4

Consider the UFOPISS (34) with polytopic uncertainties. $A_p\in co\{A_p^i, i=1, 2, \dots , n.\}$ and $B_p\in co\{B_p^i, i=1, 2, \dots , n.\}$, $A_p^i$ is a Metzler matrix and $B_p^i\succeq 0$ for each $p\in \underline{\mathrm{S}}$. For given constants $T_f$, $\lambda$ and vectors $\delta \succ \varepsilon \succ 0$, if there exist constants $\xi _1$, $\xi _2$, $\mu _p(\mu _p\ge 1)$ and positive vectors $v_p$, $p\in \underline{\mathrm{S}}$, such that the following conditions hold:

$$\begin{aligned}&\begin{array}{lll} A_p+B_p K_{2p}~are~Metzler~matrices, \end{array}\end{aligned}$$

(41)

$$\begin{aligned}&{A_p^i}^\mathrm{T}v_p+f_p\preceq \lambda _p v_p\end{aligned}$$

(42)

$$\begin{aligned}&J_p^\mathrm{T}v_p\preceq \mu _p v_q\end{aligned}$$

(43)

$$\begin{aligned}&\xi _1\varepsilon \prec v_p\prec \xi _2\delta \end{aligned}$$

(44)

$$\begin{aligned}&\frac{\lambda (\alpha T_f-\alpha +1)}{\varGamma (\alpha +1)}<\ln \frac{\xi _1}{\xi _2} \end{aligned}$$

(45)

where $f_p=K_{2p}{B_p^i}^\mathrm{T} v_p$, $\underline{\mathrm{A}}_p\preceq A_p^i\preceq \bar{A}_p$, $\underline{\mathrm{B}}_p\preceq B_p^i\preceq \bar{B}_p$, then under the control law $u(t)=K_{2p}x(t)$, the resulting closed-loop system (34) is finite-time stable with the MDADT scheme (12).

Proof

From (41) and Lemma 2, the system (34) is positive. From $\underline{\mathrm{A}}_p\preceq A_p^i\preceq \bar{A}_p$, $\underline{\mathrm{B}}_p\preceq B_p^i\preceq \bar{B}_p$, $A_p=\sum _{i=1}^n\gamma _iA_p^i$ and $B_p=\sum _{i=1}^n\gamma _iB_p^i$, we have

$$\begin{aligned} \underline{\mathrm{A}}_p=\sum _{i=1}^n\gamma _i\underline{\mathrm{A}}_p^i\preceq A_p=\sum _{i=1}^n\gamma _iA_p^i\preceq \sum _{i=1}^n\gamma _i\bar{A}_p=\bar{A}_p \end{aligned}$$

(46)

and

$$\begin{aligned} \underline{\mathrm{B}}_p=\sum _{i=1}^n\gamma _i\underline{\mathrm{B}}_p^i\preceq B_p=\sum _{i=1}^n\gamma _iB_p^i\preceq \sum _{i=1}^n\gamma _i\bar{B}_p=\bar{B}_p \end{aligned}$$

(47)

Therefore,

$$\begin{aligned} \underline{\mathrm{A}}_p+\underline{\mathrm{B}}_pK_{2p}= & {} \sum \limits _{i=1}^n\gamma _i(\underline{\mathrm{A}}_p^i+\underline{\mathrm{B}}_p^iK_{2p})\preceq A_p+B_pK_{2p}\nonumber \\&=\sum \limits _{i=1}^n\gamma _i(A_p^i+B_p^iK_{2p})\preceq \sum \limits _{i=1}^n\gamma _i\bar{B}_p=\bar{A}_p+\bar{B}_pK_{2p} \end{aligned}$$

(48)

for each $p\in \underline{\mathrm{S}}$. Obviously, the finite-time stabilization problem about polytopic uncertainties is transformed into the one of interval uncertainties. Following the proof line of Theorem 3, we can get the same result and the proof is omitted.$\square$

Remark 8

In order to obtain more results, the following two aspects will be considered in our future work. Firstly, some disturbances would be considered to obtain some more generalized stability conditions, such as the non-Gaussian noise [12, 25,26,27, 33]. Secondly, time-delays, which are widespread in various systems [9, 23], should also be discussed to obtain some delay-dependent sufficient conditions.

4 Example

A fractional electrical circuit model was presented in [22]. Accordingly, a switching-type positive fractional-order electrical circuit can be described by a fractional-order positive switched system. When the impulsive effect at switching instant and uncertainties are simultaneously considered, the parameters of the fractional-order positive impulsive switched circuit are given as

$$\begin{aligned}&{\bar{A}}_1 =\left[ \begin{array}{cc} -2 &{}\quad 0 \\ 0 &{}\quad -1 \end{array}\right] , \underline{\mathrm{A}}_1=\left[ \begin{array}{cc} -2.5 &{}\quad 0 \\ 0 &{}\quad -2 \end{array}\right] , \bar{B}_{1}=\left[ \begin{array}{cc} 2 &{}\quad 0 \\ 0 &{}\quad 1 \end{array}\right] , \underline{\mathrm{B}}_{1}=\left[ \begin{array}{cc} 1.2 &{}\quad 0 \\ 0 &{}\quad 0.6 \end{array}\right] ,\\&\bar{A}_2 =\left[ \begin{array}{cc} -1 &{}\quad 0 \\ 0 &{}\quad -1 \end{array}\right] , \underline{\mathrm{A}}_2=\left[ \begin{array}{cc} -1.5 &{}\quad 0 \\ 0 &{}\quad -1.6 \end{array}\right] , \bar{B}_{2}=\left[ \begin{array}{cc} 1.1 &{}\quad 0 \\ 0 &{}\quad 0.8 \end{array}\right] , \underline{\mathrm{B}}_{2}=\left[ \begin{array}{cc} 0.6 &{}\quad 0 \\ 0 &{}\quad 0.6 \end{array}\right] ,\\&\bar{J}_{1}=\left[ \begin{array}{cc} 1.5 &{}\quad 0 \\ 0 &{}\quad 2 \end{array}\right] , \bar{J}_{2}=\left[ \begin{array}{cc} 2 &{}\quad 0 \\ 0 &{}\quad 2 \end{array}\right] , \varepsilon =\left[ \begin{array}{cc} 0.05&\quad 0.03\end{array}\right] ^\mathrm{T}, \delta =\left[ \begin{array}{cc} 0.2&\quad 0.3\end{array}\right] ^\mathrm{T}, \end{aligned}$$

Let $\alpha =0.8$, $\mu _1=1.1$, $\mu _2=1.2$, $\lambda _1=0.1$, $\lambda _2=0.12$, $\lambda =\max \{\lambda _1, \lambda _2\}=0.12$. According to Algorithm 1, solving the inequalities in Theorem 3 by linear programming, we have

$$\begin{aligned}v_1 =\left[ \begin{array}{c} 0.9120\\ 0.5910\end{array}\right] , v_2=\left[ \begin{array}{c} 0.7871\\ 0.5755\end{array}\right] ,\\ f_1 =\left[ \begin{array}{c} 0.9588\\ 0.5808\end{array}\right] , f_2=\left[ \begin{array}{c} 0.8924\\ 0.5904\end{array}\right] ,\\ \xi _1=5.6710, \xi _2=1.0706,\end{aligned}$$

By $f_p=K_p^\mathrm{T}\bar{B}_p^\mathrm{T}v_p$, $p=1,2$, we have

$$\begin{aligned}K_{11}= & {} \left[ \begin{array}{cc} 0.4271 &{}\quad 0.3042 \\ 0.4271 &{}\quad 0.3042 \end{array}\right] , K_{12}=\left[ \begin{array}{cc} 0.4846 &{}\quad 0.2968\\ 0.4846 &{}\quad 0.2968 \end{array}\right] ,\\ \bar{A}_1+\bar{B}_1 K_{11}= & {} \left[ \begin{array}{cc} -1.1458 &{}\quad 0.6084 \\ 0.4271 &{}\quad -0.6958 \end{array}\right] , \underline{\mathrm{A}}_1+\underline{\mathrm{B}}_1 K_{11}=\left[ \begin{array}{cc} -1.9875 &{}\quad 0.3650 \\ 0.2562 &{}\quad -1.8175 \end{array}\right] ,\\ \bar{A}_2+\bar{B}_2 K_{12}= & {} \left[ \begin{array}{cc} -0.4679 &{}\quad 0.3265 \\ 0.3877 &{}\quad -0.7642 \end{array}\right] , \underline{\mathrm{A}}_2+\underline{\mathrm{B}}_2 K_{12}=\left[ \begin{array}{cc} -1.2092 &{}\quad 0.1781 \\ 0.2908 &{}\quad -1.4219 \end{array}\right] . \end{aligned}$$

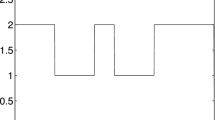
It is easy to verify that $\underline{\mathrm{A}}_p+\underline{\mathrm{B}}_p K_{1p}$ and $\bar{A}_p+\bar{B}_p K_{1p}$ are Metzler matrices for each $p\in \underline{\mathrm{S}}$. Then, according to (12), we can obtain $T_{\alpha 1}^*=1.8794, T_{\alpha 2}^*=3.2391$. Choosing $T_{\alpha 1}=1.9>T_{\alpha 1}^*$ and $T_{\alpha 2}=3.3>T_{\alpha 2}^*$. Under the state feedback controller, the simulation results are shown in Figs. 1, 2, 3 and 4. The initial conditions of the system (5) are $x(0)=[0.5\;0.3]^\mathrm{T}$, which satisfies $x^\mathrm{T}(0)\delta \le 1$. According to the MDADT scheme, we give the impulsive sequence in Fig. 1. The switching signal $\sigma (t)$ with MDADT is depicted in Fig. 2. The state trajectories of the closed-loop system with MDADT are shown in Fig. 3. Figure 4 plots the evolution of $x^\mathrm{T}(t)\varepsilon$ of system (5).

Fig. 1

Impulsive sequence of the system (5)

Fig. 2

Switching signal of system (5) with MDADT

Fig. 3

State trajectories of closed-loop system (5)

Fig. 4

The evolution of $x^\mathrm{T}(t)\varepsilon$ of system (5)

5 Conclusions

This paper has investigated the problem of finite-time stability and stabilization for UFOPISS with interval and polytopic uncertainties. FTS analysis of UFOPISS is firstly discussed. By using MDADT approach and constructing multiple linear copositive Lyapunov functions, two state feedback controllers are designed; then a series of switching signals and some sufficient conditions are obtained to guarantee that the corresponding closed-loop systems are finite-time stable. Such sufficient conditions can be solved by linear programming. Finally, an example is given to show the effectiveness of the proposed method.