1 Introduction

Spectrum sensing (SS) in cognitive radio (CR) periodically and dynamically monitors the radio spectrum to determine spectral holes in order to provide non-interfered reliable communication [9]. In wideband scenario which requires high sampling rate, the filter bank technique is a better choice since processing clock requirements are brought down after analog to digital conversion and decimation [9, 11]. Filter bank-based methods have the inherent advantage of providing better spectrum sensing. This leads to efficient spectrum utilization in CR. For wideband spectrum sensing, the available spectrum is split into multiple subbands and sensed with DFT filter banks [14].

We consider IEEE 802.22 wireless regional area network (WRAN) standard as an application for the validation of the proposed spectrum sensing algorithm using multistage DFT filter banks. In IEEE 802.22 WRAN standard, spectrum sensing has to be done to allow television (TV) services and wireless microphones (WM) to coexist. WM are low-power licensed users and are allowed by federal communications commission (FCC) to operate on vacant TV channels without causing interference. The detection of WM is difficult because of the low-power transmission (typically 50 mW for 100 m coverage) and small bandwidth occupancy (200 kHz). In IEEE 802.22 WRAN standards, when WM appears anywhere in the TV channel, the whole channel of 6 MHz has to be evacuated to avoid interference [3]. However, TV channels can be utilized fractionally when the exact position of the WM is detected [5, 13]. Hence, the detection of WM signals has several challenges [17, 22]. Some of the conventional techniques available in literature are blind spectrum sensing based on eigenvalue algorithm and power spectral density (PSD) to detect the peak of WM signal regardless of modulation type [2, 10, 15, 19].

The sensing of wireless microphone is still an open research problem as there are no common transmission standards. Some of the filter bank techniques existing in literature are DFT filter banks, polyphase realization of DFT filter banks, and multistage coefficient decimation filter banks [6, 8, 23]. Even though multistage coefficient decimation filter bank reduces computational complexity, they are not suitable for detecting narrowband spectrum [16]. Reconfigurable filter bank methods have also been exploited for spectrum sensing [18]. Multistage filter bank technique was proposed earlier for the detection of a single WM and estimation of the center frequency appearing in the TV channels. However, this method required an additional modulation component to the existing DFT filter bank to move the filter response to desired spectral region [6, 7].

The goal of the proposed multistage polyphase filter bank method is to detect the presence of WM and estimate the center frequency of the WM with better precision by using the centroid method. The important contribution of our work is the detection and estimation of center frequency with high-precision and reduced computational complexity. The proposed algorithm for detection of unused spectrum (spectrum holes) starts with a coarser spectral resolution (smaller number of subbands) in the first stage to reduce computational complexity. The novelty of the proposed centroid-based technique is that the presence of WM can be detected in the first stage itself, when spectrum of WM lies partly in one subband and partly in adjacent subband. This in turn reduces the computational complexity, latency and achieves fast sensing. However, if WM appears exclusively within a single subband, an additional stage is required to detect and estimate the center frequency of WM with finer spectral resolution. This implies WM can be detected in the second stage without ambiguity.

The paper is organized as follows: In Sect. 2 implementation of polyphase filter banks is explained and Sect. 3 details the proposed multistage polyphase filter bank. The estimation of center frequency using centroid method is discussed in Sect. 4. Simulation results are discussed in Sect. 5 followed by conclusion.

2 Polyphase Filter Bank

Filter banks are often implemented based on the modulation of a prototype filter. The prototype filter is a low-pass FIR filter. The magnitude of sidelobes of the filter determines leakage to other subbands [23]. The polyphase filter bank structure reduces the complexity of the filter bank implementation to a large extent. Polyphase filter banks are efficiently designed using FFT when the number of subbands M is a power of two. M subbands are obtained by the polyphase decomposition of the prototype filter h(n) having a transfer function H(z). The polyphase decomposition of the prototype filter can be written as [21]

$$\begin{aligned} H_{0}(z)= \sum _{l=0}^{M-1}z^{-l}E_{l}(z^M),\quad l=0,1,\ldots , M-1. \end{aligned}$$
(1)

The \(l \mathrm{th}\) polyphase component can be defined as

$$\begin{aligned} E_{l}(z)= \sum _{n=0}^{N-1}h(Mn+l)z^{-n}. \end{aligned}$$
(2)

The polyphase structure of a M band filter bank is equivalent to the realization of the prototype filter and one M point FFT, i.e., the computational complexity is \(N+M\log _{2}M\), where N is the length of the prototype filter. The polyphase filter banks reduce the computational complexity to a large extent compared to the complexity NM for direct implementation. The polyphase filter bank structure can further be simplified using noble identities of multirate signal processing [21]. The efficient polyphase filter bank structure is shown in Fig. 1.

Fig. 1
figure 1

Polyphase filter bank structure [21]

Full size image

3 Proposed Multistage Polyphase Filter Bank Structure

The proposed multistage polyphase filter bank method detects the presence of WM and also estimates the center frequency of the WM with higher precision using the centroid method. It is well known that the detection accuracy depends on the number of subbands M in the filter bank. The computational complexity of the filter bank increases with higher value of M. However, the complexity is reduced by using multistage polyphase filter bank structure. The WM is detected by computing the signal energy (power) at output of the individual subbands. To reduce computational complexity, the detection of WM is performed from a coarser to finer spectral resolutions depending on the energy distribution at each stage.

The proposed system can be used to detect WM in the presence of a signal following IEEE 802.22 WRAN standard. This scheme is designed to detect the presence of WM anywhere within a TV channel (6 MHz) and to estimate the center frequency of WM taking into account the following scenarios:

Case 1 If the signal spectrum of WM lies partly in one subband and partly in the adjacent subband as shown in Fig. 2, then the center frequency of WM can be either in one of the subbands or between two subbands. The center frequency in such a case is estimated using the centroid method as described in Sect. 4.

Case 2 If the signal spectrum of WM is in the middle of two adjacent subbands as shown in Fig. 3, the energy at the output of two subbands will be equal. This implies that the center frequency of WM is at the midpoint of the two subbands. Therefore, finer level of detection is not necessary. This in turn reduces the computational complexity and latency.

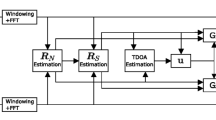
Case 3 If the signal spectrum of WM appears exclusively within a subband as shown in Fig. 4, then output of the first stage is passed to the input of the next stage filter bank to estimate the center frequency with finer spectral resolution. The process is illustrated in Fig. 5, where only two stages are required to detect the presence of the WM and to accurately estimate the center frequency of WM. The center frequency is estimated in the second stage using DFT polyphase filter bank and centroid method. The procedure followed for multistage spectrum sensing is summarized below in two steps:

Fig. 2
figure 2

Case 1: WM appears anywhere between two consecutive subbands

Full size image
Fig. 3
figure 3

Case 2: WM appears exactly between two subband

Full size image
Fig. 4
figure 4

Case 3: WM appears exclusively within a subband

Full size image

Step 1 The bandwidth of sensing is divided coarsely into \(M_{1}\) subbands and sensed through the \(M_{1}\) subband DFT polyphase filter bank. Energy detection is performed at the output of each subband, considering energy (power) as the test statistic to decide the presence or absence of the WM in the subbands. The detection and estimation of center frequency of WM as per Case 1 or Case 2 is done in the first stage. If the signal spectrum of WM is as per Case 3, the output of the sensed subband is further processed with finer resolution as in Step 2.

Step 2 The output of the first stage is sensed in the next level with \(M_{2}\) subbands. The signal energy (power) at the output of the subband is considered as the test statistic. At this level, the spectrum is sensed with a spectral resolution of \(\pi /M_{1}M_{2}\).

The proposed method can be summarized as: (1) If WM appear anywhere within the consecutive subbands (Case 1 and Case 2), the center frequency of WM is estimated accurately using the centroid method in single stage, (2) if WM appears anywhere exclusively within any subband (Case 3), the output of the sensed subband is further processed with finer resolution as in Step 2.

Fig. 5
figure 5

Detection of WM in a two stage filter bank

Full size image

3.1 Complexity Analysis

The complexity of the filter is estimated with the number of complex multiplications performed in the filter bank structure. For an M subband filter with conventional polyphase structure, complexity is equivalent to the length of the prototype filter and the M point FFT, \(N+M\log _{2}M\). If the M bank is divided into two stages \(M_{1}\) and \(M_{2}\) such that \(M=M_{1}M_{2}\), then the complexity is \(2N+M_{1}\log _{2}M_{1}+M_{2}\log _{2}M_{2}\). The complexity of the first stage is \(N+M_{1}\log _{2}M_{1}\) and the complexity of second stage is \(N+M_{2}\log _{2}M_{2}\), where N is the length of the prototype filter. The computational complexity of the filter bank structure for different stages and subband resolution are given in Table 1. In IEEE 802.22 standard, if the spectrum sensing is done in a 6-MHz channel to detect a WM having a bandwidth of 200 kHz, different filter bank structures can be considered. If the latency has to be reduced, a 32 subband filter can be considered in the first stage. This is sufficient to detect WM in all possible scenarios, as the spectral resolution of the subbands is 187.5 kHz. For a trade-off between complexity and latency, a two stage with either \(M_{1}=16\) and \(M_{2}=2\) subbands or \(M_{1}=8\) and \(M_{2}=4\) subbands may be considered. The comparison of computational complexity of the proposed method with existing methods using filter bank structures is shown in Table 2.

Table 1 Computational complexity in terms of multiplications for the proposed method for different stages and number of subbands
Full size table
Table 2 Comparison of computational complexity in terms of multiplications for different filter bank methods
Full size table

3.2 Calculation of Threshold and Test Statistics

Energy detection has been chosen due to its simplicity and less knowledge requirement on the signal to be detected [20]. The energy at the output of the individual subbands in the filter bank is considered as the test statistics.

$$\begin{aligned} Y_k=\frac{1}{L}\sum _{n=0}^{L-1}y_{k}^{2}\left( n \right) \end{aligned}$$
(3)

where \(L={N}/{M}\) is the number of samples in each subband k, \(k=1,2,\ldots , M\), and M is the total number of subbands. When the number of samples is increased, Chi-square distribution approximates to a normal distribution from the central limit theorem. The presence and absence of a primary user signal are written in terms of the following two hypotheses [12]:

$$\begin{aligned}&y_k(n)\sim \mathcal {N}\left( \sigma _\mathrm{v}^{2},\frac{1}{N}\sigma _\mathrm{v}^{4}\right) ; \text {for hypothesis}\ {H_{0}}\\&y_k(n)\sim \mathcal {N}\left( \sigma _\mathrm{v}^{2}+\sigma _\mathrm{s}^{2}, \frac{1}{N}\left( \sigma _\mathrm{v}^{2}+\sigma _\mathrm{s}^{2}\right) ^2\right) ; \text {for hypothesis}\ H_{1} \end{aligned}$$

The presence of an active signal in a specified subband can be determined by comparing the energy in that subband with a predetermined threshold.

3.3 Calculation of Threshold

The threshold \(\lambda \) is calculated with the knowledge of probability of false alarm \(P_\mathrm{fa}\) and noise variance \(\sigma _v^2\) of the received signal. Here, we assume that the noise variance and probability of false alarm are known depending on the channel conditions. For single channel, the threshold is determined from the probability of false alarm and noise variance using Eq. (4).

$$\begin{aligned} P_\mathrm{fa}=Q\left( \frac{\lambda -\sigma _\mathrm{v}^{2}}{\sqrt{1/N}\sigma _\mathrm{v}^{2}} \right) \end{aligned}$$
(4)

where N is the total number of samples in the channel. The threshold is determined as

$$\begin{aligned} \lambda =\left( Q^{-1}(P_\mathrm{fa})\sqrt{1/N}+1\right) \sigma _\mathrm{v}^{2}. \end{aligned}$$
(5)

For subband filters, the threshold is given as \(\lambda =(Q^{-1}(P_\mathrm{fa})\sqrt{1/L}+1)\sigma _\mathrm{v}^{2}\), where L is the number of samples in each subband. Different thresholds are calculated depending on the percent probability of false alarm. The threshold varies dynamically in each stage depending on the number of samples. The number of samples in each stage needs to be large enough to perform energy detection even with low SNR. The minimum number of samples required in each stage is obtained using the relation [1],

$$\begin{aligned} N_{\min } =2\left[ Q^{-1}(P_\mathrm{fa})-Q^{-1}(P_\mathrm{d})(1+\mathrm{SNR})\right] ^{2}\mathrm{SNR}^{-2}. \end{aligned}$$
(6)

The threshold value reduces when sensing is performed from a coarser to finer levels of spectrum sensing as the number of samples for processing is reduced.

4 Calculation of Center Frequency

4.1 Centroid Method

The center frequency can be estimated using the centroid method considering a trapezoid. The center of each subband represents the energy in that subband resolution as shown in Fig. 6. The top edge of the distribution can be defined by a linear function \(f(x)=b+\frac{x}{h}(a-b)\). The area of a trapezoid is given as \(A=\frac{h}{2}(a-b)\). The centroid in the x direction is computed as

$$\begin{aligned} A\bar{x}=\int _{0}^{h}xf(x)\mathrm{d}x =\int _{0}^{h}x\left( b+\frac{x}{h}(a-b)\right) \mathrm{d}x =\frac{h^2}{6}(2a+b), \end{aligned}$$
(7)

where \(\bar{x}=\frac{h}{3}(\frac{2a+b}{a+b})\), and A is the area of the trapezoid. Here, \(\bar{x}\) represents the centroid of the trapezoid. This is verified for equal energy in the subbands, i.e., when \(a=b,\ \bar{x}=h/2\). The center frequency of WM is related to \(\bar{x}\), h represents the granularity of filter bank M, a and b are related to the energies of the adjacent subbands with energies \(E_1\) and \(E_2\). The minimum of two subband energies is represented as a, i.e., \(a=\min (E_1,E_2)\), and maximum as \(b=\max (E_1,E_2)\). Then the estimated center frequency \(\hat{f}_\mathrm{c}\) can be expressed as follows:

$$\begin{aligned} \hat{f}_\mathrm{c}=\frac{M}{3}\left( \frac{2a+b}{E_1+E_2}\right) \end{aligned}$$
(8)

A generalized expression is obtained by considering the energies of subband \(E_i\) and adjacent subband \(E_{i+1}\).

$$\begin{aligned} \hat{f}_\mathrm{c}=\frac{M}{3}\left( \frac{2\min (E_i,E_{i+1})+\max (E_i,E_{i+1})}{E_i+E_{i+1}}\right) \end{aligned}$$
(9)
Fig. 6
figure 6

Centroid method

Full size image
Fig. 7
figure 7

Center of mass method

Full size image
Table 3 WM operating conditions
Full size table
Fig. 8
figure 8

WM operating conditions. a Soft mode, b loud mode, c silent mode

Full size image

4.2 Center of Mass Method

The center of mass method can also be used to estimate the center frequency. The energy of the subbands is related to the mass, and the distance is related to the frequency. Consider the energy in two subbands as \(E_{1}\) and \(E_{2}\), let \(\varDelta _{1}\) and \(\varDelta _{2}\) be the center point of spectral resolution in the subband bins as shown in Fig. 7. The center frequency for the energy bins can be obtained using the law of center of mass as

$$\begin{aligned} \hat{F}_\mathrm{c}=\frac{E_{1}\varDelta _{1}+E_{2}\varDelta _{2}}{E_{1}+E_{2}}. \end{aligned}$$
(10)

The expression can be extended for different subbands, and the center frequency can be calculated using the relation,

$$\begin{aligned} {\hat{F}}_\mathrm{cn}=\frac{\sum _{k=1}^{n}E_{k}\varDelta _{k}}{\sum _{k=1}^{n}E_{k}}. \end{aligned}$$
(11)
Table 4 Simulation parameters
Full size table

5 Simulation Results

The sensing performance (detection and estimation of center frequency) of the WM is determined using simulation model provided in [4]. The WM signals are simulated using frequency modulation as in [2]. The sensing bandwidth is considered as 6 MHz.

Stage 1 has a spectral resolution of 750 kHz \((\pi /M_{1})\) for \(M_{1}=8\), and Stage 2 has the number of subbands \(M_{2}=4\), with spectral resolution 187.5 kHz \((\pi /M_{1}M_{2})\). The polyphase decomposition of the spectrum in Stage 1 is \([0{-}0.375{-}1.125{-}1.875{-}2.625{-}3.375{-}4.125{-}4.875{-}5.625{-}6]\,\mathrm{MHz}\). WM has three different operating modes as silent, soft, and loud mode. These three different operating modes in indoor environment recommended in [4] are used to generate frequency-modulated WM signals in simulations. The power spectral density of the frequency-modulated WM as per specification in Table 3 is shown in Fig. 8.

The different simulation parameters are given in Table 4. Three different scenarios are considered here.

Case 1 If WM appears with a center frequency of 1.1 MHz, the subband 2 and subband 3 are sensed as shown in Fig. 9 and the center frequency is determined using the centroid method.

Case 2 If the WM appears with a center frequency of 1.125 MHz, the subband 2 and subband 3 have equal energy as shown in Fig. 10. The center frequency of WM is at the midpoint of the two subbands.

Fig. 9
figure 9

Energy distribution for Case 1

Full size image
Fig. 10
figure 10

Energy distribution for Case 2

Full size image
Fig. 11
figure 11

Energy distribution for Case 3

Full size image
Fig. 12
figure 12

Energy distribution at the output of subband 2 in Case 3 for a spectral resolution of \(M_{2}=4\)

Full size image
Fig. 13
figure 13

Comparison of proposed method with conventional methods

Full size image

Case 3 If the WM appears with a center frequency of 0.65 MHz, the subband 2 has higher energy compared to other subbands as shown in Fig. 11, and the output of this subband is further sensed with finer resolution in Stage 2 to locate the center frequency precisely using centroid method. This is shown in Fig. 12 for a spectral resolution of \(M_2=4\).

It can be inferred that except for Case 3, the detection and center frequency estimation of WM is completed in Stage 1 reducing the computational complexity and latency.

The accuracy of center frequency estimation of the WM using the proposed method was compared with conventional polyphase DFT filter bank methods for different spectral resolution of \(M=8\), \(M=16\), and \(M=32\). The accuracy of the method proposed in [6] is the same as the conventional polyphase DFT filter bank method [5]. In the proposed method, the number of subbands in the first stage was chosen to be \(M_1=8\) and the second stage \(M_2=4\). The simulation was performed for different center frequencies with different operating modes of WM over a sensing bandwidth of 6 MHz with SNR varying from 0 to −20 dB. The comparison of the proposed method with the conventional methods for center frequency estimation in terms of percentage error is shown in Fig. 13. It can be inferred from Fig. 13 that the proposed method has percentage error less than 4 % and better than the conventional methods. It was also observed that for coarser resolution \(M=8\), the percentage error is much higher compared to finer resolutions \(M=16\) and \(M=32\). The computational complexity of the proposed method along with the other methods is tabulated in Table 2. The proposed method has reduced computational complexity and provides better accuracy in estimation of center frequency in WM.

6 Conclusions

The algorithm proposed in the paper has unique features of reduced latency, low computational, and hardware complexities. In addition, in the proposed method the percentage error in detection of center frequency in WM for various noise levels is less than 4 %. A trade-off is achieved between complexity and latency depending on the choice of number of subbands and stages in the filter bank structure. The algorithm uses centroid method to calculate center frequency for WM in TV channels. The rationale behind adapting this method along with the mathematical derivation for calculation of center frequency using centroid method is discussed in this paper. The proposed method detects the presence of WM depending on the energy distribution at the output of the subbands. Compared to the existing schemes, the proposed method has less computational complexity. In addition, this method estimates center frequency of WM with a higher precision.