1 Introduction

Recently, research on speech enhancement using so-called acoustic sensor networks consisting of spatially distributed microphones has gained significant interest [1–12]. Compared with a microphone array at a single position, spatially distributed microphones are able to acquire more information about the sound field. The usage of spatially distributed microphones allows to employ beamforming techniques for speech quality improvement in reverberant and noisy conditions. Several methods were introduced that use a reference channel. These include the relative transfer function—generalized sidelobe canceler (RTF-GSC) [13], the minimum variance distortionless response (MVDR) beamformer [14], and the speech distortion weighted—multichannel Wiener filter (SDW-MWF) [15, 16].

The MWF is a well-established technique for speech enhancement. It produces a minimum-mean-squared error (MMSE) estimate of an unknown desired signal. The desired signal of the standard MWF (S-MWF) is usually the speech component in one of the microphone signals, referred to as the reference microphone signal. For spatially distributed microphones, the selection of the reference microphone may have a large influence on the performance of the MWF depending on the positions of the speech/noise sources and the microphones [5–7, 17].

With the S-MWF, the overall transfer function from the speakers to the output of the MWF equals the acoustic transfer function (ATF) from the speaker to the reference microphone. Hence, the reference microphone selection determines the amount of speech distortion. Moreover, the overall transfer function has an impact on the broadband output SNR of the MWF [17]. In [5], an MWF formulation with partial equalization (P-MWF) was presented, where the overall transfer function was chosen as the envelope of the individual ATFs with the phase of an arbitrary reference microphone. This results in a partial equalization of the acoustic system and an improved broadband output SNR. While this approach has advantages with respect to background noise reduction, the reverberation caused by the acoustic environment is not reduced.

Recently, the generalized MWF was proposed in order to improve the broadband output SNR [7] (see also [6]). With the G-MWF, the speech reference is a weighted sum of the speech components, such that the output signal has the same phase as the speech component in the reference microphone. The overall transfer function is the weighted sum of squared amplitudes of all ATFs.

In this work, we consider the phase of the speech reference. That is, we present a further generalization of the G-MWF approach in [7], which enables different phase references. We demonstrate that the phase of the speech reference shapes the overall transfer function and hence impacts the speech distortion. Moreover, the overall transfer function influences the broadband output SNR. We propose two speech references that achieve a better signal-to-reverberation ratio and an improvement in broadband output SNR. The proposed references are based on the phase of a delay-and-sum beamformer (DSB) [18].

As shown in [19], the temporal smearing and therefore the reverberation relies on the all-pass component of the overall transfer function. This suggests that a suitable phase reference can improve the output SRR of the system. As a consequence, the phase term of a delay-and-sum beamformer is applied as a phase reference of the G-MWF. Similar concepts were proposed in [20–22]. The DSB needs an estimate of the TDOA to align the signals properly. In the literature, several methods for TDOA estimation were proposed [23–30]. Many of these techniques are summarized in [29].

The work is a sequel to [21]. In addition to the concept proposed in [21], we present a new approach that combines the delay-and-sum beamformer and the P-MWF. Both approaches for the G-MWF can improve the SRR and SNR compared with the S-MWF and P-MWF. Furthermore, we present a theoretical analysis of the broadband output SNR of the G-MWF.

The paper is organized as follows: in Section 2, we introduce the signal model and notation. The G-MWF formulation and the analysis of the output SNR are presented in Sections 3 and 4, respectively. The design of the overall transfer function is explained in Section 5. The block diagram structure of the system is presented in Section 6, together with the necessary TDOA estimation and the challenge of acquiring these estimates in noisy and reverberated environments. In Section 7, the simulation results in terms of SNR and SRR improvement are given, followed by a conclusion in Section 8.

2 Signal model and notation

We consider a linear and time-invariant acoustic system. The beamformer array consists of M microphones. The ith microphone signal y i (k) can be expressed as the convolution of the speech signal s(k) with the acoustic impulse response h i (k) from the speech source to the ith microphone plus an additive noise term n i (k). In the short time frequency domain, the resulting microphone signals can be written as follows

$$ Y_{i}(\kappa,\nu) = H_{i}(\nu)S(\kappa,\nu) + N_{i}(\kappa,\nu). $$
(1)

Y i (κ,ν), S(κ,ν), and N i (κ,ν) correspond to the short time spectra of the time domain signals. H i (ν) represents the ATF corresponding to the the acoustic impulse response and X i (κ,ν)=H i (ν)S(κ,ν) is the speech component at the ith microphone. κ and ν denote the subsampled time index and the frequency bin index, respectively. In the following, these indices are often omitted when possible. The short time spectra and the ATF can be written as M-dimensional vectors:

$$\begin{array}{*{20}l} \qquad\qquad\qquad\boldsymbol{X} &= [X_{1},X_{2},\ldots,X_{M}]^{T} & \end{array} $$
(2)
$$\begin{array}{*{20}l} \boldsymbol{N} &= [N_{1},N_{2},\ldots, N_{M}]^{T} & \end{array} $$
(3)
$$\begin{array}{*{20}l} \boldsymbol{H} &= [H_{1},H_{2},\ldots,H_{M}]^{T} & \end{array} $$
(4)
$$\begin{array}{*{20}l} \boldsymbol{Y} &= [Y_{1},Y_{2},\ldots,Y_{M}]^{T} & \end{array} $$
(5)
$$\begin{array}{*{20}l} \boldsymbol{Y} &= \boldsymbol{X} + \boldsymbol{N} \end{array} $$
(6)

T denotes the transpose of a vector, ∗ the complex conjugate, and † denotes the conjugate transpose. Vectors and matrices are written in bold and scalars are normal letters.

We assume that the speech and noise signals are zero-mean random processes with the power spectral densities (PSDs) Φ N i 2 and Φ S 2. Assuming a single speech source, the speech correlation matrix R S has rank one and therefore can be expressed as

$$\begin{array}{*{20}l} \boldsymbol{R}_{S} &= \mathbb{E} \left\{ \boldsymbol{X}\boldsymbol{X}^{\dag} \right\} = P_{S}\boldsymbol{H}\boldsymbol{H}^{\dag}, \end{array} $$
(7)

where \(\mathbb {E}\) denotes the mathematical expectation. Similarly, \(\boldsymbol {R}_{N}=\mathbb {E} \bigl \{ \boldsymbol {N}\boldsymbol {N}^{\dag } \bigr \}\) denotes the noise correlation matrix. It is assumed, that the speech and noise terms are uncorrelated.

The output signal Z of the beamformer with filter coefficients G=[G 1,G 2,…,G M ]T is obtained by filtering and summing the microphone signals, i.e.,

$$\begin{array}{@{}rcl@{}} Z &=& \mathbf{G}^{\dag}\mathbf{Y}= \mathbf{G}^{\dag}\mathbf{X} + \mathbf{G}^{\dag}\mathbf{N} \\ &=& Z_{S} + Z_{N} \end{array} $$
(8)

where Z S and Z N denote the speech and the noise components at the beamformer output.

3 Generalized MWF

The MWF aims to estimate an unknown signal \(\tilde {H}_{d} S\), where \(\tilde {H}_{d}\) denotes the overall transfer function of the speech component [15, 16, 31]. The parametric MWF minimizes the weighted sum of the residual noise energy and the speech distortion energy, i.e., the cost function

$$ \xi (\mathbf{G})= \mathbb{E} \left\{ \left|\tilde{H}_{d} S - \mathbf{G}^{\dag}\mathbf{X} \right|^{2} \right\}+ \mu\mathbb{E} \left\{ |\mathbf{G}^{\dag}\mathbf{N}|^{2} \right\}, $$
(9)

where μ is a trade-off parameter between noise reduction and speech distortion. The filter minimizing (9) is given by

$$ \mathbf{G} = (\boldsymbol{R}_{S} + \mu\boldsymbol{R}_{N})^{-1} P_{S} \boldsymbol{H}\tilde{H}_{d}^{\ast}. $$
(10)

Commonly, the MWF is implemented as

$$ \mathbf{G} = (\boldsymbol{R}_{S} + \mu\boldsymbol{R}_{N})^{-1} \boldsymbol{R}_{S}\mathbf{u}, $$
(11)

where u is a vector that selects the reference microphone, i.e., the vector u contains a single one and all other elements are zero. Therefore, the overall transfer function is equal to the ATF of a reference microphone, i.e. H d =H ref.

Since, R S is a rank one matrix, it should be noted that any non-zero vector u achieves the same (optimal) narrow-band output SNR. In [7], the generalized MWF was presented, where the elements u i of the vector u define a speech reference for the MWF which is a weighted sum of the speech components in the different microphones with the phase of the speech component in the reference microphone signal. The vector u can be used to define the desired complex-valued response as

$$ \tilde{H}_{d} = \mathbf{u}^{\dag} \boldsymbol{H} =\sum_{i} u_{i}^{\ast} \cdot H_{i}\text{~~for~~} u_{i} \in \mathbb{C}. $$
(12)

In [7], the magnitude of the response \(\tilde {H}_{d} \) was designed to improve the broadband output SNR, whereas the phase term of \(\tilde {H}_{d}\) was set equal to the phase of the ATF in the reference microphone. In contrast to the approach in [7], we consider a complex-valued selection vector u which enables different phase references. In the following, we demonstrate that \(\tilde {H}_{d}\) can be considered as the overall transfer function.

3.1 MWF overall transfer function

According to [5] and many others, the MWF in (10) can be decomposed using the matrix inversion lemma as

$$\begin{array}{@{}rcl@{}} \mathbf{G} &=& \frac{P_{S}}{P_{S} + \mu(\boldsymbol{H}^{\dag}\boldsymbol{R}_{N}^{-1}\boldsymbol{H})^{-1}}\,\frac{\boldsymbol{R}_{N}^{-1}\boldsymbol{H}}{\boldsymbol{H}^{\dag}\boldsymbol{R}_{N}^{-1}\boldsymbol{H}}\,\tilde{H}_{d}^{\ast} \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} &=& G_{WF}\,\mathbf{G}_{MVDR}\,\tilde{H}_{d}^{\ast}, \end{array} $$
(14)

i.e., a MVDR beamformer

$$ \mathbf{G}_{MVDR}=\frac{\boldsymbol{R}_{N}^{-1}\boldsymbol{H}}{\boldsymbol{H}^{\dag}\boldsymbol{R}_{N}^{-1}\boldsymbol{H}}, $$
(15)

a filter \(\tilde {H}_{d}\), and a single-channel Wiener post filter

$$ G_{WF}=\frac{P_{S}}{P_{S} + \mu(\boldsymbol{H}^{\dag}\boldsymbol{R}_{N}^{-1}\boldsymbol{H})^{-1}}. $$
(16)

Without noise reduction, i.e., for μ=0, the overall transfer function equals \(\tilde {H}_{d}\), because G MVDR has a unity gain transfer function. The output signal can be written as

$$ Z_{S} = \tilde{H}_{d} \cdot S. $$
(17)

In the following, we consider some special cases of the G-MWF. Note that the different formulations of the G-MWF differ only with respect to the vector u and the corresponding transfer function \(\tilde {H}_{d}\).

3.2 MVDR beamformer

The MVDR beamformer obtains perfect equalization of the acoustic system, where the overall transfer function is chosen to be \(\tilde {H}_{d}=1\). Hence, the elements of the vector u are

$$ u_{i} = \frac{H_{i}}{\boldsymbol{H}^{\dag}\boldsymbol{H}}. $$
(18)

However, the resulting G-MWF requires perfect knowledge about the ATF from the speaker to the microphones. The corresponding issue of blind channel estimation is a challenging task in noisy environments and so far an unsolved problem. A further issue is the inversion of the squared norm of the ATFs, since they may contain zeros in their magnitude response.

3.3 Selection of a reference channel

In the S-MWF, the overall transfer function \(\tilde {H}_{d}\) is equal to the ATF from the speaker to one of the microphones, i.e., \(\tilde {H}_{d}=H_{\text {ref}}\) where ref denotes the index of the reference microphone. In this case, the numerator of the S-MWF can be written as

$$ \boldsymbol{R}_{S} \boldsymbol{u} = P_{S} \boldsymbol{H}\boldsymbol{H}^{\dag} \boldsymbol{u} = P_{S} \boldsymbol{H}\tilde{H}_{\text{ref}}^{\ast}, $$
(19)

where u is a column vector of length M that selects the reference microphone, i.e., the corresponding entry is equal to one, while all other entries are equal to zero. As a result, the corresponding ATF remains as the overall transfer function.

Compared to the MVDR beamformer in Section 3.2, the advantage of the S-MWF is that it only depends on estimates of the signal statistics, i.e., R S and R N and no explicit knowledge of the ATFs is required. However, it should be noted that the output signal is as reverberant as the input signal.

3.4 Partial equalization approach

In [5], the P-MWF has been presented, where the amplitude of the overall transfer function is defined as the envelope of the individual ATFs, and the phase is chosen as the phase ϕ ref of an arbitrary (reference) ATF, i.e.,

$$ \tilde{H}_{d} = \sqrt{\boldsymbol{H}^{\dag} \boldsymbol{H}} \, e^{j\phi_{\text{ref}}}. $$
(20)

This formulation results in a partial equalization of the acoustic system, since the dips in the magnitude response of the individual ATFs can be avoided. The elements of the vector u can be computed as

$$ u_{i} = \sqrt{\frac{r_{S_{i,i}}}{\text{tr}(\boldsymbol{R}_{S})}} \frac{r_{S_{i,\text{ref}}}}{|r_{S_{i,\text{ref}}}|} = \frac{H_{i}}{\sqrt{\boldsymbol{H}^{\dag} \boldsymbol{H}}} \, e^{-j\phi_{\text{ref}}}, $$
(21)

where tr(·) denotes the trace of the matrix and \(r_{S_{i,j}}\) denotes the element of R S in the ith row and jth column. Hence, for the P-MWF, we have

$$ \boldsymbol{R}_{S}\boldsymbol{u} = \boldsymbol{R}_{S}\frac{\boldsymbol{H}}{\sqrt{\boldsymbol{H}^{\dag} \boldsymbol{H}}} \, e^{-j\phi_{\text{ref}}}=P_{S} \boldsymbol{H}\sqrt{\boldsymbol{H}^{\dag} \boldsymbol{H}} \,e^{-j\phi_{\text{ref}}}. $$
(22)

Similar to the S-MWF, the P-MWF only depends on the signal statistics and therefore no explicit knowledge of the ATFs is required. It should be noted that the phase of the output speech component is equal to the phase of the reverberant speech component in the reference microphone signal. As a result, the P-MWF approach equalizes the amplitude of the desired overall transfer function, but the output signal is as reverberant as the selected microphone signal.

4 Output SNR

In this section, we investigate the narrow-band and broadband output SNR of the different MWF formulations. Firstly, we consider the narrow-band output SNR

$$ \gamma(\nu) = \frac{\mathbb{E} \left\{|Z_{S}(\nu)|^{2}\right\}}{\mathbb{E} \left\{|Z_{N}(\nu)|^{2}\right\}} =\frac{\boldsymbol{G}^{\dag}\boldsymbol{R}_{S}\boldsymbol{G}}{\boldsymbol{G}^{\dag}\boldsymbol{R}_{N}\boldsymbol{G}}. $$
(23)

Using Eq. (14), we have

$$\begin{array}{@{}rcl@{}} \gamma(\nu) &=&\frac{\left(G_{\text{WF}}\,\mathbf{G}_{\text{MVDR}}\,\tilde{H}_{d}^{\ast}\right)^{\dag}\boldsymbol{R}_{S}\left(G_{\text{WF}}\,\mathbf{G}_{\text{MVDR}}\,\tilde{H}_{d}^{\ast}\right)}{\left(G_{\text{WF}}\,\mathbf{G}_{\text{MVDR}}\,\tilde{H}_{d}^{\ast}\right)^{\dag}\boldsymbol{R}_{N}\left(G_{\text{WF}}\,\mathbf{G}_{\text{MVDR}}\,\tilde{H}_{d}^{\ast}\right)}\\ &=&\frac{|G_{\text{WF}}|^{2}|\tilde{H}_{d}|^{2}\mathbf{G}_{\text{MVDR}}^{\dag}\boldsymbol{R}_{S}\mathbf{G}_{\text{MVDR}}}{|G_{\text{WF}}|^{2}|\tilde{H}_{d}|^{2}\mathbf{G}_{\text{MVDR}}^{\dag}\boldsymbol{R}_{N}\mathbf{G}_{\text{MVDR}}}\\ &=&\frac{\mathbf{G}_{\text{MVDR}}^{\dag}\boldsymbol{R}_{S}\mathbf{G}_{\text{MVDR}}}{\mathbf{G}_{\text{MVDR}}^{\dag}\boldsymbol{R}_{N}\mathbf{G}_{\text{MVDR}}}. \end{array} $$
(24)

Consequently, the narrow-band output SNR is independent of the particular choice of \(\tilde {H}_{d}\). Nevertheless, \(\tilde {H}_{d}\) impacts the broadband output SNR, which is defined as

$$\begin{array}{@{}rcl@{}} \gamma_{\text{out}} &=& \frac{\sum_{\nu}\mathbb{E} \left\{|Z_{S}(\nu)|^{2}\right\}}{\sum_{\nu}\mathbb{E} \left\{|Z_{N}(\nu)|^{2}\right\}} \\ &=& \frac{\sum_{\nu}\boldsymbol{G}(\nu)^{\dag}\boldsymbol{R}_{S}(\nu)\boldsymbol{G}(\nu)}{\sum_{\nu}\boldsymbol{G}(\nu)^{\dag}\boldsymbol{R}_{N}(\nu)\boldsymbol{G}(\nu)}. \end{array} $$
(25)

Note that the PSD of the speech component at the output of the MVDR beamformer is P S . Hence, the PSD of the speech component Z S at the output of the G-MWF is \(\mathbb {E} \left \{|Z_{S}(\nu)|^{2}\right \}=|G_{WF}|^{2}|\tilde {H}_{d}|^{2} P_{S}\). Similarly, the PSD of the noise component at the output of the MVDR beamformer is \(P_{N,\text {MVDR}}=\mathbf {G}_{\text {MVDR}}^{\dag }\boldsymbol {R}_{N}\mathbf {G}_{\text {MVDR}}\), such that the PSD of the noise component at the output of the G-MWF is \(\mathbb {E} \left \{|Z_{N}(\nu)|^{2}\right \}=|G_{WF}|^{2}|\tilde {H}_{d}|^{2} P_{N,\text {MVDR}}\) and

$$\begin{array}{@{}rcl@{}} \gamma_{\text{out}} &=& \frac{\sum_{\nu}P_{S}(\nu)|G_{\text{WF}}(\nu)|^{2}|\tilde{H}_{d}(\nu)|^{2}}{\sum_{\nu}P_{N,\text{MVDR}}(\nu)|G_{\text{WF}}(\nu)|^{2}|\tilde{H}_{d}(\nu)|^{2}}. \end{array} $$
(26)

From this equation, it can be seen that the overall transfer function as well as the single-channel Wiener post filter impact the broadband output SNR.

Next, we consider the response \(\tilde {H}_{d}\) that maximizes the broadband output SNR. Equation (26) can be written as

$$\begin{array}{@{}rcl@{}} \gamma_{\text{out}} &=& \frac{{\sum_{\nu}}\alpha_{\nu}|\tilde{H}_{d}(\nu)|^{2}}{{\sum_{\nu}}\beta_{\nu}|\tilde{H}_{d}(\nu)|^{2}}=\frac{{\tilde{\mathbf{H}}^{\dag}}\mathbf{A}{\tilde{\mathbf{H}}}} {{\tilde{\mathbf{H}}^{\dag}}\mathbf{B}{\tilde{\mathbf{H}}}}. \end{array} $$
(27)

with

$$\begin{array}{@{}rcl@{}} \alpha_{\nu}&=&P{_{S}}(\nu)|{G}_{\text{WF}}(\nu)|^{2}\\ \beta_{\nu}&=&P{_{N,\text{MVDR}}}(\nu)|{G}_{\text{WF}}(\nu)|^{2}\\ \tilde{\mathbf{H}}&=&[\tilde{H}_{d}(0),\ldots,\tilde{H}_{d}(F-1)]^{T}\\ {A}&=&\left(\begin{matrix} \alpha_{0} & 0 & \ldots & 0 \\ 0 & \alpha_{1} & \ldots & 0 \\ 0 & \ldots & \ddots & 0 \\ 0 & \ldots & 0 & \alpha_{F-1} \end{matrix}\right) \\ {B}&=&\left(\begin{matrix} \beta_{0} & 0 & \ldots & 0 \\ 0 & \beta_{1} & \ldots & 0 \\ 0 & \ldots & \ddots & 0 \\ 0 & \ldots & 0 & \beta_{F-1} \end{matrix}\right). \end{array} $$

where F denotes the total number of frequency bins. Maximizing γ out is equivalent to solving the generalized eigenvalue problem \(\mathbf {A}\tilde {\mathbf {H}}=\lambda \mathbf {B}\tilde {\mathbf {H}}\) or \(\mathbf {B}^{-1}\mathbf {A}\tilde {\mathbf {H}}=\lambda \tilde {\mathbf {H}}\). The solution to the eigenvalue problem is the eigenvector corresponding to the largest eigenvalue λ max. Since B −1 A is a diagonal matrix, the largest eigenvalue is

$$ \lambda_{\text{max}}=\max_{\nu}\frac{\alpha_{\nu}}{\beta_{\nu}}=\max_{\nu}\frac{P{_{S}}(\nu)}{P{_{N,\text{MVDR}}(\nu)}}. $$
(28)

Comparing Eqs. (28) with (26), we obtain the corresponding eigenvector \(\tilde {\mathbf {H}}=[0,\ldots,1,\ldots,0]^{T}\), with a one in the frequency bin corresponding to the largest eigenvalue and zero elsewhere. Although this overall transfer function maximizes the broadband output SNR, the corresponding speech distortion will not be acceptable, because only one frequency bin will pass the beamformer.

Hence, we conclude that the design of the desired response \(\tilde {H}_{d}\) requires additional constraints on the speech distortion. The optimal solution with respect to speech distortion is the MVDR beamformer which is, however, hardly attainable in practice.

5 MWF reference selection

It was shown in [19] that the temporal smearing and therefore the reverberation relies on the all-pass component of the overall ATF. This suggests that a suitable phase reference can improve the output SRR. In this section, we present two formulations of the G-MWF that improve the SRR and the broadband output SNR compared with the S-MWF or the P-MWF. Both formulations use a phase reference from a DSB, which delays the microphone signals to compensate for the different times of arrival. Hence, the DSB enhances the direct path component and, as we will see in Section 7, improves the SRR.

5.1 Delay-and-sum beamformer

In the first approach, we propose to simply use the output of a delay-and-sum beamformer as the speech reference. The corresponding elements of the vector u can be described as

$$ u_{i} = \frac{1}{M}\cdot e^{j2\pi\frac{\nu}{F}\tau_{i}}\text{ for } \nu \in 0,\ldots,F-1, $$
(29)

where τ i is a delay (in samples), which compensates the TDOA of the direct path speech components at the microphones. The speech components are typically aligned to the microphone with the latest arrival time to obtain a causal DSB. Using (12) we obtain the overall transfer function

$$ \tilde{H}_{d} =\frac{1}{M}\sum_{i} H_{i}e^{-j2\pi\frac{\nu}{F}\tau_{i}}. $$
(30)

5.2 Partial equalization with DSB phase reference

The second approach is a combination of the P-MWF with the DSB as the phase reference. As already described in Section 3.4, the phase reference of the P-MWF is the phase of an arbitrary ATF. In order to improve the SRR, we can use the DSB as the phase reference. The resulting vector u can be described as

$$ u_{i} = \sqrt{\frac{r_{S_{i,i}}}{\text{tr}(\boldsymbol{R}_{S})}}\cdot e^{j2\pi\frac{\nu}{F}\tau_{i}}\text{~~for~~} \nu \in 0,\ldots,F-1. $$
(31)

Note that the phase term impacts the magnitude of the overall transfer function \(\tilde {H}_{d}\), cf. (12). Comparing (21) and (31), we have \(u_{i}=\frac {|H_{i}|}{\sqrt {\boldsymbol {H}^{\dag } \boldsymbol {H}}}e^{j2\pi \frac {\nu }{F}\tau _{i}}\) and

$$ \tilde{H}_{d} =\frac{1}{\sqrt{\boldsymbol{H}^{\dag} \boldsymbol{H}}}\sum_{i} |H_{i}|H_{i}e^{-j2\pi\frac{\nu}{F}\tau_{i}}. $$
(32)

Hence, the direct path speech components in the microphones are aligned, but additionally the microphone signals are weighted with the magnitude of the ATFs similar to the P-MWF approach.

6 System structure of the G-MWF

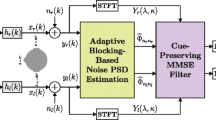
Figure 1 depicts the block diagram of the G-MWF for an array with two microphones. Since the filtering is performed in the frequency domain, the microphone signals are first windowed and then transformed using the fast Fourier transform (FFT).

Fig. 1
figure 1

System structure for multichannel Wiener filtering with vector u

Full size image

A frequency-dependent voice activity detector (VAD) as proposed in [32] is used to estimate the required correlation matrices for the G-MWF. During speech pauses and in frequency bins where no speech activity is detected, the estimate of the noise correlation matrix R N is updated. The estimate of the speech correlation matrix R S is obtained from the input correlation matrix R Y as

$$ \mathbf{R}_{S} = \mathbf{R}_{Y} - \mathbf{R}_{N}. $$
(33)

Furthermore, for the phase reference proposed in Section 5, the TDOA from the speaker to the microphones is required, to achieve a coherent summation of the microphone signals. Depending on the TDOA, a suitable vector u is derived to compensate the phase differences of the microphone signals, as calculated in Eq. (29). A very popular TDOA estimation approach is the generalized cross correlation (GCC) method [23, 28, 29], where the cross-correlation between the microphone signals is calculated in the frequency domain as the cross power spectral density (CPSD). Depending on the application and the environmental conditions, the CPSD is typically weighted with a coherence or noise-based weighting using the magnitude spectrum of the CPSD. The weighted CPSD is transformed to the time domain using the inverse Fourier transform, resulting in the cross correlation vector. The main peak in the cross correlation vector indicates the time delay. It should be noted that the TDOA estimate is only valid in signal blocks where the speaker is active, which can be determined based on a VAD.

It should be noted that the phase of the CPSD is equal to the phase of the relative transfer function (RTF) between the microphones, since both only differ from a different magnitude response. Since in general the microphone signals contain correlated noise components, estimating the RTFs directly from the noisy microphone signals leads to biased RTF estimates. Several methods for unbiased RTF estimation have been proposed, e.g., by exploiting the non-stationarity of speech signals [13, 33] or based on the generalized eigenvalue decomposition of R Y and R N [34, 35]. In [36], an approach for unbiased RTF estimation was proposed, requiring estimates of the PSDs and CPSDs of the speech and noise components, which can be obtained from the estimated speech and noise correlation matrices R S and R N . The RTF estimate between microphones i and j is computed as a combination of two weighted coefficients

$$\begin{array}{@{}rcl@{}} \hat{W}_{\text{unbiased}} &=& f_{i}\frac{r_{S_{i,j}}}{r_{S_{i,i}}} + f_{j}\frac{r_{S_{j,j}}}{r_{S_{j,i}}}, \end{array} $$
(34)

where the terms f i and f j are SNR-based weighting coefficients which are defined as

$$\begin{array}{@{}rcl@{}} f_{i} &=& \frac{\frac{r_{S_{i,i}}}{r_{N_{i,i}}}}{\frac{r_{S_{i,i}}}{r_{N_{i,i}}}+\frac{r_{S_{j,j}}}{r_{N_{j,j}}}} \end{array} $$
(35)
$$\begin{array}{@{}rcl@{}} f_{j} &=& \frac{\frac{r_{S_{j,j}}}{r_{N_{j,j}}}}{\frac{r_{S_{i,i}}}{r_{N_{i,i}}}+\frac{r_{S_{j,j}}}{r_{N_{j,j}}}}. \end{array} $$
(36)

We propose a slightly modified approach based on frequency-dependent VAD [32], where the RTF estimate is updated only in frequency bins where speech activity is detected. Furthermore, a smoothing parameter to average the RTF estimate is used, which is the rate of all frequency bins where speech activity is detected. By applying the inverse Fourier transform, \(\hat {W}_{\text {unbiased}}\) can be transformed back into the time domain, which results in the vector \(\hat {W}_{\text {unbiased}}\). The location of the peak value that indicates the delay to the microphone j can be calculated as

$$ \tau_{i} = \arg\max_{n=0,\ldots,F-1} \hat{w}_{\text{unbiased}}(n), $$
(37)

where \(\hat {w}_{\text {unbiased}}(n)\) is the nth element of the vector \(\hat {W}_{\text {unbiased}}\).

7 Simulation results

To verify the SRR and SNR improvements provided by the proposed approaches, different simulations were carried out. In the following, G-MWF-1 denotes the G-MWF that uses the DSB as the speech reference, i.e., (29), whereas G-MWF-2 denotes the partial equalization approach, using the DSB only as a phase reference, i.e., (31). For the S-MWF and the P-MWF, the first microphone was used as the reference. All simulations were performed with a sampling rate of 16 kHz and an FFT length F=512. We consider a noisy car environment as well as a reverberant classroom. The signals for testing the algorithms are ITU speech signals convolved with measured impulse responses. For the car scenario, this was done with an artificial head and two cardioid microphones that were mounted close to the rear-view mirror. For the classroom scenario [37] impulse responses were recorded with a loudspeaker and omnidirectional microphones at two different spatial locations with a microphone distance of 0.5 m. The reverberation time R T 60 of the classroom has a value between 1.5 and 1.8 s over all frequencies. To evaluate the dereverberation capabilities of the algorithms, the energy decay curves (EDCs) [38] of the resulting overall transfer functions \(\tilde {H}_{d}\) using the measured impulse responses were calculated (for μ=0). For the car environment, the resulting EDCs are shown in Fig. 2.

Fig. 2
figure 2

EDC of the resulting acoustic transfer functions of the car environment: (a) ATF from the speech signal source to microphone 1 (S-MWF), (b) overall transfer function of P-MWF with phase reference of microphone 1, (c) overall transfer function of G-MWF-1, (d) overall transfer function of G-MWF-2

Full size image

Curve (a) depicts the EDC of the overall transfer function for the S-MWF. Curve (b) depicts the resulting EDC of the overall transfer function of the P-MWF. Compared with (a), it can be observed that the decay time is increased, but the energy of the first reflections is reduced due to the partial equalization as can be seen from the first 230 samples of the EDC. Curves (c) and (d) depict the EDC of the overall transfer function for the G-MWF-1 and G-MWF-2, respectively. Compared with (a) and (b), a reduced decay time is observed due to the coherent combining of the phase terms. As a result, the direct components of the ATF are enhanced, which leads to an improvement in speech quality of the overall system.

For the classroom scenario, the resulting EDCs are shown in Fig. 3. Due to the longer reverberation time, compared with the car environment, the resulting EDCs show a different behavior. Curves (e) and (f) depict the EDCs of the resulting transfer function for the S-MWF and the P-MWF, respectively. Curves (g) and (h) depict the EDCs of the overall transfer functions for the G-MWF-1 and the G-MWF-2. Compared to (e), it can be observed in (f) that the direct signal component for the first few samples is augmented, due to the partial equalization, but that the decay time is increased. While (h) still shows a slightly better performance than (g) for the first 7000 samples, the decay time is increased by a small amount compared with (h) during the samples 7000–10,000. However, the reverberation energy for the G-MWF-1 and G-MWF-2 in (g) and (h) is noticeably reduced compared with (e) and (f).

Fig. 3
figure 3

EDC of the resulting acoustic transfer functions of the classroom environment: (e) ATF from the speech signal source to microphone 1 (S-MWF), (f) overall transfer function of P-MWF with phase reference of microphone 1, (g) overall transfer function of G-MWF-1, (h) overall transfer function of G-MWF-2

Full size image

As a measure of reverberation, the direct-to-reverberation ratio (DRR) can be calculated from the resulting overall transfer functions \(\tilde {H}_{d}\). The DRR is defined as [39]

$$ \text{DRR} = 10\log_{10}\left(\frac{\sum\limits_{n=0}^{n_{d}} {h_{d}^{2}}(n)}{\sum\limits_{n=n_{d}+1}^{\infty} {h_{d}^{2}}(n)}\right) \text{dB}, $$
(38)

where h d is the impulse response of the overall transfer function \(\tilde {H}_{d}\) in the time domain and n d are the samples of the direct path. For n d , we considered a time interval of 8 ms after the first arrival of the direct sound. In Table 1, the DRR values for the different overall transfer functions \(\tilde {H}_{d}\) are presented. From the table, it can be seen that the G-MWF approaches improve the DRR in both scenarios compared with the S-MWF and P-MWF.

Table 1 DRR of the overall transfer function for choosing a different phase and magnitude reference
Full size table

Both versions of the G-MWF result in similar overall transfer functions. This can be observed in Figs. 4 and 5. Figure 4 presents the magnitude response of the ATFs of the car environment for both microphones as well as the overall transfer function of G-MWF-2 for frequencies between 2600 and 4000 Hz. Clearly, the resulting partial equalization of the G-MWF-2 can be seen. Figure 5 depicts the overall transfer function of both G-MWF versions for the same frequency section. It is shown that the magnitude response of both approaches looks quite similar.

Fig. 4
figure 4

Magnitude response of G-MWF2

Full size image
Fig. 5
figure 5

Comparison of G-MWF1 and G-MWF2

Full size image

Finally, we consider a noisy car scenario. The noise was recorded at a driving speed of 100 km/h with the same microphone setup as specified above. For μ>0, the MWF performs an adaptive noise reduction and therefore the resulting overall transfer function is time varying. As a result, signal-based performance measures for the noise reduction and dereverberation performance need to be used. For the dereverberation performance, the signal-to-reverberation ratio (SRR) after [39] is used, i.e.,

(39)

where s d (k) is the direct path signal component of the first microphone and \(\hat {s}(k)\) is the output signal of the beamformer in the time domain. It should be noted that this measure is only valid for signal segments, where speech activity is detected.

Table 2 presents the results for the SRR and the broadband output SNR for two settings of the trade-off parameter μ, where a larger value of μ results in more noise reduction. The SRR was measured in time frames where speech was present. The performance of both G-MWF approaches are compared with the S-MWF and P-MWF. It can be observed that both G-MWF approaches outperform the S-MWF in terms of SRR and SNR. G-MWF-1 outperforms the P-MWF in terms of SRR and SNR, whereas G-MWF-2 improves the SRR compared to G-MWF-1 at the expense of a small SNR loss.

Table 2 SRR and SNR comparison for different MWF formulations
Full size table

8 Conclusions

For the multichannel Wiener filter, the influence of the phase reference is often neglected, because it has no impact on the narrow-band output SNR. In this work, we have shown that the phase reference influences the overall transfer function. Moreover, the overall transfer function determines the speech distortion and impacts the broadband output SNR. We have proposed two generalized formulations for the MWF where the phase reference is based on the phase of a delay-and-sum beamformer. The proposed G-MWF technique requires an estimate of the time-difference-of-arrival, which can be acquired from the estimates of the speech and noise correlation matrices. Thus, the G-MWF requires only information about the second order statistics of the signals. The presented simulation results indicate that both G-MWF versions can achieve a better signal-to-reverberation ratio and an improvement in broadband output SNR compared to previously known MWF formulations.