Comparison of $(1+\alpha )$ Fractional-Order Transfer Functions to Approximate Lowpass Butterworth Magnitude Responses

Abstract

Three fractional-order transfer functions are analyzed for differences in realizing ($1+\alpha$) order lowpass filters approximating a traditional Butterworth magnitude response. These transfer functions are realized by replacing traditional capacitors with fractional-order capacitors ($Z=1/s^{\alpha }C$ where $0\le \alpha \le 1$) in biquadratic filter topologies. This analysis examines the differences in least squares error, stability, $-$3 dB frequency, higher-order implementations, and parameter sensitivity to determine the most suitable ($1+\alpha$) order transfer function for the approximated Butterworth magnitude responses. Each fractional-order transfer function for $(1+\alpha )=1.5$ is realized using a Tow–Thomas biquad a verified using SPICE simulations.

1 Introduction

Fractional-order filter circuits are an emerging field of electronics incorporating concepts from fractional calculus into circuit theory for signal processing [5]. In the past decade, there has been a surge of research regarding the theory [1, 2, 13, 14, 17, 21] and implementation [3, 20, 23, 24] of these circuits. Early works highlight the precise control of attenuation they provide. Integer-order filters yield $-20n$ dB/decade stopband attenuations, where n is the integer order of the filter; fractional-order filters provide greater control with $-20(n+\alpha )$ dB/decade stopband attenuations where $0\le \alpha \le 1$ is the fractional component of the order. They also provide an avenue to design band-pass [2] and band-reject [13] filters with asymmetric stopband characteristics. These features allow the design of filters with fractional-step attenuations between the integer orders and is where this class of circuits derives their name.

Significant work has been devoted to designing fractional-order filters that approximate the Butterworth responses with flat passband characteristics [1, 3], but has recently been expanded to also include Chebyshev responses [8, 25]. Multiple approaches have been taken toward the realization of these fractional-order filters that can be divided into two families: (1) Using approximations of $s^{\alpha }$ to realize integer-order filters that implement the fractional response [6, 15, 24, 26] and (2) using fractional-order capacitors ($Z=1/s^{\alpha }C$ where $0\le \alpha \le 1$ and C is a pseudocapacitance with units F sec$^{\alpha -1}$) in the realizations of traditional filter topologies [7, 20–23]. Many of these works focus on the design and implementation of fractional-order transfer functions of the form

$$\begin{aligned} T_{1}^{1+\alpha }(s)=\frac{k_1}{s^{1+\alpha }+k_2 s^{\alpha }+k_3} \end{aligned}$$

(1)

Where the $k_{2,3}$ coefficients are selected to yield a flat passband response. These coefficients have been selected when $k_1$ has been fixed at a value of 1 yielding a DC gain equal to $1 / k_3$. Using (1) provides an alternative to earlier fractional-order filters with transfer function:

$$\begin{aligned} H(s) = \frac{1}{s^{1+\alpha }+1} \end{aligned}$$

(2)

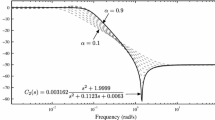
that exhibited peaking in the passband [16]. An example of the passband peaking exhibited by (2) and a response using (1) designed to approximate a Butterworth response is given in Fig. 1 as dashed and solid lines, respectively.

Fig. 1

Comparison of FLPF transfer functions (1) and (2) when $\alpha )= 0.9$ as solid and dashed lines, respectively

The transfer function (1) has been implemented in [7] using a Tow–Thomas biquadratic filter and a fractional-order capacitor with $\alpha =0.5$ realized using a photolithographic process [9], approximated with field programmable analog array hardware [6], switched-capacitor realizations [15], current mirrors [25, 26], and with sinh-domain and log-domain integrators [24]. While acknowledged in [7] that transfer function and magnitude characteristics were impacted by the choice of capacitor replaced with a fractional-order component, these impacts were not investigated. As the field matures, it becomes important to explore further $(1+\alpha )$ order transfer functions to quantify the differences between them and for the design situations where each will be most suitable to implement.

This provides the motivation for this work, where three fractional-order transfer functions are analyzed to determine differences in realizing $(1+\alpha )$ order lowpass filters to approximate a traditional Butterworth magnitude response. These transfer functions are realized by replacing traditional capacitors with fractional-order capacitors in biquadratic filter topologies. This analysis examines the differences in least squares error, stability, $-3$ dB frequency, higher-order implementations, parameter sensitivity, and circuit realizations for each transfer function.

2 Fractional-Order Low-Pass Filter (FLPF) Transfer Functions

While there are currently no fractional-order components commercially available to implement fractional-order circuits, there has been much progress toward realizing fractional-order capacitors [4, 9, 19]. These components have an order $0 < \alpha < 1$ placing them between the traditional components of a resistor ($\alpha =0$) and capacitor ($\alpha =1$). It is from this property that the name fractional-order capacitor is derived, though it is also referred to in many other fields as a constant phase element (CPE) due to the constant phase angle that is dependent on the order $\alpha$ and is independent of frequency. With the availability of these components on the horizon, it is important to explore how their use in traditional circuit topologies will impact performance [22, 23] and uncover potential improvements over their integer-order counterparts that designers can take advantage of in the future. Expanding these integer-order circuits to the fractional domain requires replacing their integer-order capacitors with their fractional-order counterparts. Applying this process to the biquadratic filter circuits given in Fig. 2 yields general $(\alpha _1+\alpha _2)$ order transfer functions given by:

$$\begin{aligned} H_1(s)= & {} \frac{\frac{1}{R_1 R_2 C_1 C_2}}{s^{\alpha _1 + \alpha _2} + s^{\alpha _2}\frac{\left[ R_1 R_2 + R_1R_3 + R_2R_3 \right] }{R_1 R_2 R_3 C_1} + \frac{1}{R_2 R_3 C_1 C_2}} \end{aligned}$$

(3)

$$\begin{aligned} H_2(s)= & {} \frac{\frac{1}{R R_2 C_1 C_2}}{s^{\alpha _1 + \alpha _2} + \frac{s^{\alpha _2}}{G R C_1} + \frac{1}{R^2 C_1 C_2}} \end{aligned}$$

(4)

$$\begin{aligned} H_3(s)= & {} \frac{\frac{R_6}{R_1 R_4 R_5 C_1 C_2}}{s^{\alpha _1 + \alpha _2} + \frac{s^{\alpha _2}}{R_3 C_1} + \frac{R_6}{R_2 R_4 R_5 C_1 C_2}} \end{aligned}$$

(5)

where $H_1(s)$, $H_2(s)$, and $H_3(s)$ describe the responses of the circuits in Fig. 2a–c, respectively, when $C_{1,2}$ are replaced with fractional-order capacitors with orders ($0 \le \alpha _{1,2} \le 1$). It should be noted that to obtain (4) from Fig. 2b requires setting $R_1=R_3=\infty$ (open circuits). Each of (3)–(5) realizes the transfer function (1) when $C_1$ is a traditional capacitor ($\alpha _1=1$) and $C_2$ is a fractional-order capacitor ($0 \le \alpha _2 \le 1$). Alternatively, each circuit can realize the transfer function:

$$\begin{aligned} T_{2}^{1+\alpha }(s)=\frac{k_1}{s^{1+\alpha }+k_2 s+k_3} \end{aligned}$$

(6)

when $C_1$ is a fractional-order capacitor ($0 \le \alpha _1 \le 1$) and $C_2$ is a traditional capacitor ($\alpha _2=1$). Both (1) and (6) are $(1+\alpha )$ order transfer functions that differ in the order of the denominator term with the $k_2$ coefficient. The general case results when both $C_1$ and $C_2$ are fractional-order capacitors ($0 \le \alpha _{1,2} \le 1$) yielding the transfer function:

$$\begin{aligned} T_{3}^{1+\alpha }(s)=\frac{k_1}{s^{\alpha _1+\alpha _2}+k_2 s^{\alpha _2}+k_3}=\frac{k_1}{s^{2\beta }+k_2 s^{\beta }+k_3} \end{aligned}$$

(7)

where $1+\alpha =2\beta =\alpha _1+\alpha _2$. Note that this work has been limited to the case where $\alpha _1=\alpha _2$ to simplify the analysis as there are near infinite combinations that could be explored otherwise.

Fig. 2

Circuit topologies realizing biquadratic filter responses

Each of the fractional transfer functions (1), (6), and (7) offers stopband attenuations of $-20(1+\alpha )$ dB/decade but potentially different stability margins, bandwidths, and transition characteristics while being simple to realize using existing topologies and fractional-order components. In the following sections, the coefficients to approximate Butterworth passband behavior for each $(1+\alpha )$ order transfer function are determined and further used to explore the differences between their stability, $-3$ dB frequencies, higher-order implementations, sensitivities, and circuit realizations.

2.1 Coefficient Selection

In [6] the $k_{2,3}$ coefficients for (1) were selected to approximate the flat passband response of the Butterworth filters using a numerical search comparing the fractional transfer function and first-order Butterworth passbands over the frequency range $\omega =0.01$–1 rad/s. The coefficients yielding the lowest error during the search, which was limited to $0<k_{2}<2$ and $0<k_{3}<1$ when $k_1=1$, from [6] are

$$\begin{aligned} k_2^{FPAA}= & {} 1.0683 \alpha ^2 + 0.161\alpha + 0.3324 \end{aligned}$$

(8)

$$\begin{aligned} k_3^{FPAA}= & {} 0.2937 \alpha + 0.7122 \end{aligned}$$

(9)

In this work, a similar routine is implemented using the optimization tools available in MATLAB rather than a brute-force search. The purpose of this is to improve the returned coefficients, increase the search speed, and provide a controlled search process for evaluating all $(1+\alpha )$ order transfer functions. The search was implemented using the MATLAB lsqcurvefit routine, which uses nonlinear least squares fitting that attempts to solve the problem

$$\begin{aligned} \min _{x}\parallel | H\left( x, \omega \right) |-|B_1(\omega )|\parallel _{2}^{2}&= \min _{x}\sum _{i=1}^{k}\left( |H\left( x, \omega _i \right) -|B_1(\omega _{i})|\right) ^{2} \nonumber \\&\quad {\mathrm {s.t.}} \quad 0 \le k_{2,3} \le 2 \end{aligned}$$

(10)

where x is the vector of filter coefficients [$k_2$, $k_3$], | H(x) | is the magnitude response using (1), (6), or (7) calculated using x, $|B_1(\omega )|$ is the normalized first-order Butterworth magnitude response, $|H(x, \omega _i)|$ and $|B_1(\omega _{i})|$ are the magnitude responses of (1), (6), or (7) and the first-order Butterworth approximation at frequency $\omega _{i}$, and k is the total number of data points in the magnitude response. This is not the first application of optimization routines in the field of fractional filters. Previously, they have been employed in [10] to generate approximations of $1/(s+1)^{\alpha }$ for audio applications and to determine coefficients to approximate fractional Chebyshev responses [8].

Fig. 3

a $k_{2,3}$ coefficients to approximate a Butterworth magnitude response using (1) and (6) as solid and dashed lines, respectively, compared to coefficients presented in [6] with b LSE from optimization process

The $k_{2,3}$ coefficients that yielded the lowest least squares error (LSE) for (1), (6), and (7) with $k_1=1$ when the order is increased from 1.01 to 1.99 in steps of 0.01 are given in Fig. 3a as solid, dashed, and dotted lines, respectively. Values for $k_2$ and $k_3$ are given as blue and black lines, respectively. For further comparison, the coefficients from [6] are given as hatched lines. The interpolated quadratic and linear equations that describe $k_{2,3}$ for (1), (6), and (7) as functions of $\alpha$ determined using the raw data are:

$$\begin{aligned} k_2^{TF_1}= & {} 1.008 \alpha ^2 + 0.2867\alpha + 0.2366 \end{aligned}$$

(11)

$$\begin{aligned} k_3^{TF_1}= & {} 0.2171 \alpha + 0.7914 \end{aligned}$$

(12)

$$\begin{aligned} k_2^{TF_2}= & {} -0.4838 \alpha ^2 + 2.023\alpha + 0.0104 \end{aligned}$$

(13)

$$\begin{aligned} k_3^{TF_2}= & {} -0.0992 \alpha ^2 + 0.0989 \alpha + 1.004 \end{aligned}$$

(14)

$$\begin{aligned} k_2^{TF_3}= & {} 0.2305 \alpha ^2 + 1.315\alpha + 0.0032 \end{aligned}$$

(15)

$$\begin{aligned} k_3^{TF_3}= & {} 0.013 \alpha + 0.98 \end{aligned}$$

(16)

with norm of residuals of 0.0727, 0.0267, 0.0178, 0.0138, 0.1677, and 0.0713 for (11)–(16), respectively. This norm of residuals is calculated from the fit residuals, defined as the difference between the ordinate data point and the resulting fit for each abscissa data point; with a lower norm value indicating a better fit than a larger value. It should also be noted that for (15) and (16) that the value $\alpha$ is the fractional component of the order between the integer cases 1 and 2 and not the order of each fractional capacitor, which are instead related by $1+\alpha =\alpha _1+\alpha _2$.

Using the MATLAB optimization routines improved the coefficients over the brute-force numerical search used in [6] yielding lower LSE, given in Fig. 3b, calculated as:

$$\begin{aligned} {\mathrm {LSE}}=\sum _{i=1}^{k} \left( |H\left( k_{2,3}, \omega _i \right) -|B_1(\omega _{i})|\right) ^{2} \end{aligned}$$

(17)

The LSE for all $\alpha$ using the optimization coefficients in (1) is lower than the LSE using the coefficients from [6], highlighting that the optimization routine can be used to find much better coefficients for the approximated magnitude response than the brute-force search routine. From the LSEs, (7) has the lowest error for $(1+\alpha )<1.85$, with (1) having the lowest for $(1+\alpha )>1.85$; though each case approaches a common error value as $(1+\alpha )$ approaches 2. This is similarly reflected in Fig. 3 with all the $k_{2}$ and $k_3$ coefficients approaching common values regardless of transfer function as $(1+\alpha )$ approaches 2.

Comparing the solid and dashed lines in Fig. 3b, the LSE using the optimization coefficients in (1) and (6) is similar for $(1+\alpha ) < 1.4$. While for $(1+\alpha )>1.4$, (1) provides lower LSE than (6). Therefore, using (11) and (12) in (1) provides a better approximated Butterworth filter response than (13) and (14) in (6) when designing for filters with orders greater than 1.4 using only a single fractional capacitor in the implementation. Using two fractional-order capacitors in the implementation and coefficients (15) and (16) in (7) result in the lowest LSE for all cases while $(1+\alpha )<1.83$, above which the optimization coefficients in (1) yields the lowest LSE.

The magnitude response of (1), (6), and (7) using the $k_{2,3}$ optimization coefficients for orders 1.2, 1.5, and 1.8 are given in Fig. 4 as solid lines, dashed lines, and circles, respectively. Confirming that all transfer functions with the optimization coefficients realize low pass filter responses with fractional stepping in the stopband attenuation. For all further references to (1), (6), and (7) throughout this work, unless stated otherwise, it can be assumed that the optimization coefficients (11)–(16) are being used in their respective transfer functions.

Fig. 4

Magnitude response of (1), (6), and (7) as solid lines, dashed lines, and circles, respectively, using $k_{2,3}$ optimization coefficients when the order is 1.2, 1.5, and 1.8

2.2 Stability

Another useful criteria to evaluate differences between the transfer functions is the margin of stability, described here as the margin between the region of instability and the closest pole angle. To analyze this stability for the fractional filters using traditional analysis methods requires conversion of the s-domain transfer functions to the W-plane defined in [18]. This transforms the transfer function from fractional order to integer order which is much easier to analyze. This process can be broken into the following steps:

• 1. Convert the fractional transfer function to the W-plane using the transformations $s=W^m$ and $\alpha =k/m$ [18],

• 2. Select k and m for the desired $\alpha$ value,

• 3. Solve the transformed transfer function for all poles in the W-plane,

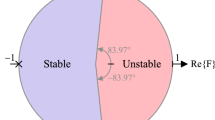
• 4. Observe the absolute pole angles, $\left| \theta _W\right|$, if any are less than $\frac{\pi }{2m}$ rad/s then the system is unstable, otherwise if all $\left| \theta _W\right| >\frac{\pi }{2m}$ then the system is stable.

Applying this process to the denominators of (1), (6), and (7) yields the characteristic equations:

$$\begin{aligned} W^{m+k} + k_2W^{k} + k_3= & {} 0 \end{aligned}$$

(18)

$$\begin{aligned} W^{m+k} + k_2W^{m} + k_3= & {} 0 \end{aligned}$$

(19)

$$\begin{aligned} W^{2k} + k_2W^{k} + k_3= & {} 0 \end{aligned}$$

(20)

Though it should be noted that we have set $\beta =k/m$ for (7) which yields (20). The minimum root angles of (18) and (19) for $\alpha =0.01$–0.99 and minimum root angles of (20) for $\beta =0.505$–0.995 calculated with $k=10$ to 990 in steps of 10 when $m=1000$ are given in Fig. 5 as solid, dashed, and dotted lines, respectively. The minimum root angles, $|\theta _W|_{{\mathrm {min}}}$, for all values of $\alpha$ are greater than the minimum required angle, $\left| \theta _W\right| >\frac{\pi }{2m}=0.09^{\circ }$, confirming that each transfer function using (11)–(16) are stable and physically realizable.

While each transfer function has a similar minimum root angle at an order of 2, (7) shows the highest margin from the region of stability for $(1+\alpha )<1.74$. Above 1.74 (6) shows a slightly higher margin with all three converging on a similar value as the order approaches 2. Minimum root angles for (1) and (6) are similar for $1+\alpha <1.2$, but for $1+\alpha >1.2$ the minimum root angle for (6) shows a visibly higher margin until converging at approximately $(1+\alpha )=1.99$. For further comparison, the minimum root angle for (1) using (8)–(9) is given in Fig. 5 as a hatched line. Interestingly, the optimization coefficients for (1) yield a worse margin of stability than (8)–(9) indicating that the improved LSE comes at the cost of the stability margin.

Fig. 5

Minimum root angle in W-plane for (1), (6), and (7) as a solid, dashed, and dotted line respectively, compared to that presented in [6] (hatched line)

2.3 $-$3 dB Frequencies

To further evaluate differences between (1), (6), and (7) the frequency at which each magnitude response reaches $-3$ dB is compared. The ideal Butterworth response reaches $-3$ dB below its DC value at a frequency of 1 rad/s; then the approximation which most closely meets this criteria would prove the best choice for implementation. The $-3$ dB frequencies (numerically calculated with errors less than 0.1 %) for each order from 1.01 to 1.99 in steps of 0.01 for (1), (6), and (7) are given in Fig. 6 as solid, dashed, and dotted lines, respectively.

Fig. 6

$-3$ dB frequency for (1), (6), and (7) as solid, dashed, and dotted lines, respectively. Each using the optimization coefficients and further compared to those from numerical search in [6] (hatched line)

The fractional transfer functions only match 1 rad/s at orders of approximately 1.04 and 1.81 using (1), at no orders using (6), and at approximately 1.04 using (7). The transfer function given by (7) shows the least variation of $-3$ dB frequencies over the full range of orders.

Both (1) and (6) show similar magnitudes of deviation from 1 rad/s. The transfer function given by (1) has frequencies greater than 1 rad/s for $1.04<1+\alpha <1.81$ and (6) lower for all orders. Each reaching extremes of 1.127 rad/s and 0.856 rad/s at $(1+\alpha =1.41)$ and 1.58 for (1) and (6), respectively. For further comparison, the $-3$ dB frequencies of (1) using (8)–(9) are given in Fig. 6 as a hatched line, which shows closer agreement to 1 rad/s over orders $1.1<(1+\alpha )<1.73$ than when the optimization coefficients are used, indicating that the optimization coefficients do not universally improve the filter response and that while the LSE is lower the bandwidth has not been improved, hinting at an unexplored avenue regarding how the optimization search routine for $k_{2,3}$ coefficients can be executed to achieve different design objectives, but leave that research for future exploration.

Fig. 7

Magnitude response of $(4+\alpha )$ order filters using (1) and (6) as a solid line and circles, respectively, with $k_{2,3}$ optimization coefficients when $\alpha =0.2$, 0.5, and 0.8

2.4 Higher-Order $-$3 dB Frequencies

To realize stable higher-order FLPFs, it was previously suggested in [14] to employ (1) divided by a higher-order normalized Butterworth polynomial creating a ($n+\alpha$) order filter given by:

$$\begin{aligned} T_{n+\alpha }(s) = \frac{T_1^{1+\alpha }(s)}{B_{n-1}(s)} \end{aligned}$$

(21)

where $B(\cdot )$ represents the Butterworth polynomial. While filters using this method have been realized in [6, 14, 15], the impact on the $-$3 dB frequency compared to the Butterworth responses it approximates has not been explored. Further, using (6) and (7) in the numerator of (21) instead of (1) provides another opportunity to evaluate the differences between each transfer function.

Magnitude responses of $(4+\alpha )$ order FLPFs using (21) and either (1), (6) or (7) are given in Fig. 7 as solid, dashed, and dotted lines, respectively, for orders of 1.2, 1.5, and 1.8. From this figure, the fractional attenuations between the fourth- and fifth-order Butterworth responses indicated as $B_4$ and $B_5$, respectively, are evident. Observing the responses near $\omega =1$ rad/s the FLPFs do not share the same $-3$ dB frequency of the Butterworth responses. To quantify these differences, the frequencies where each FLPF response reaches $-3$ dB are calculated (with an error less than $0.1\%$) for steps of 0.01 in the fractional component of the order from 0.01 to 0.99. These calculations used (1), (6), and (7) and first-, second-, or third-order normalized Butterworth polynomials to realize $(2+\alpha )$, $(3+\alpha )$, and $(4+\alpha )$ order FLPFs. The calculated $-3$ dB frequencies are given in Fig. 8a–c for the $(2+\alpha )$, $(3+\alpha )$, and $(4+\alpha )$ order FLPFs, respectively. Solid lines in Fig. 8 indicate frequencies for (1), dashed for (6), dotted for (7), and hatched for (1) using $k_{2,3}$ from [6].

The general trends from Fig. 8 indicate the magnitude responses of (21), regardless of the fractional transfer function in the numerator, reduces the frequency at which the magnitude responses reach $-3$ dB. This impact decreases as the order of the FLPF is increased using a higher-order Butterworth polynomial. That is, the $(4+\alpha )$ $-3$ dB frequencies are the closest to the ideal value while the $(2+\alpha )$ show the highest deviation from the ideal. Further, using (7) results in a smaller range of $-3$ dB frequencies than using (1) or (6). However, even with the widest range of $-3$ dB frequencies for each order, (1) is closest to the ideal Butterworth responses ($\omega =1$ rad/s) over the largest range of orders for all cases, making it the superior choice to realize higher-order FLPFs using (21).

Fig. 8

$-3$ dB frequency for a $(2+\alpha )$, b $(3+\alpha )$, and c $(4+\alpha )$ order lowpass filter implementations using (1) and (6) as solid and dashed lines respectively

2.5 Stopband Attenuations

Each of the fractional-order transfer functions has different roll-off characteristics, that is how the magnitude response changes from the flat passband attenuation to the ideal stopband attenuation of $-20(1+\alpha )$ dB/decade. This provides another avenue to explore differences, with sharper roll-off characteristics being the most desirable. To compare these characteristics, the slope of the magnitude of each transfer function between frequencies $\omega =1$ and 10 rad/s as well as $\omega =10$ and 100 rad/s for $(1+\alpha )=1.01$ to 1.99 in steps of 0.01 are given in Fig. 9. The slopes between frequencies $\omega =1$ and 10 rad/s are given as black lines, while those between $\omega =10$ and 100 rad/s are given as blue lines. With values for each of the transfer functions (1), (6), and (7) are given as solid, dashed, and dotted lines, respectively. The solid red line is the ideal characteristic of $-20(1+\alpha )$ dB/decade, transitioning from a value of $-20$ dB/decade when $(1+\alpha )=1$ to $-40$ dB/decade when $(1+\alpha )=2$; corresponding to the traditional integer-order attenuations available.

From Fig. 9, the attenuation for $\omega =1-10$ of (6) is closest to the ideal when $(1+\alpha )<1.45$ but for $(1+\alpha )>1.45$ (1) is closer until all transfer functions converge to a common value at $(1+\alpha )=2$, indicating that for lower orders, (6) has the sharpest roll-off, though comparing the attenuations for $\omega =10$ and 100 both (1) and (7) are closer to the ideal than (6), which shows the greatest deviation. Overall, (1) provides the best overall attenuation characteristics.

Fig. 9

Stopband attenuation for $(1+\alpha )$ order lowpass filter implementations using (1), (6), and (7) over frequency ranges $\omega \,\epsilon \left[ 1,10\right]$ (black) and $\omega \,\epsilon \left[ 10,100\right]$ rad/s compared to the ideal attenuation (red) (Color figure online)

2.6 Sensitivity to Parameter Variation

With each $(1+\alpha )$ transfer function having different orders for the s term with the $k_2$ coefficient, there is potential for them to have different sensitivities to $k_{2,3})$ variations. To explore these sensitivities, the $-3$ dB frequency deviations and attenuation deviations over the frequency bands $\omega =1-10$ rad/s and $\omega =10-100$ rad/s for each transfer function were calculated for three cases; i) $k_2$ varied by 1 %, ii) $k_3$ varied by 1 %, and iii) $k_2$ and $k_3$ varied by 1 %.

Fig. 10

Deviation of $-3$ dB frequency for $(1+\alpha )$ order lowpass filter implementations using (1), (6), and (7) when parameters a $k_2$, b $k_3$, and c $k_{2,3}$ are varied by 1 %

Fig. 11

Deviations of stopband attenuation for $(1+\alpha )$ order lowpass filter implementations using (1), (6), and (7) over frequency ranges $\omega \,\epsilon \left[ 1,10\right]$ (black) and $\omega \,\epsilon \left[ 10,100\right]$ (blue) rad/s when parameters a $k_2$, b $k_3$, and c $k_{2,3}$ are varied by 1 % (Color figure online)

2.6.1 $-$3 dB Frequency Sensitivity

The $-3$ dB frequency deviations for the $(1+\alpha )$ order transfer functions, calculated as the absolute deviation (in percent) from their ideal, are given in Fig. 10a–c for cases (i), (ii), and (iii), respectively. In each figure, the values for (1), (6), and (7) are given as solid, dashed, and dotted lines, respectively. From Fig. 10a there is a general trend of increasing deviation with increasing order for each of the three transfer functions when $k_2$ has a $1\%$ variation. There is no single transfer function that has the lowest sensitivity for all orders; both (6) and (7) show similar errors for $(1+\alpha )<1.2$, (1) for $1.2<(1+\alpha )<1.44$, (6) for $1.44<(1+\alpha )<2$, and each converging at $(1+\alpha )=2$. The reverse is seen in Fig. 10b for the sensitivity to $k_3$ for all transfer functions. The deviation for all three transfer functions decreases with increasing order. Comparing each deviation, for $(1+\alpha )>1.15$ (6) shows the lowest sensitivity until all three converge at an order of 2; while for $(1+\alpha )<1.15$ (1) shows the lowest sensitivity. From the deviations in Fig. 10c, (6) has the lowest sensitivity to the 1 % variation in $k_2$ and $k_3$ for orders $(1+\alpha )>1.04$ until all converge at an order of 2. Though for the region $(1+\alpha )<1.04$ (7) shows the lowest sensitivity. Comparing all three cases, (6) has the lowest sensitivity over the widest range of orders to the $1\%$ variations in the coefficients $k_{2,3}$. Overall, (6) has the lowest sensitivity over the widest range of orders for each case.

Table 1 Component values to realize 1.5-order fractional-order transfer functions (TF) using Tow–Thomas biquad

Fig. 12

a RC ladder circuit to approximate fractional-order capacitor and b impedance magnitude of approximated fractional-order capacitors (dashed) compared to the ideal (solid) with pseudocapacitances of 12.62 $\upmu$F sec$^{\alpha -1}$ with $\alpha =0.5$ (black) and 1.42 $\upmu$F sec$^{\alpha -1}$ with $\alpha =0.75$ after scaling to a center frequency of 1 kHz

2.6.2 Stopband Attenuation

The deviation (in percent) of the stopband attenuations for the $(1+\alpha )$ order transfer functions compared to their ideal case is given in Fig. 11a–c for the cases (i), (ii), and (iii), respectively. In each figure, the errors of (1), (6), and (7) are given as solid, dashed, and dotted lines, respectively, while errors over the frequency band $\omega =1-10$ rad/s are given as black lines and errors over $\omega =10-100$ rad/s are given as blue lines.

Table 2 Component values to realize fourth-order RC ladder approximation of fractional-order capacitors

From Fig. 11, the deviation in stopband attenuation for the 1 % variations of $k_2$, $k_3$, and $k_{2,3}$ are very low. All showing less than 1 % deviation over both frequency bands. The sensitivity is generally less for $\omega =10-100$ than $\omega =1-10$, with sensitivities so low ($<$0.5 %) in the band $\omega =10-100$ that differences between them for each transfer function would be negligible in practical application. For each case over $\omega =1-10$, (1) tends to show the lowest sensitivity for $(1+\alpha )<1.4$ with (6) showing the lowest sensitivity above 1.4.

Fig. 13

SPICE simulations of $(1+\alpha )=1.5$ order fractional Tow–Thomas filters implementing the transfer functions a (1), b (6), and c (6) (dashed blue lines) compared to the ideal responses (solid black lines) (Color figure online)

3 Circuit Simulations

The ($1+\alpha$) order transfer functions can be physically realized using the circuit in Fig. 2c, known as the Tow–Thomas biquadratic filter. This topology has been previously employed in [7] to realize the transfer function given by (1) and is employed here to further verify the operation of each fractional-order transfer function. Using the design equations presented in [7], the component values to realize (1), (6), and (7) for $(1+\alpha )=1.5$ are given in Table 1. Each component value has been magnitude scaled by 1000 and frequency scaled to 1 kHz to realize realistic values. Comparing the values no transfer function has an advantage in terms of the range of values required, all are within the same order of magnitude, though (1) and (6) have the advantage requiring a single fractional-order capacitor over the two required by (7).

3.1 Approximated Fractional-Order Capacitors

To simulate these circuits, approximations of the fractional-order capacitors were implemented and realized using the RC ladder network given in Fig. 12a. To determine the component values for this approximation, the method presented in [11] was employed, based on collecting terms of a Continued Fraction Expansion (CFE) and realizing a fourth-order approximation when 8 CFE terms are collected. Applying this process to realize approximations of 12.62 $\upmu$F sec$^{\alpha -1}$ and 1.42 $\upmu$F sec$^{\alpha -1}$ fractional-order capacitors with orders 0.5 and 0.75, respectively, yields the resistor and capacitor values given in Table 2. These values have been selected such that the frequency band around which the RC ladder is a good approximation is centered at 1 kHz. The impedance magnitude of the ideal (solid) and approximated (dashed) fractional-order capacitors are presented in Fig. 12b from which it is clear that the approximations are very good over almost 4 decades, from approximately 10 Hz–100 kHz.

Using the component values in Tables 1 and 2, the Tow Thomas biquad was simulated in LTSPICE IV using LT1354 op amps, realizing the 1.5-order fractional low-pass filter responses. The SPICE-simulated magnitude responses (blue dashed lines) compared to the ideal responses (black solid lines) are shown in Fig. 13a–c for the transfer functions (1), (6), and (7). The SPICE-simulated magnitude responses show very good agreement with the MATLAB-simulated ideal responses, though there are significant deviations above 100 kHz which can be attributed to the approximations of the fractional-order capacitors which show larger error from their ideal behavior above this frequency. The greatest deviations are seen in Fig. 13c from 10-100 kHz. This results from using two approximated fractional-order capacitors that compounds the impact of their individual deviations. These simulations verify that each of the fractional-order transfer functions given by (1), (6) , and (7) can be realized at the circuit level and realizes the expected responses using approximated fractional-order capacitors.

4 Conclusion

The $(1+\alpha )$ order transfer functions given by (1), (6), and (7) are used to implement a magnitude response that approximates the passband of a traditional Butterworth response with fractional-step stopband attenuation. Each transfer function, using coefficients determined through a MATLAB-implemented optimization routine, realizes FLPF magnitude responses with differing LSEs, stability margins, $-3$ dB frequencies, transition characteristics from passband to stopband, and sensitivities. This research could be further expanded to determine differences using different fractional transfer functions to implement fractional-order Chebyshev, Inverse Chebyshev, and Cauer magnitude responses, or differences in phase and group delay; all of which have not yet been thoroughly investigated.