1 Introduction

The goal in the Blind Source Separation (BSS) problem [7] is to estimate and separate an unobserved vector of M source signals \(\mathbf{s}\in \mathbf{R}^{M}\), from N observations of their mixture \(\mathbf{x}\in \mathbf{R}^{N}\) while the source signals and the mixture process are all unknown. In the noise-free case, BSS model can be expressed as \(\mathbf{x}=\mathbf{As}\), where \(\mathbf{A}\in \mathbf{R}^{N\times M}\) is the mixing matrix. To solve the BSS problem, independent component analysis (ICA) is one of the most widely used techniques and ICA is essentially a method for extracting individual signals from mixtures [26]. The ICA is said to be complete when the mixing matrix A is squared and invertible, \(N=M\); to be overcomplete when it contains more sources than observations, \(M\,>\,N\); to be undercomplete when it contains fewer sources than observations, \(M\,<\,N\) [26]. For undercomplete ICA, the number of independent sources in the given mixture has to be determined before performing ICA. In [25, 27], the authors demonstrated that normalized determinant of the global matrix is a measure of the number of independent sources, M, in a mixture of N observations. With the rapid development of BSS/ICA technologies and their applications, a series of new BSS/ICA methods have emerged [1]. For audio BSS/ICA, the research has progressed to real-world scenarios today [43], with the following applications. The broadband ICA was used to minimize the statistical independence and can be successfully exploited for acoustic source localization [23]. For speech BSS, a joint approach for single-channel speaker identification and speech BSS was proposed in [24]. In [40], the authors proposed a single-channel BSS algorithm. The proposed method assumed that the sources were characterized as autoregressive processes and constructed a pseudo-stereo mixture by time-delaying and weighing the observed single-channel mixture. Ensemble empirical mode decomposition (EEMD)-based methods are often used for single-mixture BSS. To solve the edge effect problem, Guo [13] proposed an edge effect elimination method which was based on principal component analysis (PCA), ICA and edge effect elimination of EEMD. For microphone array processing, in [30] the authors designed a unified framework for joint optimization and estimating the sound sources under auditory uncertainties such as reverberation or unknown number of sounds, and a unified model was proposed for sound source localization and separation based on Bayesian nonparametrics. In distributed microphone arrays, the source location information can be defined as the intra- and inter-node levels. Souden et al. [37] utilized both of them to cluster and separate multiple competing speech signals. The normalized recording vector was used to capture the intra-node information, and different features including the energy level differences with and without the phase differences between nodes were used to deal with the inter-node level. In [29], the authors addressed the problem of sound BSS from a multi-channel microphone array capture via estimation of source spatial covariance matrix of a short-time Fourier transformed mixture signal. It had been proved that multi-channel BSS can separate the deterministic sinusoidal signals by using ICA technique, and in [19], the authors derived a single-channel BSS method for deterministic sinusoidal signals with ICA, this method can achieve separation by utilizing additional filters to virtually provide a mixture matrix for BSS.

Overcomplete ICA is a hard problem to solve since the mixing matrix A is not invertible. As was mentioned above, the single-channel BSS is overcomplete or underdetermined BSS (UBSS). To perform UBSS, identification of the mixing matrix and source recovery becomes two distinct problems, thus the “two-step approach” is often used. The first step is to estimate the mixing matrix and the second step is to separate the source signals. The most critical step of UBSS is to estimate the mixing matrix. In the two-sensor case, based on sparse representation, the classical potential function method [4] can be used to estimate the mixing matrix. Based on sparse component analysis (SCA), a discriminatory K-weighted hyperline clustering algorithm [46] was developed via weighing scheme to deal with the blind identification problem of the underdetermined mixing matrix of multiple dominants. The K-mean clustering algorithms are commonly used to solve the UBSS problem given sufficiently sparse sources, but in any case other than deterministic sources, this lacks theoretical justification. Indeed, mean-based clustering does not possess any equivariance (performance independent of A). Based on this consideration, Theis [41] proposed a median-based clustering method and proved its equivariance and convergence; and in [44] the authors proposed a method combining the fuzzy clustering and eigenvalue decomposition technique to estimate the mixing matrix in order to deal with the nonstrictly sparse sources. For underdetermined convolutive mixtures of audio sources, a two-stage method based on frequency bin-wise clustering and permutation alignment was proposed in [34]; and in [28], the authors proposed a convolutive UBSS through weighted interleaved ICA and spatio-temporal source correlation. In addition, the observed signals in the frequency domain were normalized into positive values and became compact clustering. In [14], the authors proposed an ant colony clustering algorithm to estimate the pivotal datum in the data stack so as to estimate the column vectors of the mixing matrix. From the above analysis, the clustering algorithms are the most important methods to estimate the mixing matrix of UBSS and the precondition of cluster analysis is that the sources are sparse. Therefore, sparse representation is actually of paramount importance in UBSS; without it, the estimation of the mixing matrix is not possible at all. If the mixing matrix has been successfully estimated, some methods can be used to separate the sources. For a given overcomplete basis matrix, the corresponding sparse solution (coefficient matrix) with minimum \(l_{1}\) norm is unique with a probability of one, which can be obtained using a standard linear programming algorithm [21]. Based on this, Li et al. [22] gave a development of a recoverability analysis and obtained a necessary and sufficient condition under which a source column vector can be recovered by solving a linear programming problem. And often such methods are fit to data by solving mixed \(l_{1}-l_{2}\) convex optimization problems [47].

In signal processing, the first and foremost task is to represent a signal. The traditional representation is to ideally sample a signal in space or time. This representation, while convenient for the purposes of displaying or playback, is mostly inefficient for analysis tasks. Signal processing techniques commonly require more meaningful representations which capture the useful characteristics of the signal [31]. Sparse representations offer a powerful emerging model for signals and approximate a data source as a linear combination of few elementary signals (atoms) from a pre-specified dictionary [9]. This is mainly due to the fact that important classes of signals such as audio and images have naturally sparse representations with respect to fixed bases (i.e., Fourier, wavelet), or concatenations of such bases [45]. Moreover, efficient and provably effective algorithms based on convex optimization or greedy pursuit are available for computing such representations with high fidelity [9].

In this paper, we investigate audio UBSS and the basic scheme is as follows: Since audio signal may not be sparse enough in the time domain, we do the UBSS in the frequency domain in which the signals are sufficiently sparse. Furthermore, the linear clustering characteristic of sparse signal in the time domain is translated into compact cluster by normalizing the observed data in the frequency domain. Through estimating the pivotal datum in a normalized data stack, the column vector of the underdetermined mixing matrix can be estimated. In the traditional processing methods of UBSS, the number of source signals is assumed to be known and the K-means algorithm is used to estimate the mixing matrix. In practice, however, the sources and the number of sources are unknown, so the K-means is not suitable for the actual situation of UBSS. Based on this consideration, this paper employs affinity propagation (AP) clustering to estimate the exact number of clusters (the number of sources); then the K-means algorithm with AP clustering as the initialization is used to estimate the mixing matrix. The rest of this paper is organized as follows: The signal sparse representation and normalization for the UBSS problem are discussed in Sect. 2. The estimation of the mixing matrix is discussed in Sect. 3. First, we utilize AP clustering to search the initial cluster centers (the number of sources) as a preprocessing, and then the K-means is used to estimate the column vectors of the mixing matrix. In Sect. 4, we use the linear programming method to separate the source signals. The simulations are made in Sect. 5 to test and validate the performance of the proposed method. Finally, Sect. 6 summarizes the results and presents the conclusions.

2 Signal Sparse Representation and Normalization

In the case of noise-free, the UBSS model of time domain can be expressed as \(\mathbf{x}(t)=\mathbf{As}(t)\), where t is the time sampling point, \(\mathbf{s}(t)=[s_{1}(t),{\ldots },s_{M}(t)]^{T}\) is the source signal vector, \(\mathbf{x}(t)=[x_{1}(t),{\ldots },x_{N}(t)]^{T}\) is the observed signal vector, and A is the \(N \times M (N < M)\) underdetermined mixing constant matrix. That is

$$\begin{aligned} \left[ {{\begin{array}{c} {x_1 (t)} \\ {x_2 (t)} \\ \vdots \\ {x_N (t)} \\ \end{array} }} \right] =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {a_{11} }&{} {a_{12} }&{} \cdots &{} {a_{1M} } \\ {a_{21} }&{} {a_{22} }&{} \cdots &{} {a_{2M} } \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {a_{N1} }&{} {a_{N2} }&{} \cdots &{} {a_{NM} } \\ \end{array} }} \right] \left[ {{\begin{array}{c} {s_1 (t)} \\ {s_2 (t)} \\ \vdots \\ {s_M (t)} \\ \end{array} }} \right] \end{aligned}$$
(1)

where \(a_{ij}\) \((1\le i\le N, 1\le j\le M)\) is the ijth element of the matrix A. To obtain a useful formulation of this system, the mixing matrix A is decomposed into its column vector \(\mathbf{a}_{j}\) \((j=1,{\ldots },M)\):

$$\begin{aligned} \mathbf{A}=\left[ {{\begin{array}{llll} {\mathbf{a}_1 }&{} {\mathbf{a}_2 }&{} \ldots &{} {\mathbf{a}_M } \\ \end{array} }} \right] \end{aligned}$$
(2)

and

$$\begin{aligned} \mathbf{a}_j =\left[ {{\begin{array}{llll} {a_{1j} }&{} {a_{2j} }&{} \ldots &{} {a_{Nj} } \\ \end{array} }} \right] ^{T} \end{aligned}$$
(3)

Thus, Eq. (1) can be rewritten as

$$\begin{aligned} \mathbf{x}(t)=\mathbf{a}_1 s_1 (t)+\mathbf{a}_2 s_2 (t)+\ldots +\mathbf{a}_M s_M (t) \end{aligned}$$
(4)

In general, an important audio signal processing framework is as follows: segment the signal into (overlapping) frames; process each frame separately; then reconstruct audio signal using the processed frames. For the UBSS problem, estimating the mixing matrix and sources are usually carried out in the time–frequency (T–F) domain, since these signals are sparser than those in the time domain alone. In addition, considering the frame pattern of audio signal processing, we use the short-time Fourier transform (STFT) to realize the transformation from time domain into frequency domain, since STFT can be achieved by selecting the audio frame using the window function. In the frequency domain, the audio signal is sufficiently sparse, i.e., at a given discrete frequency point k, we suppose that only \(S_{j}(k)\) is nonzero and the other source signals are zero or near to zero. Using the signal sparse representation in the frequency domain, the Eq. (4) becomes

$$\begin{aligned} \mathbf{X}(k)=\mathbf{a}_j S_j (k)\quad (j=1,\ldots ,M) \end{aligned}$$
(5)

where k is the discrete frequency index, \( {{\mathbf {X}}}(k)\) and \(S_{j}(k)\) are the STFT of time signals \(\mathbf{x}(t)\) and \(s_{j}(t)\), respectively. Equation (5) is the vector form, and we can also rewrite (5) as its component form:

$$\begin{aligned} \frac{X_1 (k)}{a_{1j} }=\frac{X_2 (k)}{a_{2j} }=\cdots =\frac{X_N (k)}{a_{N j} }=S_j (k) \end{aligned}$$
(6)

Equation 6 is a linear equation and the direction vector \(\mathbf{a}_{j}=[a_{1j},{\ldots },a_{Nj}]^{T}\) of the straight line is the jth column of the mixing matrix A. That is, sparse signals have the linear clustering characteristics and every source signal will determine such a straight line. Therefore, the estimation of the mixing matrix will be translated into the direction estimation of the straight line.

A straight line can be depicted by two directions. For example, a straight line in three-dimensional space can be depicted by direction vector (1, 1, 1) or another vector (\(-\)1, \(-\)1, \(-1\)). To depict the straight line by unique vector, we can take mirroring mapping of the direction vectors to the positive side of the plane or sphere (super-sphere). For example, map vector (\(-\)1, \(-\)1, \(-1\)) to (1, 1, 1). This mapping process can be realized by normalizing the observed signals in frequency domain:

$$\begin{aligned} X^{\# }(k)=\left\{ {\begin{array}{l} \frac{X(k)}{||X(k)||}\quad \;X(k)\ge 0 \\ \frac{-X(k)}{||X(k)||}\quad \;X(k)<0 \\ \end{array}} \right. \end{aligned}$$
(7)

where \({\vert }{\vert }\cdot {\vert }{\vert }\) denotes Euclidean norm.

In the frequency domain, the normalization (7) maps the points to the half unit circle (sphere or hyper-sphere) to form data-intensive clusters. Each straight line maps to a unique point on the half unit circle. That is, the linear clustering characteristic of sparse signal is translated to compact clustering. Thus, the estimation of the column vectors of the mixing matrix A is changed into clustering the point \(X^{\# }(k)\) on the half unit circle. In each dense data stack, there is a pivotal datum (cluster center) that its direction can denote the direction of the straight line. Based on this consideration, we can estimate the direction of the straight line by searching the pivotal datum in the data stack; consequently, the estimation of the mixing matrix of UBSS can be realized.

3 Mixing Matrix Estimation

Cluster analysis aims to seek a partition of the data in which data objects in the same clusters are homogenous while data objects in different groups are well separated [32]. This homogeneity and separation are evaluated through the criterion functions. One such criterion function is the sum-of-squared-error criterion, which is the most widely used criterion function in clustering practice. Suppose we have a set of data objects \(\mathbf{x}_{j} (j =1,{\ldots },N)\) and we want to organize them into K clusters \(\mathbf{C}=\{C_{1}, \ldots , C_{K}\}\). The sum-of-squared-error criterion is defined as

$$\begin{aligned} J(\mathbf{U},\mathbf{M})= & {} \sum \limits _{k=1}^K {\sum \limits _{j=1}^N {u_{kj} } ||\mathbf{x}_j -\mathbf{m}_k ||^{2}} \nonumber \\= & {} \sum \limits _{k=1}^K {\sum \limits _{j=1}^N {u_{kj} } (\mathbf{x}_j -\mathbf{m}_k )^{T}(\mathbf{x}_j -\mathbf{m}_k )} \end{aligned}$$
(8)

where \(\mathbf{U}=\{u_{kj}\}\) is a partition matrix,

$$\begin{aligned} u_{kj} =\left\{ {\begin{array}{ll} 1,&{}\quad \hbox {if }\mathbf{x}_j \in \hbox {cluster }k \\ 0,&{}\quad \hbox {otherwise} \\ \end{array}} \right. \end{aligned}$$
(9)

with

$$\begin{aligned} \sum _{k=1}^K {u_{kj} } =1\;\;\forall j \end{aligned}$$
(10)

\(\mathbf{M}=\{{{\mathbf {m}}}_{1}, \ldots , {{\mathbf {m}}}_{K}\}\) is the cluster prototype or centroid (means) matrix, and

$$\begin{aligned} \mathbf{m}_k =\frac{1}{N_k }\sum _{j=1}^N {u_{kj} \mathbf{x}_j } \end{aligned}$$
(11)

is the sample mean for the kth cluster with \(N_{k}\) data objects. The partition that minimizes the sum-of-squared-error criterion is regarded as optimal and is called the minimum variance partition. Clearly, the sum-of-squared-error criterion is appropriate for the clusters that are compact and well separated.

Based on the criterion function, we must find a clustering algorithm that can realize the goal of minimizing the sum-of-squared-error. In various clustering methods, the K-means algorithm seeks an optimal partition of the data by minimizing the sum-of-squared-error criterion with an iterative optimization procedure, which belongs to the category of hill-climbing algorithms.

3.1 K-means Algorithm

The K-means algorithm is one of the best-known and most popular iterative clustering algorithms. Each iteration consists of two basic steps: (a) partitioning the training signal space into K regions or clusters; and (b) computing the centroid of each region. The basic clustering procedure of K-means is summarized as follows:

  1. (1)

    Initialize a K-partition randomly or based on some prior knowledge. Calculate the cluster prototype matrix \(\mathbf{M}=\{ {{\mathbf {m}}}_{1}, \ldots , {{\mathbf {m}}}_{K}\}\);

  2. (2)

    Assign each object in the data set to \(C_{k}\) using the so-called nearest-neighbor rule, i.e.,

    $$\begin{aligned} \begin{array}{l} \mathbf{x}_j \in C_k ,\hbox { if } ||\mathbf{x}_j -\mathbf{m}_k ||< || \mathbf{x}_j -\mathbf{m}_i || \\ \hbox {for } j=1,\ldots ,N, \, i\ne k,\hbox { and } i=1,\ldots ,K \\ \end{array} \end{aligned}$$
    (12)
  3. (3)

    Recalculate the cluster prototype matrix based on the current partition,

    $$\begin{aligned} \mathbf{m}_k =\frac{1}{N_k }\sum _{\mathbf{x}_j \in C_k } {\mathbf{x}_j } \end{aligned}$$
    (13)
  4. (4)

    Repeat steps (2) and (3) until there is no change for each cluster.

The algorithm described above performs batch mode learning, since the update of the prototypes occurs after all the data points have been processed. Correspondingly, the on-line or incremental mode K-means adjusts the cluster centroids each time a data point is presented,

$$\begin{aligned} \mathbf{m}^\mathrm{new}=\mathbf{m}^\mathrm{old}+\eta (\mathbf{x}-\mathbf{m}^\mathrm{old}) \end{aligned}$$
(14)

where \({\eta }\) is the learning rate.

K-means algorithm is regarded as a staple of clustering methods, due to its ease of implementation. It works well for many practical problems, particularly when the resulting clusters are compact and hyper-spherical in shape [32]. This means that K-means algorithm is well suited for clustering the normalized data as in (7), that is, it can be well used to estimate the mixing matrix of UBSS.

While K-means has these desirable properties, it also suffers several major drawbacks, particularly the inherent limitations when hill-climbing methods are used for optimization. The first problem that plagues K-means is that the iteratively optimal procedure cannot guarantee the convergence to a global optimum. Since K-means can only converge to a local optimum, different initial points generally lead to different convergence centroids, which makes it important to start with a reasonable initial partition to achieve high-quality clustering solutions. However, in theory, there exist no efficient and universal methods for determining such initial partitions. The second problem is that K-means assumes that the number of clusters K is known by the users, which, unfortunately, usually is not true in practice. Like the situation for cluster initialization, there are also no efficient and universal methods for the selection of K. Therefore, identifying K in advance becomes a very important topic in cluster validity. In addition, K-means is sensitive to outliers and noise. The calculation of the means considers all the data objects in the cluster, including the outliers. Even if an object is quite far away from the cluster centroids, it is still forced into a cluster and used to calculate the prototype representation, which therefore distorts the cluster shapes. These disadvantages of the K-means algorithm attract a great deal of effort from different communities, and as a result, many variants of K-means have appeared to address these obstacles.

3.2 Cluster Validity Analysis

There are many clustering algorithms that attempt to expose the inherent partitions in the underlying data. Each algorithm can partition data, but different algorithms or input parameters cause different clusters, or reveal different clustering structures. Thus, the problem of objectively and quantitatively evaluating the resulting clusters, or whether the clustering structure derived is meaningful, which is referred to as cluster validation, is particularly important. For example, if there is no clustering structure in a data set, the output from a clustering algorithm becomes meaningless and is just an artifact of the clustering algorithm. In this case, it is necessary to perform some type of tests to assure the existence of the clustering structure before performing any further analysis. Such problems are called clustering tendency analysis.

With respect to three types of clustering structures (i.e., partitional clustering, hierarchical clustering and individual clusters), there are three categories of testing criteria, known as external criteria, internal criteria and relative criteria. Given a data set X and a clustering structure \({{\mathbf {C}}}\) derived from the application of a certain clustering algorithm on X, external criteria compare the obtained clustering structure \({{\mathbf {C}}}\) to a pre-specified structure, which reflects a priori information on the clustering structure of X. In contrast to external criteria, internal criteria evaluate the clustering structure exclusively from X, without any external information. Relative criteria compare \({{\mathbf {C}}}\) with other clustering structures, obtained from the application of different clustering algorithms or the same algorithm but with different parameters on X, and determine which one may best represent X in some sense. For example, a relative criterion would compare a set of values of K for the K-means algorithm to find the best fit of the data. Both external criteria and internal criteria are closely related to statistical methods and hypothesis tests. They require statistical testing, which could become computationally intensive. Relative criteria eliminate such requirements and concentrate on the comparison of clustering results generated by different clustering algorithms or the same algorithm but with different input parameters. In this section, we only discuss cluster validity approaches based on relative criteria and focus on the problem of how to estimate the number of clusters K.

For many partitional clustering algorithms, K is required as a user-specified parameter. Although in some cases, K can be estimated in terms of the user’s expertise or a priori information for more applications, K still needs to be estimated exclusively from the data themselves. Either over-estimation or under-estimation of K will affect the quality of resulting clusters. A partition with too many clusters complicates the true clustering structure, therefore making it difficult to interpret and analyze the results. On the other hand, a partition with too few clusters causes the loss of information and misleads the final decision. Therefore, to estimate the number of clusters is called the fundamental problem of cluster validity.

Perhaps the most direct method to estimate the value of K is to project data points onto a two- or three-dimensional Euclidean space, using data visualization methods. In that way, visual inspections can provide some useful insight on the number of clusters, and for that matter, even the assignment of data points to different clusters could be determined. However, the complexity of many real data sets makes the 2 or 3-dimensional projections far from sufficient to represent the true data structures; therefore, the visual estimation of K can only be restricted to a very small scope of applications.

For probabilistic mixture, model-based clustering (e.g., K-means), finding the correct number of clusters K is equivalent to fitting a model with observed data and optimizing some criterion. Usually, the expectation maximization (EM) algorithm is used to estimate the model parameters for a given K, which also goes through a predefined range of values. The value of K that maximizes or minimizes the defined criterion is considered optimal. A Monte Carlo cross validation (MCCV) method was proposed in [36], which randomly divides data into training and test sets a certain number of times using a fraction \(\beta \) (e.g., a half-half division of training and test set works well based on the empirical results). K can be selected either directly based on the criterion function or through the calculated posterior probabilities. The most widely used model selection criteria are Akaike’s information criterion (AIC) [2], Bayesian information criterion (BIC) [35], deviance information criterion (DIC) [38], and Bayes factors (BF) [17, 18]. There are several important differences between AIC, BIC, DIC, and BF. All maximum likelihood and Bayesian criteria are alike, in that model selection is linked to parameter estimation. In the calculation of AIC and BIC, parameter estimation is done by maximizing the likelihood in an attempt to find the single best point estimate. Parameters for DIC and BF are estimated using Bayesian methods, which integrate rather than maximize over the parameter space. While both DIC and BF incorporate parameter uncertainty and correlation in the sampling of the joint posterior distribution, one criticism of AIC and BIC is that neither consider parameter uncertainty in their calculations. This is not a maximum likelihood versus Bayesian issue; several maximum likelihood criteria, including the information complexity criterion (or non-coding information theoretic criterion, ICOMP) [5, 6], do include parameter correlation and uncertainty. In [10], the author analyzed and compared the performance of five model selection criteria (AIC, BIC, DIC, BF, and ICOMP). In Monte Carlo comparisons of model selection performance, the true model is almost always considered among the candidate models. While the goal of Monte Carlo comparisons is to estimate the frequency of selecting the true model, the goal of model selection applied to real data is to find a model that best approximates truth. If the simulation-based rules were applied to inference in the real world, all criteria would be wrong 100 % of the time.

From the above analysis, validity criteria are used to examine hierarchical clustering structures, partitional clustering structures, or individual clusters. Particularly, estimating the number of clusters in underlying data is a central task in cluster validation, attracting efforts from a wide variety of disciplines and leading to a large number of indices, criteria, and ad hoc methods. With all these validation criteria, indices, and methods, it is important to keep in mind that no criterion, index, or method is superior to any other for all problems encountered. In general, clustering algorithms search the space of cluster locations and number of clusters to optimize the AIC, BIC ,or DIC measure, and the splitting decision is done by computing the BIC or AIC for Gaussian dataset. In this paper, we mainly investigate the UBSS of audio sources (super-Gaussian dataset) rather than the division criterion, so we expect to find an existent clustering method to accurately estimate the number of sources. And this clustering method is used as preprocessing of the K-means algorithm, since K-means is well qualified for solving the UBSS problem if the number of sources is known in advance. Fortunately, affinity propagation (AP) clustering [12] can be applied to the case of an unknown number of clusters. The novel AP clustering doesn’t need the initialization and it can quickly search the exact number of clusters. Thus, we use AP clustering to search the initial cluster prototype matrix; based on this, the K-means is performed with this initial partition to improve the estimated accuracy of the mixing matrix of UBSS.

3.3 AP Clustering

Clustering data based on a measure of similarity is a critical step in scientific data analysis and in engineering systems [12]. A common approach is to use data to learn a set of centers such that the sum of squared errors between data points and their nearest centers is small. When the centers are selected from actual data points, they are called exemplars [12]. The most obvious feature of AP clustering is that it simultaneously considers all data points as potential exemplars.

AP is a fast algorithm and has advantages in searching speed, general applicability, and good clustering performance. Differing from the K-means algorithm, AP works based on similarities between pairs of data points, and simultaneously considers all the data points as potential cluster centers (called exemplars). The similarity \(s_\mathrm{im}(i, k)\) indicates how well the data point with index k is suited to be the exemplar for data point i. When the goal is to minimize squared error (Euclidean distance), each similarity is set to a negative squared error. For points \(x_{i}\) and \(x_{k}\), the similarity is defined as [12]

$$\begin{aligned} s_\mathrm{im} (i,k)=-||x_i -x_k ||^{2} \end{aligned}$$
(15)

AP takes as input a real number \(s_\mathrm{im}(k, k)\) for each data point k so that data points with larger values of \(s_\mathrm{im}(k, k)\) are more likely to be chosen as cluster centers. These values are referred to as preferences. The number of clusters is influenced by the values of the input preferences, but also emerges from the message-passing procedure.

In order to find appropriate exemplars, AP accumulates evidence, responsibility r(i, k), from data point i for how well-suited point k is to serve as the exemplar for point i, and accumulates evidence, availability \(a_{v}(i, k)\), from candidate exemplar point k for how appropriate it would be for point i to choose point k as its exemplar. From the view of evidence theory [16], larger the value \(r(:, k)+a_{v}(:, k)\), the more probability the point k as a final cluster center. Based on the evidence accumulation, AP searches for clusters through an iterative process until a high-quality set of exemplars and corresponding clusters emerges.

The messages r(i, k) and \(a_{v}(i, k)\) can be viewed as log-probability ratios. To begin with, the availabilities are initialized to zero: \(a_{v}(i, k)=0\). Then, the responsibilities are computed using the rule [12]:

$$\begin{aligned} r(i,k)=s_\mathrm{im} (i,k)-{\mathop {\max }\limits _{j\hbox { s.t.} j\ne k}} \{a_v (i,j)+s_\mathrm{im} (i,j)\} \end{aligned}$$
(16)

In the first iteration, the availabilities are zero, r(i, k) is set to the input similarity between point i and point k as its exemplar, minus the largest of the similarities between point i and other candidate exemplars. In later iterations, when some points are effectively assigned to other exemplars, their availabilities will drop below zero as prescribed by the update rule below. These negative availabilities will decrease the effective values of some of the input similarities s(i, j) in the above rule, removing the corresponding candidate exemplars from competition. For \(k=i\), the responsibility r(k, k) is set to the input preference that point k be chosen as an exemplar, s(k, k), minus the largest of the similarities between point i and all other candidate exemplars. This self-responsibility reflects accumulated evidence that point k is an exemplar, based on its input preference tempered by how ill-suited it is to be assigned to another exemplar.

The above responsibility update rule (16) lets all candidate exemplars compete for ownership of a data point, and the following availability update rule gathers evidence from data points as to whether each candidate exemplar would make a good exemplar:

$$\begin{aligned} a_v (i,k)=\min \left\{ {0,\;r(k,k)+\sum _{j \hbox { s.t}. j\notin \{i,k\}} {\max [0,r(j,k)]} } \right\} \end{aligned}$$
(17)

the availability \(a_{v}(i, k)\) is set to the self-responsibility r(k , k) plus the sum of the positive responsibilities candidate exemplar k receives from other points. Only the positive portions of incoming responsibilities are added, because it is only necessary for a good exemplar to explain some data points well (positive responsibilities), regardless of how poorly it explains other data points (negative responsibilities). If the self-responsibility r(k, k) is negative, the availability of point k as an exemplar can be increased if some other points have positive responsibilities for point k being their exemplar. To limit the influence of strong incoming positive responsibilities, the total sum is thresholded so that it cannot go above zero. The self-availability \(a_{v}(k, k)\) is updated differently:

$$\begin{aligned} a_v (k,k)=\sum _{j \hbox { s.t}. j\ne k} {\max \{0,r(j,k)\}} \end{aligned}$$
(18)

This message reflects accumulated evidence that point k is an exemplar, based on the positive responsibilities sent to candidate exemplar k from other points.

In addition, there are two important parameters in AP: the preferences \(p(k)=s_\mathrm{im}(k, k)\) in diagonal of similarity matrix \(\mathbf{S}_\mathrm{im}=\{s_\mathrm{im}(i, k)\}\) and the damping factor \(\lambda \). Obviously,

$$\begin{aligned} r(k,k)=p(k)-{\mathop {\max }\limits _{j \hbox { s.t.} j\ne k}} \{a_v (k,j)+s_\mathrm{im} (k,j)\} \end{aligned}$$
(19)

The larger the p(k) value, the larger the r(k, k) and \(a_{v}(i, k)\) values, so that it has more probability that the point k is as a final cluster center, i.e., the p(k) value influences which and how many exemplars will win as final cluster centers. This means that the number of identified clusters is increased or decreased by adjusting p(k) accordingly, and usually a good choice is to set all the p(k) values to be the median of all the similarities between data points.

Furthermore, when updating the messages, it is important that they be damped to avoid numerical oscillations that arise in some circumstances. In each iterative step i, the values of r(i, j) and \(a_{v}(i, j)\) are updated with the one in last iteration

$$\begin{aligned} \begin{array}{l} a_v (i,k)=(1-\lambda )a_v (i,k)+\lambda a_v (i-1,k) \\ r(i,k)=(1-\lambda )r(i,k)+\lambda r(i-1,k) \\ \end{array} \end{aligned}$$
(20)

where the damping factor \(\lambda \in [0, 1]\) and the default value is \(\lambda =0.5\). Another function of the damping factor is to improve convergence when AP fails to converge on account of oscillations (or identified exemplars are in periodic variation), where \(\lambda \) needs to be increased to eliminate oscillations [12].

The above update rules require only simple, local computations that are easily implemented, and messages need only be exchanged between pairs of points with known similarities. At any point during AP, availabilities and responsibilities can be combined to identify exemplars. For point i, the value of k that maximizes \(a_{v}(i, k)+r(i, k)\) either identifies point i as an exemplar if \(k=i\), or identifies the data point that is the exemplar for point i.

Obviously, AP clustering can effectively overcome the inherent defect of the K-means algorithm. With AP as initialization, the traditional K-means is used to estimate the underdetermined mixing matrix of UBSS; this is the innovation point of this paper.

4 Source Signals Estimation

In Sect. 3, we have obtained the underdetermined mixing matrix A by the clustering algorithms. Based on this matrix, the second step of the “two-step approach” is to separate the source signals.

In the noise environment, the UBSS model is \(\mathbf{x}=\mathbf{As}+\mathbf{v}\), where \(\mathbf{v}\in \mathbf{R}^{N}\) is a vector of additive Gaussian noise. For sparse signals, the model \(\mathbf{x}=\mathbf{As}+\mathbf{v}\) has the property that only a small number of the components \(x_{i} (i =1, \ldots , N)\) are significantly nonzero at the same time. In the frequency domain, the observed signals are sufficiently sparse, only a component is nonzero. That is, the given nonzero component has a sparse distribution. A random variable \(x_{i}\) is called sparse when \(x_{i}\) has a distribution with a peak at zero and heavy tails, as is the case, for example, with the double exponential (Laplace) distribution. For all practical purposes, sparsity is equivalent to super-Gaussianity or leptokurtosis. In this paper, we only investigate the UBSS of audio signals which are super-Gaussian sources, so the separation process is as follows.

For sparse signals, source separation is achieved by solving the following optimization problem [4]:

$$\begin{aligned} \mathop {\min }\limits _{\mathbf{A},\mathbf{S}} \frac{1}{2\sigma ^{2}}||\mathbf{AS}(k)-\mathbf{X}^{\# }(k)||^{2}+\sum _{i,k} {|S_i (k)|} \end{aligned}$$
(21)

where \(\sigma ^{2}\) is the variance of the noise. The first term of (21) is the sum of squared reconstruction error (the log-likelihood of the Gaussian noise); the second term is the penalty for non-sparsity (assuming independent Laplacian source or super-Gaussian source).

Obviously, (21) is a multi-variable optimization problem. It is difficult to estimate the mixing matrix and the sources at the same time. Since the mixing matrix A was given in Sect. 3, problem (21) becomes

$$\begin{aligned} \mathop {\min }\limits _\mathbf{S} \frac{1}{2\sigma ^{2}}||\mathbf{AS}(k)-\mathbf{X}^{\# }(k)||^{2}+\sum _{i=1}^M {|S_i (k)|} \end{aligned}$$
(22)

In this paper, we only consider the case of noise-free, problem (22) is reduced into

$$\begin{aligned} \mathop {\min }\limits _\mathbf{S} \sum _{i=1}^M {|S_i (k)|} \quad \hbox {s.t. }\mathbf{AS}(k)=\mathbf{X}^{\# }(k)\;\;(k=1,\ldots ,F) \end{aligned}$$
(23)

The problem (23) is a linear programming problem, and it can be separated into F problems at each k, which are easier to solve.

5 Simulation and Analysis

To check the effectiveness of the proposed method, three simulations are done in different cases (with different mixing matrices). In all simulations, we also compare the traditional K-means and the direction estimation of mixing matrix (DEMIX) method [3] with the proposed method. All the methods are carried out under the same conditions in order to get a fair conclusion.

5.1 Simulation Environment and Performance Index

All the simulations are carried out in MATLAB 7.10.0 (R2010a), system of the PC is Windows 7, CPU is Intel(R) Celeron(R) 1007U-1.5GHz, and memory is 4 GB (gigabyte).

All the methods are tested using the SixFlutes data set [4]: the sound of a flute playing steady, isolated notes are recorded at high quality in an acoustically isolated booth without reverberation, and sampled at 44,100 Hz with 16 bits resolution. Six 743 ms excerpts (32,768 samples) are selected for the source signals, corresponding to notes \(s_{1}(t), s_{2}(t), s_{3}(t), s_{4}(t), s_{5}(t)\) and \(s_{6}(t)\).

We use the angular deviation [39] to check the estimated accuracy of the mixing matrix:

$$\begin{aligned} d(\mathbf{a},{{\hat{\mathbf{a}}}})=\frac{180}{\pi }\arccos \frac{\left\langle {\mathbf{a},{{\hat{\mathbf{a}}}}} \right\rangle }{||\mathbf{a}||\cdot ||{\hat{\mathbf{a}}}||} \end{aligned}$$
(24)

where a is the column vector of the original mixing matrix A, and \({\hat{\mathbf{a}}}\) is the column vector of the estimated matrix \({\hat{\mathbf{A}}}\). When the angular deviation is smaller, the accuracy of the estimation is higher.

In addition, we use the correlative coefficients [11] to check the similarity between the original sources and the recovered sources.

$$\begin{aligned} \rho _{ij} =\frac{\sum \nolimits _{t=1}^T {s_i (t)\hat{{s}}_j (t)} }{\sqrt{\sum \nolimits _{t=1}^T {[s_i (t)]^{2}} \sum \nolimits _{t=1}^T {[\hat{{s}}_j (t)]^{2}} }} \end{aligned}$$
(25)

where \(s_{i}(t)\) is the ith source signal, \(\hat{{s}}_j (t)\) is the \(j\mathrm{th}\) recovered signal, and T is the number of sampling points in time domain. If the algorithm is effective \(\rho _{ii}\) will approximate to 1 or \(-\)1, and \(\rho _{ij}(i\ne j)\) approximates to 0.

In order to compare the DEMIX method with the proposed method, we also use the source to interference ratio (SIR), the source to distortion ratio (SDR) and the source to artifacts ratio (SAR) [42].

$$\begin{aligned} \hbox {SIR}= & {} 10\log _{10} \frac{||s_{\mathrm{target}} ||^{2}}{||e_{\mathrm{interf}} ||^{2}} \end{aligned}$$
(26)
$$\begin{aligned} \hbox {SDR}= & {} 10\log _{10} \frac{||s_{\mathrm{target}} ||^{2}}{||e_{\mathrm{interf}} +e_{\mathrm{artif}} ||^{2}} \end{aligned}$$
(27)
$$\begin{aligned} \hbox {SAR}= & {} 10\log _{10} \frac{||s_{\mathrm{target}} +e_{\mathrm{interf}} ||^{2}}{||e_{\mathrm{artif}} ||^{2}} \end{aligned}$$
(28)

Here the recovered time domain signal is decomposed into the sum of three terms, with reference to the original unmixed source signal

$$\begin{aligned} s_{\mathrm{recov}} =s_{\mathrm{target}} +e_{\mathrm{interf}} +e_{\mathrm{artif}} \end{aligned}$$
(29)

where \(s_\mathrm{recov}\) is the recovered source signal, \(s_\mathrm{target}\) is the portion of the recovered signal that relates to the original or target source, \(e_\mathrm{interf}\) is the portion that relates to interference from other sources, and \(e_\mathrm{artif}\) is the portion that relates to artifacts generated by the separation technique and/or the re-synthesis method. The SIR provides a measure of the presence of other sources in the separated source; the SDR provides a measure of the overall quality of the sound source separation; the SAR provides a measure of the artifacts present in the signal due to separation and/or re-synthesis.

In [42], the authors discussed the performance measures SIR, SDR and SAR in detail. The assumptions are as follows: (1) the true source signals and noise signals (if any) are known; (2) the user chooses a family of allowed distortions \(\mathcal{F}\) according to the application (but independently of the kind of mixture or the algorithm used). The mixing system and the de-mixing techniques do not need to be known. Depending on the exact applications, different distortions can be allowed between an estimated (recovered) source and the wanted true source. In [42], the authors considered four different sets of such allowed distortions, from time-invariant gains to time-varying filters. In each case, the estimated source was decomposed into a true source part plus error terms corresponding to interferences, additive noise, and algorithmic artifacts.

Separate performance measures are computed for each estimated source \(\hat{{s}}_j \) by comparing it to a given true source \(s_{j}\). Note that the measures do not take into account the permutation indeterminacy of BSS. If necessary, \(\hat{{s}}_j \) may be compared with all the sources \((s_{j^{\prime }})_{1\le j^{\prime }\le N}\) and the “true source” may be selected as the one that gives the best results. In [42] the estimated source was decomposed as \(\hat{{s}}_j =s_{\mathrm{target}} +e_{\mathrm{interf}} +e_{\mathrm{noise}} +e_{\mathrm{artif}} \), where \(s_\mathrm{target}=f(s_{j})\) was a version of \(s_{j}\) modified by an allowed distortion \(f\in {\mathcal {F}}\), and where \(e_\mathrm{interf}\), \(e_\mathrm{noise}\) and \(e_\mathrm{artif}\) were, respectively, the interferences, noise, and artifacts error terms. These four terms should represent the part of \(\hat{{s}}_j \) perceived as coming from wanted source \(s_{j}\), from other unwanted source \((s_{j^{\prime }})_{ j^{\prime }\ne j}\), from sensor noise \((n_{i})_{1\le i\le M}\), and from other causes (like forbidden distortions of the sources and/or “burbling” artifacts). The decomposition was based on orthogonal projections. Let \(\prod \{y_{1}, {\ldots }, y_{k}\}\) denote the orthogonal projector onto the subspace spanned by the vector \(y_{1}\), ..., \(y_{k}\), and the projector was a \(T \times T\) matrix, where T was the length of these vectors. The three orthogonal projectors [42] were as follows:

$$\begin{aligned} P_{s_j }= & {} \prod \{s_j \} \end{aligned}$$
(30)
$$\begin{aligned} P_\mathbf{s}= & {} \prod \left\{ (s_{j^{\prime }} )_{1\le j^{\prime }\le N} \right\} \end{aligned}$$
(31)
$$\begin{aligned} P_{\mathbf{s},\mathbf{n}}= & {} \prod \left\{ (s_{j^{\prime }} )_{1\le j^{\prime }\le N} ,(n_i )_{1\le i\le M} \right\} \end{aligned}$$
(32)

where \(s_{j}\) was the wanted source, \(s_{j^{\prime }}\) was a unwanted source, and \(n_{i}\) was a component of the noise vector n. The estimated source \(\hat{{s}}_j \) was decomposed as the sum of the four terms [42]:

$$\begin{aligned} s_{\mathrm{target}}= & {} P_{s_j } \hat{{s}}_j \end{aligned}$$
(33)
$$\begin{aligned} e_{\mathrm{interf}}= & {} P_\mathbf{s} \hat{{s}}_j -P_{s_j } \hat{{s}}_j \end{aligned}$$
(34)
$$\begin{aligned} e_{\mathrm{noise}}= & {} P_{\mathbf{s},\mathbf{n}} \hat{{s}}_j -P_\mathbf{s} \hat{{s}}_j \end{aligned}$$
(35)
$$\begin{aligned} e_{\mathrm{artif}}= & {} \hat{{s}}_j -P_{\mathbf{s},\mathbf{n}} \hat{{s}}_j \end{aligned}$$
(36)

The computation of \(s_\mathrm{target}\) was as follows [42]:

$$\begin{aligned} s_{\mathrm{target}} =\frac{\langle \hat{{s}}_j ,s_j \rangle s_j }{||s_j ||^{2}} \end{aligned}$$
(37)

where \(\langle a\), \(b \rangle \) was the inner product between two signals a and b, and \({\vert }{\vert }a{\vert }{\vert }^{2}=\langle a\), \(a \rangle \) was the energy of a.

The computation of \(e_\mathrm{interf}\) was a bit more complex [42]. If the sources were mutually orthogonal, then

$$\begin{aligned} e_{\mathrm{interf}} =\frac{\sum _{j^{\prime }\ne j} {\langle \hat{{s}}_j ,s_{j^{\prime }} \rangle } s_{j^{\prime }} }{||s_{j^{\prime }} ||^{2}} \end{aligned}$$
(38)

Otherwise, if we use a vector c of the coefficients such that [42]

$$\begin{aligned} P_\mathbf{s} \hat{{s}}_j =\sum \limits _{j^{\prime }=1}^N {\bar{{c}}_{j^{\prime }} s_{j^{\prime }} } =\mathbf{c}^{H}\mathbf{s} \end{aligned}$$
(39)

where \(\bar{{c}}_{j^{\prime }} \) was the complex conjugate of \(c_{j^{\prime }}\), and \((\cdot )^{H}\) denoted Hermitian transposition. Then

$$\begin{aligned} \mathbf{c}=\mathbf{R}_{\mathbf{ss}}^{-1} [\langle \hat{{s}}_j ,s_1 \rangle ,\ldots ,\langle \hat{{s}}_j ,s_N \rangle ]^{H} \end{aligned}$$
(40)

where \(\mathbf{R}_\mathbf{ss}\) was the Gram matrix of the source defined by \((\mathbf{R}_\mathbf{ss})_{jj^{\prime }}=\langle s _{j}\), \(s _{j^{\prime }} \rangle \).

The computation of \(\hbox {P}_\mathbf{s,n}\) proceeds in a similar fashion; however, most of the time we can make the assumption that the noise signals are mutually orthogonal and orthogonal to each source, so that [42]

$$\begin{aligned} P_{\mathbf{s},\mathbf{n}} \hat{{s}}_j \approx P_\mathbf{s} \hat{{s}}_j +\frac{\sum _{i=1}^M {\langle \hat{{s}}_j ,n_i \rangle } n_i }{||n_i ||^{2}} \end{aligned}$$
(41)

In this paper, we only discuss the BSS model in the noise-free case; the second term of the right-hand side of (41) will not be considered. Similarly, the error term \((e_\mathrm{noise})\) is not considered. That is, the estimated source \(s_\mathrm{recov}\) is decomposed into the sum of three terms as in (29).

When the powers of \(s_\mathrm{target}\), \(e_\mathrm{interf}\), and \(e_\mathrm{artif}\) vary across time, the perceived separation quality also varies. We take this into account by defining local numerical performance measures in the following way [42].

First, we compute \(s_\mathrm{target}\), \(e_\mathrm{interf}\), and \(e_\mathrm{artif}\) as in (30)–(34), (36). Then, denoting w a finite-length centered window, we compute the windowed signals \(s_{\mathrm{target}}^r \), \(e_{\mathrm{interf}}^r \), and \(e_{\mathrm{artif}}^r \)centered in r, where \(s_{\mathrm{target}}^r (t)=w(t-r)s_{\mathrm{target}} (t)\), and so on. Finally, for each r, we compute the local measures \(\hbox {SIR}^{r}\), \(\hbox {SDR}^{r}\), and \(\hbox {SAR}^{r}\) as in (26)–(28) but replacing the original terms by the windowed terms centered in r.

\(\hbox {SIR}^{r}\), \(\hbox {SDR}^{r}\), and \(\hbox {SAR}^{r}\) thus measure the separation performance on the time frame centered in r. All these values can be visualized more globally by plotting them against or by summarizing them into cumulative histograms. Global performance measures can also be defined in the spirit of segmental SNR [8]. The shape of the window has not much importance generally, only its duration is relevant.

5.2 The Procedures of Simulations

The observed signals \(\mathbf{x}(t)\) in time domain are processed in frame format of length L samples and they are multiplied by a Hanning window. A hop distance d is used between the starting points of successive frames, leading to an overlap of \(L-d\) samples between consecutive frames. Each frame is transformed with STFT (a standard Fast Fourier transform (FFT) of length L), and the real and imaginary parts of the positive half spectrum are taken, for a total of L coefficients. For each signal, the coefficients of successive frames are concatenated in a single vector \(\mathbf{X}(k)\), which is the actual input to the separation procedure. Using Eq. (7), the signals \(\mathbf{X}(k)\) in frequency domain are normalized to \(\mathbf{X}^{\# }(k)\).

The window function selection needs explaining in the case of the Hanning window to deal with the STFT. In the frequency domain, spectral amplitude estimation forms the basis of most signal restoration systems and the simplest form of spectral amplitude estimation is spectral subtraction [33]. The audio signals \(\mathbf{x}(t)\) in the time domain are generally divided into frames (or blocks) of L sample length. Each frame is windowed, using a window and then transformed via discrete Fourier transform (DFT) to L spectral samples. The main function of the window and the overlap operations is to alleviate discontinuities at the endpoints of each output block. Although there are a number of useful windows (for example, rectangular window, Hamming window, Barlett window, Blackman window) with different frequency/time characteristics, in most implementations of the spectral subtraction, a Hanning window is used [33]. In removing distortions introduced by spectral subtraction, the postprocessor algorithm makes use of such information as the correlation of each frequency channel from one block to the next, and the durations of the signal events and the distortions.

FFT-based measurements are subject to errors from an effect known as leakage. This effect occurs when the FFT is computed from of a block of data which is not periodic. To correct this problem, appropriate window functions must be applied. In a signal analyzer, the time record length is adjustable but it must be selected from a set of predefined values. Since most signals are not periodic in the predefined data block time periods, a window must be applied to correct for leakage. A window is shaped so that it is exactly zero at the beginning and end of the data block and has some special shape in between. This function is then multiplied with the time data block forcing the signal to be periodic. A special weighting factor must also be applied so that the correct FFT signal amplitude level is recovered after the windowing. A window function minimizes the effect of leakage to better represent the frequency spectrum of the data. Window functions are most easily understood in the time domain; however, they are often implemented in the frequency domain instead. Mathematically there is no difference when the windowing is implemented in the frequency or time domains, though the mathematical procedure is somewhat different. When the window is implemented in the frequency domain, the FFT of the window function is computed one time and saved in memory and then it is applied to every FFT frequency value correcting the leakage in the FFT. This gives rise to one measure of the window’s characteristics, known as the side lobe. The FFT of a window has a peak at the applied frequency and other peaks, called side lobes, on either side of the applied frequency. The height of the side lobes indicates what affect the windowing function will have on frequencies around the applied frequency. In general, lower side lobes reduce the leakage in the measured FFT but increase the bandwidth of the major lobe. FFT windows reduce the effects of leakage but cannot eliminate leakage entirely. In effect, they only change the shape of the leakage. In addition, each type of window affects the spectrum in a slightly different way. Many different windows have been proposed over time, each with its own advantage and disadvantage relative to the others. Some are more effective for specific types of signal types such as random or sinusoidal. Some improve the frequency resolution, that is, they make it easier to detect the exact frequency of a peak in the spectrum. Some improve the amplitude accuracy, that is, they most accurately indicate the level of the peak. The best type of window should be chosen for each specific application. The most common windows and their features [20] are given in Table 1.

Table 1 Window functions and their features
Full size table

According to Table 1, Hanning, Hamming, Tukey and Welch produce good frequency resolution. Hanning is the most commonly used window function for random signals because it provides good frequency resolution and leakage protection with fair amplitude accuracy [20]. The advantage of the Hanning window is very low aliasing, and the tradeoff is slightly decreased resolution (widening of the main lobe). If the Hanning window is used to sample a signal in order to convert to frequency domain, it is complex to reconvert to the time domain without adding distortions [15].

On the other hand, one of the disadvantages of window functions is that the beginning and end of the signal is attenuated in the calculation of the spectrum. This means that more averages must be taken to get a good statistical representation of the spectrum, increasing the time to complete the measurement. Overlap processing is a feature that is available in most signal processing that can recover the lost data and reduce the measurement time. This processing reduces the total measurement time by recovering a portion of each previous frame that otherwise is lost due to the effect of the windowing function. Overlap processing is particularly effective at reducing the measurement time for low frequency tests (generally under 50 Hz) for which the frame acquisition times are very long.

For the normalized data \(\mathbf{X}^{\# }(k)\), the K-means is carried out to estimate the cluster centers by setting the number of clusters in advance; for the DEMIX method, the directions of the mixing matrix is counted and estimated based on a clustering algorithm; for the proposed method, the number of clusters and the initial cluster centers are evaluated by AP clustering, and the results are regarded as the initial values of the K-means to estimate the ideal cluster centers which are the column vectors of the underdetermined mixing matrix.

In the following experiments, we use the traditional K-means algorithm, and the main parameters are the following: the initial cluster centroid positions are chosen randomly from the observed signals, the number of times to repeat the clustering is 1, and the maximum number of iterations is 100. The stopping criterion of K-means is that the assignments no longer change.

After obtaining the mixing matrix, the source signals are separated by the linear programming as in (23). The solutions give the estimation of M sparse source signals in the frequency domain. For each estimated source, the coefficient vector is split back into frames. The real and imaginary components are regrouped into complex coefficients, and the spectra are extended to negative frequencies. For each spectrum, the standard IFFT is used to obtain time domain frames of length L. Each frame is multiplied by the inverse window, and the overlap between frames is removed, 50 % on either side, by keeping only the central part of the frame (thus avoiding the distortion at the edges that often appears after frequency domain manipulation). The re-synthetized signals are finally built by simple concatenation of the resulting pieces.

5.3 Simulations

To evaluate the performances of the above algorithms, some simulations are given here, in different cases.

  1. 1.

    UBSS of three source signals from two mixed signals.

The three source signals are \(s_{1}(t), s_{2}(t),\) and \(s_{6}(t)\) respectively. The number of samples of each signal is 7500. Two different mixing matrices are used; one is the white noise channel and the other is the Gaussian channel. For each type of the mixing matrices and each algorithm, we carry out ten trials, respectively. For the white noise channel, the mixing matrix is randomly generated by MATLAB command \(\mathbf{A}=2* \hbox {rand}(2, 3)-1\) and one of the mixing matrices is:

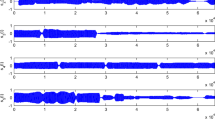
$$\begin{aligned} \mathbf{A}=\left[ {{\begin{array}{ccc} {-0.7808}&{} {0.4757}&{} {-0.3481} \\ {-0.2011}&{} {0.7464}&{} {0.8084} \\ \end{array} }} \right] \end{aligned}$$

The mixed signals are obtained by \(\mathbf{x}(t)=\mathbf{As}(t)=[x_{1}(t)\), \(x_{2}(t)]^{T}\). The waveforms of the source signals and the mixed signals are shown in Fig. 1.

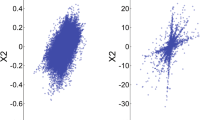
We take STFT of the two mixed signals \(x_{1}(t)\) and \(x_{2}(t)\) in frame. For each frame with \(L=2048\), we multiply a Hanning window. Since the number of samples of each signal is 7500 and the number of frames must be an integer, we take the hop distance \(d= \hbox {round}(0.15*L*4)=1229\), where \(\hbox {round}(x)\) rounds x to nearest integer. Thus, every signal is decomposed into six frames and the very end of the signal is removed. The overlap between the successive frames is \(L-d=819\). After the STFT operation, the transformed signals \(X_{1}(k)\) and \(X_{2}(k)\) are the coefficients in frequency domain and k is the discrete frequency index. A simple and useful representation of mixture space is a scatter plot of the data, which shows \(X_{2}(k)\) against \(X_{1}(k)\) for every data point k. The scatter plot is shown in Fig. 2a.

Fig. 1
figure 1

Three source signals and two mixed signals

Full size image
Fig. 2
figure 2

The scatter plot \(X_{1}\) versus \(X_{2}\) of the three sparse source signals

Full size image

From Fig. 2a, we can see that the three sources gave three straight lines, this reflects the linear clustering characteristic of sparse signals. In the scatter plot, the column vectors of the mixing matrix are mapped into the directions of the lines and the matrix A can be estimated via line clustering. In this paper, to depict each line by a unique vector, the signals are normalized in scale and mapped the directional vectors to the positive side of the plane. Figure 2b shows the data points to the half unit circle and the sources are embodied in the data stack.

For convenience, the proposed method is expressed as “AP-K-Means,” the conventional K-means algorithm is expressed as “K-means” and the direction estimation of mixing matrix method is expressed as “DEMIX.” For the normalized data, we use AP clustering to seek the number of clusters and the initial cluster centers. To speed the convergence of AP, we set the damping factor \(\lambda =0.9\). For the given mixing matrix A, we use AP-K-Means and DEMIX to estimate the mixing matrix. The results are as follows:

$$\begin{aligned} { \hat{\mathbf{A}}}_{\mathrm{AP-K}} =\left[ {{\begin{array}{ccc} {-0.9685}&{} {0.5211}&{} {-0.4009} \\ {-0.2488}&{} {0.8514}&{} {0.9153} \\ \end{array} }} \right] \quad {\hat{\mathbf{A}}}_{\mathrm{DEMIX}} =\left[ {{\begin{array}{ccc} {-0.9685}&{} {0.5375}&{} {-0.3961} \\ {-0.2492}&{} {0.8433}&{} {0.9182} \\ \end{array} }} \right] \end{aligned}$$

For K-means, we set the number of clusters K = 3 in advance and the estimated mixing matrix is

$$\begin{aligned} { \hat{\mathbf{A}}}_\mathrm{K} =\left[ {{\begin{array}{ccc} {-0.5539}&{} {0.6329}&{} {-0.3942} \\ {0.8326}&{} {0.7008}&{} {0.9189} \\ \end{array} }} \right] \end{aligned}$$

Based on the estimated mixing matrix, we separate the sources by linear programming and do IFFT to obtain the signals in the time domain.

To compare the similarity between the original source and the estimated source, we compute the correlative coefficient of each signal of the three methods. The results are shown in Table 2.

Table 2 Correlative coefficients of the three methods
Full size table

From Table 2 we can see that the similarity index of AP-K-Means is superior to that of DEMIX though the correlative coefficients of these two methods are very similar. For K-means, the correlative coefficient of signal2 is only slightly better than that of AP-K-Means and DEMIX, but the performance indices of the other signals are poor. On the whole, the UBSS performances of AP-K-Means and DEMIX are better than that of K-means. This trial illustrates that AP-K-Means can commendably recover the sources.

For AP-K-Means, the waveforms of the separated sources and the original sources are shown in Fig. 3. From Fig. 3, we can know that the estimated sources precisely recover the original sources.

To have a better performance comparison of the three methods, we consider the data of all the ten trials. The angular deviations and the correlative coefficients of the ten trials are shown in Figs. 4 and 5.

Fig. 3
figure 3

Three original sources and the recovered sources of AP-K-Means

Full size image
Fig. 4
figure 4

The angular deviations of the three methods

Full size image
Fig. 5
figure 5

The correlative coefficients of the three methods

Full size image
Fig. 6
figure 6

The relationship among the SDR, SIR and SAR for \(s_{1}(t)\) of AP-K-Means

Full size image
Fig. 7
figure 7

The SDR comparison of the three methods

Full size image

From Figs. 4 and 5, we can clearly see that the angular deviation curve and the correlative coefficient curve of DEMIX almost coincide with that of AP-K-Means. However, the curves of K-means have larger fluctuation; this illustrates the limitation of K-means since it can only converge to a local optimum.

To compare the indices of SDR, SIR and SAR, we first verify the relationship among the SDR, SIR and SAR using AP-K-Means. In all the ten trials, when time-invariant (TI) filters distortion and TI gains distortion are allowed [42], the SDR, SIR and SAR for single signal \(s_{1}(t)\) are shown in Fig. 6.

From Fig. 6 we can know that the SIR has the maximum values and the SDR has the minimum values, but the SDR can provide a measure of the overall quality of BSS [42]. Thus, for the signal \(s_{1}(t)\), we compute the SDR of the three methods and the results are shown in Fig. 7.

From Fig. 7, we clearly see that the separation performance of AP-K-Means is almost the same as that of DEMIX, and these two methods are greatly superior to the K-means.

For the three estimated source signals, we also compute the average SDR, SIR and SAR values of all the ten trials; the results of the three methods are shown in Table 3.

From Table 3, we can see that the average SDR, SIR and SAR indices of DEMIX are best for signal1, the indices of K-means are best for signal2, and the indices of AP-K-Means are best for signal3. In spite of this, from Table 3 we can still see that the average indices for signal1 and signal3 of K-means are very poor, especially since the SDR value of signal1 is only 7, and this shows the estimated signal has serious distortion. On average, the performance indices of DEMIX and AP-K-Means are nearly the same and they are better than that of K-means. In addition, from Table 3 we can also know that the quantitative indices for IT-filters allowed distortion are bigger than that of IT-gains allowed distortion. This shows that the factor of IT-gains allowed distortion has more influence on the performance of UBSS.

Table 3 The average SDR, SIR and SAR of the three methods
Full size table

For Gaussian channel, the mixing matrix is randomly generated by MATLAB command \(\mathbf{A}=\hbox {randn}(2, 3)\), and we have also made ten trials. In the experiment, we found that the source signals could not be correctly separated in several trials using the estimated matrix of K-means method, and AP-K-Means and DEMIX were able to separate the source signals successfully. Thus, we picked a matrix in which K-means can be used:

$$\begin{aligned} \mathbf{A}=\left[ {{\begin{array}{ccc} {1.5357}&{} {-1.9171}&{} {1.2744} \\ {0.4344}&{} {0.4699}&{} {0.6385} \\ \end{array} }} \right] \end{aligned}$$

Since AP-K-Means and DEMIX have almost the same performance, here we only compared AP-K-Means and K-means method. The estimated matrices of these two methods are:

$$\begin{aligned} {\hat{\mathbf{A}}}_{\mathrm{AP-K}} =\left[ {{\begin{array}{ccc} {0.9623}&{} {-0.9704}&{} {0.8925} \\ {0.2720}&{} {0.2411}&{} {0.4509} \\ \end{array} }} \right] \quad {\hat{\mathbf{A}}}_\mathrm{K} =\left[ {{\begin{array}{ccc} {-0.9591}&{} {-0.9711}&{} {-0.9194} \\ {0.2830}&{} {0.2388}&{} {0.3821} \\ \end{array} }} \right] \end{aligned}$$

For AP-K-Means, the angular deviations for each column vector of the estimated mixing matrix are 0.0112, 0.1806, 0.1916 and that of K-means are 147.7658, 0.0431, 4.0442. Obviously, the first column of the mixing matrix was not truly estimated using K-means. For the sake of observing the separation results more intuitively, we gave the waveforms of the recovered source signals of these two methods. The results are shown in Fig. 8.

Fig. 8
figure 8

The waveforms of the recovered source signals of the two methods. a AP-K-Means method, b K-means method

Full size image

Compared with the source signals in Fig. 1, we know that AP-K-Means can accurately recover the source signals. Unfortunately, K-means cannot recover the first source signal, and the recovery effects of the other two signals are also very poor. This fully shows that the local optimum of K-means is fatal in some cases.

  1. 2.

    UBSS of four source signals from two mixing signals

The four source signals are \(s_{1}(t)\),\( s_{2}(t)\),\( s_{5}(t)\) and \(s_{6}(t)\). The white noise and Gaussian mixing matrices are randomly generated by MATLAB commands \(\mathbf{A}=2 * \hbox {rand}(2, 4)-1\) and \(\mathbf{A}= \hbox {randn} (2, 4)\). For each method, we carried out five trials for the white noise mixing matrix and five trials for Gaussian mixing matrix, respectively.

When TI-filters distortion and TI-gains distortion are allowed, for the four estimated source signals, the average SDR, SIR and SAR of the ten trials are shown in Table 4.

Table 4 The average SDR, SIR and SAR of the ten trials
Full size table

From Table 4, we can see that the average SIR, SDR and SAR for the first three signals of AP-K-Means are superior to that of DEMIX, while the performance indices for the signal4 of DEMIX are better than that of AP-K-Means. On the contrary, the performance indices of K-means are the worst; in particular, the SDR values for the signal4 are only 3.9907 and 5.2553, which are unacceptable for the UBSS.

We also computed the average correlative coefficients of all the ten trials to compare the similarity indices between the original sources and the recovered sources. The results are shown in Table 5.

Table 5 The average correlative coefficients of the ten trials
Full size table

From Table 5, we also know that AP-K-Means can more precisely recover the source signals compared with the other two methods, and the average indices of DEMIX are also very close to that of AP-K-Means.

In order to illustrate the performance indices more specifically, we only carried out one trial to compare these three methods. The white noise mixing matrix is:

$$\begin{aligned} \mathbf{A}=\left[ {{\begin{array}{cccc} {-\hbox {0.7276}}&{} {-\hbox {0.9949}}&{} {-\hbox {0.7414}}&{} {-\hbox {0.5072}} \\ {-\hbox {0.6884}}&{} {\hbox {0.1365}}&{} {\hbox {0.6652}}&{} {\hbox {0.8593}} \\ \end{array} }} \right] \end{aligned}$$

The mixed signals are obtained by \(\mathbf{x}(t)=\mathbf{As}(t)=[x_{1}(t)\), \(x_{2}(t)]^{T}\). As in the previous simulation, we also transformed the mixed signals to the frequency domain and normalized the signals into positive data. Then, using the three methods to estimate the mixing matrix, the results are, respectively:

$$\begin{aligned} \mathbf{A}_{\hbox {AP-K}}= & {} \left[ {{\begin{array}{cccc} {-\hbox {0.7225}}&{} {-\hbox {0.9907}}&{} {-\hbox {0.7447}}&{} {-\hbox {0.4998}} \\ {-\hbox {0.6884}}&{} {\hbox {0.1360}}&{} {\hbox {0.6672}}&{} {\hbox {0.8637}} \\ \end{array} }} \right] \\ \mathbf{A}_{\hbox {DEMIX}}= & {} \left[ {{\begin{array}{cccc} {-\hbox {0.7265}}&{} {-\hbox {0.9907}}&{} {-\hbox {0.7433}}&{} {-\hbox {0.5087}} \\ {-\hbox {0.6872}}&{} {\hbox {0.1359}}&{} {\hbox {0.6690}}&{} {\hbox {0.8609}} \\ \end{array} }} \right] \\ \mathbf{A}_\mathrm{K}= & {} \left[ {{\begin{array}{cccc} {-\hbox {0.7225}}&{} {-\hbox {0.3271}}&{} {-\hbox {0.7959}}&{} {-\hbox {0.5156}} \\ {-\hbox {0.6884}}&{} {\hbox {0.9439}}&{} {\hbox {0.5565}}&{} {\hbox {0.8565}} \\ \end{array} }} \right] \end{aligned}$$

In this trial, the correlative coefficients of these three methods are shown in Table 6.

Table 6 Correlative coefficients of the specific trial
Full size table

From Table 6, we see that the similarity index of AP-K-Means is better than that of the other two methods. In addition, the similarity index of DEMIX is still similar to that of AP-K-Means, so we only compare the SDR, SIR and SAR values of these two methods. The results of this trial are shown in Table 7.

Table 7 The SDR, SIR and SAR of AP-K-Means and DEMIX
Full size table

From Table 7 we see that the performance indices for signal1 and signal2 of DEMIX are better than that of AP-K-Means; however, the performance indices for signal3 and signal4 of AP-K-Means are better than that of DEMIX. These results again show that the UBSS performance of AP-K-Means is very close to that of DEMIX.

  1. 3.

    UBSS of five source signals from two mixing signals.

The five source signals are \(s_{1}(t)\),\( s_{2}(t)\),\( s_{3}(t)\),\( s_{4}(t)\) and \(s_{5}(t)\), respectively. The white noise and Gaussian mixing matrices are randomly generated by MATLAB commands \(\mathbf{A}=2* \hbox {rand} (2, 5)-1\) and \(\mathbf{A}= \hbox {randn} (2, 5)\). For the three methods, we, respectively, carry out five trials for each type of the mixing matrix.

For each signal, the average SDR, SIR and SAR of all the ten trials are shown in Figs. 9 and 10.

With the increase in the number of sources for the fixed number of mixed signals (two sensors), from Figs. 9 and 10 we can know that the performance indices SDR, SIR and SAR became worse since the difficulty of blind separation increased. In spite of this, the indices of DEMIX and AP-K-Means are still very similar and very good. Conversely, the performance indices of K-means are relatively poor. In particular, when IT-filters distortion is allowed the SDR for signal4 of K-means is 1.7053, and when IT-gains distortion is allowed the SDR for signal4 of K-means is only 1.1841. These results show that the performance index of K-means has dropped dramatically with the increase in the number of source signals.

Fig. 9
figure 9

The average SDR, SIR and SAR of IT-filters allowed distortion

Full size image
Fig. 10
figure 10

The average SDR, SIR and SAR of IT-gains allowed distortion

Full size image

In order to compare more intuitively, we only carried out one trial. In this trial, the white noise mixing matrix is

$$\begin{aligned} \mathbf{A}=\left[ {{\begin{array}{ccccc} {0.2400}&{} {0.5802}&{} {-0.7245}&{} {-0.8791}&{} {0.3181} \\ {-0.9664}&{} {-0.8170}&{} {0.6818}&{} {-0.4808}&{} {0.9426} \\ \end{array} }} \right] \end{aligned}$$

Given the mixing matrix A, the estimated mixing matrices of the three methods are respectively:

$$\begin{aligned} \mathbf{A}_{\hbox {AP-K}}= & {} \left[ {{\begin{array}{ccccc} {\hbox {0.2437}}&{} {\hbox {0.5705}}&{} {-\hbox {0.7289}}&{} {-\hbox {0.8827}}&{} {\hbox {0.3221}} \\ {-0.9682}&{} {-0.8191}&{} {0.6816}&{} {-0.4678}&{} {0.9418} \\ \end{array} }} \right] \\ \mathbf{A}_{\hbox {DEMIX}}= & {} \left[ {{\begin{array}{ccccc} {\hbox {0.2406}}&{} {\hbox {0.5799}}&{} {-\hbox {0.7280}}&{} {-\hbox {0.8755}}&{} {\hbox {0.3194}} \\ {-0.9706}&{} {-0.8147}&{} {0.6856}&{} {-0.4831}&{} {0.9476} \\ \end{array} }} \right] \\ \mathbf{A}_\mathrm{K}= & {} \left[ {{\begin{array}{ccccc} {\hbox {0.2546}}&{} {\hbox {0.6581}}&{} {\hbox {0.9023}}&{} {-\hbox {0.8687}}&{} {\hbox {0.3221}} \\ {-0.9643}&{} {-0.7444}&{} {0.4307}&{} {-0.4944}&{} {0.9418} \\ \end{array} }} \right] \end{aligned}$$

We computed and compared the correlative coefficients of the three methods. The results are in Table 8.

Table 8 Correlative coefficients comparison
Full size table

From Table 8, the similarity index of K-means for the signal2 is better than that of AP-K-Means and DEMIX. However, for the other signals the similarity indices of K-means are worse than that of the other two methods. Particularly, the similarity index of K-means for the signal4 is only 0.5593 which resulted in severe distortion of the recovered signal. Moreover, all the similarity indices of AP-K-Means are superior to that of DEMIX, and this proves once again that AP-K-Means can obtain high degree of similarity between the original sources and the recovered sources.

6 Conclusion

We have proposed a new approach to estimate the number of sources and the mixing matrix of underdetermined audio BSS. The simulations on stereophonic recordings have illustrated the performance of the proposed method: (a) to accurately estimate the number of sources in the instantaneous case for the fixed two sensors; (b) to robustly estimate the underdetermined mixing matrix and recover the source signals that classical clustering algorithms like K-means failed to estimate. The UBSS performance of the proposed method is slightly better than that of the DEMIX method while the performance indices of these two methods are very similar.

The proposed method exploits a certain level of sparsity of the time–frequency representations to estimate the underdetermined mixing matrix. Our main contribution is the use of AP clustering to accurately estimate the number of sources, together with the K-means to estimate the mixing matrix. The proposed method seems essentially limited by the fact that it relies on the assumption that each target source is sufficiently sparse in time–frequency regions. This condition is likely to fail when the sources representations are not sparse enough. This would require adequate modifications of the clustering algorithm which may become significantly more complex. Another interesting perspective is to extend the present method to the convolutive case; this points out the orientation of future study.