Reduced Order Observer for Linear Time-Invariant Multivariable Systems with Unknown Inputs

Abstract

This paper presents the design of a new reduced order observer to estimate the state for a class of linear time-invariant multivariable systems with unknown inputs. The proposed design approach is a combination of the approaches proposed by Hou and Muller (IEEE Trans. Autom. Control 37:871–875, 1992) and Boubaker (Int. J. Autom. Control Syst. Eng. 5:45–51, 2005); matrix decompositions, state transformations, and substitutions based on coordinate changes are used. It is shown that the problem of reduced order observers for linear systems with unknown inputs can be reduced to a standard one (the unknown input vector will not interfere in the observer equations). The effectiveness of the suggested design algorithm is illustrated by a numerical example (aircraft lateral motion), and, for the same aircraft dynamics, we compare our new observer with other already existing observers from the existence conditions and dynamic characteristics point of view; the superiority of the new designed observer is demonstrated.

1 Introduction

1.1 Antecedents and Motivations

A state observer is a dynamical system allowing the state reconstruction from the system model and the measurements of its inputs and outputs. The plant input and output signals are used to estimate the plant state, which is then employed to close the control loop [13]. The aim of the observers is to augment or replace sensors in a control system. Starting from the first observers, introduced by Luenberger, observers for plants with both known and unknown inputs have been developed, resulting in the unknown input observer (UIO) architectures, such as, for example, those in [6, 7, 12, 17, 23].

A physical process is often subjected to disturbances which have as origin the noises due to its environment, uncertainty of measurements, and sensor or actuator faults. These disturbances affect the normal behavior of the process, and an estimation of these disturbances is needed in order to conceive a control strategy to minimize their effects. Disturbances are called unknown inputs if they affect the process input, and their presence makes the state estimation difficult [1].

The state estimation problem for linear time-invariant (LTI) multivariable systems, subjected to unknown inputs, has received considerable attention in the last decades [3, 7, 15, 24, 26]. The dimension of the observer is considerably increased in [1], and that is why the approach of Wang et al. [26] is more interesting: they proposed a method to design reduced order observers without any knowledge of these inputs. Existence conditions for this observer have been provided by Kudva et al. [15]. Silverman’s inverse method [24], the use of generalized inverse matrices, and singular value decomposition are useful in the linear observer design process [7].

Generally, observers can be designed for singular systems, unknown input systems, delay systems, and also uncertain systems with time-delay perturbations [1, 8, 26]. There are two categories of papers describing observer design methods: the first one supposes a priori knowledge of information on these unmeasurable inputs, while the second category proceeds either by estimation of the unknown inputs, or by their complete elimination from the equations of the system [1].

The design of the observers depends on the type and the complexity of the considered model. Two types of models are distinguished according to the linear or nonlinear character of the system [14]. Linear models have simple structures, and they are the base of several applications and research works. In these cases, observers can be designed for uncertain systems with time-delay perturbations [26] and unknown input systems [7]. However, in the majority of real cases the nonlinear nature of the process cannot be neglected. The assumption of linearity is checked only locally around an operating point. Real physical processes present complex behaviors with nonlinear laws. Because it is not easy to design an observer for a nonlinear system, the multiple model approaches constitute tools which are largely used in the modeling of nonlinear systems [14].

Easily verifiable system theoretic conditions, which are necessary and sufficient for the existence of UIOs, have been established (see [10] or [11]). One possible statement of these conditions is that the transfer function matrix between the unmeasurable input and the measured outputs must be of minimum phase and relative degree one [9]. New conditions for the existence of reduced order linear functional state observers for linear systems with unknown inputs were presented in [25]. Systematic procedures for the synthesis of reduced order functional observers have been given, the attractive feature of the proposed observer being the simplicity with which the design process can be accomplished [25].

One of the most important algorithms for the design of reduced order observers for LTI systems with unknown inputs was suggested by Hou and Muller [11]; their reduced order observer for linear systems with unknown inputs decomposes the state equation of the system into two subsystems: the first one depends on the unknown inputs, while, in the second one, the unknown inputs may be dropped. One of this approach’s assumptions is that the state of the second subsystem may be obtained through the measurement equation. The designed observer has good results, but there are many situations in which this hypothesis does not hold [11]. Maquin et al. made some modifications to the observer of Hou and Muller, and a straightforward treatment allowing the unknown input estimation is proposed in [19]. Another important algorithm for the design of reduced order observers for LTI systems with unknown inputs was suggested by Boubaker [4]: any reduced order observer has the advantage of avoiding redundancy caused by reconstructing accessible states; transformations and substitutions based on a coordinate system are used, and existence conditions are provided.

The observer design problem is a very important problem that has various applications in, e.g., output feedback control, system monitoring, process identification, and fault detection [5]. The basic idea behind the use of observers for fault detection is to estimate the outputs of the system from the measurements by using some type of observer, and then construct the residual by a properly weighted output estimate error. By means of a fixed or adaptive threshold, the residual is examined for the likelihood of faults, and certain decision rules can then be applied to determine if a fault has occurred [22].

For the majority of the existing approaches, the number of unknown inputs must be less than the number of outputs; moreover, additional structural requirements on the system to be observed are met [28]. Those conditions turn out to be rather restrictive; for instance, they cannot cover the simplest class of mechanical systems with unknown inputs wherein only the position is measurable [2]. Another disadvantage of these observers is that only asymptotic convergence to zero of the observation and error is guaranteed [20]. However, for instance, for hybrid systems, the finite-time exact observation is quite important, because the time of observation convergence must be less than the dwell time. This happens, for example, in the case of walking robots [16].

We may conclude that there are numerous observers for linear systems with unknown inputs. There are three important design methods: geometrical methods (first introduced by Bhattacharyya [3]), algebraic methods (used in observer design by Kudva et al. [15], Hautus [10], Hou and Muller [11], Darouach et al. [7], Yang and Wild [27], O’Reilly [21], and others), and methods that use the generalized inverse [4]. Each of them has advantages and disadvantages; achieving less restrictive existence conditions and more direct design procedures has always been a challenge in this area [5].

1.2 Main Contribution

The classical reduced order observers are easier to implement from the software point of view; their disadvantages are related to the important number of constraints (existence conditions). This paper presents a new reduced order observer design for the estimation of the system state vector and unknown inputs. It will be shown that the problem of reduced order observers for linear systems with unknown inputs can be reduced to a standard one (the unknown input vector does not interfere in the observer equations). The existence conditions for the obtained observer are also given. The new observer will be obtained by combining two other reduced order observers: the first one has been suggested by Hou and Muller [11], while the second one is that of Boubaker [4]. Moreover, a comparison of our new observer, the Boubaker observer, and the Hou and Muller observer is achieved, and the superiority of the new designed observer is demonstrated from both a dynamic characteristics and a constraints point of view. The main advantage of our new observer is proved to be the lack of a priori restrictions on the class of systems that can be considered.

The paper is organized as follows. The design approach of the new reduced order observer (ALGLIN algorithm) is given in Sect. 2; in the same section, the observer is validated by means of a numerical simulation for the case of an aircraft lateral motion. A comparison of our new algorithm and the other two design approaches is given in Sect. 3. The conclusions are presented in Sect. 4.

2 Design of the New Reduced Order Observer

2.1 Problem Statement

In this section of the paper we design a new observer for the state estimation problem in the case of LTI systems with unknown inputs. The approach is original, and it represents the main contribution of the paper. The observer has been obtained by combining two other reduced order observers: the observer designed by Hou and Muller [11] and the Boubaker observer [4]. Two additional “while” loops have been added in the design procedure in order to obtain a reduced order observer without existence conditions. The new algorithm must make the design problem equivalent to the standard problem of the observers’ design when all inputs are known. In order to obtain a better observer, we will also focus on the design procedure, which must be direct and simple.

Let us consider an LTI system described by [4]

$$ \dot{x} = Ax + Bu + Dd,\qquad y = Cx, $$

(1)

where x∈R ^n×1 is the system state vector, u∈R ^p×1—system known input vector, d∈R ^s×1—system unknown input vector, and y∈R ^m×1—output vector; the known matrices A,B,C,D have appropriate dimensions (A∈R ^n×n, B∈R ^n×p, C∈R ^m×n, D∈R ^n×s).

The state vector is divided into two state vectors: the first one is associated with the unknown inputs, while the second one depends on the system known inputs. We make a coordinate change by choosing a matrix N∈R ^n×(n−s) such that $T = [ \begin{array}{c@{\ }c} N & D \end{array} ]$ is nonsingular, and we transform the old system state (x) into a new one $( \bar{x} )$ by using the transformation [19]

$$ x = T\bar{x} = T\left[ \begin{array}{c@{\quad}c} \bar{x}_{1}^{T} & \bar{x}_{2}^{T} \end{array} \right]^{T}, $$

(2)

with $\bar{x}_{1} \in R^{m \times 1}$, $\bar{x}_{2} \in R^{( n - m ) \times 1}$. Equation (1) is then equivalent to [4]

$$ \dot{\bar{x}} = \bar{A}\bar{x} + \bar{B}u + \bar{D}d,\qquad y = \bar{C}\bar{x}, $$

(3)

where the matrices $\bar{A}$, $\bar{B}$, $\bar{C}$, and $\bar{D}$ have the following forms:

$$ \begin{array}{l} \bar{A} = T^{ - 1}AT = \left[ \begin{array}{c@{\quad}c} \bar{A}_{11} & \bar{A}_{12} \\\bar{A}_{21} & \bar{A}_{22} \end{array} \right],\qquad\bar{B} = T^{ - 1}B = \left[ \begin{array}{c} \bar{B}_{1} \\\bar{B}_{2} \end{array} \right], \\\bar{D} = T^{ - 1}D = \left[ \begin{array}{c} 0_{\left( n - s \right) \times s} \\I_{s} \end{array} \right],\qquad\bar{C} = CT = \left[ \begin{array}{c@{\quad}c} CN & CD \end{array} \right] = \left[ \begin{array}{c@{\quad}c} \bar{C}_{1} & \bar{C}_{2} \end{array} \right]; \end{array} $$

(4)

the matrices in the above equation have appropriate dimensions$: \bar{A}_{11} \in R^{m \times m},\bar{A}_{12} \in R^{m \times ( n - m )}$, $\bar{A}_{21} \in R^{( n - m ) \times m}$, $\bar{A}_{22} \in R^{( n - m ) \times ( n - m )}$, $\bar{B}_{1} \in R^{m \times p}$, $\bar{B}_{2} \in R^{( n - m ) \times p}$, $\bar{C}_{1} \in R^{m \times m}$, $\bar{C}_{2} \in R^{m \times ( n - m )}$.

The partitioning of $\bar{x}$ points out the decomposition of the system (1) into an unknown-input-dependent subsystem and an unknown-input-free subsystem. Therefore, combining (2) and (4), we obtain [4]

$$ \left\{ \begin{array}{l} \dot{\bar{x}}_{1} = \bar{A}_{11}\bar{x}_{1} + \bar{A}_{12}\bar{x}_{2} + \bar{B}_{1}u, \\ \dot{\bar{x}}_{2} = \bar{A}_{21}\bar{x}_{1} + \bar{A}_{22}\bar{x}_{2} + \bar{B}_{2}u + I_{s}d, \\ y = \bar{C}_{1}\bar{x}_{1} + \bar{C}_{2}\bar{x}_{2}. \end{array} \right. $$

(5)

$\bar{x}_{2}$ depends on the unknown input d, while $\bar{x}_{1}$ does not; therefore, it is more judicious to estimate $\bar{x}_{1}$ rather than $\bar{x}_{2}$. As a consequence, we design a reduced order observer for the estimation of the state $\bar{x}_{1}$ by using the equations

$$ \left\{ \begin{array}{l} \dot{\bar{x}}_{1} = \bar{A}_{11}\bar{x}_{1} + \bar{A}_{12}\bar{x}_{2} + \bar{B}_{1}u, \\ y = \bar{C}_{1}\bar{x}_{1} + \bar{C}_{2}\bar{x}_{2}; \end{array} \right. $$

(6)

$\hat{\bar{x}}_{2}$ and $\hat{d}$ (the estimations of $\bar{x}_{2}$ and d, respectively) will be calculated with respect to $\hat{\bar{x}}_{1}$ (the estimation of $\bar{x}_{1}$).

2.2 Design of the Reduced Order Observer

The design of the new observer is concentrated into the following theorem.

Theorem 1

Consider the LTI multivariable system (1); using the assumptions n>m, n>s, and with (C, A) an observable pair of matrices, we design the convergent reduced order observer for LTI systems with unknown inputs described by the equations

$$ \begin{array}{l} \dot{\hat{\bar{x}}}_{1} = ( \tilde{A}_{1} - LC_{1} )\hat{\bar{x}}_{1} + \bigl( LH_{22}^{T} + \tilde{E}_{1} \bigr)y + \tilde{B}_{1}u,\qquad \hat{\bar{x}}_{2} = K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T} ( y - \bar{C}_{1}\hat{\bar{x}}_{1} ),\\ \hat{d} = U_{1}\dot{y} - U_{2}y - U_{3}\hat{ \bar{x}}_{1} - U_{4}u,\qquad \hat{x} = T\hat{\bar{x}} = T \left [ \begin{array} {c@{\quad}c} \hat{\bar{x}}_{1}^{T} & \hat{\bar{x}}_{2}^{T} \end{array} \right ]^{T}, \end{array} $$

(7)

where H ₂₂∈R ^m×m is a submatrix of an orthogonal matrix $H_{2} = [ \begin{array}{c@{\ }c} H_{21} & H_{22} \end{array} ] \in R^{m \times n}$, $C_{1} = H_{22}^{T}\bar{C}_{1}$, $\tilde{A}_{1} = \bar{A}_{11} - \bar{A}_{12}K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T}\bar{C}_{1}$, $\tilde{B}_{1} = \bar{B}_{1}$, $\tilde{E}_{1} = \bar{A}_{12}K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T}$, $G^{T} = [ \begin{array}{c@{\ }c} I_{n - m} & 0 \end{array} ]$, while R ₂ (a nonsingular matrix) and K ₂ (an orthogonal matrix) are obtained by expanding the full column rank matrix $\bar{C}_{2}$ as follows:

$$ \bar{C}_{2} = H_{2}\left[ \begin{array}{c@{\quad}c} R_{2}^{T} & 0 \end{array} \right]^{T}K_{2}^{T}; $$

(8)

L is calculated by choosing desired eigenvalues for the matrix $( \tilde{A}_{1} - LC_{1} )$, such that $( \tilde{A}_{1} - LC_{1} )$ is stable, while the matrices U ₁,U ₂,U ₃, and U ₄ have the expressions

$$ \begin{array}{rcl} U_{1} &=& K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T}, \\ U_{2} &=& K_{2}R_{2}G^{T}H_{2}^{T}\bar{C}_{1}\bigl( LH_{22}^{T} + \tilde{E}_{1} \bigr) + \bar{A}_{22}K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T}, \\ U_{3} &=& K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T}\bar{C}_{1}( \tilde{A}_{1} - LC_{1} ) + \bar{A}_{21} - \bar{A}_{22}K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T}\bar{C}_{1}, \\ U_{4} &=& K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T}\bar{C}_{1}\tilde{B}_{1} + \bar{B}_{2}. \end{array} $$

(9)

Proof

The expansion of the matrix $\bar{C}_{2}$ (Eq. (8)) [11, 19] allows us to obtain the following matrices: H ₂∈R ^m×n, R ₂∈R ^{(n−m)×(n−m)}, K ₂∈R ^{(n−m)×(n−m)}; analyzing the dimensions of the matrices R ₂, K ₂, and $\bar{D}$, new necessary conditions for the observer design result:

$$ n - m > 0,\qquad n - s > 0. $$

(10)

In (8) the matrix H ₂ must be orthogonal $( H_{2} \cdot H_{2}^{T} = I_{m} )$, while R ₂ must be nonsingular.

Next, by partitioning the matrix H ₂ as follows [11, 19]: $H_{2} = [ \begin{array}{c@{\ }c} H_{21} & H_{22} \end{array}]$, we obtain the matrices H ₂₁∈R ^m×(n−m), H ₂₂∈R ^m×m, and we denote [11]:

$$ \bar{y} = H_{2}^{T}y = \left[ \begin{array}{c@{\quad}c} H_{21} & H_{22} \end{array} \right]^{T}y = \left[ \begin{array}{c@{\quad}c} \bar{y}_{1}^{T} & \bar{y}_{2}^{T} \end{array} \right]^{T}; $$

(11)

then the third equation of (5) becomes $y = \bar{C}_{1}\bar{x}_{1} + H_{2}[ \begin{array}{c@{\ }c} R_{2}^{T} & 0 \end{array}]^{T}K_{2}^{T}\bar{x}_{2}$. Left pre-multiplying both sides of the previous equation by $H_{2}^{T}$, we obtain

$$\begin{aligned} &H_{2}^{T}y = H_{2}^{T}\bar{C}_{1}\bar{x}_{1} + \underbrace{H_{2}^{T}H_{2}}_{I_{m}}\left[ \begin{array}{c} R_{2} \\0 \end{array} \right]K_{2}^{T}\bar{x}_{2} \\& \quad \Longleftrightarrow\quad \left[ \begin{array}{c} H_{21}^{T} \\ H_{22}^{T} \end{array} \right]y = \left[ \begin{array}{c} H_{21}^{T} \\ H_{22}^{T} \end{array} \right]\bar{C}_{1}\bar{x}_{1} + \left[ \begin{array}{c} R_{2} \\0 \end{array} \right]K_{2}^{T}\bar{x}_{2} \end{aligned}$$

(12)

and the measurement equation may be decomposed as follows:

$$ \left\{ \begin{array}{l} \bar{y}_{1} = H_{21}^{T}\bar{C}_{1}\bar{x}_{1} + R_{2}K_{2}^{T}\bar{x}_{2},\\ \bar{y}_{2} = C_{1}\bar{x}_{1}, \end{array} \right. $$

(13)

where $C_{1} = H_{22}^{T}\bar{C}_{1}$. Now, with the notation $G^{T} = [ \begin{array}{c@{\ }c} I_{n - m} & 0 \end{array} ]$, we have

$$ \bar{y}_{1} = \left[ \begin{array}{c@{\quad}c} I_{n - m} & 0 \end{array} \right]\left[ \begin{array}{c@{\quad}c} \bar{y}_{1}^{T} & \bar{y}_{2}^{T} \end{array} \right]^{T} \quad \Longleftrightarrow\quad \bar{y}_{1} = G^{T}\bar{y}. $$

(14)

Using the first equation of (13) we write [11]

$$ \bar{x}_{2} = \bigl( R_{2}K_{2}^{T} \bigr)^{ - 1} \bigl( \bar{y}_{1} - H_{21}^{T} \bar{C}_{1}\bar{x}_{1} \bigr) = \bigl( R_{2}K_{2}^{T} \bigr)^{ - 1} \bigl( G^{T}\underbrace{H_{2}^{T}y}_{\bar{y}} - H_{21}^{T}\bar{C}_{1}\bar{x}_{1} \bigr) $$

(15)

or

$$ \bar{x}_{2} = K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T} ( y - \bar{C}_{1}\bar{x}_{1} ); $$

(16)

Equation (16) has been obtained by using the equality $( R_{2}K_{2}^{T} )^{ - 1} = K_{2}R_{2}^{ - 1}$ (K ₂—orthogonal matrix) and the equation $G^{T}H_{2}^{T} = [ \begin{array}{c@{\ }c} I_{n - m} & 0 \end{array} ][ \begin{array}{c@{\ }c} H_{21} & H_{22} \end{array} ]^{T} = H_{21}^{T}$.

Substituting $\bar{x}_{2}$ (Eq. (16)) into the first equation of (6), we find [11]

$$ \dot{\bar{x}}_{1} = \tilde{A}_{1}\bar{x}_{1} + \tilde{B}_{1}u + \tilde{E}_{1}y, $$

(17)

with

$$\begin{aligned} \tilde{A}_{1} = \bar{A}_{11} - \bar{A}_{12}K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T}\bar{C}_{1},\qquad\tilde{B}_{1} = \bar{B}_{1},\qquad\tilde{E}_{1} = \bar{A}_{12}K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T}. \\ \end{aligned}$$

(18)

In order to design the observer, the pair $( \tilde{A}_{1},C_{1} )$ must be observable or at least detectable. After the fulfillment of this condition, following the conventional Luenberger observer design procedure, we design a reduced order observer for the unknown-input-free equation (17) as follows [11, 19]:

$$ \dot{\hat{\bar{x}}}_{1} = ( \tilde{A}_{1} - LC_{1} )\hat{\bar{x}}_{1} + \bigl( LH_{22}^{T} + \tilde{E}_{1} \bigr)y + \tilde{B}_{1}u. $$

(19)

Equation (19) has been obtained by using the expression $LC_{1}\bar{x}_{1} = L\bar{y}_{2} = LH_{22}^{T}y$; the matrix L is chosen such that $\sigma ( \tilde{A}_{1} - LC_{1} ) \subset \mathrm{C}_{ -}$ (the matrix $\tilde{A}_{1} - LC_{1}$ is stable). If the condition is fulfilled, L has been obtained properly, and the observer error converges asymptotically to zero (the proof is presented in [11] and [4]).

By means of (19), we determine $\hat{\bar{x}}_{1}$ and, after that, by using (16) we obtain

$$ \hat{\bar{x}}_{2} = K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T} ( y - \bar{C}_{1}\hat{\bar{x}}_{1} ); $$

(20)

the unknown input vector d is then calculated from (5) as follows:

$$ \hat{d} = \dot{\hat{\bar{x}}}_{2} - \bar{A}_{21}\hat{ \bar{x}}_{1} - \bar{A}_{22}\hat{\bar{x}}_{2} - \bar{B}_{2}u, $$

(21)

where $\dot{\hat{\bar{x}}}_{2}$ has the form

$$\begin{aligned} \dot{\hat{\bar{x}}}_{2} =& K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T} \bigl[ \dot{y} - \bar{C}_{1} ( \tilde{A}_{1} - LC_{1} )\hat{\bar{x}}_{1} \bigr] \\&{}- K_{2}R_{2}^{ - 1}G^{T}H_{2}^{T} \bigl[ \bar{C}_{1} \bigl( LH_{22}^{T} + \tilde{E}_{1} \bigr)y + \bar{C}_{1}\tilde{B}_{1}u \bigr]. \end{aligned}$$

(22)

Next, substituting (22) into (21) we find

$$ \hat{d} = U_{1}\dot{y} - U_{2}y - U_{3}\hat{\bar{x}}_{1} - U_{4}u, $$

(23)

where the matrices U ₁, U ₂, U ₃, and U ₄ have the forms given in (9).

The vector $\hat{\bar{x}}$ is determined by the concatenation of the vectors $\hat{\bar{x}}_{1}$ and $\hat{\bar{x}}_{2}$, while the estimated state vector $\hat{x}$ is calculated by means of an equation similar to (2). Theorem 1 is now demonstrated. □

Remark 1

The second set of conditions (10) has been considered an assumption in Theorem 1, because the number of system unknown inputs (s) is commonly less than the number of states (n); moreover, the first condition of (10) is an assumption for the approach because it generally holds. Otherwise, it may be easily fulfilled by a judicious choice of matrix C.

Remark 2

In order to reduce the number of observer constraints and to obtain a reduced order observer without existence conditions, we add in the design procedure two “while” loops. Because one of the existence conditions of the observer is related to the matrix $\bar{C}_{2}$, the first “while” loop is used to obtain a full column rank matrix $\bar{C}_{2}$, an orthogonal matrix H ₂, and a nonsingular matrix R ₂. On the other hand, to eliminate another constraint of our new approach (the pair $( \tilde{A}_{1},C_{1} )$ must be observable or at least detectable), a second “while” loop is introduced. Thus, if the pair $( \tilde{A}_{1},C_{1} )$ is not observable or at least detectable, we return to the selection of the matrix N, with the coordinates change (2), calculation of the matrices $\bar{A},\bar{B},\bar{C},\bar{D}$, and so on; we repeat all these operations, in a second “while” loop, until this existence condition is fulfilled. There is no risk of an infinite “while” loop; therefore, the approach will always provide an observable or at least detectable pair of matrices $( \tilde{A}_{1},C_{1})$.

Remark 3

In the two similar approaches (Boubaker observer and Hou and Muller observer) no remedy for the non-observability of the pair $( \tilde{A}_{1},C_{1} )$ is presented. That is why these two approaches have a disadvantage with respect to our new approach and, as a consequence, we obtained a design algorithm with a greater generality due its second “while” loop.

The observer design procedure for the state estimation problem in the case of an LTI multivariable system, subjected to unknown inputs, is based on the ALGLIN algorithm, which is summarized below.

Step 1: :

We check if $\operatorname{rank}( CD ) = \operatorname{rank}( D )$, n>m, and n>s; if the first two conditions are not met, we choose another matrix C to satisfy the two conditions; the number of system unknown inputs (s) is commonly less than the number of states (n).

Step 2: :

We choose the matrix N such that the matrix T=[ND] is nonsingular.

Step 3: :

The change of coordinates (2) is performed and the matrices $\bar{A},\bar{B},\bar{C},\bar{D}$ are calculated; these four matrices are partitioned and the matrices $\bar{A}_{11},\bar{A}_{12},\bar{A}_{21}$, $\bar{A}_{22},\bar{B}_{1},\bar{B}_{2},\bar{C}_{1},\bar{C}_{2}$ are determined.

Step 4: :

We check if $\bar{C}_{2}$ is a full column rank matrix. If $\bar{C}_{2}$ is not a full column rank matrix, we return to step 2 and we repeat steps 2–4 until the condition is fulfilled; otherwise, $\bar{C}_{2}$ is written in the form (8) and the matrices H ₂,R ₂,K ₂ are obtained. The three matrices are calculated until we obtain a nonsingular matrix R ₂ and two orthogonal matrices H ₂,K ₂.

Step 5: :

H ₂ is partitioned $( H_{2} = [ \begin{array}{c@{\ }c} H_{21} & H_{22} \end{array} ] )$ and the matrices H ₂₁ and H ₂₂ result.

Step 6: :

C ₁ is calculated by means of the equation $C_{1} = H_{22}^{T}\bar{C}_{1}$.

Step 7: :

Using (18), we determine $\tilde{A}_{1},\tilde{B}_{1},\tilde{E}_{1}$. We check if pair $( \tilde{A}_{1},C_{1} )$ is observable and, if the condition holds, we go to the next step; otherwise, we return to step 2 and we repeat steps 2–7 until the fulfillment of the observer existence conditions.

Step 8: :

The Luenberger observer described by Eq. (19) is designed, the matrix L being chosen such that $\sigma ( \tilde{A}_{1} - LC_{1} ) \in \mathrm{C}_{ -}$. The reduced order observer estimates the vector $\bar{x}_{1}$; its estimation $( \hat{\bar{x}}_{1} )$ is obtained.

Step 9: :

$\hat{\bar{x}}_{2}$ is calculated by means of (20).

Step 10: :

We calculate the matrices U ₁,U ₂,U ₃,U ₄ (Eq. (9)) and, after that, the unknown input vector $\hat{d}$ is obtained by using (23).

Step 11: :

$\hat{\bar{x}}$ is determined by the concatenation of the vectors $\hat{\bar{x}}_{1}$ and $\hat{\bar{x}}_{2}$, while the estimated state vector $\hat{x}$ is obtained by using an equation similar to (2).

The new reduced order observer with unknown inputs reconstruction has three assumptions (n>m, n>s,(C,A)—observable pair of matrices) and four existence conditions (constraints): (1) $\operatorname{rank}( CD ) = \operatorname{rank}( D )$; (2) $\bar{C}_{2}$ is a full column matrix; (3) the matrix R ₂ is nonsingular, while the matrix H ₂ is orthogonal; (4) the pair $( \tilde{A}_{1},C_{1} )$ is observable or at least detectable. Condition (1) is sometimes called the observer matching condition, and it is the analogue of the well-known matching condition for a sliding mode controller to be insensitive to matched perturbations. This condition may be met easily by a judicious choice of matrix C (the choice of the output vector y). The existence conditions (2) and (3) are met in the first “while loop” by choosing a suitable matrix N, while the fulfillment of the constraint (4) is made in the second “while” loop. If condition (4) is fulfilled, the observer gain matrix L has been obtained properly, the dynamics of the observer error has a homogeneous form, and, therefore, the observer error converges asymptotically to zero.

In conclusion, choosing a suitable matrix C, a suitable matrix N (first “while” loop), and an observable pair of matrices $( \tilde{A}_{1},C_{1} )$-second “while” loop, all the existence conditions for the observer design are met. In these circumstances, our approach has no existence conditions and only three assumptions.

Remark 4

The only minor disadvantage of our new observer with respect to other design algorithms in the literature is related to the use of the pole placement technique, which is easy to implement but has some disadvantages: (1) it becomes difficult to use for systems of large order or for poorly controlled systems; (2) if we choose fast poles for the observer, the advantage is that the observer estimation error decays rapidly, but the disadvantage is that the system needs perfect sensors and/or a noise-free environment; (3) if we choose slow poles for the observer, the advantage is that the system is less sensitive to process disturbances and measurement noise, but the disadvantage is that the observer estimation error decays slowly. The use of the pole placement technique is not a fundamental problem since most observers use this method for determination of the observer gain matrix; therefore the disadvantage of our new observer is a minor one.

2.3 Validation of the ALGLIN Algorithm

The validation of our new algorithm for a reduced order observer design is performed here, in a Matlab/Simulink environment, for the case of lateral motion of a Boeing 747 flying with 0.8 Mach number at an altitude of H=40,000 ft [18]. Aircraft flight is often influenced by disturbances like longitudinal or vertical wind shears, atmospheric turbulence, or sensor errors. From the aircraft dynamics point of view, these represent unknown inputs; an observer for systems with unknown inputs must estimate these unknown inputs and, at the same time, estimate the system states with very small errors. Here, we validate our new reduced order observer for the case of an aircraft flight, but the observer may be used, with good results, in any other examples due to its general character. Because the main advantage of our new observer is the lack of a priori restrictions, we only have to know the system linear dynamics and then put the dynamics in the form of the state equations (1). In our case, the state equations associated to the Boeing 747 lateral motion have the form (1) with [18]

$$ \begin{array}{l} x = \left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \Delta \beta & \Delta r & \Delta p & \Delta \varphi \end{array} \right]^{T},\qquad u = \left[ \begin{array}{c@{\quad}c} \delta _{r} & \delta _{a} \end{array} \right]^{T}, \\ A = \left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} - 0.0558 & - 0.9968 & 0.0802 & 0.0415 \\0.598 & - 0.115 & - 0.0318 & 0 \\0.305 & 0.388 & - 0.465 & 0 \\0 & 0.0805 & 1 & 0 \end{array} \right],\\ B = D = \left[ \begin{array}{c@{\quad}c} 0.0073 & 0 \\- 0.475 & 0.123 \\0.153 & 1.063 \\0 & 0 \end{array} \right],\qquad C = \left[ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 & 0 & 0 & 0 \\0 & 0 & 1 & 0 \end{array} \right]; \end{array} $$

(24)

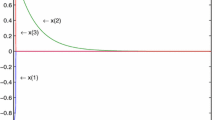
β is the aircraft sideslip angle, r and p are the yaw and roll angular rates, φ—the roll angle, δ _r —the rudder deflection, and δ _a —the aileron deflection, while Δ is associated with the deviation of the variables from their nominal values; d∈R ^s×1 is considered to be a vertical wind shear. In this simulation, the input signal is calculated by using the ALGLX algorithm [18]; thus, we consider the gain matrix $\bar{K}$ (feedback of the closed-loop system) and the input vector of the system $u = [ \begin{array}{c@{\ }c} \delta _{r} & \delta _{a} \end{array} ]^{T} = - \bar{K}\hat{x}$. We obtained the graphic characteristics as shown in Fig. 1 (the four states x _i , $i = \overline{1,4}$—solid line and the four estimated states $\hat{x}_{i}$, $i = \overline{1,4}$—dashed line). The graphics of the system states are superposed over the estimated states’ graphics.

Fig. 1

State estimation errors by using the ALGLIN algorithm

3 Comparison of Our New Observer and Other Observers for LTI Systems with Unknown Inputs

In this section, we compare our new observer with other already existing observers for LTI systems with unknown inputs. We briefly present two important observers, representative for the research area of LTI systems with unknown inputs, and we compare these observers with our new observer. These observers have been designed by Boubaker [4] and Hou and Muller [11], respectively.

To briefly present the Boubaker observer, we consider the same LTI system described by (1). All the equations (1)–(6) and the notation remain valid. The observer design is concentrated into the following theorem.

Theorem 2

[4]

Consider the LTI multivariable system (1); using the assumptions that n>m and (C,A) is an observable pair of matrices, we design the convergent observer for LTI systems with unknown inputs described by the equations [4]

$$ \begin{array}{l} \dot{\hat{\bar{x}}}_{1} = ( \tilde{A}_{1} - L \tilde{C}_{1} )\hat{\bar{x}}_{1} + \bar{B}_{1}u + \tilde{L}y,\qquad \hat{\bar{x}}_{2} = U_{1}y - U_{1}CN\hat{ \bar{x}}_{1}, \\ \hat{d} = U_{1}\dot{y} + G_{1}\hat{\bar{x}}_{1} + G_{2}y + G_{3}u,\qquad\hat{x} = T\hat{\bar{x}} = T\left [ \begin{array} {c@{\quad}c} \hat{\bar{x}}_{1}^{T} & \hat{ \bar{x}}_{2}^{T} \end{array} \right ]^{T}, \end{array} $$

(25)

where $\tilde{A}_{1} = \bar{A}_{11} - \bar{A}_{12}U_{1}CN$, $\tilde{C}_{1} = U_{2}CN$, $E_{1} = \bar{A}_{12}U_{1}$, $\tilde{L} = LU_{2} + E_{1}$, and L has been calculated by choosing desired eigenvalues for the matrix $( \tilde{A}_{1} - L\tilde{C}_{1} )$ such that $\sigma ( \tilde{A}_{1} - L\tilde{C}_{1} ) \subset \mathrm{C}_{ -}$, while U ₁∈R ^m×p and U ₂∈R ^(p−m)×p have been obtained by choosing a nonsingular matrix $U = [ \begin{array}{c@{\ }c} CD & Q \end{array} ]$, Q∈R ^p×(p−m); U ⁻¹ has been partitioned as $U^{ - 1} = [ \begin{array}{c@{\ }c} U_{1}^{T} & U_{2}^{T} \end{array} ]^{T}$. The matrices U and U ⁻¹ must fulfill the condition [4]

$$ U^{ - 1}U = \left[ \begin{array}{c} U_{1} \\U_{2} \end{array} \right]\left[ \begin{array}{c@{\quad}c} CD & Q \end{array} \right] = \left[ \begin{array}{c@{\quad}c} U_{1}CD & U_{1}Q \\U_{2}CD & U_{2}Q \end{array} \right] = \left[ \begin{array}{c@{\quad}c} I_{m} & 0 \\0 & I_{p - m} \end{array} \right]; $$

(26)

the matrices G ₁,G ₂,G ₃ are calculated as follows [4]:

$$\begin{array}{l} G_{1} = U_{1}CN ( LU_{2}CN + \bar{A}_{12}U_{1}CN ) - U_{1}CN\bar{A}_{11} - \bar{A}_{21} + \bar{A}_{22}U_{1}CN, \\ G_{2} = - U_{1}CNLU_{2} - U_{1}CN \bar{A}_{12}U_{1} - \bar{A}_{22}U_{1},\qquad G_{3} = - U_{1}CN\bar{B}_{1} - \bar{B}_{2}. \end{array} $$

The theorem proof is presented in [4]. Our new observer design approach has borrowed five steps from the Boubaker design procedure: steps 1, 2, 3, 10, and 11).

The Boubaker observer has two assumptions (n>m, (C,A)—observable pair of matrices) and three existence conditions (constraints). The first existence condition of the Boubaker observer is related to the dimensions of the matrix Q; thus, the first observer constraint is p>m. This constraint is sometimes difficult to meet, and no remedy is presented in the Boubaker approach; for example, if the LTI multivariable system has only one known input, the observer cannot be designed (matrix C does not exist). Therefore, the observer may be designed and used only for LTI multivariable systems with multiple known inputs. The other two Boubaker observer existence conditions are given by the following two theorems [11].

Theorem 3

[11]

For the given system (1), observer (25) exists if and only if:

$$\begin{array}{l} (1)\quad \operatorname{rank}( CD ) = \operatorname{rank}( D );\\ (2)\quad \operatorname{rank}\left[ \begin{array}{c@{\quad}c} \mathbf{s}I_{n - s} - \bar{A}_{11} & - \bar{A}_{12} \\CN & CD \end{array} \right] = n,\quad ( \forall )\mathbf{s} \in \mathrm{C},\operatorname{Re}\{ \mathbf{s}\} \ge 0. \end{array} $$

Theorem 4

[11]

If $\operatorname{rank}( CD ) = \operatorname{rank}( D ) = s$, then the following statements are equivalent:

$$\begin{array}{l} (1)\quad \mathrm{pair}\ ( \tilde{A}_{1},\tilde{C}_{1} )\ \mathit{is}\ \mathit{observable}\ \mathrm{or}\ \mathit{at}\ \mathit{least}\ \mathit{detectable};\\ (2)\quad \operatorname{rank}\left[ \begin{array}{c@{\quad}c} \mathbf{s}I_{n - s} - \bar{A}_{11} & - \bar{A}_{12} \\CN & CD \end{array} \right] = n,\quad ( \forall )\mathbf{s} \in \mathrm{C},\operatorname{Re}\left\{ \mathbf{s} \right\} \ge 0;\\ (3)\quad \operatorname{rank}\left[ \begin{array}{c@{\quad}c} \mathbf{s}I_{n} - A & D \\C & 0 \end{array} \right] = n +s,\quad ( \forall )\mathbf{s} \in \mathrm{C},\operatorname{Re}\{ \mathbf{s}\} \ge 0. \end{array} $$

The disadvantages of this observer are related to the number of existence conditions: (1) the number of system outputs is less than the number of system known inputs; (2) $\operatorname{rank}( CD ) = \operatorname{rank}( D )$; (3) the pair $( \tilde{A}_{1},\tilde{C}_{1} )$ is observable or at least detectable. Condition (2) is not a serious problem because it may be easily fulfilled by a judicious choice of matrix C; condition (1) is very restrictive and represents a serious problem in the case of LTI systems with only one known input. If condition (3) is not met, the algorithm stops; no solution for solving this problem is included in the Boubaker approach. In contrast with the Boubaker observer, our observer solves this problem by means of a “while” loop which includes steps 2–7. By a judicious choice of matrix C ₁, our algorithm has no existence condition due to the “while” loops, while the Boubaker observer has two constraints without any remedy. Our new observer has one additional assumption which generally holds (the number of states is greater than the number of unknown inputs). Both design procedures use the pole placement technique, which is a minor disadvantage.

The second observer presented in this section is that of Hou and Muller [11]. We consider the observable LTI system described by (1); the Hou and Muller observer can be designed only if C is a full row rank matrix and D is a full column rank matrix [11]. The matrix C can be conveniently chosen by selecting the system outputs, while the matrix D, associated to the unknown inputs of the system, cannot be chosen by the designer. Considering the set consisting of these two conditions as the first assumption of the observer for the state estimation of an observable system, we perform the first matrix decomposition [11]:

$$ D = H\left[ \begin{array}{c@{\quad}c} R^{T} & 0 \end{array} \right]^{T}K^{T}, $$

(27)

where H∈R ^n×n and K∈R ^s×s are orthogonal matrices, while R∈R ^s×s is a nonsingular matrix. Using the coordinates change $\bar{x} = H^{T}x,\bar{d} = K^{T}d$, and the decomposition of the new state vector $\bar{x} = [ \begin{array}{c@{\ }c} \bar{x}_{1} & \bar{x}_{2} \end{array}]^{T}$, $\bar{x}_{1} \in R^{s \times 1}$, $\bar{x}_{2} \in R^{( n - s ) \times 1}$, system (1) obtains the form [11]

$$ \left\{ \begin{array}{l} \dot{\bar{x}}_{1} = \bar{A}_{11}\bar{x}_{1} + \bar{A}_{12}\bar{x}_{2} + \bar{B}_{1}u + R\bar{d}, \\ \dot{\bar{x}}_{2} = \bar{A}_{21}\bar{x}_{1} + \bar{A}_{22}\bar{x}_{2} + \bar{B}_{2}u, \\ y = \bar{C}_{1}\bar{x}_{1} + \bar{C}_{2}\bar{x}_{2}, \end{array} \right. $$

(28)

with

$$\begin{aligned} &\bar{A} = H^{T}AH,\qquad\bar{B} = H^{T}B,\qquad\bar{C} = CH,\\&\bar{A} = \left[ \begin{array}{c@{\quad}c} \bar{A}_{11} & \bar{A}_{12} \\\bar{A}_{21} & \bar{A}_{22} \end{array} \right],\qquad \bar{B} = \left[ \begin{array}{c} \bar{B}_{1} \\\bar{B}_{2} \end{array} \right],\qquad \bar{C} = \left[ \begin{array}{c@{\quad}c} \bar{C}_{1} & \bar{C}_{2} \end{array} \right]; \end{aligned}$$

the matrices in the previous equation have appropriate dimensions: $\bar{A}_{11} \in R^{s \times s}$, $\bar{A}_{12} \in R^{s \times ( n - s )}$, $\bar{A}_{21} \in R^{( n - s ) \times s}$, $\bar{A}_{22} \in R^{( n - s ) \times ( n - s )}$, $\bar{B}_{1} \in R^{s \times p}$, $\bar{B}_{2} \in R^{( n - s ) \times p}$, $\bar{C}_{1} \in R^{m \times s},\bar{C}_{2} \in R^{m \times ( n - s )}$. After analyzing the dimensions of the matrices $\bar{A}_{12},\bar{A}_{21}$, or $\bar{A}_{22}$, the result is a new necessary condition for the design of the observer: n>s (the number of system unknown inputs must be less than the number of system states). Because $\bar{x}_{1}$ depends on the unknown input d, while $\bar{x}_{2}$ does not, it is more judicious to estimate $\bar{x}_{2}$; as a consequence, the Hou and Muller observer estimates the state $\bar{x}_{2}$, while the estimations of $\bar{x}_{1}$ and d are calculated with respect to $\hat{\bar{x}}_{2}$ (the estimation of $\bar{x}_{2}$).

The Hou and Muller observer design is concentrated into the following theorem.

Theorem 5

[11]

Consider the LTI multivariable system (1) written in the form (28); using the assumptions n>s, (C, A) is an observable pair of matrices, C is a full row rank matrix, and D is a full column rank matrix, we design the convergent reduced order observer for LTI systems with unknown inputs described by the equations

$$ \begin{array}{l} \dot{\hat{\bar{x}}}_{2} = ( A_{2} - LC_{2} )\hat{ \bar{x}}_{2} + B_{2}u + \bigl( D_{2} + LH_{12}^{T} \bigr)y,\qquad\hat{\bar{x}}_{1} = K_{1}R_{1}^{ - 1}G^{T}H_{1}^{T} [ y - \bar{C}_{2}\hat{\bar{x}}_{2} ], \\ \hat{d} = KR^{ - 1}\dot{\hat{\bar{x}}}_{1} - KR^{ - 1} \bar{A}_{11}R_{1}^{ - 1}G^{T}H_{1}^{T}y + \bigl( KR^{ - 1}R_{1}^{ - 1}G^{T}H_{1}^{T} \bar{C}_{2}\\ \hphantom{\hat{d} =} {}- KR^{ - 1}\bar{A}_{12} \bigr)\hat{ \bar{x}}_{2} - KR^{ - 1}\bar{B}_{1}u, \end{array} $$

(29)

where $\bar{C}_{1} = H_{1}[ \begin{array}{c@{\ }c} R_{1}^{T} & 0 \end{array}]^{T}K_{1}^{T}$ ($\bar{C}_{1}$ must be a full column rank matrix, H ₁∈R ^m×m, K ₁∈R ^s×s —orthogonal matrices, R ₁∈R ^s×s —nonsingular matrix), $H_{1} = [ \begin{array}{c@{\ }c} H_{11} & H_{12} \end{array}]$, H ₁₁∈R ^m×s, H ₁₂∈R ^m×(m−s), $C_{2} = H_{12}^{T}\bar{C}_{2}$, $G^{T} = [ \begin{array}{c@{\ }c} I_{s} & 0 \end{array} ]$, $A_{2} = \bar{A}_{22} - \bar{A}_{21}K_{1}R^{ - 1}G^{T}H_{1}^{T}$, $B_{2} = \bar{B}_{2}$, $D_{2} = \bar{A}_{21}K_{1}R^{ - 1}G^{T}H_{1}^{T};L$ is calculated by choosing desired eigenvalues for the matrix (A ₂−LC ₂) such that σ(A ₂−LC ₂)⊂C₋. Vector $\hat{\bar{x}}$ is determined by the concatenation of the vectors $\hat{\bar{x}}_{1}$ and $\hat{\bar{x}}_{2}$, while the estimated state vector $\hat{x}$ is calculated by means of an equation similar to (2). The ALGLIN observer design procedure has borrowed six steps (steps 4–9) from the Hou and Muller approach.

The Hou and Muller observer has four assumptions (n>s, (C,A)—observable pair of matrices, C—full row rank matrix, and D—full column rank matrix) and five constraints: (1) $\operatorname{rank}( CD ) = \operatorname{rank}( D )$; (2) $\bar{C}_{1}$ is a full column matrix; (3) matrix R is nonsingular, while matrix H is orthogonal; (4) matrix R ₁ is nonsingular, while the matrix H ₁ is orthogonal; (5) the pair (A ₂,C ₂) is observable or at least detectable.

Two of the four assumptions (n>s, (C,A)—observable pair of matrices) are common to the ALGLIN observer and the Hou and Muller observer; the observability of the pair (C,A) is met easily by a judicious choice of matrix C, while the assumption n>s is generally valid. The other two assumptions make the Hou and Muller observer less general than the ALGLIN observer, this being the first disadvantage of the Hou and Muller observer with respect to our new observer. The existence condition (1) is not a serious problem because it may be fulfilled easily by a judicious choice of the matrix C. Constraint (2) is solved in the ALGLIN algorithm by using a “while” loop; in the Hou and Muller observer no solution is presented for the case when this existence condition is not fulfilled, this being the second disadvantage of the Hou and Muller observer. Constraint (3) of the ALGLIN algorithm is similar to the existence conditions (3) and (4) in the Hou and Muller approach. If in the ALGLIN design procedure, the constraint is eliminated by introducing the first “while” loop, in the Hou and Muller design procedure no remedy is presented for the case when these two conditions are not met (the third disadvantage of the observer presented in [11]). Finally, constraint (4) of the ALGLIN algorithm is similar to the existence condition (5) of the Hou and Muller approach. If the pair (A ₂,C ₂) is not observable, the Hou and Muller design procedure stops (the fourth disadvantage of the observer presented in [11]) unlike the ALGLIN algorithm, where the second “while” loop (the loop which includes steps 2–7) ensures the fulfillment of this constraint.

From the constraints and design point of view, the ALGLIN observer is better, its main advantages being the lack of a priori restrictions on the class of systems that can be considered. Next, we want to make a brief comparison between our new observer and the two observers summarized in this section from the dynamic characteristics point of view. Therefore, we have implemented in Matlab/Simulink all three observers using the same aircraft dynamics, the same flight data, and the same unknown input vector. Thus, in Fig. 2 we represent the time histories of the four state estimation errors for the ALGLIN observer (solid line), for the Boubaker observer, and for the Hou and Muller observer, respectively.

Fig. 2

Comparison of the ALGLIN observer, Boubaker observer, and Hou and Muller observer

From the dynamic characteristics point of view, the comparison between the three reduced order observers for systems with unknown inputs leads to the following conclusions: (1) all three observers are convergent—the four components of the state estimation error tend to zero; (2) the ALGLIN observer is characterized by a convergence speed of 3 s, while the convergence speed associated to the other two observers is about 4–5 s; this means an advantage of our new observer from the convergence speed point of view (a decrease of 33.3–66.6 % of the convergence speed); (3) the oscillation amplitudes of the state estimation errors are smallest if the ALGLIN observer is used. For a correct comparison, the same desired eigenvalues have been used for all the three observers. Moreover, in Remark 4 we specified the following well-known issue: “if we choose slow poles for the observer, the advantage is that the system is less sensitive to process disturbances and measurement noise, but the disadvantage is that the observer estimation error decays slowly.” Thus, for a correct comparison, the solution was to choose the same slow poles for all three observers; this way, the sensor errors will not affect the measurements. On the other hand, although slow poles have been chosen, our observer estimation error does not decay slowly, 3 s representing a very good convergence speed in the research area of LTI systems with unknown inputs.

4 Conclusions

In this paper we have designed a new approach for the state estimation problem in the case of LTI multivariable systems with unknown inputs. The approach is original and it represents the main contribution of the paper; the observer has been obtained by combining two other reduced order observers: the observer designed by Hou and Muller [11] and the Boubaker observer [4]. The effectiveness of the suggested design algorithm is illustrated by a numerical example (aircraft motion), and, for the same aircraft dynamics, we compared our new observer, the Boubaker observer, and the Hou and Muller observer; the superiority of the new designed observer has been demonstrated, especially from the constraints point of view (our new algorithm has four existence conditions, but all of them can be eliminated by means of a judicious choice of the system outputs and two “while” loops). The design procedure presented in this paper can be extended in future work, and a new observer with unknown inputs reconstruction can be designed; it can be a subsystem (fault detection/diagnosis scheme) of a typical fault-tolerant control system.