1 Introduction

Because of their simplicity and robustness, the least mean square (LMS) algorithms are widely used in applications such as echo cancellation, unknown channel estimation, and speech signal processing [1, 7–12]. One notable characteristic of the LMS method is that the weight coefficients are obtained by the stochastic gradient descent method, which brings about the effect that different step sizes produce different misadjustment errors [7]. A large step size is associated with a high-level steady-state error, while a small step size does not ensure fast convergence. In practice, the convergence performance of LMS algorithms often deteriorates with high-level measurement noise or colored input signals [1].

In the past two decades, several step-size updating adaptive algorithms have been developed to achieve improved LMS performance [1–3, 5, 6, 8, 13–15]. For instance, Kwong and Johnston [8] used the squared instantaneous error to derive a variable step size LMS filter, which gives an improved performance in processing correlated signals. To have better control of the step size, Ang and Farhang-Boroujeny [1] developed a scheme using the inner product between adjacent gradient vectors, and Zhang et al. [15] applied the squared Euclidean norm of the gradient vector. Also, Costa and Bermudez [2] proposed a robust variable step size LMS (VSLMS) algorithm, whose performance is less sensitive to the power of measurement noise than that of [8]. Hwang and Li [6] proposed a scheme using a gradient-based weighted average to control the step size. This scheme enables a faster convergence rate and has lower misadjustment error than the VSLMS schemes reported in [1, 8, 15]. The averaged gradient vector used in [6], however, is affected by the noise power after the algorithm converges. Other VSLMS methods include the wavelet-based affine projection algorithm [14] and the normalized LMS algorithm with robust regulation [3].

This paper proposes a new VSLMS method, which selects an appropriate function to control the step size. The proposed algorithm aims to attain lower steady-state misadjustment errors under the same convergence rates obtained by other VSLMS algorithms mentioned above. Guidelines on the selection of the control function and the updating parameter are presented. In addition, the excess MSE of the proposed method is theoretically derived and verified by the simulation results.

2 Algorithm Formulation

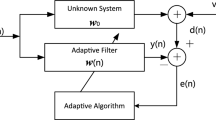
The recurrence formula of the variable step size LMS algorithm is described as follows:

(1)
(2)

where e(k) is the instantaneous error, (⋅)∗ denotes the conjugate operator, and (⋅)H the conjugate transpose operator. \({\bf{x}}(k) = {[x(k), \ldots,x(k - M + 1)]^{T}}\) is the input signal vector, (⋅)T denotes the transpose operator, and M is the length of the filter. \({\bf{w}}(k) = {[w(k), \ldots,w(k - M + 1)]^{T}}\) is the weight vector. d(k) is the desired signal and μ(k) the step size of the algorithm. The widely used step size control scheme is [7, 8]

$$ \mu(k + 1) = \alpha\mu(k) + \gamma{\bigl \vert {e(k)} \bigr \vert ^2}, $$
(3)

where 0<α<1 and γ>0. The updating parameter γ, which is a constant, plays an important role in the filter convergence rate as well as the level of steady-state misadjustment error. However, a better LMS performance can be achieved when γ is considered a varied parameter [1, 2, 6, 8, 15]. A relatively large γ at the earlier iterations enables faster convergence, whereas a small γ at the later iterations may ensure a smaller misadjustment level. Moreover, it would be better for the noise power to have less influence on the step size. A higher noise power often results in a larger step size, which leads to greater steady-state error, and the algorithm loses its efficiency.

The proposed function-controlled VSLMS scheme has better control on the step size so that the impact of high-level noise is alleviated. The idea is that we use an appropriate function to control the updating parameter γ and, at the same time, make the steady-state step size free from the interference of noise through the use of the estimated mean square error (MSE). The proposed step size update recursion is expressed in the form

$$ \mu(k + 1) = \alpha\mu(k) + {\gamma_s}f(k)\frac{{{{\vert {e(k)} \vert }^2}}}{\hat{e}_\mathrm{ms}^2(k)}, $$
(4)

where 0<α<1, γ s >0 is an updating parameter for the proposed algorithm, and \(\hat{e}_{\mathrm{ms}}^{2}(k)\) is the estimated MSE defined as

$$ \hat{e}_\mathrm{ms}^2(k) = \beta\hat{e}_\mathrm{ms}^2(k - 1) + (1 - \beta){\bigl \vert {e(k)} \bigr \vert ^2}. $$
(5)

The weighting factor β lies in the range of 0<β<1 and is close to one.

As the adaptation progresses, the weight of the instantaneous error e(k) of (1) on the step size should be gradually reduced. To achieve this goal, the control function f(k) is introduced and chosen as a decreasing function. The control function f(k) selected for the proposed VSLMS algorithm is

$$ f(k) = \left \{ { \begin{array}{l@{\quad}l} 1/k,& k < N, \\ 1/N,& k \ge N. \\ \end{array} } \right . $$
(6)

N is a relatively large constant number, say N>100. Other candidates for the control function are

(7)
(8)

3 Performance Analysis

The following assumptions are used to conduct the performance analysis [4, 5]:

  1. (1)

    The input signal x(k) and system noise v(k) are zero-mean, wide sense stationary processes. They are independent of each other.

  2. (2)

    x(k) and d(k) are jointly Gaussian random processes.

  3. (3)

    The weight vector \({\bf{w}}(k)\) is independent of the input signal \({\bf{x}}(k)\) and desired signal d(k).

It follows from (5) that the estimated MSE \(\hat{e}_{\mathrm{ms}}^{2}(k)\) can be obtained recursively:

$$ \hat{e}_\mathrm{ms}^2(k) = {\beta^k}\hat{e}_\mathrm{ms}^2(0) + (1 - \beta)\sum\limits _{i = 1}^k {{\beta^{k - i}}} {\bigl \vert {e(i)} \bigr \vert ^2}. $$
(9)

Taking the expectation on both sides, (9) becomes

(10)

In the steady state, i.e., k→∞ , (10) becomes

$$ E\bigl\{ \hat{e}_\mathrm{ms}^2(\infty)\bigr\} = E\bigl\{ {\bigl \vert {e(\infty)} \bigr \vert ^{\rm {2}}}\bigr\}. $$
(11)

Similarly, we can obtain E{μ(k)} recursively, when k≫N,

$$ E\bigl\{ \mu(k)\bigr\} \approx{\alpha^k}\mu(0) + { \gamma_s}\frac{{({\alpha ^k} - 1)}}{{N(\alpha - 1)}}\frac{{E\{ {{\vert {e(k)} \vert }^2}\} }}{{E\{ \hat{e}_\mathrm{ms}^2(k)\} }}. $$
(12)

Letting k→∞ , we have

$$ E\bigl\{ \mu(\infty)\bigr\} \approx\frac{{{\gamma_s}}}{{N(1 - \alpha)}}. $$
(13)

The excess MSE ξ ex of the LMS algorithm can be expressed as [7]

$$ {\xi_\mathrm{ex}} \approx\frac{{{\mu_c}}}{2}M\sigma_x^2{ \xi_{\min}}, $$
(14)

where \(\sigma_{x}^{2}\) is the variance of the input signal, μ c the steady-state step size, and ξ min the least MSE of the filter. Substituting (13) into (14), we obtain the excess MSE

$$ {\xi_\mathrm{ex}} = \frac{{{\gamma_s}M\sigma_x^2}}{{2N(1 - \alpha)}}{\xi _{\min}} $$
(15)

and the misadjustment of the proposed algorithm

$$ \eta = \frac{{{\xi_\mathrm{ex}}}}{{{\xi_{\min}}}} = \frac{{{\gamma _s}M\sigma_x^2}}{{2N(1 - \alpha)}}. $$
(16)

Let μ(0) and \(\hat{e}_{\mathrm{ms}}^{2}(0)\) be set to zero; from (10) and (12), we have

$$ E\bigl\{ \mu(k)\bigr\} = \frac{{{\gamma_s}(1 - {\alpha^k})}}{{N(1 - \alpha)(1 - {\beta^k})}}. $$
(17)

Then the upper bound of E{μ(k)} is

$$ \frac{{{\gamma_s}}}{{N(1 - \alpha)(1 - \beta)}}. $$
(18)

To guarantee the convergence of the LMS algorithm, a sufficient condition is [7]

$$ 0 < \mu < \frac{2}{{\operatorname{tr}({\bf{R}})}}, $$
(19)

where \(\bf{R}\) is the autocorrelation matrix of \({\bf{x}}(n)\). It follows from (17) and (19) that the parameter γ s can be selected according to

$$ 0 < {\gamma_s} < \frac{{{\rm{2}}N(1 - \alpha)(1 - \beta)}}{{\operatorname{tr}({\bf{R}})}}. $$
(20)

Next, we discuss the condition the control function f(k) should fulfill. From (9), suppose that \(\hat{e}_{\mathrm{ms}}^{2}(0) = 0\); then we have

(21)

Substituting (21) into (4) and taking the expectation operation yields

$$ E\bigl\{ \mu(k + 1)\bigr\} \le\alpha E\bigl\{ \mu(k)\bigr\} + \frac{{{\gamma_s}}}{{1 - \beta}}f(k). $$
(22)

Letting μ(0)=0, the upper bound of E{μ(k)} can be obtained recursively:

$$ E\bigl\{ \mu(k)\bigr\} \le\frac{{{\gamma_s}}}{{1 - \beta}}\sum\limits _{i = 1}^k {{\alpha^{k - i}}f(i)}. $$
(23)

It follows from (19) and (23) that the control function f(k) should be chosen to satisfy the following condition:

$$ \sum\limits _{i = 1}^k {{\alpha^{k - i}}f(i)} \le \frac{{2(1 - \beta )}}{{{\gamma_s}\operatorname{tr}({\bf{R}})}}. $$
(24)

As for the computational complexity, the proposed algorithm requires 2M+9 multiplications and 2M+1 additions to compute one filter output. This complexity is slightly higher than that of [8], but lower than that of [6].

4 Simulation Results

In this section, the performance of the proposed algorithm is evaluated in the situation of unknown channel estimation, similar to the simulations used in [8] and [13], and compared with the adaptive LMS algorithms reported in [1, 2, 6, 8, 14, 15]. The adaptive filter and the FIR system are assumed to have the same number of taps. The unknown channel is chosen as \({\bf{w}}_{o} = [0.307, 0.463, 0.617, 0.463, 0.307]^{T}\), and the output signal is d(k)=y(k)+v(k), where \(y(k) = {\bf{w}}_{o}^{T}{\bf{x}}(k)\) and v(k) is the measurement noise. The parameter values of the proposed algorithm used in the simulation are α=0.993, β=0.92, N=200, and γ s =0.002. The trace of the matrix \(\bf{R}\) is set as 5. Note that the upper bound of the updating parameter γ s is 0.0448, computed from (20). The excess MSE of (15) is employed as the performance metric for various LMS algorithms. Results are averaged over 100 independent runs. The step size update equations and the parameter values for other VSLMS algorithms are listed in Table 1.

Table 1 Step size updates and simulation parameters of the other VSLMS algorithms
Full size table

Two types of input signals are considered. One is a white Gaussian signal of zero mean and unit variance; another is a colored signal obtained by filtering the zero-mean, unit variance white Gaussian noise through a third-order system:

$$H(z) = \frac{{0.75}}{{(1 - 0.5{z^{ - 1}} + 0.7{z^{ - 2}} - 0.25{z^{ - 3}})}}. $$

Results are compared at 10 dB and 0 dB of the signal-to-noise ratio (SNR) calculated by

$${\rm{SNR}} = 10\log_{10} \biggl( {\frac{{E \{ {{{\vert {y(k)} \vert }^2}} \}}}{{E \{ {{{\vert {v(k)} \vert }^2}} \} }}} \biggr). $$

Simulation results on the excess MSE for the proposed VSLMS method and other adaptive LMS algorithms are shown in Figs. 1 and 2. Figure 1 compares the excess MSE for a white Gaussian input signal, and Fig. 2 for the colored signal. Performance under the low-SNR environment is shown in Figs. 1(b) and 1(b). We observe from Figs. 1 and 2 that the proposed VSLMS method enables as fast a convergence as other VSLMS algorithms, and is able to achieve a lower misadjustment error. The excess MSE by the proposed method at SNR = 10 dB is −35 dB, and at SNR = 0 dB it is −24.8 dB. These simulation results are almost the same as the excess MSEs of −34.5 dB and −24.5 dB calculated by (15). This implies that the proposed method is able to achieve a misadjustment of 0.0035, as expected from (16). On the other hand, all the other VSLMS algorithms only attain the excess MSE in the neighborhood of −30 dB at SNR = 10 dB and −20 dB at SNR = 0 dB, which points to misadjustments of around 0.01.

Fig. 1
figure 1

Plots of excess MSE for various VSLMS algorithms. The input signal is white Gaussian noise with zero mean and unit variance. (a) SNR = 10 dB, ξ min=0.1, (b) SNR = 0 dB, ξ min=1

Full size image
Fig. 2
figure 2

Plots of excess MSE for various VSLMS algorithms. The input is a colored signal. (a) SNR = 10 dB, ξ min=0.1, (b) SNR = 0 dB, ξ min=1

Full size image

The behavior of step size adaptation by different VSLMS algorithms is illustrated in Fig. 3, which shows that the steady-state step size of the proposed method approaches 0.0012. This value is slightly smaller than the expected 0.0014 calculated by (13). The step size of the proposed method is controlled to have a relatively large value in the beginning for fast convergence, and is slowly decreased to ensure good control to reach a lower level of misadjustment.

Fig. 3
figure 3

Plots of step size versus the number of iterations for various VSLMS algorithms (white Gaussian input, SNR = 10 dB, and ξ min=0.1)

Full size image

The performance of different control functions is shown in Fig. 4. We observe that the control function (8) gives better performance than the other two when the input is a colored signal, whereas there is not much difference in performance among the three control functions for a white Gaussian input.

Fig. 4
figure 4

Performance comparison of different control functions (SNR = 10 dB and ξ min=0.1). (a) White Gaussian input, (b) colored input

Full size image

5 Conclusion

This paper has presented a function-controlled, variable step size LMS algorithm. The proposed method exploits an adjustable adaption scheme to enhance the LMS performance and alleviates the influence of the high-level noise power. Guidelines on the selection of the control functions and the updating parameter have been given. In addition, the excess MSE of the proposed method is theoretically derived and verified by experiment. The simulation results have demonstrated the improved performance of the proposed VSLMS scheme in terms of speed of convergence and level of misadjustment error. In conclusion, the proposed VSLMS method is suitable for unknown channel estimation applications.