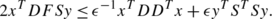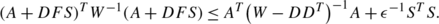1 Introduction

Recently, lots of significant researches focused on the design of dynamic anti-windup compensator for the systems with input saturation. In many practical systems, saturation causes the nonlinearity which may lead to performance degradation. In the past decades, a great number of results have been reported in [2, 3, 12, 13, 18, 19, 42, 43]. For instance, by using passivity theorem to deal with input saturation, some analysis results were presented in [12]. An optimization-based approach was proposed to design feedback and anti-windup gains of a controller subject to saturation in [3]. The static anti-windup synthesis problem for a class of linear systems with actuator amplitude and rate saturation was considered in [18]. The method based on multiobjective convex optimization was used to deal with the problem of anti-windup controller synthesis in [19]. By employing dynamic anti-windup scheme, the stability analysis and control synthesis problems for linear system with saturation were studied in [42, 43]. In addition, time delays which may cause difficulty in stability analysis and controller design are often encountered in many practical systems, and the stabilization problem of time-delay systems has attracted many researchers; see, e.g., [1, 5–7, 11, 15, 16, 29, 36–38], and the references therein. More recently, for time-delay systems with input saturation, the robust stabilization and optimal control problems were investigated in [27, 28].

On the other hand, considerable attention has been devoted to the study of Markovian jump systems in [9, 10, 20, 23–25, 30, 34, 41]. When taking time delays into account Markovian jump systems, various results on stability analysis [4, 14, 21, 46], controller design [5, 35, 40] and filter design [22, 26, 33, 45] have been presented, where the transition rates of the Markovian process are assumed to be completely known. While this assumption was removed in [32, 44]. Furthermore, for Markovian jump systems subject to saturation, the stability analysis and controller design problems were considered in [8, 17], respectively.

However, to the best of our knowledge, the robust stabilization problem of Markovian jump systems with time-delay and saturating actuators has not been fully investigated in the recent developed works. In this paper, we consider a class of Markovian time-delay systems with actuator saturation and partially known transition rates. By use of Lyapunov–Krasovskii function approach, a dynamic anti-windup compensator is designed to ensure the locally stability of the resulting closed-loop system. A numerical example is employed to show the potential of the proposed method. The contribution of this paper can be listed as follows:

  1. (1)

    Analyze the stability of this class of Markovian jump delayed systems with partly known transition rates;

  2. (2)

    Study the robust stabilization problem of the considered Markovian jump delayed systems with saturation and partly known transition rates by using the dynamic compensation scheme.

Notation

Throughout the paper, for symmetric matrices X and Y, the notation X≥Y (respectively, X>Y) means that the matrix X−Y is positive semi-definite (respectively, positive definite). I is the identity matrix with appropriate dimension. The notation M T represents the transpose of the matrix M; \((\varOmega,\mathcal{F},\mathcal{P})\) is a probability space; Ω is the sample space, \(\mathcal{F}\) is the σ-algebra of subsets of the sample space and \(\mathcal{P}\) is the probability measure on \(\mathcal{F}\); \(\mathcal{E} \{ \cdot \} \) denotes the expectation operator with respect to some probability measure \(\mathcal{P}\). Matrices, if not explicitly stated, are assumed to have compatible dimensions. The symbol ∗ is used to denote a matrix which can be inferred by symmetry. He{A}=A T+A.

2 Model Descriptions and Preliminaries

Consider the following class of Markovian jump systems (Σ) in the probability space \((\varOmega ,\mathcal{F},\mathcal{P})\):

(1)
(2)
(3)

where x(t)∈ℝn is the state vector, V(t)∈ℝm is the input, y(t)∈ℝq is the measurement output. The time-delay h(t)≤τ, τ is positive constant, and \(\dot{h}(t)\leq{d}<1\). {δ(t)} is a continuous-time Markovian process with right continuous trajectories and taking values in a finite set \(S=\{1,2,\ldots ,\mathcal{N}\}\) with transition probabilities given by

$$\Pr \bigl\{ \delta ( t+\Delta ) =j\vert \delta ( t ) =i \bigr\} = \left \{ \begin{array}{l@{\quad}l} \pi_{ij}\Delta +o ( \Delta ) & i\neq j, \\ 1+\pi_{ii}\Delta +o ( \Delta ) & i=j, \end{array} \right . $$

where Δ>0, limΔ→0(o(Δ)/Δ)=0 and π ij ≥0, for j≠i, is the transition rate from mode i at time t to mode j at time t+Δ and

$$\pi_{ii}=-\sum_{j\in{S},j \neq i }\pi_{ij }. $$

In this paper, the transition rates of the jumping process are considered to be partly accessible. For instance, the transition rates matrix of the system (Σ) may be expressed as follow:

where “?” represents the unknown transition rate. For notational clarity, ∀i∈S, the set S i denotes

with

Moreover, if \(S_{k}^{i}\neq\varnothing\), it is further described as

(4)

where m is non-negation integer with \(1\leq{m}\leq\mathcal{N}\) and \(k_{j}^{i}\in{Z^{+}}, 1\leq{k_{j}^{i}}\leq\mathcal{N}, j=1, 2,\ldots, \mathcal{N}\), represent the jth known element of the set \(S_{k}^{i}\) in the ith row of the transition rate matrix.

The plant inputs are supposed to be bounded as follows:

(5)

In the system (Σ), to simplify the notation, we denote A i +ΔA it =A(δ(t),t) for each δ(t)=i∈S, and the other symbols are similarly denoted. A i , A di , B i and C i are known real constant matrices of the system (Σ) for each δ(t)=i∈S, ΔA i (t), ΔA di (t), ΔB i (t) are unknown real matrices with

(6)

Assume that the following controller has been designed for stabilizing the system disregarding the control bounds given in (5) for each δ(t)=i∈S:

(7)
(8)

where \(x_{c}(t)\in{\mathbb{R}^{n_{c}}}\), \(u_{c}(t)\in{\mathbb{R}^{n_{p}}}\) and y c (t)∈ℝm. A ci , B ci , C ci , D ci are matrices with appropriate dimensions. In consequence of the control bounds, the nominal interconnection of the controller (7)–(8) with the system (Σ) is

Since that the controller was designed disregarding the control input bounds, the following anti-windup compensator is given to ensure the closed-loop stability of the system (Σ):

(9)
(10)

with vectors \(\psi(y_{c}(t))=\operatorname{sat}(y_{c}(t))-y_{c}(t)\), \(x_{a}(t)\in{\mathbb{R}^{n+n_{c}}}\), \(y_{a}(t)\in{\mathbb{R}^{n_{c}}}\) being, respectively, the input, the state, the output of the compensator. Then it is easy to achieve the new controller as follows:

Define ξ(t)=[x(t)T x c (t)T x a (t)T]T, the corresponding augmented system will be represented by the following equations:

(11)
(12)
(13)

where

with the following matrices:

3 Main Results

In this section, we investigate the design of anti-windup compensator which guarantees the locally stability of the resulting closed-loop system. Before presenting the main results, we first give the following lemmas:

Lemma 1

[27]

For the matrix K of the system (11)–(13), the appropriate matrix \(L_{i}\in{\mathbb{R}^{m\times2(n+n_{c})}}\) is given, if ξ(t) is in the set D(u o ), where D(u o ) is defined as follows:

then for any diagonal positive matrix T∈ℝm×m, the following inequality holds:

Lemma 2

[31]

For the matrices A,D,S,W>0, the matrix F(t)T F(t)≤I with appropriate dimensions, the following inequalities hold:

  1. (1)

    ∀ϵ>0 and x,y∈R n

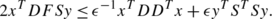
  2. (2)

    ∀ϵ>0, if W−ϵDD T>0,

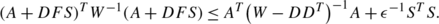
Lemma 3

[39]

For the given matrices X=X T,D,Z and the matrix R=R T>0 with appropriate dimensions, for all the F∈{F∣F T F≤R}, the following inequality holds:

if and only if there exists a scalar ϵ>0 this makes that the following holds:

Lemma 4

[3]

For the given symmetric matrix S∈ℝ(n+m)×(n+m)

where S 11∈ℝn×n, S 12∈ℝn×m, S 22∈ℝm×m, the following conditions are equivalent:

  1. (1)

    S<0.

  2. (2)

    S 11<0, \(S_{22}-S_{12}^{T}S_{11}^{-1}S_{12}<0\).

  3. (3)

    S 22<0, \(S_{11}-S_{12}S_{22}^{-1}S_{12}^{T}<0\).

Theorem 1

Consider system (Σ) with V(t)=0 and partially known transition rates, for each δ(t)=i∈S, the constant d<1 and scalars ε i >0, if there exist symmetric positive definite matrices P i ,R,W i , such that the following linear matrix inequalities (LMIs) hold:

(14)
(15)
(16)

where

and “ 0 ” is zero matrix with appropriate dimensions, then system (Σ) with V(t)=0 is stable.

Proof

Define the following Lyapunov function for each δ(t)=i∈S:

$$ V\bigl(x(t),i,t\bigr)=x(t)^{T}P_{i}x(t)+\int_{t-h(t)}^{t}x(\theta)^{T}Rx(\theta)\,d\theta, $$
(17)

then we derive

Based on the Lemma 2, it is easy to achieve that

Since \(\dot{h}(t)<d\), then we derive

where

By using the Schur complements, \(\bar{H}<0\) is equivalent to

(18)

Since ∑ j∈(s) π ij =0, it is easily shown that (18) is satisfied if LMIs in (14)–(16) are satisfied, which implies that \(\mathcal{L}V(x(t),i,t)<0\), in view of [25], it is easy to see that system (Σ) is stable. The proof is completed. □

We are now in a position to give some results on the dynamic anti-windup compensator design for the considered system (Σ).

Theorem 2

Consider the closed-loop system (11)–(13) with the partially known transition rates, for each δ(t)=i∈S, the given bound of the input u 0, the constant d<1 and scalars ϵ i >0, if there exist symmetric positive definite matrices X i ,Y i ,R i1,R i3,W i1, W i3,G 1,G 2, diagonal positive definite matrices S i , invertible matrix N i , and matrices \(\hat{A}_{ai},\hat{B}_{ai},\hat{C}_{ai},\hat{D}_{ai}, U_{i},V_{i},R_{i2},W_{i2}\), such that the following linear matrix inequalities (LMIs) hold:

(19)
(20)
(21)
(22)
(23)
(24)

where

with

and “ 0 ” is zero matrix with appropriate dimensions, then the resulting closed-loop system (11)–(13) is locally asymptotically stable for every initial condition belong to ε(P i ,1). In this case, the desired dynamic anti-windup compensator in the form of (9) and (10) can be designed with parameters as follows:

(25)
(26)

Proof

Define the following Lyapunov function for each δ(t)=i∈S

then we derive

Based on the Lemma 2, we have

(27)

where β(t)=[ξ(t)T ξ(t−h(t))T ψ(t)T]. From (27) and Lemma 1, one easily obtains the following inequality:

(28)

where

with

(29)

Due to ∑ j∈(s) π ij =0, it is easily showed that ∑ j∈(s) π ij ξ(t)T O i ξ(t)=0, where \(O_{i}=O_{i}^{T}>0\). Adding [−∑ j∈(s) π ij ξ(t)T O i ξ(t)] into \(\mathcal{L}V(\xi(t),i,t)\), we have

(30)

By employing the Schur complements, one can obtain

$$ \left [\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \varOmega_{i}&*&*&*\\[2pt] \hat{A}_{di}^{T}P_{i}&-(1-d)R&*&*\\[2pt] \hat{B}_{i}^{T}P_{i}+T_{i}L_{i}&0&-2T_{i}&*\\[2pt] \bar{N}_{i}&N_{di}&N_{bi}&-\epsilon_{i}{I} \end{array} \right ]<0, $$
(31)

then pre- and post-multiplying (31) by \(\operatorname{diag}(Q_{i},Q_{i},S_{i},I)\), respectively, we derive

$$ \left [\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \bar{\varOmega}_{i}&*&*&*\\[2pt] Q_{i}\hat{A}_{di}^{T}&-(1-d)\mathfrak{R}_{i}&*&*\\[2pt] S_{i}\hat{B}_{i}^{T}+Z_{i}&0&-2S_{i}&*\\[2pt] \bar{N}_{i}Q_{i}&N_{di}Q_{i}&N_{bi}S_{i}&-\epsilon_{i}{I} \end{array} \right ]<0, $$
(32)

where

Defining H as the left-hand side of (32), it follows that

(33)

where

with \(\bar{\varOmega}_{i0}=\hat{A}_{i}Q_{i}+Q_{i}\hat{A}_{i}^{T}+\mathfrak{R}_{i}+\epsilon_{i}\bar{M}_{i}\bar{M}_{i}^{T}\) and “0” is zero matrix with appropriate dimensions. From (33), one can easily find that if the following conditions hold, we have H<0:

(34)
(35)
(36)
(37)

Based on the conditions (34), (35) and by using the Schur complements, we derive

(38)
(39)

where

Here, we denote

then pre- and post-multiply (38) and (39) by \(\operatorname{diag} (\gamma^{T},\gamma^{T},I,\ldots,I)\) and its transpose, respectively, and define the following variable changes

and \(\hat{A}_{ai}=X_{i}\tilde{M}_{i}^{T}A_{ai}N_{i}\), \(\hat{B}_{ai}=X_{i}\tilde{M}_{i}^{T}B_{ai}S_{i}\), \(\hat{C}_{ai}=C_{ai}N_{i}\), \(\hat{D}_{ai}=D_{ai}S_{i}\), \(U_{i}=V_{i}+\tilde{U}_{i}\tilde{M}_{i}X_{i}\).

Note that it is easy to find a diagonal positive matrix G=G T≤Q i ,∀i∈S

then replace the \(Q_{k_{m}^{i}}\) of (38) and (39) by G 1 and G 2, it follows that (34) and (35) are equivalent to LMIs (19) and (20). By using Schur complements, from the condition (36) it follows that

$$ \left [\begin{array}{c@{\quad}c} -W_{i}&Q_{i}\\ Q_{i}&-Q_{j} \end{array} \right ]<0, $$
(40)

then pre- and post-multiplying (40) by \(\operatorname{diag} (\gamma^{T},I)\) and its transpose, respectively, and considering that G≤Q j , which implies the LMIs (21) is satisfied. Similarly, one can easily find that (37) is equivalent to LMIs (22). Since ε(P i ,1)⊂D(u 0), it follows that

$$ \left [\begin{array}{c@{\quad}c} P_{i}&*\\ \mathbf{K}_{i(k)}+L_{i(k)}&u_{0(k)}^{2} \end{array} \right ]>0,\quad k=1,\ldots,m, $$
(41)

then pre- and post-multiplying (41) by \(\operatorname{diag}(\gamma^{T}Q_{i},I)\) and its transpose, we derive LMIs (23). These imply that the resulting closed-loop system (11)–(13) is locally asymptotically stable for every initial condition belong to ε(P i ,1). The proof is completed. □

Algorithm:

Step 1:

: Use the LMIs (19)–(24) of Theorem 2 to get the \(\hat{A}_{ai},\hat{B}_{ai},\hat{C}_{ai},\hat{D}_{ai}\) and X i ,Y i ,N i .

Step 2:

: Based on the variable change which have been given in the proof process, and the parameters of step 1, compute the A ai ,B ai ,C ai ,D ai .

Remark 1

In this paper, a class of Markovian jump delayed systems with input saturation and partially known transition rates were considered. Different from the common proportional controller of the recent works, a dynamic anti-windup compensator is designed to deal with the robust stabilization problem of this class of Markovian jump delayed systems. Compared with recent developed works(for instance in [2]), via a dynamic anti-windup compensator, the system state response has less accommodation time and damping.

4 Simulation and Numerical Examples

In this section, a numerical example is provided to demonstrate the effectiveness of the proposed method.

Example 1

Consider the Markovian jump time-delay system (Σ) with the following parameters:

and with the following parameters of the controller:

In this example, the bounds of the input u 0=0.05, M=I, d=0.4, τ=0.1 and the transition rate matrix is given by the following:

Based on the Theorem 2, we derive dynamic anti-windup compensator parameters as follows:

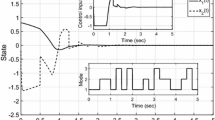
Then, from Figs. 1(a)–(d), the controller we designed guarantees that the resulting closed-loop constrained systems are mean-square stable. Note that the transition rates of the Markovian process of the systems under consideration were often assumed to be completely known in some recent developed works. In this paper, we consider a class of Markovian system with partly known transition rates and input saturation via a dynamic anti-windup compensator combined with a controller. Compared with the common proportional controller of the recent works, dynamic anti-windup compensator can reduce the accommodation time of the state response of systems.

Fig. 1
figure 1

(a) System modes evolutions r t ; (b) x(t) of open-loop system; (c) x(t) of closed-loop system; (d) the control input u(t)

Full size image

5 Conclusions

This paper considers the stabilization problem for a class of Markovian jump delayed systems with input saturation and partially known transition rates, and a methodology for synthesizing dynamic anti-windup compensators for systems is presented. By use of Lyapunov–Krasovskii function method, the sufficient conditions which ensure the system is locally stable are given in terms of linear matrix inequalities, and the trajectories of closed-loop system are bounded for every initial condition belong to ε(P i ,1). In the future work, we will study the stabilization problem for a class of singular or stochastic Markovian jump delayed systems with input saturation and partially known transition rates.