1 Introduction

Studies on dynamic systems with complicated switching law which are called switched systems have arisen in various disciplines of science and engineering in recent years [1, 2, 4, 6, 19, 27, 28]. Switched system usually consists of a family of subsystems and a switching signal. Many real-world processes and systems can be modeled as switched systems, such as power electronics, embedded systems, networked control systems, chemical processes, computer-controlled systems, automotive industry, etc.

It is well known that time delay can be encountered in various industrial systems and may be a main source of instability and poor performance of a control system. Thus, the stability of time-delay systems has been widely considered by many researchers [8, 23, 25, 26, 31]. Neutral system as a special class of time-delay systems appears in many dynamic systems, which depends on the delays of state and state derivative. Some practical examples of neutral systems include distributed networks, heat exchanges, and processes including steam [20]. In view of the strong engineering background, switched neutral systems have attracted special attention during the past decade. Some useful results have been reported in the literature (see, e.g. [3, 5, 7, 9, 21] and the references therein), primarily on the investigation of stability.

Tracking control, which can be divided into state tracking and output tracking, is an important issue in control field and has wide applications in dynamic processes in industry, economics, and biology. The main objective of output tracking control is trying to minimize the error between the output of the plant and the output of a given reference model via a designed controller [32]. The problem of H ∞ output tracking control for neutral systems with time-varying delay and nonlinear perturbations was investigated in [33, 34], and provided a less conservative result than one in the reference [32]. The issue of robust output feedback tracking control for time-delay nonlinear systems using neural network is studied in [12], where the reference signal is a given continuous bounded signal.

On the other hand, with the great development of the switched system theory, the tracking control problems of switched systems have received increasing attention in the last few years. In addition, the importance of the study of tracking control for switched systems with time-delay arises from the extensive applications in robot tracking control [22]. The issue of observer-based state tracking control and robust state tracking control for switched linear systems with time-varying delay was investigated in [15, 18], respectively. Li et al. investigated the robust tracking control problem for switched linear systems with time-varying delays and some sufficient conditions for the solvability of the robust tacking control problem were developed in [17]. In [16], the output tracking control problem for switched linear time-varying delayed systems with stabilizable and unstabilizable subsystems is investigated and some sufficient conditions for the solvability of the tracking control problem are developed. Hou et al. considered the problem of exponential l 2−l ∞ output tracking control for discrete-time switched system with time-varying delay in [11], where a class of discrete-time state feedback tracking controllers was constructed. However, the aforementioned papers on the tracking problem focus mainly on the switched time-delay systems. It is well known that neutral systems play a very important role in time-delay systems. To the best of the authors’ knowledge, the problem of tracking control of switched neutral systems with time delay has not been investigated, and this constitutes the main motivation of the present study.

In this paper, we are interested in investigating the exponential H ∞ output tracking control for switched neutral system with time-varying delay and nonlinear perturbations. By resorting to the average dwell time approach and Newton–Leibniz formula, sufficient conditions for exponential stability and H ∞ performance of switched systems with time delay are derived. Then, the problem of exponential H ∞ output tracking control is investigated. Finally, a numerical example is provided to demonstrate the potential and effectiveness of the proposed method. Compared with the previous results, the proposed results have the following highlights: (1) a new Lyapunov functional candidate is constructed to investigate exponential stability and H ∞ performance; (2) the nonlinear perturbation in this paper is quite general that include the usual Lipschitz conditions as a special case; (3) the exponential H ∞ performance is firstly introduced to study the output tracking problem of switched neutral systems.

Notations

Throughout this paper, the superscript “T” denotes the transpose, and the symmetric terms in a matrices are denoted by *. The notation X>0 (X≥,<,≤0) means that X is a positive definite (positive semi-definite, negative definite, semi-negative definite, respectively). R n denotes the n dimensional Euclidean space. ∥x(t)∥ denotes the Euclidean norm. L 2[0,∞) is the space of square integrable functions on [0,∞). λ max(P) and λ min(P) denote the maximum and minimum eigenvalues of matrix P, respectively. I is an identity matrix with appropriate dimension. Matrices, if not explicitly stated, are assumed to have compatible dimensions.

2 Problem Formulation and Preliminaries

Consider the following switched neutral systems with time-varying delay:

(1)
$$ z(t) = C_{1\sigma (t)}x(t) + C_{2\sigma (t)}x \bigl(t - d(t) \bigr) + D_{1\sigma (t)}u(t), $$
(2)
$$ x(t_{0} + \theta) = \varphi(\theta),\quad \theta\in [ - H,0 ] $$
(3)

where x(t)∈R n, u(t)∈R p, and z(t)∈R q are the state vector, input and output, respectively, w(t)∈R l is the noise input which is assumed to belong to L 2[t 0,∞),τ 1,τ 2 denotes the constant delay, d(t) denotes the time-varying state delay satisfying

(4)

with d and h being positive constant numbers, H=max{τ 1,τ 2,d,h},φ(θ) is a continuous vector-valued initial function. The function \(\sigma(t):[ t_{0}, \infty) \to\underline{N} = \{ 1,2, \ldots, N \}\) is the switching signal which is deterministic, piecewise constant and right continuous, corresponding to it, the switching sequence \(\sigma(t):\{ (t_{0},\sigma(t_{0})), (t_{1},\sigma(t_{1})), \ldots,(t_{k},\sigma(t_{k})) \ldots\},\sigma(t_{k}) \in\underline{N} ,k = 0,1, \ldots\,\), where t 0 is the initial time, and t k denotes the kth switching instant of the system. Moreover, σ(t)=i means that the ith subsystem is activated. N denotes the number of the subsystems. \(A_{i},B_{i},C_{i},D_{i},E_{i},C_{1i},C_{2i},D_{1i}, i \in\underline{N}\), are known constant matrices with appropriate dimensions. In addition, f i (⋅):R n→R n is nonlinear function satisfying

$$ \bigl(f_{i}(x) - \varTheta_{1i}x \bigr)^{T} \bigl(f_{i}(x) - \varTheta_{2i}x \bigr) \le 0,\quad x \in R^{n} $$
(5)

where Θ 1i ,Θ 2i are known real constant matrices.

Remark 1

The nonlinear function f i (x) satisfies the so-called sector condition in the sense that f i (x) belongs to the sector [Θ 1i ,Θ 2i ] (see Ref. [13]). Such a sector description is quite general and includes the usual Lipschitz conditions as a special case, and also covers several other classes of well-studied nonlinear systems (see the reference [10, 14]).

The reference model is given as

$$ \dot{x}_{r}(t) = A_{r}x_{r}(t) + D_{r}r(t), $$
(6)
$$ z_{r}(t) = C_{r}x_{r}(t), $$
(7)

where z r (t)∈R q,x r (t)∈R n is the reference state and r(t) is energy bounded reference input belonging to L 2[t 0,∞),A r is a Hurwitz matrix with appropriate dimensions.

Here, we are interested in designing a state feedback controller described by the following equation:

$$ u(t) = K_{1\sigma (t)}x(t) + K_{2\sigma (t)}x_{r}(t), $$
(8)

where K 1σ(t) and K 2σ(t) are controller gain matrices. Applying this controller to system (1)–(3), results in the following closed-loop system:

(9)
(10)

where \(\hat{A}_{\sigma (t)} = A_{\sigma (t)} + D_{\sigma (t)}K_{1\sigma (t)},\hat{D}_{\sigma (t)} = D_{\sigma (t)}K_{2\sigma (t)}\),

$$\hat{C}_{1\sigma (t)} = C_{1\sigma (t)} + D_{1\sigma (t)}K_{1\sigma (t)}, \quad \hat{D}_{1\sigma (t)} = D_{1\sigma (t)}K_{2\sigma (t)}. $$

Let \(\xi(t) = [ \begin{array}{c@{\quad}c} x^{T}(t) & x_{r}^{T}(t) \\\end{array} ]^{T},v(t) = [ \begin{array}{c@{\quad}c} w^{T}(t) & r^{T}(t) \\\end{array} ]^{T},e(t) = z(t) - z_{r}(t),y(t) = \dot{\xi} (t)\), we obtain the following augmented switched system:

(11)
$$ e(t) = \bar{C}_{1\sigma (t)}\xi(t) + \bar{C}_{2\sigma (t)}\xi \bigl(t - d(t) \bigr), $$
(12)

where

$$\bar{I}_{\sigma (t)} = \left [ \begin{array}{c} I \\ 0 \\\end{array} \right ], \quad \bar{C}_{1\sigma (t)} = \left [ \begin{array}{c@{\quad}c} \hat{C}_{1\sigma (t)} & - C_{r} + \hat{D}_{1\sigma (t)} \\\end{array} \right ],\quad \bar{C}_{2\sigma (t)} = \left [ \begin{array}{c@{\quad}c} C_{2\sigma (t)} & 0 \\\end{array} \right ]. $$

Denote

then we have \(\bar{A}_{\sigma (t)} = \tilde{A}_{\sigma (t)} + \tilde{D}_{\sigma (t)}K_{\sigma (t)},\bar{C}_{1\sigma (t)} = \tilde{C}_{1\sigma (t)} + D_{1\sigma (t)}K_{\sigma (t)}\), and the controller (8) can be rewritten as

$$ u(t) = K_{\sigma (t)}\xi(t). $$
(13)

Before moving on to the next section, we need the following definitions.

Definition 1

The system (1)–(3) with w(t)≡0 is said to be exponentially stabilizable under the controller u(t) and the switching signal σ(t), if its solution satisfies \(\| x(t) \| \le\alpha\| x(t_{0}) \|e^{ - \beta (t - t_{0})}\), where α≥1,β>0,t≥t 0.

Definition 2

For any T 2>T 1>0, let N σ (T 1,T 2) denote the switching number of σ(t) on an interval (T 1,T 2), if

(14)

holds for given N 0≥0,τ a >0. Then the constant τ a is called the average dwell time and N 0 is the chatter bound.

Remark 2

The concept of average dwell time was originally proposed for continuous-time switched systems by Hespanha and Morse (see Ref. [19]), which has been shown to be an effective tool for the stability analysis of switched systems. As commonly used in the literature, we choose N 0=0 in this paper.

Definition 3

Consider system (11)–(12), if the following conditions hold.

  1. (1)

    The system (11)–(12) is exponentially stable when v(t)≡0;

  2. (2)

    Under zero initial conditions, i.e. x(t)=0,x r (0)=0,t∈[−H,0], the system (11)–(12) satisfies \(\int_{t_{0}}^{\infty} e^{ - \alpha (t - t_{0})}e^{T}(t)e(t)\,dt \le\gamma^{2}\int_{t_{0}}^{\infty} v^{T}(t)v(t)\,dt\) when v(t)≠0.

Then system (11)–(12) is said to have exponential H ∞ performance γ, where α,γ>0 are positive constants.

Remark 3

The exponential H ∞ performance index was introduced for switched systems in [29] and was extended in [24]. In fact, the concept of exponential H ∞ performance index in the form of \(\sum_{s = k_{0}}^{\infty} (1 - \alpha)^{s}z^{T}(s)z(s) \le\sum_{s = k_{0}}^{\infty} \gamma^{2}w^{T}(s)w(s)\) is proposed for the discrete-time switched linear systems (see Definition 3 in [30]). In this paper, we modify the definition to adapt the tracking problem in switched neutral systems.

If there exists a state feedback controller (8) such that the resulting augmented switched system (11)–(12) is exponentially stable with an exponential H ∞ performance γ, then the controller (8) is said to be an exponential H ∞ output tracking controller.

The objective of this paper is to design an exponential H ∞ output tracking controller (8) such that system (11)–(12) is exponentially stable with an exponential H ∞ performance γ.

3 Main Results

3.1 Exponential Stability and H ∞ Performance Analysis

This subsection focuses on the analysis of the exponential stability and H ∞ output tracking performance.

Theorem 1

Consider the augmented system (11)–(12) with v(t)=0, if there exist positive definite matrices P i ,Q i ,R i ,S i ,T i >0, any matrices N i ,M i and scalar α>0 such that the following matrix inequality holds:

(15)

and the average dwell time satisfies

(16)

then the system is exponentially stable, where

and μ≥1 satisfying

(17)

Proof

For the ith subsystem, we define a Lyapunov functional candidate of the form

$$V_{i}(t) = V_{1i}(t) + V_{2i}(t) + V_{3i}(t) + V_{4i}(t) + V_{5i}(t) $$

with

$$ \begin{array}{l} \displaystyle V_{1i}(t) = \xi^{T}(t)P_{i}\xi(t) \\[2pt] \displaystyle V_{2i}(t) = \int_{t - d(t)}^{t} e^{\alpha (s - t)}\xi^{T}(s)R_{i}\xi(s) \,ds \\[10pt] \displaystyle V_{3i}(t) = \int_{ - d}^{0} \int_{t + \theta}^{t} e^{\alpha (s - t)}\dot{\xi}^{T}(s)Q_{i}\dot{\xi} (s) \,ds\,d\theta\\[10pt] \displaystyle V_{4i}(t) = \int_{t - \tau _{1}}^{t} e^{\alpha (s - t)}y^{T}(s)S_{i}y(s)\,ds \\[10pt] \displaystyle V_{5i}(t) = \int_{t - \tau _{2}}^{t} e^{\alpha (s - t)}f_{i}^{T} \bigl(x(s) \bigr)T_{i}f_{i} \bigl(x(s) \bigr) \,ds \end{array} $$
(18)

which is positive definite since P i ,Q i ,R i ,S i ,T i are positive definite matrices.

Along the trajectories of system (11) and (12), we have

(19)
(20)
(21)
(22)
(23)

It follows from the Newton–Leibniz formula that

(24)

Then for any matrices N i ,M i we have

(25)

The inequality (5) can be written as

(26)

Then combining (19)–(26) with v(t)=0, we have

(27)

where

and

Note that

(28)

By the Schur complement, (15) implies

(29)

Thus, it follows from (27)–(29) that

(30)

According to (17) and (18), we have

(31)

From (30)–(31) and k=N σ (t 0,t)≤(t−t 0)/τ a , for any t∈[t k ,t k+1), we have

(32)

Moreover, we obtain

(33)

Here

and

Therefore

(34)

By Definition 1, we know that system (11) and (12) is exponentially stable. This completes the proof. □

Now we are in a position to present the following theorem on the exponential H ∞ output tracking performance analysis.

Theorem 2

Consider the augmented system (11)–(12), if there exist positive definite matrices P i ,Q i ,R i ,S i ,T i >0, any matrices N i ,M i and scalar α>0 such that the following matrix inequality holds:

(35)

and the average dwell time satisfies (16), then the system (11)–(12) is exponentially stable with an exponential H ∞ output tracking performance γ. Here \(\phi_{11i}, \phi_{12i}, \phi_{22i}, \bar{\varTheta}_{1i}, \bar{\varTheta}_{2i}\) are given in (17).

Proof

From Theorem 1, we know that system (11)–(12) is exponentially stable with v(t)=0. In the sequel, we shall prove that the exponential H ∞ disturbance attenuation performance of system (11)–(12) is guaranteed for all nonzero v(t)∈L 2[t 0,∞) under the zero initial condition.

By (19)–(26), and using the same method in Theorem 1, we can obtain

(36)

when \(t \in[ \begin{array}{c@{\quad}c} t_{k} & t_{k + 1} \end{array} )\), the following matrix inequalities hold:

(37)

Let Δ(s)=e T(s)e(s)−γ 2 v T(s)v(s), from (18), (31) and (37), for \(t \in[ \begin{array}{c@{\quad}c} t_{k} & t_{k + 1} \end{array} )\), we have

(38)

Under zero initial conditions i.e. V(t 0)=0, (38) becomes

(39)

Multiplying both sides of (39) by \(e^{ - N_{\sigma} (t_{0},t)\ln \mu}\) yields

(40)

Note that N σ (t 0,s)≤(s−t 0)/τ a , and τ a >lnμ/α, we have

(41)

Therefore it follows from (40) and (41) that

(42)

Integrating both sides of (42) from t=t 0 to ∞ leads to

(43)

This means that system (11) and (12) achieves exponential H ∞ output tracking performance γ. This completes the proof. □

Remark 4

When μ=1 in (16), we have \(\tau_{a}^{*} = 0\), which implies that switching signals can be arbitrary.

Remark 5

Compared with the existing results, the proposed sufficient conditions are more general due to that the proposed Lyapunov–Krasovskii functional candidate includes the time-varying delay term d(t).

3.2 Exponential H ∞ Output Tracking Controller Design

In this subsection, we will solve the exponential H ∞ output tracking controller design problem.

Theorem 3

Consider system (1)–(3), there exists a state feedback controller of the form (13), such that the augmented closed-loop system (11)–(12) achieves the exponential H ∞ output tracking performance γ, if there exist matrices positive definite \(\bar{P}_{i} > 0,\bar{Q}_{i} > 0,\bar{R}_{i} > 0,\bar{S}_{i} > 0, T_{i} > 0\), any matrices \(\bar{N}_{i}, \bar{M}_{i},X_{i}\), and positive scalars α,γ>0 satisfying

(44)

where

and the average dwell time of the system satisfies (16), μ≥1 satisfying

(45)

Moreover, the gain matrices of a desired controller of the form (13) are given by

(46)

Proof

Performing a congruence transformation to (35) by \(\mathit{diag}\{ P_{i}^{ - 1},P_{i}^{ - 1},P_{i}^{ - 1},I,I,I,I,P_{i}^{ - 1},I,I \}\), denoting \(X_{i} = K_{i}\bar{P}_{i}\), together with the change of matrix variables defined by

and by the Schur complement, we find that (47) holds:

(47)

where \(\bar{\varPhi}_{11i} = \bar{P}_{i}\tilde{A}_{i}^{T} + \tilde{A}_{i}\bar{P}_{i} + \bar{R}_{i} + \alpha\bar{P}_{i} + \bar{N}_{i} + \bar{N}_{i}^{T} + X_{i}^{T}\tilde{D}_{i}^{T} + \tilde{D}_{i}X_{i} - \bar{P}_{i}\frac{\bar{\varTheta}_{1i}^{T}\bar{\varTheta}_{2i} + \bar{\varTheta}_{2i}^{T}\bar{\varTheta}_{1i}}{2}\bar{P}_{i}\).

Noticing that \(\bar{S}_{i},\bar{Q}_{i} > 0\), we have \((\bar{S}_{i} - \bar{P}_{i})\bar{S}_{i}^{ - 1}(\bar{S}_{i} - \bar{P}_{i}) \ge 0, (Q_{i} - \bar{P}_{i})\bar{Q}_{i}^{ - 1}(\bar{Q}_{i} - \bar{P}_{i}) \ge 0\) and \((\bar{\varTheta}_{1i} + \bar{\varTheta}_{2i})^{T}(\bar{\varTheta}_{1i} + \bar{\varTheta}_{2i}) \ge 0\), which are equivalent to

(48)
(49)
(50)

By combining (47)–(50), we readily obtain Theorem 3. This completes the proof of Theorem 3. □

Remark 6

From Theorem 3, it is easy to see that a smaller α will be favorable to the solvability of inequalities (44). On the contrary, a larger α is more desirable to relax τ a . Considering these, we can first select a smaller α to guarantee the feasible solution of inequalities (44), and then increase α to obtain the suitable α and τ a .

4 Numerical Example

In this section an example is given to illustrate the effectiveness of the proposed approach. Consider switched system (1)–(3) and reference system (6)–(7) with parameters as follows.

Subsystem 1:

Subsystem 2:

Reference system:

$$A_{r} = \left [ \begin{array}{c@{\quad}c} - 2 & - 0.2 \\ 0.3 & - 1 \end{array} \right ], \quad D_{r} = \left [ \begin{array}{c@{\quad}c} 0.1 & 0 \\ 0 & 0.1 \end{array} \right ],\quad C_{r} = \left [ \begin{array}{c@{\quad}c} 0.5 & 0.5 \end{array} \right ]. $$

It is assumed that α=0.5,τ 1=0.3,τ 2=0.2,γ=1,d(t)=0.1+0.1sin(t), from (4) we can get d=0.2,h=0.1. The nonlinear functions \(f_{1}(x) = f_{2}(x) = [ \begin{array}{c@{\quad}c} f_{a}^{T}(x) & f_{b}^{T}(x) \end{array} ]^{T}\) with

$$f_{a}(x) = - \tanh(x_{1}) + 0.5x_{1} + 0.1x_{2},\quad f_{b}(x) = 0.1x_{1} - \tanh(x_{2}) + 0.5x_{2} $$

It is easy to verify that

$$\varTheta_{11} = \varTheta_{12} = \left [ \begin{array}{c@{\quad}c} - 0.5 & 0.1 \\ 0.1 & - 0.5 \end{array} \right ],\quad \varTheta_{21} = \varTheta_{22} = \left [ \begin{array}{c@{\quad}c} 0.5 & 0.1 \\ 0.1 & 0.5 \end{array} \right ]. $$

Solving the matrix inequalities in Theorem 3, we obtain

$$K_{1} = \bigl[ 2.7538\quad {-}0.7641\quad {-}2.0955\quad {-}2.6662 \bigr], $$
$$K_{2} = \bigl[ 0.5400\quad 3.6895\quad {-}2.8241\quad {-}3.0730 \bigr]. $$

Then, according to (17), we can get μ=4, then \(\tau_{a}^{ *} = 2.7726\). In addition, the initial value of system (1)–(3) is assumed to be \(x(0) = [ \begin{array}{c@{\quad}c} 0.5 & - 0.5 \end{array} ]^{T}\), and the initial condition of reference model (6)–(7) is assumed to be \(x_{r}(0) = [ \begin{array}{c@{\quad}c} 0.1 & - 0.2 \end{array} ]^{T}\).

In the sequel, two kinds of reference signal r(t) are utilized to demonstrate the tracking results.

Case I: Sinusoidal reference signal

Let

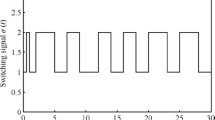
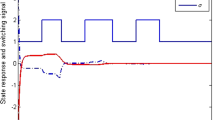
$$r(t) = \left \{ \begin{array}{l@{\quad}l} \left [ \begin{array}{l@{\quad}l} 2\sin(0.2\pi t) & 2\sin(0.2\pi t) \end{array} \right ]^{T},& 10 \le t \le25 \\ \left [ \begin{array}{c@{\quad}c} 0 & 0 \end{array} \right ]^{T},& \mathrm{others} \end{array} \right . $$
$$w(t) = \left \{ \begin{array}{l@{\quad}l} \left [ \begin{array}{c@{\quad}c} 0.2e^{- t} & 0.2e^{ - t} \end{array} \right ]^{T},&10 \le t \le 25 \\ \left [ \begin{array}{l@{\quad}l} 0 & 0 \end{array} \right ]^{T},& \mathrm{others} \\ \end{array} \right . $$

Obviously, we have v(t)∈L 2[0,∞). The switching signal σ(t) with average dwell time τ a =3 is shown in Fig. 1. The curves of output z(t) and z r (t) are shown in Fig. 2 under the sinusoidal signal. Figure 3 shows the error between the output of the system and the reference signal.

Fig. 1
figure 1

Switching signal

Full size image
Fig. 2
figure 2

Output z(t) and z r (t) under case I

Full size image
Fig. 3
figure 3

Tracking error under case I

Full size image

Case II: Step reference signal

Let

$$r(t) = \left \{ \begin{array}{l@{\quad}l} \left [ \begin{array}{l@{\quad}l} 0.5 & 0.5 \end{array} \right ]^{T},& 10 \le t \le25 \\ \left [ \begin{array}{l@{\quad}l} 0 & 0 \end{array} \right ]^{T},& \mathrm{others} \end{array} \right . $$
$$w(t) = \left \{ \begin{array}{l@{\quad}l} \left [ \begin{array}{l@{\quad}l} 0.2e^{ - t} & 0.2e^{ - t} \end{array} \right ]^{T},& 10 \le t \le 25 \\ \left [ \begin{array}{l@{\quad}l} 0 & 0 \end{array} \right ]^{T},& \mbox{others} \end{array} \right . $$

The curves of output z(t) and z r (t) are shown in Fig. 4. Figure 5 shows the error between the output of the system and the reference signal.

Fig. 4
figure 4

Output z(t) and z r (t) under case II

Full size image
Fig. 5
figure 5

Tracking error under case II

Full size image

It can be observed from Figs. 1–5 that the designed controller can guarantee the exponential stability and H ∞ output tracking performance of the closed-loop system. This shows the effectiveness of the proposed design method.

5 Conclusions

In this paper, the problem of exponential H ∞ output tracking control of switched neutral system with time-varying delay and nonlinear perturbations has been addressed. A new exponential stability criterion has been obtained. Furthermore, the desired exponential H ∞ output tracking controller has been designed. A numerical example was provided to show the effectiveness of the obtained results.