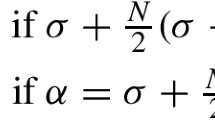Global boundedness of the immune chemotaxis system with general kinetic functions

Abstract

In this paper, we study the following reaction-diffusion-advection system

$$\begin{aligned} \left\{ \begin{aligned}{}&u_t=D_{u}\Delta u- \chi \nabla \cdot ( u\nabla v) + f(u),&(x,t)\in \Omega \times (0,\infty ), \\&v_t=D_{v}\Delta v+s_{v}uw-\mu _{v}v,&(x,t)\in \Omega \times (0,\infty ), \\&w_t=D_{w}\Delta w+s_{w}-\lambda _{w}uw-\mu _{w}w,&(x,t)\in \Omega \times (0,\infty ), \end{aligned} \right. \end{aligned}$$

in a smoothly bounded domain $\Omega \subset {\mathbb {R}}^{n}$, which describes a directed movement of immune cells toward chemokines during the immune process, where $D_{u},D_{v},D_{w},s_{v},s_{w},\lambda _{w}$, $\mu _{v},\mu _{w},\chi$ are positive parameters, and $f\in C^{1}([0,\infty ))$ is a kinetic function. When $n\ge 1$, if there exist positive constants $\alpha$ and $\theta _{0}$ such that $\sup _{s\ge 0}\{f(s)\!+\!\alpha s\}<\infty$ and $\lim _{s\rightarrow \infty }\inf \left\{ -\!\frac{f(s)}{s^{2}}\right\} =:\mu \in (\theta _{0},\infty ]$, then the solution of the system is global and uniformly bounded. In particular, when $n=2$ and $f(0)\ge 0$, the condition of f(u) could be improved as follows: if there exists $\alpha >0$ such that $\sup _{s\ge 0}\{f(s)+\alpha s\}<\infty$ and one of the conditions that $\lim _{s\rightarrow \infty }\inf \left\{ -\frac{f(s)\ln s}{s^{2}}\right\} =:\mu \in (\sqrt{2}\frac{\chi s_{v}C_{w}}{D_{v}},\infty ]$ or $\frac{2\sqrt{2}\chi s_{v}C_{GN}^{4}m_{1}C_{w}}{D_{v}}\le D_{u}$ holds, then the solution of the system is still global and uniformly bounded, where $m_{1}$ is a positive constant given by below, $C_{GN}>0$ is the Gagliardo-Nirenberg inequality’s constant and $C_{w}$ represents the uniform upper bound of w. Moreover, when $f\equiv 0$ and $\frac{2\sqrt{2}\chi s_{v}C_{GN}^{4}m_{1}C_{w}}{D_{v}}\le D_{u}$, the global and uniform boundedness of solutions can also be established.

1 Introduction

In this paper, we consider the following immune system induced by chemotaxis in [21] with general kinetic functions

$$\begin{aligned} \left\{ \begin{aligned}{}&u_t=D_{u}\Delta u- \chi \nabla \cdot ( u\nabla v) + f(u),&(x,t)\in \Omega \times (0,\infty ), \\&v_t=D_{v}\Delta v+s_{v}uw-\mu _{v}v,&(x,t)\in \Omega \times (0,\infty ), \\&w_t=D_{w}\Delta w+s_{w}-\lambda _{w}uw-\mu _{w}w,&(x,t)\in \Omega \times (0,\infty ),\\&\dfrac{\partial u}{\partial \nu }=\dfrac{\partial v}{\partial \nu }=\dfrac{\partial w}{\partial \nu }=0,&(x,t)\in \partial \Omega \times (0,\infty ), \\&u(x,0)=u_{0}(x), v(x,0)=v_{0}(x), w(x,0)=w_{0}(x),&x\in \Omega , \end{aligned} \right. \qquad \end{aligned}$$

(1.1)

where $\Omega \subset {\mathbb {R}}^{n}$ $(n\ge 1)$ is a smoothly bounded domain, the kinetic function f belongs to $C^{1}([0,+\infty ))$ and the initial data $u_{0}(x)$, $v_{0}(x)$, $w_{0}(x)$ are nonnegative functions satisfying

$$\begin{aligned} \begin{aligned}&u_{0}\in C^{0}({\overline{\Omega }}) ,v_{0}\in C^{1}({\overline{\Omega }}),w_{0}\in C^{0}({\overline{\Omega }}). \end{aligned} \end{aligned}$$

(1.2)

Moreover, the unknown functions u, v and w represent the density of immune cell, the concentrations of chemokine and antigen, respectively. $D_{u}$, $D_{v}$ and $D_{w}$ respectively denote the diffusion coefficients of the three elements and $\mu _{v}$, $\mu _{w}$ represent their own decline rates. The constant antigen $s_{w}> 0$ represents source of persistent infection and $s_{v}uw$ indicates that immune cells secrete chemokines based on the quality of the antigen. The term $-\lambda _{w}uw$ represent the depletion of phagocytosis. In addition, the source f(u) of immune cell includes its own decay and regulatory depletion. The chemosensitivity $\chi >0$ in the advection term contributes to the movement of immune cells towards the chemokine gradient.

In recent years, the researches on the immune system with chemotaxis have attracted many biologists and mathematicians (see [8, 9, 12, 13, 30, 30, 32]). Among them, the chemotactic system describes the directional movement of individual organisms in response to chemical signals, which is important in the immune system (see [7, 46]). More specifically, during immunity, immune cells secrete chemicals called chemokines at the site of inflammation. The eukaryotic cells then sense the gradient of chemokines by the polarization distribution of the receptor as they move toward a relatively high concentration of the chemical (chemical attraction) or in the opposite direction (chemical repulsion). To describe the above mentioned chemotactic movement of cells, the well-known minimal Keller-Segel chemotaxis model is proposed in [18]. However, a striking feature of this minimal Keller-Segel model is that the solution may blow up in finite or infinite time, depending largely on the spatial dimension. Therefore, in order to suppress this phenomenon, the following Keller-Segel model with source term has been proposed and studied by many authors

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial u}{\partial t}=\Delta u-\chi \nabla \cdot (u \nabla v)+f(u), &{} x \in \Omega , t>0, \\ \tau \frac{\partial v}{\partial t}=\Delta v-v+u, &{} x \in \Omega , t>0, \end{array}\right. } \end{aligned}$$

(1.3)

where $\tau \ge 0$, $\chi >0$, f(u) is a logistic source and $\Omega \subset {\mathbb {R}}^{n}$ is a bounded domain with smooth boundary $\partial \Omega$. For the case $f(u)=0$ in (1.3), there exists a finite-time blow-up solution for system (1.3) in the higher-dimensional case $n \ge 2$ (see [16, 40]). However, some rigorous results of (1.3) are shown that logistic source can prevent the occurrence of blow-up. In particular, in two-dimensional smooth bounded domain, Xiang [43] proved that the sub-logistic source f(u) can prevent the blow-up of solutions. When $f(u) \le a-b u^{\alpha }, a, b>0$ and $\alpha =2$, Winkler [37] proved the global existence and boundedness of solutions to (1.3) in a convex bounded smooth domain $\Omega \subset {\mathbb {R}}^{n}(n \ge 2)$. The finite-time blow-up of solutions for (1.3) is still possible if n and $\alpha$ are chosen in certain way [38]. Moreover, the global existence, asymptotic behavior or blow-up of solutions in more general quasilinear parabolic-parabolic chemotaxis systems with source term have been studied extensively (see [2, 6, 17, 33, 41, 44]).

Nowadays, some authors have also proposed the variants of (1.3) and obtained many interesting results (see [11, 14, 15, 24, 27, 47,48,49]). It is worth mentioning that in theoretical immunology, scholars often describe the evolution of virus populations by using the following chemotaxis May-Nowak model

$$\begin{aligned} \left\{ \begin{array}{lll} u_{t}=D_{u} \Delta u-\nabla \cdot (u f(u) \nabla v)-g(u) w+r-u, &{} x \in \Omega , &{} t>0, \\ v_{t}=D_{v} \Delta v+g(u) w-v, &{} x \in \Omega , &{} t>0, \\ w_{t}=D_{w} \Delta w+v-w, &{} x \in \Omega , &{} t>0, \\ \end{array}\right. \end{aligned}$$

(1.4)

where $\Omega \subset {\mathbb {R}}^{n}$ $(n\ge 1)$ is a smoothly bounded domain and the parameters $D_{u}, D_{v}, D_{w}, r$ are positive. When $f(u)=\chi$ and $g(u)=u$, Stancevic [31] revealed Turing-type instabilities to system (1.4) for suitably large $\chi$ by numerical simulations. If $f(u)=(1+u)^{-\alpha }$ and $g(u)=u$, Winkler [39] proved that whenever $\alpha >-1$ in $n=1$ and $\alpha >\frac{n-2}{n-1}$ in $n=2,3$, the solutions to system (1.4) are global and uniformly bounded. When $f(u)=1$ and $g(u)\le K_{f}u^{\alpha }$ with $K_{f}>0$, Fuest [10] proved that whenever $\alpha <\frac{2}{n}$, the solutions of system (1.4) exist globally and are bounded. When $f(u)=K_{f}(1+u)^{-\alpha }$ and $g(u)=K_{g}u^{\beta }$ with $K_{f} \in {\mathbb {R}}, K_{g}, \alpha , \beta >0$, Pan et.al [29] proved that the global boundedness of solutions is shown if $\alpha >\max \left\{ \frac{n \beta }{4}, \frac{\beta }{2}, \frac{n(n+2)}{6 n+8} \beta +\frac{1}{2}\right\}$. Besides, some interesting results have also been derived in [3, 4, 20, 34].

Recently, in order to describe a cross-talk between antigens and immune cells via chemokines, Lee [21] proposed a reaction-diffusion-advection system

$$\begin{aligned} \left\{ \begin{array}{lll} u_t=D_{u}\Delta u- \chi \nabla \cdot ( u\nabla v) + s_{u}-\lambda _{u}uw-\mu _{u}u, &{} x \in \Omega , &{} t>0 \\ v_t=D_{v}\Delta v+s_{v}uw-\mu _{v}v, &{} x \in \Omega , &{} t>0 \\ w_t=D_{w}\Delta w+s_{w}-\lambda _{w}uw-\mu _{w}w, &{} x \in \Omega , &{} t>0 \\ \end{array}\right. \end{aligned}$$

(1.5)

where $D_{u},D_{v},D_{w},s_{u},s_{v},s_{w},\lambda _{u},\lambda _{w},\mu _{u},\mu _{v},\mu _{w},\chi$ are positive parameters. Lee [21] analyzed the stability and instability that appeared in (1.5), and found that instability occurs when the chemosensitivity coefficient $\chi$ is suitably large; Yoon et.al [45] verified the global boundedness of solutions to system (1.5) in one and two dimensions. In the one-dimensional space, without being restricted by $\chi$ or the initial conditions, the global boundedness of solutions can be obtained. However, in the two-dimensional case, the global boundedness of solutions is obtained under some constraints of initial conditions and $\chi$. In addition, the stability of the non-constant steady state and the existence of periodic orbits are obtained, and the numerical results are given.

Moreover, the following chemotaxis model with indirect signal production and general kinetic function

$$\begin{aligned} {\left\{ \begin{array}{ll}u_{t}=\Delta u-\chi \nabla \cdot (u \nabla v)+f(u), &{} x \in \Omega , t>0 \\ v_{t}=\Delta v-v+w, &{} x \in \Omega , t>0 \\ \tau w_{t}+\lambda w=g(u), &{} x \in \Omega , t>0\end{array}\right. } \end{aligned}$$

(1.6)

has been studied by Li [22] in a bounded domain $\Omega \subset {\mathbb {R}}^{n}(n \le 3)$ with smooth boundary $\partial \Omega$, where $\chi , \tau , \lambda$ are given positive parameters, f and g are known functions. Li found several explicit conditions involving the kinetic function f, g, the parameters $\chi , \lambda$ and the initial mass $\left\| u_{0}\right\| _{L^{1}(\Omega )}$ to ensure the global-in-time existence and uniform boundedness for the corresponding $2 \textrm{D} / 3 \textrm{D}$ Neumann initial-boundary value problem.

To the best of our knowledge, there are still some gaps that need to be studied, such as the global existence and boundedness of the solutions for system (1.1) in higher dimensions. Inspired by [22], we consider the effect of the general kinetic function f(u) on the global boundedness of solutions for (1.1) in higher dimensions. Our main results are stated as follows.

Theorem 1.1

Let $\Omega \subset {\mathbb {R}}^{n}$, $n\ge 1$ be a bounded domain with smooth boundary. Suppose that the nonnegative initial data $(u_{0},v_{0},w_{0})$ satisfies (1.2) and the kinetic function f belongs to $C^{1}([0,+\infty ))$. Assume that there exists $\theta _{0}>0$ such that the following condition holds:

$$\begin{aligned} \exists \alpha >0,\text {s.t.} \sup _{s\ge 0}\{f(s)+\alpha s\}<\infty ,\lim _{s\rightarrow \infty }\inf \left\{ -\frac{f(s)}{s^{2}}\right\} =:\mu \in (\theta _{0}, \infty ]. \end{aligned}$$

Then system (1.1) has a unique global-in-time classical solution $(u,v,w)\in (C^{0}({\overline{\Omega }}\times [0,\infty )\cap C^{2,1}({\overline{\Omega }}\times (0,\infty )))^{3}$, which is uniformly bounded in the sense that there exists $C>0$ such that

$$\begin{aligned} ||u(\cdot ,t)||_{L^{\infty }(\Omega )}+||v(\cdot ,t)||_{W^{1,\infty }(\Omega )}+||w(\cdot ,t)||_{L^{\infty }(\Omega )}\le C \;\;\;\text {for all}\, t\in (0,\infty ). \end{aligned}$$

Remark 1.1

When $n=3$, this result of Theorem 1.1 is similar to that of [22], but we can cancel the restriction of dimensions. In fact, we use the result of Lemma 2.3 in [35] to derive the boundedness of $||u(\cdot ,t)||_{L^{p}(\Omega )}$, and combine the well-known $L^{p}-L^{q}$ estimate to obtain the boundedness of $||v(\cdot ,t)||_{W^{1,\infty }(\Omega )}$, which allows us to get rid of the dimensional limitation of the Gagliardo-Nirenberg inequality. However, since $\theta _{0}=\chi s_{v} C_{w}\frac{p-1}{p}C_{S}(p)^{\frac{1}{p+1}}>0$ for $p>1$, where $C_{w}>0$ represents the uniform upper bound of w(x, t), the constant $C_{S}(p)$ is produced by the maximal Sobolev regularity estimate in Lemma 3.1, which depends on p in a fairly intransparent manner, then two different cases arise: if $C_S(p)^{\frac{1}{p+1}}\rightarrow C_{S_{0}}$ as $p\rightarrow \infty$ for some constant $C_{S_{0}}\ge 0$, the condition is simplified to $\mu \in (\chi s_{v}C_{w}C_{S_{0}}, \infty ]$ for sufficiently large p; if $C_S(p)^{\frac{1}{p+1}}\rightarrow \infty$ as $p\rightarrow \infty$, then the value of $\mu$ needs to be large enough or even $\mu \rightarrow \infty$ for $p\rightarrow \infty$. In addition, this result implies that when $f(u)=\mu u(1-u)$ with $\mu$ is sufficiently large in the multi-dimensional space, the solution is globally bounded in system (1.1).

In particular, when $n=2$, the condition of f(u) could be improved by using some new estimates as follows.

Theorem 1.2

Let $\Omega \subset {\mathbb {R}}^{2}$ be a bounded domain with smooth boundary. Suppose that the nonnegative initial data $(u_{0},v_{0},w_{0})$ satisfies (1.2) and f belongs to $C^{1}([0,+\infty ))$ satisfying $f(0)\ge 0$. Assume that one of the following conditions holds:

$$\begin{aligned} \begin{aligned}&(i)\,\,\exists \alpha>0,\text {s.t. } sup_{s\ge 0}\{f(s)+\alpha s\}<\infty ,\lim _{s\rightarrow \infty }\inf \{-\frac{f(s)\ln s}{s^{2}}\}=:\mu \in (\sqrt{2}\frac{\chi s_{v}C_{w}}{D_{v}},\infty ],\\&(ii)\,\,\exists \alpha >0,\text {s.t. } sup_{s\ge 0}\{f(s)+\alpha s\}<\infty ,\frac{2\sqrt{2}\chi s_{v}C_{GN}^{4}m_{1}C_{w}}{D_{v}}\le D_{u},\\&(iii)\,\,f\equiv 0,\frac{2\sqrt{2}\chi s_{v}C_{GN}^{4}m_{1}C_{w}}{D_{v}}\le D_{u}, \end{aligned} \end{aligned}$$

where $C_{GN}>0$ is the Gagliardo-Nirenberg inequality’s constant given in Lemma 2.2, $m_{1}$ is given in (2.4) and $C_{w}$ represents the uniform upper bound of w(x, t) given in Lemma 2.1. Then system (1.1) possesses a unique global-in-time classical solution $(u,v,w)\in (C^{0}({\overline{\Omega }}\times [0,\infty )\cap C^{2,1}({\overline{\Omega }}\times (0,\infty )))^{3}$, which is uniformly bounded in the sense that there exists $C>0$ such that

$$\begin{aligned} ||u(\cdot ,t)||_{L^{\infty }(\Omega )}+||v(\cdot ,t)||_{W^{1,\infty }(\Omega )}+||w(\cdot ,t)||_{L^{\infty }(\Omega )}\le C \;\;\;\text {for all}\,\, t\in (0,\infty ). \end{aligned}$$

Remark 1.2

When $n=2$, the condition (i) is similar as in [22], but there exists a difference that the range of $\mu$ has nothing to do with the initial data $||u_{0}||_{L^{1}(\Omega )}$ in Theorem 1.2. Moreover, the condition (i) implies that the order of f(u) can ensure the boundedness of the solution in system (1.1). For example, when $f(u)=\mu u(1-u)$ with any $\mu >0$ in two-dimensional space (see [26, 28],etc), which can establish the boundedness of solutions in (1.1). Furthermore, it’s worth mentioning that when $f(u)=-\mu \frac{u^{2}}{\ln u}$ with sufficiently large $\mu$, the global boundedness of solutions can be obtained by (i) in Theorem 1.2, but it cannot be obtained by Theorem 1.1, which means that the condition of f(u) has been improved. Apart from this, the conditions (ii) and (iii) imply that when $f\equiv 0$ or $f(u)=-\alpha u$ for any $\alpha >0$, if the diffusion coefficient $D_{u}$ and $D_{v}$ are sufficiently large, the boundedness of solutions in (1.1) can also be established.

The rest of the article is organized as follows. Section 2 gives some preliminary lemmas. In Sects. 3 and 4, we shall prove Theorem 1.1 and Theorem 1.2 respectively. In addition, we let $u(\cdot ,t)=u(x,t)$ and omit the sign dx during integrating throughout this paper.

2 Preliminaries

In this section, we first give some preliminaries.

Lemma 2.1

Let $\Omega \subset {\mathbb {R}}^{n}(n\ge 1)$ be a smoothly bounded domain. Assume that the function $f\equiv 0$ or f belongs to $C^{1}([0,+\infty ))$ and the nonnegative initial data $(u_{0},v_{0},w_{0})$ satisfies (1.2). Then there exist $T_{\max }\in (0,\infty ]$ and a uniquely determined triple (u, v, w) with

$$\begin{aligned} \begin{aligned}&u\in C^{0}({\overline{\Omega }}\times [0,T_{\max }))\cap C^{2,1}({\overline{\Omega }}\times (0,T_{\max })),\\&v\in C^{0}({\overline{\Omega }}\times [0,T_{\max }))\cap C^{2,1}({\overline{\Omega }}\times (0,T_{\max })),\\&w\in C^{0}({\overline{\Omega }}\times [0,T_{\max }))\cap C^{2,1}({\overline{\Omega }}\times (0,T_{\max })), \end{aligned} \end{aligned}$$

such that (u, v, w) solves problem (1.1) classically in $\Omega \times \left( 0, T_{\max }\right)$. Moreover, if $T_{\max }<\infty$, then

$$\begin{aligned} \sup ||u(\cdot ,t)||_{L^{\infty }(\Omega )}\rightarrow \infty ,\;\;\;\hbox { as}\ t\nearrow T_{\max }. \end{aligned}$$

(2.1)

In addition, there exists a positive constant $C_{w}$ such that

$$\begin{aligned} 0\le w(x,t)\le C_{w} \;\;\;\text {for}\; (x,t)\in {\overline{\Omega }}\times (0,T_{\max }). \end{aligned}$$

Proof

By Amman’s well-established parabolic theory introduced in Theorem 7.3 of [1], we can obtain the local existence, uniqueness and blow-up criterion (2.1). By the standard comparison principle for parabolic equations (cf. Lemma 2.1 of [45] for details), we ensure the boundedness of w(x, t). $\Box$

Lemma 2.2

(see [25]) Let $\Omega \subset {\mathbb {R}}^{n}$, $n\ge 1$ be a bounded domain with smooth boundary, and let $p\geqslant 1$, $q\in (0,p)$. Then there exists a constant $C_{GN}>0$ such that

$$\begin{aligned} ||u||_{L^{p}(\Omega )}\le C_{GN}(||\nabla u||_{L^{2}(\Omega )}^{\delta }||u||_{L^{q}(\Omega )}^{1-\delta }+||u||_{L^{r}(\Omega )}), \end{aligned}$$

where $r\ge 0$ is arbitrary and $\delta =\frac{\frac{n}{q}-\frac{n}{p}}{1-\frac{n}{2}+\frac{n}{q}}\in (0,1)$.

Lemma 2.3

Assume that $f\equiv 0$ or f satisfies

$$\begin{aligned} \mathop {\sup }\limits _{s\ge 0} \{f(s)+\alpha s\}<\infty , \end{aligned}$$

(2.2)

with some positive constant $\alpha$, then the solution component u of (1.1) satisfies

$$\begin{aligned} ||u(\cdot ,t)||_{L^{1}(\Omega )}\le m_{1}, \end{aligned}$$

(2.3)

where

$$\begin{aligned} m_{1}:= {\left\{ \begin{array}{ll}{} \max \left\{ ||u_{0}||_{L^{1}(\Omega )},\frac{\sup _{s\ge 0}\{f(s)+\alpha s\}|\Omega |}{\alpha }\right\} ,\;&{}\text {if}\; \sup _{s\ge 0}\{f(s)+\alpha s\}<\infty , \\ ||u_{0}||_{L^{1}(\Omega )},\;&{}\text {if}\;f(u)=0. \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.4)

Proof

By integrating the first Eq. (1.1) with respect to $x\in \Omega$, we have

$$\begin{aligned} \frac{d}{dt}\int _{\Omega } u = \int _{\Omega } f(u)\hbox { for all}\ t\in (0,T_{\max }). \end{aligned}$$

If f(u) satisfies (2.2), we have

$$\begin{aligned} \frac{d}{dt}\int _{\Omega } u + \alpha \int _{\Omega } u = \int _{\Omega } (f(u)+\alpha u) \le \sup _{s\ge 0}\{f(s)+\alpha s\}|\Omega |\hbox { for all} \, t\in (0,T_{\max }), \end{aligned}$$

which implies that (2.3) holds by using the ODE argument.

If $f(u)=0$, then the mass of solution component u of (1.1) is conserved, i.e,

$$\begin{aligned} ||u(\cdot ,t)||_{L^{1}(\Omega )} = ||u_{0}||_{L^{1}(\Omega )}\hbox { for all} \, t\in (0,T_{\max }). \end{aligned}$$

The proof of Lemma 2.3 is complete. $\Box$

3 Proof of theorem 1.1

In this section, we shall prove the uniform boundedness of the solution of (1.1) in the space dimension $n\ge 1$. To do this, we need the following maximal Sobolev regularity estimate.

Lemma 3.1

(See Lemma 2.3 in [35]) Let $\Omega \subset {\mathbb {R}}^{n}(n\ge 1)$ be a smoothly bounded domain, and let $0\le t_{0}<T_{\max }\le \infty$ and $p\in (n,+\infty )$. Assume that each $z_{0}\in W^{2,p}(\Omega )$ with $\partial _{\nu }z_{0}=0$ on $\partial \Omega$ and $h\in L^{p}\left( [0,T_{\max });L^{p}(\Omega )\right)$, then the problem

$$\begin{aligned} \left\{ \begin{aligned}{}&z_t=D_{z}\Delta z-\mu _{z}z+h,&(x,t)\in \Omega \times (0,T_{\max }), \\&\dfrac{\partial z}{\partial \nu }=0,&(x,t)\in \partial \Omega \times (0,T_{\max }), \\&z(\cdot ,0)=z_{0},&x\in \Omega , \end{aligned} \right. \end{aligned}$$

exists a unique solution $z\in W^{1,p}\left( [0,T_{\max });L^{p}(\Omega )\right) \bigcap L^{p}\left( [0,T_{\max }); W^{2,p}(\Omega )\right)$, where $D_{z}$ and $\mu _{z}$ are positive constants. Moreover, there exists $C_{S}(p)>0$ such that

$$\begin{aligned}{} & {} \int _{t_{0}}^{t}e^{p\tau }\int _{\Omega }|\Delta z(\cdot ,\tau )|^{p}d\tau \\ {}{} & {} \quad \le C_{S}(p)\int _{t_{0}}^{t}e^{p\tau }\int _{\Omega }|h(\cdot ,s)|^{p}d\tau +C_{S}(p)e^{{pt_{0}}}||\Delta z(\cdot ,t_{0})||_{L^{p}(\Omega )}^{p} \end{aligned}$$

for any $t\in (t_{0},T_{\max })$.

Lemma 3.2

Let $\Omega \subset {\mathbb {R}}^{n}(n\ge 1)$ be a smoothly bounded domain and the kinetic function f belongs to $C^{1}([0,+\infty ))$. Assume that there exists $\theta _{0}>0$ such that the following condition holds:

$$\begin{aligned} \exists \alpha >0,\text {s.t. } \sup _{s\ge 0}\{f(s)+\alpha s\}<\infty ,\lim _{s\rightarrow \infty }\inf \left\{ -\frac{f(s)}{s^{2}}\right\} =:\mu \in (\theta _{0}, \infty ]. \end{aligned}$$

Then for any $p>1$, there exists $C>0$ such that

$$\begin{aligned} \int _{\Omega }u^{p}(\cdot ,t)\le C\;\;\;\hbox { for all} \, t\in (0,T_{\max }). \end{aligned}$$

Proof

Testing the first Eq. (1.1) by $pu^{p-1}$ for all $p>1$, we obtain

$$\begin{aligned} \begin{aligned} \dfrac{d}{dt}\int _{\Omega }u^{p}&=D_{u}p\int _{\Omega }u^{p-1}\Delta u-\chi p\int _{\Omega }u^{p-1}\nabla \cdot (u\nabla v)+p\int _{\Omega }u^{p-1}f(u)\\&=-\frac{4D_{u}p(p-1)}{p^{2}}\int _{\Omega }|\nabla u^{\frac{p}{2}}|^{2}+\chi p(p-1)\int _{\Omega }u^{p-1}\nabla u\cdot \nabla v\\&\quad +p\int _{\Omega }u^{p-1}f(u). \end{aligned} \end{aligned}$$

(3.1)

Applying Young’s inequality to the second term on the right of (3.1), we deduce

$$\begin{aligned} \begin{aligned} \chi p(p-1)\int _{\Omega }u^{p-1}\nabla u\cdot \nabla v&=-\chi (p-1)\int _{\Omega }u^{p}\cdot \Delta v\\&\le \chi (p-1)\int _{\Omega }u^{p}|\Delta v|\\&\le \epsilon \int _{\Omega }u^{p+1}+c_{\epsilon }\chi ^{p+1}(p-1)^{p+1}\int _{\Omega }|\Delta v|^{p+1}, \end{aligned} \end{aligned}$$

(3.2)

where $\epsilon >0$ shall be determined later and $c_{\epsilon }=\frac{p^{p}}{(p+1)^{p+1}\epsilon ^{p}}$. By combining (3.1) with (3.2), we have

$$\begin{aligned} \begin{aligned}&\dfrac{d}{dt}\int _{\Omega }u^{p}+\frac{4D_{u}p(p-1)}{p^{2}}\int _{\Omega }|\nabla u^{\frac{p}{2}}|^{2}\\&\le \epsilon \int _{\Omega }u^{p+1}+c_{\epsilon }\chi ^{p+1}(p-1)^{p+1}\int _{\Omega }|\Delta v|^{p+1}+p\int _{\Omega }u^{p-1}f(u). \end{aligned} \end{aligned}$$

(3.3)

By using Lemma 2.2, Lemma 2.3 and Young’s inequality, there exist positive constants $C_{1}$, $C_{2}$ and $C_{3}$ such that

$$\begin{aligned} \begin{aligned} \int _{\Omega }u^{p}&=||u^{\frac{p}{2}}||_{L^{2}(\Omega )}^{2}\\&\le C_{1} ||\nabla u^{\frac{p}{2}}||_{L^{2}(\Omega )}^{2a_{1}}||u^{\frac{p}{2}}||_{L^{\frac{2}{p}}(\Omega )}^{2(1-a_{1})}+C_{1}||u^{\frac{p}{2}}||_{L^{\frac{2}{p}}(\Omega )}^{2}\\&\le C_{2} ||\nabla u^{\frac{p}{2}}||_{L^{2}(\Omega )}^{2a_{1}}+C_{2}\\&\le \frac{4D_{u}p(p-1)}{p^{2}(p+1)}\int _{\Omega }|\nabla u^{\frac{p}{2}}|^{2}+C_{3}, \end{aligned} \end{aligned}$$

(3.4)

where $a_{1}:=\dfrac{\frac{np}{2}-\frac{n}{2}}{1-\frac{n}{2}+\frac{np}{2}}\in (0,1)$ for any $p>1$ and $n\ge 1$.

Combining (3.3) and (3.4), we obtain

$$\begin{aligned} \begin{aligned}&\dfrac{d}{dt}\int _{\Omega }u^{p}+(p+1)\int _{\Omega }u^{p}\\&\le \epsilon \int _{\Omega }u^{p+1}+c_{\epsilon }\chi ^{p+1}(p-1)^{p+1}\int _{\Omega }|\Delta v|^{p+1}+p\int _{\Omega }u^{p-1}f(u)+C_{4}, \end{aligned} \end{aligned}$$

(3.5)

where $C_{4}=(p+1)C_{3}$. Integrating (3.5) from $t_{0}$ to t, we derive

$$\begin{aligned} \begin{aligned} \int _{\Omega }u^{p}(\cdot ,t)&\le \epsilon e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }u^{p+1}(\cdot ,\tau )d\tau \\&\;\;\;+ c_{\epsilon }\chi ^{p+1}(p-1)^{p+1}e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }|\Delta v|^{p+1}(\cdot ,\tau )d\tau \\&\;\;\;+p e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }u^{p-1}f(u)(\cdot ,\tau )d\tau \\&\;\;\;+e^{(p+1)(t_{0}-t)}\int _{\Omega }u^{p}(\cdot ,t_{0})+C_{4}e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }d\tau \\&\le \epsilon e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }u^{p+1}(\cdot ,\tau )d\tau \\&\;\;\;+ c_{\epsilon }\chi ^{p+1}(p-1)^{p+1}e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }|\Delta v|^{p+1}(\cdot ,\tau )d\tau \\&\;\;\;+p e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }u^{p-1}f(u)(\cdot ,\tau )d\tau +C_{5}, \end{aligned} \end{aligned}$$

(3.6)

for any fixed time $t_{0}\in (0,T_{\max })$ and $t\in (t_{0},T_{\max })$, where $C_{5}=\int _{\Omega }u^{p}(\cdot ,t_{0})+\frac{C_{4}}{p+1}$.

Applying Lemma 3.1 to the second Eq. (1.1) and combining the boundedness of $w(\cdot ,t)$ in Lemma 2.1, there exists a positive constant $C_{S}(p)$ such that

$$\begin{aligned}&\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }|\Delta v|^{p+1}(\cdot ,\tau )d\tau \nonumber \\&\quad \le C_{S}(p) \int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }(s_{v}uw)^{p+1}d\tau +C_{S}(p)e^{(p+1)t_{0}}||\Delta v(\cdot ,t_{0})||_{L^{p+1}(\Omega )}^{p+1} \nonumber \\&\quad \le K(p)\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }u^{ p+1}(\cdot ,\tau )d\tau +C_{S}(p)e^{(p+1)t_{0}}||\Delta v(\cdot ,t_{0})||_{L^{p+1}(\Omega )}^{p+1},\nonumber \\ \end{aligned}$$

(3.7)

where $K(p)=C_{S}(p)s_{v}^{p+1}C_{w}^{p+1}$. Substituting (3.7) into (3.6), we derive

$$\begin{aligned} \begin{aligned} \int _{\Omega }u^{p}(\cdot ,t)&\le (\epsilon +c_{\epsilon }\chi ^{p+1}(p-1)^{p+1}K(p)) e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }u^{p+1}(\cdot ,\tau )d\tau \\&\;\;\;+p e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }u^{p-1}f(u)(\cdot ,\tau )d\tau +C_{6}, \end{aligned} \end{aligned}$$

(3.8)

where $C_{6}=C_{5}+c_{\epsilon }\chi ^{p+1}(p-1)^{p+1} C_{S}(p)e^{(p+1)t_{0}}||\Delta v(\cdot ,t_{0})||_{L^{p+1}(\Omega )}^{p+1}$. Setting

$$\begin{aligned} F_{1}(\epsilon ):=\epsilon +c_{\epsilon }\chi ^{p+1}(p-1)^{p+1}K(p), \end{aligned}$$

(3.9)

it follows from $c_{\epsilon }$ in (3.2) and some simple calculations that $F_{1}(\epsilon )$ can attain the minimum value

$$\begin{aligned} \min _{\epsilon >0} F_{1}(\epsilon )=\chi (p-1)K(p)^{\frac{1}{p+1}}, \end{aligned}$$

(3.10)

when $\epsilon =\frac{p}{p+1}\chi (p-1)K(p)^{\frac{1}{p+1}}$. With this $\epsilon$, we can derive

$$\begin{aligned} \begin{aligned} \int _{\Omega }u^{p}(\cdot ,t)&\le \chi (p-1)K(p)^{\frac{1}{p+1}}e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }u^{p+1}(\cdot ,\tau )d\tau \\&\;\;\;+p e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }u^{p-1}f(u)(\cdot ,\tau )d\tau +C_{6}. \end{aligned} \end{aligned}$$

(3.11)

Let

$$\begin{aligned} F_{2}(s):=\chi (p-1)K(p)^{\frac{1}{p+1}}s^{p+1}+ps^{p-1}f(s), \end{aligned}$$

(3.12)

it follows from $\lim _{s\rightarrow \infty }\inf \{-\frac{f(s)}{s^{2}}\}=:\mu \in (\theta _{0}, \infty ]$ for $\theta _{0}=\chi s_{v} C_{w}\frac{p-1}{p}C_{S}(p)^{\frac{1}{p+1}}>0$ that

$$\begin{aligned} \lim _{s\rightarrow \infty }\inf \frac{1}{s^{p+1}}F_{2}(s)=\chi (p-1)K(p)^{\frac{1}{p+1}}-p\mu <0, \end{aligned}$$

(3.13)

so that

$$\begin{aligned} \exists s_{1}>0,\hbox { s.t. }F_{2}(s) <0\;\;\;\text {for all} \, s> s_{1}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \begin{aligned}&\chi (p-1)K(p)^{\frac{1}{p+1}}e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }u^{p+1}(\cdot ,\tau )d\tau \\&\;\;\;+p e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }u^{p-1}f(u)(\cdot ,\tau )d\tau \\&=e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\Omega }[\chi (p-1)K(p)^{\frac{1}{p+1}}u^{p+1}+pu^{p-1}f(u)](\cdot ,\tau )d\tau \\&=e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\{u\le s_{1}\}}F_{2}(u)(\cdot ,\tau )d\tau \\&\;\;\;+e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\{u> s_{1}\}}F_{2}(u)(\cdot ,\tau )d\tau \\&\le e^{-(p+1)t}\int _{t_{0}}^{t}e^{(p+1)\tau }\int _{\{u\le s_{1}\}}F_{2}(u)(\cdot ,\tau )d\tau \\&\le \frac{1}{p+1}\sup _{0<s\le s_{1}}[F_{2}(s)]|\Omega |<\infty . \end{aligned} \end{aligned}$$

(3.14)

Substituting (3.14) into (3.11), we derive

$$\begin{aligned} \int _{\Omega }u^{p}(\cdot ,t)\le C \end{aligned}$$

(3.15)

for all $t\in (0,T_{\max })$. $\Box$

Lemma 3.3

Let the conditions of Lemma 3.2 hold, then there exists $C>0$ such that the solution component v of (1.1) fulfills

$$\begin{aligned} ||v(\cdot ,t)||_{W^{1,\infty }(\Omega )}\le C \hbox { for all}\ t\in (0,T_{\max }). \end{aligned}$$

(3.16)

Proof

With the uniform boundedness on $w(\cdot ,t)$ in Lemma 2.1, we can represent the second Eq. (1.1) via the heat Neumann semigroup as follows

$$\begin{aligned} \begin{aligned} v(\cdot ,t)&=e^{t(D_{v}\Delta -\mu _{v})}v_{0}+\int _{0}^{t}e^{(t-\tau )(D_{v}\Delta -\mu _{v})}s_{v}uw(\cdot ,\tau )d\tau \\&\le e^{t(D_{v}\Delta -\mu _{v})}v_{0}+s_{v}C_{w}\int _{0}^{t}e^{(t-\tau )(D_{v}\Delta -\mu _{v})}u(\cdot ,\tau )d\tau \end{aligned} \end{aligned}$$

(3.17)

for all $t\in (0,T_{\max })$.

Now, by the well-known $L^{p}-L^{q}$ estimate in [36], we can deduce the following results:

(i) By Lemma 1.3 (i) of [36], there exist positive constants $C_{7}$ and $C_{8}$ such that

$$\begin{aligned} \begin{aligned}&\Vert v(\cdot ,t)\Vert _{L^{\infty }(\Omega )}\\&\quad \le \Vert e^{t(D_{v}\Delta -\mu _{v})}v_{0}\Vert _{L^{\infty }(\Omega )}+s_{v}C_{w}\int _{0}^{t}\Vert e^{(t-\tau )(D_{v}\Delta -\mu _{v})}u(\cdot ,\tau )\Vert _{L^{\infty }(\Omega )}d\tau \\&\quad \le C_{7}\Vert v_{0}\Vert _{L^{\infty }(\Omega )}+C_{7}\int _{0}^{t}[1+(t-\tau )^{-\frac{n}{2p}}]e^{-(D_{v}\lambda _{1}+\mu _{v})(t-\tau )}\Vert u(\cdot ,\tau )\Vert _{L^{p}(\Omega )}d\tau \\&\quad \le C_{8} \end{aligned} \end{aligned}$$

$t\in (0,T_{\max })$, where $\lambda _{1}$ is the first positive eigenvalue of the Laplace operator $-D_{v}\Delta$ in $\Omega$ and we have used the fact that $-\frac{n}{2p}>-1$ by selecting the same p in Lemma 3.2 with $p>\frac{n}{2}$.

(ii) By Lemma 1.3 (ii), (iii) of [36], there exist some positive constants $C_{9}$ and $C_{10}$ such that

$$\begin{aligned} \begin{aligned}&\Vert \nabla v(\cdot ,t)\Vert _{L^{\infty }(\Omega )}\\ {}&\quad \le \Vert \nabla e^{t(D_{v}\Delta -\mu _{v})}v_{0}\Vert _{L^{\infty }(\Omega )}+s_{v}C_{w}\int _{0}^{t}\Vert \nabla e^{(t-\tau )(D_{v}\Delta -\mu _{v})}u(\cdot ,\tau )\Vert _{L^{\infty }(\Omega )}d\tau \\&\quad \le C_{9}\Vert \nabla v_{0}\Vert _{L^{\infty }(\Omega )}+C_{9}\int _{0}^{t}[1+(t-\tau )^{-\frac{1}{2}-\frac{n}{2p}}]e^{-(D_{v}\lambda _{1}+\mu _{v})(t-\tau )}\Vert u(\cdot ,\tau )\Vert _{L^{p}(\Omega )}d\tau \\&\quad \le C_{10} \end{aligned} \end{aligned}$$

for all $t\in (0,T_{\max })$, where $\lambda _{1}$ is the first positive Neumann eigenvalue of the Laplace operator $-D_{v}\Delta$ in $\Omega$ and we have used the fact that $-\frac{1}{2}-\frac{n}{2p}>-1$ by selecting the same p in Lemma 3.2 with $p>n$. The proof of Lemma 3.3 is complete. $\Box$

By Lemma 3.2 and Lemma 3.3, we can complete the proof of Theorem 1.1.

Proof of Theorem 1.1. It follows from Lemma 3.2 and Lemma 3.3, as well as Moser-Alikakos iteration (Appendix A of [33]) that there exists a constant $C>0$ such that

$$\begin{aligned} ||u(\cdot ,t)||_{L^{\infty }(\Omega )}\le C\;\;\;\hbox { for all} \, t\in (0,T_{\max }). \end{aligned}$$

(3.18)

This in conjunction with Lemma 2.1 proves Theorem 1.1.$\Box$

4 Proof of theorem 1.2

In this section, we can improve the conditions of f(u) in the space dimension $n=2$. Firstly, we give the coupled estimate of $\int _{\Omega }u\ln u$ and $\int _{\Omega }|\nabla v|^{2}$.

Lemma 4.1

Let (u, v, w) be a solution ensured in Lemma 2.1. Then the solution (u, v, w) of (1.1) satisfies

$$\begin{aligned} \begin{aligned} \frac{d}{dt}&\left\{ \int _{\Omega }u\ln u+\frac{\chi }{\sqrt{2}s_{v}C_{w}}|\nabla v|^{2}\right\} +D_{u}\int _{\Omega }\frac{|\nabla u|^{2}}{u}+\int _{\Omega }u\ln u+\frac{\sqrt{2}\mu _{v}\chi }{s_{v}C_{w}}|\nabla v|^{2}\\&\le \sqrt{2}\frac{\chi s_{v}C_{w}}{D_{v}}\int _{\Omega }u^{2}+\int _{\Omega }f(u)(\ln u+1)+M_{0}\;\;\;\hbox { for all} \, t\in (0,T_{\max }), \end{aligned} \end{aligned}$$

(4.1)

where $M_{0}=\sup _{s>0}\left\{ s\ln s-\sqrt{\frac{1}{8}}\frac{\chi s_{v}C_{w}}{D_{v}} s^{2}\right\} \left| \Omega \right| <\infty$ and $C_{w}$ is given in Lemma 2.1.

Proof

Testing the first Eq. (1.1) by $\ln u+1$ and using Young’s inequality, we have

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\int _{\Omega }u\ln u+D_{u}\int _{\Omega }\frac{|\nabla u^{2}|}{u}&=-\chi \int _{\Omega }u\Delta v+\int _{\Omega }f(u)(\ln u+1)\\&\le \epsilon \int _{\Omega }u^{2}+\frac{\chi ^{2}}{4\epsilon }\int _{\Omega }|\Delta v|^{2}+\int _{\Omega }f(u)(\ln u+1),\\ \end{aligned} \end{aligned}$$

(4.2)

where $\epsilon >0$ shall be determined later. In order to deal with the integral $\int _{\Omega }|\Delta v|^{2}$ in (4.2), we multiply the second Eq. (1.1) by $-\Delta v$, then integrate by parts over $\Omega$ and use Young’s inequality to get

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\int _{\Omega }|\nabla v|^{2}+\mu _{v}\int _{\Omega }|\nabla v|^{2}+\frac{D_{v}}{2}\int _{\Omega }|\Delta v|^{2}\le \frac{s_{v}^{2}}{2D_{v}}\int _{\Omega }(uw)^{2}. \end{aligned}$$

(4.3)

Since $w(\cdot ,t)$ is bounded due to Lemma 2.1, we obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\int _{\Omega }|\nabla v|^{2}+\mu _{v}\int _{\Omega }|\nabla v|^{2}+\frac{D_{v}}{2}\int _{\Omega }|\Delta v|^{2}\le \frac{C_{w}^{2}s_{v}^{2}}{2D_{v}}\int _{\Omega }u^{2}. \end{aligned}$$

(4.4)

By a combination (4.2) + $\frac{\chi ^{2}}{2\epsilon D_{v}} \times$ (4.4), we derive

$$\begin{aligned} \begin{aligned} \frac{d}{dt}&\left\{ \int _{\Omega }u\ln u+\frac{\chi ^{2}}{4\epsilon D_{v}}|\nabla v|^{2}\right\} +D_{u}\int _{\Omega }\frac{|\nabla u|^{2}}{u}+\frac{\mu _{v}\chi ^{2}}{2\epsilon D_{v}}|\nabla v|^{2}\\&\le \left( \epsilon +\frac{C_{w}^{2}\chi ^{2}s_{v}^{2}}{4\epsilon D_{v}^{2}}\right) \int _{\Omega }u^{2}+\int _{\Omega }f(u)(\ln u+1). \end{aligned} \end{aligned}$$

(4.5)

Setting

$$\begin{aligned} K(\epsilon ):=\sup _{s>0}\{s\ln s-\epsilon s^{2}\}, \end{aligned}$$

then we have

$$\begin{aligned} s\ln s\le \epsilon s^{2}+K(\epsilon ) \;\;\;\hbox { for all}\ \epsilon >0. \end{aligned}$$

Since

$$\begin{aligned} \lim _{s\rightarrow \infty }\frac{s\ln s-\epsilon s^{2}}{s^{2}}=-\epsilon <0, \end{aligned}$$

we obtain

$$\begin{aligned} K(\epsilon )<\infty \;\;\;\hbox { for all} \ \epsilon >0. \end{aligned}$$

Thus, by adding $\int _{\Omega }u\ln u$ to both sides of (4.5), we can obtain

$$\begin{aligned} \begin{aligned} \frac{d}{dt}&\left\{ \int _{\Omega }u\ln u+\frac{\chi ^{2}}{4\epsilon D_{v}}|\nabla v|^{2}\right\} +D_{u}\int _{\Omega }\frac{|\nabla u|^{2}}{u}+\int _{\Omega }u\ln u+\frac{\mu _{v}\chi ^{2}}{2\epsilon D_{v}}|\nabla v|^{2}\\&\le \left( 2\epsilon +\frac{C_{w}^{2}\chi ^{2}s_{v}^{2}}{4\epsilon D_{v}^{2}}\right) \int _{\Omega }u^{2}+\int _{\Omega }f(u)(\ln u+1)+K(\epsilon )\left| \Omega \right| . \end{aligned} \end{aligned}$$

(4.6)

Let

$$\begin{aligned} F_{3}(\epsilon ):=2\epsilon +\frac{C_{w}^{2}\chi ^{2}s_{v}^{2}}{4\epsilon D_{v}^{2}}\;\;\text {for all} \;\;\epsilon \in (0,\infty ), \end{aligned}$$

it follows from the elementary inequality that $F_{3}(\epsilon )$ can attain the minimum value

$$\begin{aligned} \min _{\epsilon >0} F_{3}(\epsilon )=\sqrt{2}\frac{\chi s_{v}C_{w}}{D_{v}}, \end{aligned}$$

when $\epsilon =\sqrt{\frac{1}{8}}\frac{\chi s_{v}C_{w}}{D_{v}}$. Therefore, by choosing this $\epsilon$ and setting $M_{0}=K(\sqrt{\frac{1}{8}}\frac{\chi s_{v}C_{w}}{D_{v}})\left| \Omega \right|$, we can obtain (4.1). $\Box$

Lemma 4.2

Let $n=2$ and $f(0)\ge 0$. Assume that one of the following conditions holds:

$$\begin{aligned} \begin{aligned}&(i)\,\,\exists \alpha>0,\text {s.t. } \sup _{s\ge 0}\{f(s)+\alpha s\}<\infty ,\lim _{s\rightarrow \infty }\inf \{-\frac{f(s)\ln s}{s^{2}}\}=:\mu \in (\sqrt{2}\frac{\chi s_{v}C_{w}}{D_{v}},\infty ],\\&(ii)\,\,\exists \alpha >0,\text {s.t. } \sup _{s\ge 0}\{f(s)+\alpha s\}<\infty ,\frac{2\sqrt{2}\chi s_{v}C_{GN}^{4}m_{1}C_{w}}{D_{v}}\le D_{u},\\&(iii)\,\,f\equiv 0,\frac{2\sqrt{2}\chi s_{v}C_{GN}^{4}m_{1}C_{w}}{D_{v}}\le D_{u}, \end{aligned} \end{aligned}$$

where $C_{GN}$ is given in Lemma 2.2, $m_{1}$ is given in (2.4) and $C_{w}$ is given in Lemma 2.1. Then there exists $C>0$ such that

$$\begin{aligned} \int _{\Omega }u\ln u+\int _{\Omega }|\nabla v|^{2}\le C\;\;\;\hbox { for all} \, t\in (0,T_{\max }). \end{aligned}$$

(4.7)

Proof

(i) Setting

$$\begin{aligned} \varPhi (s) := f(s)\ln s + \sqrt{2}\frac{\chi s_{v}C_{w}}{D_{v}}s^{2}, \end{aligned}$$

since $\lim _{s\rightarrow \infty }\inf \{-\frac{f(s)\ln s}{s^{2}}\}=:\mu \in (\sqrt{2}\frac{\chi s_{v}C_{w}}{D_{v}},\infty ]$, we deduce

$$\begin{aligned} \exists s_{2}>1,\hbox { s.t. }\varPhi (s) <0\;\;\;\text {for all} \, s\ge s_{2}. \end{aligned}$$

Therefore, we have

$$\begin{aligned} \begin{aligned}&\sqrt{2}\frac{\chi s_{v}C_{w}}{D_{v}}\int _{\Omega }u^{2}+\int _{\Omega }f(u)(\ln u+1)\\&=\int _{\{u<s_{2}\}}\varPhi (u)+\int _{\{u\ge s_{2}\}}\varPhi (u)+\int _{\Omega }f(u)\\&\le \sup _{0<s<s_{2}}[\varPhi (s)]|\Omega |+\sup _{s>0}f(s)|\Omega |<\infty \;\;\;\hbox { for all} \, t\in (0,T_{\max }), \end{aligned} \end{aligned}$$

(4.8)

due to the conditions that $f\in C^{1}([0,+\infty ))$, $f(0)\ge 0$ and $\sup _{s>0}f(s)<\infty$ implied by (2.2).

Let

$$\begin{aligned} y(t):=\int _{\Omega }u\ln u+\frac{\chi }{\sqrt{2}s_{v}C_{w}}\int _{\Omega }|\nabla v|^{2}+e^{-1}|\Omega |, \end{aligned}$$

(4.9)

then $y(t)\ge 0$ due to $s\ln s\ge -e^{-1}$. Moreover, it follows from (4.1) and (4.8) that y(t) satisfies

$$\begin{aligned} y'(t)+c_{1}y(t)\le c_{2}\;\;\;\hbox { for all} \, t\in (0,T_{\max }), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&c_{1}:=\min \left\{ 1,2\mu _{v}\right\} ,\\&c_{2}:=\left( \sup _{0<s<s_{2}}[\varPhi (s)]+\sup _{s>0}f(s)+e^{-1}\right) |\Omega |+M_{0}. \end{aligned} \end{aligned}$$

(4.10)

By the ODE comparison argument, we have

$$\begin{aligned} y(t)\le \max \left\{ y(0),\frac{c_{2}}{c_{1}}\right\} \;\;\text {for all}\;\; t\in (0,T_{\max }), \end{aligned}$$

which implies (4.7).

(ii) We further consider the effect of diffusion. It follows from $n=2$, Lemma 2.2 and Lemma 2.3 that

$$\begin{aligned} \begin{aligned} \int _{\Omega }u^{2}=||\sqrt{u}||^{4}_{L^{4}(\Omega )}&\le \{C_{GN}(||\sqrt{u}||^{\frac{1}{2}}_{L^{2}(\Omega )}||\nabla \sqrt{u}||^{\frac{1}{2}}_{L^{2}(\Omega )}+||\sqrt{u}||_{L^{2}(\Omega )})\}^{4}\\&\le 8C_{GN}^{4}(||\sqrt{u}||^{2}_{L^{2}(\Omega )}||\nabla \sqrt{u}||^{2}_{L^{2}(\Omega )}+||\sqrt{u}||_{L^{2}(\Omega )}^{4})\\&\le 8C_{GN}^{4}(||u||_{L^{1}(\Omega )}||\nabla \sqrt{u}||^{2}_{L^{2}(\Omega )}+||u||_{L^{1}(\Omega )}^{2})\\&\le 2C_{GN}^{4}m_{1}\int _{\Omega }\frac{|\nabla u|^{2}}{u}+ 8C_{GN}^{4}m_{1}^{2}, \end{aligned} \end{aligned}$$

(4.11)

where $C_{GN}$ and $m_{1}$ are given in Lemmas 2.2 and 2.4, respectively.

According to the elementary inequality

$$\begin{aligned} 1<\ln s+1\le s\;\;\;\text {for all} \, s\ge 1, \end{aligned}$$

and the conditions $f(0)\ge 0$ and (2.2), we have

$$\begin{aligned} 0\le \sup _{s>0}f(s)<\infty , \end{aligned}$$

which implies

$$\begin{aligned} (\ln s+1)f(s)\le (\ln s+1)\sup _{s>0}f(s)\le s\sup _{s>0}f(s)\;\;\;\text {for all} \, s\ge 1. \end{aligned}$$

Therefore, the two integrals on the right-hand side of (4.1) can be estimated as follows:

$$\begin{aligned} \begin{aligned}&\sqrt{2}\frac{\chi s_{v}C_{w}}{D_{v}}\int _{\Omega }u^{2}+\int _{\Omega }f(u)(\ln u+1)\\&\le \sqrt{2}\frac{\chi s_{v}C_{w}}{D_{v}}\int _{\Omega }u^{2}+\int _{\{u<1\}}f(u)(\ln u+1)+\int _{\{u\ge 1\}}f(u)(\ln u+1)\\&\le \sqrt{2}\frac{\chi s_{v}C_{w}}{D_{v}}\int _{\Omega }u^{2}+\sup _{u<1}[f(u)(\ln u+1)]\left| \Omega \right| +\sup _{s>0}f(s)\int _{\Omega }u\\&\le \sqrt{2}\frac{\chi s_{v}C_{w}}{D_{v}}\int _{\Omega }u^{2}+\sup _{u<1}[f(u)(\ln u+1)]\left| \Omega \right| +\sup _{s>0}f(s)m_{1}. \end{aligned} \end{aligned}$$

(4.12)

Setting

$$\begin{aligned} M_{1}=\sup _{u<1}[f(u)(\ln u+1)]\left| \Omega \right| +\sup _{s>0}f(s)m_{1}<\infty , \end{aligned}$$

we can combine (4.1), (4.11) as well as (4.12) to deduce

$$\begin{aligned} \begin{aligned} \frac{d}{dt}&\left\{ \int _{\Omega }u\ln u+\frac{\chi }{\sqrt{2}s_{v}C_{w}}|\nabla v|^{2}\right\} +D_{u}\int _{\Omega }\frac{|\nabla u|^{2}}{u}+\int _{\Omega }u\ln u+\frac{\sqrt{2}\mu _{v}\chi }{s_{v}C_{w}}|\nabla v|^{2}\\&\le \sqrt{2}\frac{\chi s_{v}C_{w}}{D_{v}}\left( 2C_{GN}^{4}m_{1}\int _{\Omega }\frac{|\nabla u|^{2}}{u}+8C_{GN}^{4}m_{1}^{2}\right) +M_{1}+M_{0}. \end{aligned} \end{aligned}$$

Thanks to the condition $\frac{2\sqrt{2}\chi s_{v}C_{GN}^{4}m_{1}C_{w}}{D_{v}}\le D_{u}$, we have

$$\begin{aligned} \begin{aligned} \frac{d}{dt}&\left\{ \int _{\Omega }u\ln u+\frac{\chi }{\sqrt{2}s_{v}C_{w}}|\nabla v|^{2}+e^{-1}|\Omega |\right\} +\int _{\Omega }u\ln u+\frac{\sqrt{2}\mu _{v}\chi }{s_{v}C_{w}}|\nabla v|^{2}\\&\le \frac{8\sqrt{2}\chi s_{v}C_{GN}^{4}m_{1}^{2}C_{w}}{D_{v}}+M_{1}+M_{0}\;\;\;\hbox { for all\;}\ t\in (0,T_{\max }). \end{aligned} \end{aligned}$$

Thus, this along with the ODE comparison argument once again then yields (4.7).

(iii) If $f\equiv 0$, it implies $m_{1}=||u_{0}||_{L^{1}(\Omega )}$. By the same argument as in the proof of (ii), we can conclude that the condition

$$\begin{aligned} \frac{2\sqrt{2}\chi s_{v}C_{GN}^{4}m_{1}C_{w}}{D_{v}}\le D_{u} \end{aligned}$$

is enough to ensure (4.7). The proof of Lemma 4.2 is complete. $\Box$

Lemma 4.3

Let the conditions of Lemma 4.2 hold, then for any $q\in (2,\infty )$, there exists $C>0$ such that the component v of (1.1) fulfills

$$\begin{aligned} ||v(\cdot ,t)||_{W^{1,q}(\Omega )}\le C \;\;\;\hbox { for all} \, t\in (0,T_{\max }). \end{aligned}$$

(4.13)

Proof

Firstly, we prove the boundedness of $||u(\cdot ,t)||_{L^{2}(\Omega )}$. Testing the first Eq. (1.1) by u, it follows from Young’s inequality that

$$\begin{aligned} \begin{aligned} \frac{1}{2}\frac{d}{dt}\int _{\Omega }u^{2}&= -D_{u}\int _{\Omega }|\nabla u|^{2}+\chi \int _{\Omega }u\nabla u\cdot \nabla v+\int _{\Omega }f(u)u\\&\le -\frac{1}{2}D_{u}\int _{\Omega }|\nabla u|^{2}+\frac{\chi ^{2}}{2D_{u}}\int _{\Omega }u^{2}|\nabla v|^{2}+m_{1}\sup _{s\ge 0}f(s). \end{aligned} \end{aligned}$$

(4.14)

By using $\nabla v\cdot \nabla \Delta v=\frac{1}{2}\Delta |\nabla v|^{2}-|D^{2}v|^{2}$, and combining with the second Eq. (1.1) we have

$$\begin{aligned}&\frac{1}{4}\frac{d}{dt}\int _{\Omega }|\nabla v|^{4}\nonumber \\ {}&\quad =-\frac{D_{v}}{2}\int _{\Omega }|\nabla |\nabla v|^{2}|^{2}+\frac{D_{v}}{2}\int _{\partial \Omega }|\nabla v|^{2}\frac{\partial |\nabla v|^{2}}{\partial \nu }-D_{v}\int _{\Omega }|\nabla v|^{2}|D^{2}v|^{2}\nonumber \\&\qquad -\mu _{v}\int _{\Omega }|\nabla v|^{4}-s_{v}\int _{\Omega }uw|\nabla v|^{2}\Delta v-s_{v}\int _{\Omega }uw\nabla v\cdot \nabla |\nabla v|^{2}. \end{aligned}$$

(4.15)

By using the estimate that $\frac{\partial |\nabla v|^{2}}{\partial \nu }\le c_{3}|\nabla v|^{2}$ on $\partial \Omega$ with some $c_{3}>0$ (see Lemma 4.2 in [23]), and the trace inequality (see Lemma 3.4 in [42]), there exists $c_{4}>0$ such that

$$\begin{aligned} \begin{aligned} \frac{D_{v}}{2}\int _{\partial \Omega }|\nabla v|^{2}\frac{\partial |\nabla v|^{2}}{\partial \nu }&=\frac{D_{v}}{4}\int _{\partial \Omega }\frac{\partial (|\nabla v|^{2})^{2}}{\partial \nu }\\&\le \frac{D_{v}}{4}\int _{\Omega }|\nabla |\nabla v|^{2}|^{2}+c_{4}\left( \int _{\Omega }|\nabla v|^{2}\right) ^{2}. \end{aligned} \end{aligned}$$

(4.16)

By using Young’s inequality on the last two terms of (4.15) and combining the pointwise inequality $|\Delta v|^{2}\le n|D^{2}v|^{2}$, we obtain

$$\begin{aligned} \begin{aligned}&-s_{v}\int _{\Omega }uw|\nabla v|^{2}\Delta v-s_{v}\int _{\Omega }uw\nabla v\cdot \nabla |\nabla v|^{2}\\&\le s_{v}\int _{\Omega }uw|\nabla v|^{2}|\Delta v|+s_{v}\int _{\Omega }uw|\nabla v|\cdot |\nabla |\nabla v|^{2}|\\&\le (\frac{ns_{v}^{2}C_{w}^{2}}{4D_{v}}+\frac{2s_{v}^{2}C_{w}^{2}}{D_{v}})\int _{\Omega }u^{2}|\nabla v|^{2}+D_{v}\int _{\Omega }|\nabla v|^{2}|D^{2}v|^{2}+\frac{D_{v}}{8}\int _{\Omega }|\nabla |\nabla v|^{2}|^{2}. \end{aligned} \end{aligned}$$

Combining this with (4.14)–(4.16), we obtain

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}\left\{ \frac{1}{2}\int _{\Omega }u^{2}+\frac{1}{4}\int _{\Omega }|\nabla v|^{4}\right\} +\frac{D_{u}}{2}\int _{\Omega }|\nabla u|^{2}+\frac{D_{v}}{8}\int _{\Omega }|\nabla |\nabla v|^{2}|^{2}\\&\le c_{5}\int _{\Omega }u^{2}|\nabla v|^{2}+c_{5}, \end{aligned} \end{aligned}$$

(4.17)

with some $c_{5}>0$. Next, invoking an extended interpolation [5], Lemma 2.3 and Lemma 4.2, then for each $\epsilon >0$ we can pick some $c_{6}(\epsilon )>0$ and $c_{7}(\epsilon )>0$ such that

$$\begin{aligned} \begin{aligned} ||u||^{3}_{L^{3}(\Omega )}&\le \epsilon ||\nabla u||^{2}_{L^{2}(\Omega )}||u\ln u||_{L^{1}(\Omega )}+c_{6}(\epsilon )(||u||^{3}_{L^{1}(\Omega )}+1)\\&\le \epsilon \int _{\Omega }|\nabla u|^{2}+c_{7}(\epsilon ) \;\;\;\text {for all} \, t\in (0,T_{\max }). \end{aligned} \end{aligned}$$

By using the Gagliardo-Nirenberg inequality and Lemma 4.2 we have

$$\begin{aligned} \begin{aligned} ||\left| \nabla v\right| ^{2}||^{3}_{L^{3}(\Omega )}&\le c_{8}||\nabla |\nabla v |^{2}||^{2}_{L^{2}(\Omega )}|| \left| \nabla v\right| ^{2}||_{L^{1}(\Omega )}+c_{8}|| \left| \nabla v\right| ^{2}||^{3}_{L^{1}(\Omega )}\\&\le c_{9}\int _{\Omega }|\nabla |\nabla v|^{2}|^{2}+c_{9} \end{aligned} \end{aligned}$$

(4.18)

with some $c_{8}>0$ and $c_{9}>0$. Due to Hölder’s and Young’s inequalities, there exists $c_{10}>0$ such that

$$\begin{aligned} \begin{aligned} c_{5}\int _{\Omega }u^{2}|\nabla v|^{2}&\le c_{5}||u||^{2}_{L^{3}(\Omega )}||\left| \nabla v\right| ^{2}||_{L^{3}(\Omega )}\\&\le c_{5}c_{9}^{\frac{1}{3}}\left\{ \epsilon \int _{\Omega }|\nabla u|^{2}+c_{7}(\epsilon )\right\} ^{\frac{2}{3}}\left\{ \int _{\Omega }|\nabla |\nabla v|^{2}|^{2}+1\right\} ^{\frac{1}{3}}\\&\le \frac{D_{v}}{16}\left\{ \int _{\Omega }|\nabla |\nabla v|^{2}|^{2}+1\right\} +c_{10}\left\{ \epsilon \int _{\Omega }|\nabla u|^{2}+c_{7}(\epsilon )\right\} . \end{aligned} \end{aligned}$$

By choosing $\epsilon :=\frac{D_{u}}{4c_{10}}$, we thus conclude from (4.17) that there exists $c_{11}>0$ such that

$$\begin{aligned} \frac{d}{dt}\left\{ \frac{1}{2}\int _{\Omega }u^{2}+\frac{1}{4}\int _{\Omega }|\nabla v|^{4}\right\} +\frac{D_{u}}{4}\int _{\Omega }|\nabla u|^{2}+\frac{D_{v}}{16}\int _{\Omega }|\nabla |\nabla v|^{2}|^{2}\le c_{11}. \end{aligned}$$

Next, since the Gagliardo-Nirenberg inequality and Young’s inequality, there exist some constants $c_{12}>0$ and $c_{13}>0$ such that

$$\begin{aligned} \int _{\Omega }u^{2}\le c_{12}\left\{ \int _{\Omega }|\nabla u|^{2}+1\right\} \;\;\;\text {and}\;\;\;\int _{\Omega }|\nabla v|^{4}\le c_{13}\left\{ \int _{\Omega }|\nabla |\nabla v|^{2}|^{2}+1\right\} . \end{aligned}$$

Then, we have

$$\begin{aligned}{} & {} \frac{d}{dt}\left\{ \frac{1}{2}\int _{\Omega }u^{2}+\frac{1}{4}\int _{\Omega }|\nabla v|^{4}\right\} +\frac{D_{u}}{4}\left( \frac{1}{c_{12}}\int _{\Omega } u^{2}-1\right) +\frac{D_{v}}{16}\left( \frac{1}{c_{13}}\int _{\Omega }|\nabla v|^{4}-1\right) \\ {}{} & {} \quad \le c_{11}. \end{aligned}$$

Let

$$\begin{aligned} y(t):=\frac{1}{2}\int _{\Omega }u^{2}+\frac{1}{4}\int _{\Omega }|\nabla v|^{4}, \end{aligned}$$

we can obtain that y(t) satisfies

$$\begin{aligned} y'(t)+c_{14}y(t)\le c_{15}\;\;\;\hbox { for all} \, t\in (0,T_{\max }), \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&c_{14}:=\min \left\{ \frac{D_{u}}{2c_{12}},\frac{D_{v}}{4c_{13}}\right\} ,\\&c_{15}:=c_{11}+\frac{D_{u}}{4}+\frac{D_{v}}{16}. \end{aligned} \end{aligned}$$

By using the ODE comparison argument, we can obtain the boundedness of $||u(\cdot ,t)||_{L^{2}(\Omega )}$.

Thus, it follows from the boundedness of $||u||_{L^{2}(\Omega )}$ and $w(\cdot ,t)$ in Lemma 2.1 that $||uw||_{L^{2}(\Omega )}$ is bounded. By using the parabolic regularity (Ref. Lemma 4.1 of [16] and Lemma 1 of [19]) when $n=2$, we can obtain (4.13). The proof of Lemma 4.3 is complete. $\Box$

Lemma 4.4

Let the conditions of Lemma 4.2 hold, then for all $p>1$ there exists $C>0$ such that

$$\begin{aligned} \int _{\Omega }u^{p}\le C\;\;\;\hbox { for all} \, t\in (0,T_{\max }). \end{aligned}$$

Proof

Multiplying the first Eq. (1.1) by $pu^{p-1}$ and integrating by parts, we see

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}\int _{\Omega }u^{p}+D_{u}p(p-1)\int _{\Omega }u^{p-2}|\nabla u|^{2}\\&\quad \quad =\chi p(p-1)\int _{\Omega }u^{p-1}\nabla u\cdot \nabla v+p\int _{\Omega }u^{p-1}f(u). \end{aligned} \end{aligned}$$

(4.19)

By using Young’s inequality to the first term on the right of (4.19) and combining Lemma 4.3, then for all $\epsilon >0$ there exist some positive constants $c_{16}$ and $c_{17}$ such that

$$\begin{aligned} \begin{aligned}&\chi p(p-1)\int _{\Omega }u^{p-1}\nabla u\cdot \nabla v\\&\le \frac{D_{u}p(p-1)}{2}\int _{\Omega }u^{p-2}|\nabla u|^{2}+\frac{\chi ^{2}p(p-1)}{8D_{u}}\int _{\Omega }u^{p}|\nabla v|^{2}\\&\le \frac{D_{u}p(p-1)}{2}\int _{\Omega }u^{p-2}|\nabla u|^{2}+\epsilon \int _{\Omega }u^{p+1}+c_{16}\int _{\Omega }|\nabla v|^{2(p+1)}\\&\le \frac{D_{u}p(p-1)}{2}\int _{\Omega }u^{p-2}|\nabla u|^{2}+\epsilon \int _{\Omega }u^{p+1}+c_{17}.\\ \end{aligned} \end{aligned}$$

(4.20)

When f satisfies (2.2), there exists a positive constant $c_{18}$ such that

$$\begin{aligned} \begin{aligned} p\int _{\Omega }u^{p-1}f(u)&= p\int _{\Omega }u^{p-1}(f(u)+\alpha u-\alpha u)\\&\le p\sup _{s>0}(f(s)+\alpha s)\int _{\Omega }u^{p-1}-\alpha p\int _{\Omega }u^{p}\\&\le -\frac{\alpha p}{2}\int _{\Omega }u^{p}+c_{18}.\\ \end{aligned} \end{aligned}$$

This in conjunction with (4.19) and (4.20) then yields

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}\int _{\Omega }u^{p}+\frac{D_{u}p(p-1)}{2}\int _{\Omega }u^{p-2}|\nabla u|^{2}+\frac{\alpha p}{2}\int _{\Omega }u^{p}\\&\le \epsilon \int _{\Omega }u^{p+1}+c_{17}+c_{18}. \end{aligned} \end{aligned}$$

(4.21)

By applying Lemma 2.2 and Lemma 2.3, we get

$$\begin{aligned} \begin{aligned} \int _{\Omega }u^{p+1}&=||u^{\frac{p}{2}}||_{L^{\frac{2(p+1)}{p}}(\Omega )}^{\frac{2(p+1)}{p}}\\&\le (2C_{GN})^{\frac{2(p+1)}{p}}(||u^{\frac{p}{2}}||^{\frac{2}{p}}_{L^{\frac{2}{p}}(\Omega )}||\nabla u^{\frac{p}{2}}||^{2}_{L^{2}(\Omega )}+||u^{\frac{p}{2}}||^{\frac{2(p+1)}{p}}_{L^{\frac{2}{p}}(\Omega )})\\&=(2C_{GN})^{\frac{2(p+1)}{p}}(||u||_{L^{1}(\Omega )}||\nabla u^{\frac{p}{2}}||^{2}_{L^{2}(\Omega )}+||u||^{p+1}_{L^{1}(\Omega )})\\&\le (2C_{GN})^{\frac{2(p+1)}{p}}(m_{1}||\nabla u^{\frac{p}{2}}||^{2}_{L^{2}(\Omega )}+m_{1}^{p+1})\\&=(2C_{GN})^{\frac{2(p+1)}{p}}(\frac{m_{1}p^{2}}{4}\int _{\Omega }u^{p-2}|\nabla u|^{2}+m_{1}^{p+1}).\\ \end{aligned} \end{aligned}$$

(4.22)

Therefore, we can choose $\epsilon =\frac{2D_{u}(p-1)}{pm_{1}}(2C_{GN})^{\frac{-2(p+1)}{p}}$ in (4.21) to obtain

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\int _{\Omega }u^{p}+\frac{\alpha p}{2}\int _{\Omega }u^{p} \le c_{19}, \end{aligned} \end{aligned}$$

(4.23)

where $c_{19}>0$. By the ODE comparison argument, we have

$$\begin{aligned} \int _{\Omega }u^{p}\le c_{20}, \end{aligned}$$

where $c_{20}>0$.

On the other hand, when $f\equiv 0$, we combine (4.19) and (4.20) to deduce that there exists a positive constant $c_{21}$ such that

$$\begin{aligned} \begin{aligned} \frac{d}{dt}\int _{\Omega }u^{p}+\frac{D_{u}p(p-1)}{2}\int _{\Omega }u^{p-2}|\nabla u|^{2}\le \epsilon \int _{\Omega }u^{p+1}+c_{21}. \end{aligned} \end{aligned}$$

(4.24)

Adding $\int _{\Omega }u^{p}$ to the both sides of (4.24) and combining Young’s inequality, we obtain

$$\begin{aligned} \begin{aligned}&\frac{d}{dt}\int _{\Omega }u^{p}+\int _{\Omega }u^{p}+\frac{D_{u}p(p-1)}{2}\int _{\Omega }u^{p-2}|\nabla u|^{2}\\&\le \int _{\Omega }u^{p}+ \epsilon \int _{\Omega }u^{p+1}+c_{21}\\&\le 2\epsilon \int _{\Omega }u^{p+1}+c_{22}, \end{aligned} \end{aligned}$$

(4.25)

where $c_{22}>0$. By using (4.22) again, we can choose $\epsilon =\frac{D_{u}(p-1)}{pm_{1}}(2C_{GN})^{\frac{-2(p+1)}{p}}$ in (4.25) to obtain that there exists $c_{23}>0$ such that

$$\begin{aligned} \frac{d}{dt}\int _{\Omega }u^{p}+\int _{\Omega }u^{p}\le c_{23}. \end{aligned}$$

(4.26)

By using the ODE comparison argument again, we get

$$\begin{aligned} \int _{\Omega }u^{p}\le c_{24}\;\;\;\hbox { for all} \, t\in (0,T_{\max }), \end{aligned}$$

where $c_{24}>0$. The proof of Lemma 4.4 is complete. $\Box$

By means of Lemmas 4.3 and 4.4, we can complete the proof of Theorem 1.2.

Proof of Theorem 1.2. By combining Lemmas 4.3 and 4.4, we can use the Moser-Alikakos iteration (Appendix A of [33]) to derive

$$\begin{aligned} ||u(\cdot ,t)||_{L^{\infty }(\Omega )}\le C\;\;\;\hbox { for all} \, t\in (0,T_{\max }), \end{aligned}$$

(4.27)

where $C>0$. This in conjunction with the extensibility criterion of Lemma 2.1 proves Theorem 1.2.$\Box$