A Geometrical Characterization of Proportionally Modular Affine Semigroups

Abstract

A proportionally modular affine semigroup is the set of nonnegative integer solutions of a modular Diophantine inequality $f_1x_1+\cdots +f_nx_n \bmod b \le g_1x_1+\cdots +g_nx_n$, where $g_1,\dots ,g_n$, $f_1,\ldots ,f_n\in \mathbb {Z}$, and $b\in \mathbb {N}$. In this work, a geometrical characterization of these semigroups is given. On the basis of this geometrical approach, some algorithms are provided to check if a semigroup S in $\mathbb {N}^n$, with $\mathbb {N}^n{\setminus } S$ a finite set, is a proportionally modular affine semigroup.

1 Introduction

An affine semigroup S is a commutative subsemigroup of $\mathbb {N}^n$; that is, S is a subset of $\mathbb {N}^n$ containing the origin and such that $x+y\in S$ for all $x,y\in S$. Semigroups satisfying the condition that $\mathbb {N}^n{\setminus } S$ is a finite set are called generalized numerical semigroups or $\mathbb {N}^n$-semigroups [4, 7]. If $n=1$, they are called numerical semigroups. Denote by $a\bmod b$ the remainder between 0 and $b-1$ of the Euclidean division of a by b for every $a,b\in \mathbb {N}$ with $b\ne 0$.

Proportionally modular numerical semigroups were introduced by Rosales et al. [10]. These numerical semigroups are the nonnegative integer solutions of the Diophantine modular inequality $a x\bmod b \le cx$, where $a,c\in \mathbb {Z}$ and $b\in \mathbb {N}$. They have been investigated from multiple points of view. For example, their relationships to the numerical semigroups generated by intervals and to Bézout sequences have been found, and some different ways to determine if a numerical semigroup is a proportionally modular numerical semigroup have been given. A comprehensive compilation of these numerical semigroups is presented in [9].

A natural generalization of proportionally modular numerical semigroups to higher dimensions is given in [8]: a proportionally modular affine semigroup is the set of nonnegative integer solutions of a modular Diophantine inequality $f_1x_1+\cdots +f_nx_n \bmod b \le g_1x_1+\cdots +g_nx_n$, where $g_1,\dots ,g_n,f_1,\ldots ,f_n\in \mathbb {Z}$ and $b\in \mathbb {N}$. In that paper, the authors determined some algorithms to obtain the minimal generating set of a semigroup from its modular Diophantine inequality, and studied some properties related to its associated ring.

The main goal of this work is to give algorithmic methods for checking if a semigroup is a proportionally modular affine semigroup. To obtain such algorithms, we provide a geometrical characterization of these semigroups. In particular, we prove that an affine semigroup is a proportionally modular semigroup if and only if it is the union of the natural points belonging to some translations of the polyhedron delimited by two hyperplanes (Theorem 1).

Based on Theorem 1, Algorithms 2 and 3 check if an $\mathbb {N}^n$-semigroup is a proportionally modular semigroup. The first algorithm tests if S is a proportionally modular semigroup when S includes no elements of the canonical basis of $\mathbb {R}^n$. For this case, we prove that the proportionally modular semigroups are the semigroups obtained from a special kind of polytopes. In a way, this is equivalent to what happens for proportionally modular numerical semigroups. The second algorithm can be applied when some element of the canonical basis belongs to S.

In any case, both algorithms solve the problem by finding real solutions to systems of polynomial inequalities constructed from some technical results (namely, Corollary 2 and Theorem 2). These inequalities are the explicit conditions that have to be satisfied by the elements in S and in $\mathbb {N}^n{\setminus } S$ so that a semigroup $S\subset \mathbb {N}^n$ is a proportionally modular semigroup. In fact, this work presents some algorithms to determine if a finite subset of $\mathbb {N}^n$ satisfies some specific geometrical configurations and arrangements. Several references concerning the solution of systems of polynomial inequalities can be found in [2].

For proportionally modular numerical semigroups, we introduce the concepts of minimal and maximal intervals defining them. These intervals have an important role in the algorithms mentioned above. Furthermore, we provide an algorithm for computing the sets of these minimal and maximal intervals.

The results of this work are illustrated with several examples. With this aim in mind, we have used the library PropModSemig.m [3] developed by the authors in Mathematica [12].

The remainder of this paper is organized as follows. Section 2 provides some basic definitions and results related to proportionally modular numerical semigroups, including algorithmic methods for computing the sets of minimal and maximal intervals defining them. Section 3 gives several definitions and some notation related to affine semigroups. Furthermore, most of the inequalities used in the main algorithms later in the paper are defined in this section. Section 4 presents the geometrical characterization of proportionally modular affine semigroups. The algorithms for checking if a semigroup is a proportionally modular affine semigroup are introduced in Sects. 5 and 7. Section 6 studies the two-dimensional case to provide a better understanding of the case 2 solved in Sect. 7.

2 Initial Results on Proportionally Modular Numerical Semigroups

In this section, we introduce some results and definitions about numerical semigroups that are useful for understanding this work.

Let $\mathbb {R}$, $\mathbb {Q}$, and $\mathbb {N}$ be the sets of real numbers, rational numbers, and nonnegative integers, respectively. Denote by $\mathbb {R}_\ge$ the set of nonnegative elements of $\mathbb {R}$, by $\mathbb {R}_>$ the set $\mathbb {R}_\ge {\setminus }\{0\}$, and by $\mathbb {N}^*$ the set $\mathbb {N}{\setminus }\{0\}$. Denote by [n] the set $\{1,\ldots , n\}$ for any $n\in \mathbb {N}$.

A numerical semigroup S is called a half-line semigroup if there exists $m\in \mathbb {N}$ such that $S{\setminus } \{0\}=\mathbb {N}\cap [m,\infty )$. Given an interval $\mathbf {I}\subset \mathbb {R}_\ge$, denote by $\mathscr {S}(\mathbf {I})$ the numerical semigroup $\bigcup _{i\in \mathbb {N}}i\mathbf {I}\cap \mathbb {N}$. Half-line semigroups can be characterized by a property of the intervals defining them. We say that a numerical semigroup S is a proper numerical semigroup whenever $S\ne \{0\}$ and $S\ne \mathbb {N}$.

Lemma 1

Let S be a proper numerical semigroup. Then, S is a half-line semigroup if and only if there exists an interval [p, q] such that $p>1$, and $S=\mathscr {S}([p,q'])$ for all $q'\ge q$.

Proof

Assume that S is a half-line semigroup, so there exists an integer $m>1$ such that S is minimally generated by $\{m,\ldots ,2m-1\}$. Then, the interval $[m,2m-1]$ satisfies the lemma.

If $S=\mathscr {S}([p,q])$ and $S=\mathscr {S}([p,q'])$ for all $q'\ge q$, then the set $\mathbb {N}{\setminus } S$ is $\{1,\ldots ,m-1\}$. So, S is a proper half-line semigroup. $\square$

We say that an interval [p, q] with $p>1$ is a half-line interval if $\mathscr {S}([p,q])=\mathscr {S}([p,q'])$ for all $q'\ge q$.

In [9], it is proved that proportionally modular numerical semigroups are numerical semigroups generated by a closed interval with lower endpoint greater than 1; that is, for any proportionally modular numerical semigroup T given by the equation $a x\bmod b \le cx$, there exists an interval [d, e] such that $d>1$ and $T=\mathscr {S}([d,e])$. In this work, we assume that the lower endpoint of every interval defining a numerical semigroup is greater than 1. Note that if $0<a\le c$ or $a=0$, then T is the proper numerical semigroup $\mathbb {N}$, and for $c\le 0$, $T=\{0\}$. The relationship between proportionally modular numerical semigroups and numerical semigroups generated by intervals is expressed in the following lemmas.

Lemma 2

(Lemma 5.9 in [9]) If $0<c<a<b$, then the proportionally modular numerical semigroup defined by $ax\bmod b\le cx$ is $\mathscr {S}([d,e])$ with $d=b/a$ and $e=b/(a-c)$.

Lemma 3

(Lemma 5.12 in [9]) Let $a_1$, $a_2$, $b_1$, and $b_2$ be positive integers such that $b_1/a_1<b_2/a_2$. Then, the semigroup $\mathscr {S}([b_1/a_1,b_2/a_2])$ is the proportionally modular numerical semigroup defined by $a_1b_2x \bmod (b_1b_2)\le (a_1b_2-a_2b_1)x$.

Note that for a closed interval [d, e], the intersection $j[d,e]\cap (j+1)[d,e]$ is empty for every nonnegative integer $j< \lfloor d/(e-d) \rfloor$, or, equivalently, $j[d,e]\cap (j+1)[d,e]$ is not empty iff $j\in [ \lceil d/(e-d) \rceil ,\infty )\cap \mathbb {N}$. Denote $\min \{j\in \mathbb {N}\mid (j+1)[d,e]\cap j[d,e]\ne \emptyset \}$ by $\phi ([d,e])$; that is, $\phi ([d,e])= \lceil d/(e-d) \rceil$.

In fact, there exist only a few proportionally modular numerical semigroups compared with the number of numerical semigroups. Table 1 compares the two sets up to genus 44. This table has been computed in a cluster of computers [11] using our modified version of [5] based on [6].

Table 1 Number of proportionally modular numerical semigroups (PMNS) compared with number of numerical semigroups (NS) up to genus 44

To achieve the main goal of this work, we need to improve our knowledge of the proportionally modular numerical semigroups. In particular, we have to introduce the minimal and maximal intervals defining them.

Given an open interval $(p,q)\subset \mathbb {R}_\ge$, the numerical semigroup $\mathscr {S}((p,q))$ is called an open modular numerical semigroup. For a given numerical semigroup, $\mathrm {EH}(S)\subset \mathbb {N}{\setminus } S$ is the set of elements in $\mathbb {N}{\setminus } S$ such that $S\cup \{x\}$ is a semigroup.

In [10], a characterization of the numerical semigroups defined from closed intervals is given.

Proposition 1

(Proposition 23 in [10]) Let $S\ne \mathbb {N}$ be a numerical semigroup minimally generated by $\{n_1,\ldots ,n_t\}$. Then, $S=\mathscr {S}([p,q])$ with $q>p>1$ if and only if the following conditions hold:

• 1. For all $i\in [t]$, there exists $k_i\in [n_i-1]$ such that $n_i/k_i\in [p,q]$.

• 2. For all $x\in \mathrm {EH}(S)$ and $k_x\in [x-1]$, $x/k_x\notin [p,q]$.

Remark 1

The previous proposition means that for each possible closed interval [p, q] such that $p>1$ and $S=\mathscr {S}([p,q])$, there must exist a sequence $p\le x_1/y_1\le \cdots \le x_{l}/y_{l}\le q$ and two integers $h,r\in \mathbb {N}$ such that

• 1. $\{x_h,\ldots ,x_{h+r}\}= \{n_1,\ldots ,n_t\}$;

• 2. $y_{h+i}\in [x_{h+i}-1]$ for $i\in \{0,\ldots ,r \}$;

• 3. $x_{h-1}/y_{h-1}\ne x_{h}/y_{h}$;

• 4. $x_{h+r}/y_{h+r}\ne x_{h+r+1}/y_{h+r+1}$;

• 5. and $x/k_x\notin [p,q]$$\forall x\in \mathrm {EH}(S)$ and $\forall k_x\in [x-1]$.

Note that if S is a proportionally modular numerical semigroup, there exists a finite set of intervals $[x_h/y_h,x_{h+r}/y_{h+r}]$ satisfying these conditions. Following this idea, an algorithm to check if a numerical semigroup is proportionally modular is given in [10, Algorithm 24].

We now introduce the concepts of minimal and maximal intervals defining proportionally modular numerical semigroups.

Definition 1

Given a proportionally modular numerical semigroup S, a closed interval $[\widetilde{p},\widetilde{q}]$ is a minimal (closed) interval defining S if $[\widetilde{p},\widetilde{q}]$ is a minimal element with respect to inclusion in $\{ [p,q]\subset (1,\infty )\mid S=\mathscr {S}([p,q]) \}$.

Note that for any proper proportionally modular numerical semigroup S, the set of minimal intervals defining S is finite. We denote this set by $\widetilde{L}_S$.

Lemma 4

Given $p,q\in \mathbb {R}_>$ with $\mathscr {S}([p,q])$ a proper numerical semigroup, there exists a unique maximal open interval (with respect to inclusion) $(\widehat{p},\widehat{q})$ such that $[p,q]\subset (\widehat{p},\widehat{q})$ and $\mathscr {S}((\widehat{p},\widehat{q}))=\mathscr {S}([p,q])$.

Proof

Let $i_0$ be the minimal integer satisfying $iq\le (i+1)p$, $X=\mathbb {N}{\setminus } \mathscr {S}([p,q])$ and $\widehat{p}=p-\min \{(ip-s)/i \mid s\in X\cap ((i-1)q,ip), \, i=1,\ldots ,i_0 \}$.

If it is assumed that [p, q] is a non-half-line interval, then the lemma holds for $\widehat{q}=q+\min \{ (s-iq)/i \mid s\in X\cap (iq,(i+1)p), \, i=1,\ldots ,i_0-1 \}$. Otherwise, $\widehat{q}=\infty$ must be considered. $\square$

Remark 2

Given a proper proportionally modular numerical semigroup S, $\widehat{L}_S$ denotes the finite set of open intervals $\cup _{[\widetilde{p},\widetilde{q}]\in \widetilde{L}_S} \{(\widehat{p},\widehat{q})\}$, where $(\widehat{p},\widehat{q})$ is the unique interval obtained from the proof of Lemma 4.

Algorithm 1 computes the sets of minimal and maximal intervals defining a proportionally modular numerical semigroup. This algorithm is based on Algorithm 24 in [10]. Note that the two algorithms are not equivalent. For example, if one applies Algorithm 24 in [10] to the proportionally modular numerical semigroup minimally generated by $\{2,3\}$, then the obtained closed intervals determining this semigroup are [3/2, 2], [2, 3], and [3/2, 3], but, trivially, the last one is not a minimal interval.

Example 1

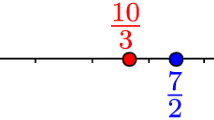
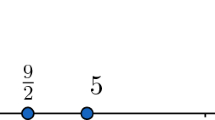
Let S be the numerical semigroup minimally generated by {10, 11, 12, 13, 27}. The set $\mathrm {EH}(S)$ is $\{28,29\}$. So, Algorithm 1 determines that S is a proportionally modular numerical semigroup defined by the minimal intervals $\widetilde{L}_S= \{[\frac{27}{25},\frac{10}{9}],[10,\frac{27}{2}]\}$ and the corresponding maximal intervals $\widehat{L}_S= \{(\frac{14}{13},\frac{29}{26}),(\frac{29}{3},14)\}$; that is,

$$\begin{aligned} S = \bigcup _{i\in \mathbb {N}} i \left[ \tfrac{27}{25},\tfrac{10}{9}\right] \cap \mathbb {N}= \bigcup _{i\in \mathbb {N}} i \left[ 10,\tfrac{27}{2}\right] \cap \mathbb {N}= \bigcup _{i\in \mathbb {N}} i \left( \tfrac{14}{13},\tfrac{29}{26}\right) \cap \mathbb {N}= \bigcup _{i\in \mathbb {N}} i \left( \tfrac{29}{3},14\right) \cap \mathbb {N}. \end{aligned}$$

In fact, S is the numerical semigroup obtained from the inequality $11 x \bmod 110 \le 3 x$.

3 Fixing Notation for Affine Semigroups

Let $\{e_1,\ldots ,e_n\}\subset \mathbb {N}^n$ be the canonical basis of $\mathbb {R}^n$. Define $\langle e_{i_0},\ldots ,e_{i_t}\rangle _\mathbb {R}$ as the $\mathbb {R}$-vector space generated by $\{e_{i_0},\ldots ,e_{i_t}\}$.

For a subset $A\subseteq \mathbb {Q}^n$, denote by $\mathtt{ConvexHull}(A)$ the convex hull of the set A, that is, the smallest convex subset of $\mathbb {Q}^n$ containing A, and by $\mathtt{VSet}(A)$ the vertex set of $\mathtt{ConvexHull}(A)$. A polyhedron is a region defined by the intersection of finitely many closed half-spaces, and a polytope is the convex hull of a finite number of points, or, equivalently, it is a bounded polyhedron (see [1] for details). From these definitions, it is easy to prove that for checking if a finite set of points are in the same region defined by a hyperplane, it is enough to test if the vertices of its convex hull hold that property.

For $\{a_1,\ldots ,a_k\}\subset [n]$ and $x\in \mathbb {N}^n$, define $\pi _{\{a_1,\ldots ,a_k\}}(x)=(x_{a_1},\ldots ,x_{a_k})$, that is, the projection of x on its $\{a_1,\ldots ,a_k\}$ coordinates. Fix $A\subset \mathbb {Q}^n$, with $\pi _{\{a_1,\ldots ,a_k\}}(A)=\{\pi _{\{a_1,\ldots ,a_k\}}(x)\mid x\in A\}$. Also, denote by $\sigma _{\{a_1,\ldots ,a_k\}}(A)$ the set $\{\pi _{\{a_1,\ldots ,a_k\}}(x)\mid x\in A \text{ and } x_i=0,\, \forall i\in [n]{\setminus } \{a_1,\ldots ,a_k\} \}$.

For fixed $f(x_1,\dots ,x_n)=f_1x_1+\dots +f_nx_n$ and $g(x_1,\dots ,x_n)=g_1x_1+\dots +g_nx_n$ with $g_1,\dots ,g_n,f_1,\ldots ,f_n\in \mathbb {Z}$, let $S\subset \mathbb {N}^n$ be the semigroup defined by the inequality $f(x)\bmod b\le g(x)$, where $x=(x_1,\dots ,x_n)$. We assume that $f_i=f_i\bmod b$ for all $i\in [n]$, so these coefficients are nonnegative integers. It is easy to prove that if $g_i>0$ for all $i\in [n]$, then $\mathbb {N}^n{\setminus } S$ is a finite set. Note that for this semigroup and for every $i\in [n]$, the set $S\cap \langle e_i \rangle _\mathbb {R}$ is isomorphic to the proportionally modular numerical semigroup given by the set of natural solutions of $f_i x_i\bmod b \le g_i x_i$.

Denote by $G_i$ the hyperplane with linear equation $g(x)=ib$, and by $G_i^+$ the closed half-space defined by $g(x)\ge ib$ ($G_i^-$ is the open half-space $g(x)< ib$). Analogously, $F_i$ is the hyperplane $f(x)=ib$ (respectively $D_i\equiv f(x)-g(x)=ib$), $F_i^+$ is $f(x)\ge ib$ (respectively $D_i^-\equiv f(x)-g(x)\le ib$), and $F_i^-$ is $f(x)< ib$ (respectively $D_i^+\equiv f(x)-g(x)> ib$).

In [1], it is proved that given a polytope $\mathbf {P}\subset \mathbb {R}^n_\ge$, the monoid $\bigcup _{i\in \mathbb {N}}i\mathbf {P}\cap \mathbb {N}^n$ is an affine semigroup if and only if $\mathbf {P}\cap \tau \cap \mathbb {Q}^n_\ge \ne \emptyset$ for all $\tau$ that are extremal rays of the rational cone generated by $\mathbf {P}$. Equivalently to the definition of $\mathscr {S}(\mathbf {I})$ for a closed real interval $\mathbf {I}$, $\mathscr {S}(\mathbf {P})$ defines the affine semigroup $\bigcup _{i\in \mathbb {N}}i\mathbf {P}\cap \mathbb {N}^n$.

For a set of closed intervals $L=\{[p_1,q_1], \ldots ,[p_t,q_t]\}$, denote by $\mathbf {P}_L$ the polytope $\mathtt{ConvexHull}(\cup _{i\in [t]} \{ p_ie_i,q_ie_i\})$, and denote $\phi (L)=\max \{\phi ([p_i,q_i])\mid i\in [t]\}$. So, $\mathtt{ConvexHull}( i\mathbf {P}_L\cup (i+1)\mathbf {P}_L) = i\mathbf {P}_L\cup (i+1)\mathbf {P}_L$ for every integer $i\ge \phi (L)$, and $\mathbb {N}^t{\setminus } \bigcup _{i\in \mathbb {N}}i\mathbf {P}_L\subset \mathtt{ConvexHull}( \{0\}\cup \phi (L)\mathbf {P}_L)$. Moreover, the polytopes $i\mathbf {P}_L$ can be determined by hyperplanes and half-spaces:

• $H_{1iL}$ is the hyperplane containing the set of points $\{ip_1e_1,\ldots ,ip_te_t\}$, its equation is $h_{1iL}(x)=0$, and $H_{1iL}^+$ is the closed half-space delimited by $H_{1iL}$ not containing the origin,

• $H_{2iL}$ is the hyperplane containing $\{iq_1e_1,\ldots ,iq_te_t\}$, its equation is $h_{2iL}(x)=0$, and $H_{2iL}^-$ is the closed half-space delimited by $H_{2iL}$ containing the origin.

So, the convex set $i\mathbf {P}_L$ is $\mathbb {R}^t_\ge \cap H_{1iL}^+\cap H_{2iL}^-$. Note that some expressions for $h_{1iL}(x)=0$ and $h_{2iL}(x)=0$ can be easily constructed by using linear algebra. Consider

$$\begin{aligned} h_{1iL}(x):= p_1\cdots p_t\!\left( i-\sum _{j\in [t]} x_j/p_j\right) \quad \text{ and }\quad h_{2iL}(x):= q_1\cdots q_t\!\left( i-\sum _{j\in [t]} x_j/q_j\right) .\nonumber \\ \end{aligned}$$

(1)

Furthermore, $H_{1iL}^+$ is defined by $h_{1iL}(x)\le 0$, and $H_{2iL}^-$ by $h_{2iL}(x)\ge 0$. We also consider the open half-spaces $H_{1iL}^-$ defined by $h_{1iL}(x)> 0$, and $H_{2iL}^+$ by $h_{2iL}(x)<0$.

Given any $P\in \mathbb {N}^n$, $\kappa _{L}(P)$ denotes the maximum integer i such that $h_{1iL}(P)<0$. In the case $h_{11L}(P)\ge 0$, $\kappa _{L}(P)=0$. Also, define by $\theta _{L}(P)$ the function such that $\theta _{L}(P)=1$ if there exists $i\in \mathbb {N}$ with $P\in i\mathbf {P}_L$, and $\theta _{L}(P)=0$ otherwise. Note that $\theta _{L}(P)$ can be determined in the following way: compute the sets $\tau _P\cap \mathbf {P}_L=\overline{AB}$ and $\{k\in \mathbb {N}\mid ||P||/||B||\le k \le ||P||/||A||\}$, where $\tau _P$ is the ray containing P, and ||X|| is the Euclidean norm of X, that is, $||X||^2=||(x_1,\dots ,x_t)||^2=\sum _{j=1}^t x_j^2$; if $\{k\in \mathbb {N}\mid ||P||/||B||\le k \le ||P||/||A||\}=\emptyset$, then $\theta _{L}(P)$ is 0, and 1 otherwise.

Assuming $n>t$, let $\mu _{1,i}e_t+\mu _{2,i}e_i$ and $-\nu _{1,i}e_t+\nu _{2,i}e_i$, where $i\in \{t+1,\ldots ,n\}$ and $\mu _{1,i},\mu _{2,i},\nu _{1,i},\nu _{2,i}\in \mathbb {Q}$ are some vectors, and $\tau _{1iL}(x)=0$ and $\tau _{2iL}(x)=0$ are equations of the hyperplanes defined by these vectors and the sets of points $\{iq_1e_1,\ldots ,iq_te_t\}$ and $\{ip_1e_1,\ldots ,ip_te_t\}$, respectively. For every $i\in \mathbb {Z}$, consider

$$\begin{aligned} \begin{aligned} \tau _{1iL}(x)&:=q_1\cdots q_t\mu _{2,t+1}\cdots \mu _{2,n}\left( i-\sum _{j\in [t]} \frac{x_j}{q_j}+ \sum _{j=t+1}^n \frac{\mu _{1,j}}{q_t \mu _{2,j}} x_j\right) ,\\ \tau _{2iL}(x)&:=p_1\cdots p_t\nu _{2,t+1}\cdots \nu _{2,n}\left( i-\sum _{j\in [t]} \frac{x_j}{p_j}- \sum _{j=t+1}^n \frac{\nu _{1,j}}{p_t \nu _{2,j}} x_j\right) . \end{aligned} \end{aligned}$$

(2)

4 A Geometrical Characterization of Proportionally Modular Affine Semigroups

Let S be the proportionally modular semigroup given by the modular inequality $f(x)\bmod b\le g(x)$, where $x=(x_1,\dots ,x_n)$, $g_1,\dots ,g_n$, $f_1,\ldots ,f_n \in \mathbb {Z}$, and $b\in \mathbb {N}^*$. Assume that $f_i=f_i\bmod b$ for all $i\in [n]$, so these coefficients are nonnegative integers.

As in previous sections, we denote by $F_i$ the hyperplane with linear equation $f(x)=ib$ (respectively $D_i\equiv f(x)-g(x)=ib$), and by $F_i^+$ the closed half-space defined by $f(x)\ge ib$ (respectively $D_i^-\equiv f(x)-g(x)\le ib$). With these hyperplanes fixed, $\mathbf {P}_i$ denotes the polyhedron $F_i^+\cap D_i^-$ with $i\in \mathbb {Z}$. Note that since $b>0$, and $f(e_j)\ge 0$ for all $j\in [n]$, on setting a negative integer i, every $P\in \mathbf {P}_i\cap \mathbb {N}^n$ satisfies $P\in F_0^+\cap D_0^-$. So, $\cup _{i\in \mathbb {N}} (F_i^+\cap D_i^-)\cap \mathbb {N}^n=\cup _{i\in \mathbb {Z}} (F_i^+\cap D_i^-)\cap \mathbb {N}^n$. Also, for all $i\in \mathbb {N}$, the points P in $F_i^+\cap D_i^-$ satisfy $g(P)\ge 0$.

Lemma 5

$P\in S$ if and only if there exists $i\in \mathbb {N}$ such that $P\in \mathbf {P}_i\cap \mathbb {N}^n$.

Proof

For any $P\in \mathbb {N}^n$, there exist two nonnegative integers i and r such that $f(P)=ib+r$ with $r\in [0,b)$. Assume that $P\in S$, so $f(P)\bmod b\le g(P)$. Furthermore, $0\le f(P)\bmod b=r=f(P)-ib\le g(P)$, and then P belongs to $\mathbf {P}_i\cap \mathbb {N}^n$.

Consider now any $P\in \mathbf {P}_i\cap \mathbb {N}^n$, with $i\in \mathbb {N}$, so $0\le f(P)-ib \le g(P)$. Since $f(P)\bmod b=f(P)-ib\bmod b\le b$, if $g(P)\ge b$, then, trivially, $P\in S$. Suppose that $g(P)<b$. In that case, $0\le f(P)-ib \le g(P)<b$, and again $f(P)\bmod b=f(P)-ib\bmod b\le g(P)$, and $P\in S$. $\square$

We now have the necessary tools to introduce a geometrical characterization of proportionally modular semigroups in the next result.

Theorem 1

$S\subset \mathbb {N}^n$ is a proportionally modular affine semigroup if and only if there exist two linear functions with integer coefficients f(x) and d(x) with $f_1,\ldots , f_n\ge 0$, an integer $b>0$, and two families of half-spaces $\{F_i^+\}_{i\in \mathbb {N}}$ and $\{D_i^-\}_{i\in \mathbb {N}}$, where $F_i^+\equiv f(x)\ge ib$ and $D_i^-\equiv d(x)\le ib$, such that $S= \cup _{i\in \mathbb {N}} (F_i^+\cap D_i^-)\cap \mathbb {N}^n$.

Proof

Given a proportionally modular semigroup S, it is the set of nonnegative integer solutions of an inequality $f(x)\bmod b\le g(x)$, where f(x) and g(x) are linear functions with integer coefficients, and $b\in \mathbb {N}^*$. From Lemma 5, taking the half-spaces $F_i^+\equiv f(x)\ge ib$ and $D_i^-\equiv (f-g)(x)\le ib$ the result holds.

Conversely, if $S= \cup _{i\in \mathbb {N}} (F_i^+\cap D_i^-)\cap \mathbb {N}^n$ with $F_i^+\equiv f(x)\ge ib$ and $D_i^-\equiv d(x)\le ib$, where f(x) and d(x) are linear functions and $b\in \mathbb {N}^*$, again, by Lemma 5, S is the proportionally modular semigroup given by the inequality $f(x)\bmod b\le (f-d)(x)$. $\square$

From previous results, the set of gaps of a proportionally modular semigroup can be described geometrically too.

Corollary 1

Let $S\subset \mathbb {N}^n$ be a proportionally modular affine semigroup. Then, $(\mathbb {N}^n{\setminus } S)\cap G_0^+=\cup _{i\in \mathbb {N}^*} (F_i^-\cap D_{i-1}^+\cap G_0^+)\cap \mathbb {N}^n$.

Proof

Note that for any $P\in F_i^-\cap D_{i-1}^+\cap G_0^+$, $0 \le g(P)<b$. Moreover, $(F_i^-\cap D_{i-1}^+\cap G_0^+)\cap (F_j^-\cap D_{j-1}^+\cap G_0^+)=\emptyset$ for every nonnegative integer $i\ne j$. In the other case, if we suppose $i<j$ and $P\in (F_i^-\cap D_{i-1}^+\cap G_0^+)\cap (F_j^-\cap D_{j-1}^+\cap G_0^+)$, then the point P satisfies $ib>f(P)$, $f(P)-g(P)>(j-1)b$, and $g(P)\ge 0$. Then, $0\ge (i-j+1)b>g(P)\ge 0$, but this is not possible.

Assume $P\in F_i^-\cap D_{i-1}^+\cap G_0^+$ for some $i\in \mathbb {N}^*$, and that there exists a nonnegative integer $j\le i-1$ such that $P\in F_j^+$. Since $f(P)-g(P)>(i-1)b$, if $jb\ge f(P)-g(P)$, $j>i-1$. So, $P\notin D_j^-$. Analogously, if $P\in F_i^+\cap D_{i}^-$ with $g(P)<b$, and we suppose that there exists an integer $j\ge i$ such that $P\in F_j^-$, then P does not belong to $D_{j-1}^+$ ($P\in D_{j-1}^+$ implies $ib\ge f(P)-g(P)>(j-1)b$, that is, $i>j-1$). So, $\cup _{i\in \mathbb {N}^*} (F_i^-\cap D_{i-1}^+\cap G_0^+)\bigcap \cup _{i\in \mathbb {N}} (F_i^+\cap D_{i}^-\cap G_b^-)= \emptyset$ and $\mathbb {N}^n\cap G_0^+\cap G_b^-= \cup _{i\in \mathbb {N}^*} (F_i^-\cap D_{i-1}^+\cap G_0^+)\bigcup \cup _{i\in \mathbb {N}} (F_i^+\cap D_{i}^-\cap G_b^-)$.

Since $\mathbb {N}^n\cap G_0^+\cap G_b^-= \cup _{i\in \mathbb {N}^*} (F_i^-\cap D_{i-1}^+\cap G_0^+)\bigcup \cup _{i\in \mathbb {N}} (F_i^+\cap D_{i}^-\cap G_b^-)$, by Theorem 1, the corollary holds. $\square$

The characterizations given in this section are illustrated by some examples in the following sections. In particular, Figs. 1 and 2 show two examples in the two-dimensional case. In these figures, the red lines correspond to the hyperplanes $D_i$ and the green ones to the hyperplanes $F_i$.

5 Testing $\mathbb {N}^n$-Semigroups for Being Proportionally Modular Affine Semigroups: Case 1

In this section, we assume that the semigroup $S\subset \mathbb {N}^n$ satisfies the conditions that for every $i\in [n]$, $e_i\notin S$ and $S_i$ is a proportionally modular numerical semigroup.

Fig. 1

$\mathbb {N}^2$-semigroup given by $11x+ 15y\bmod 110\le 3x+6y$

Fig. 2

$\mathbb {N}^2$-semigroup given by $11x+ 6y\bmod 110\le 3x+15y$

Proposition 2

S is a proportionally modular $\mathbb {N}^n$-semigroup with $b>f_i>g_i>0$ for all $i\in [n]$ if and only if there exists a set $L=\{[p_1,q_1],\ldots , [p_n,q_n]\}$ where $S_i=\mathscr {S}([p_i,q_i])$ for all $i\in [n]$, and $S=\bigcup _{i\in \mathbb {N}}i\mathbf {P}_L\cap \mathbb {N}^n$.

Proof

Assume that S is a proportionally modular $\mathbb {N}^n$-semigroup with $f_i>g_i>0$ for all $i\in [n]$. Consider $\mathbf {P}_L$, the polytope $\mathtt{ConvexHull}(\cup _{i\in [n]} \{ p_ie_i,q_ie_i\})\subset \mathbb {R}^n$, where $q_i=b/(f_i-g_i)>p_i=b/f_i>1$. Then, $S_i=\mathscr {S}([p_i,q_i])$. Note that $\mathbf {P}_L$ is the set $(F_1^+\cap D_1^-)\cap \mathbb {R}_\ge ^n$ with $F_i^+\equiv f(x)\ge ib$, and $D_i^-\equiv (f-g)x\le ib$, and $i\mathbf {P}_L$ is equal to $(F_i^+\cap D_i^-)\cap \mathbb {R}_\ge ^n$. So, the proposition holds by Theorem 1.

Now, we assume that $\mathscr {S}([p_1,q_1]),\ldots , \mathscr {S}([p_n,q_n])$ are proper proportionally modular numerical semigroups. By Lemma 3, for each $i\in [n]$, there exist three nonnegative integers $b_i$, $a_i$, and $c_i$ with $b_i>a_i>c_i>0$, such that $\mathscr {S}([p_i,q_i])$ is the set of nonnegative integers of the inequality $a_ix\bmod b_i\le c_ix$. Let $b=\mathrm {lcm}(\{b_1,\ldots ,b_n\})$ and consider the inequalities $(b/b_i)a_ix_i\bmod b\le (b/b_i)c_ix_i$. Let S be the proportionally modular $\mathbb {N}^n$-semigroup defined by the inequality $\sum _{i=1}^n (b/b_i)a_i x_i \bmod b \le \sum _{i=1}^n (b/b_i)c_ix_i$. It is an easy exercise for the reader to prove that $\bigcup _{i\in \mathbb {N}}i\mathbf {P}_L\cap \mathbb {N}^n$ is the proportionally modular $\mathbb {N}^n$-semigroup defined by the inequality $\sum _{i=1}^n (b/b_i)a_ix_i \bmod b \le \sum _{i=1}^n (b/b_i)c_ix_i$, and that $b>(b/b_i)a_i>(b/b_i)c_i$ for all $i\in [n]$. $\square$

From this proposition, we obtain a procedure to check if an $\mathbb {N}^n$-semigroup S is a proportionally modular semigroup. For that to be the case, the first necessary condition that S must satisfy is that $S_i$ must be a proper proportionally modular numerical semigroup for all $i\in [n]$. If this initial condition is satisfied, we have to determine whether there exist n intervals $L=\{[p_1,q_1],\ldots , [p_n,q_n]\}$ with $q_i>p_i>1$ such that $S_i=\mathscr {S}([p_i,q_i])$ and $S=\bigcup _{i\in \mathbb {N}}i\mathbf {P}_L\cap \mathbb {N}^n$. Let $\Lambda _S$ be the minimal generating set of S. For any interval $[p_i,q_i]$, $[\widetilde{p}_i,\widetilde{q}_i]$ and $(\widehat{p_i},\widehat{q_i})$ denote the intervals defined in Definition 1 and Remark 2, respectively.

Lemma 6

Let S be an $\mathbb {N}^n$-semigroup with $e_i\notin S$ for all $i\in [n]$. Then, S is a proportionally modular semigroup if and only if there exist $([\widetilde{p}_1,\widetilde{q}_1],\ldots , [\widetilde{p}_n,\widetilde{q}_n])\in \widetilde{L}_{S_1}\times \cdots \times \widetilde{L}_{S_n}$ and a set $L=\{[p_1,q_1],\ldots , [p_n,q_n]\}$ such that $S_i=\mathscr {S}([p_i,q_i])$ for all $i\in [n]$ satisfying

• 1. $[\widetilde{p}_i,\widetilde{q}_i]\subseteq [p_i,q_i] \subset (\widehat{p_i},\widehat{q_i})$ for all $i\in [n]$;

• 2. $\mathbb {N}^n{\setminus } S\subset \mathtt{ConvexHull}( \{0\}\cup \phi (L)\mathbf {P}_{L} )$;

• 3. for every $x\in \mathbb {N}^n{\setminus } S$ and for every $i\in [\phi (L)]$, $x\notin i\mathbf {P}_L$;

• 4. for every $s\in \Lambda _S$ such that $\theta _{\widetilde{L}}(s)=0$, $\kappa _{\widehat{L}}(s)\ne 0$, and $s/m\in \mathbf {P}_L$ for some $m\in [\kappa _{\widehat{L}}(s)]$.

Proof

If S is a proportionally modular $\mathbb {N}^n$-semigroup with $e_i\notin S$ for all $i\in [n]$, then, by Proposition 2, $S=\cup _{i\in \mathbb {N}}(i\mathbf {P}_L\cap \mathbb {N}^n)$, where $L=\{[p_1,q_1],\ldots , [p_n,q_n]\}$, is such that $S_i=\mathscr {S}([p_i,q_i])$. So, the lemma holds.

Assume that $\mathbf {P}_L$ is a polytope satisfying the hypotheses of the lemma and let $S'$ be the $\mathbb {N}^n$-semigroup $S'=\bigcup _{i\in \mathbb {N}}i\mathbf {P}_L\cap \mathbb {N}^n$. Trivially, $S'\cap \langle e_i \rangle _\mathbb {R}$ is isomorphic to $\mathscr {S}([p_i,q_i])$ for all $i\in [n]$. By conditions 2 and 3, $\mathbb {N}^n{\setminus } S\subset \mathbb {N}^n{\setminus } S'$ and then $S'\subset S$. By conditions 2 and 4, we have that $S\subset S'$ (note that if $\theta _{\widetilde{L}}(s)=1$ for some $s\in \Lambda _S$, then there exists $i\in \mathbb {N}$ with $s\in i\mathbf {P}_{\widetilde{L}}\subset i\mathbf {P}_{{L}}$). So, $s\in \bigcup _{i\in \mathbb {N}}i\mathbf {P}_L\cap \mathbb {N}^n$. $\square$

To obtain an algorithm to check if an $\mathbb {N}^n$-semigroup is a proportionally modular semigroup, for a set of closed intervals ${L}=\{[p_1,q_1],\ldots , [p_n,q_n]\}$ with $S_i=\mathscr {S}([p_i,q_i])$ for every $i\in [n]$, we establish a disjoint partition of the region $\mathbb {T}_{{L}}:=\mathtt{ConvexHull}( \{0\}\cup \phi ({L})\mathbf {P}_{{L}} )\cap \mathbb {N}^n$:

$$\begin{aligned}&\mathbb {H}_{1{L}}=\{x\in \mathbb {N}^n\mid x\in H^-_{11{L}}\} \text { and }\mathbb {H}_{i{L}}=H^-_{1i{L}} \cap H^+_{2(i-1){L}}\cap \mathbb {N}^n\\&\quad \text { for any } i\in \{2,\ldots , \phi ({L})\},\\&\mathbb {S}_{i{L}}= H^+_{1i{L}} \cap H^-_{2i{L}}\cap \mathbb {N}^n \text { for any } i\in [\phi ({L})]. \end{aligned}$$

Note that $\mathbb {T}_{{L}}= \{0\}\cup \bigcup _{i\in [\phi ({L})]} (\mathbb {H}_{i{L}}\sqcup \mathbb {S}_{i{L}})$ and $\mathbb {S}_{i{L}}=i\mathbf {P}_{{L}}\cap \mathbb {N}^n$.

For any i belonging to $[\phi ({L})]$, denote by $\mathrm {B}_{i{L}}$ the set $(\mathbb {N}^n{\setminus } S)\cap \mathbb {H}_{i{L}}$. So, a necessary condition for S to be a proportionally modular $\mathbb {N}^n$-semigroup for some $L=\{[p_1,q_1],\ldots , [p_n,q_n]\}$ is $\mathbb {N}^n{\setminus } S\subset \cup _{i\in \phi ({L})} \mathrm {B}_{i{L}} \subset \cup _{i\in \phi (\widetilde{L})} \mathrm {B}_{i\widetilde{L}}$. Otherwise, $S\ne \bigcup _{i\in \mathbb {N}}i\mathbf {P}_L\cap \mathbb {N}^n$.

Corollary 2

Let S be an $\mathbb {N}^n$-semigroup with $e_i\notin S$ for all $i\in [n]$. Then, S is a proportionally modular semigroup if and only if for some $\widetilde{L}=\{[\widetilde{p}_1,\widetilde{q}_1],\ldots , [\widetilde{p}_n,\widetilde{q}_n]\}$ with $([\widetilde{p}_1,\widetilde{q}_1],\ldots , [\widetilde{p}_n,\widetilde{q}_n])\in \widetilde{L}_{S_1}\times \cdots \times \widetilde{L}_{S_n}$, $\mathbb {N}^n{\setminus } S\subset \cup _{i\in [\phi (\widetilde{L})]} \mathbb {H}_{i\widetilde{L}}$ and there exists $L=\{[p_1,q_1],\ldots , [p_n,q_n]\}$ with $p_1,\ldots , p_n$, $q_1, \ldots ,q_n \in \mathbb {Q}$ satisfying the following inequalities:

• 1. For all $i\in [n]$ such that $[\widetilde{p}_i,\widetilde{q}_i]$ is a half-line interval, $\widehat{p}_i<p_i\le \widetilde{p}_i<\widetilde{q}_i\le q_i$; otherwise, $\widehat{p}_i<p_i\le \widetilde{p}_i<\widetilde{q}_i\le q_i< \widehat{q}_i$.

• 2. For all $x\in \mathtt{VSet}((\mathbb {N}^n{\setminus } S)\cap \mathbb {H}_{1\widetilde{L}})$, $h_{11L}(x)>0$, and for all $i\in \{2,\ldots ,\phi (\widetilde{L})\}$ and $x\in \mathtt{VSet}((\mathbb {N}^n{\setminus } S)\cap \mathbb {H}_{i\widetilde{L}})$, $h_{1iL}(x) >0$ and $h_{2(i-1)L}(x)<0$.

• 3. For every $s\in \Lambda _S$ such that $\theta _{\widetilde{L}}(s)=0$, $\kappa _{\widehat{L}}(s)\ne 0$, and for some $m\in [\kappa _{\widehat{L}}(s)]$, $h_{1iL}(s/m) \le 0$ and $h_{2iL}(s/m)\ge 0$.

Proof

The condition $\mathbb {N}^n{\setminus } S\subset \cup _{i\in [\phi (\widetilde{L})]} \mathbb {H}_{i\widetilde{L}}$ is equivalent to condition 2 in Lemma 6. Furthermore, for every integer i, the sets of inequalities appearing in the second condition are satisfied by the rational points belonging to $\mathbb {H}_{i{L}}$, while any point that satisfies the inequalities in the third condition belongs to $i\mathbf {P}_L$ for some integer i. Then, the second and third conditions of the corollary are equivalent to conditions 3 and 4 of Lemma 6, respectively. $\square$

Algorithm 2 presents a method for checking the conditions of the previous corollary. Note that some steps in this algorithm can be computed in a parallel way. Given a minimal interval $[\widetilde{p},\widetilde{q}]$, we denote by $r_{[\widetilde{p},\widetilde{q}]}$ the inequalities $\widehat{p}<p\le \widetilde{p}<\widetilde{q}\le q$ if [p, q] is a half-line interval, and $\widehat{p}<p\le \widetilde{p}<\widetilde{q}\le q< \widehat{q}$ otherwise.

Example 2

Consider the set of circles in Fig. 1 and let S be the $\mathbb {N}^2$-semigroup such that $\mathbb {N}^2{\setminus } S$ is this set, and its minimal generating set is

$$\begin{aligned}&\{(0, 8), (0, 9), (0, 10), (0, 11), (0, 12), (0, 15), (1, 7), (1, 8), (1, 9), (1, 10),\\&\quad (1, 11), (1, 14), (2, 6), (2, 7), (2, 8), (2, 9), (2, 10), (3, 6), (3, 7), (3, 8), (3, 9),\\&\quad (4, 5), (4, 6), (4, 7), (4, 8), (5, 4), (5, 5), (5, 6), (5, 7), (5, 11), (6, 3),(6, 4),\\&\quad (6, 5), (6, 6), (7, 3), (7, 4), (7, 5), (7, 6), (8, 2), (8, 3), (8, 4), (8, 5), (9, 1), (9, 2),\\&\quad (9, 3), (9, 4), (10, 0), (10, 1), (10, 2), (10, 3), (11, 0), (11, 1), (11, 2), (12, 0),\\&\quad (12, 1), (13, 0), (23, 4), (24, 3), (25, 2), (26, 1), (27, 0) \}. \end{aligned}$$

Thus, $S_1$ is minimally generated by $\{10,11,12,13,27\}$, and $S_2$ is minimally generated by $\{8,9,10,11,12,15 \}$. Using Algorithm 1, we find that both $S_1$ and $S_2$ are proportionally modular numerical semigroups with $\widetilde{L}_{S_1}= \{[\frac{27}{25},\frac{10}{9}],[10,\frac{27}{2}]\}$, $\widehat{L}_{S_1}= \{(\frac{14}{13},\frac{29}{26}),(\frac{29}{3},14)\}$, $\widetilde{L}_{S_2}= \{[\frac{12}{11},\frac{15}{13}],[\frac{15}{2},12]\}$, and $\widehat{L}_{S_2}= \{(\frac{13}{12},\frac{7}{6}),(7,13)\}$, respectively. Algorithm 2 determines that S is a proportionally modular $\mathbb {N}^2$-semigroup when $\widetilde{L}= ([10,\frac{27}{2}], [\frac{15}{2},12] )$ by computing $p_1,q_1,p_2,q_2\in \mathbb {Q}$ such that $\frac{29}{3}<p_1\le 10< \frac{27}{2} \le q_1< 14$, $7<p_2\le \frac{15}{2}<12 \le q_2< 13$, and satisfying the other inequalities in Corollary 2. Moreover, S is given by the inequality $11x+ 15y \bmod 110\le 3x+ 6y$. In Fig. 1, the blue line is $g(x)=b$, the green lines are $f(x)=kb$, and the red lines are $f(x)-g(x)=(k-1)b$ for $k\in \mathbb {N}$. The above results were obtained using our software [3]:

Note that $p_1= 163\,835/16384$, $q_1= 28\,367/2048$, $p_2= 931/128$, and $q_2= 1553/128$.

6 Some properties of proportionally modular $\mathbb {N}^2$-semigroups

To obtain an algorithm to check if an $\mathbb {N}^n$-semigroup is a proportionally modular semigroup when some $e_i$ belongs to it, we study the two-dimensional case in depth. Let $S\subset \mathbb {N}^2$ be the proportionally modular semigroup given by $f_1x_1+f_2x_2\bmod b \le g_1x_1+g_2x_2$. Again, we assume $f_1=f_1\bmod b$, $f_2=f_2\bmod b$, and $g_1,g_2>0$ which implies that $S\ne \{0\}$ and $S\ne \mathbb {N}^2$.

Without loss of generality, we assume, for example, that if $f_1>g_1$ but $g_2\ge f_2$, then $e_2$ belongs to S, and for all $x\in \mathbb {N}^2{\setminus } S$, $x-e_2\notin S$. Note that if one particularizes Theorem 1 and Corollary 1 to the two-dimensional case, then the sets $F_i^-\cap D_{i-1}^+\cap G_0^+$ are triangles with parallel edges, and their bases are the intervals given by $F_i^-\cap D_{i-1}^+\cap \langle e_1\rangle _\mathbb {R}$.

For any integer $k\in (0,f_1/g_1)$, we denote by $A_{k}$ the point

$$\begin{aligned} \frac{b}{f_1g_2-f_2g_1}(kg_2-f_2,f_1-kg_1)=\{g_1x_1+g_2x_2=b\}\cap \{f_1x_1+f_2x_2=kb\}\in \mathbb {Q}^2_\ge . \end{aligned}$$

The triangle $\mathrm {T}_{k}$ is the convex hull of the vertex set

$$\begin{aligned} \left\{ \left( \frac{kb}{f_1},0\right) , \left( \frac{(k-1)b}{f_1-g_1},0\right) ,A_{k}\right\} , \end{aligned}$$

and

$$\begin{aligned} \ddot{\mathrm {T}}_{k}=\mathrm {T}_{k}{\setminus } \left\{ \overline{\left( \frac{(k-1)b}{f_1-g_1},0\right) A_{k}}, \;\overline{\left( \frac{kb}{f_1},0\right) A_{k}}\right\} . \end{aligned}$$

This situation is illustrated in Fig. 2; the blue line is $g(x)=b$, the green lines are $f(x)=kb$, and the red lines are $f(x)-g(x)=(k-1)b$ for $k\in \mathbb {N}$.

So, a proportionally modular semigroup S with $f_1>g_1$ and $g_2\ge f_2$ can be characterized by a finite set of triangles satisfying some conditions.

Lemma 7

Let $S\ne \mathbb {N}^2$ be a proportionally modular $\mathbb {N}^2$-semigroup $f_1x_1+f_2x_2\bmod b\le g_1x_1+g_2x_2$, such that $1\in S_2$. For every $\alpha \in \mathbb {N}^2$, $\alpha \in S$ if and only if $\alpha \notin \cup _{k\in [\lfloor f_1/g_1 \rfloor ]} \ddot{\mathrm {T}}_{k}$.

Proof

By Corollary 1, if S is a proportionally modular semigroup, then $(\mathbb {N}^2{\setminus } S)\cap G_0^+=\cup _{i\in \mathbb {N}{\setminus }\{0\}} (F_i^-\cap D_{i-1}^+\cap G_0^+)\cap \mathbb {N}^n$, and $F_i^-\cap G_0^+=\overline{(kb/f_1,0) A_{k}}$ and $D_{i-1}^+\cap G_0^+=\overline{((k-1)b/(f_1-g_1),0) A_{k}}$. These are just the edges of the triangle $\mathrm {T}_{k}$. $\square$

Note that the triangles $\mathrm {T}_i$ can also be determined by the points (p, 0) and (q, 0) and the two vectors $(\mu _1,\mu _2)$ and $(-\nu _1,\nu _2)$, with $\mu _1,\nu _1\in [0,1)$, $\mu _2,\nu _2\in (0,1]$, and $\mu _1+\mu _2=\nu _1+\nu _2=1$.

Remark 3

Given a triangle with vertex set $\mathrm {T}=\{(0,0),(p,0),(\gamma _1,\gamma _2)\}\subset \mathbb {Q}^2_\ge$ such that $0\le \gamma _1\le p$, and one other point $(q,0)\in \mathbb {Q}^2_\ge$ with $q>p$, a proportionally modular $\mathbb {N}^2$-semigroup can be constructed by using the following method. Define the line containing $\{(p,0),(\gamma _1,\gamma _2)\}$ by the equation $\gamma _2x_1+(p-\gamma _1)x_2=p\gamma _2$ and consider the line $(q-p)\gamma _2x_1+( pq-\gamma _1(q-p) )x_2=pq\gamma _2$. Let $r_1$ and $r_2$ be the minimum nonnegative integers such that $\{r_1\gamma _2,r_1(p-\gamma _1),r_1p\gamma _2, r_2(q-p)\gamma _2,r_2( pq-\gamma _1(q-p) ),r_2pq\gamma _2 \}\subset \mathbb {N}$, and $b=\mathrm {lcm}(\{r_1p\gamma _2,r_2pq\gamma _2\})$. The semigroup given by the inequality

$$\begin{aligned} \frac{br_1\gamma _2}{r_1p\gamma _2}\, x_1 + \frac{b r_1(p-\gamma _1)}{r_1p\gamma _2}\,x_2 \bmod b \le \frac{b r_2(q-p)\gamma _2}{r_2pq\gamma _2}\, x_1 + \frac{br_2\left( pq-\gamma _1(q-p) \right) }{r_2pq\gamma _2}\,x_2 \end{aligned}$$

(3)

then satisfies Lemma 7 for $\mathrm {T}_{1}=\mathrm {T}$.

Example 3

Consider the $\mathbb {N}^2$-semigroup S shown in Fig. 2, that is, the nonnegative integer solutions of the modular inequality $11x+ 6y\bmod 110\le 3x+15y$. In this example, the vertex set of the triangle $\mathrm {T}_1=\mathrm {T}$ is $\{(0,0),(10,0),(\frac{300}{49},\frac{880}{174})\}$. The vertex sets of $T_2$ and $T_3$ are $\{ (\frac{55}{4}, 0), (20,0), (\frac{880}{49},\frac{550}{147})\}$ and $\{ (\frac{55}{2}, 0), (30,0), (\frac{1430}{49}, \frac{220}{147}) \}$, respectively. Also, the vectors $(\mu _1,\mu _2)$ and $(-\nu _1,\nu _2)$ determining the triangles $\mathrm {T}_i$ are $(\mu _{1,3},\mu _{2,3})=(\frac{9}{17},\frac{8}{17})$ and $(-\nu _{1,3},\nu _{2,3})=(-\frac{6}{17},\frac{11}{17})$, respectively.

7 Testing $\mathbb {N}^n$-Semigroups for Being Proportionally Modular Affine Semigroups: Case 2

In this section, $\mathbb {N}^n$-semigroups containing some $e_i$ are considered. We assume that S is an $\mathbb {N}^n$-semigroup, that the semigroup $S_i\ne \mathbb {N}$ is a proportionally modular numerical semigroup for every $i\in [t]$, and that $S_i=\mathbb {N}$ for all $i\in \{t+1,\ldots ,n\}$. To simplify our proofs, we consider that every set of closed intervals $L=\{[p_1,q_1],\ldots , [p_t,q_t]\}$ satisfies $\phi (L)=\phi ([p_t,q_t])$.

Since S is a semigroup, for every $x\in \mathbb {N}^n{\setminus } S$ and $i\in \{t+1,\ldots ,n\}$, $x-e_i\notin S$. We also consider the vectors $\mu _{1,i}e_t+\mu _{2,i}e_i$ and $-\nu _{1,i}e_t+\nu _{2,i}e_i$, where $\mu _{1,i},\nu _{1,i}\in [0,1)$, $\mu _{2,i},\nu _{2,i}\in (0,1]$, and $\mu _{1,i}+\mu _{2,i}=\nu _{1,i}+\nu _{2,i}=1$ for $i\in \{t+1,\ldots ,n\}$. We denote by $S^d$ and $S^u$ the sets $\sigma _{[t]}(S)\equiv S\cap \langle e_1,\ldots ,e_t\rangle _\mathbb {R}$ and $\{(\alpha _1,\ldots ,\alpha _n)\in S\mid \sum _{i=t+1}^n\alpha _i\ne 0\}$, respectively. Note that $S^d$ is an $\mathbb {N}^t$-semigroup and $S=(S^d\times \{0\}^{n-t+1})\cup S^u$.

In Sect. 5, we defined several objects for a given set L including n closed intervals, but here L has only t elements (note that $n>t$). In order to simplify the notation, we consider those objects defined over the $\mathbb {N}^t$-semigroup $S^d$.

If S is a proportionally modular $\mathbb {N}^n$-semigroup defined by the inequality $f(x)\bmod b\le g(x)$, then the above conditions mean that $b>f_i>g_i>0$ for all $i\in [t]$, and $g_i\ge f_i$ and $g_i>0$ for all $i\in \{t+1,\ldots ,n\}$. By Lemma 7 and Remark 3, for fixed $i\in [t]$ and $j\in \{t+1,\ldots ,n\}$, the semigroup $S\cap \langle e_i,e_j\rangle _\mathbb {R}$ is equivalent to an $\mathbb {N}^2$-semigroup determined by a triangle $\mathrm {T}_{ij}$. So, by Theorem 1 and Corollary 1, the hyperplanes defining S are determined by the points $p_1e_1,\ldots ,p_te_t,q_1e_1,\ldots ,q_te_t$ (suppose $S_i=\mathscr {S}([p_i,q_i])$ for $i\in [t]$) and the edges of the triangles $\mathrm {T}_{t\,(t+1)},\ldots ,\mathrm {T}_{t\,n}$; that is, the hyperplanes are fixed by their intersections with the planes $\langle e_t,e_j\rangle _\mathbb {R}$ for any $j\in \{t+1,\ldots ,n\}$. Moreover, the hyperplane $F_i$ is given by the points $ip_1e_1,\ldots ,ip_te_t$ and the vectors $-\nu _{1,j}e_t+\nu _{2,j}e_j$ and $D_i$ by the points $iq_1e_1,\ldots ,iq_te_t$ and $\mu _{1,j}e_t+\mu _{2,j}e_j$, with $j\in \{t+1,\ldots ,n\}$. Note that these data are enough to determine a hyperplane in $\mathbb {N}^n$.

To generalize the two-dimensional case studied in Sect. 6, for any i in $[\phi (L)]$, denote by $\mathrm {P}_{iL}$ the set $\{ (\alpha _1,\ldots ,\alpha _t,\beta _{t+1},\ldots ,\beta _n)\in \mathbb {R}_\ge ^n \mid \alpha \in \mathbb {H}_{i{L}}\}$ and define

$$\begin{aligned}&\overline{\mathrm {P}}^+_{iL}= \{\alpha \in S^u \mid \alpha -e_j \in \mathrm {P}_{iL}{\setminus } S \text { for some } j\in [t]\},\\&\overline{\mathrm {P}}^-_{iL}= \{\alpha \in S^u \mid \alpha +e_j \in \mathrm {P}_{iL}{\setminus } S \text { for some } j\in [t]\},\\&\overline{\mathrm {P}}^*_{iL}= \{\alpha \in S^u {\setminus } (\overline{\mathrm {P}}^+_{iL} \cup \overline{\mathrm {P}}^-_{iL})\mid \alpha -e_j\in \mathrm {P}_{iL}{\setminus } S \text { for some } j\in \{t+1,\ldots ,n\}\}. \end{aligned}$$

Note that $\sigma _{[t]} (\mathrm {P}_{iL})$ is equal to $\mathbb {H}_{i{L}}$ any $i\in [\phi (L)]$. So, three necessary conditions for S to be a proportionally modular $\mathbb {N}^n$-semigroup given by $L=\{[p_1,q_1],\ldots [p_t,q_t]\}$ are $\mathbb {N}^n{\setminus } S\subset \cup _{i\in [\phi (L)]} \mathrm {P}_{iL}\subset \cup _{i\in [\phi (L)]} \mathrm {P}_{i\widetilde{L}}$ for all natural vectors $\alpha \in \mathrm {P}_{iL}{\setminus } S$, $\alpha -e_j\notin S$ for every $j\in \{t+1,\ldots ,n\}$, and $(\alpha ,\beta )\in S$ for all $(\alpha ,\beta )\in (\cup _{i\in \mathbb {N}}\mathbf {P}_L\cap \mathbb {N}^{t}) \times \mathbb {N}^{n-t}$.

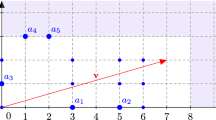
For three dimensions, Fig. 3 shows the geometrical arrangement of the case solved in this section.

Theorem 2

Let S be an $\mathbb {N}^n$-semigroup such that $S_i$ is a proper proportionally modular numerical semigroup for all $i\in [t]$ and $S_i=\mathbb {N}$ for all $i\in \{t+1,\ldots ,n\}$. Then, S is a proportionally modular semigroup if and only if for some $([\widetilde{p}_1,\widetilde{q}_1],\ldots , [\widetilde{p}_t,\widetilde{q}_t])\in \widetilde{L}_{S_1}\times \cdots \times \widetilde{L}_{S_t}$, there exist $L=\{[p_1,q_1],\ldots , [p_t,q_t]\}$, with $p_1,\ldots , p_t,q_1, \ldots ,q_t\in \mathbb {Q}$, and $\mu _{1,t+1},\mu _{2,t+1},\ldots ,\mu _{1,n},\mu _{2,n}$, $\nu _{1,t+1},\nu _{2,t+1},\ldots ,\nu _{1,n},\nu _{2,n} \in \mathbb {Q}$ satisfying the following conditions:

• 1. $\mathbb {N}^n{\setminus } S\subset \cup _{i\in [\phi (\widetilde{L})]}\mathrm {P}_{i\widetilde{L}}$.

• 2. For all $i\in [t]$ such that $[\widetilde{p}_i,\widetilde{q}_i]$ is a half-line interval, $\widehat{p}_i<p_i\le \widetilde{p}_i<\widetilde{q}_i\le q_i$; otherwise, $\widehat{p}_i<p_i\le \widetilde{p}_i<\widetilde{q}_i\le q_i< \widehat{q}_i$.

• 3. For all $x\in \mathtt{VSet}((\mathbb {N}^t{\setminus } S^d)\cap \mathbb {H}_{1\widetilde{L}})$, $h_{11L}(x)>0$, and for all $i\in \{2,\ldots ,\phi (\widetilde{L})\}$ and $x\in \mathtt{VSet}( (\mathbb {N}^t{\setminus } S^d)\cap \mathbb {H}_{i\widetilde{L}})$, $h_{1iL}(x) >0$ and $h_{2(i-1)L}(x)<0$.

• 4. For every $s\in \Lambda _S\cap (S^d\times \{0\}^{n-t+1})$ such that $\theta _{\widetilde{L}}(s)=0$, $\kappa _{\widehat{L}}(s)\ne 0$, and for some $m\in [\kappa _{\widehat{L}}(s)]$, $h_{1iL}(\sigma _{[t]}(s)/m) \le 0$ and $h_{2iL}(\sigma _{[t]}(s)/m)\ge 0$.

• 5. $\mu _{1,i},\nu _{1,i}\in [0,1)$, $\mu _{2,i},\nu _{2,i}\in (0,1]$, and $\mu _{1,i}+\mu _{2,i}=\nu _{1,i}+\nu _{2,i}=1$ for every $i\in \{t+1,\ldots ,n\}$.

• 6. For all $i\in [\phi (\widetilde{L})]$, and for every $\alpha \in \mathtt{VSet}(\{x\in \mathrm {P}_{i\widetilde{L}}\cap (\mathbb {N}^n{\setminus } S)\mid \sum _{j=t+1}^n x_j\ne 0\})$, $\beta \in \overline{\mathrm {P}}^+_{i\widetilde{L}}$, $\gamma \in \overline{\mathrm {P}}^-_{i\widetilde{L}}$, and $\delta \in \overline{\mathrm {P}}^*_{i\widetilde{L}}$:

  • (a) $\tau _{1(i-1)L}(\alpha )< 0$ and $\tau _{2iL}(\alpha )>0$;

  • (b) $\tau _{1(i-1)L}(\gamma )\ge 0$;

  • (c) $\tau _{2iL}(\beta )\le 0$;

  • (d) $\tau _{1(i-1)L}(\delta )\ge 0$ and/or $\tau _{2iL}(\delta )\le 0$.

Proof

We assume that S is a proportionally modular $\mathbb {N}^n$-semigroup such that $S_i=\mathscr {S}([p_i,q_i])$ for all $i\in [t]$ and $S_i=\mathbb {N}$ for all $i\in \{t+1,\ldots ,n\}$. By Corollary 2, conditions 2–4 hold. Also, since $\mathbb {N}^t{\setminus } S^d=\cup _{i\in [\phi (L)]} \sigma _{[t]}(\mathrm {P}_{iL})$, $\mathbb {N}^n{\setminus } S\subset \cup _{i\in [\phi (L)]} \mathrm {P}_{iL}\subset \cup _{i\in [\phi (L)]} \mathrm {P}_{i\widetilde{L}}$.

By Theorem 1 and Corollary 1, there exist two families of half-spaces $\{F_i^+\}_{i\in \mathbb {N}}$ and $\{D_i^-\}_{i\in \mathbb {N}}$, where $F_i^+\equiv f(x)\ge ib$ and $D_i^-\equiv d(x)\le ib$, such that $S= \cup _{i\in \mathbb {N}} (F_i^+\cap D_i^-)\cap \mathbb {N}^n$ and $(\mathbb {N}^n{\setminus } S)\cap G_0^+=\cup _{i\in \mathbb {N}^*} (F_i^-\cap D_{i-1}^+\cap G_0^+)\cap \mathbb {N}^n$. Let $\mathrm {T}_{t\,i}$ be the triangle $(F_1^-\cap D_{0}^+\cap G_0^+)\cap \langle e_t,e_i\rangle _\mathbb {R}$, with $i\in \{t+1,\ldots ,n\}$. As in Remark 3, for each triangle $\mathrm {T}_{t\,i}$, we fix the vectors $-\nu _{1,i}e_t+\nu _{2,i}e_i$ and $\mu _{1,i}e_t+\mu _{2,i}e_i$ satisfying $\mu _{1,i},\nu _{1,i}\in [0,1)$, $\mu _{2,i},\nu _{2,i}\in (0,1]$, and $\mu _{1,i}+\mu _{2,i}=\nu _{1,i}+\nu _{2,i}=1$. So, $F_i$ is the hyperplane containing the points $\{ p_1 e_1,\ldots ,p_t e_t\}$ and the vectors $\{-\nu _{1,(t+1)}e_t+\nu _{2,(t+1)}e_{t+1}, \ldots ,-\nu _{1,n}e_t+\nu _{2,n}e_n \}$, and $D_i$ contains $\{ q_1e_1,\ldots ,q_te_t\}$ and $\{\mu _{1,(t+1)}e_t+\mu _{2,(t+1)}e_{t+1}, \ldots ,\mu _{1,n}e_t+\mu _{2,n}e_n \}$. Then, $F_i$ is equal to the hyperplane defined by $\tau _{2iL}(x)=0$ and $D_i\equiv \tau _{1iL}(x)=0$. Furthermore, since $q_1,\ldots ,q_t$, $\mu _{2,t+1},\ldots \mu _{2,n}$, $p_1,\ldots ,p_t$, and $\nu _{2,t+1},\ldots ,\nu _{2,n}$ belong to $\mathbb {R}_>$, the closed half-space $F_i^+$ is defined by $\tau _{2iL}(x)\le 0$, and the open half-space $F_i^-$ by $\tau _{2iL}(x)> 0$. Analogously, $D_i^-\equiv \tau _{1iL}(x)\ge 0$, and $D_i^+\equiv \tau _{1iL}(x)< 0$. Again, by Theorem 1 and Corollary 1, conditions 6a–d hold.

Conversely, let $S'$ be the $\mathbb {N}^n$-semigroup $\cup _{i\in \mathbb {N}} (F_i^+\cap D_i^-)\cap \mathbb {N}^n$, where $F_i^+$ is the closed half-space defined by $\tau _{2iL}(x)\le 0$, and $D_i^-\equiv \tau _{1iL}(x)\ge 0$. By Theorem 1, $S'$ is a proportionally modular semigroup. Conditions 1–4 imply $S^d=S'^d$. Since $\mathbb {N}^n{\setminus } S^u\subset \mathbb {N}^n{\setminus } S'^u$ by conditions 1 and 6a, $S'^u \subset S^u$.

Suppose $\alpha \in S^u$. If $\alpha$ belongs to $(\cup _{i\in \mathbb {N}}\mathbf {P}_{\widetilde{L}}\cap \mathbb {N}^{t}) \times \mathbb {N}^{n-t}$, then $\alpha \in S'^u$. Otherwise, $\alpha \in \mathrm {P}_{i\widetilde{L}}$ for some $i\in [\phi (\widetilde{L})]$. If $\alpha \in \overline{\mathrm {P}}^+_{i\widetilde{L}}\cup \overline{\mathrm {P}}^-_{i\widetilde{L}}\cup \overline{\mathrm {P}}^*_{i\widetilde{L}}$, then $\alpha \in (F_{i-1}^+\cap D_{i-1}^-)\cup (F_i^+\cap D_i^-)$ (by conditions 6b–d). In the case that $\alpha \in \mathrm {P}_{i\widetilde{L}}{\setminus } (\overline{\mathrm {P}}^+_{i\widetilde{L}}\cup \overline{\mathrm {P}}^-_{i\widetilde{L}}\cup \overline{\mathrm {P}}^*_{i\widetilde{L}})$ and since $\alpha \in \mathrm {P}_{i\widetilde{L}}$, $\sigma _{[t]} (\alpha )\notin S^d$. So, there exists $\beta \in \mathrm {P}_{i\widetilde{L}}\cap (\mathbb {N}^n{\setminus } S^u)$ with $\sigma _{[t]} (\beta )=\sigma _{[t]} (\alpha )$ such that $\beta + e_j\in S^u$ and $\pi _{\{t+1,\ldots ,n\}}(\alpha -\beta -e_j)\ge 0$, for some $j\in \{t+1,\ldots ,n\}$; that is, $\alpha =(\alpha -\beta - e_j) + \beta +e_j$, with $\beta +e_j\in S^u$ but $\beta \notin S^u$. Equivalently, $\tau _{1(i-1)L}(\beta )< 0$ and $\tau _{2iL}(\beta )>0$, but $\tau _{1(i-1)L}(\beta +e_j)\ge 0$ and/or $\tau _{2iL}(\beta + e_j)\le 0$. If $\tau _{1(i-1)L}(\beta +e_j)\ge 0$, it is easy to prove that $\tau _{1(i-1)L}(\alpha )\ge 0$. In a similar way, if $\tau _{2iL}(\beta + e_j)\le 0$, then $\tau _{2iL}(\alpha )\le 0$. We can conclude that $\alpha \in (F_{i-1}^+\cap D_{i-1}^-)\cup (F_i^+\cap D_i^-)\subset S'$. $\square$

Algorithm 3 presents a computational method to check if an $\mathbb {N}^n$-semigroup is a proportionally modular semigroup by testing the conditions given in the above theorem. Note that some steps in this algorithm can be computed in a parallel way.

Fig. 3

$\mathbb {N}^3$-semigroup given by $29x+ 11y + 6z\bmod 33\le 6x+3y+15z$

Example 4

Let S be the $\mathbb {N}^3$-semigroup whose gap set is the set of black points in Fig. 3, that is,

$$\begin{aligned}&\{ (0, 1, 0), (0, 2, 0), (0, 2, 1), (0, 5, 0), (1, 0, 0), (1, 2, 0), (1,3, 0), (1, 6, 0),\\&\quad (2, 0, 0), (2, 0, 1), (2, 3, 0), (3, 0, 0), (3, 1, 0), (3, 4, 0), (4, 1, 0) \} \end{aligned}$$

So, the $\mathbb {N}^2$-semigroup $S\cap \langle e_1,e_2\rangle _\mathbb {R}$ is minimally generated by

$$\begin{aligned} \{ (0, 3), (0, 4), (1, 1), (2, 1), (4, 0), (5, 0), (5, 2),(6, 0), (7, 0) \}. \end{aligned}$$

By Algorithm 3, the semigroup S is a proportionally modular affine semigroup where the intervals $[\frac{829}{256},\frac{113}{16}]$ and $[\frac{21}{16},\frac{1589}{1024}]$ determine $S_1$ and $S_2$, respectively, and $\mu _{1,3}=\frac{39}{128}$, $\mu _{2,3}=\frac{89}{128}$, $\nu _{1,3}=\frac{1}{4}$, and $\nu _{2,3}=\frac{3}{4}$.

The above results were obtained using our software [3]: