Bayesian Estimation of the Maximum Magnitude m_max Based on the Extreme Value Distribution for Probabilistic Seismic Hazard Analyses

Abstract

This work proposes a new approach, based on Bayesian updating and extreme value statistics to determine the maximum magnitudes for truncated magnitude-frequency distributions such as the Gutenberg Richter model in the framework of Probabilistic Seismic Hazard Analyses. Only the maximum observed magnitude and the associated completeness period are required so that the approach is easy to implement and there is no need to determine and use the completeness periods for smaller events. The choice of maximum magnitudes can have a major impact on hazard curves when long return periods as required for safety analysis of nuclear power plants are considered. Here, not only a singular value but a probability distribution accounting for prior information, data and uncertainty is provided. Moreover, uncertainties related to magnitude frequency distributions, including the uncertainty related to the maximum observed magnitude are discussed and accounted for. The accuracy of the approach is validated based on simulated catalogues with various parameter values. Then the approach is applied to French data for a specific region characterized by high-seismic activity in order to determine the maximum magnitude distribution and to compare the results to other approaches.

1 Introduction

Probabilistic Seismic Hazard Assessment (PSHA) has the goal to evaluate annual frequencies of exceeding a given ground motion intensity measure. For this purpose, it is necessary to describe occurrence rates of earthquakes and the distribution of their magnitudes. In the classical PSHA (Cornell 1968), the hazard integral is evaluated for magnitudes in the range ${m}_{min}$ and${m}_{max}$, where ${m}_{max}$ is the maximum magnitude that can be expected for a given area and ${m}_{min}$ is the minimum magnitude of relevance for engineering structures (Bommer and Crowley 2017). The most popular distribution of magnitudes frequencies is the Gutenberg-Richter (Gutenberg and Richter 1944) truncated exponential distribution. Numerous studies and applications showed that the GR distribution is a good choice to model the distribution of magnitudes over a wide magnitudes range. The maximum magnitude ${m}_{max}$ is then the upper value used to truncate the GR model. The justification of the choice of ${m}_{max}$ only from physics or simple statistics is not straightforward. The largest observed earthquake in a specified area provides an unarguable lower bound on m_max in the area. However it is difficult to estimate the upper bound of the m_max because the physical reasons why earthquake rupture stops are still poorly understood. The choice of maximum magnitudes can have a major impact on the hazard curve when long return periods, as required for safety analysis of NPP (e.g., 10,000 years or longer), are considered.

There are essentially three types of approaches that have been pursued in the past to determine the maximum magnitude ${m}_{max}$(see e.g. the review in Wheeler 2009). The simplest method is purely empirical and consists in adding an increment (e.g., 0.5 magnitudes units) to the largest magnitude observed in the zone or region of interest. The physical approach consists in considering fault geometry, and length and possibly paleo-seismicity to deduce information on the energy that could be released (see also Zöller and Holschneider 2016). In addition, deformation rates from geodetic data and long-term tectonic deformation are gaining increased interest for the determination of maximum magnitudes (e.g. Anderson 1979; Main and Burton 1984; Moravos et al. 2003; Rong et al. 2017; Stevens and Avouac 2017). Alternatively, the theory of statistics of extremes has been applied in engineering seismology since the early ‘fifties’ by different authors such as Nordquist (1945), Epstein and Lomnitz (1966) and Knopoff and Kagan (1977) to estimate maximum magnitudes. The developments concern both the estimation of ${m}_{max}$ of the truncated GR distribution and the direct estimation of the tails of the magnitude distribution by the Generalized Extreme Value (GEV) and Pareto distributions. Burton and Makropoulos (1985) express the distribution of maximum magnitude by an extreme value distribution of Weibull type that has an upper bound to be estimated. The authors use no prior information so the uncertainty in the maximum magnitude is very large. Pisarenko and Sornette (2003) and Pisarenko et al. (2008, 2014) study the more general framework of GEV and Pareto distributions applied to earthquake magnitudes distribution and ${m}_{max}$.

From a theoretical point of view, extreme value statistics show that the GEV distribution is the limit distribution of the maximum of a series of independent random variables with same distribution under the condition of appropriate normalization. However, the scarcity of data in low seismicity regions can make it difficult to apply the latter statistical methods. On the other hand, it is well known that the maximum likelihood estimator (MLE) of the ${m}_{max}$ is biased (Kijko 2004, 2012). The maximum likelihood estimate corresponds to the maximum of the likelihood function which is always equal to the highest observed magnitude m_maxobs. As the number of observed earthquakes and thus the sample size increases it becomes more and more likely that m_maxobs is the true ${m}_{max}$ and the likelihood function gets more and more concentrated around this value. In consequence, the estimator converges with increasing the sample size N to the “true” value, but from below. This means that the estimated ${m}_{max}$ is always below the true value which is why the estimator is called biased. To overcome this drawback, Kijko (2012) developed a bias correction. The derivation of the correction term is however based on a couple of simplifying assumptions.

Zöller et al. (2016) and Holschneider et al. (2014) argue that the modeling context of a doubly truncated GR law allows for the inference of the maximum possible magnitude only if unrealistically large catalogs are available. Zöller et al. (2013) suggest replacing it by the maximum expected magnitude on a particular time horizon, for which confidence intervals can be computed from an earthquake catalog in the framework of Gutenberg–Richter statistics. This approach has been recently applied to evaluate maximum expected magnitudes for Iran (Salamat et al. 2019). It has to be pointed out that the distribution of the maximum magnitude on a time horizon has a fundamentally different meaning than the estimation of the ${m}_{max}$ in the truncated GR law. First, for determining the maximum magnitude in a time horizon in the framework of the GR law, it is still necessary to estimate the truncation of the GR law or, else, to work with the untruncated GR law. The latter however leads to very large expected magnitudes for large time horizons such as considered in probabilistic risk assessment in the nuclear sector. Secondly, in contrast to the distribution of the ${m}_{max}$ used to truncate the GR law, the distribution of the maximum magnitude on a time horizon does not represent epistemic uncertainty but aleatory variability (each of the maximum magnitudes could happen to be the maximum value over one such time interval, with different probabilities of occurrence). This has to be taken into account when choosing for example a deterministic design value, such as the 95% non-exceedance value on the time horizon.

The work presented here focuses on the estimation of ${m}_{max}$ distributions that could be used to propagate epistemic uncertainty in the framework of PSHA. For this purpose we develop a new approach based on Bayesian updating that allows to tackle most of the problems discussed above. It allows for the combination of different sources of information, and to overcome the problem of bias of the simple MLE. The Bayesian updating approach to estimate maximum magnitudes of the doubly truncate GR law has been initially proposed by Cornell (1994) (also referred to as EPRI-1994) for stable tectonic regions such as the Central and Eastern United States (CEUS). The development of the prior distributions relies on drawing analogies with tectonically comparable regions so as to obtain a larger dataset (Cornell 1994). The Bayesian approach has been applied in several PSHA projects worldwide, using the prior distributions developed for CEUS (e.g., USNRC (2012) in the framework of the seismic-source characterization for nuclear facilities in CEUS; Bommer et al. (2015) for the Thyspunt NPP in South Africa, Grünthal et al. (2018) in the national PSHA for Germany by Wiemer et al. (2016) in the national PSHA for Switzerland). Recently Martin et al. (2017) and Drouet et al. (2020) applied the Bayesian approach for PSHA in France using priors specifically developed for the target region (Ameri et al. 2015).

We develop here an improved version of the Bayesian updating approach allowing for more accurate estimates while accounting for uncertainty in the likelihood function.

It is noteworthy that the Bayesian updating approach for estimation of ${m}_{max}$ has also been blamed for producing results that are biased to low values (e.g. Kijko 2012). The authors however consider only the mode of the posterior as the point estimate of ${m}_{max}$, (similar to the Maximum Likelihood solution), which leads to the bias. Here we use the full posterior distribution in the application of the Bayesian approach for the ${m}_{max}$ estimation and we consider the posterior mean, sometimes called the “Bayes estimator”, which is known to be a better point estimator for ${m}_{max}$ than the mode (see e.g. Jaynes 2007). We show by means of simulated catalogues, that, when assuming the truncated GR distribution for the simulated magnitudes, it is possible obtain a meaningful estimate of m_max based on available data. Several case studies presented in USNRC (2012) confirm that the Bayesian posterior does not display any significant bias.

Finally we present an application to the French territory by considering appropriate prior distributions (Ameri et al. 2015) and a recently compiled national earthquake catalogue that includes historical and instrumental periods (Manchuel et al. 2017).

2 Methodology

2.1 Distribution of Extreme Magnitudes

Extreme value statistics provide mathematical methods and tools for the law of extremes defined by the tails of probability distributions. By the extreme value theorem, the GEV distributions is the only possible limit distribution of properly normalized maxima of a sequence of independent and identically distributed random variables.

Let us consider a sequence of n random variables ${X}_{1},{X}_{2},\dots ,{X}_{n}$ with common cumulative density function (cdf) $F\left(x\right)$ and the random variable

$${M}_{n}=\mathrm{max}\{{X}_{1},{X}_{2},\dots ,{X}_{n}\}$$

(1)

The cdf of the maxima ${M}_{n}$ of the sequence is then simply expressed as:

$$\mathrm{P}\left({M}_{n}<x\right)={F(x)}^{n}.$$

(2)

However, the function $F\left(x\right)$ is generally not known. Moreover, small errors on the quantity $F\left(x\right)$ can lead to important errors in the product ${F(x)}^{n}$. An alternative consists in the direct estimation of the quantity ${F(x)}^{n}$. It can be shown that for large n and when choosing appropriate normalizing constants a_n, b_n (see e.g. Coles 2001) we have: $P(\frac{{M}_{n}-{b}_{n}}{{a}_{n}}<z)\to G(z)$ where

$$G\left(z\right)=exp\left\{-{\left[1+\xi \left(\frac{z-\mu }{\sigma }\right)\right]}^{-1/\xi }\right\}$$

(3)

represents the family of GEV distributions, with parameters $\mu ,\sigma >0$ and $\xi$ that have to be determined. The parameters $\mu$ and $\sigma$ define localization and scale. The parameter $\xi$ is called the “shape parameter” since it determines to which of the three possible families of extreme value distributions the variable belongs.

For earthquake recurrence, if the truncated GR distribution or any other frequency-magnitude distribution is assumed, then the cdf $F\left(x\right)$ is known and the extreme value distributions can be derived analytically.

Under the assumption of Poissonian occurrence, as assumed in standard PSHA, the theorem of total probabilities allows writing the probability that all magnitudes, observed over a time horizon τ, are less than m as:

$$G\left(m\right)=\sum_{k=0}^{\infty }\frac{{\left({\lambda }_{0}\tau \right)}^{k}}{k!}{e}^{-{\lambda }_{0}\tau }{\left[{F}_{M}\left(m\right)\right]}^{k}, =exp\left[-{\lambda }_{0}\tau (1-{F}_{M}\left(m\right))\right]$$

(4)

where ${\lambda }_{0}$ is the annual rate of earthquakes and ${F}_{M}\left(m\right)$ is the cdf of magnitudes. Equation (4) expresses the cumulative density function of maximum magnitudes over the period τ, called $G\left(m\right)$. The corresponding probability density function (pdf) reads:

$$g\left(m\right)=\frac{dG(m)}{dm}={f}_{M}\left(m\right) {\lambda }_{0}\tau exp\left[-{\lambda }_{0}\tau (1-{F}_{M}\left(m\right))\right]$$

(5)

where ${f}_{M}\left(m\right)$ is the pdf of magnitudes. It is possible to derive the distribution of maxima accounting for the truncated GR law with upper bound ${m}_{max}$ and lower bound${m}_{min}$. In this case, we obtain the following expression for ${m}_{min}\le \mathrm{ m }\le {m}_{max}$:

$$G\left(m\right)=\mathrm{exp}\left[-{\lambda }_{0}\tau \left(\frac{\mathrm{exp}\left(-\beta {m}_{max}\right)-\mathrm{exp}\left(-\beta m\right)}{\mathrm{exp}\left(-\beta {m}_{max}\right)-\mathrm{exp}\left(-\beta {m}_{min}\right)}\right)\right]$$

(6)

where we have written ${\lambda }_{0}$ for the annual rate of earthquakes with magnitude larger than ${m}_{min}$ and $\beta$ represents the b-value of the GR law (ratio between earthquakes with large and small magnitude):$\beta =b ln(10)$.

The maximum likelihood estimator for ${m}_{max}$ in Eqs. (4)–(6) is biased as explained above. The Bayesian updating allows for a more robust and globally unbiased estimation as we show in what follows.

2.2 Bayesian Updating of Extreme Value Distribution

In what follows, we first give a general description of the Bayesian updating approach. We then show different ways to construct the likelihood function based on the extreme value distribution and conclude with the proposed approach (Sect. 2.3). Afterwards (Sect. 2.4), the EPRI-1994 Bayesian updating procedure (Cornell 1994) is described and advantages of the new method proposed here are highlighted.

The Bayes theorem allows us to write the posterior distribution of the maximum magnitude${m}_{max}$, denoted $f\left({m}_{max}\left|obs\right.\right)$, as a product of the prior distribution ${f}_{0}({m}_{max})$ and the likelihood:

$$\left.f\left({m}_{max}\left|obs\right.\right)=c L\left(obs\left|{m}_{max}\right.\right){f}_{0}({m}_{max}\right)$$

(7)

with an appropriate normalizing constant c. In this expression, the likelihood function $L\left(obs\left|{m}_{max}\right.\right)$ expresses the probability to observe the data (denoted by “obs”), given the model parameter ${m}_{max}$. In order to apply the Bayesian updating we have to consider a suitable prior distribution. For the maximum magnitude, EPRI-1994 proposes to develop prior distributions of m_max based on the statistical analysis of a catalogue of earthquakes that occurred globally, within regions with similar tectonics and geological configurations to the target region. Obviously, if the data available for the Bayesian update is scarce, then the posterior distribution is close to the prior such that the prior has a major impact on the estimation. We anticipate here that the studies conducted here in this work for French data showed that the available observations drive the estimations and have a significant impact on the estimates.

2.3 Different Ways to Express the Likelihood Function Based on the Distribution of Extremes

The data required to construct the likelihood functions is the observed ${m}_{maxobs}$ and the duration T (duration of catalogue). The likelihood functions are defined based on the extreme value distributions for Poissonian occurrences using the Eqs. (4) for the cdf and (5) for the pdf. If the GR law is assumed, then cdf yields Eq. (6). Nevertheless, any other magnitude distribution parameterized by m_max could be used in the likelihood functions developed below.

The first two functions (Eqs. (8) and (9)) are applicable only if ${m}_{maxobs}$ is included in the complete part of the catalogue, with completeness period T and is not a paleo-event.

(Ia) Probability to Observe m _maxobs on the Interval T (Completeness Period of ${m}_{maxobs}$ )

$$L(obs\left|{m}_{max}\right.)=g({m}_{maxobs}\left|{m}_{max}\right.)$$

(8)

(Ib) Probability to Observe a Set of m _{max_ti} on n Time Intervals ${\sum }_{i=1}^{n} t_{i}$

$$L(obs\left|{m}_{max}\right.)={\prod }_{{t}_{i}}g({m}_{\mathrm{max}\_ti}\left|{m}_{max}\right.)$$

(9)

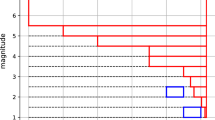
The two cases (Ia) and (Ib) are illustrated in Fig. 1 for a subset of the French catalogue, where the magnitudes are plotted as a function of the year of observation (more details will be provided in Sect. 4). On Fig. 1a, the maximum over the whole time interval is considered to construct the likelihood function of Eq. (8) while on Fig. 1b a separation in smaller time intervals is considered to construct the likelihood given by Eq. (9).

Fig. 1

Illustration of methods I a) (left) and I b) (right) for the construction of the likelihood function. The year of completeness for ${m}_{maxobs}$ is assumed to be 1600

The parameters that define the likelihood function are the durations and the values of the maxima over this time interval. Numerical analyses showed that the result is the same if the catalogue is partitioned into equal intervals and the block maxima are used or if the maximum observed over the whole duration of completeness is considered. This is also the conclusion of Zöller and Holschneider (2016). Additional information on past earthquakes is only helpful to constrain the parameters of the seismicity model, for example, the GR parameters a and b. Moreover, if the largest magnitude per interval is larger than the completeness magnitude of the considered time interval, then no special consideration of completeness is required, otherwise approach 1b cannot be applied directly.

In conclusion, the duration T together with ${m}_{maxobs}$ should be chosen (point 1 a) above) to construct the likelihood function since the completeness interval for ${m}_{maxobs}$ is generally rather large. This approach requires the determination of the completeness period of ${m}_{maxobs}$ only, without considering the issue of completeness for smaller events. The significant duration for the analyses is then the completeness period of ${m}_{maxobs}$, T(${m}_{maxobs}$). Since the catalogue it is complete for magnitudes higher than ${m}_{maxobs}$, we know that no larger event occurred during that period.

However, in some cases, the maximum observed earthquake might be outside the completeness period of the catalogue, such as for paleo-earthquakes. In this case, the likelihood function of relation (8) is not applicable, nor the likelihood function given by relation (9). In this case, we can still use the constraint that the largest magnitude in the time interval T is less than ${m}_{maxobs}$. This is the approach developed in what follows and recommended for further applications.

(II) Probability that m < m _maxobs on Interval T (Completeness Period for m _maxobs )—Proposed Approach

Since ${m}_{maxobs}$ is the largest earthquake observed in the zone, we know that all other earthquakes observed over the period T of the catalogue are less or equal than this value. We use this information to write the likelihood function as the probability that the largest magnitude in the time interval T is less than ${m}_{maxobs}$:

$$L(obs\left|{m}_{max}\right.)=G({m}_{maxobs}\left|{m}_{max}\right.)$$

(10)

Equation (10) is the most general approach and can be applied even if ${m}_{maxobs}$ is outside considered completeness interval T.

This is illustrated in Fig. 2 where the maximum magnitude occurred before 1600 which is considered as completeness period for magnitude 6 and above in this example. The method does not require any special consideration of completeness periods as long as ${m}_{maxobs}$ is in the completeness period of the duration T and this is generally the case. It can be used if ${m}_{maxobs}$ is outside the considered duration T(${m}_{maxobs}$) of the catalogue. This formulation of the likelihood will be adopted in the following applications.

Fig. 2

Illustration of approach II) for the construction of the likelihood function. m_maxobs can be outside the completeness interval. The year of completeness for ${m}_{maxobs}$ is assumed to be 1600

In what follows, we present the EPRI (Cornell 1994) approach and highlight the advantages of the new method proposed here.

2.4 EPRI Method

Cornell (1994) has developed a Bayesian updating approach where the likelihood function expresses the probability that all magnitudes in a set of N observations are less than ${m}_{maxobs}$. This method has been promoted by EPRI and is also the recommended USNRC (2012) approach. The likelihood function reads:

$$L(obs\left|{m}_{max}\right.)={{F}_{M}({m}_{maxobs})}^{N}$$

(11)

It is noteworthy that this expression (no exceedance for N observations) is close to the expression used to derive the GEV given by Eq. (3).

Using the equation for the GR law, we obtain

$$L\left(obs\left|{m}_{max}\right.\right)={{F}_{M}\left({m}_{maxobs}\right)}^{N}=c\left\{\begin{array}{ll}0& {m}_{max}\le {m}_{maxobs}\\ \frac{1}{{{(e}^{-\beta {m}_{0}}-{e}^{-\beta {m}_{max}})}^{N}}& else\end{array}\right.$$

(12)

where the constant c depends on ${m}_{maxobs}$ and ${m}_{0}$ is the chosen low-magnitude threshold (${m}_{0}$=4.5 in EPRI-1994). The data used for the EPRI-1994 method is illustrated in Fig. 3.

Fig. 3

Illustration of the EPRI method for the construction of the likelihood function. The number of earthquakes in the completeness period of m₀ is marked in violet, the vertical red line indicates the completeness interval for m₀ and m_maxobs is marked by the red dot. The black lines show the completeness period as a function of magnitude to compute the number N in the EPRI-1994 method

The EPRI-1994 Bayesian updating approach uses only the number of observations between ${m}_{0}$ and ${m}_{maxobs}$ and does not explicitly account for duration over which the N observations are made.The period over which these earthquakes can be considered in the updating depends on their completeness periods. This approach is applied to events in the completeness period of m₀ where the total number of non-exceedances is known, and to magnitudes in the completeness intervals for larger events. This is illustrated in Fig. 3 where the violet dots represent events with magnitudes lager than m₀ in the completeness period of m₀ and the black lines indicate the completeness intervals for larger events. When applying the EPRI method, then all events above the black curves are considered.The method proposed here, based on expression (10), is a more rigorous application of extreme value statistics. Since it associated the largest observed magnitude to its completeness period, it leads to smaller confidence intervals and a more accurate estimate. It is referred to as the improved likelihood function in what follows.

3 Validation with Simulated Catalogues

3.1 Convergence and Accuracy of Bayesian Updating Approach

First of all, we apply the methodology to simulated catalogues for an assessment of the accuracy and the convergence of the estimation for given periods of observation. For the simulated catalogues, we chose values for the GR parameters that are close to those of the French most active regions. The parameters assumed for the truncated GR law parameters used to simulate the catalogues are: m_min = 4.5, b = 0.79, ${\lambda }_{0}$ = 0.8. The m_max value depends on the study cases. We use the prior distribution for French active zones developed by Ameri et al. (2015) with the following characteristics (see also Drouet et al. 2020):

• Truncated normal distribution

• mean Mw = 6.8, std = 0.4

• upper truncation at Mw = 7.5, lower truncation at Mw = 5.5

We compare the results obtained with this prior to the cases where a lognormal prior or a Gaussian prior without truncation are assumed.

The case with magnitude uncertainty, depending on the date of the events, will be considered in a second step. The following two series of studies are conducted:

• 1. We assess the feasibility and accuracy of the estimations for different values of m_max. Since, in contrast to the observed earthquake data, the m_max value is known for the simulated catalogues, we can compare m_max estimated as the mean of the posterior density function to the “true” value. To check a possible bias and assess variability of the estimations, we compute N = 1000 catalogues for each study case considering T = 266 years and compute the posterior mean as an estimator for m_max. Tables 1 and 2 show the mean value of the N estimated posterior means and the standard deviation (std) for true m_max values increasing from Mw = 6.0 to Mw = 7.2. If the mean is close to the true value and the dispersion, expressed by the std is small, then this means that the application of this method to observed data (one catalogue) provides estimations close to the true value. Note that in the application to the French catalogue presented in the following section, the considered duration is actually 266 years.

• 2. We analyze the convergence of the estimations by increasing the period of observation to T = 500 years and T = 1000 years. To assess the variability, we compute again N = 1000 catalogues for each study case with m_max = 6.5. and m_max = 7.0. The reference results for T = 266 years are given in Tables 1 and 2. Tables 3 and 4 show the results for T = 500 years and T = 1000 years, respectively.

Table 1 Mean and std of the posterior means for 1000 catalogues, true m_max = 6.0 (left) and m_max = 6.5 (right) considering the 3 different priors for T = 266 years

Table 2 Mean and std of the posterior means for 1000 catalogues, true m_max = 7.0 (left) and m_max = 7.2 (right) considering the 3 different priors for T = 266 years

Table 3 Mean and std of the posterior means for 1000 catalogues, true m_max = 6.5, T = 500 years (left) and T = 1000 years (right)

Table 4 Mean and std of the posterior means for 1000 catalogues, true m_max = 7.0, T = 500 years (left) and T = 1000 years (right)

The results show that the Bayesian updating provides an accurate estimate of the maximum magnitude for observation periods available in France. The mean of the m_max values estimated over the N catalogues is very close to the true value indicating that there is no significant bias. The estimates converge towards the true value if T is increased and if there is no uncertainty in the magnitudes. For T = 1000 years, the variability of the estimate is negligible (the std decreases to ± 0.02 for magnitude ranges expected in France) and the estimated mean is equal to the true value. The error or spread of the estimations (expressed here by the standard deviation) always decreases when the period of observation is increased.

The analyses also show that the particular choice of the prior distribution (among Gaussian, lognormal and truncated Gaussian alternates) does not have a significant impact on the result in this case. In particular, the estimations of the posterior mean computed with the Gaussian and the truncated Gaussian priors are very close. This is because the data has a major impact on the posterior. The close agreement of the posterior mean with the known m_max implies that the estimation is robust, consistent with Jaynes (2007).

3.2 Accounting for Period-Dependent Magnitude Uncertainty

Earthquake magnitudes reported in catalogues are inevitably affected by uncertainties that are expected to be higher for the historical events. A value of 0.1 can be considered as the magnitude uncertainty for recent well studied events. However, such uncertainty is expected to increase for historical events and to change over time with the oldest events being characterized by the largest uncertainties. Accordingly, we introduced a Gaussian error term with time-dependent standard deviation. The std are 0.5, 0.35, 0.25 for events that occurred respectively before 1900, 1950, 1975 and 0.1 for the more recent events. These values are generally in agreement with the values given in the French catalogue FCAT17 (Manchuel et al. 2017) and the RESORCE database (Akkar et al. 2014) for French events. Note that magnitude uncertainties are also expected to be magnitude-dependent with small magnitudes being characterized by larger uncertainties. However, for purpose of m_max definition, where the interest is mostly on the largest events in the catalogue, uncertainties on small magnitudes are less relevant.

The simulations show that magnitude uncertainty leads to a systematic overestimation of m_max. The latter increases if the magnitude uncertainty increases. The overestimation of m_max is due to the fact that the observed m_maxobs of a set of earthquakes is generally higher than the “true” m_maxobs when magnitude uncertainty is included (because it becomes highly likely that m_maxobs would be governed by an overestimated magnitude due to uncertainty). This leads to a bias in the estimations.

This issue can be analyzed with the simulated catalogues by introducing the magnitude uncertainty and by comparing the observed m_maxobs to the true m_maxobs (without magnitude uncertainty). The numerical analyses showed that the relative bias, that is the observed m_maxobs/true m_maxobs, does not change considerably for different true m_max values but it does depend on the degree of magnitude uncertainty. The bias becomes more significant when the magnitude uncertainty increases. The simulation shows a bias (observed m_maxobs/true m_maxobs) of 4.5% when considering uncertainty. An illustration of the origin of the bias is given in Fig. 4.

Fig. 4

Illustration of the case where the a true m_maxobs and the observed mmaxobs do not belong to the same event and b where they do. The green stars represent the “perfect” catalogue without uncertainty while the blue stars are obtained when introducing period-dependant magnitude uncertainty

Obviously, without considering magnitude uncertainty, the m_maxobs value cannot exceed the true m_max, which equals 7.0 in this example. However, the observed m_maxobs can be larger than the true m_max within its stated error. Moreover, when the true m_maxobs value is underestimated due to uncertainty this does not mean that m_maxobs is underestimated by that same amount because the second largest magnitude might be larger and then be considered as m_maxobs. This is why, when considering higher magnitude uncertainty, then the observed m_maxobs is generally higher than the true m_maxobs which can lead to a considerable overestimation of m_max.

In consequence, not only the parameter uncertainties but also the bias has to be accounted for in the Bayesian updating procedure. The approach adopted here is detailed in what follows.

We consider uncertainty related to the GR recurrence parameters $\beta ,{\lambda }_{0}$, duration T and m_maxobs.

We evaluate the marginal posterior distribution by integrating the parameter uncertainty in the likelihood function as:

$$\begin{aligned} \bar{f}\left({m}_{max}\left|obs\right.\right)=c\int L\left(obs\left|{m}_{max},\beta ,{\lambda }_{0}\right.,\right){f}_{0}\left({m}_{max}\right)f\left(\beta ,{\lambda }_{0},{m}_{maxobs}\right)f\left(T\right)d\beta d{\lambda }_{0} d{m}_{maxobs}dT \\ L\left(obs\left|{m}_{max},\beta ,{\lambda }_{0}\right.\right)=\mathrm{exp}\left[-{\lambda }_{0}T \left(\frac{\mathrm{exp}\left(-\beta {m}_{max}\right)-\mathrm{exp}\left(-\beta {m}_{maxobs}\right)}{\mathrm{exp}\left(-\beta {m}_{max}\right)-\mathrm{exp}\left(-\beta {m}_{min}\right)}\right)\right] \end{aligned}$$

(13)

We consider here GR-statistics for French most active regions covering the French Alps and Pyrenees and corresponding to the seismotectonic domain D-1 identified by national PSHA by Drouet et al. (2020) as illustrated in Fig. 5 (upper right graph). The GR parameters derived for magnitudes larger than $Mw=4.0$ in EDF (2017) are shown in Fig. 5. According to their study, the mean estimate and the std of the GR parameters a and b are, respectively:

• $\bar{a}=4.1$ and ${\sigma }_{a}=0.13$

• $\bar{b}=0.79$ and ${\sigma }_{b}=0.05$

Fig. 5

Gutenberg-Richer parameters for French active domain “D1” encompassing the Alps and Pyrenees. (Top-left): Observed exceedance rates (blue circles for individual solutions from synthetic catalogs sampling uncertainties, see main text) compared to modeled G-R curves (gray lines for individual solutions). The mean G-R curve is shown in black and compared to the solution defined by Johnston et al. (1994) for SCR shown in purple. The red color refers to the solution obtained with the original catalogue. (Top-right): Map of the seismicity considered in the analysis. Only the epicenter shown as red circles are selected for the calculation after applying the completeness criteria. (Bottom-left): Statistics of the a-values (per 1E6 km²) and b-values obtained through the Monte-Carlo sampling (gray circles). The percentiles 2, 16, 50, 84, 98th are shown as squares. (Bottom-right): Analysis of the correlation of the individual G-R solutions (gray circles)

The GR curves are shown in Fig. 5 (upper left figure). The GR parameters are estimated using the Penalized Maximum Likelihood method by USNRC (2012) which account for uncertainties on earthquake location, magnitude and completeness periods through the use of synthetic catalogues and introduces a prior b-value to constrain the slope of the GR model. In agreement with these results we use a bivariate Gaussian distribution to express the joint law $f(a,b)$ of the two GR parameters.However, the correlation coefficient determined for French domain D-1 is close to unity which means a « nearly perfect correlation» of the two parameters. Note that this is not always the case and although a and b parameters are expected to be correlated (Ordaz and Faccioli 2018) the level or correlation depends of the specific zone under consideration.

In the light of these results, we assume perfect correlation. The two perfectly correlated Gaussian random variables $\beta$ and ${log}_{10}{\lambda }_{0}$ are then expressed as:

$$\beta =\mathrm{ln}\left(10\right)\bar{b}+{\mathrm{ln}\left(10\right)\sigma }_{b}\varepsilon$$

(14)

$${log}_{10}{\lambda }_{0}=\bar{a}+{\sigma }_{a}\varepsilon \, - {m}_{min}(\bar{b}+{\sigma }_{b}\varepsilon )=\bar{a}+{m}_{min}\bar{b}+({\sigma }_{a}+{{m}_{min}\sigma }_{b})\varepsilon$$

(15)

where $\varepsilon$ is a centered normalized (unit variance) Gaussian random variable. We adopt a Gaussian distribution for the uncertainty related to m_maxobs We furthermore assume a uniform distribution for the completeness year T, with the interval $\bar{T}\pm 50 \mathrm{years}$, where $\bar{T}$ is the mean value.

The parameter uncertainty in the likelihood function of Eq. (13) is propagated using the Latin Hypercube Sampling approach (LHS). On the one hand, the uncertainty on the duration and the GR-parameters does not change the position of the peak of the likelihood function but it results in functions more or less concentrated towards that value. On the other hand, the uncertainty on m_maxobs has an impact on the position of the peak and leads to a broadening of the latter. This is illustrated for the application to French data in Fig. 9.

First, the impact of the uncertainty on the estimates of m_max is quantified by assessing the mean and std of the difference between the observed m_maxobs and the true m_maxobs using the simulated catalogues. Secondly, the approach is applied to estimate m_max for the simulated catalogues.

The results obtained with 5000 artificial catalogues are shown in Fig. 6 where the bias, that is the mean of the difference between true and observed values, and its std are shown as a function of the true m_maxobs. According to these results, the std can be considered constant while the bias depends on the value of the true m_maxobs. The bias is a systematic error that has to be accounted for in the estimation procedure. Moreover, these simulations provide the uncertainty relative to the observed m_max in terms of the std of the difference between the true m_maxobs and the observed m_maxobs.

Fig. 6

Mean and std of the difference between the observed m_maxobs and the true m_maxobs estimated from 5000 catalogues

In consequence, m_maxobs in Eq. (13) is modelled as a Gaussian random variable with mean and std equal to the values determined by means of the simulations and shown in Fig. 6.

In what follows we show the impact of accounting for the bias and uncertainty on m_maxobs in the estimation procedure. We consider GR parameters of domain D1 assuming a true m_max equal to Mw = 7.0. We adopt again the prior distribution for active French regions with parameters as introduced in Sect. 3. Figure 7 illustrates, for an example catalogue, the prior and the posterior estimates of the m_max distribution for the case when uncertainty is neglected (left figure) and when considering uncertainty (right figure). As expected, considering uncertainty enlarges the likelihood function and in consequence the posterior distribution and allows for a smoother shape of the latter. The posterior mean (or Bayes estimator) is now close to the mode of the distribution.

Fig. 7

Illustration of posterior pdf and Bayes estimator with and without considering magnitude uncertainty for m_max = 7.0

The numerical results with and without considering uncertainty are shown in Table 5, where the mean and the std of the Bayes estimator is given for 1000 simulated catalogues. In particular, we compare the ideal case where the magnitudes in the catalogue are perfectly known (true simulated m_max) to the case where the magnitudes in the catalogue are not perfectly known. In the latter case, Table 5 shows that the introduction of the uncertainty on the parameters and, in particular on m_maxobs, allows us to improve the estimations (last column of Table 5). The posterior mean is close to the true m_max and the std of the estimations (over 1000 catalogues) decreases from 0.28 to 0.16 which is close to the lowest possible value obtained with the perfect data.

Table 5 Estimated m_max for GR parameters of domain D1 assuming a true m_max Mw=7.0  with and without improved likelihood function for 1000 simulated catalogues.

It has to be pointed out that the issue of magnitude uncertainty is unavoidable, and not specific to the new approach presented here but it also needs to be accounted for in the EPRI updating procedure (as discussed in USNRC 2012) as well as in any other method where a set of extreme magnitudes is considered. In those cases, not only the uncertain of the largest observed magnitude but the uncertainty of the full set of magnitudes used for the estimation of m_max has to be accounted for according to their occurrence time.

In what follows, we apply the EPRI-1994 method and the new Bayesian updating approach to French data from catalogue FCAT17 with and without considering magnitude uncertainty. The impact of magnitude and GR parameter uncertainty is then further analyzed and discussed.

4 Estimation of the Maximum Magnitude Distribution Using Data from French Active Zones

The methodology is now applied to determine the maximum magnitude for French domain D1 containing the most active regions in France as shown in Fig. 5 (upper right). The data available for this domain according to FCAT17 catalogue is plotted in Fig. 8. The largest observed magnitude in the domain is ${m}_{maxobs}=\mathrm{6,7}$, and it occurred within the completeness period T (1750 according to the lower bound given by Drouet et al. 2020), highlighted by the vertical red bars. The values for the GR parameters are those introduced in the previous section. We consider the truncated Gaussian distribution for French active regions developed by Ameri et al. (2015) for the prior distributions of m_max, as introduced above. The Authors used the European earthquake catalogue (Stucchi et al. 2012) and the m_max regionalization developed for the European Seismic Hazard Model, ESHM13 (Woessner et al. 2015) in order to develop two prior m_max distributions applicable to low and active seismic regions in France. The statistical approach adopted by Ameri et al. (2015) to develop the priors follow the one employed by EPRI-1994 and more details can be found in Ameri et al. (2015). We also refer to Drouet et al. (2020) who applied these priors in the EPRI-type Bayesian approach to determine m_max in the framework of the generation of probabilistic seismic hazard maps for France.

Fig. 8

Earthquakes contained in the catalogue corresponding to French domain D1 identified in the upper-right graph of Fig. 5. Vertical red bars highlight the completeness period for m_maxobs

Beside the prior developed by Ameri et al. (2015), we tested other prior distributions; in particular the lognormal and the not-truncated Gaussian distribution. We will compare results for the initial Gaussian and the truncated Gaussian prior distribution to assess the sensitivity of the estimations on this choice.

When considering uncertainty in the likelihood function according to Eq. 13, then the value of m_max has to be known in order to pick the correct bias correction value in Fig. 6, but in a realistic case this valued is not known from the start. An iterative procedure is applied, where the initial value for the bias is chosen according to the results without considering uncertainty. The bias is then updated to be in agreement with the new estimation of m_max. The iterations continue until the m_max used for bias correction coincides with the estimated m_max. Tests performed by the authors showed no dependence on the choice of the initial estimation as long as it remains in the range of reasonable values.

In what follows we show the results for the two cases:

• New approach with improved likelihood function according to Eq. (10)

• New approach with improved likelihood function and accounting for parameter uncertainty in expression (13)

For comparison, we also compute the estimations for EPRI-type approach with likelihood function based on expression (12) (as in Drouet et al. 2020). Figure 9 compares the likelihood functions corresponding to the EPRI method (light blue dashed) and the proposed method based on the cdf of extremes without uncertainties (solid blue) and when accounting for uncertainties (solid magenta). The improved likelihood function proposed here makes better use of available information and it is tighter around the observed m_max as compared to the EPRI likelihood function. The introduction of uncertainties on recurrence parameters and m_maxobs in the new approach leads to a broadening of the likelihood function. The likelihood functions are normalized for comparison. Since the likelihood functions are not proper in the sense that they cannot be normalized by integration of the pdf to infinity, we have chosen a pragmatic normalization based on the peak value (the same peak value for all functions) to facilitate visualization and comparison.

Fig. 9

Comparison of likelihood functions from the EPRI method (N = 149 events) and the proposed method (T = 266 years) with and without considering uncertainties

Figure 10 compares the posterior pdfs and the Bayes estimator corresponding to the EPRI method (Fig. 10a), N = 149 events) and the proposed method based on the cdf of extremes (Fig. 10b), T = 266 years), in both cases uncertainties in the GR parameters are neglected.

Fig. 10

Comparison the prior and the updated distributions of m_max using the EPRI method (N = 149 events) and the proposed method (T = 266 years) without considering uncertainties

Figure 11 shows the prior and the updated distributions of m_max for the improved likelihood function when considering uncertainties of the GR parameters and the completeness period of m_max.

Fig. 11

Prior and the updated distributions of m_max when considering the improved likelihood function with parameter uncertainties

The introduction of uncertainty allows for a more physical representation of possible values of maximum magnitudes, the likelihood function is smoother and the density of the updated m_max distribution is more centered on the Bayes estimator. Due to the uncertainty related to the observed m_maxobs, the likelihood function with uncertainty also allows for maximum magnitude values below the observed one, although higher magnitude values become more likely.

The Table 6 summarizes the statistics of the posterior distribution of ${m}_{max}$ for the three methods where the mean, median and 5%, 95% Bayesian Intervals (BI), that is the fractiles 5%, 95% of the posterior distribution are given. First of all, Table 6 confirms that the truncated prior and the untruncated prior distributions provide very similar results and thus only small sensitivity of the updating on the particular choice of the prior. This means that the data carries sufficient information for meaningful updating.

Table 6 Statistics of the posterior distribution of ${m}_{max}$ with and without considering uncertainties on GR parameters and m_maxobs for truncated Gaussian prior distribution: mean, median and 5%, 95% BI

5 Summary and Conclusions

We have developed a methodology for estimating the probability distribution (epistemic uncertainty) of the maximum magnitude by Bayesian updating using the analytical expressions of the extreme value distribution. For application purposes, we have adopted the truncated Gutenberg-Richter law assuming Poissonian occurrence of earthquakes. The uncertainties on the maximum observed magnitude in the catalogue and the GR parameters have been integrated in the updating procedure. The approach remains applicable when other distributions than the truncated GR law are assumed since the analytical expressions can be derived for any distribution as long as Poisson occurrence is assumed. In the Bayesian approach, the information from similar tectonic regions and expert judgment is introduced by a prior distribution of the maximum magnitude. The new method combines the distribution of extreme values of the truncated GR law with the Bayesian updating approach. Regarding the time intervals used for the derivation of the extreme value distribution, the analyses showed that the same result is obtained when considering a set of time intervals and their m_maxobs or when considering only one time interval and the associated m_maxobs.

The proposed method is more rigorous and outperforms the EPRI/USNRC Bayesian updating approach for the following reasons. The duration-based formulation of the likelihood proposed here performs better than the EPRI approach because it associates m_maxobs to its completeness period which is a stronger constraint on m_max than the number of events that can be used in the EPRI method. Only the completeness period of m_maxobs is required, so that there is no need to determine and use the completeness periods for smaller events and to introduce the associated uncertainties. This makes the approach easy to implement and to apply. The analyses conducted with simulated catalogues demonstrated the capability of the Bayesian updating approach to correctly estimate m_max. Eventually, simulated catalogues demonstrate the possibility to estimate m_max with the proposed method and for periods of observation available in France. The results were insensitive to the truncation of prior distribution, however it is important to investigate alternative priors and to conduct further sensitivity analyses. Finally, this study highlights the crucial importance of accounting of uncertainties of earthquake catalogues magnitudes. Introducing uncertainty in the process allows for a more physical and unbiased representation of possible values of maximum magnitudes. In this case, the likelihood function is smoother and the density of the updated m_max distribution is more centered around the Bayes estimator.