1 Introduction

The right rectangular prism is a good and simple way to approximate (in fact any) a 3D body. The density of this prism can be constant, if there are a large number of them and they are sufficiently small to model any density distribution. Only limitation was the calculation time. However, this problem could be almost neglected with the massive improvement of the computing technology in the present. One can say that approximation with the polyhedral bodies is better, or more suitable or more accurate. In connection with this, we can see the large “reincarnation” of the direct problem solutions for the polyhedron bodies in the geodetic literature in the last several years (e.g. Hamayun et al. 2009; Çavşak 2012; D’Urso 2014; Werner 2017 a.o.). However, any polyhedron can be approximated by a system of rectangular prisms with the constant density with a given or required accuracy of the calculated gravitational effect. Because of this, some “refreshment” of the knowledge connected with a right rectangular prism and its gravitational effect is given in this paper, while there are still some issues which have to be answered.

According to our knowledge (based on the data from the citation databases), the most cited paper dealing with the effect of the right rectangular prism is Nagy (1966). There are some problems connected with this solution (validity, completeness, singularities) and we tried to identify the right source of these problems and explain them. Next, the formula of Sorokin (1951), as representative of another solution’s type, is discussed while similar problems occur here too. Finally, the questions connected with the citations in this area of the direct problem research are investigated.

2 Theory Elements

We will start with some very elements of the direct problem branch. The gravitational potential of the 3D body in the Cartesian coordinate system is given by (e.g. MacMillan 1930):

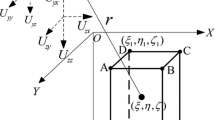
$$V(x,y,z) = G\mathop{\iiint}\limits_{\!\!\!\!\tau } {\frac{{{\text{d}}m}}{{\sqrt {(\xi - x)^{2} + (\eta - y)^{2} + (\zeta - z)^{2} } }}},$$
(1)

where dm is the mass element: \({\text{d}}m = \sigma (\xi ,\eta ,\zeta ){\text{d}}\tau ,\)σ is the function of the density distribution within the body and G is the gravitational constant, dτ is the volume element. The used symbolism is chosen as follows: the Greek letters are related with the position of a mass element and Latin letters are connected with the calculation point (Fig. 1). The vertical axis of used system is pointing upwards. This is important to mention, because one can find the publications (e.g. Li and Chouteau 1998; Nagy et al. 2000 a.o.), where this axis is orientated downwards—in “geological” way. This modification was used mostly in the past (but still occurs from time to time in the more recent publications, too) to avoid the depth to be a negative number. Note that, there is in fact no preferred orientation of coordinate system—the terms “horizontal” and “vertical” have to be understood rather as a “names” of the axis not as the expression of their orientation. When the direct problem is solved, there is only the body and the calculation point, i.e. there is none “external” gravity field to tell us “where” the vertical/horizontal direction is. So, the term “vertical” is connected with the z axis and “horizontal” is assigned with the x and y axis.

Fig. 1
figure 1

The scheme of the rectangular prism and the mass element (dm) with the position of the calculation point P in the Cartesians coordinates

Full size image

The gravitational attraction vector is then given by:

$${\mathbf{g}} = \nabla V = \frac{\partial V}{\partial x}{\mathbf{i}} + \frac{\partial V}{\partial y}{\mathbf{j}} + \frac{\partial V}{\partial z}{\mathbf{k}}.$$
(2)

Calculated like this, the resultant vector g is pointing from the calculation point to the body, as common agreement says.

3 The Gravitational Attraction of the Rectangular Prism

Basically, there are two ways to find the components of gravitational attraction vector g—to find the potential in the first step, and next, to carry out the derivatives with respect to variables x, y and z. The second option is to find the derivatives of the integrated function in Eq. (1) first, and then carry out the integration. This approach is fully valid for the potential itself and its first derivatives (e.g. Kellogg 1929) for any position of the calculation point (outside, inside, on the surface of the prism). According to this, the components of g are:

$$V_{x} = \frac{\partial V}{\partial x} = G\sigma \mathop{\iiint}\limits_{\!\!\!\!\tau } {\frac{\xi - x}{{R^{3} }}\,{\text{d}}\xi \,{\text{d}}\eta \,{\text{d}}\zeta },$$
(3)
$$V_{y} = \frac{\partial V}{\partial y} = G\sigma \mathop{\iiint}\limits_{\!\!\!\!\tau } {\frac{\eta - y}{{R^{3} }}\,{\text{d}}\xi \,{\text{d}}\eta \,{\text{d}}\zeta },$$
(4)
$$V_{z} = \frac{\partial V}{\partial z} = G\sigma \mathop{\iiint}\limits_{\!\!\!\!\tau } {\frac{\zeta - z}{{R^{3} }}\,{\text{d}}\xi \,{\text{d}}\eta \,{\text{d}}\zeta },$$
(5)

where \(R = \sqrt {(\xi - x)^{2} + (\eta - y)^{2} + (\zeta - z)^{2} } .\) We can see, that it is enough to solve the first integration (Eq. 3) and the two others are just its variations. So, now we will focus on the detailed solution of the first integration. With the substitution: \(X = \xi - x\), \(Y = \eta - y\), \(Z = \zeta - z,\) and with the corresponding change of the symbol R to: \(R = \sqrt {X^{2} + Y^{2} + Z^{2} } ,\) Eq. (3) can be rewritten:

$$V_{x} = G\sigma \int\limits_{X} {\int\limits_{Y} {\int\limits_{Z} {\frac{X}{{R^{3} }}\,{\text{d}}X\,{\text{d}}Y\,{\text{d}}Z} } } .$$
(6)

The integration with the respect to the variable X is quite simple:

$$V_{x} = - G\sigma \int\limits_{Y} {\int\limits_{Z} {\left[ {\frac{1}{R}} \right]_{X} {\text{d}}Y\,{\text{d}}Z} } .$$
(7)

The integration with the respect to the variable Y can be carried out with the help of substitution \(t = \frac{Y}{R}\) and the result is:

$$V_{x} = - G\sigma \int\limits_{Z} {[\ln (Y + R)]_{X,Y} \,{\text{d}}Z} .$$
(8)

The per partes method is used now and the result of the last integration (through the substitution \(v = \frac{t}{{\sqrt {t^{2} + b} }}\)) is:

$$V_{x} = - G\sigma \left[ {Z\ln (Y + R) + Y\ln (Z + R) - X\,{\text{arctg}}\frac{YZ}{XR}} \right]_{X,Y,Z} .$$
(9)

The result in this form is valid \(\forall X \ne 0\) and if \(X \ne Y \ne Z \ne 0\) what results in the contradiction with the potential theory, because this solution has the singularities in the source-free region. The geometrical sense of \(X = 0\) is that the calculation point (named, e.g. P) lies in the planes normal to the x-axis, assigned by the front and back facets of the prism (rectangles ABCD and EFGH), see Fig. 1, while the situation \(X = Y = Z = 0\) refers to the calculation point located in the one of the prism’s vertices.

Nagy et al. (2000) refer to this problem and calculate the limits for these crucial positions, but we see the problem in this approach. The existence of the limit in the given point P, does not necessarily mean that the function is continuous in P and more, the limit in P describe only the situation “very close” to that point, but tell us nothing about what happens directly in the given point, as clear from the definition of the limit. The theory says that potential and its first derivatives must exist, be regular, finite and continuous in the each point (e.g. Kellogg 1929), which is why we cannot be satisfied with the limits as Nagy et al. (2000). The desired solution must fulfilled all these conditions for \(X = 0,\) and so, it must be proven that the values in these calculation point’s positions are the same as the limits obtained by Nagy et al. (2000). This can be done by substituting the corresponding boundaries \((X_{1} = 0 \vee X_{2} = 0)\) directly after the integration with the respect to the variable X what will give us some partial results for these crucial positions of the calculation point (the same approach can be used for the case \(X = Y = Z = 0\)). The combination of Eq. (9) and such partial results will give us the complete continuous solution for the each position of the calculation point. It is clear that the program realization will be complicated in the form of the combination of the partial results, and so, the better alternative is to modify Eq. (9) to contain these partial solutions for the analyzed problematic positions of the calculation point. One of the possible modifications could be:

$$V_{x} = - G\sigma \left[ {\begin{array}{*{20}l} {Z\ln (Y + R + 1 - {\text{sign|}}Z |) + Y\ln (Z + R + 1 - {\text{sign|}}Y |)} \hfill \\ {\quad - X\,{\text{arctg}}\frac{YZ}{{XR + 1 - {\text{sign|}}X |}}} \hfill \\ \end{array} } \right]_{X,Y,Z} .$$
(10)

This formula is fully valid even for the calculation points located inside of the prism. There is, of course, another simple possibility—choose the sampling step precisely to avoid the calculation point hit these crucial positions, or to shift the calculation point by adding a small number ε to its coordinates (according to our testing made in the MatLab—this approach works satisfactory for \(\varepsilon \approx 10^{ - 6}\) m).

The last crucial task is the position of the calculation point on the surface of the prism—on the rest of the facets (upper, lower, right, left), the edges and the vertices (precisely, the edges are including in the facets, so they have not to be discussed separately, but the vertices have to be discussed—because of the “R” term within the solutions). The properties of the potential and its first derivatives mentioned before must hold in these points too. This is true for Eq. (10), but is not for Sorokin (1951), Nagy (1966) and the others. The calculation point located on the surface of the prism is problem for the higher order derivatives—they are not continuous here. After a similar analysis for the rest of the potential’s derivatives (Vy and Vz), we will obtain:

$$V_{y} = - G\sigma \left[ {\begin{array}{*{20}l} {Z\ln (X + R + 1 - {\text{sign|}}Z |) + X\ln (Z + R + 1 - {\text{sign|}}X |)} \hfill \\ {\quad - Y\,{\text{arctg}}\frac{XZ}{{YR + 1 - {\text{sign|}}Y |}}} \hfill \\ \end{array} } \right]_{X,Y,Z} ,$$
(11)
$$V_{z} = - G\sigma \left[ {\begin{array}{*{20}l} {X\ln (Y + R + 1 - {\text{sign|}}X |) + Y\ln (X + R + 1 - {\text{sign|}}Y |)} \hfill \\ {\quad - Z\,{\text{arctg}}\frac{XY}{{ZR + 1 - {\text{sign|}}Z |}}} \hfill \\ \end{array} } \right]_{X,Y,Z} .$$
(12)

Finally, substituting Eqs. (10)–(12) into Eq. (2) gives us the singularity-free solution of the direct problem for the rectangular prism with the constant density for all positions of the calculation point.

4 The Review of Nagy (1966) Solution

The discussed formula of Nagy (1966) Eq. (7) reads:

$$V_{z} (0,0,0) = G\rho \left[ {x\ln (y + r) + y\ln (x + r) - z\arcsin \frac{{y^{2} + z^{2} + yr}}{{(y + r)\sqrt {y^{2} + z^{2} } }}} \right]_{{z_{1} ,y_{1} ,x_{1} }}^{{z_{2} ,y_{2} ,x_{2} }} ,$$
(13)

where \(r = \sqrt {x^{2} + y^{2} + z^{2} }\), ρ is the density and xi, yi, zii = 1, 2 are the integration boundaries, which defines the size and the position of the prism. This formula is derived for the calculation point placed in the origin of the coordinate system. The calculation in the other points is made by changing of the integration boundaries.

There is important issue with this formula. If the vertical projection of the body is crossing the horizontal axis, the discussed formula cannot be used immediately. In such cases, the integration must be divided and carried out from 0 to the upper boundary (x2) and then from 0 to the lower boundary x1, where the absolute values of theses boundaries has to be used. So, the horizontal boundaries cannot have the different signs. Practically, the body is divided into the two parts, and the one with the boundary of the negative sign is placed in the positive part of the axis, in this process. The author himself mentioned this, but he does not deal with it as with the problem. Some other authors mentioned it too (e.g. Banerjee and Das Gupta 1977; Li and Chouteau 1998), but they did not explain the reason for this, nor pointed the source of this problem in the Nagy’s derivation. We will take a closer look on his derivation and try to identify where this problem begins.

The first two integrations with the respect to the variables z and y are:

$$V_{z} = G\rho \int\limits_{x} {\int\limits_{y} {\int\limits_{z} {\frac{z}{{r^{3} }}\,{\text{d}}x\,{\text{d}}y\,{\text{d}}z} } } = - G\rho \int\limits_{x} {\int\limits_{y} {\frac{1}{r}\,{\text{d}}y\,{\text{d}}x} } = - G\rho \int\limits_{x} {\ln (y + r)\,{\text{d}}x} .$$
(14)

The last integration (with respect to the variable x) is the crucial point of the whole derivation. Next, the per partes method is used:

$$V_{z} = - G\rho \left[ {x\ln (y + r) - \int\limits_{x} {\frac{{x^{2} \,{\text{d}}x}}{r(y + r)}} } \right]_{y,z} .$$
(15)

The task is reduced to find the last integration. Here is the place where author made the crucial steps which lead us to the above-mentioned problems connected with his solution. The author used the following substitution:

$$u = y + r.$$
(16)

Here is the main problem. Such substitution is valid only for the one-by-one functions (injections) (e.g. Rektorys 1968). This is why the substitution works correctly, only if the both boundaries are a positive numbers—in such interval the function is an injection. Once, the horizontal axis is crossed (the boundaries are of a different sign), the function does not meet the injection condition, because the function under the integration sign is even. Next, the author stated that:

$$x^{2} = (u - y)^{2} - y^{2} - z^{2} .$$
(17)

This expression is used to calculate dx:

$$2x{\text{d}}x = 2(u - y){\text{d}}y \Rightarrow {\text{d}}x = \frac{u - y}{x}.$$
(18)

There is another problem. Author wrote that:

$$x = \sqrt {(u - y)^{2} - y^{2} - z^{2} } ,$$
(19)

which gave him the expression of dx:

$${\text{d}}x = \frac{u - y}{{\sqrt {(u - y)^{2} - y^{2} - z^{2} } }}.$$
(20)

This step is not completely valid. Precisely it should be:

$$|x| = \sqrt {(u - y)^{2} - y^{2} - z^{2} } .$$
(21)

Author’s derivation is then valid only for the positive part of the integrated function, again. In one word, the usage of Eq. (19) instead of Eq. (20) leads to the loss of generality of the final solution. This issue can be avoided by previously mentioned procedure—splitting body into the two parts—which are taken separately. From the programming point of view, this is “unforced” complication, while more general solutions are available.

Next, it is important also to mention the fact pointed out by Banerjee and Das Gupta (1977, p. 1054), that the formula of Nagy (1966) is not independent in the choice of the x- and y-axes (i.e. when the x-and y-axes are interchanged). This is caused by the problems with the used substitution in the integration in the x-direction. Also, when setting the limits x1, x2, y2 and y2 to the infinity we should get the well-known gravitational attraction of an infinite Bouguer slab, which is a true in the case of the Sorokin’s (1951) formula (which will be discussed next), but cannot be achieved in the case of the Nagy (1966) formula (Banerjee and Das Gupta 1977, p. 1055).

5 The Review of Sorokin (1951) Solution

The discussed formula of Sorokin (1951) reads [with the symbolism similar to (1)]:

$$V_{z} (0,0,0) = - G\sigma \left[ {\xi \ln (\eta + R) + \eta \ln (\xi + R) + \zeta \text{arctg} \frac{\zeta R}{\xi \eta }} \right]_{{\xi_{1} ,\eta_{1} ,\zeta_{1} }}^{{\xi_{2} ,\eta_{2} ,\zeta_{2} }} ,$$
(22)

where G is the gravitational constant, σ is the density, and \(R = \sqrt {\xi^{2} + \eta^{2} + \zeta^{2} }\). Note that, the vertical axis of the used coordinate system is oriented downwards. In the contrast to the previously analyzed formula of Nagy (1966), it contains the inverse tangent function. Such formulae were derived earlier by, e.g. Everest (1830) or MacMillan (1930), but the Sorokin’s version is, according to our knowledge, the first in this simple and usable form (note that a very similar solution was published in the same year: Mader 1951).

The brief look show us there are the expected problems with this formula—existence of the singularities in the source-free points, and more—this solution is not continuous in the horizontal plane above (below) the prism. Several similar solutions were later derived by other authors, e.g. Haáz (1953) or Banerjee and Das Gupta (1977):

$$V_{z} (0,0,0) = - G\sigma \left[ {\xi \ln (\eta + R) + \eta \ln (\xi + R) - \zeta \text{arctg} \frac{\xi \eta }{\zeta R}} \right]_{{\xi_{1} ,\eta_{1} ,\zeta_{1} }}^{{\xi_{2} ,\eta_{2} ,\zeta_{2} }} .$$
(23)

We can see that this formula is a non singularity-free version of Eq. (12). The difference between (22) and (23) is in the argument of the inverse tangent function—it is reciprocal in the Sorokin’s formula. Li and Chouteau (1998) stated that: “these two solutions are equivalent, what can be easily demonstrated by the well-known \(\text{arctg} (a) = \frac{\pi }{2} - \text{arctg} \left( {\frac{1}{a}} \right)\) and \(\frac{\pi }{2}\) is cancelled by the summation”. This statement is not correct for the all possible positions of the prism and the calculation points. The mentioned property of the inverse tangent function is not used properly. It should be (e.g. Gradshteyn and Ryzhik 1962):

$${\text{arctg(}}a )+ {\text{arctg}}\left( {\frac{1}{a}} \right) = {\text{sign(}}a )\cdot \frac{\pi }{2}\quad a \ne 0.$$
(24)

According to this, Eq. (22) can be then modified to:

$$V_{z} (0,0,0) = - G\sigma \left[ {\xi \ln (\eta + R) + \eta \ln (\xi + R) + \zeta \left( { - {\text{sign}}\left( {\frac{\xi \eta }{\zeta }} \right) \cdot \frac{\pi }{2} + \text{arctg} \frac{\zeta R}{\xi \eta }} \right)} \right]_{{\xi_{1} ,\eta_{1} ,\zeta_{1} }}^{{\xi_{2} ,\eta_{2} ,\zeta_{2} }} .$$
(25)

Now, the factor π/2 is not cancelled in the summation, and equivalency of (25) and (23) is obtained. Another possibility is to replace the inverse tangent function in (22) by the multi-valued inverse tangent, signed as ATAN2(a, b) in the computer languages, which generalize the previously mentioned property (24).

Despite the problem with the continuousness of Sorokin’s solution, it can be easily fixed and the satisfactory solution is obtained, even though it is not a singularity-free, but still better than the previously analyzed solution of Nagy (1966).

6 Quotation Problems

The problems connected with the paper of Nagy (1966) do not stop with the less general prism’s gravitational effect formula. The subject we want to refer to is connected with the citations of the discussed paper. Let us focus on the other parts of Nagy (1966). The author mentioned the older available formulae of Sorokin (1951) and Haáz (1953). We prove these two solutions can be modified to be equivalent (even if obtained by the different approaches—Haáz applied the Euler’s theorem for the homogenous functions).

The problem we want to focus on is the fact that paper Nagy (1966) is the most cited paper dealing with the gravitational attraction of the right rectangular prism. We did check tens of these citing papers that these authors are using, in fact, the “Sorokin’s type” of the discussed formula with the inverse tangent component, because it does not require the special procedures if the body is crossing the horizontal axes. Even Nagy himself did as well in his later papers, (see, e.g. Nagy 1973 or Nagy et al. 2000), but he did not cite the Sorokin’s work.

However, it happens somehow, that the attraction of the prism and the paper Nagy (1966) is taken as the “synonyms”. This is not right because his formula has limited validity and is not easy to apply or to be programmed. One reason for this can be that Sorokin (1951) is not so easy to access, and more, there is no English translation of it. However, the precise citation should at least be something like, e.g. “Sorokin (1951) in Nagy (1966)”. Of course, it is not Nagy’s fault, that the commonly used formula is not correctly cited. However, the credit has to go to the paper, where the formula, used by majority of the community, occurs and it is definitely not Nagy (1966).

Although, Sorokin (1951) is not the first solution of the rectangular prism effect (see, e.g. Everest 1830; MacMillan 1930), but, it is for the first time (according to our knowledge) where the solution is presented in such “nice and simple” closed form (along with Mader 1951 as well). These older authors usually substitute the integration boundaries throughout the derivation, what results into the 24 terms and looks “macabre” at the first sight.

So, the question is: whom to cite to stay consistent? From those papers, which contain more general solutions for the “mathematically” orientated coordinate system (the positive part of the vertical axes is pointing upwards—the depth is a negative number) and easily accessible, it seems in our opinion, that it could be the papers Mader (1951) or Banerjee and Das Gupta (1977), despite some typographical errors. These papers did not specify how to calculate the effect in the other points outside of the origin of the coordinates, but this is not a serious problem as it can be managed by simple substitution.

7 Conclusion

In the presented paper, we have tried to explain in an analytical way the problems which occur when using the formula for a 3D rectangular prism’s gravitational effect calculation derived by Nagy (1966), as the most cited paper, and the better alternatives derived by Sorokin (1951), Mader (1951) or Banerjee and Das Gupta (1977). The main problem of the Nagy’s solution occurs when entering the negative limits of the prism in the x-direction and it is caused by the used substitution in the integration in the x-direction during the derivation of the formula. This situation results in the more complicated algorithm realization when compared with the formula of, e.g. Sorokin (1951). The much more straightforward concept of the Sorokin’s formula, during the algorithm realization is a great advantage in the comparison of the discussed and analyzed Nagy’s formula. The problems connected (discontinuousness, singularities) with the Sorokin’s formula can be fixed in a more simple manner than those of the Nagy’s solution. Next, we revisited the problem of the proper quotation of some papers connected with the direct problem for the rectangular prism where Nagy (1966) is the leading paper. We show that there are the papers available, where the solution is more general, and in fact, really used by the community. We suggest stopping the improper citations of the incomplete formula of Nagy (1966) and turning the focus to the better alternatives.

The singularity-free formula, valid in the each position of the calculation point, for all the components of the gravitational attraction vector, is presented too.