Distribution of Earthquake Interevent Times in Northeast India and Adjoining Regions

Abstract

This study analyzes earthquake interoccurrence times of northeast India and its vicinity from eleven probability distributions, namely exponential, Frechet, gamma, generalized exponential, inverse Gaussian, Levy, lognormal, Maxwell, Pareto, Rayleigh, and Weibull distributions. Parameters of these distributions are estimated from the method of maximum likelihood estimation, and their respective asymptotic variances as well as confidence bounds are calculated using Fisher information matrices. Three model selection criteria namely the Chi-square criterion, the maximum likelihood criterion, and the Kolmogorov–Smirnov minimum distance criterion are used to compare model suitability for the present earthquake catalog (Yadav et al. in Pure Appl Geophys 167:1331–1342, 2010). It is observed that gamma, generalized exponential, and Weibull distributions provide the best fitting, while exponential, Frechet, inverse Gaussian, and lognormal distributions provide intermediate fitting, and the rest, namely Levy, Maxwell Pareto, and Rayleigh distributions fit poorly to the present data. The conditional probabilities for a future earthquake and related conditional probability curves are presented towards the end of this article.

1 Introduction

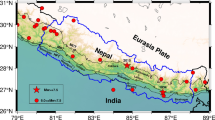
The northeast of India and its adjoining regions (20°–32°N and 87°–100°E) have been one of the most seismically active areas over historical time. Since 1846, twenty earthquakes of magnitudes greater or equal to 7.0 have occurred in this region. Among these, two great earthquakes, namely the Shillong Plateau earthquake of 12 June 1897 $\left( {Ms\,\, 8.7} \right)$ and the Independence Day Assam earthquake of 15 August 1950 $\left( {Ms\,\, 8.6} \right)$ rocked the whole northeastern region causing extensive loss of human life and property in the Indian subcontinent (Gupta et al. 1986; Gupta and Singh 1986; Bilham and England 2001).

Statistical properties of time intervals between successive earthquakes in northeast India and its surrounding regions have been the subject of numerous studies in order to provide long-term prediction for the next big earthquakes. A number of scientists, namely Parvez and Ram (1997), Yadav et al. (2010), Pasari and Dikshit (2013) have earlier carried out recurrence interval estimation of the study region. They used four probability distributions, namely exponential, gamma, lognormal, and Weibull (two-parameter and three-parameter) distributions in their analysis. Apart from these probability distributions, the ones that are commonly used in recurrence modeling are the Pareto group of distributions (Kagan and Schoenberg 2001; Ferraes et al. 2003; Pisarenko et al. 2010), the Gaussian distribution (Papazachos et al. 1987), the inverse Gaussian or Brownian passage time distribution (Matthews et al. 2002; Kagan 2007), the Rayleigh distribution (Ferraes et al. 2003; Yazdani and Kowsari 2011), the Levy distribution (Sotolongo-Costa et al. 2000), the negative binomial distribution (Dionysiou and Papadopoulos 1992), the generalized gamma distribution (Bak et al. 2002), and the triple exponential distribution (Kijko and Sellevoll 1981). Nevertheless, the most appropriate distribution function to represent earthquake interevent times still remains under debate. As a result, it has now been a common practice to apply all competing models on a given catalog, and analyze recurrence interval from the best fitted model(s).

In a similar manner, an attempt is made in this study to analyze earthquake interoccurrence times of northeast India and its adjoining regions from eleven probability distributions, namely exponential, Frechet (inverse Weibull), gamma, generalized (exponentiated) exponential, inverse Gaussian, Levy, lognormal, Maxwell, Pareto, Rayleigh, and Weibull distributions. Parameters of these distributions are estimated from the method of maximum likelihood estimation (MLE), and their respective asymptotic variances as well as confidence bounds are calculated using the concept of the Fisher information matrix (FIM). The performances of these distributions are evaluated from three statistical criteria: the Chi-square criterion, the maximum likelihood criterion and its modification, named as Akaike information criterion (AIC), and the Kolmogorov–Smirnov minimum distance criterion. In addition to the statistical model developments, we calculate conditional probability values (for different elapsed times) for a large earthquake $\left( {M \ge 7.0} \right)$ in the study region.

1.1 Study Area and Earthquake Data File Description

In the present work, we investigate earthquake inter-occurrence time by analyzing the northeastern India catalog, including events with magnitude above 7.0 (Yadav et al. 2010). This region has been tectonically very active due to the collision and ongoing convergence between Indian plate with Tibet in the north and the Burmese landmass towards the east (Nandy 1986, 2001; Bilham and England 2001). There are a number of active thrust faults, namely main frontal thrust, main boundary thrust, main central thrust, Lohit thrust, Misami thrust, and the Bame-Tuting fault (Gsi 2000). On the basis of epicentral distributions of past earthquakes, faulting pattern, ground evidences, and geotectonic features, the northeast region and its vicinity can be divided into five smaller seismotectonic zones: eastern (upper) Himalayan collision zone, Indo-Myanmar subduction zone, Syntaxis zone of Himalayan arc and Bermese arc (the Mishmi massif), the Brahmaputra valley, and the Shillong plateau (Kayal 1996; Nandy 2001; Thingbaijam et al. 2008). Besides, this region, according to the seismic zoning map of India (Bis 2002), falls under zones V, IV, and III, with magnitudes exceeding 8, 7, and 6, respectively.

Table 1 provides a list of 20 major earthquake events $\left( {M \ge 7.0} \right)$ from northeast India and its adjoining regions covering a period from 1846 to 1995. The geographical epicentral locations of these events are shown in Fig. 1. It is worthwhile to note here that the study region has not experienced any earthquake of magnitude $M \ge 7.0$ since 1995. Therefore, the present catalog (Yadav et al. 2010) essentially accounts for all main shocks with magnitude $M \ge 7.0$ for the period 1846–2013.

Table 1 List of earthquakes that occurred in the study region for magnitude M ≥ 7.0 (after Yadav et al., 2010)

Fig. 1

Epicentral locations of earthquakes of magnitude $M \ge 7$ (as listed in Table 1) that occurred in the study region (northeast India and surrounding regions) after 1846 till 2013 (after Yadav et al. 2010)

2 Probabilistic Modeling of Earthquake Recurrence

Let $T$ be a positive random variable of the recurrence time with cumulative distribution function $F\left( t \right)$, density function $f\left( t \right)$, survival function $S\left( t \right)$, and hazard function $h\left( t \right)$. Further, we assume that $\tau$ is the time elapsed since the last event and $v$ is the waiting time. Having $\tau$ as known, waiting time $v$ is random. Thus, our concern is to estimate $v$ so that an earthquake appears within $\left( {\tau ,\,\,\tau + v} \right)$, knowing that no earthquake occurred in the last $\tau \,\,\left( {0 < \tau < t} \right)$ years. Bringing the concept of reliability into the picture and calling the overall structure as an earthquake system, $S\left( t \right)$ illustrates the probability that an earthquake will occur later than time $t$ and $h\left( t \right)$ defines the instantaneous rate of earthquake occurrence. $S\left( t \right)$ and $h\left( t \right)$ are defined by $S\left( t \right) = 1 - F\left( t \right)\,\,\,{\text{and}}\,\,\,h\left( t \right) = \frac{f\left( t \right)}{1 - F\left( t \right)}$.

We further introduce a random variable $V$ corresponding to the waiting time $v$. Noting that $V$ is linearly related to the random variable $T$ (through the elapsed time $\tau$), its distribution function becomes $F\left( {\tau + v} \right)$. Therefore, the conditional probability of an earthquake in time interval $\left( {\tau ,\,\,\tau + v} \right)$, knowing that no earthquake occurred in the last $\tau$ years, can be defined as

$$ P\left( {V \le \tau + v|V \ge \tau } \right) = \frac{{F\left( {\tau + v} \right) - F\left( \tau \right)}}{1 - F\left( \tau \right)}\,\,\,\,\left( {v > 0} \right). $$

(1)

Eleven different probability distributions are considered in this study. These distributions and their probability density functions are presented in Table 2. The associated model parameters along with their generic role are also highlighted. The genesis of these distributions (except, generalized exponential), their model properties, and interrelations among themselves may be found in Johnson et al. (1995). For the generalized exponential, the same may be found in Gupta and Kundu (1999, 2007).

Table 2 Probability distributions and their density functions

Table 2 shows that the usual domains for ten distributions are the whole positive real line, while for Pareto distribution, the domain $\left( {\alpha ,\infty } \right)$ is restricted by the completeness parameter $\alpha$. Further, three distributions, namely gamma, generalized exponential, and Weibull, when $\beta = 1$, coincide with the exponential distribution, meaning these distributions are somewhat generalizations or extensions of classical exponential distribution. In addition, it is observed (Gupta and Kundu 1999) that generalized exponential distribution shares many physical properties (e.g., shapes of density function or hazard function) with gamma and Weibull models and, thus, could be a potential model to represent earthquake interevent times. Besides, Table 2 includes a number of heavy-tailed (tail is thicker than that of exponential model) distributions: Frechet, Levy, lognormal, Pareto, and Weibull $\left( {\beta < 1} \right)$. As a whole, we have tried to combine all possible type of distributions for a well-defined conclusion for the most appropriate model(s) for the present earthquake catalog of northeast India and the adjoining region.

Apart from the probability density function, characterization of hazard function has become very popular in seismic recurrence studies (Davis et al. 1989; Sornette and Knopoff 1997; Matthews et al. 2002). The various shapes of hazard functions provide salient information of earthquake reliability. More specifically, increasing hazard function implies that chances of an earthquake increase with time (similar to the elastic rebound theory, Reid 1910), whereas decreasing hazard function means the opposite, and the constant hazard function refers to the chances of an earthquake being independent of elapsed time. It is easy to observe that (a) exponential distribution has constant hazard function, (b) gamma, generalized (exponentiated) exponential, and Weibull distributions possess monotone hazard functions, (c) Frechet (inverse Weibull), inverse Gaussian, lognormal, and Weibull distributions offers both monotone and non-monotone hazard shapes, and (d) Pareto distribution has a decreasing hazard function. Different plots of these hazard functions may be available upon request to the authors.

3 Parameter Estimation

Using the interevent times of successive earthquakes (as listed in Table 1), the model parameters of all 11 distributions have been estimated using the MLE method. The detailed procedure of the MLE method may be found in Hogg et al. 2005. The estimated model parameter values are shown on Table 4.

Characterizations of the estimated parameters are essential in order to quantify the uncertainty in the estimation process. However, most of the time, the exact distributions of the estimated model parameters are not available. In such cases, the law of large samples is used as a proxy to asymptotically estimate the variance-covariance matrix $\Sigma_{{\hat{\theta }}}$ and confidence bounds of the estimated parameters $( {\hat{\theta }} )$. In this study, we have exact distribution of the estimated Pareto parameters only (Quandt 1966). The exact variances of the Pareto parameters are given (Quandt 1966) below.

$$ \begin{gathered} \sigma^{2} \left( {\hat{\alpha }} \right) = \frac{{\alpha^{2} n\beta }}{{\left( {n\beta - 2} \right)\left( {n\beta - 1} \right)^{2} }}\,\,\,\left( {n > \frac{2}{\beta }} \right) \\ \sigma^{2} \left( {\hat{\beta }} \right) = \frac{{\beta^{2} n^{2} }}{{\left( {n - 2} \right)^{2} \left( {n - 3} \right)}}\,\,\,\,\,\,\,\,\,\,\left( {n > 3} \right) \\ \end{gathered} $$

(2)

For other distributions, we calculate FIM $I\left( {\hat{\theta }} \right)$ and combine it with the Cramer–Rao lower-bound theorem defined as $\Sigma_{{\hat{\theta }}} \ge \left[ {nI\left( {\hat{\theta }} \right)} \right]^{ - 1}$. A brief discussion on FIM is provided in “Appendix 1”. In addition, the Fisher–trace information (FTI), defined as the trace of the FIM, is derived for each distribution. The FTI offers an overall measure of the total amount of uncertainty associated with the distribution (Gupta and Kundu 2006). The larger the FTI, the better is the approximation.

Now considering the asymptotic normality of the MLE estimated parameters, we derive the asymptotic confidence bounds, or confidence intervals, for each parameter (Lawless 1982). The $\left( {1 - \delta } \right)\,\%$ two-sided confidence bounds of the parameter $\theta$ is obtained as

$$ \widehat{\theta } - z_{{{\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0pt} 2}}} \sqrt {\text{var} \left( {\widehat{\theta }} \right)} < \theta < \widehat{\theta } + z_{{{\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0pt} 2}}} \sqrt {\text{var} \left( {\widehat{\theta }} \right)}, $$

(3)

$z_{{\delta} / {2}}$ is the critical value corresponding to a significance level of ${\delta \mathord{\left/ {\vphantom {\delta 2}} \right. \kern-0pt} 2}$ on the standard normal distribution.

The FIMs and FTIs corresponding to the presently studied distributions are listed in Table 3, whereas the asymptotic standard deviations and confidence bounds are shown in Table 4.

Table 3 Fisher information matrix (FIM) and Fisher trace information (FTI)

Table 4 Estimated parameter values and their asymptotic standard deviations and confidence bounds

Tables 3 and 4 provide much information related to the distribution properties; for instance, the estimated shape parameters for gamma, generalized exponential, and Weibull models are found to be greater than 1.0, meaning the associated hazard functions of these distributions are monotonically increasing; the FTI for the generalized exponential distribution is the largest, which implies that this distribution is more precise in providing estimated parameter values (which is actually true as can be seen from Table 4). At this point, however, it may also be noted that, for some parameters (e.g., shape parameter of gamma or inverse Gaussian parameters), we see that the numerical figure of the asymptotic standard deviation is quite large. But, it does not necessarily mean that the associated distribution will fit very poorly to the data. Therefore, the emphasis should be on estimating the final propagation in the conditional probability values (discussed later in Sect. 5) with model parameter uncertainties as inputs, rather than deciding directly from the numerical standard deviation values of the estimated parameters.

4 Model Selection

In order to prioritize the competing models, we apply the three model selection criteria, namely the Chi-square criterion, the maximum likelihood criterion and its modifications, known as the AIC, and the Kolmogorov–Smirnov minimum distance criterion. In “Appendix 2”, a brief discussion on each of these methods is provided.

In the Chi-square test, as there is no specified method to choose the number and size of class intervals (Johnson et al. 1995; Boero et al. 2004; Murthy et al. 2004), we calculate Chi-square values corresponding to six classes (<3, 3–6, 6–9, 9–12, 12–15, >15) as well as five classes (<3, 3–6, 6–10, 10–15, >15). This would, in fact, throw some light on the sensitivity of the Chi-square test. The model selection results are shown in Table 5.

Table 5 Model selection using three criteria: the minimum Chi-square $\left( {\chi_{\text{value}}^{ 2} } \right)$ criterion, the maximum log-likelihood criterion $\left( {\ln L} \right)$, and the Kolmogorov–Smirnov (K–S) minimum distance criterion

Table 5 shows that $\chi_{1}^{2}$ values for the exponential (2.85), gamma (2.71), and Weibull (2.76) distributions are the least (within a tolerable limit), although the generalized exponential (3.05) is not very far away. Similarly, $\chi_{2}^{2}$ value for the exponential (1.18) distribution is the minimum, and $\chi_{2}^{2}$ values for the gamma (1.19), generalized exponential (1.51), and Weibull (1.35) distributions appear next to the exponential distribution. Moreover, we see that the decision from the Chi-square criterion, for the present catalog, is not very sensible for the choice of the number or size of class intervals.

On the other hand, AIC values corresponding to the gamma (117.82), generalized exponential (117.78), and Weibull (117.73) distributions appear to be the least among all AIC values. Therefore, AIC suggests the gamma, generalized exponential, and Weibull models to be the most suitable ones to represent the present earthquake catalog of northeast India and its adjoining regions. Besides, we see that the exponential (118.18) distribution has also a quite smaller AIC value.

The Frechet distribution has the minimum K–S distance (0.1326); the Weibull (0.1440), gamma (0.1482), exponential (0.1532), and generalized exponential (0.1532) distributions have also quite smaller K–S distances, giving an impression that these distributions may suitably fit the present data. To be more certain, we assess the overall matching among these distributions with the empirical distribution function by simultaneously plotting in Fig. 2.

Fig. 2

Empirical distribution function and the fitted distributions functions

Figure 2 reveals quite interesting facts: (i) the K–S distance value for the Frechet distribution, although it is the minimum, it fits poorly to the overall data set, (ii) the gamma, generalized exponential, and Weibull distributions match quite well to the empirical distribution, and these three distributions themselves are very close to each other, almost indistinguishable, (iii) the calculated K–S values for exponential and generalized exponentials, although they were very similar, the K–S plot suggests the generalized exponential to be more appropriate than the exponential distribution.

From the above discussion on model selection, it may be inferred that broadly three categories of distributions have emerged: the gamma, generalized exponential, and Weibull distributions have the best fitting, while exponential, Frechet, inverse Gaussian, and lognormal distributions have intermediate fitting, and the rest, namely Levy, Maxwell Pareto, and Rayleigh distributions fit poorly to the present data.

5 Conditional Probability

Having identified the suitable models in the preceding section, we now apply those models to calculate conditional probability [using (1)] of an earthquake $\left( {M \ge 7.0} \right)$ for an elapsed time of 18 years (i.e., July 2013). These values are listed in Table 6.

Table 6 Estimated conditional probability for an elapsed time of 18 years (i.e., July 2013) for the study region as obtained from exponential, Frechet, gamma, generalized exponential (GE), inverse Gaussian (IG), lognormal (LN), and Weibull models

Table 6 shows that the conditional probability (from the gamma, generalized exponential, and Weibull distributions) of a large magnitude earthquake reaches 0.8–0.9 by 2020–2027. Besides, it may be observed that the gamma and generalized exponential distributions produce similar (up-to second decimal place) conditional probability values for the present catalog. This emphasizes the scope and suitability of the comparatively new generalized exponential distribution in seismic recurrence studies.

The conditional probability curves, generated from conditional probability values, for a combination of waiting time and elapsed time are presented in Fig. 3. These curves play a significant role in seismic zonation and microzonation, urban planning and insurance, designing of important structures such as schools, hospitals, mega-malls, and nuclear power plants, and related concerns (SSHAC 1997; Kagan and Schoenberg 2001; Baker 2008; Yadav et al. 2010).

Fig. 3

Conditional probability curves (hazard curves) for elapsed time $\tau = 0,5,10, \ldots ,60$ years, using gamma, generalized exponential (GE), inverse Gaussian (IG), lognormal (LN), Frechet (also called as inverse Weibull IW), and standard Weibull (SW) distribution for earthquake events of $M \ge 7$ in northeast India and its surrounding region. The dot-line represents the hazard curve corresponding to an elapsed time of 18 years, i.e., 2013

6 Summary and Conclusions

Forecasting of large earthquakes, in a specified region, has been an important task for seismologists and earthquake professionals. The present research contributes to this endeavor by focusing on eleven probability distributions, namely exponential, Frechet, gamma, generalized exponential, inverse Gaussian, Levy, lognormal, Maxwell, Pareto, Rayleigh, and Weibull to analyze earthquake interevent times of large $\left( {M \ge 7.0} \right)$ earthquakes in the seismically active northeast India and its adjoining regions. We have briefly explained several model characteristics of these distributions, parameter estimations from the maximum likelihood method, and model selections using three goodness-of-fit methods. In addition, we have paid special attention to the problem of uncertainty measurement of the estimated model parameters. Finally, towards the end of this article, we have presented a number of conditional probability curves (also known as hazard curves) for elapsed time $\tau = 0,5,10, \ldots ,60$ years. These curves reveal very high seismicity in the study region.

The present study brings out the following results:

• 1. The gamma, generalized exponential, and Weibull distributions provide the best fitting, while exponential, Frechet, inverse Gaussian, and lognormal distributions provide intermediate fitting, and the rest, namely Levy, Maxwell Pareto, and Rayleigh distributions fit poorly to the present earthquake catalog of northeast India and its adjoining regions.

• 2. The conditional probability (from the gamma, generalized exponential, and Weibull distributions) of a large magnitude earthquake $\left( {M \ge 7.0} \right)$ in the study regions reaches 0.8–0.9 by 2020–2027.

Appendices

Appendix 1

Under the standard regularity conditions (Lehmann 1998), FIM for parameter vector $\theta = \left( {\theta_{1} ,\theta_{2} } \right) ,$ say, is defined as follows:

$$ I\left( \theta \right) = E\left( {\left[ {\begin{array}{*{20}c} {\frac{\partial }{{\partial \theta_{1} }}\ln f\left( {T;\theta } \right)} \\ {\frac{\partial }{{\partial \theta_{2} }}\ln f\left( {T;\theta } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{\partial }{{\partial \theta_{1} }}\ln f\left( {T;\theta } \right)} & {\frac{\partial }{{\partial \theta_{2} }}\ln f\left( {T;\theta } \right)} \\ \end{array} } \right]} \right). $$

(4)

The FIM can also be expressed (Nelson 1982; Hogg et al. 2005) as

$$ I\left( \theta \right) = E\left( { - \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} }}{{\partial \theta_{1}^{2} }}\ln f\left( {T;\theta } \right)} & {\frac{{\partial^{2} }}{{\partial \theta_{1} \partial \theta_{2} }}\ln f\left( {T;\theta } \right)} \\ {\frac{{\partial^{2} }}{{\partial \theta_{2} \partial \theta_{1} }}\ln f\left( {T;\theta } \right)} & {\frac{{\partial^{2} }}{{\partial \theta_{2}^{2} }}\ln f\left( {T;\theta } \right)} \\ \end{array} } \right]_{2 \times 2} } \right). $$

(5)

Moreover, Efron and Johnstone (1990) observed that $I\left( \theta \right)$ can also be expressed in terms of the hazard function as

$$ I\left( \theta \right) = E\left( {\left[ {\begin{array}{*{20}c} {\frac{\partial }{{\partial \theta_{1} }}\ln h\left( {T;\theta } \right)} \\ {\frac{\partial }{{\partial \theta_{2} }}\ln h\left( {T;\theta } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{\partial }{{\partial \theta_{1} }}\ln h\left( {T;\theta } \right)} & {\frac{\partial }{{\partial \theta_{2} }}\ln h\left( {T;\theta } \right)} \\ \end{array} } \right]} \right). $$

(6)

Depending on the form of density and hazard functions of a distribution, the most convenient equation from (4, 5, 6) is used to calculate $I\left( \theta \right)$.

Appendix 2

For simplicity, we assume two competitive models $F$ and $G$ with density functions $f\left( {x;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } } \right)\,\,{\text{and}}\,\,g\left( {x;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varphi } } \right)$, respectively.

The minimum Chi-square criterion is one of the conventional techniques for model selection. The Chi-square criterion consists of three steps: (i) divide the sample observations $\left\{ {t_{1} ,t_{2} , \ldots ,t_{n} } \right\}$ into k disjoint groups of moderate length (may be equal or unequal in size) and record the observed frequencies $n_{1} ,\,n_{2} ,\,\, \ldots ,\,n_{k}$(ii) compute the expected frequencies $f_{1} ,f_{2} , \ldots ,f_{k} \,\,{\text{and}}\,\,g_{1} ,g_{2} , \ldots ,g_{k}$ based on $f\left( {x;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } } \right)\,\,{\text{and}}\,\,g\left( {x;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varphi } } \right)$, and (iii) calculate Chi-square distances $\chi_{{f,{\text{data}}}}^{2}$ and $\chi_{{g,{\text{data}}}}^{2}$ as $\chi_{{f,{\text{data}}}}^{2} = \sum\nolimits_{i = 1}^{k} {\frac{{\left( {n_{i} - f_{i} } \right)^{2} }}{{f_{i} }}},$ $\chi_{{g,{\text{data}}}}^{2} = \sum\nolimits_{i = 1}^{k} {\frac{{\left( {n_{i} - g_{i} } \right)^{2} }}{{g_{i} }}}$. If $\chi_{{f,{\text{data}}}}^{2} < \chi_{{g,{\text{data}}}}^{2},$ then distribution $F$ should be chosen, otherwise, $G$ should be chosen. In the Chi-square test, the only confusion arises in selecting the number of class intervals k. There are no hard and fast rules to select the interval size (Johnson et al. 1995; Boero et al. 2004; Murthy et al. 2004). Thus, a reasonable number of class intervals with moderate observed frequencies are preferred in all practical applications.

The maximum likelihood criterion is entirely based on the log-likelihood values obtained in MLE. Among several competitive models, the model for which the log-likelihood value is the maximum is tagged as the best model. The maximum likelihood criterion, despite its simplicity, has a few drawbacks. For instance, it assumes that the number of parameters in each competitive model is the same. However, this presumption hardly holds true in practical situations. As a result, several modifications have been proposed over decades. Among these, AIC (Akaike 1974) has been widely used. AIC is defined as ${\text{AIC}} = 2k - 2\ln L$.

The Kolmogorov–Smirnov (K–S) minimum distance criterion prioritizes the competing models based on their ‘closeness’ to the empirical distribution function of the sample data $\left\{ {t_{1} ,t_{2} , \ldots ,t_{n} } \right\}$. Unlike the maximum likelihood criterion, the K–S minimum distance method does not require any presumption on the number of parameters in the competitive models. Besides, the K–S test is a non-parametric and distribution free test, and; hence, it avoids the use of special tables unlike the Chi-square criterion defined previously (Johnson et al. 1995).