1 Introduction

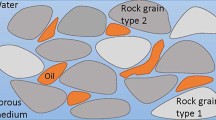
Hydrocarbon-bearing zones in continental deposits are characterized by complex pore structures in shape, size and throat (Liu, 2002, Liu and Jin, 2002). Various technologies have being adopted in order to deal with such complex issues. However, numerous methods currently used are based on statistical technologies. These methods have shown satisfying results for reservoir evaluation; however, if the pore structures are too complicated to be illustrated on the constructing graphs, the statistical methods are too limited to provide enough useful physical information for the investigation of pore structures (Westphal and Surholt, 2005).

NMR (Nuclear Magnetic Resonance) is a modern wire-line logging (or M/LWD) tool that has been used to measure the pore-size distributions in reservoirs. The pore-size distributions are calculated via NMR relaxation times, and therefore, might yield information about the relative rock properties such as porosity, bound/free fluids, wettability and permeability.. (Yan et al., 2007 , Pape et al., 2009). The descriptions of pore size and structural distribution in terms of NMR become one of the most discussed topics in reservoir evaluation in recent years. Brownstein and Tarr (1979) in their studies have regarded cells as sphere, cylinder and slab, and a diffusion relaxation was applied to investigate the relaxation rules of protons based on these geometric structures; this method is called the Brownstein & Tarr theory (B-T method). Numerous researchers in recent years (Nguyen and Mardon, 1995, Callaghan et al., 2003 , Weng et al., 2003), especially in the oil and gas industry, utilized this theory to perform the evaluations of pore structures and regard cells as spherical pores with isolated and regular sphere. Consequently, depicting pores as a sphere would be simplified to result in pore sizes that are not sensitive to connectivity because pore structure differs greatly from one to another when considering a reservoir under complicated conditions.

The oil fields in southwest China are generally distributed structurally and lithologically with a source-reservoir-cap rock background. These become the main factors to control production of oil, water and wells. In this study, a forward model (Sphere–Cylinder) for NMR is proposed to investigate pore structure based on the mechanism of proton relaxation in specialized spaces (Liu et al., 2004, 2006). This model also considered the connection for different pores in two-phase porous rocks which are saturated by oil and water.

2 Methodology

The first NMR logging was run down-hole by Schlumberger in the 1960s, which provided an improved reservoir quantitative estimation for porosity, fluid types and permeability on a foot-by-foot basis. The acquired NMR data from oil fields have displayed useful log-curve images with a very important concept of T2 distributions, which can occur in the following three ways: (1) bulk relaxation (2) surface relaxation and (3) molecular diffusion relaxation.

Assuming M0 is the protons’ magnetization, an external magnetic field H is applied clockwise along direction Z, causing the protons' spin to align along direction Z (Fig. 1). As shown in Fig. 1, when a radio frequency magnetic field (H1) is placed along the Y-axis, it will cause M0 to tilt towards the Y-axis. When the pulse is turned off, the magnetization, M0, processes back towards the Z-axis, and gradually returns to the same direction as the Z-axis. The returning process of M0 to the Z-axis direction is called relaxation. The projection of M0 on the xy plane is Mx and My (Dung and Bergman, 2002).

Fig. 1
figure 1

Transverse relaxation in magnetic field H

Full size image

On the basis of the proton relaxation mechanism, the T2 distributions give the description of pore size, and can divide fluids in pores into CBW (clay bound water), BVI (bulk volume of irreducible fluid) and BVM (bulk volume of moveable fluid). Figure 2 illustrates the T2 distributions with defined typical cut-off values for a sandstone reservoir.

Fig. 2
figure 2

T2 spectrum with fluid distributions in NMR

Full size image

2.1 Theoretical Background from NMR Relaxation Laws

Brownstein & Tarr regarded biologic cells as sphere, cylinder and slab, separately; they conducted further research in NMR relaxations based on the biologic cells. The forward model and NMR relaxation processes developed by Brownstein and Tarr are called BT theory. In proton relaxation simulations, the cell-wall in biologic tissue and the pore-wall in rock are equivalent in the proton relaxations. Therefore, the same theory has been adopted into NMR relaxations in porous media (Brownstein and Tarr, 1979; Nguyen and Mardon, 1995; Callaghan, 2003; Weng et al., 2003) as below:

$$ D\nabla^{2} m(\vec{r},t) - \left( {\frac{1}{{T_{2B} }} + \frac{1}{{T_{2D} }}} \right)m(\vec{r},t) = \frac{{\partial m(\vec{r},t)}}{\partial t}, $$
(1)
$$ \vec{n} \cdot \left. {\nabla m(\vec{r},t) + \rho_{2o} m(\vec{r},t)} \right|_{{\vec{r} \in S}} = 0, $$
(2)
$$ m(\vec{r},0) = m_{0} = \frac{{M_{0} }}{V}, $$
(3)

where S is the interface dividing pore-wall and water or the interface dividing oil and water; \( \vec{n} \) is the unit vector along the outer normal direction of S; m 0 is the specific bulk magnetic intensity of oil or water at initial time; m(r, t) is the magnetization per unit volume in location r, at time t; M 0 is the total magnetic intensity of oil & water at initial time; V is the pore volume; D is the diffusion coefficient of fluid in solution area; T 2B is the fluid’s bulk transverse relaxation time; T 2D is the fluid diffusion relaxation time and the term of 1/T 2D is omitted in our research. ρ 2o is the transverse relaxation of the oil–water interface and ρ 2o  ≈ 0 when bulk relaxations existed in oil. Equation 2 shows the NMR relaxations that limited by the pore-wall (cell wall), and Eq. 3 describes the initial condition of NMR relaxations.

To find the solutions for oil relaxation, the volume integral is performed in Eq. 1 for the entire oil volume. Ω is defined as the space occupied by oil. We obtain

$$ D\iiint\limits_{\Upomega } {\nabla^{2} m(\vec{r},t)dV} - \left( {\frac{1}{{T_{2B} }} + \frac{1}{{T_{2D} }}} \right)\iiint\limits_{\Upomega } {m(\vec{r},t)dV} = \frac{\partial }{\partial t}\iiint\limits_{\Upomega } {m(\vec{r},t)dV}. $$
(4)

According to the first Green law, the directional derivative and the boundary condition in Eq. 2, we have

$$ \begin{gathered} \iiint\limits_{\Upomega } {\nabla^{2} m(\vec{r},t)dV} = \iint\limits_{{S_{1} }} {\frac{{\partial m(\vec{r},t)}}{{\partial n_{1} }}dS} = \iint\limits_{{S_{1} }} {\vec{n}_{1} \cdot \nabla m(\vec{r},t)dS} = 0 \hfill \\ \iiint\limits_{\Upomega } {m(\vec{r},t)dV} = M_{O} (t), \hfill \\ \end{gathered} $$
(5)

where M o (t) is the magnetization induced by oil, and substituting Eq. 5 in Eq. 4, we obtain

$$ M_{\text{O}}^{ '} (t) = - \frac{1}{{T_{{ 2 {\text{B}}}} }}M_{O} (t), $$
(6)
$$ M_{O} (t) = M{}_{0}(0)\exp \left( { - \frac{t}{{T_{{ 2 {\text{B}}}} }}} \right) = S_{0} m_{0} \exp \left( { - \frac{t}{{T_{{ 2 {\text{B}}}} }}} \right), $$
(7)

where \( S_{o} = \frac{{V_{o} }}{V} \) is the ratio of oil volume to the total volume, namely, oil saturation; M o (t) is the relative magnetization of oil phase at time t without unit; m o is the initial relative magnetization of oil phase without unit; t is the relaxation time in ms. Equation 7 indicates that in the pore model saturated by oil & water, oil relaxation follows the law of bulk relaxation.

2.2 The Weakness of Relaxation Laws

When porous media is saturated by oil and water, two interfaces exist in the pores, including the oil–water interface and water–pore-wall interface. Given that no bulk water exists in the Sphere–Cylinder model, no bulk relaxation appears in the water phase either. Therefore, T 2B in water can be defined as infinite and the governing equations in the water phase can be defined as below

$$ D_{w} \nabla^{2} m(\vec{r},t) = \frac{{\partial m(\vec{r},t)}}{\partial t}, $$
(8)
$$ \left\{ \begin{gathered} D_{w} \vec{n} \cdot \nabla m(\vec{r},t)\left. { + \rho_{2w} m(\vec{r},t)} \right|_{{\vec{r} \in S_{2} }} = 0 \hfill \\ \vec{n} \cdot \left. {\nabla m(\vec{r},t)} \right|_{{\vec{r} \in S_{1} }} = 0 \hfill \\ \end{gathered} \right., $$
(9)
$$ m(\vec{r},0) = m_{0} = \frac{{M_{0} }}{V}, $$
(10)

where ρ 2w is the transverse relaxation of the pore surface; D w is the diffusivity of water; S 2 and S 1 are the interfaces between water and pore-wall, and between water and oil, respectively.

The solutions of \( m(\overrightarrow {r},t) . \) in spherical, cylindrical and planar cell, namely, the relaxation procedures of protons among the three cells, were obtained respectively by Brownstein & Tarr theory. Assuming cells are replaced by rock pores, the BT model can be used to conduct evaluations of pore structures to establish a forward model in terms of NMR data (Nguyen and Mardon, 1995; Weng et al., 2003). Brownstein and Tarr (1979) presented a general solution as below

$$ m(\overrightarrow {r} ,t) = \sum\limits_{n = 0}^{\infty } {A_{n} F_{n} (\overrightarrow {r} )e^{{\frac{ - t}{{T_{n} }}}} } , $$
(11)

where A n is a coefficient determined by the initial conditions; \( F_{\text{n}} (\overrightarrow {r} ) \) is the Eigen-function of orthogonal space, and the general solutions of \( F_{\text{n}} (\overrightarrow {r} ) \) can be found by using Eq. 8. The coefficients in the general solutions can be determined in the boundary conditions in Eq. 9 and the special solutions of \( F_{\text{n}} (\overrightarrow {r} ) \) can then be obtained (Callaghan et al., 2003; Nguyen and Mardon, 1995). Since pores are still treated as isolated pores, this approach is only valid for isolated spherical pores, cylindrical pores and planar pores separately (Liu et al., 2004).

3 Model Improvements and Relaxation Mechanism

3.1 Sphere–Cylinder Model

As described, the pores structures can be divided into spherical pore, cylindrical pore and planar pore, based on their shapes, which have been saturated by oil and water (Fig. 3a). The planar pore can be simulated by cylindrical pores lined in side-by-side. As a result, we can only define two kinds of pores in rocks (spherical pore and cylindrical pore). The Sphere–Cylinder model is the combination of two kinds of pores. The pore structures can be simulated by the ratio of cylindrical pore radius and sphere radius, and the connections of spherical pore are related to the cylindrical pore (Fig. 3b). When the Sphere–Cylinder model is saturated by oil and water, Eqs. 7 and 11 control the relaxations of oil and water. However, the relaxations of water can be simulated after coefficients and Eigen-functions are determined from Eq. 11.

Fig. 3
figure 3

a Primary pores in rocks with fluids and b the illustration of the Sphere–Cylinder model

Full size image

3.2 Validation of Eigen-Function

Since the Sphere–Cylinder model includes a spherical pore and a cylindrical pore, we ought to validate the spherical Eigen-function and cylindrical Eigen-function, respectively. Substituting Eq. 11 into the relaxation equation (Eq. 8) with boundary condition, we can get the equation that validates the Eigen-function in a spherical pore in a spherical coordinate frame as below:

$$ F_{\text{k}}^{\prime \prime } (r) + \frac{2}{r}F_{\text{k}}^{\prime } (r) + \frac{1}{{T_{\text{k}} D_{\text{w}} }}F_{\text{k}} (r) = 0, $$
(12)

The general solution of Eq. 12 can be presented as

$$ F_{\text{k}} (r) = \frac{{C_{1} }}{r}\cos \left( {\frac{r}{{\sqrt {T_{\text{k}} D_{\text{w}} } }}} \right) + \frac{{C_{2} }}{r}\sin \left( {\frac{r}{{\sqrt {T_{\text{k}} D_{\text{w}} } }}} \right) $$
(13)

Utilizing the boundary condition of water phase (Eq. 9), we acquire the coefficient from Eq. 13. Assuming C 2 = 1 without loss of generality as presented in Eq. 11, we come to

$$ C_{1} = \frac{{S_{0}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} \xi_{k} - \tan \left( {S_{0}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} \xi_{k} } \right)}}{{1 + S_{0}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} \xi_{k} \tan \left( {S_{0}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}}} \xi_{k} } \right)}}\;\underline{\underline{\text{defined as}}} \;C_{k} , $$
(14)

\( \xi_{\text{k}} = \frac{{R_{\text{s}} }}{{\sqrt {T_{\text{k}} D_{\text{w}} } }}, \) and ξ k is the positive root of the transcendental equation, and the transcendental equation is expressed as follows:

$$ \tan \xi_{\text{k}} = \frac{{D_{\text{w}} \xi_{\text{k}} - C_{\text{k}} (D_{\text{w}} - \rho \;R_{\text{s}} )}}{{D_{\text{w}} \xi_{\text{k}} C_{\text{k}} + (D_{\text{w}} - \rho \;R_{\text{s}} )}} $$
(15)

Once ξ k ,  C1 and C2 are determined, Eq. 13 is then substituted into Eq. 11. We can obtain the relaxation equation of water phase in spherical pore, which the coefficients of the Eigen-function are determined from. S o in Eq. 14 is the oil saturation and it can be expressed as the equation below

$$ S_{\text{o}} = \frac{{a_{1}^{3} }}{{R_{\text{s}}^{3} }} $$
(16)

where a 1 is the radius of oil drop in spherical pore in μm. Correspondingly, substituting Eq. 11 into Eq. 8, and then re-writing the relaxation equation in a cylindrical coordinate frame, we can obtain a new equation from the Eigen-function for water in a cylindrical pore.

$$ F_{\text{k}}^{\prime \prime } (r) + \frac{1}{r}F_{\text{k}}^{\prime } (r) + \frac{1}{{T_{\text{k}} D_{\text{w}} }}F_{\text{k}} (r) = 0 $$
(17)

The general solution for the Eigen-function can be written as

$$ F_{\text{k}} (r) = C_{1} J_{0} \left( {\frac{r}{{\sqrt {T_{\text{k}} D_{\text{w}} } }}} \right) + C_{2} N_{0} \left( {\frac{r}{{\sqrt {T_{\text{k}} D_{\text{w}} } }}} \right), $$
(18)

where J 0 is the zero-order Bessel function, and N 0 is the zero-order Neumann function. The J and N in the following text are the same function in Eq. 18. Similar to the spherical pore, assuming C 2 = 1,  we can obtain C 1 in Eq. 19.

$$ C_{1} = - \frac{{N_{1} \left( {\frac{{\eta_{\text{k}} b_{1} }}{{R_{\text{c}} }}} \right)}}{{\left( {\frac{{\eta_{\text{k}} b_{1} }}{{R_{\text{c}} }}} \right)}} = C_{\text{k}} ({\text{defined}}), $$
(19)

where \( \eta_{\text{k}} = \frac{b}{{\sqrt {T_{\text{k}} D_{\text{w}} } }} \) is the positive root of transcendental equation, and the transcendental equation can be expressed as follows

$$ \frac{{N_{1} \left( {\frac{{\eta_{\text{k}} b_{1} }}{{R_{\text{c}} }}} \right)}}{{J_{1} \left( {\frac{{\eta_{{_{\text{k}} }} b_{1} }}{{R_{\text{c}} }}} \right)}} = \frac{{D_{\text{w}} \eta_{{_{\text{k}} }} \;N_{1} (\eta_{\text{k}} ) - \rho \;R_{\text{c}} N_{0} (\eta_{\text{k}} )}}{{D_{\text{w}} \eta_{{_{\text{k}} }} \;J_{1} (\eta_{{_{\text{k}} }} ) - \rho \;R_{\text{c}} J_{0} (\eta_{\text{k}} )}} $$
(20)

Substituting the Eigen-function of cylindrical pore (Eq. 18) into Eq. 11, we can acquire the relaxation equation of water phase in cylindrical pore. b 1 in Eq. 19 is the radius of oil phase in cylindrical pore, the oil saturation (S o) in cylindrical pore is defined as

$$ S_{\text{o}} = \frac{{b_{1}^{2} }}{{R_{\text{c}}^{2} }} $$
(21)

Assuming oil is evenly distributed in the Sphere–Cylinder model, the oil saturations in a spherical pore and a cylindrical pore, therefore, should be the same.

$$ S_{\text{o}} = \frac{{b_{1}^{2} }}{{R_{\text{c}}^{ 2} }} = \frac{{a_{1}^{3} }}{{R_{\text{s}}^{ 3} }} $$
(22)

3.3 Development of Brownstein & Tarr Theory

Once the Eigen-functions for the water phase in a spherical pore and a cylindrical pore are determined, the relaxation of water phase in two kinds of pore then can also be obtained. According to Eq. 11 with F i(r) to perform volume integral for water phase, we have

$$ \iiint\limits_{\Upomega } {m(\vec{r},t)F_{i} (\vec{r})dV} = \sum\limits_{k = 0}^{\infty } {A_{k} \left[ {\iiint\limits_{\Upomega } {F_{k} (\vec{r})F_{i} (\vec{r})dV}} \right]\exp \left( { - \frac{t}{{T_{k} }}} \right)} $$
(23)

Since Eigen-functions are orthonormal set, thus

$$ \iiint\limits_{\Upomega } {m(\vec{r},t)F_{k} (\vec{r})dV} = A_{k} \left[ {\iiint\limits_{\Upomega } {F_{k}^{2} (\vec{r})dV}} \right]\exp \left( { - \frac{t}{{T_{k} }}} \right) $$
(24)

Set t = 0, and combine with the boundary conditions in Eq. 10, we then have

$$ m(\vec{r},0) = \frac{{M_{0} }}{V} = \frac{{M_{0} }}{{V_{\text{W}} }} \cdot \frac{{V_{\text{W}} }}{V} = \left( {1 - S_{\text{O}} } \right)\frac{{M_{0} }}{{V_{\text{W}} }}, $$
(25)

where V w is the volume of the water phase, combine it into Eq. 25 and Eq. 24, A k can be derived as

$$ A_{\text{k}} = \left( {1 - S_{\text{O}} } \right)\frac{{M_{0} }}{{V_{\text{W}} }}\frac{{\iiint\limits_{\Upomega } {F_{\text{k}} (\vec{r})dV}}}{{\iiint\limits_{\Upomega } {F_{\text{k}}^{2} (\vec{r})dV}}} $$
(26)

As a result, the volume integral for Eq. 11 in the water phase can perform directly as

$$ \iiint\limits_{\Upomega } {m(\vec{r},t)dV} = \sum\limits_{k = 0}^{\infty } {A_{k} \left[ {\iiint\limits_{\Upomega } {F_{k} (\vec{r})dV}} \right]\exp \left( { - \frac{t}{{T_{k} }}} \right)} $$
(27)
$$ \begin{gathered} M_{w} (t) = \left( {1 - S_{o} } \right)M_{0} \sum\limits_{k = 0}^{\infty } {\frac{1}{{V_{W} }}\frac{{\left[ {\iiint\nolimits_{\Upomega } {F_{k} (\vec{r})dV}} \right]^{2} }}{{\iiint\nolimits_{\Upomega } {F_{k}^{2} (\vec{r})dV}}}\exp \left( { - \frac{t}{{T_{k} }}} \right)} \hfill \\ = \left( {1 - S_{o} } \right)M_{0} \sum\limits_{k = 0}^{\infty } {I_{k} \exp \left( { - \frac{t}{{T_{k} }}} \right)} \hfill \\ \end{gathered} $$
(28)

where M w(t) is the magnetization induced by water and I k can be calculated in Eq. 29 as below

$$ I_{\text{k}} = \frac{1}{{V_{\text{W}} }}\frac{{\left[ {\iiint\nolimits_{\Upomega } {F_{\text{k}} (\vec{r})dV}} \right]^{2} }}{{\iiint\nolimits_{\Upomega } {F_{\text{k}}^{2} (\vec{r})dV}}} $$
(29)

4 Parameters and Functions for Modelling

4.1 Determining Relaxation Time for Oil Samples

Based on the experiments of mercury injections in the lab, the radii of cylindrical pores in the core were set as 0.1, 1.0 and 5.0 μm, separately (Fig. 4a). The relaxation times of oil samples are widely scattered, and they might range approximately from 500 to 1,500 ms (Xiao, 1998). The experimental results in our research indicate that the relaxation time is about 1,000 ms according to different measure parameters (Fig. 4b). With consideration of the general relaxation time of crude oil, it is set as 800 ms, as below

Fig. 4
figure 4

a The distributions of pore size from mercury injection experiments and b the distributions of oil sample relaxation time with relative amplitude in NMR experiments

Full size image
$$ \frac{1}{800} = \frac{1}{{T_{{2{\text{o}}}} }} \approx \frac{1}{{T_{{2{\text{B}}}} }}, $$
(30)

T 2o is the bulk relaxation for oil sample, substituting Eq. 30 into Eq. 7, the relaxation signal of oil phase can be calculated.

4.2 Input Parameters for Modelling

In order to obtain the spherical radius and cylindrical radius, the surface area restriction (Liu, 2002) is also used in our study as below

$$ \left\{ \begin{gathered} S_{\text{e}} = S_{\text{c}} + S_{\text{s}} \hfill \\ R_{\text{c}} = C_{\text{d}} R_{\text{s}} \hfill \\ \end{gathered} \right., $$
(31)

where S e, S c and S s are the surface areas of equivalent spherical pore, cylindrical pore and spherical pore in μm2, respectively; R c and R s are the radii of cylindrical pore and spherical pore in μm2; and C d is the ratio of the radius of cylindrical pore to the radius of spherical pore. Providing that the radii of cylindrical pores are 0.1, 1.0 and 5.0 μm2, respectively. The radii of an equivalent spherical pore and spherical pore can be obtained in the restriction-optimization method along with Eq. 19 and Table 1. In Table 1, R e is the radius of equivalent sphere, and has the same surface area, volume or the same ratio of volume to surface as the Sphere–Cylinder model. R c , R s and L c respectively are the radii of cylindrical pore, spherical pore and the cylindrical length shown in Fig. 2b. Oil saturation is set as 0 for the water saturated zone; 0.3 for the oil and water saturated zone and 0.65 for the oil saturated zone.

Table 1 Numerical simulation parameters for the Sphere–Cylinder model
Full size table

4.3 Simulation Functions

After the Eigen-functions are solved in terms of spherical pore and cylindrical pore, respectively, substituting the Eigen-functions into Eq. 28 we obtain the simplified equations of the relaxation procedure of the water phase.

The first and second items of functions in Tables 2 and 3 are the relaxations of spherical pores and cylindrical pores, respectively, in the Sphere–Cylinder model. In summary, the total relaxation of mono-phase fluid in the Sphere–Cylinder model is the composition of the spherical pore and cylindrical pore. According to the equations in Table 2, 3 and Eq. 7, the relaxation signal of the oil and water phase can be calculated, and the total relaxation signal is the summation of oil and water. As an example, combining Eq. 7 with the first equation in the Table 2, the total relaxation of the water-bearing Sphere–Cylinder model can be expressed as follows:

Table 2 Simulation functions for fine pores
Full size table
Table 3 Simulation functions for macro pores
Full size table
$$ \left\{ \begin{gathered} M_{\text{t}} (t) = M_{\text{o}} (t) + M_{\text{w}} (t) \hfill \\ M_{\text{t}} (t) = S_{\text{o}} m_{\text{o}} \exp ( - \frac{t}{800}) + 0.9928\exp ( - 0.1981t) + 0.007197\exp ( - 0.4399t) \hfill \\ \end{gathered} \right., $$
(32)

where S o = 0; M t, is the total relative relaxation amplitude including water and oil. The total relaxation equations in other cases can be derived also in the same way.

5 Numerical Simulations and Result Analysis

5.1 Simulation Analysis

The theoretical studies indicate that the relaxation procedures for spherical pores and cylindrical pores composed the special solutions of transcendental equations in the Sphere–Cylinder model. Therefore, in a single spherical-cylinder model, the range of special solutions is restricted by the solution of special equations. Since the solutions of Eq. 1 can be added up for different compositions, the relaxation procedure of Sphere–Cylinder can be regarded as the compound relaxation procedure that is produced by spherical pores and cylindrical pores. As presented in Eqs. 13 and 18, the special solutions of the spherical pore and cylindrical pore are combined with trigonometric functions and Bessel functions. After both trigonometric functions and Bessel functions are simplified, the two types of functions can be expressed in the multi-exponential functions in Tables 2 and 3. In addition, only one exponential function during the procedure constitutes the main part of relaxation can be named as a main relaxation procedure. Our mathematical calculations demonstrate that the main relaxations of spherical pore and cylindrical pore are all just one-exponential function, and the rest of the parts can be overlooked. Hence, the relaxation of the Sphere–Cylinder model is a dual exponential attenuation procedure.

5.2 Modelling Results

Considering the impacts of pore structures under water-wetting conditions, we come to the conclusion that the signal of oil relaxation is the interference. Furthermore, in a given pore condition, the level of abnormality of the signal fluctuates with the level of the oil saturations in proportional ratio. As a result, the illustration of relaxation will alter the reflection of pore structures if interpreting the relaxation signal of oil-bearing without removing the oil first.

The amplitudes of relaxation in Fig. 5a have been normalized; therefore, the unavailability of oil relaxation signal, total relaxation signal and brine relaxation signal will be combined into one relaxation signal. This indicates that the relaxation signal mainly responds to the pore boundary condition without interference of oil. The relaxation signal of brine-bearing core reported to be mostly fitted for pore structure evaluation (Yue et al., 2002; Liu et al., 2004), whose essences have been presented in our theoretical research.

Fig. 5
figure 5

a Relaxations in both pores for water-bearing. b The fine pore filled by water and oil

Full size image

Regardless what shape and size the pore have, the total relaxation signal in oil-bearing rock, along with the measured relaxation signal, is the superposition signal of the water relaxation signal and the oil relaxation signal (Fig. 5b). Comparing the total relaxation signal of small pores in Fig. 5a with the one in Fig. 5b, we soon discover that the total relaxation signal of oil-bearing pores becomes abnormal due to the signal superposition of oil relaxation.

Evidently, only the relaxation of water surface defines different pore sizes on the relaxation process in special Sphere–Cylinder model with the same oil saturation, as presented in Fig. 6a, b. In terms of small pores, as the relaxation of water surface is restricted by pore surface, the relaxation process appears to accelerate plus the relaxation signal shifted to shorter relaxation time.

Fig. 6
figure 6

a The comparison of relaxations in small pores and b the big pores for water and water & oil-bearing (So = 0.65)

Full size image

For oil-bearing pores, due to the superposition of the oil relaxation signal, the measured relaxation signals shifted to longer relaxation times which produced false information for bigger pores. Nevertheless, we can review the differences between two signals based on the proportions of the area surrounded by water-bearing relaxation and oil & water-bearing relaxation, and the area of water-bearing relaxation. The calculation indicates that the area of black points is 105 times more than the area of water-bearing relaxation. Note that the X-coordinate is on a logarithmic scale in Fig. 6a, hence, the oil-bearing relaxation in small pores will cause marked abnormality on the total relaxation signal. Therefore, in order to conduct pore structure evaluation on small pores, it is necessary to remove the effects of oil-bearing relaxation.

We can also obtain the proportion of area circled by the water-bearing relaxation and oil & water-bearing relaxation for big pore in Fig. 6b (black zone circled by X-coordinate and Y-coordinate). To summarize, the oil-bearing relaxation has much less impact to the big pores than small pores on the total relaxation at the same oil saturation, as the relaxation time of water surface in big pore becomes long enough to approach the oil ingredient. Therefore, in terms of NMR logging data, the log data is imprecise for small pores but high precision for large pores. In large pores, the influence of oil on relaxation signal is not significant.

5.3 Case Study from NMR Logging

Combining spherical pores with cylindrical pores as one model, the NMR relaxations in the Sphere–Cylinder model are the superimpositions of spherical pore relaxations and cylindrical pore relaxations. In terms of BT theory, only one kind of pore exists in their model. A case study for the comparison of NMR relaxation time in Fig. 7 shows both BT and our model.

Fig. 7
figure 7

NMR relaxations in Sphere–Cylinder and BT Spherical Model

Full size image

Suppose the water saturation is 0.3 and the magnetization of a BT spherical pore and the Sphere–Cylinder model can be calculated. If the volume of the Sphere–Cylinder model is equal to the BT spherical model, the relaxation in the Sphere–Cylinder model declines and the velocity increases, then the relaxations in the BT spherical model due to the pore space in the first one is smaller than the latter one. When the relaxation time is longer than 260 ms, both the magnetizations (Am) from the Sphere–Cylinder model and the BT spherical model will get down to almost zero.

The simulation results show that if dividing the total echo signal into water echo and oil echo to perform inversion, then the spherical pore and cylindrical pore can be described based on the T2 distributions from the water echo due to only the relaxation of the water phase relative to pore structures.

In the case study from a gas field in southwest China, the core NMR analysis shows that the top reservoirs have many small pore-throat structures (cylinder shape mainly) for target intervals, and this observation has been further confirmed by logging NMR processing from the Lab. Figure 8 provides an interpreted CPI plot that shows the mixture of gas and oil located at the intervals between 4,550 and 4,664 m; however, the irreducible water (gray colour in the last panel) shows poor movable oil which were caused by small pores (cylindrical) that were distributed at this depth interval.

Fig. 8
figure 8

Small pore structures with poor movable oil and high irreducible fluid

Full size image

6 Conclusions

The study of pore structure in NMR is a key matter for complex reservoirs and it is related to pore boundary conditions with the assumption that pore structures are spherical for simplification. The approach of the Sphere–Cylinder model in oil–water bearing porous media can be regarded as the superposition relaxation for both spherical pores and cylindrical pores.

The study of relaxation mechanism shows that, in water-wet rocks, the relaxation of oil phase is relevant to oil saturation and it is independent from pore structure. Since water adheres to the surface of the pore, the relaxation of water surface is relative to the pore structure of rock. The pore structure study shows that oil ingredients may impose abnormal effects in relaxation signals, especially in these small pores. Therefore, it is necessary to consider these effects in order to carry out the complicated reservoir evaluations based on NMR data.