Seismic Tomography by Monte Carlo Sampling

Abstract

The paper discusses the performance and robustness of the Bayesian (probabilistic) approach to seismic tomography enhanced by the numerical Monte Carlo sampling technique. The approach is compared with two other popular techniques, namely the damped least-squares (LSQR) method and the general optimization approach. The theoretical considerations are illustrated by an analysis of seismic data from the Rudna (Poland) copper mine. Contrary to the LSQR and optimization techniques the Bayesian approach allows for construction of not only the “best-fitting” model of the sought velocity distribution but also other estimators, for example the average model which is often expected to be a more robust estimator than the maximum likelihood solution. We demonstrate that using the Markov Chain Monte Carlo sampling technique within the Bayesian approach opens up the possibility of analyzing tomography imaging uncertainties with minimal additional computational effort compared to the robust optimization approach. On the basis of the considered example it is concluded that the Monte Carlo based Bayesian approach offers new possibilities of robust and reliable tomography imaging.

1 Introduction

Seismic velocity tomography is an inversion technique aimed at imaging the spatial distribution of velocity heterogeneities in global, regional, local or even laboratory-scale problems. It relies on high frequency approximation to the wave equation according to which seismic energy may be assumed to propagate along an infinitesimal “tube” between the source and the receiver, called the ray path. Hence, the wave travel time between two points provides information on the average seismic velocity along the ray path. If the travel-time data are available for a number of ray paths probing different parts of the studied area, it becomes possible to obtain a spatial map of local heterogeneities of the velocity distribution. The obtained velocity distribution (tomogram) is usually a starting point for further seismological, mineralogical, tectonic, or similar analysis. To make this interpretation as quantitative as possible, a quantitative estimation of the tomography uncertainties and their spatial distribution is required. Currently this can be done in two ways. Assuming a linear or linearized forward problem and Gaussian-type data, modeling and a priori errors, the imaging errors can be approximated by a covariance matrix calculated under the minimum least-squares approach assumption (Nolet et al., 1999; Yao et al., 1999). This is a very simple and efficient technique but its applicability is strongly limited by the underlying assumption of the linear/linearized forward problem. Also the assumption on the Gaussian character of the data or modeling errors is quite restrictive. The second approach relies on the Bayesian (also called probabilistic) approach which is capable of dealing with highly nonlinear forward problems and all types of errors. The limitation of the approach comes only from the available computational resources as it requires quite exhaustive numerical calculations. This is becoming an increasingly unimportant consideration, however. The advantages of using the Bayesian inversion technique for solving tomography problems are so great that it should be used whenever possible.

This paper examines new possibilities offered by applying Bayesian inversion using Monte Carlo sampling to passive seismic tomography in underground mine scenarios. First, the basic elements of the classical, travel-time based velocity tomography are sketched. Next, two classical inversion algorithms, namely the algebraic and optimization techniques are briefly reviewed. Then, the Bayesian approach-including some elements of the Monte Carlo sampling technique—is discussed in detail. Finally, all three methods are applied to two-dimensional passive tomography imaging at the Rudna (Poland) copper mine.

The basic tomographic forward problem relates the observable travel-time data d ^obs with the slowness distribution s(r) and reads (Aki and Richards, 1985)

$$ {{\mathbf{d}}}^{\text{th}}({{\mathbf{s}}}) = \int\limits_{\text{ray}[{{\mathbf{s}}}]} {{\mathbf{s}}}({{\mathbf{r}}}) dl, $$

(1)

where s(r) denotes slowness (inverse of velocity), d ^th is the predicted travel time, and the integral is taken along a seismic ray path. The ray path depends on the slowness distribution, and so Eq. 1 is highly nonlinear. However, this effect may often be neglected in the case of local seismic tomography if the slowness distribution does not have large gradients (Cardarelli and Cerrto, 2002). Such a simplification makes the tomography problem easier to solve at the cost of a slight loss of tomogram sharpness (Maxwell and Young, 1993). We follow this assumption throughout the analysis presented here.

Having a set of travel-time data d = (t ₁, t ₂, …t _N ) recorded for different source-receiver pairs and the discretized slowness distribution (for example, assuming that the imaged area may be described as a set of homogeneous cells), the linear tomographic forward problem can be written as a set of linear equations

$$ d^{\text{th}}_{i} = \sum\limits_j^{M} G^{ij} s_j\quad i = 1 \ldots N, $$

(2)

where s = (s ₁, s ₂, …s _M ) is the vector of the discretized slowness field and G is a matrix whose elements G ^ij are equal fractions of the ith ray path in the jth cell.

2 Inverse Algorithms

Inversion of the slowness parameters s can be carried out in various ways, among which the direct algebraic solution and the optimization approaches are the most common (Iyer and Hirahara, 1993). Another relatively new approach, referred to as the Bayesian (or probabilistic) approach, is based on sampling of the a posteriori probability density and is a method based on the pioneering work of Tarantola and Vallete (1982) (see also Sambridge and Mosegaard (2002) for a review of the history of applying the Monte Carlo technique in geophysics). The Bayesian approach has been gaining more and more popularity recently (Curtis and Lomax, 2001; Bosch et al., 2000; Mosegaard and Tarantola, 2002; Dȩbski, 2004). The reasons for this include the method's advantages (flexibility, ability to deal with highly nonlinear forward problems, and easy estimation of inversion errors at almost no additional cost) and the simultaneously rapid development of the computational resources which are required for large-scale tomographic tasks.

2.1 Algebraic Solution

If the forward modeling formula given by Eq. 1 is linear or can be linearized, the relation between the data d and model parameters s (slowness) takes the form of a set of linear equations

$$ {{\mathbf{d}}} = {{\mathbf{G}}} \cdot {{\mathbf{s}}}. $$

(3)

The problem of inverting for s from d ^obs can be viewed as the task of solving the set of linear equations using as d the results of measurements d ^obs. This task can be accomplished within a simple algebraic approach (Menke, 1989; Tarantola, 1987; Parker, 1994) by a matrix manipulation, as follows.

In the first step, the so-called normal equation is formed by multiplying both sides of Eq. 3 by the transposed G ^T operator (matrix)

$$ {{\mathbf{G}}}^T {{\mathbf{d}}}^{\text{obs}}=({{\mathbf{G}}}^T\cdot{{\mathbf{G}}}) {{\mathbf{s}}}. $$

(4)

The matrix G ^T G is a square matrix which usually cannot be inverted yet because of possible singularity. To fix this problem, the G ^T G matrix is regularized which, in the simplest case, is achieved by adding a small diagonal term:

$$ {{\mathbf{G}}}^T\cdot {{\mathbf{G}}} \longrightarrow {{\mathbf{G}}}^T\cdot {{\mathbf{G}}} + \gamma {{\mathbf{I}}}, $$

(5)

where I is a diagonal matrix. Finally, the analytical formula for the model s ^lsqr regarded as the solution can be cast into the form with the explicitly introduced initial (a priori) model s ^apr (Menke, 1989; Tarantola, 1987)

$$ {{\mathbf{s}}}^{\text{lsqr}} = {{\mathbf{s}}}^{\text{apr}} + ({{\mathbf{G}}}^T\cdot {{\mathbf{G}}} + \gamma{{\mathbf{I}}})^{-1}{{\mathbf{G}}}^T ({{\mathbf{d}}}^{\text{obs}} - {{\mathbf{G}}} {{\mathbf{s}}}^{\text{apr}}) + O(\gamma^2). $$

(6)

This form is particularly convenient when s ^lsqr is estimated iteratively (Tarantola, 1987) and is de facto the starting point of various linear inversion techniques (Parker, 1994; Limes and Treitel, 1983).

The above formula for s ^lsqr in fact coincides with the solution obtained by the optimization approach (method 2), when the least-squares difference between observed and modeled travel times is minimized subject to an additional “smoothness” condition. That is why this method is often called the LSQR (Damped Least- Squares) solution (Parker, 1994; Menke, 1989).

The algebraic approach described above can be classified as a back-projection technique (Deans, 1983) as it performs a direct projection of the data space ${{\mathcal{D}}}$ onto the model space ${{\mathcal{M}}}$ (Parker, 1994). The apparent advantage of this technique is its ability to cope with extremely large-scale problems as various numerical algorithms can find s ^lsqr quickly and efficiently. However, the method requires the forward problem to be linear or approximately linear, which limits its application to weakly heterogeneous media. Moreover, the method, being equivalent to the l ₂ norm-based optimization, is non-robust and requires very high quality data to yield acceptable results (Tarantola, 1987; Menke, 1989; Dȩbski, 2004).

2.2 Optimization Approach

Although the above approach is attractive due to its simplicity and ability to deal with large-scale problems, it suffers from a lack of generality as it is restricted to explicit linear problems. It also suffers from a lack of mathematical rigorousness because of ad hoc regularization and unclear physical meaning of the regularization procedure. Both drawbacks are eliminated within the so-called optimization technique (method 2).

The idea of the optimization method is to search for a model for which predicted data are as close as possible to the observed data with respect to a given norm. However, the optimization problem posed in this way is often non-unique, since the minimized differences between observed data and predictions for the current model can be multi-modal. Thus, there is often a need for regularization which could reduce the solutions non-uniqueness (Menke, 1989). This is usually achieved by requiring the optimum model to be “smooth” or, more generally, to be somehow similar to an initial a priori model. Taking this into account, the discussed approach turns the inverse task into an optimization (minimization) problem for the so-called misfit function

$$ S({{\mathbf{s}}})=|| {{\mathbf{d}}}^{\text{obs}} - {{\mathbf{d}}}^{\text{th}}({{\mathbf{s}}}) ||_{{\mathcal{D}}} + || {{\mathbf{s}}} - {{\mathbf{s}}}^{\text{apr}}||_{{\mathcal{M}}}, $$

(7)

where $|| \cdot ||_{{{\mathcal{D}}}}$ and $|| \cdot ||_{{{\mathbf{M}}}}$ denote the norms in the data (D) and the model (${{\mathcal{M}}}$) spaces. They measure the “distances” between observed and predicted data ($|| \cdot ||_{{\mathcal{D}}}$) and between current and a priori models ($|| \cdot ||_{{{\mathcal{M}}}}$) The choice of the norms and parameters through which they are defined determines the relative influence of both terms on the final solution, similar to the choice of the damping parameter γ in Eq. 6. Some of the most popular norms used in the context of geophysical data inversion are listed in Table 1.

The main difference between the various norms stems from how unexpected outliers in data or predictions are treated. The quadratic norm (l ₂ norm) is not a robust norm in the sense that it cannot properly handle data sets that include even just a few large outliers. On the other hand, the Cauchy norm (l _c ) is the most robust and can be used to invert data strongly contaminated by large errors. The performance of the l ₁ norm is a case in between the l ₂ and l _c norms (Kijko, 1994). It can efficiently and accurately handle data sets with a moderate number of outliers (Kijko, 1994). It is important to note that the more robust a given norm is, the less constrained is the final solution. In extreme situations this effect can lead to instabilities of numerical (optimization) algorithms used to find the “best” model (Dȩbski, 2004). Hence, the choice of the “best performing” norm depends on data quality and modeling accuracy.

Table 1 Examples of norms used to measure the “distance” in a data/model space. C ^ij and C _i are the constants defining the norms

For a given data set the quality of the solution found by the optimization technique depends on the quality of the optimizer used, the norms selected and often how well the a priori model approximates the true solution. If the observational data set contains outliers, the l ₂ norm will often fail to give any reasonable results (Scales, 1996; Dȩbski, 1997a, b; Tarantola, 1987). Also the choice of the initial (a priori) model s ^apr requires some attention and is quite crucial if any local optimization approach (for example, a gradient-based technique) is employed to search for the best model. If s ^apr is taken too far from the “true” model there is a great risk that the employed optimizer will converge to a model which corresponds to a local minimum and not the global minimum. This risk is significantly reduced when global optimization techniques such as Simulated Annealing, Genetic Algorithm, or Nearest Neighborhood algorithm are used (Sen and Stoffa, 1995; Michalewicz, 1996; Sambridge, 1999).

Finally, let us note that this approach is not limited to the linear forward problem like the LSQR method. The optimization approach can cope with any forward problem. Furthermore, the optimization approach reduces to an analytical approach when the forward problem is linear and the norms $|| \cdot ||_{{\mathcal{D}}}$ and $|| \cdot ||_{{{\mathcal{M}}}}$ are both l ₂ (Tarantola, 1987; Menke, 1989; Limes and Treite, 1983).

2.3 Bayesian Inversion

Due to its generality, the optimization method reviewed above is often used in geophysical tomography problems (Zhao, 2001; Iyer and Hirahara, 1993; Nolet, 1987). The main drawback of this approach is a lack of reliable estimation of the solutions quality. This is because the optimization technique provides the solution of the inverse problem in the form of a single (optimum) model and cannot evaluate the “size” of the part of the model space around the optimum model consisting of models leading to similar residua as the optimum model. Exploration of the model space for mapping such a region is necessary for systematic error evaluation (Tarantola, 2005; Dȩbski, 2004; Curtis and Lomax, 2001; Scales, 1996; Duijndam, 1988).

Actually, for the LSQR method there exists an error estimator called the LSQR posterior covariance matrix (Menke, 1989; Nolet et al., 1999; Yao et al., 1999). However, this error estimate is restricted by the assumed linear forward problem, Gaussian-type distribution of the data and forward modeling errors or approximations, to name a few factors, which often result in misleading values in real cases. The above drawbacks of the optimization approach are conveniently overcome by the application of Bayesian inverse theory to the tomography problem (Bosch, 1999; Dȩbski, 2004).

The solution of the tomographic inverse problem using the Bayesian inverse theory consists in building the a posteriori probability distribution σ(s) over the model space which describes the probability of a given model (s) being the true one (Tarantola, 1987; Dȩbski, 2004).

It has been shown by Tarantola and Vallete, (1982), Tarantola (1987), Jackson and Matsu’ura (1985) that, in general, σ(s) is the product of a distribution f(s) describing a priori information by a likelihood function L(s) which measures to what extent theoretical predictions fit the observed data:

$$ \sigma({{\mathbf{s}}}) = \text{const.} f({{\mathbf{s}}}) L({{\mathbf{s}}}), $$

(8)

where the constant represents a normalization of the probability density and the likelihood function L(s) reads (see, for instance, Tarantola, (2005); Dȩbski (2004))

$$ L({{\mathbf{s}}}) = \hbox{exp} \left(-\|{{\mathbf{d}}}-{{\mathbf{d}}}^{\text{th}}({{\mathbf{s}}})\| \right). $$

(9)

Knowing the σ(s) distribution allows not only to find the most likely model s ^ml for which σ(s ^ml) = max but also other characteristics like, for example, the average model and the variance which provides a convenient measure of imaging accuracy. These two basic characteristics of the a posteriori distribution σ(s) are very important.

The most important operational difference between the probabilistic approach and those discussed previously consists in the different form of the solutions. While the algebraic and optimization techniques provide a single, in a sense optimum estimation of the sought parameters, the probabilistic solution is a probability distribution over the model space which quantifies the “chance” that a given model is the true one. In this way it provides a natural framework for comparing different models and allows a very general estimation of inversion uncertainties.

At this point I would like to offer two comments on a popular use of the Bayesian inversion technique.

Very often, instead of sampling of the a posteriori PDF only the global maximum of the σ(s) is sought (e.g., Dȩbski and Young, 2002) and claimed to be the solution of the Bayesian inversion. It is obviously a correct procedure, but it reduces the full Bayesian inversion to the optimization method, disregarding the potential ability of the Bayesian method to deal with error analysis.

A similar situation occurs when the a posteriori PDF is a Gaussian distribution due to a specific assumption about the a priori PDF and the form of the likelihood function (linear or linearized forward problem and Gaussian error statistics). In such a case, the a posteriori PDF σ(s) is fully described by two parameters, namely the likelihood model s ^ml and the covariance matrix C ^p equivalent to the algebraic solution given by Eq. 6. (Menke, 1989; Tarantola, 1987; Parker, 1994). Solving the inverse problem is then often understood as finding their numerical values by directly solving Eq. 6 (e.g. Taylor et al., 2003) and building the covariance matrix (Menke, 1989), which is obviously correct but is more of an algebraic method than a general Bayesian technique.

3 Solving Tomography Problems—Bayesian Point of View

The important question at this point is which of the inverse methods should be chosen to solve a particular tomography problem. I argue that whenever available computational resources allow, the probabilistic approach should be used. The arguments are as follows.

First of all, it should be recognized that when solving any tomography (inverse) problem we face various types of uncertainties (Tarantola, 1987; Scales, 1996).

Any piece of information we use to solve an inverse task always represents some degree of uncertainty. For example, any travel-time measurement we perform has a finite accuracy either due to the applied method or due to the finite resolution of the hardware (usually both). Thus, it is quite natural to describe the output of a measurement by means of the appropriate probability density function (PDF) describing the statistics of the experimental errors.

Besides the observational uncertainties discussed above there are also theoretical errors caused by an approximate (or simplified) calculation of theoretical predictions necessary for a comparison with observational data. Numerical calculations are also a source of additional modeling errors. As a consequence we face a situation where the theoretical predictions are also disturbed by some errors which can be modeled conveniently by a probability distribution.

The solution to the inverse problem also includes some a priori assumptions and information. By a priori I mean all the information that is not connected with the current measurement but results from previously acquired knowledge, experience, previous measurements, and so forth. This a priori knowledge is never perfect. It is usually quite vague. If for some reason the a priori uncertainties were small, we would not need to make any inversion; we would simply know the solution. The a priori information can also be described in terms of the probability distribution interpreted according to the Bayesian point of view as a measure of “confidence” about the sought parameters (Jeffreys, 1983; Gelman et al., 1997; Scales and Snieder, 1997).

The Bayesian (probabilistic) inverse theory allows for consistent treatment of all the above-mentioned uncertainties. This is one of the most important advantages of this technique which allows incorporation of an exhaustive error analysis into solving the inverse problem.

One very important fact concerning the probabilistic technique is that it allows calculation of more statistical estimators of the true model s ^true than just the simplest, best-fitting maximum likelihood model s ^ml , as discussed below.

Finally, a typical tomography problem is characterized by a highly nonlinear forward modeling relation (ray-path bending) which leads to a complex form of the misfit function often having a number of secondary minima. In such a situation solving the tomography problem by seeking the model which best fits the data within the optimization technique requires a very careful choice of the numerical optimization algorithms: Local, gradient-based optimization algorithms should generally be avoided. In the case of the Bayesian approach the complex, non-Gaussian form of the a posteriori PDF function is also a problem, especially when local maxima of the a posteriori PDF are significantly separated in the model space, however there exist many quite efficient Monte Carlo samplers that can sample quite complicated “non-bell-shaped” functions (Robert and Casella, 1999).

3.1 Bayesian Solutions

More than just a technical problem emerges at this point. Specifically, the problem is how to inspect the a posteriori PDF distribution to extract the required information when in most practical cases the a posteriori PDF is a complicated, multi-parameter function. Basically, there are three different strategies to explore the a posteriori probability density function: evaluating the point estimators, calculating the marginalPDF distributions, or sampling the a posteriori PDF.

3.1.1 Point Estimators

The first approach relies on searching for the point estimators among which the most popular are the lowest-order moments of the a posteriori PDF (Jeffreys, 1983):

• 1. The maximum likelihood model

  $$ {{\mathbf{s}}}^{\text{ml}}: \sigma({\bf s}^{\text{ml}}) = \hbox{max}, $$

  (10)

• 2. The average model

  $$ {{\mathbf{s}}}^{\text{avr}} = \int\limits_{{{\mathcal{M}}}} {{\mathbf{s}}} \sigma({\bf s})\hbox{d}{{\mathbf{s}}}, $$

  (11)

• 3. The covariance matrix

  $$ {{\mathbf{C}}}^{p}_{ij} = \int\limits_{{{\mathcal{M}}}}({{\mathbf{s}}}_i - {{\mathbf{s}}}^{\text{avr}}_i) ({{\mathbf{s}}}_j - {{\mathbf{s}}}^{\text{avr}}_j) \sigma({{\mathbf{s}}}) \hbox{d}{{\mathbf{s}}}. $$

  (12)

If a more comprehensive description of σ(s) is required, higher-order moments can also be calculated (Jeffreys, 1983).

Solving the inverse problem by searching for the s ^ml model in fact reduces the probabilistic approach to the optimization technique (Tarantola, 1987; Dȩbski, 2004). Since this approach does not require full knowledge of σ(s), obtaining the s ^ml solution is usually easier than full sampling of σ(s) . Two other point estimators, namely the average model s ^avr and the covariance matrix C ^p, provide significantly more information than s ^ml but their evaluation requires full knowledge of σ(s) in order to calculate the appropriate integrals. This is trivial when σ(s) is a Gaussian distribution (this implies that G(s) = G·s). In such a case s ^avr = s ^ml is given by Eq. 6 and the covariance a posteriori matrix reads (Tarantola, 1987; Menke, 1989; Parker, 1994):

$$ {{\mathbf{C}}}^{p} = ({{\mathbf{G}}}^T {{\mathbf{C}}}_d^{-1}{{\mathbf{G}}}+ {{\mathbf{C}}}_m^{-1}))^{-1} $$

(13)

where C _d describes the variance of the sum of the observational and modeling errors and C _m stands for the variance of the a priori uncertainties.

The important point is to recognize the significant difference between the first two point-like estimators, namely s ^ml and s ^avr.

The interpretation of s ^ml is obvious—this is the model which maximizes the a posteriori PDF function which, roughly speaking, means that s ^ml is the model which best explains the data and a priori expectations. The importance of the average model s ^avr stems from the fact that it provides not only information on the best-fitting model but also includes information about other plausible models from the neighborhood of s ^ml. If sub-optimum models defined as those for which σ(s)  ∼ σ(s ^ml) are similar to s ^ml, then s ^avr ∼ s ^ml. Otherwise both estimators can be quite different. Thus, a simple comparison of s ^avr and s ^ml provides a qualitative evaluation of the reliability of the inversion procedure: The more s ^avr differs from s ^ml, the more complex and non-Gaussian is the form of the a posteriori PDF. This immediately implies that in such a case more care must be taken when interpreting the inversion results, especially inversion uncertainties. In fact, using confidence levels instead of the covariance matrix is highly recommended in such situations (Jeffreys, 1983). In addition, the average model s ^avr is usually a much considerably reliable estimator of the true values s ^true than a single, even best fitting model like s ^ml. The reason for this is that the integration (averaging) procedure acts in the manner weighted stacking (Claerbout, 1985) which filters out the random part of the inversion errors which contributes to s ^ml. In other words, averaging smoothes out a posteriori noise by removing individual variations among all sub-optimum models and leaves only the features common for all reasonable models if such a common part exists at all. This reasoning assumes that the a posteriori distribution is somehow reasonably concentrated around the optimum model. If this is not the case and the a posteriori PDF is, for example, multi-modal, the average model has no meaning and eventually a more exhaustive analysis is required (Jeffreys, 1983; Brandt, 1999).

The diagonal elements of the a posteriori covariance matrix C ^p are convenient estimators of the inversion uncertainties for each component of s while the non-diagonal elements measure the degree of correlation between pairs of parameters (Menke, 1989; Jeffreys, 1983). In fact, C ^p given by Eq. 12 is a generalization of the LSQR covariance matrix to the case of an arbitrary statistics σ(s) including possibly nonlinear forward problems. As in the case of the average model, the posterior covariance matrix is meaningful only if the σ(s) distribution is unimodal. In cases of multi-modality, the existence of non-resolved directions in the model space, or other “pathologies”, a more exhaustive error analysis is necessary by a full inspection of the a posteriori distribution (Tarantola, 1987; Wiejacz and Dȩbski, 2001).

3.1.2 Marginal PDF Distributions

While the point estimators discussed previously provide a very convenient means of synthetic representation of the inversion results, the a posteriori marginal distributions give a deeper insight into the form of σ(s) and their inspection is extremely important for the correct interpretation of the inversion results.

The one-dimensional (1-D) marginal a posteriori PDF distribution is defined by integrating out all but one parameter from σ(s)

$$ \sigma_i(s_i) = \int \sigma({{\mathbf{s}}}) \prod\limits_{j \ne i} \hbox{d}s_j. $$

(14)

Multi-dimensional marginals are defined similarly. It is important to realize that marginal PDF distributions contain the same information on s _i as σ(s) except for the correlation with other parameters (Jeffreys, 1983). However, inspections of the full a posteriori PDF σ(s) and marginal PDF sigma _i (s _i ) are not equivalent (Dȩbski, 1997a). To see the difference let us consider two maximum likelihood solutions derived from the σ(s) and σ _i (s _i ) a posteriori distributions. In the first case, when seeking the s ^ml model we consider the set of N _m parameters which simultaneously maximizes σ(s). In the second case we solve the 1-D optimization problem seeking the optimum value of only one parameter s _i , regardless of the values of the other components of s. In other words, in the former case we obtain information about all the parameters simultaneously while the inspection of the marginal distributions provides information only about selected parameters, ignoring any relations with the remaining ones.

In the most frequently encountered circumstances, point estimators calculated from the marginal distributions and from σ(s) differ slightly (Dȩbski et al., 1997; Wiejacz and Dȩbski, 2001). A difference significantly larger than the corresponding elements of the a posteriori covariance matrix indicates a very strong correlation among parameters which, besides the case of intrinsically correlated parameters, may indicate that some parameters or their combinations are not resolved by the data (Wiejacz and Dȩbski, 2001).

Inspection of marginal PDF’s is always recommended to verify if σ(s) is a multi-modal distribution or not. This is especially important if s ^avr is used as the numerical estimator of s ^true. Moreover, the inspection of the marginal PDF provides conclusive verification of whether estimating the inversion errors by a posteriori covariance is justified or not.

3.1.3 Sampling a posteriori PDF

Whenever we look for a solution of the inverse problem other than the maximum likelihood model, we face the problem of sampling of σ(s), usually in the context of calculating multidimensional integrals as in Eqs. 11 and 12 or 14. More generally, we may need to calculate the integrals represented in a general form as

$$ \langle F \rangle = \int\limits_{{{\mathcal{M}}}} F({{\mathbf{s}}}) \sigma({{\mathbf{s}}}) \hbox{d}{{\mathbf{s}}}, $$

(15)

where F(s) stands for a generic function.

If the number of parameters is very small (smaller than, say, 10), the integral in Eq. 15 can be calculated by sampling σ(s) over a predefined regular grid, such as, for example, in the case of the seismic source location problem (Wiejacz and Dȩbski, 2001; Lomax et al., 2000; Sambridge and Kennett, 2001). Otherwise, the stochastic (Monte Carlo) sampling technique has to be used (Mosegaard and Tarantola, 1995; Bosch et al., 2000; Dȩbski, 2004).

The mathematical aspects of Monte Carlo (MC) sampling of the a posteriori PDF and some algorithms are discussed later and here I would like to point out only a few advantages of this approach in solving inverse problems.

Generally speaking, the MC technique allows generation an ensemble of models which can be regarded as a set of samples drawn from the σ(s) distribution so the average integrals 〈F〉 can be approximated by (Robert and Casella, 1999)

$$ \langle F \rangle \approx {\frac{1}{N}} \sum\limits_{{{\mathbf{s}}}^\alpha} F({{\mathbf{s}}}^\alpha) $$

(16)

where the sum is taken over an ensemble of all (N) generated models s ^α.

One of the biggest advantages of the possibility of calculating the statistical averages with respect to the a posteriori PDF, as in Eq. 16, is that inversion errors can be easily estimated at no additional cost. If they can be approximated by variance of the a posteriori PDF then the choice

$$ F = ({{\mathbf{s}}}-{{\mathbf{s}}}^{\text{ml}})^2 \quad \hbox{or, better} \quad F = ({{\mathbf{s}}}-{{\mathbf{s}}}^{\text{avr}})^2 $$

(17)

leads to an extremely simple, easy to calculate estimator of the a posteriori errors

$$ \epsilon_m^2 = {\frac{1}{N}} \sum\limits_{{{\mathbf{s}}}^\alpha} ({{\mathbf{s}}}^\alpha - {{\mathbf{s}}}^{\text{ml}})^2 $$

(18)

or

$$ \epsilon_a^2 = {\frac{1}{N}} \sum\limits_{{{\mathbf{s}}}^\alpha} ({{\mathbf{s}}}^\alpha - {{\mathbf{s}}}^{\text{avr}})^2. $$

(19)

Moreover, if the variance is not a satisfactory estimator of the inversion errors due to the complexity of the a posteriori PDF, higher-order moments of σ(s) or the marginal distributions such as, for example,

$$ \sigma_i(s) = {\frac{N_i}{N}} $$

(20)

where N _i is the number of generated models whose ith component has value s can easily be calculated. This means that even an exhaustive error analysis becomes almost trivial, no matter how many parameters are estimated. Meanwhile, classical error analysis based on calculating the covariance matrix is neither general, due to approximation of σ(s) by the multivariate Gaussian distribution, nor easy to obtain, especially in the case of tomographic high dimensional problems (Yao et al., 1999, 2001; Nolet et al., 2001; Zhang and McMechan, 1996; Deal and Nolet, 1996).

Having generated a set of model samples drawn from σ(s), one can inspect them one by one or, better, by making a “movie”, as suggested by Mosegaard and Tarantola, (1995), explore their common properties. Such an inspection can provide deep insight into plausible solutions and allows for the discovery of some hidden correlations, particularly macroscopic features, some trends and other features which can even be difficult to quantify. This is rather an important point because searching for correlations is quite a difficult task, especially for numerical algorithms. In fact, any feature which appears in a large fraction of generated models leads to non-vanishing average values of some functionals F such as, for example, multi-parameter correlation moments F _i,j,…n = s _i s _j …s _n . However, finding the F which is the best indicator of a particular “feature” is usually extremely difficult (Van Kampen, 1992).

3.2 Markov Chain Monte Carlo Sampling

The choice of a scheme of sampling σ(s) is by no means a trivial task, especially when the number of estimated parameters is large (Mosegaard and Tarantola, 2002; Bosch et al., 2000). This is due to the fact that with an increasing number of parameters the model space becomes extremely large but only a very small part contributes to the a posteriori distribution (Curtis and Lomax, 2001). In such a case any geometrical sampler, meaning a deterministic algorithm which explicitly depends on the size of the model space, such as the neighborhood algorithm for example (Sambridge, 1999), becomes prohibitively inefficient. A similar situation occurs if blind (random) stochastic sampling is used. This difficulty can, however, be overcome if a posteriori PDF is sampled by the Markov Chain Monte Carlo (MCMC) technique (Mosegaard and Tarantola, 1995; Tierney, 1994; Robert and Casella, 1999).

The MCMC technique is a class of numerical algorithms which originally aimed to simulate so-called short-memory stochastic processes (Gillespie, 1992; Robert and Casella, 1999). By a short-memory stochastic process I mean here a dynamical process (an evolution of a given physical system in time) which fulfills the following two conditions.

• 1. The future state of the system depends only on its current state and not on the entire evolution history-previous states are “forgotten”. This feature is commonly called a short-memory of the process.

• 2. The next state of the system cannot be predicted deterministically but only a probability of transition to other states can be provided (stochastic process).

As can be deduced from the above conditions, the state of the short-memory stochastic process is never uniquely determined at any time. Instead, it assumes the form of a probability distribution evolving in time over the space of all the possible states of the system (Gillespie, 1992). If some conditions are fulfilled (Robert and Casella, 1999) this probability is stationary-it does not change in time. As a consequence, the subsequent states of such a stationary process are distributed according to the same probability distribution. Actually, they can be regarded as correlated samples drawn from the same distribution. Short-memory processes with a discrete evolution time are called Markov chains and have been used in analyses of various scientific and engineering problems (e.g. Gamerman, 1997; Gilks et al., 1995; Tierney, 1994; Casella, 1999; Dȩbski, 2008).

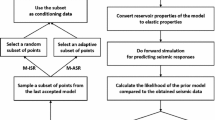
A mathematical procedure for building a Markov chain with the prerequisite stationary distribution σ(s) was put forward by Hastings (1970) who generalized the algorithm proposed by Metropolis et al. (1953). The simplest form of such an algorithm (the original Metropolis algorithm) is shown in Fig. 1 (Tierney, 1994; Mosegaard and Tarantola, 2002; Robert and Casella, 1999).

Fig. 1

The Metropolis algorithm for sampling a posteriori PDF σ(s)

The important feature of the Metropolis algorithm (also the more general Metropolis-Hastings algorithms) is that it does not depend explicitly on the size of the sampled space. Such a dependence appears only when solving the forward problem necessary for calculating σ(s ^β). This independence gives the Metropolis-Hastings sampling algorithms very high efficiency when applied to large parameter problems, such as seismic tomography. More details on the application of the Metropolis or Metropolis-Hastings algorithms, setting the parameters, monitoring convergence, and so forth, can be found in the literature of the subject (Robert and Casella, 1999; Gamerman, 1997; Gilks et al., 1995; Dȩbski, 2004).

4 Rudna Copper Mine Case

The three algorithms described above, namely LSQR, the optimization technique based on genetic algorithm optimization and MC sampling, were used to image the velocity distribution in a part of the Rudna copper mine in southwestern Poland. The same data set and the same initial (a priori) velocity model was used in each case to make a comparison between the different methods as straightforward as possible. The remaining inversion parameters, namely the damping factor γ in the LSQR method, the weights C _d and C _v in the optimization technique, and the form of the a priori and likelihood functions, were chosen to assure the methods’ maximum compatibility. Their choice is briefly discussed below.

4.1 Algorithms

The algebraic approach to the tomography task, referred to as the LSQR method, requires setting of the damping factor γ. So that the optimization and Monte Carlo approaches are consistent with each other, I define the damping factor as the ratio

$$ \gamma = C_{d}/ C_{v} ,$$

(21)

where the parameters C _d and C _v can be interpreted as the estimator of data uncertainties (C _d ) and the expected variation of velocity around the a priori model (C _v ).

In the case of the optimization technique I assumed the l ₂ norms in both the data (||·|| _D ) and model (||·|| _M ) spaces with diagonal covariance matrices. Specifically, I assumed that

$$ \begin{aligned} C_{d}^{ij} &= C_{d}^{-2} \delta^{ij} \quad \hbox{for \; the \; data\; space} \\ C_{v}^{ij} &= C_{v}^{-2} \delta^{ij} \quad \hbox{for \; the \; model\; space} \\ \end{aligned} $$

(22)

where δ^ij is the Kronecker delta function (δ^ij =  1 if i = j, otherwise 0).

To solve the optimization problem, the Genetic algorithm-based optimizer was used with parameter settings assuring maximum robustness of the calculation, but at the cost of a rather slow convergence rate (for details see Dȩbski (2002) and references therein). The velocity tomograms obtained by this method are marked from here forward as the GA solutions.

Finally, the Monte Carlo (Metropolis) sampler was run assuming Gaussian probability densities for both the a priori distribution f(s) and the likelihood function L(s) with the same covariance matrices as in the GA case defined in Eq. 22. The Metropolis sampler was used to generate 100,000 models according to the a posteriori distribution. The update step was always selected to keep the acceptance ratio at around 50% (see flowchart in Fig. 1). The generated models (samples) were used to approximate the a posteriori distribution and to calculate the maximum likelihood model (MC-ML), the average velocity model (MC-AV), and the a posteriori covariance matrix.

Within this selection the velocity images provided by each method should be identical, since from a mathematical point of view the solutions provided by all three methods are equivalent with the analytical solution given in Eq. 6. In reality, they will differ and the difference can be used to evaluate the performance of each of the inversion methods.

4.1.1 Data and Velocity Parameterization

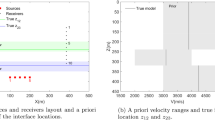
The three described algorithms were applied to a set of events occurring in 1998 at the Rudna copper mine, Poland. This mine, located in southwestern Poland, is monitored by a digital seismic network composed of 32 vertical Willmore MK-II and MK-III sensors located underground at depths from 550 to 1,150 m. The data is digitized with a frequency band ranging from 0.5 to 150 Hz, and the recording dynamics is about 70 dB. The sampling frequency is F _s = 500 Hz and determines the absolute accuracy of travel-time estimate (C _d = 2 ms). The uncertainty in event location is better than 100 m, typically around 50 m.

For the current study I selected a set of 36 events which were recorded by at least 4 of the 8 nearest stations located approximately at the same depth as the estimated hypocenters. This resulted in a subset of 177 travel times used in the P-wave velocity inversion. The distribution of selected events, employed stations and considered ray paths is shown in Fig. 2. The events were located assuming a constant background velocity, V _a = 5,800 m/s. This value was also assumed as the initial a priori velocity distribution for the inversion.

Fig. 2

Ray paths (left), ray path coverage—sum of fractions of lengths of all rays passing through cells used to parameterize the studied region (center) and cells selected for a posteriori PDF analysis (right). Seismometer positions are marked by circles and the locations of seismic sources used in the current study are depicted by stars. The events used in the current study formed four spatial clusters marked A, B, C and D , respectively

The studied area of around 5 × 5 km was discretized into 250 m by 250 m square cells, for a total of 400 blocks. However, the ray paths did not sample most of these cells, as shown in Fig. 2. In fact, only 109 cells marked in Fig. 2 in gray colors were touched by at least one ray path. Only such cells were effectively considered during the inversion, and the a priori velocity V _a = 5,800 m/s was assigned to the remaining, untouched cells.

4.1.2 Damping Parameters

Inversion of travel-time data requires two parameters to be specified, namely C _d and C _v , or at least their ratio γ = C _d /C _v in the case of the LSQR method. Usually, the optimum γ coefficient can be determined by analyzing the trade-off between the variance (complexity) of the final model and the reduction of the data variance with respect to the initial (a priori) model (Menke, 1989; Parker, 1994). In this study the analysis encountered a problem: because of the very short distances between the event epicenters and the recording stations, even very complex models led to a reduction of the residua by less than 10%, as shown in Fig. 3. In such cases the standard trade-off analysis is meaningless, therefore I introduced physical constraints to estimate C _d and C _v . Firstly, I assumed on the basis of mining practice that velocity changes generally do not exceed 20% of background velocity at a 95% confidence level. This a priori assumption corresponds approximately to the choice C _v = 400 m/s. The value of C _d which expresses the joint accuracy of the travel-time measurements and travel-time modeling (Dȩbski, 2004) is limited by the sampling period (picking accuracy) which is 2 ms as well as by the location uncertainties (travel-time modeling uncertainties). Location errors of about 100 m lead to modeled travel-time inaccuracies of about 17 ms.

Fig. 3

Trade-off curve: the correlation between reduction of data and model variance for different values of damping factor γ

For the analysis presented here I used C _v = 400 m/s and two limiting values of data variances: C _d = 20 ms and C _d =  4 ms, which roughly corresponds to the uncertainties due to location errors and those due to the travel time onset picking accuracy.

4.2 Tomography Images

The main results of the tomography imaging are shown in Figs. 4 and 5.

Fig. 4

Velocity images obtained by the LSQR method (upper-left), genetic algorithm (GA) optimization approach (upper-right) and the maximum likelihood (MC-ML) and average (MC-AV) models obtained by the Monte Carlo sampling technique (lower row). All models were calculated assuming data uncertainties C _d = 20 ms, which corresponds to γ = 5 × 10⁻⁵. Note that the LSQR and GA tomograms are practically identical, while the MC tomogram exhibits the same pattern as the LSQR and GA distributions but with a reduced amplitude of velocity variations

Fig. 5

Velocity images obtained by the LSQR method (upper-left), genetic algorithm (GA) optimization approach (upper-right) and the maximum likelihood (MC-ML) and average (MC-AV) models obtained by the Monte Carlo sampling technique (lower row). All models were calculated assuming data uncertainties C _d = 4 ms, which corresponds to γ = 10⁻⁵. The LSQR image is apparently destroyed by numerical artifacts, nonetheless due to “insufficient” damping. The GA image has also been seriously contaminated by numerical artifacts, but due to the robustness of the GA optimizer the basic structure of the velocity distribution visible in Fig. 4 is preserved. The MC-based tomogram has only been slightly influenced by the change of damping and shows only slightly larger velocity variations when compared to the previous solution (see Fig. 4)

Figure 4 shows the images obtained assuming data uncertainties C _d = 20 ms, while the velocity images obtained for the choice C _d = 4 ms are shown in Fig. 5. Only the cells well probed by ray paths (at least 10% of the maximum ray path coverage, see Fig. 2) are plotted in both figures. The remaining cells were excluded, as small coverage (below 10%) creates large imaging uncertainties and leads to unreliable results (Menke, 1989; Limes and Treitel, 1983; Backus and Gilbert, 1970).

The results from the images presented in Fig. 4 show that the two classical methods, namely the LSQR approach (left-hand figure) and the GA optimization approach (center figure) led to practically identical images. This suggests that the a posteriori imaging errors have a Gaussian distribution, and thus the use of the LSQR formula (Eq. 6) with the damping factor γ = 5 × 10⁻⁵ is justified and consistent with the result provided by the GA optimization.

The maximum likelihood solution (MC-ML) which maximizes the a posteriori PDF function has a structure similar to the GA and the LSQR solutions, but differs in terms of small-scale variations. The reason for this might be that the Metropolis sampler was unable to find the global optimum solution found by the genetic algorithm. The MC-ML solution represents the optimum solution among all the MC generated models, but only approaches the true global optimum found by the GA approach. Indeed, a comparison of the RMS residua for the LSQR GA and the MC-ML models listed in Table 2 shows that the MC-ML model leads to the largest residua. Thus the MC-ML solution is only an example of “sub-optimum” models. That is why we prefer to consider the MC-AV model as the “final” MC-based solution.

Table 2 Root mean square (RMS) values of residua calculated for the models obtained by LSQR, GA, and MC (the maximum likelihood (MC-ML) and average (MC-AV) models) for two considered data uncertainties

The average image found by the MC method is somewhat different. Although the main structure of the velocity distribution is the same as in the LSQR and GA cases, the amplitude of spatial velocity variation is slightly reduced and smoother. This is because the solution is obtained by averaging over a number of sub-optimum models generated with respect to the a posteriori PDF. Thus, any individual variations among the models which are almost equally probable as the optimum solution (for example, the MC-ML model) average out and only the basic structure common for all the models remains. If the sampled models are strongly dispersed, the average procedure will naturally lead to a smoother solution. The degree of smoothing in the MC-AV solution with respect to the MC-ML solution is a relative measure of the accuracy and reliability of the tomogram. The smoother the average solution is with respect to the MC-ML, the less reliable is the MC-ML tomogram.

Figure 5 shows the velocity images obtained when data uncertainties were taken near the limit of travel-time picking accuracy, namely C _d  = 4 ms. This choice corresponds to a much lower damping factor γ = 10⁻⁵, as shown in Fig. 3, consequently a better fit to the data at the cost of a “rougher” model is expected. The upper-left panel in Fig. 5 shows that the velocity model obtained by the LSQR approach is significantly different from the previous result calculated for γ = 5 × 10⁻⁵ ms. It exhibits very large velocity variations, in some places exceeding the imposed physical limit of a 20% range. Thus this model cannot be regarded as physically reasonable.

The image provided by the GA procedure (upper-right panel) still resembles the smooth model from Fig. 4, but is characterized by smaller-scale variations likely due to noise. Thus, the optimization method still produces a reasonable velocity distribution although with exaggerated velocity contrasts. The fact that the GA and LSQR solutions are so different in this case is a consequence of the GA optimization method’s much greater robustness. The MC-ML solution (lower-left panel) also behaves similarly to the GA method, where decreasing the damping leads to an increased roughness of the solution.

The situation is different for the MC-AV solution (lower-right panel). It is the smoothest model among the considered four solutions and, like the other models obtained for C _d = 4 ms, it shows a broadening of the high velocity zone located around the region x = 2 km, y = 2 km. In contrast to the GA and MC-ML models, changing the damping factor had very little influence on the “roughness” of the model. In fact, comparing the MC-AV solutions for the two damping factors, the main differences in the solutions are the aforementioned broadening of the high velocity zone as well as an increase in the velocity amplitude heterogeneities. Since choosing a proper regularization (damping) factor is always a difficult task and often subjective in any tomographic imaging problem, it is obvious why the weak sensitivity of the MC-AV solution to the damping factor is an important issue.

To explore this in more detail, let us consider the following. Let us assume that we can divide the inverted velocity image into a “noisy part” (v _n ) due to all the uncertainties, such as data noise, forward modeling inaccuracy, optimization errors, etc., and the remaining “true” distribution (v _b ) we would expect in the ideal case. What type of behavior would we expect for these two parts when γ or C _d change? A change in the damping factor will influence v _b and v _n in different ways. While v _b is expected to interpolate more or less smoothly between the a priori (γ → ∞) model and the model which exactly fits the observational data (γ = 0), v _n will behave in an unpredictable way due to the randomness of all the uncertainties. This type of expected behavior is visible in the considered cases. In all but the LSQR solutions, the region of high velocity broadened when the damping factor was decreased. However, for the GA and MC-ML solutions, there is an additional increase in roughness . This increase in roughness or “noise” is much weaker in the case of the MC-AV solution. This suggests that the average model is a considerably more robust estimator of the true (noise-free part v _b ) velocity distribution than any of the maximum likelihood models. When averaged, this noise suppression effect is, in fact, very similar to noise reduction in the case of seismogram stacking (Claerbout, 1985) and follows from the incoherent nature of the noise (Jeffreys, 1983; Claerbout, 1985). Assuredly, any optimization algorithm which searches for a single, best solution, cannot perform noise reduction.

4.3 Imaging accuracy

The very first step in evaluating tomography results relies on inspecting the residuals for the “best” fit models. Figs. 6 and 7 display the residuals for the models obtained for C _d = 20 and 4 ms, respectively. Table 2 displays the root mean squares of the residuals calculated for all the models.

Fig. 6

Travel time residua for the LSQR (upper left), GA (upper right), MC-ML (lower left), and MC-AV (lower right) velocity models obtained using C _d = 20 ms setting. In this case the GA and LSQR algorithms performed equally well. The average MC solution provides slightly more scattered residua. The MC-ML model leads to the largest residua

Fig. 7

Travel time residua for the LSQR (upper left), GA (upper right), MC-ML (lower left), and MC-AV (lower right) velocity models obtained using C _d = 4 ms setting. Although all histograms are very similar, the corresponding models are quite different (see Fig. 5)

Note that all the residua histograms (for both C _d = 20 ms and C _d = 4 ms) are very similar, with a variance around 30 ms. The residuals exceed 50 ms only for a few data points. Thus the residuals suggest that the approximation of the sum of the travel time measurement and ray tracing errors by a Gaussian distribution (Gaussian Likelihood function) with variance C _d = 20 ms is justified. Furthermore Figs. 6 and 7 indicate that the choice C _d = 4 ms as the variance for the sum of observational and model errors is incompatible with the calculated residuals.

In the case of the well-damped inversion (C _d = 20 ms), all the methods led to similar residuals and hence, similar velocity images. It is interesting to note, however, that in the under-damped case (C _d = 4 ms) the differences between the velocity models are very substantial, yet the residuals are still similar for all four models. This demonstrates that evaluating the accuracy of a tomographic solution by inspecting the a posteriori residua alone is not sufficient. As in the studied case, there exist completely different models leading to, similar travel-time predictions.

A more comprehensive insight into imaging accuracy is obtained by inspecting the a posteriori covariance matrix which can be calculated easily as part of the MC technique. Figure 8 shows the spatial distribution of the velocity imaging errors estimated from the diagonal elements of the covariance matrix calculated from the a posteriori PDF for the MC solutions. Note that the a priori value C _v = 400 m/s is attached to cells probed by no rays. The obtained distribution shows that within the applied velocity parameterization (cell size) the imaging errors are almost homogeneously distributed over the imaged area and are approximately δ _v  ∼ 160 m/s for the image obtained, assuming C _d = 20 ms and δ _v  ∼ 50 m/s for C _d =  4 ms.

Fig. 8

Plot of the spatial distribution of imaging errors expressed by diagonal elements of the a posteriori covariance matrix for C _d = 20 ms (left) and C _d = 4 ms (right) The black contour defines the area probed by seismic rays. An increase of the imaging errors at the boundary of the imaged area is due to poorer sampling at the edges. Note the significant reduction of imaging uncertainties for C _d = 4 ms with respect to the C _d = 20 ms case

Comparing these results with the images in Figs. 4 and 5 indicates that great care must be taken when interpreting covariances as imaging errors. While such an interpretation seems to be justified in the case of the well-damped solution (Fig. 4), it is meaningless for the GA and LSQR in the case of the under-damped solutions, in which the final velocity images are strongly influenced by additional numerical artifacts far exceeding δ _v . The interpretation of the covariance matrix as a “measure” of inversion errors still seems to be justified (at least for this case) when the average model is taken as an estimator of the sought velocity distribution.

Estimating the imaging errors by the covariance matrix is justified if the a posteriori PDF has a “bell-shaped” and approximately symmetric, unimodal distribution. To verify whether this assumption is fulfilled in this study, I have selected a few cells (see Fig. 2) for which 1-D a posteriori marginal PDF’s were calculated according to Eq. 20. The results are shown in Figs. 9 and 10 for well-damped and under-damped cases, respectively. In both cases the marginal distributions resemble the Gaussian PDF, which means that the assumptions regarding the data and modeling error having a Gaussian distribution as well as the specific choice of the Gaussian a priori PDF were justified and consistent.

Fig. 9

Examples of the a posteriori 1D PDF functions for a few selected cells (see Fig. 2) for the C _d = 20 ms case. Note that the velocity heterogeneities shown in Fig. 4 are lower than the imaging errors

Fig. 10

Examples of the a posteriori 1-D marginal PDF functions for a few selected cells (see Fig. 2) for the C _d =  4 ms case. In this case the velocity resolution is sufficient to identify regions with velocity contrasts larger than the imaging errors

Finally, a question that remains to be addressed is which of the tomographic inversion methods is the preferred approach to estimate the true velocity distribution. Figures 11 and 12 compare the differences between the LSQR, GA, MC-ML models and the MC-AV model obtained for the two damping factors. For the case of a properly chosen damping factor all the models are compatible within one standard deviation range. For the LSQR solution, decreasing the damping factor leads to an unphysical solution. The remaining GA, MC-ML and MC-AV models are still compatible. However, for the reasons discussed above, the GA solution is expected to be a more reliable MLL estimator of the true velocity distribution than the MC-ML solution.

Fig. 11

The difference between LSQR (left), GA (middle) and MC-ML solutions and the MC-AV model obtained for C _d = 20 ms scaled down by the a posteriori imaging errors. Note that the differences between the LSQR, GA and MC-AV models are smaller than half the standard deviation (imaging error) in the whole imaged area. This means that the LSQR, GA, and MC-AV models are compatible with each other at a 68% confidence level. Only in the case of the MC-ML solutions the difference occasionally increases to one standard deviation

Fig. 12

The difference between LSQR (left), GA (middle) and MC-ML solutions and the MC-AV model obtained for C _d = 4 ms scaled down by the a posteriori imaging errors. Note that the LSQR solution differs in most of the imaged area by more than two standard deviations (imaging errors) from the MC-AV solution. On the other hand the GA and MC-ML models are compatible with MC-AV as the differences reach one standard deviation (value of the imaging errors) only in part of the imaged area. This means that the three solutions, namely GA, MC-ML and—MC-AV are statistically equivalent at a 68% confidence level

5 Discussion

Two types of conclusions can be drawn on the basis of the analyzed case study. The first concerns the performance of different inversion algorithms when applied to small-scale seismic tomography tasks. The second concerns a very preliminary quantitative interpretation of the obtained velocity images.

The MC sampling technique seems to provide the most robust estimation of the velocity distribution compared to any of the other inversion techniques based on the maximum likelihood estimator. In fact, the average image found by the MC technique was much smoother and, more importantly, provided a more realistic solution than the other two methods.

This indicates that sub-optimum models which lead to similar residua such as the GA or LSQR solutions and provide the main contribution to the MC-AV model are quite different. However, when summed up, the individual variations among them are smoothed out and the basic structure common to all the models remains. This is an important point and suggests that the MC technique is the most favorable and robust inversion approach.

In fact, this noise suppression effect is similar to that encountered in seismic stacking procedures (Claerbout, 1985). This possibility of enhancing the imaging accuracy by the proper choice of the inversion approach makes the MC technique more versatile than any other tomography technique known today.

Another important feature of the MC approach when compared with the classical (optimization and algebraic) techniques is its robustness with respect to the choice of the damping parameters. In fact, while all three methods perform rather similarly in a well-damped case, they differ when the algorithms are significantly under-damped. In an under-damped case, the algebraic approach completely fails to produce a reasonable solution. The optimization technique, due to the robustness of the used optimizer, is still able to produce an acceptable image. However, the solution is strongly influenced by numerical noise. On the other hand, in spite of apparently insufficient damping, the MC technique provides an image which differs only slightly from the result obtained for an optimum choice of γ.

Following these arguments, one can state that the Bayesian probability inversion approach with Monte Carlo sampling for the tomographic imaging problem is a very promising technique which is able to provide robust and generally more reliable images than currently used techniques. Its application is only limited by the size of the problem in hand. In the studied case, the simple Metropolis sampling algorithm was efficient enough to sample the a posteriori PDF due to the very small scale of the problem (109 model parameters and 177 data). In the case of larger-scale problems, when significantly more parameters have to be estimated (sampled), more complicated sampling techniques such as multi-step Metropolis (Bosch et al., 2000; Mosegaard and Tarantola, 1995) or more general random walk techniques will have to be employed (Robert and Casella, 1999; Mosegaard and Tarantola, 2002).

Finally, having obtained velocity distribution images, it is natural to attempt to infer information on the correlation of the velocity field and the structure of the observed seismicity. Although the current investigation was carried out primarily to evaluate various numerical algorithms for tomographic inversion, the obtained MC results seem to be robust enough to draw preliminary conclusions. Firstly, note that the events used in the current studies formed four different spatial clusters, as shown in Fig. 2. Excessively large uncertainties in clusters A and C prevent any reasonable correlation of seismicity in these two clusters with velocity distribution. In clusters B and D the MC velocity image has a high enough resolution to distinguish between fine velocity heterogeneities with sufficient precision. The obtained tomograms indicate that clusters B and D are located in regions of high spatial velocity gradients. The geomechanical interpretation of this fact is not quite clear. One possible explanation of this fact is the hypothesis on the existence of a spatially complex zone consisting of “hard” and “weak” parts. Physically, the “hard” part may consist of intact rock masses which have the possibility of accommodating larger stresses and thus showing higher velocities. The weaker part could be partially crushed rock masses. In such a condition we can expect a transfer of large stresses from the hard part to the weak one which cannot withstand them and will crush. Such a process would result in localized (clustered) seismicity.