1 Introduction

Let a plane curve \({\mathcal {C}}\) and an angle \(\theta \) be given. If it exists, the geometric locus of points through which passes a pair of tangents to \({\mathcal {C}}\) making an angle equal to \(\theta \) is called an \(\theta \)-isoptic curve of \({\mathcal {C}}\) and is denoted by \(\mathbf{Opt} ({\mathcal {C}}, \theta )\). The name comes from the fact that from points on this geometric locus the curve \({\mathcal {C}}\) is seen under a fixed angle equal to \(\theta \). We will call \(\theta \) the isoptic angle.

The study of isoptic curves has been an active field of research for a long time, both for strictly convex curves and for open curves [1, 4,5,6,7,8, 11]. An example of a non convex non smooth closed curve, namely isoptics of an astroid, is studied in [3]. The following important result is proven in [1]:

Theorem 1.1

If \({\mathcal {C}}\) is a convex closed curve, then for any angle \(\theta \), its \(\theta \)-isoptic is a closed and periodic curve with period \(2 \pi \).

The determination of isoptics can be done by purely computational means, but is also a wonderful topic for computerized experimentation using a dynamical geometry system of various online applets (see [6]). Illustrations of this theorem are given in [4, 5, 7, 8, 11]. In [4, 5] work followed an algebraic path:

  • Translate the question into equations.

  • Transform the equations into polynomial equations.

  • Solve the equations/systems of equations using computations of Gröbner bases. This generally yields a parametric representation of the desired isoptic curve.

  • Implicitize the parametric presentation using elimination ideals.

This can be viewed as a standard pattern for numerous questions around algebraic plane curves.

A central feature of the situation in Theorem 1.1 is as follows: if \({\mathcal {C}}\) is smooth convex closed curves, then it defines three regions in the plane:

  1. a.

    The exterior: through any point in that region pass a pair of tangents to \({\mathcal {C}}\).

  2. b.

    The curve \({\mathcal {C}}\) itself: through every point on the curve passes a unique tangent.

  3. c.

    The interior: through any point in that region no tangent passes.

Definition 1.2

Let \({\mathcal {C}}\) be a plane smooth closed curve and let \(\theta \) be a given angle. For any point \(P_0\) exterior to \({\mathcal {C}}\), we denote by \(T_1\) and \(T_2\) the points of contact of the tangents with \({\mathcal {C}}\). If it exists, the envelope of the family of lines \((T_1T_2)\) when \(P_0\) runs over an isoptic curve of \({\mathcal {C}}\) will be called an inner isoptic of \({\mathcal {C}}\).

In this paper, we study inner isoptics of ellipses. First, we perform experimentations using a dynamical geometry system (DGS),Footnote 1 then we will study the general case using a computer algebra system (CAS).

We use now the equations derived in [4], where a complete study of the isoptics of an ellipse can be found. WLOG, consider a general ellipse \({\mathcal {E}}_k\) whose equation is

$$\begin{aligned} x^2+k^2y^2=1, \quad k \in (0,+\infty ). \end{aligned}$$
(1.1)

Note that this equation is general enough, as the parameter k encodes the eccentricity of the ellipse. Therefore considering the general canonical equation \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) is not necessary. The topology remains the same.

Denote by \(\theta \) an isoptic angle and let \(t=\tan \theta \). Then a equation for the \(\theta \)-isoptic is as follows:

$$\begin{aligned} 4k^2 \; ( k^2y^2+x^2-1 )-t^2 \;(1-k^2 (x^2+y^2-1))^2 = 0. \end{aligned}$$
(1.2)

Actually this equation, derived in [4], describes both the \(\theta \)-isoptic and the \(\pi - \theta \)-isoptic, therefore the name of bisoptic curve given there. In each case, the curve given by Eq. (1.2) has two components. For acute \(\theta \), the \(\theta \)-isoptic is the external loop, the internal loop being the \(\pi -\theta \)-isoptic (in this last case, the isoptic angle is obtuse). In general we will denote by \(\mathbf{Opt} (k,\theta )\) the \(\theta \)-isoptic of the ellipse corresponding to k. In Fig. 1, the external loop is \(\mathbf{Opt} (1/2,45^{\circ })\) and the internal one is \(\mathbf{Opt} (1/2,135^{\circ })\).

Fig. 1
figure 1

Bisoptic curve of an ellipse

Full size image

For the algebraic computations in the present work, we will need to distinguish the components. This will be done later using parametrizations. For general descriptions of the problems posed by parameterizing curves, we refer to [10].

2 Experimentation with a DGS

Consider the ellipse \({\mathcal {E}}_2\) whose equation is \(x^2+4y^2=1\), and take an angle \(\theta =45^{\circ }\). In this case, the equation of the bisoptic curve \({\mathcal {C}}\) is

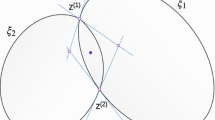
$$\begin{aligned} (x^2 + y^2)^2 - \frac{7}{2} x^2- \frac{13}{2}y^2 + \frac{41}{16} =0. \end{aligned}$$

Mark a point A on one of the components of the curve \({\mathcal {C}}\), then plot the tangents to \({\mathcal {E}}_2\) through A. We denote the tangency points by B and C and plot he segment BC. Using the Trace On feature of the DGS, we move slowly the point A along the curve. Figure 2a leads to conjecture the existence of an envelope for the segments BC, what we called an inner isoptic, for the acute angle \(45^{\circ }\). Figure 2b leads to a similar conjecture for the angle \(135^{\circ }\). We wish to mention that, at this step, we were unable to obtain an analytic presentation (i.e. an equation) for these envelopes using the DGS.

Fig. 2
figure 2

Examples of inner isoptics of an ellipse

Full size image

In order to find an equation for the envelopes of the family of segments BC parameterized by the point A, i.e. the desired inner isoptics, we have to switch to a CAS and to work with explicit equations. This is an example where a dialog between DGS and CAS is necessary.

3 The automated study of inner isoptics of a given ellipse

3.1 The tangency points and the line through them

Consider a point \(P_0 (x_0,y_0)\) on the isoptic. Through \(P_0\) passes a pair of tangents to \({\mathcal {E}}_k\), whose respective slopes are given by:

$$\begin{aligned} m_1= & {} \frac{\sqrt{k^2y_0^2+x_0^2-1}-kx_0y_0}{k(-x_0^2+1)} \\ m_2= & {} -\frac{\sqrt{k^2y_0^2+x_0^2-1}+kx_0y_0}{k(-x_0^2+1)} \end{aligned}$$

and the respective equations of the tangents are:

$$\begin{aligned} y= & {} y_0+ m_1(x-x_0) \\ y= & {} y_0+m_2(x-x_0) \end{aligned}$$

Now we look for the coordinates of the tangency points, by solving the systems of equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} y=y_0+ \frac{\sqrt{k^2y_0^2+x_0^2-1}-kx_0y_0}{k(-x_0^2+1)}\; (x-x_0)\\ x^2+k^2y^2=1 \end{array}\right. } \end{aligned}$$
(3.1)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} y=y_0 -\frac{\sqrt{k^2y_0^2+x_0^2-1}+kx_0y_0}{k(-x_0^2+1)} \; (x-x_0)\\ x^2+k^2y^2=1. \end{array}\right. } \end{aligned}$$
(3.2)

In both systems of equations, the obvious condition of existence for solutions is that \(x_0^2+k^2y_0-1>0\), i.e. that the point \(P_0\) is exterior to the curve \({\mathcal {E}}_k\). The solutions of system (3.1) are the coordinates of a point \(P_1\), namely:

$$\begin{aligned} \left\{ \begin{array}{l} x_1 = \frac{kxl_0^2y_0 \; \sqrt{k^2y_0^2 + x_0^2 - 1} - 2k^2x_0y_0^2 + ky_0 \; \sqrt{k^2y_0^2 + x_0^2 - 1} - x_0^3 + x_0}{-k^2x_0^2y_0^2 + 2kx_0y_0; \sqrt{k^2y_0^2 + x_0^2 - 1} - k^2y_0^2 - x_0^4 + x_0^2}\\ y_1= \frac{x_0 \sqrt{k^2y_0^2 + x_0^2 - 1} + ky_0}{k \; (k^2y_0^2 + x_0^2)} \end{array}\right. \end{aligned}$$
(3.3)

and the solutions of system (3.2) are the coordinates of a point \(P_2\), namely:

$$\begin{aligned} \left\{ \begin{array}{l} x_2= \frac{ kx_0^2y_0 \; \sqrt{k^2y_0^2 + x_0^2 - 1} + 2k^2x_0y_0^2 + ky_0 \; \sqrt{k^2y0^2 + x0^2 - 1} + x_0^3 - x0}{k^2x_0^2y_0^2 + 2kx_0y_0 \sqrt{k^2y0^2 + x0^2 - 1} + k^2y_0^2 + x_0^4 - x_0^2})\\ y_2= -\frac{x_0 \; \sqrt{k^2y_0^2 + x_0^2 - 1} - ky_0}{k\; (k^2y_0^2 + x_0^2)}.\\ \end{array}\right. \end{aligned}$$
(3.4)

The computation of an equation of the line \((P_1P_2)\) is theoretically an easy task, but technically it is heavy. In order to use the CAS efficiently, we use a determinant whose vanishing locus is the desired line. We obtain:

$$\begin{aligned} 2(x_0 - 1)^2(x_0 + 1)^2(k^2y_0^2 + x_0^2)(k^2yy_0 + xx_0 - 1)\sqrt{y_0^2k^2 + x_0^2 - 1}=0,\qquad \end{aligned}$$
(3.5)

which is equivalent to

$$\begin{aligned} xx_0+k^2yy_0 - 1=0. \end{aligned}$$
(3.6)

Note that if the point \(P_0\) is on the ellipse \({\mathcal {E}}_k\), this is exactly the equation of the tangent to the ellipse through \(P_0\).

3.2 A parametrization of \(\mathbf{Opt} (k,t)\)

Equation (1.2) determines bisoptic curves of the ellipse \({\mathcal {E}}_k\). As we described previously, this curve is the disjoint union of two smooth closed curves. It has been proven in [4] that this curve is a special case of a Spiric of Perseus, namely the intersection of a torus with a plane parallel to the torus axis. In the case of bisoptic of ellipses (and also of hyperbolas, as shown in [5], but this not our concern here), the torus is self-intersecting. Anyway, the two loops forming the bisoptic curve are not self-intersecting, and they can be decomposed into 4 arcs by cutting them along the x-axis.

Solving Eq. (1.2) for y, we obtain the following equations, which provide easily parametrizations for the arcs:

$$\begin{aligned} {\left\{ \begin{array}{ll} \text {Arc 1:} \quad &{}y=\frac{\sqrt{-k^2t^2x^2 + k^2t^2 + 2k^2 + t^2 + 2\sqrt{-k^4t^2x^2 + k^4t^2 + k^2t^2x^2 + k^4}}}{tk} \\ \text {Arc 2:} \quad &{}y=-\frac{\sqrt{-k^2t^2x^2 + k^2t^2 + 2k^2 + t^2 + 2\sqrt{-k^4t^2x^2 + k^4t^2 + k^2t^2x^2 + k^4}}}{tk} \\ \text {Arc 3:} \quad &{}y=\frac{\sqrt{-k^2t^2x^2 + k^2t^2 + 2k^2 + t^2 - 2\sqrt{-k^4t^2x^2 + k^4t^2 + k^2t^2x^2 + k^4}}}{tk} \\ \text {Arc 4:} \quad &{}y= - \frac{\sqrt{-k^2t^2x^2 + k^2t^2 + 2k^2 + t^2 - 2\sqrt{-k^4t^2x^2 + k^4t^2 + k^2t^2x^2 + k^4}}}{tk} \end{array}\right. } \end{aligned}$$

3.3 The inner isoptics

Take a point \(P_0\) on Arc 1; it is defined by the following parametrization:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_0 = u \\ y_0= \frac{\sqrt{-k^2t^2u^2 + k^2t^2 + 2k^2 + t^2 + 2\sqrt{-k^4t^2u^2 + k^4t^2 + k^2t^2u^2 + k^4}}}{tk} \end{array}\right. }, \end{aligned}$$
(3.7)

where u is now the parameter instead of x. By substitution into the equation of the line \(P_1P_2\), we have:

$$\begin{aligned} xu+k^2y \left( \frac{\sqrt{-k^2t^2u^2 + k^2t^2 + 2k^2 + t^2 + 2\sqrt{-k^4t^2u^2 + k^4t^2 + k^2t^2u^2 + k^4}}}{tk} \right) -1=0. \end{aligned}$$

Denote by F(x, y, u) the right-hand side of this equation. An envelope of the family of lines, if it exists, is determined by the following system of equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} F(x,y,u)=0\\ \frac{\partial F}{\partial u} F(x,y,u)=0. \end{array}\right. } \end{aligned}$$
(3.8)

We obtain:

$$\begin{aligned} {\left\{ \begin{array}{ll} x = \frac{u((1 + (-u^2 + 1)k^4 + (u^2 + 2)k^2)\sqrt{-k^2((u^2 - 2)k^2 - u^2)} + (u^2 - 1)k^6 - 3k^4 - k^2u^2}{(u^4 + u^2 - 2)k^6 + (-2u^4 + 5u^2 - 12)k^4 + (u^4 - 5u^2 - 2)k^2 - u^2}\\ y = \frac{\left( ((-u^2 + 4)k^2 + u^2)\sqrt{-k^2((u^2 - 2)k^2 - u^2)} + 3(k^2 + \frac{1}{3})((u^2 - 2)k^2 - u^2)\right) \; \sqrt{2 \sqrt{-k^2((u^2 - 2)k^2 - u^2)} + 1 + (-u^2 + 3)k^2}}{((u^4 + u^2 - 2)k^6 + (-2u^4 + 5u^2 - 12)k^4 + (u^4 - 5u^2 - 2)k^2 - u^2)k} \end{array}\right. } \end{aligned}$$

Back to the DGS, we use the command Curve to plot the curve defined by these equations. We plotted it in a GeoGebra file with general k. The slider bar enabled us to show that in the case where \(k=2\), the arc defined by the parametrization coincides exactly with what has been conjectured in Sect. 2. Two examples are displayed in Fig. 3, with emphasis on the chord BC.

Fig. 3
figure 3

Examples of chords and inner isoptics of an ellipse

Full size image

For the other arcs, work follows exactly the same path. We may leave it to the interested reader.

Remark 3.1

An important question is implicitization of the parametric presentation of the inner isoptic that we have found. In other (simpler) settings, when the data could be put into polynomial from, we could use algorithms such as computation of elimination ideals or resultants (see [2]), in the way it has been done e.g. in [4]. Here the transformation of Eq. (3.8) into rational, then polynomial expressions seems hopeless.

For example, let \(k=2\). Transforming Eq. (3.2) into polynomial data, by means of transfer from side to side and successive raising to the square provides the following polynomial equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} 110592u^{14} - 608256u^{12} - 147456u^{11}y + 1057536u^{10} + 602112u^9*y + 1296u^8x^2 \\ \qquad + 49152u^8y^2 - 591872u^8 - 9216u^7x - 557056u^7y + 8856u^6x^2 - 131072u^6y^2 \\ \qquad + 16384u^6 - 15360u^5x - 8487u^4x^2 - 57344u^4 + 139072u^3x - 80688u^2x^2 \\ \qquad + 50176u^2 - 146944ux + 107584x^2=0\\ 26873856u^{16}y^4 - 2654208u^{16}y^2 + 367276032u^{14}y^4 + 65536u^{16} + 275816448u^{14}y^2\\ \qquad + 902886912u^{12}y^4 + 15592448u^{14} + 1105416576u^{12}y^2 - 5751440640u^{10}y^4 \\ \qquad + 61000192u^{12} - 8064265152u^{10}y^2 - 17252143344u^8y^4 + 668471424u^{10}\\ \qquad - 12938192552u^8y^2 + 52402014720u^6y^4 + 1938827977u^8 + 79391817472u^6y^2 \\ \qquad + 74950760448u^4y^4 - 14469805664u^6 - 73272450048u^4y^2 - 277783609344u^2y^4 \\ \qquad + 8493420928u^4 + 20904001536u^2y^2 + 185189072896y^4 + 3487442944u^2\\ \qquad - 29359243264y^2 + 282300416=0 \end{array}\right. } \end{aligned}$$

We tried with different packages, but until now, no CAS was unable to eliminate the parameter u in a “reasonable” time. In the particular case of \(\theta = \pi /2\), computations are easier. We show this case in the next section.

3.4 An implicit equation for the inner orthoptic of an ellipse

We consider now the case where \(\theta = \frac{\pi }{2}\). If it exists, the \(\frac{\pi }{2}\)-isoptic of a curve \({\mathcal {C}}\) is generally called the orthoptic of \({\mathcal {C}}\). The best known cases are for conics, the equations are displayed in Table 1 and the curves in Fig. 4.

Table 1 Orthoptics of conics
Full size table
Fig. 4
figure 4

Orthoptics of conics

Full size image

Let \({\mathcal {E}}\) be the ellipse whose equation is \(x^2+k^2y^2=1\), for \(k>0\). Its director circle has equation \(x^2+y^2=1+\frac{1}{k^2}\). Following the same path as in previous subsection, a parametric presentation of the inner orthoptic is obtained:

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}x= \frac{1}{2 \left( 1+\frac{1}{k^2}\right) \left( \sqrt{ \sin ^2t+\frac{1}{k^2} \cos ^2t} \sqrt{ \cos ^2t+\frac{1}{k^2} \sin ^2t}+(1-\frac{1}{k^2}) \sin t \cos t\right) } \left( -2 \sin ^3t \sqrt{ \cos ^2t+\frac{1}{k^2} \sin ^2t}+\right. \\ &{}\qquad +\sqrt{2} \left( 1- \frac{2}{k^2}\right) \sin t \cos ^2t \sqrt{\left( 1-\frac{1}{k^2}\right) \cos 2t+1+\frac{1}{k^2}}+ 2 \cos ^3t \sqrt{ \sin ^2t+\frac{1}{k^2} \cos ^2t}-\\ &{}\qquad \left. -\sqrt{2} \left( 1-2 (1/k)^2\right) \sin ^2t \cos t \sqrt{\left( \frac{1}{k^2}-1\right) \cos 2t+1+\frac{1}{k^2}}\right) \\ &{}y=\frac{1}{2k^2 \left( 1+\frac{1}{k^2}\right) \left( \sqrt{ \sin ^2t+\frac{1}{k^2} \cos ^2t} \sqrt{ \cos ^2t+\frac{1}{k^2} \sin ^2t}+\left( 1-\frac{1}{k^2}\right) \sin t \cos t\right) } \left( \frac{2}{k^2} \sin ^3(t) \sqrt{ \sin ^2t +\frac{1}{k^2} \cos ^2t}+\right. \\ &{}\qquad +\sqrt{2} \left( 2 -\frac{1}{k^2}\right) \sin t \cos ^2t \sqrt{\left( \frac{1}{k^2}- 1\right) \cos 2t+1+\frac{1}{k^2}}+\frac{2}{k^2} \cos ^3t \sqrt{ \cos ^2t+\frac{1}{k^2} \sin ^2t}+\\ &{}\qquad \left. +\sqrt{2} \left( 2 -\frac{1}{k^2}\right) \sin ^2t \cos t \sqrt{\left( 1-\frac{1}{k^2}\right) \cos 2t+1+\frac{1}{k^2}}\right) \end{array}\right. } \end{aligned}$$

In this specific case, an implicit equation can be derived for the inner-orthoptic, namely

$$\begin{aligned} (x^2+k^4y^2)(k^6y^2 + k^4y^2 + k^2x^2 - k^2 + x^2)=0 \end{aligned}$$
(3.9)

Equation (3.9) has been obtained using methods based on support functions; see [9].

Actually, the first factor defines the origin only, and is irrelevant. The second factor determines the desired inner-orthoptic. Finally we have the following result:

Proposition 3.2

Let \({\mathcal {E}}\) be the ellipse whose equation is \(x^2+k^2y^2=1\), for \(k>0\).

  1. 1.

    \({\mathcal {E}}\) has an inner-orthoptic.

  2. 2.

    This inner-orthoptic is an ellipse whose equation is \((1+k^2)x^2+(k^4+k^6)y^2=k^2\).

Fig. 5
figure 5

Inner orthoptic of an ellipse

Full size image

It is easy to prove that the given ellipse and its inner orthoptic have different eccentricity and foci. An interactive GeoGebra applet is available at https://www.geogebra.org/m/z9aqyuun.