Regular polygons on isochordal-viewed hedgehogs

Abstract

A curve $\alpha$ is said to be isochordal viewed if there is a smooth motion of a constant length chord with its endpoints along $\alpha$ such that their tangents to the curve at these points form a constant angle. In this paper some properties of isochordal-viewed hedgehogs and Holditch curves are studied. It is proved that, under some conditions, the construction of some closed regular polygons whose vertices move smoothly along the curve $\alpha$ is possible. The property is illustrated with some examples. Moreover, Holditch curves of isochordal-viewed hedgehogs are considered and it is seen that they feature similar regular polygon properties although they are, in general, not parameterized by a support function. Finally, a recursive iteration of some Holditch curves for isochordal-viewed hedgehogs is shown to converge to the curve of polygon centers.

1 Introduction

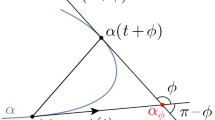
Given and a planar closed curve $\alpha :\mathbb {S}^1\rightarrow \mathbb {R}^2$, the $\phi$-isoptic of $\alpha$ is defined as a curve $\alpha _{\phi }:\mathbb {S}^1\rightarrow \mathbb {R}^2$ from which the curve $\alpha$ is seen under a constant angle $\pi -\phi$ (see for instance [3, 4] or [7]). For general curves (convex or not) the $\phi$-isoptic of $\alpha$ is understood as the locus of points through which a pair of supporting lines to $\alpha$ pass making an angle of $\phi$ (see Fig. 1). If the $\phi$-isoptic of $\alpha$ has constant curvature (i.e., if it is circular), then $\alpha$ is said to be of constant $\phi$-width [13].

We say that the curve $\alpha$ is $(\phi ,\ell )$-isochordal viewed if the chord joining the contact points of the supporting lines that define the $\phi$-isoptic of $\alpha$ has constant length $\ell$ (see Fig. 1). For an introduction to this kind of curves and some of their properties, the reader can see [6] and [15].

Fig. 1

Definition of the $\phi$-isoptic of $\alpha$, $\alpha _{\phi }$. If the length $\ell$ is constant, then $\alpha$ is $(\phi ,\ell )$-isochordal viewed.

In this paper we will consider $(\phi ,\ell )$-isochordal-viewed hedgehogs parameterized by a support function. A hedgehog $\alpha$ (see e.g. [8] or [9]) is a curve which has one and only one tangent line in each oriented direction. Its parameterization in terms of a support function h can be written follows:

$$\begin{aligned} \alpha (t) = h(t)\,(\cos t,\,\sin t) + h'(t)\,(-\sin t,\,\cos t),\quad t\in \mathbb {S}^1. \end{aligned}$$

Henceforth, we will identify $\mathbb {S}^1$ with the interval , where a curve defined there will be assumed to be extendable by periodicity.

Convex curves are particular cases of hedgehogs without singularities. A hedgehog is called projective if its support function h is such that $h(t) + h(t+\pi ) = 0$. Later on, we will show some examples of projective hedgehogs which are also isochordal-viewed. But isochordal-viewed hedgehogs are not necessarily projective (see Example 2).

The motion of a constant length chord along a curve, as it happens with isochordal-viewed curves, corresponds to the kind of kinematics considered in Holditch’s theorem and some related scenarios. Works like [1] or [17], as well as some recent works, such as [2, 11, 12] or [14], are found in the literature where this type of motion is studied. In particular, another curve is generated from the initial one, the so-called Holditch curve. Given and the motion of a chord of constant length $\ell$ around a closed curve $\alpha$, the p-Holditch curve of $\alpha$ for the chord length $\ell$ is the locus of points dividing the length $\ell$ in the ratio $p:1-p$ (see Fig. 2).

Fig. 2

A closed curve $\alpha$ and its p-Holditch curve $H_p$ for a chord length $\ell$.

If the chord movement can be done without retrograde motion, then the Holditch function for a parameterization $\alpha :\mathbb {S}^1\rightarrow \mathbb {R}^2$ is defined as the homeomorphism $f:\mathbb {S}^1\rightarrow \mathbb {S}^1$ that for each $t\in \mathbb {S}^1$, if $\alpha (t)$ is the rear endpoint of the moving chord, it produces the front one as $\alpha \bigl (f(t)\bigr )$ (see [11] and Fig. 2).

In general, Holditch functions are very difficult to compute analytically. However, for a $(\phi ,\ell )$-isochordal-viewed curve, the Holditch function for a chord length $\ell$ becomes trivial as it is just a translation: $f(t) = t + \phi$.

In this paper, $(\phi ,\ell )$-isochordal-viewed hedgehogs and their Holditch curves for the chord length $\ell$ are considered. The main result of Sect. 2 is Proposition 2.1 where it is shown that, under certain conditions, in addition to the chord of constant length $\ell$, a whole regular polygon of side length $\ell$ can travel smoothly around the curve. Some examples exhibiting this property are shown in Examples 1 and 2. Later, in Sect. 3, thanks to the regular polygon property, we show in Theorem 3.1 that Holditch curves of Holditch curves still maintain the Holditch function being a translation, so that they are also easy to compute, although any p-Holditch curve of $\alpha$ is parameterized by a support function (Proposition 3.3 and Corollary 3.4). Finally, in Sect. 4, the construction of new regular polygons from a given one maintaining the same polygon center (Proposition 4.1) allows us to relate the recursive generation of new polygons with the recursive computation of Holditch curves. As a consequence, the sequence of Holditch curves is shown to be convergent to the curve of polygon centers (Theorem 4.3).

2 Closed polylines on isochordal-viewed curves

By its definition, we know that a chord of constant length $\ell$ is allowed to move smoothly (without retrograde motion) along a $(\phi ,\ell )$-isochordal-viewed hedgehog $\alpha$ parameterized by a support function. The aim of this section is to show that actually, under some conditions, not only this chord can move along the curve $\alpha$, but also a closed equilateral polyline. The main result is presented below.

Proposition 2.1

Let $\ell >0$, and let $\alpha$ be a piecewise-$\mathcal {C}^2$ $(\phi ,\ell )$-isochordal-viewed hedgehog parameterized by a support function $h\in \mathcal {C}^3$. For each $t\in \mathbb {S}^1$, consider the polyline $\Gamma (t)$ obtained by joining the vertices $\alpha (t)$, $\alpha (t+\phi )$, $\alpha (t+2\,\phi )$, etc. Then:

• (i) The polyline $\Gamma (t)$ is formed by segments of constant length $\ell$.

• (ii) If there exist $m\in \mathbb {Z}$ and $n\in \mathbb {N}$, relatively prime, such that $\phi =\frac{m}{n}\,\pi ,$ (assuming $\alpha$ is projective if m is odd), then the polyline $\Gamma (t)$ is closed and has n sides.

• (iii) If $\alpha$ is also a curve of constant $\phi$-width, then the angle between two consecutive segments of $\Gamma (t)$ is constant.

Proof

The hedgehog $\alpha$ is defined by

$$\begin{aligned} \alpha (t)=h(t)\,(\cos t,\,\sin t) + h'(t)\,(-\sin t,\,\cos t) \end{aligned}$$

and the isochordal condition is satisfied by the hypothesis:

$$\begin{aligned} \bigl \Vert \alpha (t+\phi )-\alpha (t)\bigr \Vert =\ell ,\quad \text {for all } t\in \mathbb {S}^1. \end{aligned}$$

Notice that thanks to the isochordal condition we also have

$$\begin{aligned} \bigl \Vert \alpha (t+2\,\phi )-\alpha (t+\phi )\bigr \Vert =\ell \end{aligned}$$

and

$$\begin{aligned} \bigl \Vert \alpha (t+3\,\phi )-\alpha (t+2\,\phi )\bigr \Vert =\ell , \end{aligned}$$

etc. In fact, in general, for any $k\in \mathbb {Z}$ we have

$$\begin{aligned} \Bigl \Vert \alpha (t+k\,\phi )-\alpha \bigl (t+(k-1)\,\phi \bigr )\Bigr \Vert =\ell ,\quad \text {for all } t\in \mathbb {S}^1. \end{aligned}$$

This procedure generates a polyline of side length $\ell$ with its vertices on the curve $\alpha$, which is $\Gamma (t)$, so that (i) is proved. Such a polyline will be closed if there exists $n\in \mathbb {N}$ such that

$$\begin{aligned} \alpha (t+n\,\phi )=\alpha (t),\quad \text {for all }t\in \mathbb {S}^1. \end{aligned}$$

A simple computation shows that

$$\begin{aligned} \alpha '(t+n\,\phi )-\alpha '&(t)=\bigl (h(t)+h''(t)\bigr )\,(\sin t,\,-\cos t)\\&- \bigl (h(t+n\,\phi )+h''(t+n\,\phi )\bigr )\,\bigl (\sin (t+n\,\phi ),\,-\cos (t+n\,\phi )\bigr ). \end{aligned}$$

There are only two ways for this expression to be equal to zero. The first option is that $n\,\phi = \pi \,m,$ for some even integer m. The second option is that $n\,\phi = \pi \,m$ for an odd integer m and, in addition, $\alpha$ is a projective hedgehog, so that

$$\begin{aligned} h(t) + h(t + \pi \,m) = 0. \end{aligned}$$

In any case, we deduce that $\phi$ must be of the form

$$\begin{aligned} \phi =\frac{m}{n}\,\pi , \end{aligned}$$

which is fulfilled by hypothesis. Finally, notice that

$$\begin{aligned} \alpha (t+n\,\phi ) = \alpha (t+m\,\pi )=\alpha (t). \end{aligned}$$

The last equality is immediate if m is even. If m is odd, it holds because $\alpha$ is assumed to be projective. An irreducible fraction $\frac{m}{n}$ leads to a denominator n which is the lowest natural number that satisfies the property above, so that it is the number of sides of the closed polyline $\Gamma (t)$. Thus, we have proved (ii).

Suppose now that $\alpha$ is of constant $\phi$-width. The cosine of the angle between two consecutive segments of $\Gamma (t)$ is given by

$$\begin{aligned} \frac{1}{\ell ^2}\,\Bigl \langle \alpha \bigl (t+(k+2)\,\phi \bigr )-\alpha \bigl (t+(k+1)\,\phi \bigr ),\,\alpha (t+k\,\phi )-\alpha \bigl (t+(k+1)\,\phi \bigr )\Bigr \rangle , \end{aligned}$$

where $k\in \mathbb {Z}$. We will show geometrically that the angle is constant.

By the definition of oriented angle functions $\nu$ and $\mu$ introduced in [15] (see Fig. 3 in the case $k=0$), the angle will be equal to

$$\begin{aligned} \pi -\Bigl (\mu (t+k\,\phi )+\nu \bigl (t+(k+1)\,\phi \bigr )\Bigr ). \end{aligned}$$

(2.1)

Fig. 3

The angle between two consecutive segments of $\Gamma (t)$ can be written in terms of the angles $\mu (t)$ and $\nu (t+\phi )$.

Now, since $\alpha$ is of constant $\phi$-width, by Theorem 5.4 of [15] we know that $\nu '(t)=a$ and $\mu '(t)=-a$ are constant. This directly implies (2.1) being constant because its derivative is equal to zero. Thus, we have proved (iii). $\square$

Thanks to Proposition 2.1 we can construct a regular polygon (closed, equilateral and equiangular polyline) which moves smoothly along a $(\phi ,\ell )$-isochordal-viewed hedgehog of constant $\phi$-width. These polygons can be either convex or star as we will see in Examples 1 and 2 below.

We remark that many examples of this kind of curves can be given, so that the hypothesis on the curve is not very restrictive. In fact, finding an example of a $(\phi ,\ell )$-isochordal-viewed hedgehog which is not of constant $\phi$-width or to prove a relation between these two types of curves is still an open problem (see Remark 5.5 of [15]). In the convex case, for , it can be proved that the circle is the only example of a $(\phi ,\ell )$-isochordal-viewed curve of constant $\phi$-width (see Theorem 2 of [6]), but this is not the case for non-convex curves.

From now on, if the angle $\phi$ is of the kind given in Proposition 2.1-(ii), we will call it admissible.

Corollary 2.2

Let $\ell >0$ and suppose that is admissible. Let $\alpha$ be a $\mathcal {C}^2$-piecewise $(\phi ,\ell )$-isochordal-viewed hedgehog parameterized by a support function $h\in \mathcal {C}^3$ which is also a curve of constant $\phi$-width. Then $\alpha$ is also $(2\,\phi ,\tilde{\ell })$-isochordal-viewed, where

$$\begin{aligned} \tilde{\ell } = \sqrt{2}\,\ell \,\sqrt{1-\cos \theta }, \end{aligned}$$

with $\theta$ being the constant angle of the regular polygon associated with $\alpha$.

Proof

Fig. 4

The length $\tilde{\ell }$ is constant by the cosine rule.

By Proposition 2.1, for each $t\in \mathbb {S}^1$ we have a regular polygon $\Gamma (t)$ with vertices at $\alpha (t)$, $\alpha (t+\phi )$, $\alpha (t+2\,\phi )$, etc. Since $\Gamma (t)$ has constant side lengths and angles, we have that

$$\begin{aligned} \bigl \Vert \alpha (t)-\alpha (t+2\,\phi )\bigr \Vert \end{aligned}$$

is also constant for all $t\in \mathbb {S}^1$ by the cosine rule (see Fig. 4), which yields the expression of the statement. $\square$

Next, we are going to consider a 1-parameter family of examples. In Example 1 we will consider projective hedgehogs and we will make the computations in detail. Later, in Example 2, examples of isochordal-viewed hedgehogs which are not projective will also be shown.

Example 1

Let n be an odd natural number, i.e. $n=2\,k+1$ for $k\in \mathbb {Z}$. Consider the curve $\alpha _n:\mathbb {S}^1\rightarrow \mathbb {R}^2$ parameterized by the support function

$$\begin{aligned} h_n(t)=\sin (n\,t). \end{aligned}$$

First, let’s compute all the possible angles $\phi$ that make $\alpha _n$ an isochordal-viewed curve. It can be computed explicitly that

$$\begin{aligned}\frac{\text {d}}{\text {d}t}\bigl \Vert&\alpha (t+\phi )-\alpha (t)\bigr \Vert ^2\\&= 16\,k\,(k+1)\,(2\,k+1)\sin (k\,\phi )\sin \bigl ((k+1)\,\phi \bigr )\sin \bigl ((2\,k+1\bigr )\,\bigl (2\,t+\phi )\bigr ). \end{aligned}$$

The curve $\alpha _n$ is isochordal viewed if the expression above is equal to zero for all $t\in \mathbb {S}^1$. This happens if and only if

$$\begin{aligned} \phi = \frac{m}{k}\,\pi \quad \text {or}\quad \phi =\frac{m}{k+1}\,\pi \end{aligned}$$

for any $m\in \mathbb {Z}$. The length of the isoptic chord,

$$\begin{aligned} \ell = \bigl \Vert \alpha _n(t+\phi )-\alpha _n(t)\bigr \Vert , \end{aligned}$$

can be explicitly computed. If $\phi = m\,\pi /k$, then

and if $\phi = m\,\pi /(k+1)$, then

In addition, it can be proved that for any of the $\phi$ values above, the curve $\alpha _n$ is of constant $\phi$-width. The calculations are a bit complicated but it can be seen that

is constant. This is a sufficient condition for $\alpha _n$ to be a curve of constant $\phi$-width. The interested reader can see the expression of the curvature of the $\phi$-isoptic of $\alpha$ in Equation (5.4) of [15], which comes from Equation (5.7) of [3].

For each $t\in \mathbb {S}^1$, consider now the polyline $\Gamma (t)$ defined in Proposition 2.1. By construction, its segments have a constant length $\ell$ and it is equiangular. Moreover, in this case, if $\phi =m\,\pi /k$, for $k\in \mathbb {N}$, then

$$\begin{aligned} \alpha _n\bigl (t+k\,\phi \bigr ) = \alpha _n(t), \end{aligned}$$

so that $\Gamma (t)$ is a regular polygon of k sides. If $\phi = m\,\pi /(k+1)$, for $k\in \mathbb {N}$, then

$$\begin{aligned} \alpha _n\bigl (t+(k+1)\,\phi \bigr ) = \alpha _n(t) \end{aligned}$$

and $\Gamma (t)$ is a regular polygon of $k+1$ sides. See in Fig. 5 some frames of the movement of the regular polygon $\Gamma (t)$ in a particular example with $k=5$.

Fig. 5

Example of $\alpha _{11}$ with $\phi = \pi /5$, where $\Gamma (t)$ is a regular pentagon moving along $\alpha _{11}$.

That $\Gamma (t)$ is closed can also be deduced using Proposition 2.1(ii), because notice that for any odd integer n, $\alpha _n$ is a projective hedgehog. Indeed, we have $h(t)+h(t+\pi ) = 0.$ This means that the curves $\alpha _n$ are examples of “curves of constant width 0” and they are traced out twice in .

The same example is considered in Fig. 6 but for different admissible $\phi$ values, where different regular polygons are produced.

Fig. 6

Examples of $\alpha _{11}$ with $\phi = \pi /6$, $\phi = \pi /3$, $\phi = \pi /2$ and $\phi = 2\pi /5$.

Example 2

Let n be an even natural number, i.e. $n=2\,k$ for $k\in \mathbb {Z}$. Consider the curve $\alpha _n:\mathbb {S}^1\rightarrow \mathbb {R}^2$ parameterized by the same support function as in the previous example:

$$\begin{aligned} h_n(t)=\sin (n\,t). \end{aligned}$$

The main difference now is that $\alpha _n$ is not a projective hedgehog. A similar discussion to that of Example 1 can be done and it can be seen that for angles of the kind

$$\begin{aligned} \phi =\frac{2\,m\,\pi }{1-2\,k},\quad \text {or}\quad \phi =\frac{2\,m\,\pi }{1+2\,k}, \end{aligned}$$

for any $m\in \mathbb {Z}$, the expression

$$\begin{aligned} \ell = \bigl \Vert \alpha _n(t+\phi )-\alpha _n(t)\bigr \Vert \end{aligned}$$

is constant, so that $\alpha _n$ is $(\phi ,\ell )$-isochordal viewed. Moreover, it can also be seen that every $\alpha _n$ is a curve of constant $\phi$-width.

See in Fig. 7 some examples of the curves $\alpha _n$ (for different k values) and the regular polygons defined in Proposition 2.1 for different angles (of the kind above).

Fig. 7

Some regular polygons on non-projective isochordal-viewed hedgehogs $\alpha _n$.

3 Holditch curves of isochordal-viewed curves

In addition to the very interesting feature of $(\phi ,\ell )$-isochordal-viewed hedgehogs of constant $\phi$-width presented in Proposition 2.1 and visualized in Examples 1 and 2, we also have a direct consequence regarding the behaviour of their Holditch curves.

As it has been said, because of the parameterization by a support function of $(\phi ,\ell )$-isochordal-viewed curves, we already know that their Holditch curves for a chord length $\ell$ are easy to compute. This is because the Holditch function turns out to be just a translation by the angle $\phi$: $f(t) = t + \phi$. But what about the Holditch curves of a Holditch curve? The following theorem essentially states that in this case the iterated Holditch curves for a particular chord length are also easy to compute because the Holditch function is still the same translation.

Theorem 3.1

For each $t\in \mathbb {S}^1$, suppose that $\Gamma (t)$ is a regular polygon of constant side length $\ell$ with vertices $\alpha (t)$, $\alpha (t+\phi )$, $\alpha (t+2\phi )$, etc. lying on a closed piecewise-$\mathcal {C}^2$ curve $\alpha :\mathbb {S}^1\rightarrow \mathbb {R}^2$. Then every p-Holditch curve of $\alpha$, $H_p$, for a chord length $\ell$ satisfies that

$$\begin{aligned} \bigl \Vert H_p(t+\phi )-H_p(t)\bigr \Vert \end{aligned}$$

(3.1)

is constant.

Proof

The p-Holditch curve $H_p$ of $\alpha$ for the chord length $\ell$ can be parameterized as

$$\begin{aligned} H_p(t)=(1-p)\,\alpha (t)+p\,\alpha (t+\phi ). \end{aligned}$$

We have that

$$\begin{aligned} \bigl \Vert H_p(t&+\phi )-H_p(t)\bigr \Vert ^2\nonumber \\&=\Bigl \Vert (1-p)\,\bigl (\alpha (t+\phi )-\alpha (t)\bigr )+p\,\bigl (\alpha (t+2\,\phi )-\alpha (t+\phi )\bigr )\Bigr \Vert ^2\nonumber \\&=(1-p)^2\,\bigl \Vert \alpha (t+\phi )-\alpha (t)\bigr \Vert ^2+p^2\,\bigl \Vert \alpha (t+2\,\phi )-\alpha (t+\phi )\bigr \Vert ^2\nonumber \\&+2\,p\,(1-p)\,\bigl \langle \alpha (t+\phi )-\alpha (t),\,\alpha (t+2\,\phi )-\alpha (t+\phi )\bigr \rangle . \end{aligned}$$

(3.2)

Since $\Gamma (t)$ is a regular polygon, its segments have constant length $\ell$ and two consecutive segments subtend a constant angle. In particular, this means that

$$\begin{aligned} \bigl \Vert \alpha (t+\phi )-\alpha (t)\bigr \Vert = \ell , \end{aligned}$$

$$\begin{aligned} \bigl \Vert \alpha (t+2\,\phi )-\alpha (t+\phi )\bigr \Vert = \ell \end{aligned}$$

and

$$\begin{aligned} \bigl \langle \alpha (t+\phi )-\alpha (t),\,\alpha (t+2\,\phi )-\alpha (t+\phi )\bigr \rangle \end{aligned}$$

is constant. Therefore, the expression (3.2) is constant. $\square$

Corollary 3.2

Let $\ell >0$, and let $\alpha$ be a piecewise-$\mathcal {C}^2$ $(\phi ,\ell )$-isochordal-viewed hedgehog parameterized by a support function $h\in \mathcal {C}^3$. If $\alpha$ is of constant $\phi$-width, then every p-Holditch curve of $\alpha$, $H_p$, for a chord length $\ell$ satisfies that

$$\begin{aligned} \bigl \Vert H_p(t+\phi )-H_p(t)\bigr \Vert \end{aligned}$$

is constant.

Proof

Use Proposition 2.1 to define the regular polygon $\Gamma (t)$ and then use Theorem 3.1. $\square$

See in Fig. 8 an example of a Holditch curve for a $(\phi ,\ell )$-isochordal-viewed curve of constant $\phi$-width. The constant length chord for $H_p$ given in Theorem 3.1 or Corollary 3.2 is also shown.

Fig. 8

The isochordal-viewed hedgehog given by $h(t)=\sin (5\,t)$ and $\phi =\pi /3$ and its p-Holditch curve, $H_{p}$, for $p=1/3$.

Notice that the conclusion of Theorem 3.1 does not imply that the Holditch curve of $\alpha$ is isochordal-viewed. This is because, in general, Holditch curves are not parameterized by a support function. In the next proposition, we provide a characterization of when this happens.

Proposition 3.3

Let $\ell >0$, and let $\alpha$ be a piecewise-$\mathcal {C}^2$ $(\phi ,\ell )$-isochordal-viewed hedgehog parameterized by a support function $h\in \mathcal {C}^3$. For any $p\ne 0$, the p-Holditch curve of $\alpha$ for a chord length $\ell$ is parameterized by a support function if and only if the supporting lines at $\alpha (t)$ and $\alpha (t+\phi )$ are parallel.

Proof

The condition of writing the p-Holditch curve of $\alpha$ in terms of a support function a(t) can be set as follows:

$$\begin{aligned} H_p(t)=(1-p)\,\alpha (t)+p\,\alpha (t+\phi )=a(t)\,(\cos t,\,\sin t)+b(t)\,(-\sin t,\,\cos t), \end{aligned}$$

(3.3)

where b(t) must be $a'(t)$. The equality (3.3) produces a system of two equations with two unknowns a(t) and b(t). The solution is

$$\begin{aligned} a(t)&= -p \sin (\phi )\,h'(t+\phi )+p \cos (\phi )\,h(t+\phi )-p\,h(t)+h(t),\\ b(t)&= p \cos (\phi )\,h'(t+\phi )-(p-1)\,h'(t)+p \sin (\phi )\,h(t+\phi ). \end{aligned}$$

Now, we have that

$$\begin{aligned} a'(t)-b(t) = -p \sin (\phi ) \bigl (h''(t+\phi )+h(t+\phi )\bigr ). \end{aligned}$$

Since $p\ne 0$, this can only be equal to zero for all $t\in \mathbb {S}^1$ if $\phi = \pi$, which is the limiting case where the supporting lines to $\alpha$ at $\alpha (t)$ and at $\alpha (t+\phi )$ are parallel for all $t\in \mathbb {S}^1$. $\square$

The result above can be easily related to constant width curves if we consider curves of constant $\phi$-width as a hypothesis.

Corollary 3.4

Let $\ell >0$, and let $\alpha$ be a piecewise-$\mathcal {C}^2$ $(\phi ,\ell )$-isochordal-viewed hedgehog parameterized by a support function $h\in \mathcal {C}^3$ which is also a curve of constant ${\phi }$-width. For any $p\ne 0$, the p-Holditch curve of $\alpha$ for a chord length $\ell$ is parameterized by a support function if and only if $\alpha$ is of constant width $\ell$.

Proof

It is a direct consequence from Proposition 3.3 and the fact that a“curve of $\pi$-width”corresponds to a classical constant width curve, which are examples of“$(\pi ,\ell )$-isochordal-viewed curves”(with $\ell$ being the constant width). $\square$

4 Iterated Holditch curves for an isochordal-viewed hedgehog

In this section we will see that the conclusion of Theorem 3.1 can be extended to a recursive computation of some Holditch curves thanks to a recursive computation of regular polygons starting from the one given by Proposition 2.1. This is what we are about to see in the next proposition (see Fig. 9 for a visualization in an example).

Proposition 4.1

Let . For all $t\in \mathbb {S}^1$, let $\Gamma (t)$ be a regular polygon of side length $\ell$ whose vertices lie on a closed curve $\alpha :\mathbb {S}^1\rightarrow \mathbb {R}^2$. Divide (following an orientation) each segment of $\Gamma (t)$ in the ratio $p:1-p$ and let $\Gamma _1(t)$ be the polyline obtained by joining the resulting points of these divisions (which lie on the p-Holditch curve of $\alpha$ for a chord length $\ell$). Then $\Gamma _1(t)$ is also a regular polygon and for each $t\in \mathbb {S}^1$ it has the same polygon center as $\Gamma (t)$.

Fig. 9

Illustration of a regular polygon $\Gamma _1(t)$ of side length $\tilde{\ell }$ constructed from a regular polygon $\Gamma (t)$ of side length $\ell$ and angle $\theta$.

Proof

Notice that, for any $t\in \mathbb {S}^1$, the regular polygon $\Gamma (t)$ realizes the position of the moving chord at some points of $\alpha$ when generating any of its p-Holditch curves for the chord length $\ell$. Thus, by construction, the vertices of $\Gamma _1(t)$ lie on the p-Holditch curve of $\alpha$ and $\Gamma _1(t)$ is closed.

Moreover, the length $\tilde{\ell }$ of the segments of $\Gamma _1(t)$ is constant. Indeed, if $\theta$ is the constant angle of $\Gamma (t)$, then by the cosine rule we have that

$$\begin{aligned} \tilde{\ell }=\ell \,\sqrt{p^2+(1-p)^2-2\,p\,(1-p)\cos \theta }, \end{aligned}$$

which is constant. Similarly, by simple trigonometry, the angle $\theta _1$ between two consecutive segments of $\Gamma _1(t)$ is also constant (it only depends on p, $\ell$ and $\theta$).

Thus, the closed polyline $\Gamma _1(t)$ is in fact a regular polygon. Suppose that $P_0(t)$, $P_1(t)$, ..., $P_{n-1}(t)$ are the n vertices of $\Gamma (t)$ (consider $P_{n} = P_0$). On the one hand, the polygon center c(t) of $\Gamma (t)$ can be computed as its centroid:

$$\begin{aligned} c(t)=\frac{1}{n}\,\sum _{k=0}^{n-1}P_k(t). \end{aligned}$$

On the other hand, the centroid of $\Gamma _1(t)$ is

$$\begin{aligned} \frac{1}{n}\sum _{k=0}^{n-1}\bigl ((1-p)\,P_k(t)+p\,P_{k+1}(t)\bigr ) = (1-p)\,c(t) +p\,c(t) = c(t), \end{aligned}$$

which is coincident with that of $\Gamma (t)$. $\square$

Notice that Proposition 4.1 can be applied recursively for the next regular polygon that is found at each step, so that we can find a sequence of regular polygons $\{\Gamma _k(t)\}_k$ starting from a $(\phi ,\ell )$-isochordal-viewed curve of constant $\phi$-width (with $\Gamma _0(t)$ being the one provided in Proposition 2.1).

Similarly, we can compute Holditch curves of Holditch curves easily by Theorem 3.1. At each step, the chord length $\ell _k$ changes according to Proposition 4.1 and we have a free parameter to compute a particular $p_k$-Holditch curve. Thus, we have a sequence of chord lengths $\{\ell _k\}_k$, a sequence of free parameters $\{p_k\}_k$ and the corresponding sequence $\{H^k_{p_k}\}_k$ of Holditch curves. Each regular polygon $\Gamma _k(t)$ is associated with a particular iteration $H_{p_k}^k$ of Holditch curves (see in Fig. 10 some steps of these sequences in an example).

Fig. 10

A $(\phi ,\ell )$-isochordal-viewed hedgehog of constant $\phi$-width $\alpha$ and a recursive computation of Holditch curves $H_{1/2}^k$. The curve c is the curve of the associated regular polygon centers.

From now on, along the next two results, the sequences described above will be considered following the same notation.

Lemma 4.2

Let $\{\Gamma _k(t)\}_k$ be the sequence of regular polygons $\Gamma _k(t)$ of side length $\ell _k$. If $\{p_k\}_k$ is a sequence that converges in , then the sequence of chord lengths $\{\ell _k\}_k$ is convergent to zero.

Proof

As seen in the proof of Proposition 4.1, the side length $\ell _{k+1}$ of $\Gamma _{k+1}(t)$ can be computed in terms of the side length $\ell _k$, the constant angle $\theta _k$ and the free parameter $p_k$ of the previous iteration $\Gamma _k(t)$:

$$\begin{aligned} \ell _{k+1}=\ell _k\,\sqrt{p_k^2+(1-p_k)^2-2\,p_k\,(1-p_k)\cos \theta _k}. \end{aligned}$$

(4.1)

As we already know that each $\Gamma _k(t)$ is a regular polygon with the same number of sides, we actually have $\theta _k = \theta$, where $\theta$ is the angle of the first regular polygon.

Since $\{p_k\}_k$ is convergent to some $p\in \left]0,1\right[$, we have that

$$\begin{aligned} \lim _{k\rightarrow +\infty }\frac{\ell _{k+1}}{\ell _k}=\sqrt{2\,\bigl (1+\cos (\theta )\bigr )\,p^2-2\,\bigl (1+\cos (\theta )\bigr )\,p+1}. \end{aligned}$$

The expression inside the square root is a parabola for the variable p which is always less than 1. Thus, since $\{\ell _k\}_k$ is a sequence of positive real numbers such that

$$\begin{aligned} \lim _{k\rightarrow +\infty }\frac{\ell _{k+1}}{\ell _k} < 1, \end{aligned}$$

by D’Alembert criterion, the sequence $\{\ell _k\}_k$ is convergent to zero. $\square$

As a consequence of Lemma 4.2 we have that, for each $t\in \mathbb {S}^1$, the sequence $\{\Gamma _k(t)\}_k$ is convergent to a single point (degenerated polygon):

$$\begin{aligned} c(t) = \lim _{k\rightarrow +\infty }\Gamma _k(t). \end{aligned}$$

This point is the polygon center of all the regular polygons $\Gamma _k(t)$, for $k\in \mathbb {N}$. Therefore, for each $t\in \mathbb {S}^1$,

$$\begin{aligned} \lim _{k\rightarrow +\infty }H_{p_k}^k(t) = c(t). \end{aligned}$$

We can state this as follows.

Theorem 4.3

The sequence $\{H_{p_k}^k\}_k$ of Holditch curves tends to the curve of polygon centers.

Remark 4.4

At each step k, since the parabola of Equation (4.1), namely

$$\begin{aligned} 2\,\bigl (1+\cos (\theta )\bigr )\,p_k^2-2\,\bigl (1+\cos (\theta )\bigr )\,p_k+1, \end{aligned}$$

achieves its minimum at $p_k=1/2$, faster convergence will correspond to a choice of the midpoint Holditch curve at each step.

See in Fig. 11 an example illustrating the convergence stated in Theorem 4.3, where the curve of polygon centers turns out to be a circle (this can also be seen in the example of Fig. 10).

Fig. 11

The curve of Example 2 for $k=1$ and $\phi = 2\,\pi /3$. The sequence of Holditch curves tends to the curve of polygon centers, which is a triple-traced circle of radius 1/2.

Remark 4.5

(Open problems) There are still some open questions that are interesting to answer. All the examples of isochordal-viewed hedgehogs that we have considered have some rotational symmetry. But is every isochordal-viewed curve rotationally symmetric? We have also seen in our examples that the curve of polygon centers is always a circle. Will this always be the case or further assumptions are needed to ensure it?

Finally, we want to remark that some of the results of this paper may be extended to multihedgehogs, that is, to curves which have m cooriented supporting lines in each direction (with $m\in \mathbb {Z}$). In particular, any rosette (see e.g. [5, 10] or [18]) is a multihedgehog. The interested reader to this and further questions is referred to [16] for more details.