1 Introduction

Infectious diseases are one of the threat to humanity. Due to increase in world population and mobility, pathogen transmission is easy and it is difficult to control the spread of disease. Viral transmission depends both on the interaction with host population and with the environment.

Mathematical models can project how infectious diseases progress. The model can suggest the possible outcome of an epidemic which will help agencies to take well thought measures. In 1927, Kermack and McKendrick [6] introduced a model (called SIR model) by considering a given population having three compartments. The compartments are divided into individuals in susceptible S, infected I, and removed R classes. It is very important to study infectious diseases and their possible nature of spread.

In most instances, it is presumed that infectious diseases are spread through direct contacts between individuals. But some infectious diseases can also spread through indirect contacts like contact with contaminated surface having virus on it. Transmission through the indirect contacts occurs when there is no direct physical contact between individuals. Contact occurs from a reservoir to contaminated surfaces or objects, or to vectors such as mosquitoes, flies, mites, fleas, ticks, rodents or dogs. Through many studies, it is observed that coronaviruses (including SARS-Cov-2) may persist on objects or surfaces for some hours to many days. The persistence depends on different factors (e.g., surface type, humidity or temperature of the environment). Fomites consist of both permeable and non-permeable objects or surfaces that can be contaminated with pathogenic micro-organisms and serve as a vehicle in transmission. SARS-CoV-2, the coronavirus (CoV) causing COVID-19 is creating the most severe health issues for individuals above the age of 60—with particularly fatal results for those individuals having age above 80. In the United States, 31–59% of individuals ages 75–84 diagnosed with the virus having severe symptoms due to which hospitalization is necessary, in comparison with 14–21% of confirmed patients ages between 20 and 44. These data are based on US Centers for Disease Control and Prevention (CDC) report. Therefore, it is natural to consider age structure while modeling the infectious disease transmission. The risk of transmission of infectious disease varies in different environments, for example at school, at home, at work place or in the community. Prem et al. [14] studied projected age-specific contact rates for countries in different stages in development and with different demographic structures from those studied in POLYMOD (a European Commission project), which provides validated approximations to social contact patterns when directly measured data are not available. The data plotted in Fig. 1a–d show the relation between age of individual and age of contact, i.e., number of contacts made by individuals at all locations, at home, school and work, respectively. Yellowish color on the diagonal of Fig. 1a, b shows that individuals of same age have more chances of direct contacts, so the transmission coefficient will be large for same age individuals.

Fig. 1
figure 1

Heat maps in Fig. 1a–d shows number of contacts made by individuals at all locations, homes, schools and work respectively

Full size image

From the above heat maps, it is clear that it is natural to add age structure in ordinary differential equation (ODE)-based SIR models. Therefore, after adding age structure, the ODE-based SIR models become partial differential equation (PDE) models that are more complex to analyze. There is extensive literature available on age-structured SIR models (for more details see [2, 4, 5, 7,8,9,10, 12, 13]). In [11], an epidemiological model which studies the impact of decline in population on the dynamics of infectious diseases especially childhood diseases is considered and also an example of measles in Italy is considered. Hsieh et al. [3] studied the SARS outbreak in Taiwan, using the data of daily reported cases from May 5 to June 4, 2003 to study the spread of virus. Inaba [4] discussed threshold and stability results for an age-structured SIR model, Franceschetti et al. [2] generalized the work of [4] and also considered immigration of infected individuals in all epidemiological compartments. We considered an age-structured SIR model in which individuals can also get infected due to contaminated surfaces. We also assume that the net reproduction rate of the host population is unity which also makes our model different from the model considered in [2].

Our work is divided into five sections. In Sect. 2, we formulate our age-structured SIR model. In Sect. 3, we discuss the existence of solution to our model. In Sect. 4, we discuss steady-state solutions and show that there is no disease-free steady-state solution as long as there is transmission due to indirect contacts in the environment. Last section is devoted to numerical simulation.

2 Model Formulation

Let U(a, t) be the density of individuals of age a at time t. \(\mu (a)\) and \(\beta (a)\) be age-dependent mortality and fertility rates, respectively. Let \(a_{m}\) be the maximum age which an individual can attain, i.e., the maximum life span of an individual. Then, the evolution of U(a, t) can be modeled by the following McKendrick–Von Foerster PDE with initial and boundary conditions:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial U(a,t)}{\partial t} + \frac{\partial U(a,t) }{\partial a}= - \mu (a)U(a,t) \quad (a,t) \in (0,a_{m}) \times (0,\infty ) \\ U(0,t)= \int _{0}^{a_{m}} \beta (a)U(a,t)da \quad t \in (0, \infty ) \\ U(a,0)=U_{0}(a) \quad a \in (0,a_{m}),\\ \end{array}\right. } \end{aligned}$$
(2.1)

where U(0, t) denotes the number of newborns per unit time at time t. We assume that the mortality rate \( \mu \in L_{loc}^{1}([0,a_{m}))\) with the condition \(\int _{0}^{a_{m}} \mu (a) da= + \infty \) and the fertility rate \(\beta \in L^{\infty }(0,a_{m}).\) \(e^{-\int _{0}^{a} \mu (s) \mathrm{d}s}\) indicates the proportion of individuals who are still living at age a and \(\int _{0}^{a_{m}} \beta (a)e^{-\int _{0}^{a} \mu (s) \mathrm{d}s} da\) represents the net reproduction rate. Let us assume that the net reproduction rate is 1. Therefore, steady-state solution is given by \(U(a,t)=U(a)=\beta _{0} e^{-\int _{0}^{a} \mu (\tau ) d \tau }\), where \(\beta _{0}\) is given by

$$\begin{aligned} \beta _{0}= \frac{\int _{0}^{a_{m}} U_{0}(a) da}{\int _{0}^{a_{m}} e^{-\int _{0}^{a}\mu (\tau ) d \tau } da}. \end{aligned}$$

Let S(a, t), I(a, t) and R(a, t) be the densities of susceptible, infected and recovered individuals of age a at time t. Let \({\hat{I}}(t)\) be defined by

$$\begin{aligned} {\hat{I}}(t) = \int _{0}^{a_{m}} \gamma (a) I(a,t)da, \end{aligned}$$

where \(\gamma (a)\) denotes the weight factor for age class. Here, \({\hat{I}}(t)\) is the total number of infected individuals at time t with weight factor \(\gamma \). In addition, let r(a, b) is the age-dependent transmission coefficient which describes the contact process between susceptible and infected individuals, i.e., r(a, b)S(a, t)I(b, t)dadb is the number of individuals who are susceptible and whose age lies between a and \(a+da\) and contract the disease after contact with an infected individual aged between b and \(b+db\). We assume the form of force of infection is given in the following functional form:

$$\begin{aligned} \lambda (a,t) = \int _{0}^{a_{m}} r(a,\eta ) I(\eta ,t) \mathrm{d}\eta . \end{aligned}$$

Then, the disease spread according to the following system of partial differential equations:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial S(a,t)}{\partial t} + \frac{\partial S(a,t) }{\partial a}= -\lambda (a,t)S(a,t)-c(a,{\hat{I}}(t))S(a,t) - \mu (a)S(a,t) \\ \frac{\partial I(a,t)}{\partial t} + \frac{\partial I(a,t) }{\partial a}= \lambda (a,t)S(a,t)+c(a,{\hat{I}}(t))S(a,t)-b(a) I(a,t) - \mu (a)I(a,t) \\ \frac{\partial R(a,t)}{\partial t} + \frac{\partial R(a,t) }{\partial a}= b(a)I(a,t) - \mu (a)R(a,t) \\ S(0,t)= \int _{0}^{a_{m}} \beta (a)(S(a,t)+I(a,t)+R(a,t))da, ~~ I(0,t)=0,~~ R(0,t)=0 \\ S(a,0)=S_{0}(a),~~I(a,0)=I_{0}(a)~\text {and}~ R(a,0)=R_{0}(a). \\ \end{array}\right. }\qquad \end{aligned}$$
(2.2)

Here, b(a) is the recovery rate of individuals and \(c(a,{\hat{I}}(t))\) is the proportion of individuals which are infected due to indirect contacts. This factor \(c(a,{\hat{I}}(t))\) depends on the number of infected individuals, because this proportion is directly proportional to the total number of infected individuals. Here, we are assuming that spread of disease already started and fomites are present in the environment even if the transmission coefficient r(a, b) is zero. Assume that \(b, \gamma \in L^{\infty }(0,a_{m})\) and \(r \in L^{\infty }((0,a_{m}) \times (0,a_{m}))\) and also assume that all are non-negative. [1] studied how respiratory and viral disease spread in the presence of fomites. It is observed that enveloped respiratory viruses remain viable for less time and the non-enveloped enteric viruses remain viable for longer time. They calculated the inactivation coefficients of various respiratory viruses. Figure 2 shows the respiratory virus inactivation rates \((K_{j})\). In Fig. 2, we have used the short forms flu and cov for influenza and coronavirus, respectively.

Fig. 2
figure 2

Respiratory virus inactivation rates

Full size image

We impose the following simplifying conditions on our model:

  1. (i)

    Although there may be an incubation period for some diseases, here we assume that there is no incubation period and the individuals become infected instantaneously after contact with infected individuals or fomites.

  2. (ii)

    We assume that the age zero individuals are not infected.

  3. (iii)

    The transmission coefficient r(a, b) only summarizes the contact process between susceptible and infected individuals.

  4. (iv)

    Population is in stationary demographic state.

  5. (v)

    The susceptible individuals who got infected due to contact with infected individuals have not infected due to the indirect contacts.

  6. (vi)

    We did not take into account social interventions such as hospitalization, and quarantine. Therefore, c is not dependent on infected individuals.

Let \({\overline{S}}(a,t), {\overline{I}}(a,t)\) and \({\overline{R}}(a,t)\) be defined in the following way:

$$\begin{aligned} {\overline{S}}(a,t)=\frac{S(a,t)}{U(a,t)}, {\overline{I}}(a,t)=\frac{I(a,t)}{U(a,t)}~ \text { and }~ {\overline{R}}(a,t)=\frac{R(a,t)}{U(a,t)}, \end{aligned}$$

and the force of infection is given by

$$\begin{aligned} \lambda (a,t) = \int _{0}^{a_{m}} r(a,\eta ) U(\eta ) {\overline{I}}(\eta ,t) \mathrm{d}\eta . \end{aligned}$$

Then, our new system becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial {\overline{S}}(a,t)}{\partial t} + \frac{\partial {\overline{S}}(a,t) }{\partial a}= -\lambda (a,t){\overline{S}}(a,t)-c(a,{\hat{I}}(t)){\overline{S}}(a,t) \\ \frac{\partial {\overline{I}}(a,t)}{\partial t} + \frac{\partial {\overline{I}}(a,t) }{\partial a}= \lambda (a,t){\overline{S}}(a,t)+c(a,{\hat{I}}(t)){\overline{S}}(a,t)-b(a) {\overline{I}}(a,t) \\ \frac{\partial {\overline{R}}(a,t)}{\partial t} + \frac{\partial {\overline{R}}(a,t) }{\partial a}= b(a){\overline{I}}(a,t) \\ {\overline{S}}(0,t)= 1, ~~ {\overline{I}}(0,t)=0,~~ {\overline{R}}(0,t)=0 \\ {\overline{S}}(a,0)={\overline{S}}_{0}(a),~~{\overline{I}}(a,0)={\overline{I}}_{0}(a)~\text {and}~ {\overline{R}}(a,0)={\overline{R}}_{0}(a) \\ {\overline{S}}(a,t)+{\overline{I}}(a,t)+{\overline{R}}(a,t)=1, \\ \end{array}\right. } \end{aligned}$$
(2.3)

where

$$\begin{aligned} {\hat{I}}(t) = \int _{0}^{a_{m}} \gamma (\eta ) U(\eta ) {\overline{I}}(\eta ,t) \mathrm{d}\eta . \end{aligned}$$

Therefore, new transformations reduced our system into a simpler form, i.e., boundary conditions now become constant and there is no term involving the natural mortality rate.

3 Existence of Solution

If we observe system (2.3) carefully, then it is clear that once susceptible and infected individuals are known, recovered individuals can be obtained easily so, it is enough to show the existence of solution to the following SI system instead of full SIR system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial {\overline{S}}(a,t)}{\partial t} + \frac{\partial {\overline{S}}(a,t) }{\partial a}= -\lambda (a,t){\overline{S}}(a,t)-c(a, {\hat{I}}(t)){\overline{S}}(a,t) \\ \frac{\partial {\overline{I}}(a,t)}{\partial t} + \frac{\partial {\overline{I}}(a,t) }{\partial a}= \lambda (a,t){\overline{S}}(a,t)+c(a,{\hat{I}}(t)){\overline{S}}(a,t)-b(a) {\overline{I}}(a,t) \\ {\overline{S}}(0,t)= 1, ~~ {\overline{I}}(0,t)=0. \\ \end{array}\right. } \end{aligned}$$
(3.1)

We will analyze the system (3.1) only, because force of infection does not explicitly depends on recovered individuals. Let \({\tilde{S}}(a,t)={\overline{S}}(a,t)-1, {\tilde{I}}(a,t)={\overline{I}}(a,t),\) then the system (3.1) reduces to

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial {\tilde{S}}(a,t)}{\partial t} + \frac{\partial {\tilde{S}}(a,t) }{\partial a}= -\lambda (a,t)(1+{\tilde{S}}(a,t))-c(a,{\hat{I}}(t))(1+{\tilde{S}}(a,t)) \\ \frac{\partial {\tilde{I}}(a,t)}{\partial t} + \frac{\partial {\tilde{I}}(a,t) }{\partial a}= \lambda (a,t)(1+{\tilde{S}}(a,t))+c(a,{\hat{I}}(t))(1+{\tilde{S}}(a,t))-b(a) {\tilde{I}}(a,t) \\ {\tilde{S}}(0,0147 t)= 0, ~~ {\tilde{I}}(0,t)=0. \\ \lambda (a,t) = \int _{0}^{a_{m}} r(a,\eta ) U(\eta ) {\tilde{I}}(\eta ,t) \mathrm{d}\eta . \\ \end{array}\right. }\nonumber \\ \end{aligned}$$
(3.2)

Let \(X=L^{1}(0,a_{m} ; {\mathbb {C}}^{2})\) equipped with the \(L^{1}\) norm and \({\mathcal {A}}\) be a linear operator defined as

$$\begin{aligned} ({\mathcal {A}} \xi )(a)= & {} \left( -\frac{d}{d a} \xi _{1}(a),-\frac{d}{da} \xi _{2}(a)-b(a) \xi _{2}(a)\right) \\ \text {where}~ \xi= & {} (\xi _{1}(a),\xi _{2}(a)) \in D({\mathcal {A}})\\ D({\mathcal {A}})= & {} \{ \xi = (\xi _{1},\xi _{2}) \in X~|~ \xi _{1},\xi _{2} \in AC[0,a_{m}], \xi (0)=(0,0) \}, \end{aligned}$$

where \(AC[0,a_{m}]\) is the set of absolutely continuous functions. Suppose that \(r(a,b) \in L^{\infty }((0,a_{m}) \times (0,a_{m}))\) and for \(x \in {\mathbb {R}}^{+},~c(\cdot ,x) \in L_{loc}^{1}(0,a_{m})\). In addition, for all \({\tilde{C}}>0\), there exists a constant \(L({\tilde{C}})\) such that

$$\begin{aligned} |c(a,x_{1})-c(a,x_{2})| \le L({\tilde{C}})|x_{1}-x_{2}|,~~\mathrm{if } |x_{1}|<{\tilde{C}}, |x_{2}| \le {\tilde{C}}. \end{aligned}$$
(3.3)

Let us define

$$\begin{aligned} (F \xi )(a)= & {} (-(P_{1} \xi _{2})(a)(1+\xi _{1}(a))\\&-(P_{2} \xi _{2})(a)(1+\xi _{1}(a)),(P_{1} \xi _{2})(a)(1+\xi _{1}(a))+c(a))\\&+(P_{2} \xi _{2})(a)(1+\xi _{1}(a)), ~ \xi \in X, \end{aligned}$$

where the bounded linear operator \(P_{1}, P_{2}\) are defined by

$$\begin{aligned} (P_{1} \psi )(a)= & {} \int _{0}^{a_{m}} r(a,\eta )U(\eta ) \psi (\eta ) \mathrm{d}\eta , ~ \psi \in L^{1}(0,a_{m}),\\ (P_{2} \psi )(a)= & {} c(a,{\hat{I}}),~~ {\hat{I}} = \int _{0}^{a_{m}} \gamma (\eta ) U(\eta ) \psi (\eta ) d\eta . \end{aligned}$$

Remark 3.1

If we take \(c(a,{\hat{I}}) = c(a) {\hat{I}}\), then condition (3.3) is automatically satisfied.

Now, system (3.2) can be written as an abstract semilinear Cauchy problem in Banach space X

$$\begin{aligned} \begin{aligned}&{\left\{ \begin{array}{ll} \frac{dZ(t)}{\mathrm{d}t}= {\mathcal {A}}Z(t)+F(Z(t)) \\ Z(0)=Z_{0} \in X \end{array}\right. }\\&\text {where }~ Z(t) = ({\tilde{S}}(\cdot ,t), {\tilde{I}}(\cdot ,t)) \in Z, ~ Z_{0}(a)=({\tilde{S}}_{0}(a),{\tilde{I}}_{0}(a)). \end{aligned} \end{aligned}$$
(3.4)

In the same manner as proved in [4], we can prove that \({\mathcal {A}}\) generates a \(C_{0}\) semigroup \(T(t), t \ge 0\) and F is continuously Fréchet differentiable on X.

Therefore, for each \(Z_{0} \in X\), there exists a maximal interval of existence \([0,t_{0})\) and a unique solution \(t \longrightarrow Z(t;Z_{0})\) which is continuous from \([0,t_{0})\) to X such that

$$\begin{aligned} Z(t,Z_{0})=T(t)Z_{0}+\int _{0}^{t} T(t-\sigma ) F(Z(\sigma ;Z_{0})) \mathrm{d}\sigma ~~ \forall ~ t \in [0,t_{0}]. \end{aligned}$$
(3.5)

Moreover, if \(Z_{0} \in D({\mathcal {A}}),\) then \(Z(t;Z_{0}) \in D({\mathcal {A}})\) for \(0 \le t < t_{0}\) and \(t \longrightarrow Z(t;Z_{0})\) is continuously differentiable and satisfies (3.2) on \([0,t_{0}).\)

Now, our aim is to prove the global existence and uniqueness of solution of (3.4). We will prove the existence of unique global classical solution which in turn gives the existence of unique global mild solution.

Theorem 3.2

The abstract Cauchy problem (3.4) has a unique global solution on X with initial data \(Z_{0} \in V \cup D({\mathcal {A}})\), where V is defined by

$$\begin{aligned} V = \{ ({\tilde{S}}, {\tilde{I}}) \in X~|~{\tilde{S}} \ge -1, {\tilde{I}} \ge 0 \}. \end{aligned}$$

Proof

Let

$$\begin{aligned} V_{0} = \{ ({\tilde{S}}, {\tilde{I}}) \in X~|~ -1 \le {\tilde{S}} \le 0, 0 \le {\tilde{I}} \le 1 \} . \end{aligned}$$

We will prove that after a finite time t, the mild solution enters into V and the set \(V_{0}\) is positively invariant. First, let us observe that

$$\begin{aligned} {\tilde{S}}(a,t) = {\left\{ \begin{array}{ll} \exp \left( -\int _{0}^{a} (\lambda (\xi ,t-a+\xi )+c(\xi ,{\hat{I}}(t-a+\xi )) \right) d\xi , &{} t>a \\ {\bar{S}}_{0}(a-t) \exp \left( -\int _{0}^{t}(\lambda (a-t+\xi ,\xi ) + c(a-t+\xi ,{\hat{I}}(\xi )) )d \xi \right) , &{} t<a. \end{array}\right. } \end{aligned}$$

Observe that if \({\bar{S}}_{0}(a) \ge 0,\) then \({\tilde{S}}(a,t) \ge -1\). Now, let us write the remaining problem as abstract Cauchy problem

$$\begin{aligned} \frac{d {\tilde{I}}}{\mathrm{d}t}= & {} {\mathcal {B}} {\tilde{I}}(t) + (P_{1}{\tilde{I}}(t))(1+{\tilde{S}}(t)) + (P_{2}{\tilde{I}}(t))(1+{\tilde{S}}(t)) \end{aligned}$$
(3.6)
$$\begin{aligned} {\tilde{I}}(0)= & {} {\tilde{I}}_{0}, \end{aligned}$$
(3.7)

where \({\mathcal {B}} = -\frac{d}{da} - b\) with

$$\begin{aligned}&D({\mathcal {B}}) = \{ \phi \in L^{1}(0,a_{m})~|~ \phi ~\text { is absolutely continuous function on } [0,a_{m}],\\&\phi (0)=0 \}. \end{aligned}$$

Then, we have

$$\begin{aligned} {\tilde{I}}(t) = {\tilde{T}}(t) {\tilde{I}}_{0} + \int _{0}^{t} {\tilde{T}}(t-s)[(P_{1} {\tilde{I}}(s))(1+{\tilde{S}}(s))+(P_{2}{\tilde{I}}(s))(1+{\tilde{S}}(s))]\mathrm{d}s, \end{aligned}$$

where \({\tilde{T}}(t)\) is the strongly continuous semigroup generated by the operator \({\mathcal {B}}\). Here, \({\tilde{I}}(t)>0\) if \({\tilde{S}}(t) \ge -1,~{\tilde{I}}_{0} \ge 0\) and \({\tilde{I}}(t)\) can be evaluated using monotone iteration scheme

$$\begin{aligned} {\tilde{I}}(t) = {\tilde{T}}(t) {\tilde{I}}_{0} + \int _{0}^{t} {\tilde{T}}(t-s)[(P_{1} {\tilde{I}}(0))(1+{\tilde{S}}(s))+P_{2}({\tilde{I}}(0))(1+{\tilde{S}}(s))]\mathrm{d}s + \cdots . \end{aligned}$$

Therefore, \(Z(t;Z_{0}) \in V\) for non-negative t, when \(Z_{0} \in V\). Now, let us define

$$\begin{aligned} U(t):= {\tilde{S}}(t) + {\tilde{I}}(t), \end{aligned}$$

then it satisfies

$$\begin{aligned} \frac{\mathrm{d}U(t)}{\mathrm{d}t} = {\mathcal {C}}U(t) - b U(t),~~U(0) = {\tilde{S}}_{0}+{\tilde{I}}_{0}, \end{aligned}$$

where

$$\begin{aligned} {\mathcal {C}} = -\frac{d}{da},~D({\mathcal {C}}) = D({\mathcal {B}}). \end{aligned}$$

Then, we have

$$\begin{aligned} U(t) = W(t)U(0) - \int _{0}^{t} W(t-s)b {\tilde{I}}(s) \mathrm{d}s, \end{aligned}$$

where W(t) is the positive strongly continuous translation semigroup with the generator \({\mathcal {C}}\). Since W(t) is nilpotent semigroup, therefore, we have

$$\begin{aligned} U(t)a \le {\tilde{S}}_{0}(a-t) + {\tilde{I}}_{0}(a-t),~a-t>0 \end{aligned}$$

and \(U(t) \le 0\) for \(t \ge a_{m},\) which shows that \(Z(t;z_{0}) \in V_{0}\) for \(Z_{0} \in V_{0}\) for all non-negative t. Therefore, the norm of local solution \(Z(t,Z_{0}),~Z_{0} \in V\) is finite as far as it is defined, which gives the existence of unique global mild solution. \(\square \)

4 Steady-State Solutions

In this section, we are choosing \(c(a,{\hat{I}}(t))=c(a)\). The possible reason is that since we do not know how many infected are coming into contact with susceptible, we can assume this as a constant rate.

In addition, the calculation of \(c(a, {\hat{I}}(t))\) is difficult, because not all new infections are reported, and it is often difficult to know how many susceptibles were exposed. However, \(\lambda \) can be calculated for an infectious disease in an endemic state if homogeneous mixing of the population and a rectangular population distribution (such as that generally found in developed countries) is assumed. In this case, \(\lambda \) is given by \(\lambda =\frac{1}{A}\), where A is the average age of infection. In other words, A is the average time spent in the susceptible group before becoming infected. The rate of becoming infected \((\lambda )\) is, therefore, \({\frac{1}{A}}\) (since rate is 1/time). The advantage of this method of calculating \(\lambda \) is that data on the average age of infection are very easily obtainable, even if not all cases of the disease are reported. In addition, in the absence of social interventions such as quarantine, we can assume \(c(a,{\hat{I}}(t)) = c(a).\) Therefore, our model in steady state can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d {\overline{S}}(a) }{da}= -\lambda (a){\overline{S}}(a)-c(a){\overline{S}}(a) \\ \frac{d {\overline{I}}(a) }{da}= \lambda (a){\overline{S}}(a)+c(a){\overline{S}}(a)-b(a) {\overline{I}}(a)\\ {\overline{S}}(0)= 1, ~~ {\overline{I}}(0)=0\\ \end{array}\right. } \end{aligned}$$
(4.1)

with \( \lambda (a) = \int _{0}^{a_{m}} r(a,\eta ) U(\eta ){\overline{I}}(\eta ) \mathrm{d}\eta \).

Steady-state solution can be obtained as

$$\begin{aligned} {\overline{S}}(a)= & {} \exp \left( -\int _{0}^{a} (\lambda (\sigma )+c(\sigma )) \mathrm{d}\sigma \right) \\ {\overline{I}}(a)= & {} \int _{0}^{a} \exp \left( -\int _{\sigma }^{a} b(\eta ) \mathrm{d}\eta \right) (\lambda (\sigma )+c(\sigma )) \exp \left( -\int _{0}^{\sigma } (\lambda (\eta )+c(\eta )) \mathrm{d}\eta \right) \mathrm{d}\sigma . \end{aligned}$$

The force of infection depends on the number of infected individuals which, in turn depends on the proportion of individuals getting infected due to indirect contacts (steady-state solution shows this). Therefore, force of infection will automatically take care of fomites present in the environment.

The force of infection is given by

$$\begin{aligned} \lambda (a)= & {} \int _{0}^{a_{m}} r(a,\zeta ) U(\zeta ){\overline{I}}(\zeta ) d \zeta \end{aligned}$$
(4.2)
$$\begin{aligned}= & {} \int _{0}^{a_{m}} r(a,\zeta )U(\zeta ) \int _{0}^{\zeta } \exp \left( -\int _{\sigma }^{\zeta } b(\eta ) \mathrm{d}\eta \right) (\lambda (\sigma )\nonumber \\&+c(\sigma )) \exp \left( -\int _{0}^{\sigma }(\lambda (\eta )+c(\eta )) \mathrm{d}\eta \right) \mathrm{d}\sigma d \zeta . \nonumber \\= & {} \int _{0}^{a_{m}} \phi (a,\sigma ) (\lambda (\sigma )+c(\sigma )) \exp \left( -\int _{0}^{\sigma }(\lambda (\eta )\nonumber \right. \\&\left. +c(\eta )) \mathrm{d}\eta \right) \mathrm{d}\sigma \end{aligned}$$
(4.3)
$$\begin{aligned} \text {where }~ \phi (a,\sigma )= & {} \int _{\sigma }^{a_{m}} r(a,\zeta )U(\zeta ) \exp \left( -\int _{\sigma }^{\zeta } b(\eta ) \mathrm{d}\eta \right) d \zeta \end{aligned}$$
(4.4)

Using (4.2), we can get the following estimate:

$$\begin{aligned} | \lambda (a) | \le U \Vert r \Vert _{\infty } \Vert {\overline{I}} \Vert _{1} \end{aligned}$$

where \(\Vert \cdot \Vert _{\infty }\) and \(\Vert \cdot \Vert _{1}\) are the \(L^{\infty }\) and \(L^{1}\) norms, respectively, and U is the total population.

$$\begin{aligned} \text {Therefore, }~ \lambda \in L^{\infty }(0,a_{m}). \end{aligned}$$

It is clear that there is no disease-free equilibrium as long as there is transmission due to indirect contacts. That means if there are fomites present in the environment contaminated with pathogenic micro-organisms, disease still can spread without direct contact between susceptible and infected individuals.

On Banach space \(E=L^{1}(0,a_{m})\), with positive cone \(E_{+}= \{ \psi \in E ~|~ \psi \ge 0 ~ a.e. \},\) let us define

$$\begin{aligned} \Phi (\psi )(a) = \int _{0}^{a_{m}} \phi (a,\sigma ) (\psi (\sigma )+c(\sigma )) \exp \left( -\int _{0}^{\sigma }(\psi (\eta )+c(\eta )) \mathrm{d}\eta \right) \mathrm{d}\sigma \nonumber \\ \end{aligned}$$
(4.5)

Suppose that we have the following assumptions:

  1. (A1)

    \(r(\cdot ,\cdot )\) satisfies \( \lim _{h \longrightarrow 0} \int _{0}^{a_{m}} \Vert r(a+h,s) - r(a,s) \Vert da = 0 \) uniformly for \(s \in {\mathbb {R}}\) with \(r(\cdot ,\cdot )\) extended by defining \( r(a,s) = 0\) for a.e. \(a,s \in (-\infty , 0) \cup (a_{m}, \infty ).\)

  2. (A2)

    There exist \(m >0, 0< \alpha < a_{m}\) such that \(r(a,b) \ge m\) for a.e. \((a,b) \in (0,a_{m}) \times (a_{m}-\alpha , a_{m})\).

  3. (A3)

    There exist \(a_{1},a_{2}\) satisfying \(0 \le a_{1} < a_{2} \le a_{m}\) such that \( c(a) >0 \) a.e. \(a \in (a_{1},a_{2})\).

Observe that

$$\begin{aligned} \Phi (0)(a) = \int _{0}^{a_{m}} \phi (a,\sigma ) \exp \left( - \int _{0}^{\sigma }c(\eta ) \mathrm{d}\eta \right) c(\sigma ) \mathrm{d}\sigma . \end{aligned}$$
(4.6)

Since force of infection is non-negative, we have

$$\begin{aligned} \lambda (a) \ge \Phi (0)(a) ~~ \text {a.e.}~ a \in (0,a_{m}) \end{aligned}$$

and because of assumption (A2), we have \( \Phi (0)(a) >0 \). Now, we will prove an important theorem which will help us to show the existence of fixed point to (4.5).

Theorem 4.1

Let \({\mathcal {D}} \!=\! \{ \psi \in L_{+}^{1}(0,a_{m})~|~ \Vert \psi \Vert _{1} \!\le \! M,~\text {M is a positive constant} \} \) and suppose that the assumptions (A1)–(A3) hold, then

  1. (a)

    \({\mathcal {D}}\) is bounded, closed, convex and also \(\Phi ({\mathcal {D}}) \subseteq {\mathcal {D}}\).

  2. (b)

    \(\Phi \) is completely continuous.

Hence, Schauder’s principle gives existence of fixed point of (4.5).

Proof

Boundedness of set \({\mathcal {D}}\) is clear and also for any \(\psi _{1},\psi _{2} \in {\mathcal {D}}, 0 \le p \le 1\) we have

$$\begin{aligned} p \psi _{1} + (1-p) \psi _{2} \in {\mathcal {D}}. \end{aligned}$$

Closedness also follows from the definition of \({\mathcal {D}}\). Now, we will show that \( \Phi ({\mathcal {D}}) \subseteq {\mathcal {D}}\).

$$\begin{aligned} \Phi (\psi )(a)\le & {} \Vert \phi \Vert _{\infty } \int _{0}^{a_{m}} (\psi (\sigma )+c(\sigma )) \exp \left( -\int _{0}^{\sigma }(\psi (\eta )+c(\eta )) \mathrm{d}\eta \right) \mathrm{d}\sigma \\\le & {} M_{1} \Vert \phi \Vert _{\infty } \Vert c \Vert _{\infty } \int _{0}^{a_{m}} \exp \left( -\int _{0}^{a_{m}} \psi (\eta ) \mathrm{d}\eta \right) \mathrm{d}\sigma \\&+ M_{1} \Vert \phi \Vert _{\infty }\int _{0}^{a_{m}} \psi (\sigma ) \exp \left( -\int _{0}^{a_{m}} \psi (\eta ) \mathrm{d}\eta \right) \mathrm{d}\sigma \\= & {} M_{1} \Vert \phi \Vert _{\infty } \Vert c \Vert _{\infty } \int _{0}^{a_{m}} \exp \left( -\int _{0}^{a_{m}} \psi (\eta ) \mathrm{d}\eta \right) \mathrm{d}\sigma \\&+M_{1} \Vert \phi \Vert _{\infty } \left[ 1- \exp \left( - \int _{0}^{a_{m}} \psi (s) \mathrm{d}s \right) \right] \end{aligned}$$

where \(M_{1}\) is an upper bound on \(\exp \left( -\int _{0}^{\sigma } c(\eta ) \mathrm{d}\eta \right) \). Now , using the fact that \( | \psi |_{1} \le M\), we can easily prove that

$$\begin{aligned} | \Phi (\psi )(a) |_{1} \le M \end{aligned}$$

for some generic constant M. Now,

$$\begin{aligned}&(\Phi (\varphi _{1}))(a)-(\Phi (\varphi _{1}))(a)\nonumber \\&\quad = \int _{0}^{a_{m}} \left[ \varphi _{1} e^{-\int _{0}^{\sigma } \varphi _{1}(\eta ) \mathrm{d}\eta } - \varphi _{2} e^{-\int _{0}^{\sigma } \varphi _{2}(\eta ) \mathrm{d}\eta } \right] \phi (a,\sigma ) e^{-\int _{0}^{\sigma }c(\eta ) \mathrm{d}\eta } \mathrm{d}\sigma \nonumber \\&\qquad + \int _{0}^{a_{m}} \left[ e^{-\int _{0}^{\sigma } \varphi _{1} (\eta ) \mathrm{d}\eta } - e^{-\int _{0}^{\sigma } \varphi _{2}(\eta ) \mathrm{d}\eta } \right] \phi (a,\sigma ) e^{-\int _{0}^{\sigma }c(\eta ) \mathrm{d}\eta } \mathrm{d}\sigma . \end{aligned}$$
(4.7)

Let us first estimate the first integral as follows:

$$\begin{aligned}&\left| \int _{0}^{a_{m}} \left[ \varphi _{1} e^{-\int _{0}^{\sigma } \varphi _{1}(\eta ) \mathrm{d}\eta } - \varphi _{2} e^{-\int _{0}^{\sigma } \varphi _{2}(\eta ) \mathrm{d}\eta } \right] \phi (a,\sigma ) e^{-\int _{0}^{\sigma }c(\eta ) \mathrm{d}\eta } \mathrm{d}\sigma \right| \\&\quad \le \Vert \phi \Vert _{\infty } M_{1} \left[ e^{-\int _{0}^{a_{m}} \varphi _{2}(\eta ) \mathrm{d}\eta } -1 - e^{-\int _{0}^{a_{m}} \varphi _{1}(\eta ) \mathrm{d}\eta } +1 \right] \\&\quad = M_{1} \Vert \phi \Vert _{\infty } \left( e^{-\Vert \varphi _{2} \Vert _{1}} - e^{- \Vert \varphi _{1} \Vert _{1}} \right) \le M_{1} \Vert \phi \Vert _{\infty } \Vert \varphi _{2} - \varphi _{1} \Vert _{1} \le M \Vert \varphi _{2} - \varphi _{1} \Vert _{1} \end{aligned}$$

where M is a generic constant. Similarly,

$$\begin{aligned}&\left| \int _{0}^{a_{m}} \left[ e^{-\int _{0}^{\sigma } \varphi _{1} (\eta ) \mathrm{d}\eta } - e^{-\int _{0}^{\sigma } \varphi _{2}(\eta ) \mathrm{d}\eta } \right] \phi (a,\sigma ) e^{-\int _{0}^{\sigma }c(\eta ) \mathrm{d}\eta } \mathrm{d}\sigma \right| \\&\quad \le \!\! M_{1} \Vert \phi \Vert _{\infty } \int _{0}^{a_{m}} \left[ e^{\!-\!\int _{0}^{a_{m}} \varphi _{1} (\eta ) \mathrm{d}\eta } e^{\int _{\sigma }^{a_{m}} \varphi _{1} (\eta ) \mathrm{d}\eta }\! -\! e^{-\!\int _{0}^{a_{m}} \varphi _{2} (\eta ) \mathrm{d}\eta } e^{\int _{\sigma }^{a_{m}} \varphi _{2} (\eta ) \mathrm{d}\eta } \right] \mathrm{d}\sigma \\&\quad = M_{1} \Vert \phi \Vert _{\infty } \int _{0}^{a_{m}} \left[ e^{-\Vert \varphi _{1} \Vert _{1}} e^{\int _{\sigma }^{a_{m}} \varphi _{1}(\eta ) \mathrm{d}\eta } - e^{-\Vert \varphi _{2} \Vert _{1}} e^{\int _{\sigma }^{a_{m}} \varphi _{2} (\eta ) \mathrm{d}\eta } \right] \mathrm{d}\sigma \\&\quad \le M \left( e^{\Vert \varphi _{1} \Vert }-e^{\Vert \varphi _{2} \Vert } \right) \le M \Vert \varphi _{2}-\varphi _{1} \Vert _{1} \end{aligned}$$

which proves the continuity of \(\Phi \).

Now, we will prove that \(\Phi \) is a compact operator, so let us define \(T_{1}, T_{2} : L_{+}^{1}(0,a_{m}) \longrightarrow L_{+}^{1}(0,a_{m})\) by

$$\begin{aligned} T_{1}(\psi )(a)= & {} \int _{0}^{a_{m}} \psi (\sigma ) k_{1}(a,\sigma ) \mathrm{d}\sigma \end{aligned}$$
(4.8)
$$\begin{aligned} T_{2}(\psi )(a)= & {} \int _{0}^{a_{m}} \psi (\sigma ) k_{2}(a,\sigma ) \mathrm{d}\sigma \end{aligned}$$
(4.9)
$$\begin{aligned} k_{1}(a,\sigma )= & {} \phi (a,\sigma ) \exp \left( -\int _{0}^{\sigma } c(\eta ) d\eta \right) ,~ k_{2}(a,\sigma )\nonumber \\= & {} \phi (a,\sigma ) c(\sigma ) \exp \left( -\int _{0}^{\sigma } c(\eta ) d\eta \right) . \end{aligned}$$
(4.10)

The operators \( T_{1} , T_{2} \) are linear, continuous and positive. By applying Riesz–Fréchet–Kolmogorov theorem on compactness in \( L^{1} \), we can conclude that \( T_{1}, T_{2} \) are compact operators. Now, let us define the nonlinear operators \(F_{1}, F_{2} : L_{+}^{1}(0,a_{m}) \longrightarrow L_{+}^{1}(0,a_{m})\) by

$$\begin{aligned} F_{1}(\psi )(\sigma )= & {} \psi (\sigma ) \exp \left( -\int _{0}^{\sigma } \psi (\tau ) d \tau \right) \end{aligned}$$
(4.11)
$$\begin{aligned} F_{2}(\psi )(\sigma )= & {} \exp \left( -\int _{0}^{\sigma } \psi (\tau ) d \tau \right) . \end{aligned}$$
(4.12)

Here, \(F_{1}, F_{2}\) are continuous and hence \(T \circ F_{1},T \circ F_{2} \) are compact operators in \(L_{+}^{1}(0,a_{m})\).

Therefore, \(\Phi = T \circ F_{1}+T \circ F_{2} \) is compact operator. Hence, Schauder’s principle gives existence of fixed point of (4.5). \(\square \)

Let \(T = \Phi ^{'}(0)\) denote the Fréchet derivative of \(\Phi \) at 0, i.e.,

$$\begin{aligned} T(\psi )(a)= & {} \int _{0}^{a_{m}} \phi (a,\sigma ) \psi (\sigma ) \exp \left( -\int _{0}^{\sigma }c(\eta ) \mathrm{d}\eta \right) \mathrm{d}\sigma ~~ \text {for}~~ a\\\in & {} (0,a_{m}), \psi \in L^{1}(0,a_{m}). \end{aligned}$$

Clearly, T is a positive linear, continuous and also compact operator. Let us define

$$\begin{aligned} T_{0}(\psi )(a)= & {} \int _{0}^{a_{m}} \phi (a,\sigma ) \psi (\sigma ) \mathrm{d}\sigma \end{aligned}$$
(4.13)
$$\begin{aligned} T_{n}(\psi )(a)= & {} \int _{0}^{a_{m}} \phi (a,\sigma ) \psi (\sigma ) \exp \left( -\int _{0}^{\sigma } c_{n}(\eta ) \mathrm{d}\eta \right) \mathrm{d}\sigma \end{aligned}$$
(4.14)

where \(c_{n}\) is the sequence of the proportion of individuals infected due to indirect contacts. The spectral radius \((\rho (T))\) of the operator T plays an important role in deciding the nature of equilibrium solutions, i.e., whether disease-free equilibrium solution exists or not. In our case if there is a proportion of individuals who are infected due to fomites, disease-free equilibrium point will not exists. Our aim is to prove the following theorem:

Theorem 4.2

Let \(T_{0}\) be as defined in (4.13) and \(\Phi _{n}\) be analogous to \(\Phi \) in which c is replaced by \(c_{n}\).

  1. (a)

    If the spectral radius \(\rho (T_{0}) \le 1 \), then the sequence \(\{ \psi _{n} \}\) of fixed points of \(\Phi _{n}\) converges to zero.

  2. (b)

    If the spectral radius of \(T_{0}\) is larger than 1, then \(\exists \gamma >0 \) such that \(\Vert \psi _{n} \Vert \ge \gamma ~ \forall n \in {\mathbb {N}}.\)

Our aim is also to prove that

$$\begin{aligned} \lim _{n \rightarrow \infty } \rho (T_{n}) = \rho (T_{0}) \end{aligned}$$

which gives dependence of force of infection on \(c_{n}\). Before proving the above theorem, we will prove some lemmas and also state some theorems.

Definition 4.3

Let \(E_{+} \subset E\) be a cone in the Banach space E, then the cone \(E_{+}\) is called total if the following set:

$$\begin{aligned} \{ f - g : f,g \in E_{+} \} \end{aligned}$$

is dense in the Banach space E.

Theorem 4.4

(Krein-Rutman 1948) Let E be a real Banach space and \(E_{+}\) be total order cone in E. Let \({\mathbb {A}} : E \longrightarrow E\) be positive linear and compact operator w.r.t. \(E_{+}\) and also \(\rho ({\mathbb {A}}) >0\). Then, \(\rho ({\mathbb {A}})\) is an eigenvalue of \({\mathbb {A}}\) and \({\mathbb {A}}^{*}\) with eigenvectors in \(E_{+}\) and \(E_{+}^{*}\), respectively.

In SIR model without fomites the transmission coefficient c, Inaba [4] proved the following results:

Theorem 4.5

([4] Proposition 4.6). Let T be the Fréchet derivative of \(\Phi \) at 0

  1. (a)

    If the spectral radius \(\rho (T) \le 1\), then there is a disease-free fixed point \(\psi =0\) to the operator \(\Phi \).

  2. (b)

    If the spectral radius \(\rho (T) >1\), then there exist at least one nonzero fixed point of \(\Phi \).

Theorem 4.6

([15] Theorem V6.6). Let \( E= L^{p}(\mu ) \), \(p \in [1,\infty ]\) and \((Z,{\mathcal {S}},\mu )\) be a \(\sigma -\) finite measure space. Suppose \({\mathbb {A}} \in {\mathcal {L}}(E)\) is defined by

$$\begin{aligned} {\mathbb {A}} g(t) = \int {\mathcal {K}}(s,t)g(s) d \mu (s),~ g \in L^{p}(\mu ), \end{aligned}$$

non-negative \({\mathcal {K}}\) is \({\mathcal {S}} \times {\mathcal {S}}\) measurable kernel which satisfy the following assumptions:

  1. (a)

    Some power of \({\mathbb {A}}\) is compact.

  2. (b)

    \(C \in {\mathcal {S}}\) and \(\mu (C)> 0, \mu (Z \setminus C) >0 \)

    $$\begin{aligned} \implies \int _{Z \setminus C} \int _{C} {\mathcal {K}}(s,t) d \mu (s) d \mu (t) >0. \end{aligned}$$

Then, \(\rho ({\mathbb {A}}) > 0\) is an eigenvalue of \({\mathbb {A}}\) with a unique normalized eigen function g satisfying \(g(C) >0 ~ \mu \)-a.e. Moreover, if \({\mathcal {K}}(s,t) >0~ \mu \otimes \mu \)-a.e, then every other eigenvalue \(\lambda \) of \({\mathbb {A}}\) has the bound \(| \lambda | < \rho ({\mathbb {A}}).\)

Let \( \{ c_{n} \} \) be a sequence in \(L_{+}^{\infty }(0,a_{m})\) such that \( c_{n}(a)\longrightarrow 0\) as \( n \longrightarrow \infty \) a.e. \(a \in (0,a_{m})\), i.e., proportion of individuals who are susceptible to fomite infection are becoming less and \(\Phi _{0}\) is defined as in (4.5) with \(c=0\).

Proposition 4.7

There exist a converging subsequence \(\{ \psi _{n_{k}} \}\) of \(\{ \psi _{n} \}\) such that if \( \psi = \lim _{k \rightarrow \infty } \psi _{n_{k}} \), then \(\psi \) is the fixed point of \(\Phi _{0}\).

Proof

Since \(\Phi _{0}\) is compact and \(0 \le \Vert \psi _{n} \Vert \le M, ~ \exists \) a converging subsequence \(\{ \Phi _{0} (\psi _{n_{k}}) \}\) and let

$$\begin{aligned} \psi = \lim _{k \rightarrow \infty } \Phi _{0} (\psi _{n_{k}}). \end{aligned}$$

Since

$$\begin{aligned}&\Phi _{n_{k}} (\psi _{n_{k}})-\Phi _{0} (\psi _{n_{k}})= \int _{0}^{a_{m}} \phi (a,\sigma ) \psi (\sigma ) \exp \left( -\int _{0}^{\sigma }c_{n_{k}}(\eta ) \mathrm{d}\eta \right) \mathrm{d}\sigma \\&\qquad - \int _{0}^{a_{m}} \phi (a,\sigma ) \psi (\sigma ) \mathrm{d}\sigma \\&\quad = \int _{0}^{a_{m}} \phi (a,\sigma ) \psi (\sigma ) \left[ \exp \left( -\int _{0}^{\sigma }c_{n_{k}}(\eta ) \mathrm{d}\eta \right) -1 \right] \mathrm{d}\sigma \\&\qquad \text {because}~ \lim _{n \rightarrow \infty } c_{n}(a) =0 ~ a.e. ~ a \in (0,a_{m}),\\&\qquad \text {we have} ~ \lim _{k \rightarrow \infty } \left[ \Phi _{n_{k}} (\psi _{n_{k}})-\Phi _{0} (\psi _{n_{k}}) \right] =0.\\&\qquad \text {Therefore,}~ \lim _{k \rightarrow \infty } \psi _{n_{k}} = \lim _{k \rightarrow \infty } \Phi _{n_{k}}(\psi _{n_{k}})\\&\quad = \lim _{k \rightarrow \infty } \left[ \Phi _{0} (\psi _{n_{k}}) + \Phi _{n_{k}} (\psi _{n_{k}})-\Phi _{0} (\psi _{n_{k}}) \right] = \psi . \end{aligned}$$

Since \(\Phi _{0}\) is continuous, we have

$$\begin{aligned} \lim _{k \rightarrow \infty } \Phi _{0} (\psi _{n_{k}}) = \Phi _{0}(\psi ) = \psi \end{aligned}$$

which proves that

$$\begin{aligned} \Phi _{0}(\psi ) = \psi . \end{aligned}$$

\(\square \)

Lemma 4.8

Suppose \(T_{0}\) be as defined in (4.13), then \(\rho (T_{0})\) is an eigenvalue of both \(T_{0}\) and \(T_{0}^{*}\) with unique strictly positive normalized eigenvectors \(\psi \) and f, respectively.

Proof

We know that

$$\begin{aligned} T_{0}(\psi )(a) = \int _{0}^{a_{m}} \phi (a,\eta ) \psi (\eta ) \mathrm{d}\eta \end{aligned}$$

and is a compact operator by Theorem 4.1. Comparing \(T_{0}\) with \({\mathbb {A}}\), conditions of Theorem 4.6 are satisfied, and therefore, \(\rho (T_{0}) >0\) is the only eigenvalue of \(T_{0}\) with a unique normalized eigenvector \(\psi \in L_{+}^{1}(0,a_{m})\), satisfying \(\psi (a) > 0 ~ a.e. \) and every other eigenvalue \(\lambda \) of \(T_{0}\) satisfy \( | \lambda | < \rho (T_{0})\). In addition, \(T_{0}\) and \(T_{0}^{*}\) both have the same nonzero eigenvalues with same multiplicities. Since \(\rho (T_{0})\) is the only eigenvalue of \(T_{0}\) with a unique normalized eigenvector \(\psi \), \(\rho (T_{0})\) is also an algebraically simple eigenvalue of \(T_{0}^{*}\) with unique normalized eigen function f. Now our task is to prove that eigen function f is strictly positive. Suppose function \({\hat{f}} \in L_{+}^{\infty } \setminus \{0\}\) representing the functional f be defined as

$$\begin{aligned} \langle f,\psi \rangle= & {} \int _{0}^{a_{m}} {\hat{f}}(\eta ) \psi (\eta ) \mathrm{d}\eta ~~ \forall \psi \in L^{1}(0,a_{m}).\\ \text {Now},~ T_{0}^{*}(\varphi )(a)= & {} \int _{0}^{a_{m}} \varphi (\eta ) \phi (\eta ,a) \mathrm{d}\eta ~~ \forall \varphi \in L^{\infty }(0,a_{m}), \end{aligned}$$

there exist a function \(g : [0,a_{m}] \longrightarrow {\mathbb {R}}\) which is continuous and \(g(a)>0 ~~ \forall a \in [0,a_{m})\) and vanishes at \(a_{m}\) (because of assumption (A2)) such that \(\phi (\eta ,a) \ge g(a) ~~ a.e.~ \eta ,a \in (0,a_{m}). \)

$$\begin{aligned} \text {Then},~ {\hat{f}}(a) = \frac{1}{\rho (T_{0})} T_{0}^{*}({\hat{f}})(a) \ge \frac{1}{\rho (T_{0})} g(a) \int _{0}^{a_{m}} {\hat{f}}(\eta ) \mathrm{d}\eta >0 \end{aligned}$$

Therefore, f is strictly positive as \({\hat{f}} \in L_{+}^{\infty }(0,a_{m}) \setminus \{0\}\). \(\square \)

Lemma 4.9

Let \(T_{0}\) and \(T_{n}\) be as defined in (4.13) and (4.14), respectively. Then,

$$\begin{aligned} \lim _{n \rightarrow \infty }\rho (T_{n}) = \rho (T_{0}) ~ \text {and}~ \rho (T_{n}) \ge \rho (T_{0})~ \forall n. \end{aligned}$$

Proof

Clearly, \(T_{n} \longrightarrow T_{0} \) uniformly. Since \(T_{0}\) and \(T_{n}\) are compact operators and \(\rho (T_{0})\) and \(\rho (T_{n})\) are simple eigenvalues of \(T_{0}\) and \(T_{n}\), respectively, we have the conclusion of our lemma. \(\square \)

Now, we are ready to prove our Theorem 4.2.

Proof

We know that any converging subsequence \(\{\psi _{n_{k}}\}\) of \(\{ \psi _{n} \}\) converges to \(\psi \), the fixed point of \(\Phi _{0}\). By Theorem 4.5, for \(\rho (T_{0}) \le 1, \Phi _{0}\) has only one fixed point which is 0. Therefore, every convergent subsequence of \(\{\psi _{n}\}\) converges to zero, i.e., the sequence \(\{\psi _{n} \}\) converges to zero. Now, we will prove the part (b) of the theorem.

Given \(\rho (T_{0}) > 1\), by lemma 4.9 we have \( \rho (T_{n}) >1 ~~ \forall n .\)

Let \( f_{n} \in (L_{+}^{1}(0,a_{m}))^{*} \setminus \{0\} \) be the strictly positive eigenvector of \(T_{n}^{*}\) with eigenvalue \(\rho (T_{n})\). Then, for all n, we have

$$\begin{aligned} \langle f_{n},\psi _{n} \rangle= & {} \langle f_{n},\Phi _{n} \psi _{n} \rangle ~=~ \langle f_{n}, {\bar{\Phi }}_{n} \psi _{n}+u_{n} \rangle \end{aligned}$$

where \({\bar{\Phi }}_{n} = \Phi _{n}-u_{n}\) and \(u_{n}\) is defined by integral on R.H.S. of (4.6) with c replaced by \(c_{n}\).

Observe that

$$\begin{aligned} \exp (-\Vert \psi \Vert _{1}) T_{0} \psi \le {\bar{\Phi }} \psi \le T_{0} \psi ~~~ \forall \psi \in L_{+}^{1}(0,a_{m}) \end{aligned}$$

Therefore,

$$\begin{aligned} \langle f_{n},\psi _{n} \rangle\ge & {} \langle f_{n},\exp (-\Vert \psi _{n} \Vert _{1}) T_{n} \psi _{n}+u_{n} \rangle > \langle f_{n},\exp (-\Vert \psi _{n} \Vert _{1}) T_{n} \psi _{n} \rangle \\= & {} \exp (-\Vert \psi _{n} \Vert _{1}) \langle T_{n}^{*}f_{n},\psi _{n} \rangle = \exp (-\Vert \psi _{n} \Vert _{1}) \rho (T_{n}) \langle f_{n},\psi _{n} \rangle \end{aligned}$$

which implies

$$\begin{aligned}&\exp (-\Vert \psi _{n} \Vert _{1}) \rho (T_{n}) <1~~ \forall n,\\&i.e., ~~ \Vert \psi _{n} \Vert _{1}> \log (\rho (T_{n})) \ge \log (\rho (T_{0}))\\&\text {choose}~~ \gamma = \log (\rho (T_{0})) >0 \end{aligned}$$

then the conclusion of our theorem holds. \(\square \)

5 Numerical Simulation

We applied finite-difference scheme to solve our model numerically. It is assumed that r(a, b) is of the form \(k_{1}(a)k_{2}(b)\) and \(a_{m}\) is taken 60 Years. We take initial age distributions of the following form

$$\begin{aligned} S_{0}(a)= & {} \exp (-0.09a) + 0.7(\sin (0.05a))^2\\ I_{0}(a)= & {} 0.0001 \exp (-a^2) + 0.09(\sin (0.05a))^2\\ R_{0}(a)= & {} 0.001\exp (-0.05a) + 0.1(\sin (0.055a))^2 . \end{aligned}$$

Age-dependent mortality rate is taken as \(\mu (a) = \frac{1}{0.001+a}\) and recovery rate is taken as \(\frac{1}{\exp (a)+1}\). Other age-dependent functions are

$$\begin{aligned} \beta (a) = \frac{a}{a+80},~k_{1}(a) = k_{2}(a) = \exp (-a). \end{aligned}$$
Fig. 3
figure 3

c(a) is taken as zero in (a) and \(\frac{1}{400+a}\) in (b)

Full size image

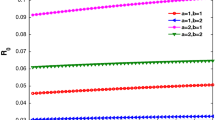
From Fig. 3a, b, it is clear that c(a) affect the density of infected individuals. For next two plots Fig. 4a and Fig. 4b, we take c(a) as

$$\begin{aligned} c(a) = {\left\{ \begin{array}{ll} 0, &{} 0 \le a \le 20 \\ \frac{1}{20+a}, &{} 20 < a \le 60 \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} c(a) = {\left\{ \begin{array}{ll} 0, &{} 0 \le a \le 20 \\ \frac{1}{a}, &{} 20 < a \le 60 \end{array}\right. }, \end{aligned}$$

respectively. We are assuming that the individuals with age between 20 and 60 are highly susceptible to infection due to indirect contacts. This assumption makes sense because most of the individuals in working class lies in this age group. Especially, front-line workers lie in this age class (Fig. 4).

Fig. 4
figure 4

The figure depicts the effect of c(a), the peak is attained at a higher value in the age interval (20, 60]

Full size image

It is clear that the peak will be attained at higher value as long as there is infection through indirect contacts.

6 Discussion

The figures on data related to interaction show that the age plays a crucial role in SARS diseases and especially in COVID-19 infection as well as in recovery. Therefore, we have studied an age-structured SIR model in which susceptible individuals not only get infected due to direct contact with infected person, but can also get infected due to indirect contacts. We proved that there is no disease-free equilibrium as long as there is transmission due to indirect contacts in the environment. That means for instance if there are fomites present in the environment contaminated with pathogenic micro-organisms, disease still can spread without direct contact between susceptible and infected individuals. Therefore, removing fomites present on the surfaces is one of the effective measure to slow the infection. Hence sanitization of surfaces and proper care to front-line workers will help to fight with such diseases. Main idea in this work is to study the role of indirect contacts in the dynamics of infectious diseases.