TbGAL: A Tensor-Based Library for Geometric Algebra

Abstract

Geometric algebra is a powerful mathematical framework that allows us to use geometric entities (encoded by blades) and orthogonal transformations (encoded by versors) as primitives and operate on them directly. In this work, we present a high-level C++ library for geometric algebra. By manipulating blades and versors decomposed as vectors under a tensor structure, our library achieves high performance even in high-dimensional spaces ($\bigwedge \mathbb {R}^{n}$ with $n > 256$) assuming (p, q, r) metric signatures with $r = 0$. Additionally, to keep the simplicity of use of our library, the implementation is ready to be used both as a C++ pure library and as a back-end to a Python environment. Such flexibility allows easy manipulation accordingly to the user’s experience, without impact on the performance.

1 Introduction

Geometric algebra (GA) is a mathematical formalism with several applications in Physics [10, 19, 20], Engineering [27], and Computer Science [11]. By considering linear subspaces (blades) and orthogonal transformations (versors) as primitives with a geometric interpretation, we can compute intersections and decompositions of subspaces, subspace spans, and transformations in an intuitive way that allows us to focus on the problem by leveraging the geometric meaning of the operations. An important feature of GA is its ability to encompass and generalize concepts that emerge in different mathematical formalisms. Quaternions and Plücker coordinates, for example, are fundamental in Computer Graphics, and both can be easily translated to a unified GA language or emerge from other concepts present in this toolset.

Fig. 1

Mean execution times for some products implemented by TbGAL for $\bigwedge \mathbb {R}^{256}$ under Euclidean metric. Here, lhs and rhs correspond, respectively, to the grade of the left and right blades involved in the operations. Notice that the geometric product execution times are presented on a different scale from the other operations

Many practical applications of GA demand the achievement of good computational performance. Thus, most computational solutions are libraries developed in C/C++ [7, 12, 24, 31] or code generators that produce libraries or source code optimized for those languages [2, 6, 8, 15, 21], sometimes considering also the use of parallelism with OpenCL and CUDA [6, 21]. A common strategy adopted by those solutions is the representation of data as multivectors, i.e., the weighted sum of basis blades of the multivector space $\bigwedge \mathbb {R}^{n}$. This strategy, however, imposes restrictions over the maximum dimensions n that the solutions support (usually, from $n = 7$ to $n = 20$) since the number of basis blades in $\bigwedge \mathbb {R}^{n}$ is $2^{n}$. Even considering the sparsity of blades and versors in their multivector form, those primitives may include up to $n! / (\lfloor n / 2 \rfloor !)^{2}$ and $2^{n-1}$ components, respectively. Thus, handling hundreds of dimensions becomes impractical by using conventional multivector-based libraries, library generators, and code optimizers. For instance, by assuming $n = 256$, the multivector space has about $1.16 \times 10^{77}$ dimensions, a blade representing a subspace with 128 dimensions may have $\sim 5.77 \times 10^{75}$ components while a versor may have $\sim 5.79 \times 10^{76}$ components. For an example of a practical problem in high dimensionality, we can mention the application of k-Discretizable Molecular Distance Geometry Problem ($^k\text {DMDGP}$) [25] on the classification of weighted graphs in machine learning [4].

The main contribution of this work is a flexible high-level library for GA called TbGAL (Tensor-based Geometric Algebra Library). This library represents blades (and versors) in their decomposed state as the outer product (and geometric product), rather than using their representation as a weighted summation of basis blades in $\bigwedge \mathbb {R}^{n}$. This implementation strategy is discussed by Fontijne [9, Chapter 5]. But to our surprise, it is not adopted by existing libraries. The main advantage of the factorized approach is that it is able to compute GA operations in higher dimensions, i.e., assume multivectors space $\bigwedge \mathbb {R}^{n}$ with $n > 256$. In terms of memory, TbGAL stores only $1 + n^{2}$ coefficients per blade or versor in worst case, while operations have maximum complexity of ${\mathcal {O}}\left( n^{3}\right)$. Figure 1 depicts the performance of our approach for four basic operations in $\bigwedge \mathbb {R}^{256}$ under Euclidean metric: geometric product, outer product, left contraction, and Hestenes’ inner product. In our experiments, we compared TbGAL against other libraries, library generators, and code optimizers designed for low dimensions: Gaalop [6], Garamon [2], GluCat [24], and Versor [7]. They supported GAs defined on up to 16-, 20-, 16-, and 7-dimensional vector spaces, respectively.

In Sects. 2 and 3, we present basic GA concepts and discuss existing implementations of them, respectively. In Sect. 4, we present the internal structure of our library. The performance of the above-mentioned libraries is compared to TbGAL in Sect. 5. Finally, we draw our conclusions in Sect. 6.

2 Background on GA Operations

In this section, we present some of the main operations associated with GA. Please refer to [11, 27] for a complete reference on the subject.

2.1 Multivector Space

Table 1 Multivector space $\bigwedge \mathbb {R}^{4}$

To define the operations in GA, we first shall introduce the basis where this algebra is defined. For this purpose, we are assuming a vector space with a set of basis vectors $\{ e _{i}\}_{i=1}^{n}$, where $n = p + q + r$. Here, (p, q, r) defines the signature of the metric space, i.e.,:

(2.1)

In Eq. (2.1), denotes the vector inner product.

Notice that the vector space considers only of 1-dimensional primitives (i.e., vectors). In GA we define from the multivector space $\bigwedge \mathbb {R}^{n}$, where we can represent GA primitives as multivectors $M$. A multivector is the linear combination of basis elements of $\bigwedge \mathbb {R}^{n}$. The set of basis elements defined in $\bigwedge \mathbb {R}^{4}$, for example, is depicted in Table 1. The rightmost column refers to the particular denomination used for the linear combinations of basis elements from the 0-dimensional, 1-dimensional, 2-dimensional, $(n - 1)$-dimensional, and n-dimensional spaces. Altogether, there are $2^{n}$ basis elements (a.k.a basis blades) in the multivector space $\bigwedge \mathbb {R}^{n}$. Formally, a k-vector is a linear combination of basis elements of $\bigwedge \nolimits ^{\!k}\mathbb {R}^{n}$ only.

2.2 Outer Product

The outer product (denoted by ) is a metric-free operation that corresponds to the mapping:

(2.2)

It has the following properties:

• antisymmetry: , thus

• distributivity:
• associativity:
• scalar commutativity:

Here, $\alpha \in \bigwedge \nolimits ^{\!0}\mathbb {R}^{n}$ is a real scalar value and $a , b , c \in \bigwedge \nolimits ^{\!1}\mathbb {R}^{n}$ are vectors.

The outer product allows the definition of blades with higher dimensionalities from low-dimensional blades. Therefore, it is clear that the outer product implements the idea of a subspace span. For instance, the outer product of two linearly independent 1-dimensional blades (i.e., vectors) defines a 2-blade, while the outer product of three linearly independent vectors defines a 3-blade, and so on. Formally, a k-blade $A _{\langle k\rangle } \in \bigwedge \nolimits ^{\!k}\mathbb {R}^{n}$ is any linear subspace spanned as the outer product of k linearly independent vectors. Furthermore, we say that $A _{\langle k\rangle }$ has grade k. It is important to emphasize that all k-blades are also k-vectors, but not all k-vectors are k-blades. For instance, is a 2-vector but it is not a 2-blade. Under the Euclidean metric, 1-blades can be interpreted as straight lines that include the origin of , 2-blades correspond to planes, 3-blades to volumes, and so on.

2.3 Left and Right Contractions

Another important operation of GA is the left contraction (denoted by ). It is a metric product that represents removing from the right-side operand the portion that is most like the left-side operand in the metric sense (i.e., the like portion of the right-side operand with respect to the left-side operand is the subspace having the same dimensionality than the left-side subspace and whose inner product between them is nonzero). Thus, it is the mapping:

(2.3)

As an embodiment of this mapping applied to blades we use:

(2.4)

The left contraction has the following properties:

• symmetry: , if and only if $r = s$

• distributivity:
• scalar commutativity:

Besides those properties, there are a few other useful relations between the left contraction and the outer product, whose applications are better illustrated in Sects. 2.5 and 4. The first relation is valid for any blade:

(2.5)

The second relation is:

(2.6)

and is valid if and only if $A _{\langle r\rangle } \subseteq C _{\langle t\rangle }$.

The geometric intuition describing the left contraction is clearly asymmetric for the general case, since when $r > 0$. Symmetry is obtained if and only if $r = s$. It is not difficult to imagine that the same intuition of removing from one operand the portion that is most like the other may applied in the definition of the right contraction , where the result is the portion in $A _{\langle r\rangle }$ that is “less like” $B _{\langle s\rangle }$ in the given metric of the space. Thus, the right contraction is the mapping:

(2.7)

with the same properties than the left contraction. The relationship between the two contractions is [11]:

(2.8)

2.4 Other Metric Products

The Hestenes’ inner product is a metric product that has a different and somewhat more symmetrical grade than the left and right contractions:

(2.9)

The literature on applied GA that use the Hestenes’ inner product as their only inner product, and it is usually denoted using the same symbol as the vector inner product (Eq. 2.1). Here, we followed the notation $\bullet _{H}$ adopted by Dorst et al. [11].

Another metric product described in the literature is the dot product:

(2.10)

The dot product is similar to the Hestenes’ inner product, except that when one of the arguments is a scalar value (i.e., $r = 0$ or $s = 0$), the result of the dot product is not necessarily zero.

Finally, the scalar product always returns a scalar value. It operates on k-blades or k-versors as a contraction, otherwise the result is zero:

(2.11)

From Eqs. (2.8, 2.10), and (2.11) it is easy to see that:

(2.12)

2.5 Dualization

The dualization is the operation denoted by $\square ^{*}$. It defines the mapping:

$$\begin{aligned} \square ^{*} : \bigwedge \nolimits ^{\!k}\mathbb {R}^{n} \rightarrow \bigwedge \nolimits ^{\!n-k}\mathbb {R}^{n}. \end{aligned}$$

(2.13)

The geometrical interpretation of $A _{\langle k\rangle }^{*}$ is that it takes from the whole n-dimensional space, i.e, from the unit pseudoscalar , the $(n - k)$-dimensional portion that is orthogonal to the blade $A _{\langle k\rangle }$.

The dualization operation can be expressed using the left contraction:

(2.14)

where

$$\begin{aligned} X _{\langle r\rangle }^{-1} = \frac{1}{\Vert X _{\langle r\rangle }\Vert ^{2}} \widetilde{X} _{\langle r\rangle } \end{aligned}$$

(2.15)

denotes the inverse of $X _{\langle r\rangle }$,

(2.16)

is the squared reverse norm, and

$$\begin{aligned} \widetilde{X} _{\langle r\rangle } = (-1)^{\frac{r (r - 1)}{2}} X _{\langle r\rangle } \end{aligned}$$

(2.17)

denotes the reverse operation. The reverse operation is distributive over the sum. Therefore, it can be applied to general multivectors, even to those having mixed grade, and evaluated regarding the grade of their components.

Fig. 2

Dualization operation. The vectors $d$ is the dual of a plane $B _{\langle 2\rangle }$ in under Euclidean metric

Recall that the left contraction induces the geometric meaning of removing from the pseudoscalar all that is similar to the given blade, keeping only the blade that is orthogonal to it. Figure 2 exemplifies the dualization operator. This image was originally available in [13]. In this example, $I _{\langle 3\rangle }$ is the whole 3-dimensional space and $d = B _{\langle 2\rangle }^{*}$ is the vector dual to the 2-blade $B _{\langle 2\rangle }$.

The dualization is invertible. The undualization operation is defined as:

(2.18)

Such invertibility allows the retrieval of the original blade using the relation defined by Eq. (2.6):

(2.19)

Equations (2.5) and (2.6) also help to define universal relations between the outer product and left contraction in terms of duality. The first relation shows that the left contraction can replace the dual of the outer product:

(2.20)

The second relation, used in our implementation (Sect. 4.5), shows how the dual of the left contraction and the outer product are connected:

(2.21)

2.6 Geometric Product

The most important product in GA is the geometric product. In practice, most of the other products can be extracted from it (see [11, Section 6.3] for details). The geometric product consists of a mapping

$$\begin{aligned} \bigwedge \mathbb {R}^{n} \times \bigwedge \mathbb {R}^{n} \rightarrow \bigwedge \mathbb {R}^{n}. \end{aligned}$$

(2.22)

Its properties include:

• distributivity: $A ( B + C ) = A B + A C$

• associativity: $A ( B C ) = ( A B ) C$

• non-commutativity in general: $\exists A , B \in \bigwedge \mathbb {R}^{n}: A B \ne B A$

An embodiment of the mapping in Eq. (2.22) involving vectors and general multivectors can be defined as:

(2.23)

where $a$ is a vector and $B$ is a multivector. From Eq. (2.23) and the properties of the geometric product, it is possible to define the geometric product of any pair of multivector operands. However, this definition is rather involving. Refer to [11] for details.

Notice in Eq. (2.23) that the multivector resulting from the geometric product $a B$ has a portion that relies on the metric () and a metric-free portion (). Such composition makes this product invertible, as long as the right-hand side operand is also invertible, i.e.,

$$\begin{aligned} A \mathbin {/} B = A B ^{-1}, \end{aligned}$$

(2.24)

where $\mathbin {/}$ denotes the inverse geometric product.

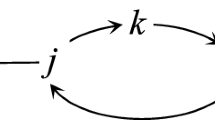
One of the main application of the geometric product is in the definition of orthogonal (i.e., length-preserving) transformations like reflection, rotation and translation, and other conformal (i.e., angle-preserving) transformations like uniform scale. These transformations can be modeled as a sequence of reflections in pseudovectors. In practice, given a pseudovector $M _{\langle n-1\rangle }$ and its dual vector $v = M _{\langle n-1\rangle }^{*}$, the vector $a$ reflected in $M _{\langle n-1\rangle }$ can be expressed as

$$\begin{aligned} a ^{\prime } = - v a v ^{-1}, \end{aligned}$$

(2.25)

where $v ^{-1}$ denotes the inverse of $v$ (Eq. 2.15). An example of the application of Eq. 2.25 is depicted by Fig. 3, originally available in [13].

Fig. 3

Reflection of a vector $a$ in a blade $M _{\langle n-1\rangle }$ producing a vector $a ^{\prime }$. In order to produce this reflection, one shall use the vector $v = M _{\langle n-1\rangle }^{*}$

Notice that reflections can be combined. Thus, one can apply a reflection after another reflection, and so on:

$$\begin{aligned} a ^{\prime \prime } = u a ^{\prime } u ^{-1} = u ( v a v ^{-1}) u ^{-1}, \end{aligned}$$

(2.26)

where $a ^{\prime \prime }$ is the reflection of the vector $a ^{\prime }$ on the blade $N _{\langle n-1\rangle }$ using its dual, given by $u = N _{\langle n-1\rangle }^{*}$. Using the associativity of the geometric product, we can write Equation 2.26 as:

$$\begin{aligned} a ^{\prime \prime } = u ( v a v ^{-1}) u ^{-1} = ( u v ) a ( v ^{-1} u ^{-1}) = ( u v ) a ( u v )^{-1}. \end{aligned}$$

(2.27)

In Eq. (2.27), $u v$ is called a 2-versor. Formally, a k-versor $\mathcal {V}$ is defined as the geometric product of k invertible vectors. Those mixed-grade primitives encode orthogonal transformations.

Although Eqs. (2.25) and (2.26) only show vectors being transformed by versors, it is important to emphasize that the sandwiching construction of the versor product can be applied to any multivector since the geometric product is distributive over the sum and versors preserves the structure of the outer product, e.g,:

(2.28)

where $\mathcal {V}$ is a versor and $i \ne j$.

3 Related Work

Many libraries, library generators, and code optimizers implementing GA concepts have been proposed in different programming languages. Table 2 present some of the most popular solutions. Notice that most of them are available in C++ and Python.

Table 2 Comparison of libraries (L), library generators (LG), and code optimizers (CO) for GA regarding programming languages, practical maximum dimensionality of the vector space, and supported metrics

Table 3 Bitset representation of basis blades in $\bigwedge \mathbb {R}^{3}$

A possible approach adopted by libraries and library generators is to store multivectors as a collection of pairs representing the linear combination of basis blades. In this case, each pair includes a bitset that identifies the corresponding basis blade unequivocally and a real coefficient. Table 3 shows the bitset representation of each of the basis blades in the multivector space $\bigwedge \mathbb {R}^{3}$. Notice that each bit corresponds to a basis vector. The on-bits indicate the basis vectors spanning the basis blades. By using the bitset approach, some parts of operations like the outer and geometric products of basis blades under orthogonal metrics can be reduced to, respectively, efficient OR and XOR bitwise operations. For instance, lets consider that the basis blade $e _{1}$ is represented by the bitset 001, and the basis blade $e _{2}$ is represented by the bitset 010. The basis blade can be computed using the bitwise OR operation between 001 and 010, which results in 011. The signal change of the resulting coefficient is a consequence of the antisymmetry property of the outer product. It is computed by checking whether there are common on-bits in the given bitsets (resulting in zero) or by counting the number of swaps necessary to arrange the basis vectors into the canonical order (even amount of swaps leads to $+1$, while odd swaps count results on $-1$). We believe that this kind of computational trick and the direct application of typical multivector algebraic manipulations may have attracted developers to the classical multivector representation.

In the following sections, we will briefly discuss each of the solutions presented in Table 2, grouped according to their type.

3.1 Libraries

Leopardi [24] provided the template-based C++ library GluCat which supports algebras having (p, q, 0) metric signatures. GluCat includes two data structures to represent GA primitives: the framed_multi class is based on an optimized version of the bitset approach described above, while the matrix_multi class implements a matrix-based approach. Thus, this library has as its core a combination of bitsets and matrices in an adaptive form. It handles low dimensionalities with dense matrix manipulations and (theoretically) higher dimensionalities with sparse matrices. The amount of dimensions n supported by Leopardi’s library is limited by the word size (in bits) assumed by the compiler. It is important to comment that libraries like GluCat, which is built to work with (p, q, 0) signatures, often provide a front-end that allows the manipulation of elements in specific cases of non-orthogonal metric spaces, like the conformal model of geometry (see the ad. note in Table 2). For the user, the mapping between the general metric and the (p, q, 0) metric space is transparent.

Colapinto created a C++ template-based library called Versor [7]. His library assumes that the basis blades of the multivector components are known in compile-time. By doing so, GA products and operations can be specialized via template meta-programming while the program is compiled. The meta-functions discard operations that lead to coefficients equal to zero and evaluate the remaining base blades operations on compilation-time while keeping track of the operations to be applied to the remaining coefficients on runtime. Gaalet, the C++ template-based library developed by Seybold [31], extends the compile-time optimization capabilities of Versor by also implementing the lazy-evaluation concept [23] on the expressions involving basis blades. Such a concept allows compile-time algebraic manipulations beyond the native routines of the library, performing optimizations on code snippets implemented by the user in his/her application. However, Gaalet is not capable of handling the coefficients of multivectors as labeled variables in expressions. As a result, the possible optimizations are not as deep as the algebraic manipulation that an expert would perform. Recently, Fernandes made his C++ template-based library, GATL, public available [12]. In contrast to Gaalet, not only basis blades but also coefficients are treated as variables in algebraic manipulations performed by the lazy-evaluation scheme of GATL in compilation time. Also, GATL allows the inclusion of compile-time defined coefficients and the optimization of complete routines written by the user. In theory, the number of dimensions n supported by Versor, Gaalet, and GATL is limited by the compiler. According to our experience, $n \le 7$ for Versor and GATL. Unfortunately, Due to technical issues, we were unable to verify the Gaalet’s limits. GATL is the only of those three libraries that currently support arbitrary metric spaces (i.e., assume any metric matrix, including degenerated ones) as a ready-to-use feature (see Table 2).

Arsenovic et al. [1] presented a Python 3 library for GA called clifford. Although the library uses a just-in-time compiler to improve the implementation’s performance (whose functionality was extended by the Gajit [18]), the authors claim that the algebras over 6 dimensions have a bad impact on the runtime, which is reasonable since the library aims pedagogical purposes or proofs of concept. The symbolic GA module galgebra was originally developed by Bromborsky [3] for Python 2. The project’s fork maintained by the Pythonic Geometric Algebra Enthusiasts supports Python 3 [29]. In contrast to clifford, galgebra supports general metric spaces.

Reed [30] developed Grassmann.jl, a package for GA written in Julia. Reed’s package is based on sparse tensor operations and uses staged caching and precompilation, which allows it to support $n = 62$ dimensions under orthogonal (p, q, r) metric spaces. Liga [5] is a Julia package written by Castelani. According to Castelani, Liga supports orthogonal (p, q, 0) metric spaces and $n > 9$ dimensions. It’s practical limits have not yet been tested.

3.2 Library Generators

Fontijne presented the first version of Gaigen [15] in 2006. It is a software that generates GA libraries. The current version of Gaigen generates C, C++, C#, and Java libraries that are optimized for a given program after profiling. To use Gaigen, first one has to write your program assuming full implementation of the GA library provided by Gaigen in one of the supported programming languages. Then, one has to run the program using the profiling functionalities of the library. Profiling data is then interpreted by Gaigen, which produces an optimized version of the GA library by pruning unused multivector components. Fontijne claims that, although the code generated has an inferior performance when compared to a manually optimized code, it is still better than a full GA library. Currently, Gaigen can handle, besides Euclidean and Conformal metric spaces, GAs having arbitrary metric spaces. According to our experience, when a pseudo-Euclidean metric is assumed, the generator can work with up to $n = 8$ dimensions.

Breulis et al. [2] developed the library generator Garamon using as a premise a precomputed algebra for lower dimensions (lower than 10) which smoothly changes to a recursive scheme based on a prefix tree for higher dimensions. The prefix tree allows mapping the position of a node in a tree to the key it is associated with. For Garamon, the level of a node in the prefix tree defines the grade of the basis blade associated with it, i.e., nodes at level k corresponds to k-blades. This approach allows resolving outer and geometric product in a recursive process that corresponds to going up or down in the prefix tree. By construction, this library generator supports Euclidean, Conformal and arbitrary metric spaces and dimensionality up to 32 dimensions. Garamon supports $n \le 18$ dimensions for non-Euclidean and $n \le 20$ for Euclidean spaces.

The ganja.js solution [8] is another GA generator that supports Euclidean, conformal and arbitrary metric spaces. The libraries produced by ganja.js does not explore the sparse nature of blades and versors in the multivector space. As a result, the multivector data structure includes $2^{n}$ components. Also, products have to execute full multivector computations, making the solution infeasible for large n. On the other hand, ganja.js provides one of the most complete visualization mechanisms among existing solutions.

3.3 Code Optimizers

CLUCalc is an interpreter for the GA script language called CLUScript, developed by Perwass et al. [28]. When combined with CLUViz, this toolset provides an environment for manipulating and visualizing elements from GA.

Gaalop [21] is a software to optimize GA procedures implemented using CLUCalc scripts and convert them into C, C++, CUDA, OpenCL, or MATLAB code. Recently, Charrier et al. [6] developed a Gaalop pre-compiler for C++, CUDA, and OpenCL that takes CLUCalc scripts declared in pragma directives and optimize them producing inline code for a given source file. By performing algebraic manipulation of whole procedures, this code optimizer can achieve good performance when compared to other solutions that only optimize operations inside the library (e.g., Gaigen and Versor). Since the pre-compiling process runs when the compiling process is triggered, it does not show any performance issues in runtime. The limitation in terms of compile-time performance is that higher dimensionalities require larger configuration files and more challenging algebraic manipulations, which may turn the compilation process unfeasible.

In contrast to the above mentioned libraries (Sect. 3.1), library generators (Sect. 3.2), and code optimizers (Sect. 3.3), TbGAL does not represent blades and versors as multivectors described by the weighted sum of basis blades of $\bigwedge \mathbb {R}^{n}$. The product of their vector factors represents such primitives. As a result, TbGAL is less sensitive to the curse of dimensionality, allowing operations between blades and versors on GAs defined over vector spaces with hundreds of dimensions ($n > 256$). In our experiments, we were able to run the implemented products with up to $n = 1536$ due to memory restrictions. Runtime and numerical instability impose restriction for more than $n = 300$ dimensions. For this reason, we report results up to $n = 256$. Such high-dimensional support tackles part of the challenges involving the $^k\text {DMDGP}$ problem [25], Clifford neural networks [26], hypercomplex Clifford analysis [17], among others, as summarized by Hitzer et al. in [22].

Our solution is closed related to the paradigm employed by Fontijne in implementing the Java package called Gallant [9, 14]. The main difference is that the evaluation of the geometric product performed by Gallant is restricted to metric spaces having (n, 0, 0), (0, n, 0), $(n-1, 1, 0)$, and $(n, n-1, 0)$ signatures [9, Section 5.4]. Our solution, on the other hand, accepts spaces having (p, q, 0) metric signatures. The benchmarks presented in Fontijne’s in [9] shows results up to $n = 22$, but we believe that his implementation can go beyond. Gallant does not appear to be available in a public repository.

4 Proposed Architecture and Implementation

The proposed library was designed to operate blades and versors in multivectors space $\bigwedge \mathbb {R}^{n}$ with arbitrary metric spaces having (p, q, 0) signature, where $n = p + q$. We developed TbGAL in C++. We used Eigen and Boost.Python for, respectively, matrix operations and Python 2 and Python 3 ports. The main idea behind the Python ports is to make the library more accessible to the community. The source code is available in our GitHub repository¹.

A toy example of the usage of our library is provided in Fig. 4. In this example, we present an embodiment of the reflection depicted in Fig. 3, where the goal is to reflect the vector $a = 0.5 e _{1} + 0.5 e _{2}$ (line 8 of Fig. 4) over the plane (line 10 of Fig. 4) using its dual, the vector $v$ (line 11 of Fig. 4), producing the vector $a ^{\prime }$ (line 13 of Fig. 4). It is important to notice that the user of the TbGAL library doesn’t have to worry about the way data is stored in variables, or the matrix operations performed during the evaluation of library functions. He/she only needs to include the header that determines which matrix library to use for processing (line 1 of Fig. 4) and the header that indicates which geometry model is assumed (line 2 of Fig. 4). Another possibility is to define his/her own geometry model by following one of the existing tbgal/assuming_ModelName.hpp files as example. Also, the placeholder auto (available since C++11) helps to set the data type of each variable (lines 8, 10, 11, and 13 of Fig. 4). With this placeholder, the type of the variable that is being declared will be automatically deduced from its initializer on the right-side of the assign operator.

Tables 4 and 5 enumerate some of the data structures and operations implemented by our library. Implementation details are discussed in the following sections.

Fig. 4

Code snippet of the usage of TbGAL. In this example, we are reflecting the vector $a$ onto blade $M _{\langle 2\rangle }$ to produce $a ^{\prime }$. The comments in lines 8, 10, 11, and 13 show the meaning of the content of each variable

4.1 Data Structures

All metric spaces implemented by TbGAL are subclasses of the abstract class BaseSignedMetricSpace. In its current version, TbGAL allows the user to choose among n-dimensional models having arbitrary metric matrices (GeneralMetricSpace class), orthogonal models with arbitrary (p, q, 0) metric signatures (SignedMetricSpace class), n-dimensional Euclidean models (EuclideanMetricSpace class), d-dimensional homogeneous models (HomogeneousMetricSpace class), and d-dimensional conformal models (ConformalMetricSpace class). The P, Q, D, and N template parameters presented in Table 4 may be set by the user to non-negative integer values before compiling his/her program, or set to Dynamic if he/she wants to define the dimensionality of the vector space in runtime. The MaxN and MaxD template parameters are optional. In most cases, one just leaves these parameters to the default values. These parameters mean the maximum number of dimensions that the vector space may have. They are useful in cases when the exact numbers of dimensions are not known at compile-time, but it is known at compile-time that they cannot exceed a certain value.

For practical reasons, TbGAL evaluates the products and operations assuming a diagonal metric matrix $\mathrm {M}$ encoding the metric signature of the space (Eq. 2.1). The actual metric defined by the user is only adopted externally. Therefore, TbGAL converts the inputs and outputs appropriately. The conversion is implemented by subclasses of BaseSignedMetricSpace.

Table 4 Basic data structures implemented by TbGAL

Table 5 Some operations implemented by TbGAL, the respective function prototypes, and overloaded operators

The FactoredMultivector class is the most important data structure declared in our library. It encodes k-blades and k-versors with $k \in \{0, 1, \ldots , n\}$. Handling k-blades and k-versors with arbitrary k as multivectors is too expensive when n is large. It is because handling the nonzero coefficients may become unfeasible by the amount of memory required. In the worst case, multivectors encoding blades have $n! / (\lfloor n / 2 \rfloor !)^{2}$ coefficients, while versors have $2^{n-1}$ coefficients. Therefore, in contrast to conventional implementations based on storing multivector components, the FactoredMultivector class stores blades and versors as a scalar value of type ScalarType multiplying k unit vector factors (unit under the Euclidean metric). Thus, TbGAL stores only $1 + n^{2}$ coefficients per blade or versor in worst case.

When the FactoringProductType parameter of the FactoredMultivector class is set to OuterProduct (see Table 4), the class stores the factors as the first k columns of a orthogonal second-order tensor under Euclidean metric. The remaining $n - k$ columns correspond to the orthogonal complement of the factors with respect to the unit pseudoscalar of the n-dimensional space, also under Euclidean metric. For instance, the 2-blade $C _{\langle 2\rangle }$ resulting from the outer product of vectors and is encoded as:

$$\begin{aligned} \gamma = 7.8102 \text {, and } \mathrm {C} = \begin{bmatrix} c _{1}&c _{2}&c _{3} \end{bmatrix} = \begin{bmatrix} -0.5547 &{} -0.3196 &{} -0.7682 \\ 0.8320 &{} -0.2131 &{} -0.5121 \\ 0.0000 &{} -0.9233 &{} 0.3841 \end{bmatrix} \text {.} \end{aligned}$$

Thus, .

By setting the FactoringProductType parameter of the FactoredMultivector class to GeometricProduct, the unit vector factors are stored as the columns of a $n \times k$ matrix, but in this case the stored factors may not be orthogonal under Euclidean metric. As an example, the 2-versor , resulting from the geometric product of vectors $a$ and $b$, is encoded as:

$$\begin{aligned} \delta = 8.0623 \text {, and } \mathrm {D} = \begin{bmatrix} d _{1}&d _{2} \end{bmatrix} = \begin{bmatrix} 0.4472 &{} -0.5547 \\ 0.0000 &{} 0.8320 \\ 0.8944 &{} 0.0000 \end{bmatrix}. \end{aligned}$$

The initialization of FactoredMultivector instances is performed as result of the evaluation of products and other operations, like in lines 8, 10, 11, and 13 of Fig. 4, or by calling auxiliary functions defined for each model of geometry. For instance, the vector(coord1, ..., coordN) function produces an instance of type:

FactoredMultivector$\mathtt {<}$ScalarType,  OuterProduct$\mathtt {<}$MetricSpaceType$\mathtt {>>}$,

where ScalarType is deduced from the types of the given coordinates and MetricSpaceType is the assumed model of geometry. All implemented models include this function. The point(coord1, ..., coordD) function, on the other hand, is declared with models where it makes sense to have finite points, such as the homogeneous and the conformal models.

4.2 Outer Product

TbGAL implements the outer product in the op(arg1, arg2 [, ...]) function. This function expects conventional numerical values (e.g., int, float, double, etc.) and instances of FactoredMultivector encoding blades as arguments, and produces a new instance of FactoredMultivector by:

• 1. Concatenating the k factors encapsulated by the FactoredMultivector arguments, producing the $n \times k$ input matrix $\mathrm {A}$;

• 2. Verifying whether the rank of $\mathrm {A}$ is equal to k;

• 3. Producing, under Euclidean metric, a new set of orthonormal vector factors that span the same k-dimensional subspace than the input blades; and

• 4. Computing the resulting scalar factor accordingly.

In our implementation, steps (2) and (3) are performed at the same time by evaluating the Householder rank-revealing QR Decomposition [16] of the matrix $\mathrm {A}$ with column-pivoting. This algorithm is based on Householder reflections, which are more stable than the Gram–Schmidt algorithm. The Householder method works by finding appropriate Householder reflection matrices and multiplying them from the left by the original matrix $\mathrm {A}$ to construct the upper triangular matrix $\mathrm {R}$ of the QR decomposition. The matrix $\mathrm {Q}$ and the rank of $\mathrm {A}$ are byproducts of this operation at a smaller cost when compared to the application of Singular Value Decomposition. If the rank of $\mathrm {A}$ is smaller than k, the scalar value and the number of factors in the resulting FactoredMultivector are set to zero. Otherwise, the new set of factors computed in step (3) correspond to the first k columns of the resulting $\mathrm {Q}$ matrix. It is clear that if one of the input blades is not a 0-blade (i.e., a scalar value) then steps (1) and (3) are not necessary, and if one of the arguments is equal to zero, then the resulting blade is also zero. The same happens when the number of columns of $\mathrm {A}$ is bigger than the number of rows.

Describing the process by equations, we compute the decomposition:

$$\begin{aligned} \mathrm {A} = \mathrm {Q} \, \mathrm {R}, \end{aligned}$$

(4.1)

and get the rank k of $\mathrm {A}$ as a byproduct. If the columns of $\mathrm {A}$ are linearly independent then k is equals the number of columns of $\mathrm {A}$ because the outer product of the vector factors will be different than zero. In this case, we set the orthogonal matrix

$$\begin{aligned} \mathrm {Q} = \begin{bmatrix} q _{1}&q _{2}&\ldots&q _{n} \end{bmatrix}, \end{aligned}$$

with $k \le n$, as the orthogonal second-order tensor stored by the resulting FactoredMultivector . The resulting stored scalar value is given by:

$$\begin{aligned} \gamma = \alpha \, \det \left( \begin{bmatrix} q _{1}&q _{2}&\ldots&q _{k} \end{bmatrix}^{T}\, \mathrm {A}\right) \text {,} \end{aligned}$$

(4.2)

where $\alpha$ is computed as the product of the scalar factors of the given arguments, k is the grade of the resulting blade, $\square ^{T}$ denotes the transpose of a matrix, and $\det \left( \square \right)$ computes the determinant of a matrix.

4.3 Dualization

The computation of the dual of a blade is an important operation in TbGAL since it is used as one of the steps of the implementation of the left contraction, as will be explained in Sect. 4.5. The use of the function dual(arg) can be seen in the code snippet presented in Fig. 4 (line 11).

Consider an orthogonal second-order tensor $\mathrm {A} = \begin{bmatrix} a _{1}&a _{2}&\ldots&a _{n}\end{bmatrix}$ and a scalar value $\alpha$ representing the data stored by a FactoredMultivector assuming OuterProduct as its FactoringProductType, and grade k. This FactoredMultivector encodes a k-blade $A _{\langle k\rangle }$ spanned by the first k columns of $\mathrm {A}$. The orthogonal tensor $\mathrm {D}$ representing the orthogonal vector factors of the dual of $A _{\langle k\rangle }$, i.e., $D _{\langle n-k\rangle } = A _{\langle k\rangle }^{*}$ (Eq. 2.13), can be computed as

$$\begin{aligned} \mathrm {D} = \mathrm {M} \, \begin{bmatrix} a _{k+1}&\ldots&a _{n}&a _{1}&\ldots&a _{k} \end{bmatrix}, \end{aligned}$$

(4.3)

where $\mathrm {M} = \mathrm {M}^{-1} = \mathrm {M}^{T}$ is a diagonal matrix encoding the (p, q, 0) metric signature of the space. The scalar factor $\delta$ of $D _{\langle n-k\rangle }$ is computed as:

$$\begin{aligned} \delta = \left( -1\right) ^{\frac{k (k - 1) + n (n - 1)}{2}} \, \alpha \, \det {\left( \mathrm {A}\right) }. \end{aligned}$$

(4.4)

The $\det {\left( \mathrm {A}\right) }$ term in Eq. (4.4) is used to fix the orientation of the resulting subspace with respect to the unit pseudoscalar under Euclidean metric (whose factors define an identity matrix).

Undualization is implemented by undual(arg) in the TbGAL. Given Eqs. (4.3) and (4.4), the computation of the undual $U _{\langle n-k\rangle } = A _{\langle k\rangle }^{-*}$ of a k-blade $A _{\langle k\rangle }$ (Eq. 2.18) is straightforward. Using

$$\begin{aligned} \mathrm {B} = \begin{bmatrix} b _{1}&b _{2}&\ldots&b _{n} \end{bmatrix} = \mathrm {M} \, \mathrm {A}, \end{aligned}$$

(4.5)

we compute the orthogonal second-order tensor encoding the vector factors of $U _{\langle n-k\rangle }$ as:

$$\begin{aligned} \mathrm {U} = \begin{bmatrix} b _{k+1}&\ldots&b _{n}&b _{1}&\ldots&b _{k} \end{bmatrix}, \end{aligned}$$

(4.6)

and the scalar factor as:

$$\begin{aligned} \gamma = \left( -1\right) ^{\frac{k (k - 1)}{2}} \, \alpha \, \det {\left( \mathrm {B}\right) }. \end{aligned}$$

(4.7)

Notice that the dualization and undualization procedures presented in this section do not work with (p, q, r) metric signatures when $r \ne 0$. This is because when some element in the main diagonal of $\mathrm {M}$ is zero, $\mathrm {D}$ (Eq. 4.3) and $\mathrm {B}$ (Eq. 4.5) will not be orthogonal tensors ($\det \left( \mathrm {D}\right) = \det \left( \mathrm {B}\right) = 0$ in this case). This issue was inherited from Eq. (2.14), since $I _{\langle n\rangle }$ is not invertible when $r \ne 0$.

4.4 Geometric Product

The gp(arg1, arg2 [, ...]) function implements the geometric product of conventional numerical values (e.g., int, float, double, etc.) and instances of FactoredMultivector assuming GeometricProduct or OuterProduct as FactoringProductType. However, each argument assuming OuterProduct must be converted to its equivalent factorization using GeometricProduct before the actual evaluation of gp because the factors of the latter may be different of the factors of former on non-Euclidean metric signatures.

Let $\kappa$ and $\mathrm {K}$ be, respectively, the scalar factor and the $n \times k$ matrix whose orthonormal columns (under Euclidean metric) store the vector factors of a k-blade $K _{\langle k\rangle }$ factored by the outer product. The vector factors of the same blade factored by the geometric product are the columns of the matrix:

$$\begin{aligned} \mathrm {K}^{\prime } = \mathrm {K} \, \mathrm {Q}_{\mathrm {K}} \text {,} \end{aligned}$$

(4.8)

where the matrix $\mathrm {Q}_{\mathrm {K}}$ is given by the QR Decomposition of the metric matrix of the space spanned by the columns of $\mathrm {K}$, i.e., $\mathrm {K}^{T} \, \mathrm {M} \, \mathrm {K} = \mathrm {Q}_{\mathrm {K}} \, \mathrm {R}_{\mathrm {K}}$, and $\mathrm {M}$ is the metric matrix encoding the metric signature of the n-dimensional space. The scalar factor of $K _{\langle k\rangle }$ factored by the geometric product is:

$$\begin{aligned} \kappa ^{\prime } = \kappa \, \det \left( \mathrm {K}^{T} \, \mathrm {K}^{\prime }\right) \text {.} \end{aligned}$$

(4.9)

Assuming that all arguments of gp(arg1, arg2 [, ...]) are factored by the geometric product (or were converted by TbGAL using Eqs. (4.8) and (4.9), the evaluation of the geometric product consists on:

• 1. Multiply all scalar factors, producing a (temporary) scalar factor $\alpha$ for the resulting FactoredMultivector;

• 2. Copy the vector factors of arg1 to the (temporary) matrix $\mathrm {A}$ stored by the resulting FactoredMultivector; and

• 3. Decide which vector factors of arg2, arg3, etc. will be appended to $\mathrm {A}$ and which ones will “consume” vector factors from it, leading to updated $\alpha$ and $\mathrm {A}$ values.

Figure 5 presents the algorithm that evaluates step (3) considering:

$$\begin{aligned} A ^{\prime } = A b = \alpha a _{1} a _{2} \ldots a _{k} b , \end{aligned}$$

(4.10)

where $\alpha$ and $\mathrm {A} = \begin{bmatrix} a _{1}&\ldots&a _{k}\end{bmatrix}$ are the factors of the (temporary) resulting multivector $A$ factored by the geometric product, $b$ is the current vector factor to be considered while updating $A$, and $A ^{\prime }$ is the updated version of $A$. The successive application of Eq. (4.10) (and hence of the algorithm in Fig. 5) considering all vector factors from arg2, arg3, etc. is straightforward and lead to the computation of the final set of factors of the resulting FactoredMultivector structure.

Fig. 5

The algorithm to evaluate the geometric product of a multivector $A$ factored by the geometric product and a vector $b$. Here, the n-dimensional space has orthogonal metric matrix $\mathrm {M}$ defined by its (p, q, 0) signature

Notice that the algorithm in Fig. 5 receives two more arguments. $\mathrm {M}_{\mathrm {A}}$ encodes the metric of the space spanned by the columns of $\mathrm {A}$. $\mathrm {F}_{\mathrm {A}}$ encodes the reciprocal frame of this space. In the first call of the algorithm, we set:

$$\begin{aligned} \mathrm {M}_{\mathrm {A}} = \begin{bmatrix} \mu _{1,1} &{} \cdots &{} \mu _{1,k} \\ \vdots &{} \ddots &{} \vdots \\ \mu _{k,1} &{} \cdots &{} \mu _{k,k} \end{bmatrix} = \mathrm {A}^{T} \, \mathrm {M} \, \mathrm {A} \text {, and } \mathrm {F}_{\mathrm {A}} = \begin{bmatrix} f _{1}&\cdots&f _{k} \end{bmatrix} = \mathrm {A} \, \mathrm {M}_{\mathrm {A}}^{-1} \text {.} \end{aligned}$$

The subsequent calls of the algorithm use the updated versions of the $\alpha$, $\mathrm {A}$, $\mathrm {M}_{\mathrm {A}}$, and $\mathrm {F}_{\mathrm {A}}$ returned by the line 35.

Lines 5–8 handle the situation where the vector $b$ is not linearly dependent on the space spanned by the columns of $\mathrm {A}$. In this case, the number of factors in $\mathrm {A}$ increase by one unit and $b$ becomes the new factors of the resulting multivector (line 6). In line 7, the inverse of $\mathrm {M}_{\mathrm {A}}$ can be efficiently computed using blockwise inversion. So, in practice, we also carry $\mathrm {M}_{\mathrm {A}}^{-1}$ as part of the function arguments.

When $b$ is linear dependent on the space spanned by $\mathrm {A}$, the part of the geometric product involving the exterior product is zero (Eq. 2.23). Thus, the result is the contraction of a vector factor from multivector $A$. Lines 10–33 perform this contraction by transforming the factors in $\mathrm {A}$ in such a way that the last factor become parallel to $b$. To do so, a set of $k - 1$ transformations $\mathrm {T}$ are applied to pairs of vectors $a _{i}, a _{i+1}$ in order to make the first $k - 1$ factors orthogonal to $b$. In lines 12, 14, and 17, $\mathrm {0}^{(m, n)}$ and $\mathrm {I}^{(m)}$ denote, respectively, $m \times n$ zero matrices and $m \times m$ identity matrices. Our implementation explores blockwise matrix multiplication since only two columns (or rows) of $\mathrm {A}$, $\mathrm {M}_{\mathrm {A}}$, and $\mathrm {F}_{\mathrm {A}}$ are affected on each iteration.

The procedure in lines 10–33 is inspired by the equations presented by Fontijne in his thesis [9, Section 5.4]. The difference is that we explore the reciprocal frame in a slightly different way in order to avoid to transform more than two columns of $\mathrm {A}$ when a non-Euclidean metrics is assumed. A key observation in our procedure was that when $\omega = 0$ (line 22), the vector $a _{i+1}$ in the $(i+1)$th column of the updated matrix $\mathrm {A}$ (line 22) must be replaced by its reciprocal vector. It is because the new factor $a _{i+1}$ is a null vector in this case, and . In the correct factorization, is expected, i.e.,$a _{i}$ and $a _{i+1}$ must be reciprocal to each other when one of them is null. Since we are evaluating the geometric product using an orthogonal metric matrix $\mathrm {M}$ defined by the metric signature of the space, the reciprocal of $a _{i+1}$ can be easily computed as $\mathrm {M} \, a _{i+1}$ (line 24).

The reason for the metric signature (p, q, r) of the space have $r = 0$ in TbGAL is that with $r \ne 0$, the matrix $\mathrm {M}_{\mathrm {A}}$ may not be invertible, leading to an invalid operation on line 7 of the algorithm.

4.5 Metric Products

The scalar product (Eq. 2.11) is implemented by the sp(arg1, arg2) function. Our implementation accepts blades as arguments and returns a scalar value. When the arguments have a different number of factors the result is zero. Otherwise, the resulting $\gamma$ value is computed as:

$$\begin{aligned} \gamma = (-1)^{\frac{k (k - 1)}{2}} \alpha \beta \det \left( \begin{bmatrix} a _{1}&a _{2}&\ldots&a _{k} \end{bmatrix}^{T} \mathrm {M} \begin{bmatrix} b _{1}&b _{2}&\ldots&b _{k} \end{bmatrix}\right) , \end{aligned}$$

(4.11)

where $\alpha$ and $\{ a _{i}\}_{i=1}^{k}$ denote the scalar and vector factors stored in arg1, and $\beta$ and $\{ b _{i}\}_{i=1}^{k}$ denote the scalar and vector factors stored in arg2. The matrix $\mathrm {M}$ in Eq. (4.11) is a diagonal matrix encoding the metric signature.

The other metric products implemented by TbGAL expect as input arguments the blades arg1 and arg2 having grades r and s, respectively, and return a FactoredMultivector encoding a blade factored by the outer product. In the current version of TbGAL, the evaluation of the left contraction rely on the duality relationship presented in Eq. (2.21) and the implementations described so far. By calculating the outer product between arg1 with the dual of arg2, we get the dual of the left contraction. By undualizing this result, we get the left contraction between the first and the second arguments. In practice, it means that

lcont(arg1, arg2)$\mathtt {\sim }$undual(op(arg1, dual(arg2))).

It is clear that when r is bigger than s, the resulting blade can be set to zero without the need to evaluate any operation.

The right contraction, Hestenes’ inner product, and dot product were implemented following Eqs. (2.8), (2.9), and (2.10), respectively:

$$\begin{aligned} \begin{aligned} {\texttt {rcont(arg1, arg2)}}&\quad \sim (-1)^{s (r + 1)} \text { \texttt {lcont(arg2, arg1),}} \\ {\texttt {hip(arg1, arg2)}}&\quad \sim {\left\{ \begin{array}{ll} {\texttt {lcont(arg1, arg2)}}, &{}\quad \, r \le s\text { and }r \ne 0, \\ {\texttt {rcont(arg1, arg2)}}, &{}\quad r > s\text { and }s \ne 0, \\ \texttt {0}, &{} \quad \text { otherwise}, \end{array}\right. } \\ {\texttt {dot(arg1, arg2)}}&\quad \sim {\left\{ \begin{array}{ll} {\texttt {lcont(arg1, arg2)}}, &{}\quad \, r \le s, \\ {\texttt {rcont(arg1, arg2)}}, &{}\quad \text { otherwise}, \end{array}\right. } \end{aligned} \end{aligned}$$

where r and s denote the grade of the blades encoded by arg1 and arg2, respectively.

4.6 Other Operations

There are other important operations implemented by TbGAL that can be derived from the basic ones presented so far, or by applying simple computations. For example, the reverse of FactoredMultivector objects using the OuterProduct as FactoringProductType is implemented by the reverse(arg) function as the multiplication of the stored scalar factor by $-1$ according to the number of factors (Eq. 2.17). On the other hand, when the FactoringProductType is set to GeometricProduct, the operation is evaluated by explicitly reverting the order of the component vectors.

The rnorm_sqr(arg) function computes the squared reverse norm of a blade or versor as the product of the square of its scalar factor and the squared (metric) norm of their vector factors assuming the geometric product as the factoring product. Therefore, when arg is factored using the outer product, it must be converted to the geometric product factoring representation using Eqs. (4.8) and (4.9).

The inverse of blades and versors is efficiently evaluated by the function inverse(arg) by simplifying the combination of the rnorm_sqr(arg) and reverse(arg) functions according to Eq. (2.15).

The implementation of the unary plus (unary_plus(arg)) and unary minus (unary_minus(arg)) operations are also straightforward since those operators return, respectively, a copy of the given argument and a copy of the given argument having the signal of the stored scalar factor changed. The use of unary minus is depicted in Fig. 4 (line 13).

The addition and subtraction of blades and versors, however, is a challenging task in this factored approach because we are using a multiplicative basis. Thus, addition and subtraction are only implemented in our library for pairs of blade arguments having the same grade, and limited to k-blades with $k \in \{0, 1, n - 1, n\}$. It is because those are the only cases where it is guaranteed that adding or subtracting two blades will result in a blade.

5 Experiments and Discussion

Our experiments were performed to assess the execution time and the supported dimensionality of the presented library in comparison to other C++ libraries, library generators, and code optimizers. We performed the comparison in a workstation running Ubuntu 16.04 operating system on bare metal. The workstation was equipped with two Intel Core i7-4960X processors with 3.60 GHz ($2 \times 6$ cores), and 64 Gb of RAM. The C++ source codes were compiled using GCC 7 (single thread) with O3 optimization in release mode.

Fig. 6

Histograms of mean execution times for the compared solutions assuming $n = 4$, Euclidean metric, and all possible combinations of grades

Fig. 7

Histograms of mean execution times for the compared solutions assuming $n = 7$, Euclidean metric, and all possible combinations of grades

We compared TbGAL against the four most used GA solutions developed for scientific purposes. The compared solutions are: Gaalop [6], Garamon [2], frame-based version of GluCat [24], and Versor [7]. The decision of not including the matrix-based version of GluCat is based on the higher execution times achieved by this version of the library. Since both matrix and frame-based versions belong to the same library, we used the one with better performance. In this paper, we do not include results for GATL [12] because its performance regarding the operations considered in our analysis is equivalent to Versor’s. It is important to emphasize that we did not consider handcrafted solutions in our experiments, even though they would allow higher dimensionalities. Therefore, the libraries, library generators, and code optimizers where evaluated as is.

We orchestrated the solutions to load blades having grade $0 \le k \le n$ defined for $\bigwedge \mathbb {R}^{n}$ with $n \in \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 16, 32, 64, 128, 256\}$ under Euclidean metric, and measured the mean execution times of 10 evaluations of the geometric product, outer product, left contraction, and Hestenes’ inner product. The only exceptions were Gaalop and Versor, which do not implement, respectively, the left contraction and Hestenes’ inner product as native functions. In those cases, we performed the execution-time analysis only for the operations that are implemented.

We used sets of k-blades defined by k linearly independent vectors. Double-precision floating-point values represented the coefficients of the factor vectors. They were randomly generated using a normal distribution.

In this section, we discuss the results related to $\bigwedge \mathbb {R}^{4}$, $\bigwedge \mathbb {R}^{7}$, $\bigwedge \mathbb {R}^{16}$, and $\bigwedge \mathbb {R}^{256}$. The full set of results is available as Supplementary Material. We have chosen to discuss the results for $n = 4$ (Fig. 6) because this is the dimensionality of the vector space in the 3-dimensional homogeneous/projective model of GA. In our opinion, this is the smallest useful dimensionality in practical geometric problems. We present results for $n = 7$ (Fig. 7) because this is the largest dimensionality supported by all compared solutions. Besides that, we present results for $n = 16$ (Fig. 8) because this is a relatively high dimensionality, when considering the libraries in general. Finally, this section also discusses results regarding $n = 256$ (Fig. 1) because it is the maximum practical dimensionality supported by TbGAL. Runtime and numerical instability restrict the workstation used in the experiments for more than $n = 300$ dimensions. The maximum dimensionality were TbGAL was capable to evaluate the implemented procedures was $n = 1536$. The bottleneck for higher dimensionalities is the amount of RAM available.

For the geometric product in $n = 4$ (leftmost column of Fig. 6), Gaalop and Versor showed the same behavior, with low execution times distributed nearby zero. It was expected, since the operations of both libraries are resolved, each one in its way, in compilation time. For the same operation and dimensionality, the execution time of GluCat is concentrated around 0.0015 ms. The execution times of Garamon, on the other hand, are scattered along the time axis between 0.001 and 0.005 ms. TbGAL shows a scattered histogram with values ranging from 0.002 to 0.013 ms. We believe that such behavior is related to the overhead of performing matrix operations. Such overhead is proportionally less expressive at higher dimensionalities.

The second column of Fig. 6 shows the execution times for the outer product in $n = 4$. Here, we notice the similarity between Gaalop and Versor again. For Garamon, the times are scattered between 0.0007 and 0.0016 ms, while the range of GluCat is larger and slightly right-shifted on the histogram, ranging from 0.0013 to 0.0030 ms. TbGAL shows a bimodal distribution on the histogram. The distribution refers to the evaluations of the outer product when there is linear dependency between the operands. When this happens, the operation returns zero as a result without performing any other computation. When there is no linear dependency, the execution time of the operations range from 0.0024 to 0.0037 ms.

The execution times for the left contraction in $n = 4$ are depicted in the third column of the Fig. 6. Versor, similarly to its results for the geometric product, shows small execution times concentrated in one bin, i.e., the execution times are not scattered along the time axis of the histogram. Since Gaalop does not implement this operation directly, its histogram is empty. Garamon and GluCat show similar results for this, while TbGAL presents small but distributed execution times. It is important to notice the concentration of values close to zero in TbGAL results. Those executions are associated to a grade checking of the blades being operated, i.e., if the grade of the right-hand side ($\texttt {rhs}$) argument is smaller than the grade of the left-hand side ($\texttt {lhs}$) then the operation returns zero without performing any extra computation. This result can also be seen in Fig. 1 as the blue upper triangle w.r.t. the anti-diagonal of the heatmap that summarizes the execution times.

As depicted in Fig. 6, there is a bimodal distribution for TbGAL for Hestenes’ inner product in $n = 4$. Garamon and GluCat shows less scattered distributions, with execution times up to 0.0044 and 0.0022 ms, respectively. In this dimensionality, TbGAL has execution times from 0.0065 to 0.0087 ms, which leads to a higher concentration of the bars on the right side of the plot.

When increasing the dimensionality of the space, we notice that Gaalop and Versor still very similar when considering $n = 7$ and the geometric product (Fig. 7, first column). The execution times for both libraries is smaller than 0.0034 ms for all the grade combinations. Although the execution times are slightly different, the distribution of execution times for Garamon and GluCat is very similar. Both are less scattered along the time axis than TbGAL. This behavior is inverted for when $n \ge 8$, i.e., TbGAL has a less distributed and a smaller execution time than GluCat and Garamon, respectively. Please refer to Supplementary Material in order to view this information.

For the outer product in $n = 7$ (Fig. 7, second column) we notice that most of TbGAL executions times are between 0 and 0.0067 ms, while mostly of execution times of Garamon and GluCat, which are very similar, are between 0 and 0.0034 ms. In this experiment, we noticed that Garamon is slightly faster than Glucat but the difference, just like the difference between Gaalop and Versor, can be neglected.

For the left contraction in $n = 7$, depicted in Fig. 7 (third column), we notice execution times for Versor close to zero. Both GluCat and TbGAL avoids computations where the difference of the grades for each operand leads to zero. Their histogram, however, shows smaller execution times for GluCat with times ranging from 0.001 to 0.0055 ms while the execution times for TbGAL ranges from 0.0025 to 0.0087 ms, when ignoring execution times close to zero. Garamon, despite not performing a pre-checking of the grades before computing the left contraction, achieved good execution times, ranging from 0.001 to 0.008 ms. the empty histogram for Gaalop is due to the fact that this operation is not directly implemented in this library.

Differently from $n = 4$, Hestenes’ inner product in $n = 7$ shows that TbGAL outperforms Garamon with a less scattered distribution on the left portion of the histogram. On the other hand, it is outperformed by GluCat (Fig. 7, fourth column). Besides that, while the operation between scalars is computed with an execution time close to zero for GluCat and TbGAL, it seems to be linearly increased in Garamon. For Gaalop, as expected, the execution times are close to zero.

Fig. 8

Histograms of mean execution times for the compared solutions assuming $n = 16$, Euclidean metric, and all possible combinations of grades. For the sake of clarity, results for Garamon are on a different scale

We were able to run the experiments for $n = 16$ for only three libraries: Garamon, GluCat, and TbGAL. For Gaalop, the size of the configuration file assuming $n = 16$ is about 96.6 Gb, making the pre-compilation impossible for $n \ge 16$ in our current setup. We present the results of Garamon in a different scale for $n = 16$ due to its higher execution times.

In Fig. 8 (top and middle), the time histograms for GluCat and TbGAL show that the bars are higher on the left portion of the plot, which indicates smaller execution times. Notice, however, that Glucat distribution has a longer tail than TbGAL. This means that, although the execution times are reduced for both implementations, GluCat presents more variation in execution times. Garamon has the highest execution times for this dimensionality (Fig. 8, bottom), with most operations taking about 37 s to run.

For the outer product in $n = 16$ (second column of Fig. 8), similarly to the geometric product histograms, GluCat presents more occurrences scattered across the time axis, which shows that for some operands the execution time can reach 1.2 ms, while TbGAL concentrates its execution times in only one bin that goes up to 0.15 ms.

For the left contraction in $n = 16$ (Fig. 8), about a half of the operations has execution time lesser than 0.002 ms) for TbGAL due to the grade checking before the operations. The other half of the operations are performed in times between 0.006 and 0.026 ms, which led to all those operations concentrated in one bin. GluCat, on the other hand, has execution times between 0 and 0.2855 ms.

For the Hestenes’ inner product, whose results for $n = 16$ are depicted in the fourth column of Fig. 8, we notice that Glucat has one extra bin when compared to TbGAL. For both libraries, the operation when one of the operands is a scalar value has the shortest execution times.

Figure 1 shows the execution times of TbGAL for $n = 256$. The left plot refers to execution times of each pair of operands, while the right plot corresponds to the histogram of the execution times. The execution time of the geometric product (a) is deeply related to the grade of the left-hand side operand. Notice that the execution times vary more when increasing the grade of the lhs operand. This behavior can also be observed for other cases of n (refer to the Supplementary Material for details). The reason for the lack of symmetry on the processing time is that the cost of the algorithm implemented by TbGAL is cubic on the number of factors in lhs when the current factor in rhs is linear dependent on the space spanned by the vector factors in lhs (see the algorithm in Fig. 5).

The geometric product is the most costly operation in our library, with a histogram of execution time scattered along the time axis with values ranging from 0 to 2100 ms. That is the reason why it is presented on a different scale from the other operations. The outer product (b), left contraction (c), and Hestenes’ inner product (d) have the distribution of execution times slightly shifted to the left or the right. For both outer product and left contraction, there are about half of the operations concentrated in bins close to zero (represented on the heatmaps as the blue triangular portions). It is because the grade of operators and the expected grade of the result are checked. The execution times for the outer product (without considering the values close to zero), ranges from 2 to 13 ms. Both left contraction and Hestenes’ inner product have execution times ranging from 5 to 16 ms.

6 Conclusions and Future Work

We presented TbGAL, a C++ library for GA and its front-end for Python 2 and 3. Our solution is based on blades and versors factorizations. It can handle higher dimensionality when compared to other existing GA libraries, library generators, and code optimizers. As limitations, we consider the maximum practical limit of $n = 256$ dimensions, even though we were able to run the library in higher dimensionalities at the cost of longer processing time and round-off error. Besides that, for now, our library is limited to arbitrary metric spaces having (p, q, 0) signatures. As expected, general multivectors are not handled by TbGAL. However, in practice, it is not a limitation when one is working with GA. As pointed by Dorst et al. [11, Section 7.7.2], in contrast to Clifford algebra, GA permits exclusively multiplicative constructions and combinations of elements. The only exceptions are the addition and subtraction of scalar values, vectors, pseudovectors, and pseudoscalars. It is because all results produced by multiplication using any of the products derived from the geometric product do have a geometrical interpretation. A practical interpretation of general multivectors is not known.

We are currently working on the implementation of TbGAL as a full-parallel library for real-time processing on GPU, and extending its capabilities to arbitrary (p, q, r) metric spaces with $r \ne 0$. Also, our library does not include visualization routines. We believe that this capability is well performed by other solutions, like ganja.js. Therefore, we are planning to call ganja.js from a sub-module of our Python ports to render GA objects.