Application of Wavelets in Numerical Evaluation of Hankel Transform Arising in Seismology

Abstract

The computation of electromagnetic (EM) fields for 1-D layered earth model requires evaluation of Hankel transform. In this paper we propose a stable algorithm for the first time that is quite accurate and fast for numerical evaluation of the Hankel transform using wavelets arising in seismology. We have projected an approach depending on separating the integrand tf(t)J _ν (pt) into two components; the slowly varying components tf(t) and the rapidly oscillating component J _ν (pt). Then either tf(t) is expanded into wavelet series using wavelets orthonormal basis and truncating the series at an optimal level or approximating tf(t) by a quadratic over the subinterval using the Filon quadrature philosophy. The solutions obtained by proposed wavelet method applied on three test functions indicate that the approach is easy to implement and computationally very attractive. We have supported a new efficient and stable technique based on compactly supported orthonormal wavelet bases.

17.1 Introduction

Electromagnetic (EM) depth sounding is, under favorable conditions, extremely useful in petroleum exploration, groundwater exploration, permafrost thickness determination exploration of geothermal resources, and foundation engineering problems. However, for data interpretation one needs fast and efficient computations of geoelectromagnetic anomaly equations. These equations appear as Hankel Transform (HT) (also known as Bessel Transform).

17.1.1 Hankel Transform

The efficient and accurate evaluation of the Hankel transform is required in a number of applications. This paper reviews a number of algorithms that have only recently been exposed in the literature. It is found that the performance of all algorithms depends on the type of function to be transformed. The wavelet based methods provide acceptable accuracy with better efficiency than numerical quadrature.

17.1.2 Mathematical Background

The general Hankel transform pair with the kernel being J _ν is defined as [1]

$$ F_{\nu } (p) = \int\limits_{0}^{\infty } {tf(t)J_{\nu } (pt){\text{d}}t} , $$

(17.1)

and Hankel transform being self reciprocal, its inverse is given by

$$ f(t) = \int\limits_{0}^{\infty } {pF_{\nu } (p)J_{\nu } (pt){\text{d}}p} , $$

(17.2)

where $J_{\nu }$ is the νth-order Bessel function of first kind. Due to oscillatory behaviour of J _ν (pt), standard quadrature methods applied to these integrals can be slow to convergence or may fail if the integral is divergent. It is only recently, mainly in the last 20 years, that attention has been turned to discovering algorithms useful for numerical evaluation of the Hankel transform. In this time a variety of algorithms of various strengths, weakness, and applicability’s have been reported. As sometimes happens, the relevant literature is distributed through a number of journals, some of it in apparent ignorance of other research.

We believe it is now timely to bring this literature together, giving a review of the main methods available and providing pointers to some of the less efficient, but nevertheless elegant, methods.

17.1.3 Historical Background of Numerical Transforms Techniques

The literature concerning numerical Hankel transform techniques is very sparse from Longman until the late seventies when a flurry of papers were published on the topic. The various algorithms that have been published during and since the seventies can be filled into a few general categories. They are:

• (1) Numerical quadrature

• (2) Logarithmic change of variables

• (3) Asymptotic expansion of the Bessel function

• (4) Projection-slice/back projection method

Numerical evaluation of Hankel transforms is ubiquitous in the mathematical treatment of physical problems involving cylindrical symmetry, optics, electromagnetism and seismology. Many different types of algorithms and software have been developed to evaluate numerically hankel transform integrals in Geophysics [2, 3]. The ubiquity of these integrals in EM geophysics motivates the need for accurate and efficient numerical integral techniques.

17.1.4 Motivation of Present Work

• (A) The Hankel transform arises naturally in the discussion of problems posed in cylindrical coordinates (with axial symmetry) and hence, as a result of separation of variables involving Bessel functions.

• (B) Analytical evaluations are rare and hence numerical methods become important. The usual classical methods like Trapezoidal rule, cotes rule etc. connected with replacing the integrand by sequence of polynomials have high accuracy if integrand is smooth. But tf(t) J _ν (pt) and pF _ν (p) J _ν (pt) are rapidly oscillating functions for large t and p, respectively.

To overcome these difficulties, various different techniques are available in the literature.

• (1) Fast Hankel Transform Here, by substitution and scaling, the problem is transformed in the space of the logarithmic co-ordinates and the fast Fourier transform in that space.

• (2) Filon quadrature philosophy In Filon quadrature philosophy, the integrand is separated into the product of an (assumed) slowly varying component and a rapidly oscillating component. In the context of the Hankel transform, the former is tf(t) and the latter is J _ν (pt). This method works quite well for computing F ₀(p), for p ≥ 1, but the calculation of inverse Hankel transform is more difficult, as F ₀(p) is no longer a smooth function but a rapidly oscillating one. Moreover the error is appreciable between 0 < p < 1.

Several papers have been written to the numerical evaluation of the HT in general and the zeroth-order in particular [4–12]. There are two general methods of the effective calculation in this area. The first is the fast Hankel transform [13, 14]. The specification of that method is transforming the function to the logarithmical space and fast Fourier transform in that space. This method needs a smoothing of the function in log space. The second method is based on the separation of the integrand into product of slowly varying component and a rapidly oscillating Bessel function [15]. But it needs the smoothness of the slow component for its approximation by lower-order polynomials.

17.2 Preliminaries

17.2.1 Wavelets

Wavelets are a class of function constructed from dilation and translation of a single function called the mother wavelet. When the dilation and translation parameters a and b vary continuously, the following family of continuous wavelets are obtained

$$ \psi_{a,b} (t) = \left| a \right|^{{ - \frac{1}{2}}} \left( {\frac{t - b}{a}} \right),\quad a,b \in R,a \ne 0. $$

When the parameters a and b are restricted to discreet values as $a = 2^{ - k} ,b = n2^{ - k}$,

Then, we have the following family of discrete wavelets

$$ \psi_{kn} (t) = 2^{{\frac{k}{2}}} \psi \left( {2^{k} t - n} \right),\quad k,n \in Z, $$

where the function $\psi$, the mother wavelet, satisfies $\int {_{R} \psi (t)} {\text{d}}t = 0.$

We are interested in the case where $\psi$ _kn constitutes and orthonormal basis of L ²(R). A systematic way to do this is by means of multiresolution analysis (MRA).

In 1910, Haar [16] constructed the first orthonormal basis of compactly supported wavelets for L ²(R). It has the form $\{ 2^{{\frac{j}{2}}} \psi (2^{j} t - k):j,k \in Z\}$ where the fundamental wavelet $\psi$ is constructed as follows:

Construct a compactly supported scaling function ϕ by the two-scale scaling relation $\phi (t) = \phi (2t) + \phi (2t - 1)$ together with the normalization constraint $\int {\varphi (t){\text{d}}t} = 1$. A solution of this recursion that represents φ in L ²(R) is $\chi_{[0,\,1)}$.

Then $\psi (t) = \varphi (2t) - \varphi (2t - 1)$. The Haar wavelets are piecewise continuous and have discontinuities at certain dyadic rational numbers.

In seminal papers; Daubechies [17, 18], constructed the first orthonormal basis of continuous compactly supported wavelets for L ²(R). They have led to a significant literature and development, both in theoretical and applied arenas.

Later in 1989, Mallat [19] studied the properties of multiresolution approximation and proved that it is characterized by a 2π-periodic function. From any MRA, one can derive a function $\psi$(t) called a wavelet such that $\left\{ {2^{{\frac{j}{2}}} \psi \left( {2^{j} t - k} \right):\,\,j,\,k \in Z} \right\}$ is an orthonormal basis of L ²(R). The MRA showed the full computational power that this new basis for L ²(R) possessed. In the same year, Mallat [20] applied MRA for analysing the information content of the images.

Note that a system $\left\{ {\varphi_{k} :k \in Z} \right\}$ is called a Riesz basis if it is obtained from an orthonormal basis by means of a bounded invertible operator.

Definition

The increasing sequence $\left\{ {V_{k} } \right\}_{k \in Z}$ of closed subspaces of L ²(R) with scaling function $\varphi \in V_{0}$ is called MRA if

• (i) $\bigcup\nolimits_{k} {V_{k} }$ is dense in L ²(R) and $\bigcap\nolimits_{k} {V_{k} } = \left\{ 0 \right\}$,

• (ii) $f(t) \in V_{k}$ iff $f(2^{ - k} t) \in V_{0}$,

• (iii) $\left\{ {\varphi \left( {t - n} \right)} \right\}_{n \in Z}$ is a Riesz basis for V ₀.

Note that (iii) implies that the sequence {2^k/2 φ(2^k t − n)} _n∊Z is an orthonormal basis for $V_{k}$. Let $\psi$(t) be the mother wavelet, then $\psi (t) = \sum\limits_{n \in Z} {a_{n} \varphi \left( {2t - n} \right)}$ and $\left\{ {2^{k/2} \psi \left( {2^{k} t - n} \right)} \right\}_{k,n \in Z}$ forms an orthonormal basis for L ²(R) under suitable conditions [21–24].

CAS Wavelets $\psi_{nm} (t)\, = \,\psi (k,n,m,t)$ involve four arguments n, k, m and t, where $n = 0,1, \ldots ,2^{k} - 1,k$ is assumed any nonnegative integer, m is any integer and t is normalized time. CAS wavelets are defined as [25]

$$ \psi_{nm} (t) = \left\{ {\begin{array}{*{20}c} {2^{{\frac{1}{2}}} {\text{CAS}}_{m} (2^{k} t - n),} \hfill & {{\text{for}}\;\frac{n}{2}\; \le \;t\; < \;\frac{n + 1}{{2^{k} }},} \hfill \\ {0,} \hfill & {{\text{otherwise}},} \hfill \\ \end{array} } \right. $$

(17.3)

where

$$ {\text{CAS}}_{m} (t)\, = \,\cos (2m\pi t)\, + \,\sin (2m\pi t). $$

(17.4)

It is clear that the set of CAS wavelets also forms and orthonormal basis for L ²([0, 1]).

17.3 Function Approximation

The function f(t) representing physical fields are either zero or have an infinitely long decaying tail outside a disk of finite radius R. Hence, in most practical applications either the signal f(t) has a compact support or for a given ɛ > 0 there exists a R > 0 such that $\left| {\int\nolimits_{R}^{\infty } {tf(t)J_{\nu } (pt)\,{\text{d}}t} } \right| < \varepsilon .$

Therefore, in either case,

$$ \begin{aligned} \hat{F}_{\nu } (p) & = \int\limits_{0}^{R} {tf(t)\,J_{\nu } (pt)\,{\text{d}}t} \\ & = \int\limits_{0}^{1} {tf(t)\,J_{\nu } (pt)\,{\text{d}}t} ,({\text{by}}\,{\text{scaling}}) \\ \end{aligned} $$

(17.5)

known as the finite Hankel transform (FHT) is a good approximation of the HT as given by (17.1). Writing tf(t) = g(t) in Eq. (17.5), we get

$$ \hat{F}_{\nu } (p) = \int\limits_{0}^{1} {g(t)J_{\nu } (pt){\text{d}}t} . $$

(17.6)

We may expand g(t) as follows

$$ g(t) = \sum\limits_{m = 0}^{\infty } {\sum\limits_{n = 0}^{{2^{k} - 1}} {c_{nm} \psi_{nm} (t)} } , $$

(17.7)

where $c_{nm} = \;\left\langle {g(t),\;\psi_{nm} \left( t \right)} \right\rangle$.

with (.,.) denoting the inner product.

By truncating the infinite series (17.7) at levels m = 2L and $n\, = \,2^{k} - 1$, we obtain an approximate representation for g(t) as

$$ g(t) \approx \sum\limits_{m = 0}^{2L} {\sum\limits_{n = 0}^{{2^{k} - 1}} {c_{nm} \psi_{nm} (t)} } = C^{T} \psi (t), $$

(17.8)

where the matrices C and $\psi$(t) are $2^{k} (2L + 1)\, \times \,1$ matrices given by

$$ C = [c_{0,0} ,c_{0,1} ,, \ldots ,c_{0,2L - 1} ,c_{10} , \ldots ,c_{1,2L} , \ldots ,c_{{2^{k} - 1,0}} , \ldots ,c_{{2^{k} - 1,2L}} ]^{T} $$

(17.9)

and

$$ \psi (t) = [\psi_{0,0} (t),\psi_{0,1} (t), \ldots ,\psi_{0,2L} (t),\psi_{1,0} (t), \ldots ,\psi_{1,2L} (t),\psi_{{2^{k} - 1,0}} (t), \ldots ,\psi_{{2^{k} - 1,2L}} (t)]^{T} . $$

(17.10)

Substituting (17.8) in (17.6), we get

$$ \hat{F}_{\nu } (p) \approx C^{T} \int\limits_{0}^{1} {\psi (r)J_{\nu } (pr){\text{d}}r} . $$

(17.11)

Now (17.11) reduces to

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{\nu } (p) \approx C^{\rm T} \left[ {\begin{array}{*{20}c} {\int\limits_{0}^{1} {\psi_{0,0} (r)J_{\nu } (pr){\text{d}}r,} \int\limits_{0}^{1} {\psi_{0,1} (r)J_{\nu } (pr){\text{d}}r} ,\int\limits_{0}^{1} {\psi_{0,2} (r)} J_{\nu } (pr){\text{d}}r, \ldots ,} \hfill \\ {\int\limits_{0}^{1} {\psi_{1.0} } (r)J_{\nu } (pr){\text{d}}r, \ldots ,\int\limits_{0}^{1} {\psi_{1,4} (r)J_{\nu } (pr){\text{d}}r} } \hfill \\ \end{array} } \right]^{\rm T} $$

(17.12)

where $\psi_{0,0} ,\psi_{0,1} \ldots \ldots \ldots \psi_{1,4}$ are defined through Eq. (17.3). We re-label and write (17.12) as

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F}_{\nu } (p) \approx [c_{0,0} ,c_{0,1} , \ldots ,c_{1,4} ][I_{n}^{0} ,I_{n}^{1} , \ldots ,I_{n}^{10} ]^{\rm T} , $$

(17.13)

where I ^l _ν ’s are the lth place integral in Eq. (17.12).

The integrals arising in Eq. (17.12) are evaluated by using the following formulae [26].

$$ \int\limits_{0}^{a} {J_{\nu } (t){\text{d}}t = 2\mathop {\lim }\limits_{N \to \infty } \sum\limits_{z = 0}^{N} {J_{\nu+2z+1} (a)} } ,\text{Re} \nu > {-}1 $$

(17.14)

and is calculated with the help of Simpson’s one third rule, Simpson’s three eight rule.

17.4 Numerical Implementation

Since it is always desirable to test the behaviour of a numerical scheme using simulated data, for which the exact results are known and thus making a comparison between the chosen well known test functions which are widely used by researchers in the area to validate the reliability of proposed method. Here we consider three examples for the numerical solutions on the prescribed method, in order to check the accuracy of our scheme. The simplicity and accuracy of sine-cosine wavelet method is illustrated by computing the absolute error graphically.

$$ E\hat{F}_{\nu } (p) = F_{\nu } (p) - \hat{F}_{\nu } (p) $$

In this section, we test the proposed algorithm (17.13) by evaluating the approximate Hankel transforms of 2 well known test function with known analytical Hankel transforms. Note that in all the examples the truncation is done at level m = 2L and L = 2, we observed that the accuracy of the method is very high even at such a low level of truncation. Note that the various graphs in the examples are plotted and sample points are chosen as p = 0.01(0.01)N, where N = 60 in all the figures.

Example 1

Let $f(r) = r^{\nu } \sin (\frac{{\pi r^{2} }}{4}),0 \le r < 1,$ then

$$ F_{\nu } (p) = \frac{1}{\sqrt 2 }\left( {\frac{\pi }{2}} \right)^{ - \nu - 1} p^{\nu } \left[ {U_{\nu + 1} \left( {\frac{\pi }{2},p} \right) - U_{\nu + 2} \left( {\frac{\pi }{2},p} \right)} \right] $$

(obtained from (p. 34, (16), [26] by putting $a\, = \,\frac{\pi }{4},\,\,\,\,b\, = \,1$),

where $U_{\nu } (w,\,\,p)$ is a Lommel’s function of two variables,

$$ = \frac{1}{\sqrt 2 p}\left[ {\sum\limits_{\eta \, = 0}^{L} {\left[ {( - 1)^{\eta } \left( {\frac{\pi }{2p}} \right)^{2\,\eta } \left( {J_{\nu + 2\eta \, + 1} (p) - \frac{\pi }{2p}J_{\nu + 2\eta + 2} (p)} \right)} \right]} } \right]\,{\text{as}}\,L \to \infty $$

(17.15)

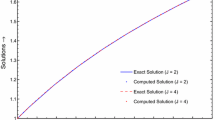
The comparison of the approximation Hν(p) (dotted line) with the exact Hankel transform Fν(p) (solid line) is shown in Figs. 17.1 and 17.3 and the error $E(p)\, = \,H\nu (p) - F\nu (p)$ in Figs. 17.2 and 17.4.

Fig. 17.1

The exact transform, Fν(p) (solid line) and the approximate transform, Hν(p) (dotted-line) where ν = 0

Fig. 17.2

Comparison of the errors

Simpson’s one third rule

Simpson’s three eight rule

Fig. 17.3

The exact transform, Fν(p) (solid line) and the approximate transform, Hν(p) (dotted-line) where ν = 0

Fig. 17.4

Comparison of the errors

Example 2

In this example, we choose as a test function the generalized version of the top-hat function, given as

$f(r) = r^{\nu } \,[H(r) - H(r - a)],\,\,a > 0$ and H(r) is the step function given by

$$ H(r) = \left\{ {\begin{array}{*{20}c} {1,} \hfill & {r \ge 0} \hfill \\ {0,} \hfill & {r < 0} \hfill \\ \end{array} } \right.. $$

Then,

$$ F_{\nu } (p) = \frac{{J_{\nu + 1} (p)}}{p}. $$

(17.16)

Guizar-Sicairos [27], took a = 1 and ν = 4 for numerical calculations. We take a = 1, ν = 0, and observe that the error is quite small as shown in Fig. 17.5 and 17.7. The comparison of the approximate with exact transform is shown in Figs. 17.6 and 17.8.

Fig. 17.5

The exact transform, Fν(p) (solid line) and the approximate transform, Hν(p) (dotted-line)

Fig. 17.6

Comparison of the errors

Simpson’s one third rule

Simpson’s three eight rule

Fig. 17.7

The exact transform, Fv(p) (solid line) and the approximate transform, Hv(p) (dotted-line)

Fig. 17.8

Comparison of the errors

Example 3

Let $f(r) = (1 - r{}^{2})^{1/2}$, 0 ≤ r ≤ 1, then,

$$ F_{1} (p) = \left\{ {\begin{array}{*{20}c} {\pi \frac{{J_{1}^{2} (p/2)}}{2p},} \hfill & {0 < p < \infty } \hfill \\ {0,} \hfill & {p = 0} \hfill \\ \end{array} } \right.. $$

(17.17)

Barakat et al., evaluated F ₁(p) numerically using Filon quadrature philosophy but again the associated error is appreciable for p < 1; whereas our method give almost zero error in that range. The comparison of the approximation F(p) (dotted line) with the exact Hankel transform F1(p) (solid line) is shown in Figs. 17.9 and 17.11 and the error E(p) = F(p) − F1(p) in Figs. 17.10 and 17.12.

Fig. 17.9

The exact transform, F1(p) (solid line) and the approximate transform, F(p) (dotted-line)

Fig. 17.10

Comparison of the errors

Simpson’s one third rule

Simpson’s three eight rule

Fig. 17.11

The exact transform, F1(p) (solid line) and the approximate transform, F(p) (dotted-line)

Fig. 17.12

Comparison of the errors

17.5 Summary and Conclusion

Since the basis functions used to construct the wavelets are orthogonal and have compact support, it makes them more useful and simple in actual computations. Also, since the numbers of mother wavelet’s components are restricted to one, so they do not lead to the growth of complexity of calculations.

Wavelet method is very simple and attractive [27]. The implementation of current approach in analogy to existed methods is more convenient and the accuracy is high. The numerical example and the compared results support our claim. The difference between the exact and approximate solutions for each example plotted graphically to determine the accuracy of numerical solutions.

17.5.1 Future Work

Since computational work is fully supportive of compatibility of proposed algorithm and hence the same may be extended to other physical problems also. A very high level of accuracy explicitly reflects the reliability of this scheme for such problems. We would like to stress that the approximate solution includes not only time information but also frequency information due to the localization property of wavelet basis; with some change we can apply this method with the help of other wavelet basis.