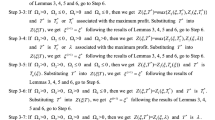Inventory Modelling of Deteriorating Item and Preservation Technology with Advance Payment Scheme Under Quadratic Demand

Abstract

This chapter comprises a single retailer and single product which deteriorates continuously. For the time-dependent deteriorating item with seasonal demand, quadratic demand is debated here which is suitable for the items whose demand with starting of the season increases initially and after end of the season, it starts to decrease. To reduce deterioration of the product, retailer needs preservation technology and due to preservation technology retailer minimizes total cost. In this chapter, the retailer has to pay a fraction of the purchase cost before the time of delivery and rest of the payment must be paid at the time of delivery. In this chapter, the optimal number of equal instalments before receiving the order quantity, replenishment time and investment of preservation technology are the decision variables that minimize the total cost. This chapter is an extension of the earlier work, as it provides the best optimal rather than the nearest minimum solution. A numerical example is delivered to demonstrate the performance of the model and to highlight certain decision-making insights.

4.1 Introduction

It is a corporate exercise by the vendor to request a retailer to advance credits for purchasing periodic and instantaneous perishable items. By doing so, a retailer may get a price reduction or an on-time distribution in return. In the current study, Taleizadeh [1] studied a model for deteriorating product for an economic order quantity (EOQ). Simultaneously, Taleizadeh [2] elaborated partial backlogging, where he obtained a near-best minimum solution using a truncated Taylor series expansion. In his circumstance, the deterioration rate reaches to zero but never extends to null. Ishii et al. [3] developed joint policies for three players, viz., vendor, wholesaler and retailer. Haq et al. [4] established the concept of joint inventory system with one vendor, several wholesalers and several retailers. Goyal and Nebebe [5] determined a model for deteriorating item under shipment policy and production for a two-layered supply chain. Woo et al. [6] studied a coordinated strategies for a manufacturer and multi-retailers. Authors measured manufacturer to be produced. Rau et al. [7] minimized an objective function of the supply chain under deteriorating items with three-echelon system. Shah et al. [8] discussed a coordinated decision when demand is quadratic. Shah et al. [9,10,11] developed optimal payment policies, pricing and shipment for a two-echelon system for deteriorating items under buoyant demand and up- and downstream trade credit. Shah and Shukla [12] analysed a two-layered inventory model for optimum pricing strategies and ordering under the retailer partial trade credit when demand is declining.

Due to extreme changes in the environment, most of the items loss their efficiency over time, termed as deterioration. Deterioration of goods like fruits (mango, i.e. seasonal famous fruit of India) and root vegetables. Out of many studies on deterioration product, only rare of them have considered fixed lifetime issue of deteriorating items. Ghare and Schrader [13] analysed inventory model with deterioration. Raafat [14], Shah and Shah [15], Goyal and Giri [16], and Bakker et al. [17] analysed the research articles on deteriorating items for inventory system. Chung and Cardenas-Barrón [18] developed an algorithm of stock-dependent demand and two-level trade credit in a supply chain comprising of three players for deteriorating items. Furthermore, Shah and Barrón [19] determined the retailer’s verdict for credit policies and ordering for deteriorating items when a supplier offers order-linked credit period or cash discount.

On the other hand, to reduce the deterioration, Hsu et al. [20] studied an inventory model to minimize the deterioration rate of inventory for constant demand with preservation technology investment. Dye and Hsieh [21] evaluated a model for optimal cycle time with effective investment in preservation technology for deteriorating items. Hsieh and Dye [22] analysed when demand is fluctuating with time, a production inventory model incorporating the effect of protection technology investment. Recently, Shah and Shah [23] evaluated an inventory model for demand depending on price and time under inflation to optimal cycle time and preservation technology asset for deteriorating items. Later on Shah, et al. [24] developed an integrated inventory model for deteriorating item which depends on time under price and time-sensitive demand. Moreover, Shah et al. [25] established optimal policies under selling price and trade credit-dependent quadratic demand in a supply chain for time-varying deteriorating item with preservation technology.

This chapter develops an inventory model for a retailer to minimize his total cost. It is assumed that the demand rate decreases quadratically. To reduce deterioration of the product, retailer needs preservation technology and due to preservation technology retailer minimizes his total cost. In this chapter, the retailer has to pay a fraction of the purchase cost before the time of delivery and rest of the payment must pay at the time of delivery. Under above assumptions, the objective is to minimize the cost of retailer with respect to the optimal number of equal instalment before receiving the order quantity replenishment time and preservation technology investment.

The remaining of the chapter is systematized as follows. Section 4.2 contains the notations and the assumptions part that are used in model. Section 4.3 is about formulation of the proposed mathematical model. Section 4.4 validates the derived inventory model with numerical instances and its sensitivity analysis. This section also provides some managerial insights. Finally, Sect. 4.5 provides a conclusion and future research directions.

4.2 Notation and Assumptions

Following are the notation and assumption that are used in mathematical inventory model.

4.2.1 Notation

Retailer’s parameters
$a$	Total scale demand of the product, $a\, > \,0$
$b$	Linear rate of change of demand of the product, $0\, \le \,b\, < 1$
$c$	Quadratic rate of change of demand of the product, $0\, \le \,c\, < 1$
$A_{r}$	Ordering cost per order incurred by the retailer ($/order)
$C_{r}$	Purchasing cost per unit item (in $)
$T_{t}$	The length of time during which the prepayments are paid, $T_{t} > 0$(in year)
$r$	The interest rate of capital cost per dollar per year, $0\, \le \,r \le 1$
$\alpha$	The fraction of the purchase cost to be prepaid before the time of delivery, $0\, \le \,\alpha \le 1$
$CC$	Capital total cost
$\theta (t)$	Deterioration rate; $0 \le \theta \left( t \right) \le 1$
$m$	Fixed lifetime of the product (in years)
$n$	The number of equal prepayments before receiving the order quantity (decision variable)
$u$	Investment of preservation technology investment per unit time (in $)(decision variable)
$f\left( u \right)$	$= 1 - \frac{1}{1 + \mu u}$ amount of reduced deterioration item (in year), $\mu > 0$
$I_{r} \left( t \right)$	Inventory level for the retailer of item at any time $t$(units)
$T$	Cycle time (unit time) of the retailer (decision variable)
$Q$	Retailer’s order quantity at time $t$
$h_{r}$	Holding cost rate for retailer per unit per annum for the product
$HC_{r} \left( t \right)$	Time-dependent holding cost of retailer for item ($/unit/unit time)

Relations between parameters:

• $T \le m$

• $0 \le \theta \left( t \right) < 1$

• Parameters of retailer:

$R\left( t \right)$	Time-dependent quadratic demand rate; $R\left( t \right) = a \cdot \left( {1 + bt - ct^{2} } \right)$, where $a > 0$ is scale demand, $0 < b,c < 1$ are rates of change of demand, respectively.
$TC_{r} \left( {n,T,u} \right)$	Total cost of the retailer per unit time ($/unit/unit time)

Minimization of the problem for the retailer is expressed as follows:

$$ \hbox{min} \,\,TC_{r} \left( {n,T,u} \right) $$

$$ \begin{aligned} & {\text{Subject to constraints}} \\ & \quad \quad \quad \quad \quad T \le m \\ \end{aligned} $$

4.2.2 Assumptions

• 1. The inventory system involves single retailer and single non-instantaneous deteriorating item.

• 2. The demand rate, $R\left( t \right) = a \cdot \left( {1 + bt - ct^{2} } \right)$ (say), is function of time, $a\, > \,0$ is total scale demand, $0\, \le \,b\, < 1$ denotes the linear rate of change of demand with respect to time and $0\, \le \,c\, < 1$ denotes the quadratic rate of change of demand.

• 3. Time prospect is infinite.

• 4. Shortages are not permitted.

• 5. Lead time is zero or negligible.

• 6. The instantaneous rate of deterioration is $\theta \left( t \right) = \frac{1}{1 + m - t},\;0 \le t \le T \le m$; for any finite value of $m$, we have $\theta \left( t \right) < 1$. If $m \to \infty$, then $\theta \left( t \right) \to 0$, i.e. the item is non-deteriorating.

• 7. For extremely periodic items or perishable product, the vendor frequently demands $\alpha$ fractions of purchasing cost $PC_{r}$ to be prepaid (i.e.$\alpha \cdot PC_{r}$) before the time of delivery. Then the outstanding purchase cost $\left( {1 - \alpha } \right) \cdot PC_{r}$ is paid at the point of delivery. Notice that if $\alpha = 0$ then the vendor does not request prepayment. Instead of if $\alpha = 1$, then the vendor requests the retailer to prepay the entire purchase cost.

• 8. The vendor settles to prepay $\alpha \cdot PC_{r}$ by $n$ equal payments in $T_{t}$ years previous to the time of delivery and pay the rest of $\left( {1 - \alpha } \right) \cdot PC_{r}$ at the time of receiving.

In the next section, the proposed inventory model for the retailer is developed.

4.3 Mathematical Model

The proposed models for deteriorating items with equally multiple instalments of $\alpha$ fractions of the purchase cost and remaining instalment would be paid at the time of purchasing the product.

In general, the retailer pays the vendor α portions of the purchasing cost by $n$ equal instalments in $T_{t}$ years earlier to the time of purchasing. The vendor receives the remaining unpaid balance $\left( {1 - \alpha } \right) \cdot PC_{r}$ instantly at the product delivery. Thereafter, the retailer’s inventory level is regularly exhausted to zero by the end of the cycle $T$, due to the mixture of demand and deterioration. Hence, the inventory level at time t as follows:

$\frac{{dI_{r} \left( t \right)}}{dt} = - R\left( t \right) - \left( {1 - f\left( u \right)} \right)\theta \left( t \right)I_{r} \left( t \right)$, $0 \le t \le T$ with the boundary condition $I_{r} \left( T \right) = 0$. Solving above differential equations, we get

$$ I_{r} \left( t \right) = \frac{1}{{\left( {6\mu^{2} + 7\mu u + 2} \right)\mu u}}\left( {1 + \mu u} \right)\left( \begin{aligned} \left( {1 + m - t} \right)^{{1 - \frac{1}{\mu u + 1}}} a\left( {\begin{array}{*{20}l} { - 2cm^{2} \mu^{2} u^{2} - 2cm\mu^{2} tu^{2} } \hfill \\ { - 2c\mu^{2} t^{2} u^{2} + 3bm\mu^{2} u^{2} } \hfill \\ { + 3b\mu^{2} tu^{2} - 4cm\mu^{2} u^{2} } \hfill \\ { - 2c\mu^{2} tu^{2} + 3b\mu^{2} u^{2} } \hfill \\ { - 4cm^{2} \mu u - 2cm\mu u} \hfill \\ {2c\mu^{2} u^{2} - c\mu t^{2} u} \hfill \\ { + 5bm\mu u + 2b\mu tu} \hfill \\ { - 8cm\mu u - 2c\mu tu} \hfill \\ { + 6\mu^{2} u^{2} + 5b\mu u - 2cm^{2} } \hfill \\ { - 4c\mu u + 2bm - 4cm} \hfill \\ { + 7\mu u + 2b - 2c + 2} \hfill \\ \end{array} } \right) \hfill \\ - \left( {1 + m - T} \right)^{{1 - \frac{1}{\mu u + 1}}} a\left( {\begin{array}{*{20}l} { - 2cm^{2} \mu^{2} u^{2} - 2cm\mu^{2} Tu^{2} } \hfill \\ { - 2c\mu^{2} T^{2} u^{2} + 3bm\mu^{2} u^{2} } \hfill \\ { + 3b\mu^{2} Tu^{2} - 4cm\mu^{2} u^{2} } \hfill \\ { - 2c\mu^{2} Tu^{2} + 3b\mu^{2} u^{2} } \hfill \\ { - 4cm^{2} \mu u - 2cm\mu u} \hfill \\ {2c\mu^{2} u^{2} - c\mu T^{2} u} \hfill \\ { + 5bm\mu u + 2b\mu Tu} \hfill \\ { - 8cm\mu u - 2c\mu Tu} \hfill \\ { + 6\mu^{2} u^{2} + 5b\mu u - 2cm^{2} } \hfill \\ { - 4c\mu u + 2bm - 4cm} \hfill \\ { + 7\mu u + 2b - 2c + 2} \hfill \\ \end{array} } \right) \hfill \\ \end{aligned} \right) $$

Therefore, the order quantities per replenishment cycle are $Q = I_{r} \left( 0 \right)$.

Now, the total cost per unit time of retailer included the following:

• $\text{Ordering\,cost\,per\,unit}: OC_{r} = A_{r}$

• $\text{Purchase\,cost\,per\,unit}: PC_{r} = C_{r} Q$

• $\text{Inventory\,holding\,cost\,per\,unit}: HC_{r} = h_{r} \left[ {\int\limits_{0}^{T} {I_{r} (t)\,\,dt} } \right]$

• $\text{Investment\,for\,preservation\,technology}: PTI = u \cdot T$

• $\text{From\,Taleizadeh (2014), the\,capital\,cost\,per\,cycle\,is}\,CC = \frac{n + 1}{2n}\,\left( {\alpha \,T_{t} \,\,r\,\,} \right)PC_{r}$

The total appropriate cost of the retailer for the product is

$$ TC_{r} \left( {n,T,u} \right) = \frac{1}{T}\left( {OC_{r} + PC_{r} + HC_{r} + PIT + CC} \right) $$

The total cost function $TC_{r} \left( {n,T,u} \right)$ is a continuous function of number of instalment $n$, cycle time $T$ and investment of preservation technology ‘$u$’. We will establish endorsement of the proposed model using numerical example. The minimization of the total cost will be shown graphically for the obtained results.

4.4 Numerical Example and Sensitivity Analysis

4.4.1 Numerical Example

Example: Consider $a = 1000$ units, $b = 0.85$, $c = 0.01$, $A_{r} = \$ 100$, $C_{r} = \$ \,40\,$, $h_{r} = \$ \,10$, $\alpha = 0.4$, $T_{t} = 0.17$ year, $r = 0.1$, $m = 0.25$ year,$\mu = 1.7$. The values of the decision variables are total idle instalment of the prepayments that are $n = 6$, cycle time of replenishment is $T = 0.066$ years and $u = \$ 25.19$. This results in retailer’s minimum cost as $ 43,192.90.

The convexity of the total cost function is obtained by the well-known Hessian matrix. Now, for a fixed value of $n = 6$, Hessian matrix for the above retailer is

$$ H\left( {6,T,u} \right) = \left( {\begin{array}{*{20}c} {\frac{{\partial^{2} TC_{r} \left( {n,T,u} \right)}}{{\partial T^{2} }}} & {\frac{{\partial^{2} TC_{r} \left( {n,T,u} \right)}}{\partial T\,\partial u}} \\ {\frac{{\partial^{2} TC_{r} \left( {n,T,u} \right)}}{\partial u\,\partial T}} & {\frac{{\partial^{2} TC_{r} \left( {n,T,u} \right)}}{{\partial u^{2} }}} \\ \end{array} } \right) $$

By the above example, we get the Hessian matrix $H\left( {6,T,u} \right)$ at the point $\left( {6,T,u} \right)$

$$ H\left( {6,T,u} \right) = \left( {\begin{array}{*{20}c} {502336.28} & { - 18.36} \\ { - 18.36} & {6.079} \\ \end{array} } \right) $$

As in Barrón and Sana [26], if the eigenvalues of the Hessian matrix at the solution $\left( {6,T,u} \right)$ are all positive, then the total cost $TC_{r} \left( {6,T,u} \right)$ is minimum at that solution. Here, eigenvalues of above Hessian matrix are $\lambda_{1} = 502336.23$ and $\lambda_{2} = 6.079$. So, the cost function $TC_{r} \left( {6,T,u} \right)$ is minimum. Also, the convexity of the cost function is obtained in Fig. 4.1 with respect to cycle time and investment of preservation technology with $n = 6$.

Fig. 4.1

Convexity behaviour of the cost function for $n = 6$

4.4.2 Sensitivity Analysis for the Inventory Parameters

Therefore, for the changed inventory parameters, the sensitivity study of example is agreed out by changing one variable at a time as −20, −10, 10 and 20%.

In imperative to detect the sensitivity of the inventory parameters on the optimal solution, we consider the data as given in numerical example. Optimal solutions for different values of $a$, $b$, $c$,$A_{r}$, $C$,$h_{r}$,$\alpha$, $T_{t}$, $r$, $m$ and $\mu$ are presented in Table 4.1. The resulting statement could be made from Table 4.1.

Table 4.1 Sensitivity analysis

• 1. In Table 4.1, holding cost rate decreases cycle time slowly. However, ordering cost per order incurred by the retailer increases cycle time rapidly, whereas scale demand, linear rate of change of demand and purchase cost decreases cycle time rapidly. In addition, change in the quadratic rate of change of demand, the fraction of the purchase cost to be prepaid before the time of delivery, a time at which prepayments are paid, the interest rate of capital cost, fixed lifetime of the product and rate of preservation technology cycle time remain constant.

• 2. From Table 4.1, scale demand, ordering cost per order incurred by the retailer and holding cost rate increase investment of preservation technology slowly, whereas linear rate of change of demand and fixed lifetime of the product decreases investment of preservation technology slowly. However, purchase cost increases investment of preservation technology rapidly although the rate of preservation technology decreases investment of preservation technology rapidly. Furthermore, change in quadratic rate of change of demand, the fraction of the purchase cost to be prepaid before the time of delivery, a time at which prepayments are paid and the interest rate of capital cost investment of preservation technology remain constant.

• 3. From Table 4.1, linear rate of change of demand, holding cost rate, ordering cost per order incurred by the retailer, the fraction of the purchase cost to be prepaid before the time of delivery and t a time at which prepayments are paid and the interest rate of capital cost increases total cost slowly, whereas the rate of preservation technology decreases total cost slowly. However, scale demand and purchase cost increase total cost rapidly. In addition, change in quadratic rate of change of demand and fixed lifetime of the product total cost remain constant.

4.5 Conclusion

In this chapter, we consider retailer’s model for the instantaneous deteriorating item under replenishment time, the optimal number of equal instalments before receiving the order quantity and preservation technology with quadratic demand. Due to time-dependent deteriorating item, retailer invests money on preservation technology to reduce deterioration. Moreover, the retailer has to pay a fraction of the purchase cost in an equal number of instalment before the time of delivery. The total cost of the retailer with respect to the optimal number of equal instalments before receiving the order quantity, replenishment time and investment of preservation technology is minimized. The decision policies are analysed for the decision-maker. For numerical examples, retailer reaches the minimum cost and carries out sensitivity analysis. This study will extend as the model can be further generalized by taken more items at a time. One can also analyse three-layered supply chain.