Transient Analysis of an M/M/c Queue Subject to Multiple Exponential Vacation

Abstract

In this paper, we consider an M/M/c queueing model subject to multiple exponential vacation wherein arrivals occur according to a Poisson distribution and the c servers provide service according to an exponential distribution. When the system is empty, all the c servers go on a vacation and the vacation times are assumed to follow exponential distribution. Further arrivals are allowed to join the queue when servers are in vacation. Explicit analytical expressions for the time dependent probabilities of the number in the system are presented using matrix geometric method.

1 Introduction

Queueing system with multiple server is useful and important as it finds a wide range of applications in computer system, communication networks, production management, etc. For example, congestion in vehicular network pose a major threat due to varied reasons like high mobility, short link lifetime and spectrum efficiency. Therefore, cognitive radio (CR) plays a predominant role in the effective management of the available spectrum. More recently, Daniel et al. [1] proposed a multi server queueing model design for CR vehicular traffic and showed its effectiveness in terms of reducing the average waiting time for a vehicle or equivalently the optimal use of the available spectrum resource. Vijayalakshmi and Jyothsna [2] presents the steady state analysis of a renewal input multiple working vacations queue with balking, reneging and heterogeneous servers thereby obtaining the various system performance measures like expected system length, expected balking rate etc. Lin and Ke [3] discusses the multi-server system with single working vacation and obtains the stationary probabilities using matrix geometric method. Tian et al. [4] considers an M/M/c queue with multiple vacations and obtains the conditional stochastic decompositions of the stationary queue length and waiting time.

Parthasarathy [5] provided an explicit analytical expression for the time dependent probabilities of the number in the system at time t in terms of modified Bessel function of first kind using generating function methodology for a multi server queueing model. Recently, Al-seedy et al. [6] extended the results by introducing the concept of balking and reneging in the multi server queueing model. Using the similar technique as above, Ammar [7] obtains an explicit expression for the transient system size probabilities for the queue with heterogeneous servers and impatient behavior. In this paper, explicit analytical expressions for the stationary probabilities of the number in the system for an M/M/c queueing model are presented using matrix geometric method. However, for the transient analog, the system size probabilities are recursively obtained in the Laplace domain. As a special case, when c = 1, the transient probabilities in Laplace domain are seen to coincide with the results of an M/M/1 queueing model subject to multiple vacation.

2 Model Description

Consider an M/M/c queueing model subject to multiple exponential vacations. Arrivals are assumed to follow Poisson distribution with parameter λ. The c servers provide service according to an exponential distribution with parameter $\mu .$ When the system is empty, all the ‘c’ servers go on a vacation wherein the vacation times follow exponential distribution with parameter $\theta$. Further, arrivals are allowed to join the queue during the vacation period. Let N(t) denote the number of customers in the system at time t. Define J(t) = 1 when the server is busy and J(t) = 0 when the server is on vacation at time, t. It is well known that {(J(t), N(t)), t ≥ 0} is a Markov process with state space $\varOmega = \{ (0,k)\,\cup\,(1,k),k = 1,2,\; \ldots \} .$ The state transition diagram for the model is given in Fig. 1.

Fig. 1

State transition diagram

3 Stationary Analysis

This section presents explicit expressions for the stationary probabilities of the above described model. Let $\pi_{jk}$ denote the stationary probability for the system to be in state j with k customers. Define $\varvec{\pi}= [\varvec{\pi}_{0} ,\varvec{\pi}_{1} ,\varvec{\pi}_{2} , \ldots$] where $\varvec{\pi}_{0} = \pi_{00}$ and $\varvec{\pi}_{0k} = \left[ {\pi_{0k} ,\pi _{1k} } \right]\quad k \ge 1,$ then the system of equations governing the state probabilities under steady state are given by

$$ \varvec{\pi}\,{\mathbb{Q}} = 0 $$

(3.1)

The infinitesimal generator ${\mathbb{Q}}$ is given by

where $\varvec{A}_{0} = -\uplambda$, $\varvec{C}_{0} = \left( {\uplambda,0} \right)$, $\varvec{ B}_{0} = \left( {\begin{array}{*{20}c} 0 \\ \mu \\ \end{array} } \right)$, $\varvec{B}_{\varvec{k}} = \left( {\begin{array}{*{20}c} 0 & 0 \\ 0 & {k\mu } \\ \end{array} } \right)\quad k = 2,3, \ldots c - 1,$ $\varvec{C} = \left( {\begin{array}{*{20}c}\uplambda & 0 \\ 0 &\uplambda \\ \end{array} } \right)$ $\varvec{A}_{\varvec{k}} = \left( {\begin{array}{*{20}c} { - \left( {\uplambda + \theta } \right)} & \theta \\ 0 & { - (\lambda + k\mu )} \\ \end{array} } \right)\quad k = 1,2 \ldots c - 1,\varvec{B} = \left( {\begin{array}{*{20}c} 0 & 0 \\ 0 & {{\text{c}}\mu } \\ \end{array} } \right)$, $\varvec{A} = \left( {\begin{array}{*{20}c} { - \left( {\uplambda + \theta } \right)} & \theta \\ 0 & { - (\uplambda + c\mu )} \\ \end{array} } \right).$

Expanding the matrix equation represented by Eq. (3.1) leads to

$$ \varvec{\pi}_{0} \varvec{A}_{0} +\varvec{\pi}_{1} \varvec{B}_{0} = 0, $$

(3.2)

$$ \varvec{\pi}_{0} \varvec{C}_{0} +\varvec{\pi}_{1} \varvec{A}_{1} +\varvec{\pi}_{2} \varvec{B}_{2} = 0, $$

(3.3)

$$ \varvec{\pi}_{k - 1} \varvec{C} +\varvec{\pi}_{k} \varvec{A}_{k} +\varvec{\pi}_{k + 1} \varvec{B}_{k + 1 } = 0;\quad 2 \le k \le c - 1, $$

(3.4)

and

$$ \varvec{\pi}_{k - 1} \varvec{C} +\varvec{\pi}_{k} \varvec{A} +\varvec{\pi}_{k + 1} \varvec{B} = 0,\quad k \ge c. $$

(3.5)

Lemma 1

If $\rho = \frac{\uplambda}{c\mu } < 1$ and $r = \frac{\uplambda}{{\uplambda + \theta }},$ then the matrix quadratic equation

$$ \varvec{R}^{2} \varvec{B} + \varvec{RA} + \varvec{C} = 0 $$

(3.6)

has the minimal non-negative solution given by

$$ \varvec{R} = \left( {\begin{array}{*{20}c} r & {\frac{\theta r}{c\mu (1 - r)}} \\ 0 & \rho \\ \end{array} } \right). $$

(3.7)

Proof

Since B, A and C are all upper triangular matrices, we assume R has the same structure as $\varvec{R} = \left( {\begin{array}{*{20}c} {r_{11} } & {r_{12} } \\ 0 & {r_{22} } \\ \end{array} } \right).$ Substituting R into $\varvec{R}^{2} \varvec{B} + \varvec{RA} + \varvec{C} = 0$ leads to

$$ \begin{aligned}\uplambda - r_{11} \left( {\uplambda + \theta } \right) & = 0, \\ r_{11} \theta - \left( {\uplambda + c\mu } \right)r_{12} + c\mu \left( {r_{11} r_{12} + r_{12} r_{22} } \right) & = 0, \\ \end{aligned} $$

and

$$ \uplambda - \left( {\uplambda + c\mu } \right)r_{22} + c\mu r_{22}^{2} = 0. $$

On solving the above equations, it is seen that $r_{11} = \frac{\lambda }{\lambda + \theta },r_{22} = \frac{\lambda }{c\mu },$ and $r_{12} = \frac{\theta r}{c\mu (1 - r)}.$ Hence, we obtain $\varvec{R} = \left( {\begin{array}{*{20}c} r & {\frac{\theta r}{c\mu (1 - r)}} \\ 0 & \rho \\ \end{array} } \right).$ Observe that for $k = 1,2,3, \ldots$

$$ \varvec{R}^{k} = \left( {\begin{array}{*{20}c} {r^{k} } & {\frac{\theta r}{c\mu (1 - r)}\mathop \sum \limits_{j = 0}^{k - 1} \rho^{k - 1 - j} r^{j} } \\ 0 & {\rho^{\text{k}} } \\ \end{array} } \right). $$

(3.8)

Theorem 1

If $\rho < 1,$ then the stationary probabilities of the system state are given by

$$ \begin{aligned} \pi_{0k} & = \pi_{00} \left( {\frac{\lambda }{\lambda + \theta }} \right)^{k} ;k \ge 1, \\ \pi_{1k} & = \pi_{00} \left\{ {\frac{1}{k!}\left( {\frac{\lambda }{\mu }} \right)^{k} \left( {1 + \mathop \sum \limits_{i = 1}^{k - 1} i!\left( {\frac{r\mu }{\lambda }} \right)^{i} } \right)} \right\};1 \le k \le c - 1, \\ \pi_{1k} & = \pi_{00} \left\{ {\frac{1}{c !}\left( {\frac{\lambda }{\mu }} \right)^{c} \left( {1 + \mathop \sum \limits_{i = 1}^{c - 1} i!\left( {\frac{r\mu }{\lambda }} \right)^{i} } \right)} \right\} + \pi_{00} r^{c} \frac{\theta r}{c\mu (1 - r)}\mathop \sum \limits_{i = 0}^{k - c - 1} \rho^{k - c - 1 - i} r^{i} ;k \ge c. \\ \end{aligned} $$

and $\pi_{00}$ is found using the normalization condition.

Proof

On substituting the corresponding matrices in Eq. (3.2), we get, $- \lambda \pi_{00} + \mu \pi_{11} = 0,$ which yields $\pi_{11} = \frac{\lambda }{\mu }\pi_{00}$. Similarly, substituting the corresponding matrices in Eq. (3.3) yields

$$ \pi_{00} \lambda - \left( {\lambda + \theta } \right)\pi_{01} = 0, \theta \pi_{01} - \left( {\lambda + \mu } \right)\pi_{11} + 2\mu \pi_{12} = 0, $$

which simplifies to $\pi_{01} = r\pi_{00}$ and $\pi_{12} = \pi_{00} \left\{ {\frac{1}{2!}\left( {\frac{\lambda }{\mu }} \right)^{2} \left( {1 + \left( {\frac{r\mu }{\lambda }} \right)} \right)} \right\}.$ Also, substituting the corresponding matrices in Eq. (3.4), we get

$$ \lambda \pi_{0k - 1} - \left( {\lambda + \theta } \right)\pi_{0k} = 0;2 \le k \le c - 1, $$

and

$$ \lambda \pi_{1k - 1} + \theta \pi_{0k} - \left( {\lambda + k\mu } \right)\pi_{1k} + \left( {k + 1} \right)\mu \pi_{1k + 1} = 0; 2 \le k \le c - 1. $$

Therefore, $\pi_{0k} = r^{k} \pi_{00} , 1 \le k \le c - 1$ and $\pi_{1k} = \pi_{00} \left\{ {\frac{1}{k!}\left( {\frac{\lambda }{\mu }} \right)^{k} \left( {1 + \sum\nolimits_{i = 1}^{k - 1} {i!\left( {\frac{r\mu }{\lambda }} \right)^{i} } } \right)} \right\}.$ Assume, $\varvec{\pi}_{k} =\varvec{\pi}_{c} \varvec{R}^{k - c}$ for $k \ge c$, then from Eq. (3.5) and using Eq. (3.8), we get $\pi_{0k} = r^{k} \pi_{00} ;k \ge c$ and $\pi_{1k} = \pi_{00} \left\{ {\frac{1}{c !}\left( {\frac{\lambda }{\mu }} \right)^{c} \left( {1 + \sum\nolimits_{i = 1}^{c - 1} {i!\left( {\frac{r\mu }{\lambda }} \right)^{i} } } \right)} \right\} + \pi_{00} r^{c} \frac{\theta r}{{c\mu \left( {1 - r} \right)}}\sum\nolimits_{i = 0}^{k - c - 1} {\rho^{k - c - 1 - i} r^{i} } ;$ $k \ge c.$ Hence all the stationary probabilities are expressed in terms of $\pi_{00}$ and $\pi_{00}$ can be found using the normalization condition.

4 Transient Analysis

This section provides an analytical expression for the time dependent probabilities of the number in the system in Laplace domain, using matrix analytic method. Let $P_{jk} (t) = P\left( {J(t) = j, N(t) = k} \right), j = 0,1;$ and $k = 0,1,2 \ldots$. Using standard methods, the system of equations that governs the process $\{ \left( {J(t),N(t)} \right), t \ge 0\}$ are given by

$$ \begin{aligned} P_{00}^{'} (t) & = - \lambda P_{00} (t) + \mu P_{11} (t), \\ P_{0k}^{'} (t) & = - (\lambda + \theta ) P_{0k} (t) + \lambda P_{0k - 1} (t),\quad k \ge 1, \\ P_{11}^{'} (t) & = - (\lambda + \mu ) P_{11} (t) + 2\mu P_{12} (t) + \theta P_{01} (t). \\ P_{1k}^{'} (t) & = - (\lambda + k\mu ) P_{1k} (t) + \lambda P_{1k - 1} (t) + \left( {k + 1} \right)\mu P_{1k + 1} (t) + \theta P_{0k} (t), 2 \le k \le c - 1, \\ \end{aligned} $$

and

$$ P_{1k}^{'} (t) = - (\lambda + c\mu ) P_{1k} (t) + \lambda P_{1k - 1} (t) + c\mu P_{1k + 1} (t) + \theta P_{0k} (t),\quad k \ge c, $$

subject to the condition $P_{00} (0) = 1.$ Let $\varvec{P}_{0} (t) = P_{00} (t),\varvec{P}_{\varvec{k}} (t) = \left[ {P_{0k} (t),P_{1k} (t)} \right],k = 1,2, \ldots$ Then, the above system of equations can be expressed in the matrix form as

$$ \frac{{d\varvec{P}(t)}}{dt} = \varvec{P}(t){\mathbb{Q}}, $$

where $\varvec{P}(t) = \left[ {\varvec{P}_{0} (t),\varvec{P}_{1} (t),\varvec{P}_{2} (t) \ldots \ldots } \right].$ Let $\hat{P}_{jk} (s)$ denote the Laplace transform of $P_{jk} (t)$ for $j = 0,1$ and $k = 0,1,2, \ldots$. Taking Laplace Transform of the above equation yields $\hat{\varvec{P}}(s)\left[ {{\mathbb{Q}} - s\varvec{I}} \right] = - \varvec{P}(0)$ which on expansion leads to

$$ \hat{\varvec{P}}_{0} (s)\left( {\varvec{A}_{0} - s} \right) + \hat{\varvec{P}}_{1} (s)\varvec{B}_{0} = - 1, $$

(4.1)

$$ \hat{\varvec{P}}_{0} (s)\varvec{C}_{0} + \hat{\varvec{P}}_{1} (S)\left( {\varvec{A}_{1} - s\varvec{I}} \right) + \hat{\varvec{P}}_{2} (s)\varvec{B}_{2} = 0, $$

(4.2)

$$ \hat{\varvec{P}}_{{\varvec{K} - 1}} (s)\varvec{C} + \hat{\varvec{P}}_{K} (s)\left( {\varvec{A}_{k} - s\varvec{I}} \right) + \hat{\varvec{P}}_{k + 1} (s)\varvec{B}_{k + 1} = 0;\quad 2 \le k \le c - 1, $$

(4.3)

and

$$ \hat{\varvec{P}}_{{\varvec{k} - 1}} (s)\varvec{C} + \hat{\varvec{P}}_{\varvec{k}} (s)\left( {\varvec{A} - s\varvec{I}} \right) + \hat{\varvec{P}}_{{\varvec{k} + 1}} (s)\varvec{B} = 0;\quad k \ge c $$

(4.4)

where $\varvec{I}$ is the identity matrix of the corresponding order.

Lemma 2

The quadratic matrix equation

$$ \varvec{R}^{2} (s)\varvec{B} + \varvec{R}(s)\left( {\varvec{A} - s\varvec{I}} \right) + \varvec{C} = 0 $$

(4.5)

has the minimal non-negative solution given by

$$ \varvec{R}(s) = \left( {\begin{array}{*{20}c} {\rho (s)} & {\beta_{c} (s)} \\ 0 & { r_{c} (s)} \\ \end{array} } \right) $$

(4.6)

where $\rho (s) = \frac{\lambda }{s + \lambda + \theta },\beta_{c} (s) = \frac{{\theta r_{c} (s)}}{{s + \lambda + \theta - c\mu r_{c} (s)}},$ and $r_{c} (s) = \frac{{\left( {s + \lambda + c\mu } \right) - \sqrt {\left( {s + \lambda + c\mu } \right)^{2} - \,4\lambda c\mu } }}{2c\mu }.$

Proof

By an analysis similar to the proof of Lemma 1***, we assume R(s) as a upper triangular matrix since $\varvec{B},\varvec{A} - s\varvec{I}$ and C are all upper triangular matrices. Substituting R(s) into Eq. (4.5) and upon solving the corresponding equations leads to Eq. (4.6). Observe that for $\varvec{ }k = 1,2,3, \ldots$

$$ \varvec{R}^{k} (s) = \left( {\begin{array}{*{20}c} {\rho^{k} \left( s \right)} & {\beta (s)\mathop \sum \limits_{i = 0}^{k - 1} \rho^{k - 1 - i} (s)r_{c}^{i} (s)} \\ 0 & {r_{c}^{k} (s)} \\ \end{array} } \right). $$

(4.7)

where $\varvec{R}^{1} (s) = \varvec{R}(s)$ and $\varvec{R}\left( 0 \right) = \varvec{R}.$

Lemma 3

Let $\varvec{R}_{\varvec{k}} (s) = \left( {\begin{array}{*{20}c} {\rho (s)} & {\lambda \beta_{k} (s)} \\ 0 & {r_{k} (s)} \\ \end{array} } \right),\quad 1 \le k \le c - 1,$

where

$$ \rho (s) = \frac{\lambda }{s + \lambda + \theta }, $$

(4.8)

$$ \beta_{c - 1} (s) = \frac{{\theta + c\mu \beta_{c} (s)}}{{\left( {s + \lambda + \theta } \right)(s + \lambda + (c - 1)\mu - c\mu r_{c} \left( s \right))}}, $$

(4.9)

$$ \beta_{k} (s) = \frac{{\theta + (k + 1)\lambda \mu \beta_{k + 1} (s)}}{{\left( {s + \lambda + \theta } \right)(s + \lambda + k\mu - \left( {k + 1} \right)\mu r_{k + 1} \left( s \right))}},\quad 1 \le k \le c - 2, $$

(4.10)

and

$$ r_{k} (s) = \frac{\lambda }{{s + \lambda + k\mu - \left( {k + 1} \right)\mu r_{k + 1} (s)}},\quad 1 \le k \le c - 1. $$

(4.11)

Then $\{ \varvec{R}_{\varvec{k}} (s),1 \le k \le c - 1\}$ are satisfied by the following recurrence relation

$$ \varvec{C} + \varvec{R}_{k} (s)\left( {\varvec{A}_{k} - s\varvec{I}} \right) + \varvec{R}_{\varvec{k}} (s)\varvec{R}_{{\varvec{k} + 1}} (s)\varvec{B}_{{\varvec{k} + 1}} = 0. $$

(4.12)

Proof

For $n = c - 1,$ let $\varvec{R}_{{\varvec{c} - 1}} \left( \varvec{s} \right) = \left( {\begin{array}{*{20}c} {\rho (s)} & { \lambda \beta_{c - 1} (s)} \\ 0 & {r_{c - 1} (s)} \\ \end{array} } \right).$ Then the recurrence relation becomes $\varvec{C} + \varvec{R}_{{\varvec{c} - 1}} (\varvec{s})\left( {\varvec{A}_{{\varvec{c} - 1}} - s\varvec{I}} \right) + \varvec{R}_{{\varvec{c} - 1}} (\varvec{s})\varvec{R}_{\varvec{c}} (\varvec{s})\varvec{B}_{\varvec{c}} = 0.$ Substituting the corresponding matrices and upon simplification yields

$$ \begin{aligned} \lambda - \left( {\lambda + \theta + s} \right)\rho (s) & = 0, \\ \theta \rho (s) - \lambda \beta_{c - 1} (s)\left( {\lambda + \left( {c - 1} \right)\mu + s} \right) + c\mu (\lambda \rho (s)\beta_{c} (s) + \lambda \beta_{c - 1} (s)r_{c} (s) & = 0, \\ \end{aligned} $$

and

$$ \lambda - r_{c - 1} (s)\left( {\lambda + \left( {c - 1} \right)\mu + s} \right) + c\mu r_{c} (s)r_{c - 1} (s) = 0, $$

which on solving leads to $\rho (s) = \frac{\lambda }{\lambda + \theta + s}, \beta_{c - 1} (s) = \frac{{\theta + c\mu \beta_{c} (s)}}{{\left( {\lambda + \theta + s} \right)\left( {\lambda + \left( {c - 1} \right)\mu + s - c\mu r_{c} (s)} \right)}}$ and $r_{c - 1} (s) = \frac{\lambda }{{\lambda + (c - 1)\mu + s - c\mu r_{c} (s)}}.$

Therefore,

$$ \varvec{R}_{{\varvec{c} - 1}} (\varvec{s}) = \left( {\begin{array}{*{20}c} {\frac{\lambda }{\lambda + \theta + s}} & {\frac{{\theta + c\mu \beta_{c} (s)}}{{\left( {\lambda + \theta + s} \right)(\lambda + (c - 1)\mu + s - c\mu r_{c} \left( s \right))}}} \\ {0 } & {\frac{\lambda }{{\lambda + (c - 1)\mu + s - c\mu r_{c} (s)}}} \\ \end{array} } \right) $$

(4.13)

is completely determined. In general, assuming $\varvec{R}_{{\varvec{k} + 1}} (\varvec{s}) = \left( {\begin{array}{*{20}c} {\rho (s)} & { \lambda \beta_{k + 1} (s)} \\ 0 & { r_{k + 1} (s)} \\ \end{array} } \right),$ it can be proved that $\varvec{R}_{\varvec{k}} (\varvec{s}) = \left( {\begin{array}{*{20}c} {\rho (s)} & {\lambda \beta_{k} (s)} \\ {0 } & {r_{k} (s)} \\ \end{array} } \right),$ satisfies Eq. (4.12). Consider $\varvec{C} + \varvec{R}_{\varvec{k}} (\varvec{s})\left( {\varvec{A}_{\varvec{k}} - s\varvec{I}} \right) + \varvec{R}_{\varvec{k}} (\varvec{s})\varvec{R}_{{\varvec{k} + 1}} (\varvec{s})\varvec{B}_{{\varvec{k} + 1}} = 0$ substituting the corresponding matrices and on simplification leads to

$$ \rho (s) = \frac{\lambda }{s + \lambda + \theta },r_{k} (s) = \frac{\lambda }{{s + \lambda + k\mu - \left( {k + 1} \right)\mu r_{k + 1} (s)}}, $$

and

$$ \beta_{k} (s) = \frac{{\theta + (k + 1)\mu \beta_{k + 1} (s)\lambda }}{{\left( {s + \lambda + \theta } \right)(s + \lambda + k\mu - \left( {k + 1} \right)\mu r_{k + 1} (s))}}. $$

Therefore Eqs. (4.8), (4.9), (4.10) and (4.11) are true for all $n = 1,2, \ldots ,c - 1.$ Having determined $\varvec{R}_{{\varvec{c} - 1}} (\varvec{s})$ in Eq. (4.13), from the matrix Eq. (4.12), we get $\varvec{R}_{{\varvec{c} - 2}} (\varvec{s}) = \left( {\begin{array}{*{20}c} {\rho (s)} & {\lambda \beta_{c - 2} (s)} \\ 0 & {r_{c - 2} (s)} \\ \end{array} } \right)$ where

$$ \rho (s) = \frac{\lambda }{s + \lambda + \theta },r_{c - 2} (s) = \frac{\lambda }{{s + \lambda + (c - 2)\mu - \left( {c - 1} \right)\mu r_{c - 1} (s)}}, $$

and

$$ \beta_{c - 2} (s) = \frac{{\theta + (c - 1)\mu \beta_{c - 1} (s)\lambda }}{{\left( {s + \lambda + \theta } \right)(s + \lambda + (c - 2)\mu - \left( {c - 1} \right)\mu r_{c - 1} (s))}}. $$

Similarly $\varvec{R}_{{\varvec{c} - 3}} (\varvec{s}),\varvec{R}_{{\varvec{c} - 4}} (\varvec{s}), \ldots \varvec{R}_{1} (\varvec{s})$ can be recursively determined. Hence the proof.

Theorem 2

The Laplace transform of the transient state probability distribution functions sequence, $\hat{\varvec{P}}_{k} (s)$ are satisfied with the following relations.

$$ \hat{\varvec{P}}_{k} (s) = \hat{\varvec{P}}_{c - 1} (s)R^{k - c + 1} (s),k \ge c $$

(4.14)

$$ \hat{\varvec{P}}_{k} (s) = \hat{\varvec{P}}_{k - 1} (s)R_{k} (s) = R_{K}^{*} (s)e_{1} \hat{P}_{0} (s),1 \le k \le c - 1 $$

(4.15)

where $R_{K}^{*} (s) = R_{K} (s)R_{K - 1} (s) \ldots R_{1} (s)$ for $k = 1,2 \ldots c - 1,e_{1} = (\begin{array}{*{20}c} 1 & {0)} \\ \end{array}$ and $\hat{\varvec{P}}_{0} (s) = \left[ {s - \varvec{A}_{0} - \varvec{e}_{1} \varvec{R}_{1} (s)\varvec{B}_{0} } \right]^{ - 1}$.

Proof

For $k \ge c,$ substituting Eq. (4.14) in (4.4) leads to

$$ \begin{aligned} \hat{\varvec{P}}_{{\varvec{k} - 1}} (s)\varvec{C} + \hat{\varvec{P}}_{\varvec{k}} (s)\left( {\varvec{A} - s\varvec{I}} \right) + \hat{\varvec{P}}_{{\varvec{k} + 1}} (s) & = \hat{\varvec{P}}_{{\varvec{c} - 1}} (s)\varvec{R}^{{\varvec{k} - \varvec{c}}} (s)\left[ {\varvec{C} + \varvec{R}(s)\left( {\varvec{A} - s\varvec{I}} \right) + \varvec{R}^{2} (s)\varvec{B}} \right] \\ & = 0\,\left( {{\text{from}}\,{\text{Lemma}}\, 2} \right). \\ \end{aligned} $$

Similarly for $2 \le k \le c - 1,$ substituting Eq. (4.15) in Eq. (4.3) leads to

$$ \begin{aligned} \hat{\varvec{P}}_{{\varvec{k} - 1}} \left( s \right)\varvec{C} + \hat{\varvec{P}}_{k} \left( s \right)\left( {\varvec{A}_{\varvec{k}} - s\varvec{I}} \right) + \hat{\varvec{P}}_{{\varvec{k} + 1}} (s)\varvec{B}_{{\varvec{k} + 1}} & = \hat{\varvec{P}}_{{\varvec{k} - 1}} (s)\varvec{R}_{{\varvec{k} - 2}} (s)\varvec{C} + \hat{\varvec{P}}_{{\varvec{k} - 1}} (s)\varvec{R}_{\varvec{k}} (s)\left( {\varvec{A}_{\varvec{k}} - s\varvec{I}} \right) + \hat{\varvec{P}}_{k} (s)\varvec{R}_{{\varvec{k} + 1}} \left( s \right)\varvec{B}_{k + 1} \\ & = \hat{\varvec{P}}_{{\varvec{k} - 2}} \left( s \right)\varvec{R}_{{\varvec{k} - 1}} (s)\left[ {\varvec{C} + \varvec{R}_{\varvec{k}} \left( s \right)\left( {\varvec{A}_{\varvec{k}} - s\varvec{I}} \right) + \varvec{R}_{\varvec{k}} (s)\varvec{R}_{{\varvec{k} + 1}} (s)\varvec{B}_{k + 1} } \right] \\ & = 0\,\left( {{\text{from}}\,{\text{Lemma}}\, 3} \right). \\ \end{aligned} $$

Also, substituting Eq. (4.15) in Eq. (4.2) and noting that $\varvec{C}_{0} = \varvec{e}_{1} \varvec{C }$ yields

$$ \begin{aligned} \hat{\varvec{P}}_{0} (s)\varvec{C}_{0} + \hat{\varvec{P}}_{1} (s)\left( {\varvec{A}_{1} - s\varvec{I}} \right) + \hat{\varvec{P}}_{2} (s)\varvec{B}_{2} & = \hat{\varvec{P}}_{0} (s)\varvec{e}_{1} \varvec{C} + \hat{\varvec{P}}_{0} (s)\varvec{e}_{1} \varvec{R}_{1}^{* } (s)\left( {\varvec{A}_{1} - s\varvec{I}} \right) + \hat{\varvec{P}}_{0} (s)\varvec{e}_{1} \varvec{R}_{2}^{*} (s)\varvec{B}_{2} \\ & = \hat{\varvec{P}}_{0} (s)\varvec{e}_{1} \left[ {\varvec{C} + \varvec{R}_{1} (s)\left( {\varvec{A}_{1} - s\varvec{I}} \right) + \varvec{R}_{2} (s)\varvec{R}_{1} (s)\varvec{B}_{2} } \right] \\ & = 0\,({\text{from}}\,{\text{Lemma}}\, 3\,{\text{for}}\,k{ = 1)} .\\ \end{aligned} $$

Therefore, it is verified that $\hat{\varvec{P}}_{\varvec{n}} (s)$ expressed by Eqs. (4.14) and (4.15) satisfies the governing system of differential equations in the Laplace domain as represented by Eqs. (4.2)–(4.4). Hence, from Eq. (4.1), we get

$$ \hat{\varvec{P}}_{0} (s) = \left[ {s - \varvec{A}_{0} - \varvec{e}_{1} \varvec{R}_{1} (s)\varvec{B}_{0} } \right]^{ - 1} $$

(4.16)

where $\varvec{A}_{0} ,\varvec{B}_{0}$ are known and $\varvec{R}_{1} (s)$ can be recursively determined from Lemma 3. Thus, the transient state probabilities of the model under consideration are given by

$$ \begin{aligned} \hat{\varvec{P}}_{k} (s) & = \hat{\varvec{P}}_{c - 1} (s)R^{k - c + 1} (s), k \ge c \\ \hat{\varvec{P}}_{k} (s) & = \hat{\varvec{P}}_{k - 1} (s)R_{k} (s) = R_{K}^{*} (s)e_{1} \hat{P}_{0} (s);1 \le k \le c - 1 \\ \end{aligned} $$

where $\hat{\varvec{P}}_{0} (s)$ is given by Eq. (4.16), $\varvec{R}^{\varvec{k}} (s)$ for all k is given by Eq. (4.7) and $\varvec{R}_{\varvec{k}}^{\varvec{*}} (s)$ for $k = 1,2, \ldots$ are recursively determined using Lemma 3.

Remark

When c = 1, the model reduces to the transient analysis of an M/M/1 queue subject to multiple exponential vacation. Accordingly, the above solution reduces $\hat{\varvec{P}}_{k} (s) = \hat{\varvec{P}}_{0} (s)e_{1} R^{k} (s),$ for $k \ge 1,$ which on simplification yields

$$ \hat{\varvec{P}}_{0k} (s) = \hat{\varvec{P}}_{00} (s)\rho^{k} (s) $$

(4.17)

and

$$ \hat{\varvec{P}}_{1k} (s) = \hat{\varvec{P}}_{00} (s)\beta_{c} (s)\mathop \sum \limits_{i = 0}^{k - 1} \rho^{k - 1 - i} (s)r_{c}^{i} (s) $$

(4.18)

for $k \ge 1$. On simplification, Eq. (4.17) reduces to $\hat{\varvec{P}}_{0k} (s) = \hat{\varvec{P}}_{00} (s)\left( {\frac{\lambda }{s + \lambda + \theta }} \right)^{k} ;k \ge 1$ which is seen to coincide with the equation below (23) obtained by Sudhesh and Raj [8]. When k = 1, Eq. (4.18) reduces to $\hat{\varvec{P}}_{1k} (s) = \hat{\varvec{P}}_{00} (s)\beta_{c} (s) = \hat{\varvec{P}}_{00} (s)\frac{{\theta \,r_{c} (s)}}{{\left( {s + \lambda + \theta } \right)\left( {1 - \frac{{c\mu \,r_{c} (s)}}{s + \lambda + \theta }} \right)}}$ which on simplification reduces to $\hat{\varvec{P}}_{1k} (s) = \hat{\varvec{P}}_{00} (s)\frac{\theta }{c\mu }\mathop \sum \limits_{m = 1}^{ \propto } \left( {\frac{{\frac{\lambda }{\beta }}}{s + \lambda + \theta }} \right)^{m} \left( {\frac{{p - \sqrt {p^{2} - \alpha^{2} } }}{\alpha }} \right)^{m}$ which is seen to coincide with the Eq. (25) obtained by Sudhesh and Raj [8].

5 Numerical Illustrations

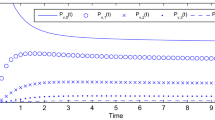
This section illustrates the behaviour of time dependent state probabilities of the system during busy and vacation states for varying values of k. Figure 2 depicts the variation of the functional state probabilities against time for $c = 3,\lambda = 1,\mu = 2\,{\text{and}}\,\theta = 0.5$. Since the system is assumed to be initially in vacation state, the curves for $P_{1,k} (t)$ (k = 1, 2, 3, 4, 5) begins at 0. The value of $P_{1,k} (t)$ decreases with increase in. It is seen that $P_{1,k} (t)$ increases with time and converges to the corresponding steady state probabilities, $\pi_{1,k}$ as t tends to infinity. The values of $\pi_{1,k} ,k = 1,2,3,4,5$ are depicted in the figure. Figure 3 depicts the variation of probabilities of functional state against time for $= 3,\lambda = 1,\mu = 2\,{\text{and}}\,\theta = 0.5$. Since the system is assumed to be initially in vacation state, the curve for $P_{0,0} (t)$ begins at 1. The value of $P_{0,k} (t)$ decreases with increase in. It is seen that $P_{0,k} (t) \left( {k = 0,1,2,3,4} \right)$ converges to the corresponding steady state probabilities, $\pi_{0,k}$ as t tends to infinity. The values of $\pi_{0,k} ,k = 0,1,2,3,4$ are depicted in the figure.

Fig. 2

Variation of probabilities of busy state of against time t

Fig. 3

Variation of probabilities vacation state against time t

Figures 4 and 5 depicts the variations the probability for the system to be in vacation state and functional state respectively against time for varying values of c and the same choice of the other parameter values. Mathematically

Fig. 4

Variation of vacation state probability for varying values of c

Fig. 5

Variation of functional state probability for varying values of c

$$ P_{0} (t) = P\left( {J(t) = 0} \right) = \mathop \sum \limits_{k = 0}^{\infty } P_{0k} (t)\,{\text{and}}\,P_{1} (t) = P\left( {J(t) = 1} \right) = \mathop \sum \limits_{k = 1}^{\infty } P_{1k} (t) $$

Since the system is assumed to be initially in vacation state, the curve or $P_{0} (t)$ begins at 1 and that of $P_{1} (t)$ begins at 0. The value of $P_{0} (t)$ decreases with increase in time and the that of increase with increase in time and converges to the corresponding steady state value. Observe that when c = 1, the model reduces to that of an M/M/1 queue subject to multiple exponential vacation.

6 Conclusion

Queueing system with multiple server plays a vital role owing of their applications in computer system, communication network, production management etc.,. In particular, M/M/c queue subject to vacation is of a great interest in view of their real time applications. Extensive work on both the steady state and transient analysis of M/M/c queueing model and its variations are done by many authors. This paper is the first of its kind to present the transient analysis of multi server model subject to multiple exponential vacation. Explicit solution for the state probabilities are presented in the stationary regime, however due to the complexity of the problem, the transient solution are presented in the Laplace domain using matrix analytic method.