Abstract
This survey is devoted to analytical-numerical methods for hidden attractors’ localization and their application to well-known problems and systems. From the computation point of view, in nonlinear dynamical systems the attractors can be regarded as self-exciting and hidden attractors. Self-exciting attractors can be localized numerically by the following standard computational procedure : after a transient process a trajectory, started from a point of an unstable manifold in a small neighborhood of unstable equilibrium, reaches an attractor and computes it. In contrast, a hidden attractor is an attractor whose basin of attraction does not contain neighborhoods of equilibria. In well-known Van der Pol, Belousov-Zhabotinsky, Lorenz, Chua, and many other dynamical systems classical attractors are self-exciting attractors and can be obtained numerically by the standard computational procedure. However, for localization of hidden attractors it is necessary to develop special analytical-numerical methods, in which at the first step the initial data are chosen in a basin of attraction and then the numerical localization (visualization) of the attractor is performed. The simplest examples of hidden attractors are internal nested limit cycles (hidden oscillations) in two-dimensional systems (see, e.g., the results concerning the second part of the 16th Hilbert’s problem). Other examples of hidden oscillations are counterexamples to Aizerman’s conjecture and Kalman’s conjecture on absolute stability in the automatic control theory (a unique stable equilibrium coexists with a stable periodic solution in these counterexamples). In 2010, for the first time, a chaotic hidden attractor was computed first by the authors in a generalized Chua’s circuit and then one chaotic hidden attractor was discovered in a classical Chua’s circuit.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Periodic Solution
- Quadratic System
- Stable Periodic Solution
- Hide Attractor
- Nonsingular Linear Transformation
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
In the first half of last century, during the initial period of development of the theory of nonlinear oscillations [2, 11, 32, 33], main attention has been given to analysis and synthesis of oscillating systems, for which the existence problem of oscillations can be solved relatively easily. The structure of many mechanical, electromechanical, and electronic systems is such that the existence of oscillations in them is almost obvious, namely the oscillations are excited from unstable equilibria. From the computational point of view it means that one can use a standard numerical method, in which after a transient process a trajectory, started from a point of an unstable manifold in a small neighborhood of equilibrium, reaches an attractor and identifies it.
Consider the following classical examples.
Example 3.1
(The Rayleigh string oscillator)
In studying string oscillations [31] Rayleigh discovered first that in the two-dimensional nonlinear dynamical system
undamped vibrations (namely limit cycles—this term was introduced later by Poincare) can arise. A well-known generalization of this system is the Van der Pol equation [34] that describes the nonlinear electrical circuits used in radio engineering. The result of the simulation of this system (3.1) for a=1, b=0.1 is presented in Fig. 3.1.
Example 3.2
(The Belousov-Zhabotinsky (BZ) reaction)
In 1951 B.P. Belousov discovered the first oscillations in the chemical reactions [3]. Consider one of the Belousov-Zhabotinsky dynamical models
and perform its simulation, using standard parameters: f=2/3, q=8×10−4, ε=4×10−2 (see Fig. 3.2).
Consider now the examples of numerical localization of well-known chaotic attractors in three-dimensional dynamical models.
Example 3.3
(The Lorenz system)
Consider the Lorenz system [27]
and carry out its simulation with standard parameters σ=10, β=8/3, ρ=28 (see Fig. 3.3). Here the computed trajectory is started from a small neighborhood of an unstable zero stationary point.
Example 3.4
(The Chua system)
Consider the classical Chua circuit [7] and its dynamical model in dimensionless coordinates
Here the function
characterizes a nonlinear element called the Chua diode. In this system, strange attractors [29] then called the Chua attractors were discovered. To date all the known classical Chua attractors are those excited from unstable equilibria. This makes it possible to compute different Chua attractors with relative ease [5]. Perform the simulation of the Chua attractor with the following parameters: α=9.35, β=14.79, γ=0.016, m 0=−1.1384, m 1=0.7225 (see Fig. 3.4).
Here, in all examples, the limit cycles and attractors are those excited from unstable equilibria (i.e., self-excited attractors).
2 Hidden Oscillations and Hidden Attractors
In the middle of the last century, oscillations of another type were found, so-called hidden oscillations : the oscillations, the existence of which is not obvious. They are not “connected” with equilibrium (i.e. in this case it is impossible to localize a periodic solution by the computing of trajectory with the initial data from a small neighborhood of equilibrium). In addition, in this case it is unlikely that the integration of trajectories with random initial data will lead to localization of such hidden oscillation since the basin of attraction can be very small and the considered system dimension can be large.
For the first time the problem of finding hidden oscillations arose in the 16th Hilbert problem (1900) for two-dimensional polynomial systems. For more than a century, in the framework of the solution of this problem, the numerous theoretical and numerical results were obtained. However, the problem is still far from being resolved even for the simple class of quadratic systems. In the 1940s and 1950s, academician A.N. Kolmogorov became the initiator of a few hundred of the following computational experiments [16]: he asked students (at Moscow State University) to find limit cycles in two-dimensional quadratic systems with randomly chosen coefficients. The result was absolutely unexpected: limit cycles were not found in any of the experiments, though it is known that quadratic systems with limit cycles form open domains in the space of coefficients and, therefore, for a random choice of polynomial coefficients, the probability of hitting in these sets is positive.
Note that numerical localization of small and nested limit cycles [13, 16, 20, 22, 24, 25] is a difficult problem.
Example 3.5
(Four limit cycles in a quadratic system)
Nowadays the application of special analytical-numerical methods [17, 25] allows one to visualize four limit cycles in a quadratic system [12].
Consider the following quadratic system:
In Fig. 3.5 for the coefficients
three “large” (normal size) limit cycles around the zero point and one “large” limit cycle to the left of the straight line x=−1 are visualized.
Further the problem of analysis of hidden oscillations arose in engineering problems of automatic control. In 1961 Gubar’ [8] showed analytically the possibility of existence of hidden oscillation in a two-dimensional system of a phase locked-loop with piecewise-constant impulse nonlinearity. In the 1950s and 1960s, the investigations of widely known Markus-Yamabe [28], Aizerman [1], and Kalman [9] conjectures on absolute stability had led to the finding of hidden oscillations in automatic control systems with a unique stable stationary point and the nonlinearity belonging to the sector of linear stability (see, e.g., [4, 6, 18, 30]).
Later, in 2010, for the first time, a chaotic hidden attractor was computed, by the authors, in a generalized Chua circuit [14] and then one chaotic hidden attractor was discovered in the classical Chua circuit [23].
Since the key factor, providing the possibility of computing the oscillation, is a basin of attraction, the following definition can be formulated.
Definition 3.1
Hidden attractors are those attractors whose basin of attraction does not contain neighborhoods of equilibria.
Here it is of the essence to consider a basin of attraction in forward and backward time since the computation in backward time may allow one to localize an unstable oscillation.
2.1 Analytical-Numerical Method for Localization of Hidden Oscillations in Multidimensional Dynamical Systems
For numerical localization of hidden oscillations the methods based on homotopy turned out to be the most effective ones. In this case a sequence of similar systems is considered such that for the first starting system the initial data for numerical localization of a periodic solution (starting periodic solution) can be obtained analytically and then the transformation of this starting periodic solution in the transition from one system to another is followed numerically.
Further we consider an effective analytical-numerical approach for localization of hidden oscillations in multidimensional dynamical systems, which are based on the method of a small parameter, the method of harmonic linearization (the describing function method), numerical methods, and an applied bifurcation theory.
Consider a system with one scalarFootnote 1 nonlinearity:
Here P is a constant (n×n)-matrix, q,r are constant n-dimensional vectors, ∗ is a transposition operation, ψ(σ) is a scalar function, and ψ(0)=0. Define a coefficient of harmonic linearization k in such a way that the matrix
has a pair of purely imaginary eigenvalues ±iω 0 (ω 0>0) and the rest of its eigenvalues have negative real parts. Assume that such k exists. Rewrite the system (3.7) as
where φ(σ)=ψ(σ)−kσ.
Introduce a finite sequence of functions φ 0(σ),φ 1(σ),…,φ m(σ) such that the graphs of the neighboring functions φ j(σ) and φ j+1(σ) slightly differ from one another, the function φ 0(σ) is small, and φ m(σ)=φ(σ). Using a smallness of the function φ 0(σ), one can apply and mathematically strictly justify [15, 16, 18, 26] the method of harmonic linearization (the describing function method) for the system
and find a stable nontrivial periodic solution x
0(t). For the localization of the oscillating solution (attractor) of the original system (3.9), we shall follow numerically the transformation of this periodic solution (a starting oscillating attractor, i.e. an attractor not including equilibria, denoted further by  ), with increasing j in passing from nonlinearity φ
j(σ) to φ
j+1(σ). Here two cases are possible:
), with increasing j in passing from nonlinearity φ
j(σ) to φ
j+1(σ). Here two cases are possible:
- Case 1::
-
All the points of
 are in the attraction domain of the attractor
are in the attraction domain of the attractor  , being an oscillating attractor of the system
$$ \frac{d\mathbf{x}}{dt}=\mathbf{P}_{\mathbf{0}} \mathbf{x}+\mathbf{q}\varphi^j\bigl(\mathbf{r}^{*}\mathbf{x} \bigr) $$(3.11)
, being an oscillating attractor of the system
$$ \frac{d\mathbf{x}}{dt}=\mathbf{P}_{\mathbf{0}} \mathbf{x}+\mathbf{q}\varphi^j\bigl(\mathbf{r}^{*}\mathbf{x} \bigr) $$(3.11)with j=1.
- Case 2::
-
In the change from the system (3.10) to the system (3.11) with j=1 a loss of stability (bifurcation) and the vanishing of
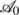 are observed.
are observed.
In Case 1 the solution x
1(t) can be determined numerically by starting a trajectory of the system (3.11) with j=1 from the initial point x
0(0). If in the process of computation the solution x
1(t) has not fallen to an equilibrium and it is not increased indefinitely (here a sufficiently large computational interval [0,T] should always be considered), then this solution reaches an attractor  . Then it is possible to proceed to the system (3.11) with j=2 and to perform a similar procedure of computation of
. Then it is possible to proceed to the system (3.11) with j=2 and to perform a similar procedure of computation of  , by starting a trajectory of the system (3.11) with j=2 from the initial point x
1(T) and computing the trajectory x
2(t).
, by starting a trajectory of the system (3.11) with j=2 from the initial point x
1(T) and computing the trajectory x
2(t).
Proceeding this procedure and sequentially increasing j and computing x
j(t) (being a trajectory of the system (3.11) with the initial data x
j−1(T)), one either arrives at the computation of  (being an attractor of the system (3.11) with j=m, i.e. the original system (3.9)), either, at a certain step, observes a loss of stability (bifurcation) and the vanishing of the attractor.
(being an attractor of the system (3.11) with j=m, i.e. the original system (3.9)), either, at a certain step, observes a loss of stability (bifurcation) and the vanishing of the attractor.
2.1.1 System Reduction
To determine the initial data x 0(0) of the starting periodic solution, one transforms the system (3.10) with nonlinearity φ 0(σ) by the linear nonsingular transformation S to the form
Here y 1, y 2 are scalar values, y 3 is an (n−2)-dimensional vector, b 3 and c 3 are (n−2)-dimensional vectors, b 1 and b 2 are real numbers, and A 3 is an ((n−2)×(n−2))-matrix, all eigenvalues of which have negative real parts. Without loss of generality, it can be assumed that for the matrix A 3 there exists a positive number d>0 such that
In practice, for determining k and ω 0 the transfer function W(p) of the system (3.7) is used:
where p is a complex variable. The number ω 0 is obtained from the equation \(\operatorname{Im} W(i\omega_{0})=0\) and k is computed then by the formula \(k=-(\operatorname{Re} W(i\omega_{0}))^{-1}\).
Let us write a transfer function of the system (3.10):
and a transfer function of the system (3.12):
Here I is a unit matrix, η and θ are certain real numbers, Q(p) is a stable polynomial of the degree (n−2), R(p) is a polynomial of a degree smaller than (n−2). Suppose that the polynomials R(p) and Q(p) have no common roots. Since the systems (3.10) and (3.12) are equivalent, the transfer functions of these systems coincide. This implies the following relations:
2.1.2 Justification of Harmonic Balance in Non-critical Case
Consider the system (3.10) with differentiableFootnote 2 nonlinearity φ 0(σ)=εφ(σ), where ε is a small positive parameter.
Introduce the describing function
Theorem 3.1
Let the number a 0>0 exist such that the conditions
are satisfied. Then for sufficiently small ε>0 the system (3.12) with nonlinearity φ 0(σ)=εφ(σ) has a periodic solution of the form
with the initial data
and with the period
Here O n−2 (ε) is an (n−2)-dimensional vector such that its components are O(ε).
Taking into account the relations (3.16), this theorem can be reformulated in the following way.
Corollary 3.1
Let the number a 0>0 exist such that the conditions
are satisfied. Then for sufficiently small ε>0 the system (3.10) with the transfer function (3.14) and the nonlinearity φ 0(σ)=εφ(σ) has a T-periodic solution such that
Theorem 3.1 coincides with the procedure of the search of stable periodic solutions by means of the standard describing function method (see, for example, [10]). Similar assertions can be proved in the case of vector nonlinearity [26].
It should be noted that the condition (3.20) cannot be satisfied in the case when conditions of the Aizerman and Kalman conjectures are fulfilled (i.e. nonlinearity φ belongs to the sector of linear stability). In this case the methods of harmonic balance and describing function lead to a wrong result, namely nonexistence of periodic solutions and global stability of unique equilibrium, but nowadays the counterexamples are well known [6, 16].
2.1.3 Justification of Harmonic Balance in the Critical Case
In 1957 R.E. Kalman formulated the following conjecture [9]:
Conjecture 3.1
Suppose that for all k∈(μ 1,μ 2) a zero solution of the system (3.9) with φ(σ)=kσ is asymptotically stable in the large (i.e., a zero solution is Lyapunov stable and any solution of the system (3.9) tends to zero as t→∞. In other words, a zero solution is a global attractor of the system (3.9) with φ(σ)=kσ).
If at the points of differentiability of φ(σ) the condition
is satisfied, then the system (3.9) is stable in the large.
The Kalman conjecture is a strengthening of the Aizerman conjecture, where in place of the condition (3.22) on the derivative of nonlinearity it is required that the nonlinearity itself belongs to a linear sector.
To justify the method of harmonic balance in this critical case special nonlinearities will be considered. Let us assume first that μ 1=0, μ 2>0 and consider the system (3.12) with nonlinearity φ 0(σ) of a special form
Here μ<μ 2 and M are certain positive numbers and ε is a small positive parameter.
Then the following result is valid.
Theorem 3.2
If the inequalities
are satisfied, then for small enough ε the system (3.12) with nonlinearity (3.23) has an orbitally stable periodic solution
with the initial date
The methods for the proof of this theorem are developed in [6, 15, 16, 21].
2.2 Hidden Oscillations in Counterexamples to the Aizerman and Kalman Conjectures
Based on this theorem, it is possible to apply the described above multi-step procedure for the localization of hidden oscillations: the initial data, obtained analytically, allows one to step aside from stable zero equilibrium and to start a numerical localization of possible oscillations.
Consider a finite sequence of piecewise-linear functions
Here the function φ m(σ) is a monotone continuous piecewise-linear function sat(σ) (“saturation”). Choose m in such a way that the graphs of the functions φ j and φ j+1 are slightly distinct from each other outside small neighborhoods of points of discontinuity.
Suppose that the periodic solution x m(t) of the system (3.9) with the monotone and continuous function φ m(σ)=sat(σ) is computed. In this case a similar computational procedure for the sequence of systems with nonlinearities can be organized:
Note that, using the similar technique of small changes, it is also possible to approach other continuous monotonic increasing functions [26]. The finding of periodic solutions for a system with nonlinearity (3.27) gives a certain counterexample to the Kalman conjecture for each i=1,…,10.
Consider the following system:
Here for φ(σ)=kσ the linear system (3.28) is stable for k∈(0,9.9) (see (3.25)). For piecewise-continuous nonlinearity φ(σ)=φ 0(σ) with sufficiently small ε there exists a periodic solution.
Now let us use the algorithm for construction of periodic solutions. Suppose μ=M=1, ε 1=0.1, ε 2=0.2,…,ε 10=1. For j=1,…,10, the solutions of the system (3.28) with nonlinearity φ(σ) equal to φ j(σ) can be constructed sequentially. Here for all ε j , j=1,…,10 there exists a periodic solution.
At the first step, for j=0, the initial data of stable periodic oscillation take the form
Therefore for j=1 a trajectory starts from the point x 1(0)=x 3(0)=x 4(0)=0, x 2(0)=−1.7513. The projection of this trajectory on the plane (x 1,x 2) and the sector of linear stability are shown in Fig. 3.6 for the odd steps.
From Fig. 3.6 it follows that at each step after a transient process a stable periodic solution is reached. At each step, the last trajectory point is used as the initial data for the next step of the computational procedure.
Proceeding this procedure for j=3,…,10, one sequentially approximates a periodic solution of the initial system (3.28) (Fig. 3.7). It should also be noted that if in place of sequential increasing ε j to compute, for ε=1, a solution with the initial data according to (3.29), then the solution will “fall down” to zero.
Change the nonlinearity φ(σ) to the increasing function θ i(σ), and continue sequential construction of periodic solutions of the system (3.28) for i=1,…,10. The obtained periodic solutions are shown in Fig. 3.8.
At the last step for the system (3.28) with smooth strictly increasing nonlinearity
there exists a periodic solution (Fig. 3.9).
2.3 Hidden Chaotic Attractors in the Chua Circuit
The development of modern computers allows one to perform numerical simulation of nonlinear chaotic systems and to obtain new information on the structure of their trajectories. In the well-known Lorenz, Chen, Chua, and many other chaotic dynamical systems the classical attractors are self-exciting attractors and can be obtained numerically by means of a standard computational procedure. In contradiction, there are attractors of another type: hidden chaotic attractors, which cannot be obtained by a standard computational procedure and show limitations of such a simple computational approach.
In 2010, for the first time, a chaotic hidden attractor was discovered [14, 23] in the Chua circuit, which is described by a three-dimensional dynamical system. Let us demonstrate the application of the above algorithm for localization of a hidden chaotic attractor in the Chua system. For this purpose, rewrite the Chua system (3.4) as (3.7)
Here

Introduce the coefficient k and the small parameter ε, and represent the system (3.31) as (3.10), namely
where

By the nonsingular linear transformation x=Sy the system (3.32) is reduced to the form (3.12), namely
where

The transfer function W A (p) of the system (3.33) can be represented as
Further, using the equality of the transfer functions of the systems (3.32) and (3.33), one obtains
This implies the following relations:
Since the system (3.32) can be reduced to the form (3.33) by the nonsingular linear transformation x=Sy, for the matrix S the relations
are valid. Having solved these matrix equations, one obtains the transformation matrix

Here
By (3.19), for small enough ε initial data for the first step of multistage localization procedure take the form
Returning to the Chua system’s denotations, for determining the initial data of the starting solution of the multistage procedure we have the following formulas:
Consider the system (3.32) with the parameters
Note that in this case for the considered values of parameters there are three equilibria in the system: a locally stable zero equilibrium and two saddle equilibria.
Now we apply the above procedure of hidden attractors’ localization to the Chua system (3.31) with the parameters (3.37). For this purpose let us compute a starting frequency and a coefficient of harmonic linearization. We have
Then, one computes solutions of the system (3.32) with nonlinearity εφ(x)=ε(ψ(x)−kx), sequentially increasing ε from the value ε 1=0.1 to ε 10=1 with the step 0.1 (see Fig. 3.10).
By (3.34) and (3.36) we obtain the initial data
for the first step of the multistage procedure for the construction of solutions. For the value of the parameter ε
1=0.1, after the transient process the computational procedure reaches the starting oscillation x
1(t). Further, by the sequential transformation of x
j(t) with increasing the parameter ε
j
, using the numerical procedure, for the original Chua system (3.31) the set  is computed. This set is presented in Fig. 3.11.
is computed. This set is presented in Fig. 3.11.
It should be noted that the decreasing of the integration step, the increasing of integration time, and the computation of different trajectories of the original system with initial data from a small neighborhood of  lead to the localization of the same set
lead to the localization of the same set  (all the computed trajectories densely trace the set
(all the computed trajectories densely trace the set  ). Note also that for the computed trajectories Zhukovsky instability and the positiveness of the Lyapunov exponent [19] is observed.
). Note also that for the computed trajectories Zhukovsky instability and the positiveness of the Lyapunov exponent [19] is observed.
The behavior of system trajectories in the neighborhood of equilibria is presented in Fig. 3.11. Here \(M_{1,2}^{\mathrm{unst}}\) are unstable manifolds, \(M_{1,2}^{\mathrm{st}}\) are stable manifolds. Thus, in a phase space of the system there are stable separating manifolds of saddles.
The above and the remark on the existence, in the system, of a locally stable zero equilibrium F
0, attracting the stable manifolds \(M_{1,2}^{\mathrm{st}}\) of two symmetric saddles S
1 and S
2, lead to the conclusion that in  a hidden strange attractor is computed.
a hidden strange attractor is computed.
3 Conclusion
The study of hidden oscillations and hidden chaotic attractors requires the development of new analytical and numerical methods. This survey includes discussion on new analytical-numerical approaches to investigation of hidden oscillations in dynamical systems, based on the development of numerical methods, computers, and an applied bifurcation theory, which suggests revising early ideas on the application of the small parameter method and the harmonic linearization [16, 18, 23, 26].
References
Aizerman MA (1949) On a problem concerning the stability “in the large” of dynamical systems. Usp Mat Nauk 4(4):187–188. In Russian
Andronov AA, Vitt AA, Khaikin SE (1966) Theory of oscillators. Pergamon Press, Oxford
Belousov BP (1959) A periodic reaction and its mechanism. In: Collection of abstracts on radiation medicine, 1958. Medgiz, Moscow, pp 145–147
Bernat J, Llibre J (1996) Counterexample to Kalman and Markus-Yamabe conjectures in dimension larger than 3. Dyn Contin Discrete Impuls Syst 2(3):337–379
Bilotta E, Pantano P (2008) A gallery of Chua attractors. World Scientific series on nonlinear science. Series A: monographs and treatises, vol 61. World Scientific, Hackensack, NJ
Bragin VO, Vagaitsev VI, Kuznetsov NV, Leonov GA (2011) Algorithms for finding hidden oscillations in nonlinear systems. The Aizerman and Kalman conjectures and Chua’s circuits. J Comput Syst Sci Int 50(4):511–543
Chua LO (1992) A zoo of strange attractors from the canonical Chua’s circuits. In: Proceedings of the 35th midwest symposium on circuits and systems, vol 2. IEEE, New York, pp 916–926
Gubar’ NA (1961) Investigation of a piecewise linear dynamical system with three parameters. J Appl Math Mech 25(6):1519–1535
Kalman RE (1981) Physical and mathematical mechanisms of instability in nonlinear automatic control systems. Trans Am Soc Mech Eng 79(3):553–566
Khalil HK (2002) Nonlinear systems, 3rd edn. Prentice Hall, Upper Saddle River
Krylov AN (1936) Vibration of ships. Gl Red Sudostroit Lit, Moscow. In Russian
Kuznetsov NV, Kuznetsova OA, Leonov GA (2011) Investigation of limit cycles in two-dimensional quadratic systems. In: Proceedings of the 2nd international symposium rare attractors and rare phenomena in nonlinear dynamics (RA’11), pp 120–123
Kuznetsov NV, Leonov GA (2008) Lyapunov quantities, limit cycles and strange behavior of trajectories in two-dimensional quadratic systems. J Vibroeng 10(4):460–467
Kuznetsov NV, Leonov GA, Vagaitsev VI (2010) Analytical-numerical method for attractor localization of generalized Chua’s system. In: Periodic control systems, vol 4, Part 1. IFAC
Leonov GA (2009) On a harmonic linearization method. Dokl Math 79(1):144–146
Leonov GA (2010) Effective methods in the search for periodic oscillations in dynamical systems. J Appl Math Mech 74(1):24–50
Leonov GA (2011) Four normal size limit cycles in two-dimensional quadratic systems. Int J Bifurc Chaos Appl Sci Eng 21(2):425–429
Leonov GA, Bragin VO, Kuznetsov NV (2010) Algorithm for constructing counterexamples to the Kalman problem. Dokl Math 82(1):540–542
Leonov GA, Kuznetsov NV (2007) Time-varying linearization and the Perron effects. Int J Bifurc Chaos Appl Sci Eng 17(4):1079–1107
Leonov GA, Kuznetsov NV (2010) Limit cycles of quadratic systems with a perturbed third-order focus and a saddle equilibrium state at infinity. Dokl Math 82(2):693–696
Leonov GA, Kuznetsov NV (2011) Algorithms for searching for hidden oscillations in the Aizerman and Kalman problems. Dokl Math 84(1):475–481
Leonov GA, Kuznetsov NV, Kudryashova EV (2011) A direct method for calculating Lyapunov quantities of two-dimensional dynamical systems. Proc Steklov Inst Math 272(Suppl 1):119–126
Leonov GA, Kuznetsov NV, Vagaitsev VI (2011) Localization of hidden Chua’s attractors. Phys Lett A 375(23):2230–2233
Leonov GA, Kuznetsova OA (2009) Evaluation of the first five Lyapunov exponents for the Liénard system. Dokl Phys 54(3):131–133
Leonov GA, Kuznetsova OA (2010) Lyapunov quantities and limit cycles of two-dimensional dynamical systems. Analytical methods and symbolic computation. Regul Chaotic Dyn 15(2–3):354–377
Leonov GA, Vagaitsev VI, Kuznetsov NV (2010) Algorithm for localizing Chua attractors based on the harmonic linearization method. Dokl Math 82(1):663–666
Lorenz EN (1963) Deterministic nonperiodic flow. J Atmos Sci 20(2):130–141
Markus L, Yamabe H (1960) Global stability criteria for differential systems. Osaka Math J 12:305–317
Matsumoto T (1984) A chaotic attractor from Chua’s circuit. IEEE Trans Circuits Syst 31(12):1055–1058
Pliss VA (1958) Some problems in the theory of the stability of motion. Izd LGU, Leningrad
Rayleigh JWS (1877) The theory of sound. MacMillan, London
Stoker JJ (1950) Nonlinear vibrations in mechanical and electrical systems. Interscience, New York
Timoshenko S (1928) Vibration problems in engineering. Van Nostrand, New York
van der Pol B (1926) On “relaxation-oscillations”. Philos Mag Ser 7 2(11):978–992
Acknowledgements
This work was partly supported by Academy of Finland, Ministry of Education and Science of the Russian Federation (Federal target program “Scientific and Scientific-Pedagogical Cadres for Innovative Russia” for the years 2009–2013), Russian Foundation for Basic Research and Saint-Petersburg State University.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Leonov, G.A., Kuznetsov, N.V. (2013). Analytical-Numerical Methods for Hidden Attractors’ Localization: The 16th Hilbert Problem, Aizerman and Kalman Conjectures, and Chua Circuits. In: Repin, S., Tiihonen, T., Tuovinen, T. (eds) Numerical Methods for Differential Equations, Optimization, and Technological Problems. Computational Methods in Applied Sciences, vol 27. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-5288-7_3
Download citation
DOI: https://doi.org/10.1007/978-94-007-5288-7_3
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-007-5287-0
Online ISBN: 978-94-007-5288-7
eBook Packages: EngineeringEngineering (R0)










 are in the attraction domain of the attractor
are in the attraction domain of the attractor  , being an oscillating attractor of the system
, being an oscillating attractor of the system
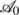 are observed.
are observed.




