Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1.1 History

The eddy covariance method for measuring exchanges of heat, mass, and momentum between a flat, horizontally homogeneous surface and the overlying atmosphere was proposed by Montgomery (1948), Swinbank (1951), and Obukhov (1951). Under these conditions, net transport between the surface and atmosphere is one-dimensional and the vertical flux density can be calculated by the covariance between turbulent fluctuations of the vertical wind and the quantity of interest.

Instrumentation limitations hampered early implementation of this approach. In 1949, Konstantinonov (Obukhov 1951) developed a wind vane with two hot wire anemometers to measure the shear stress but the full potential of the eddy covariance method only emerged after the development of sonic anemometers, for which the basic equations were given by Schotland (1955). After the development of the first sonic thermometer (Barrett and Suomi 1949), a vertical sonic anemometer with a 1 m path length (Suomi 1957) was used during the O’Neill experiment in 1953 (Lettau and Davidson 1957). The design of today’s anemometers was developed by Bovscheverov and Voronov (1960) and later by Kaimal and Businger (1963) and Mitsuta (1966). These phase shift anemometers have now been replaced by running time anemometers with delay time measurements (Hanafusa et~al. 1982; Coppin and Taylor 1983).

Early micrometeorological experiments from the 1950s to 1970s were designed to study fundamental aspects of atmospheric turbulence over homogeneous surfaces, whereas studies in the 1980s investigated the turbulent fluxes of momentum, sensible, and latent heat over heterogeneous surfaces. Similar experiments were conducted in the United States (FIFE, Sellers et~al. 1988), in France (Hydrological Atmospheric Pilot Experiment (HAPEX), André et~al. 1990), and in Russia (KUREX, Tsvang et~al. 1991). These experiments were to become the basis of many further micrometeorological experiments (Foken 2008) that needed researchers who were highly experienced in micrometeorology and sensor handling.

The possibility of continuous eddy flux measurements arose in the 1990s with the development of a new generation of sonic anemometers (see reviews by Zhang et~al. 1986; Foken and Oncley 1995) and infrared gas analyzers for water vapor and carbon dioxide, together with the first comprehensive software packages for the eddy covariance method (McMillen 1988). In the early 1990s, the eddy covariance method became more and more widely used by the ecological community for the measurement of the carbon dioxide and water exchange between an ecosystem and the atmosphere. The first measuring towers of what later became the international FLUXNET network (Baldocchi et~al. 2001) were installed, and introductions into techniques new for nonmicrometeorologists were written (Aubinet et~al. 2000; Moncrieff et~al. 1997a, b). In parallel, the development of new analyzer types allowed an extension of the investigated trace gas spectrum. In particular, Tunable Diode Laser and Quantum Cascade Laser spectrometers were used for the measurement of methane and nitrous oxide (Smith et~al. 1994; Laville et~al. 1999; Hargreaves et~al. 2001; Kroon et~al. 2010), Proton Transfer Reaction Mass Spectrometers for volatile organic compounds (Karl et~al. 2002; Spirig et~al. 2005), and Chemiluminescent sensors for Ozone (Güsten and Heinrich 1996; Gerosa et~al. 2003; Lamaud et~al. 1994, a.o.).

Some milestones in the development of the eddy covariance method are given in Table 1.1 with the reference to the Chapters of this book.

Table 1.1 History of the development of the eddy covariance method
Full size table

1.2 Preliminaries

1.2.1 Context of Eddy Covariance Measurements

Eddy covariance measurements are typically made in the surface boundary layer, which is approximately 20–50 m high in the case of unstable stratification and a few tens of meters in stable stratification (see Stull 1988; Garratt 1992; Foken 2008; for complete definitions of layers in the atmosphere). Fluxes are approximately constant with height in the surface layer; hence measurements taken in this layer are representative of the fluxes from the underlying surfaces which are desired to be known. Here atmospheric turbulence is the dominant transport mechanism, justifying the use of the eddy covariance approach to measure the fluxes.

Some preliminary definitions are necessary before discussing the eddy covariance approach in detail.

1.2.2 Reynolds Decomposition

The description of turbulent motions in the following theory sections requires the decomposition of the time-series of each variable ζ into a time-mean part, \( \bar{\zeta } \), and a fluctuating part, ζ’, the so-called Reynolds decomposition (Fig. 1.1). This can be written as:

$$ \zeta = \bar{\zeta }{ + }\zeta ^\prime $$
(1.1a)

where:

$$ \bar{\zeta } = \frac{1}{T}\int_t^{{t + T}} {\zeta (t)dt} $$
(1.1b)
Fig. 1.1
figure 1_1

Schematic presentation of Reynolds decomposition of the value ζ (Foken 2008)

Full size image

The application of Reynolds decomposition requires some averaging rules for the turbulent value ζ’ which are termed Reynolds postulates:

$$ \begin{aligned}[b] \mathbf{{\rm I}}\;\overline {\zeta ^\prime } &= 0 \\ \mathit{II}\;\overline {\zeta \xi } &= \bar{\zeta }\,\bar{\xi } + \overline {\zeta ^\prime \xi ^\prime } \\ \mathit{III}\;\overline {\bar{\zeta }\xi } &= \overline \zeta \,\overline \xi \\ \mathit{IV}\;\overline {a\zeta } &= a\bar{\zeta } \\V\;\overline {\zeta + \xi } &= \overline \zeta + \overline \xi \\ \end{aligned} $$
(1.2)

where a is a constant.

Stricto sensu, these relations are valid only when averages are by “ensemble” averaging (i.e., averaging over many realizations under identical conditions, Kaimal and Finnigan 1994). However, this is never possible in atmospheric measurements, so averages are most often computed on the basis of time series of statistical quantities by making use of the ergodic hypothesis which states that time averages are equivalent to ensemble averages (Brutsaert 1982; Kaimal and Finnigan 1994). To fulfil this assumption, the fluctuations have to be statistically stationary during the averaging time chosen (see Chap. 4).

1.2.3 Scalar Definition

The following variables are commonly used in the literature (and throughout this book) to define the scalar intensity of an atmospheric constituent s: density (ρ s, kg m−3) and molar concentration (c s mol m−3) represent the mass and the number of moles of s per volume of air, respectively. The mole fraction (mole mole−1) is the ratio of the moles of s divided by the total number in the mixture (also equal to the ratio of the constituent partial pressure to the total pressure), the molar mixing ratio (χ s,m, mole mole−1) is the ratio of the constituent mole number to those of dry air, and the mass mixing ratio (χ s, kg kg−1) is the ratio of the mass of the constituent to the mass of dry air. These variables are related by the perfect gas and the Dalton laws.

However, among these variables, only the molar and mass mixing ratios are conserved quantities in the presence of changes in temperature, pressure, and water vapor content (see Kowalski and Serrano-Ortiz (2007) for a more complete discussion). Unfortunately, the variables that are directly measured in the field by infrared gas analyzers are rather density and molar concentration, quantities that are not conserved during heat conduction, air compression/expansion or evaporation, and water vapor diffusion. Therefore, variations in these quantities may appear even in the absence of production, absorption, or transport of the component. The corrections (Webb-Pearman-Leuning (WPL) corrections) that are necessary to take these effects into account were extensively discussed by Webb et~al. (1980) and reexamined by Leuning (2003, 2007). They will be presented in Sect. 4.1.4.

The conservation equations developed in the section below are written using the mass mixing ratio but, for convenience, the other variables will also appear in this book. Conversion factors of one variable into another are given in Table 1.2.

Table 1.2 Conversion factors between different variables characterizing scalar intensity
Full size table

1.3 One Point Conservation Equations

The equation describing the conservation of any scalar or vector quantity ζ in the atmosphere may be written as

$$ \underbrace{{\frac{{\partial {\rho_{{d}}}\mathop{\zeta }\limits^{ - } }}{{\partial t}}}}_I + \underbrace{{\vec{\nabla }(\vec{u}{\rho_{\text{d}}}\,\zeta )}}_{\mathit{II}} + \underbrace{{{K_{{{\zeta }}}}\Delta ({\rho_{{d}}}\,\zeta )}}_{\mathit{III}} = \underbrace{{{S_{{{\zeta }}}}}}_{\mathit{IV}} $$
(1.3)

where \( \overrightarrow u \) is the wind velocity vector, \( \overrightarrow \nabla \) and \( \Delta \) represent the divergence \( \left( {\frac{\partial }{{\partial x}},\frac{\partial }{{\partial y}},\frac{\partial }{{\partial z}}} \right) \) and Laplacian \( \left( {\frac{{{\partial^2}}}{{\partial {x^2}}} + \frac{{{\partial^2}}}{{\partial {y^2}}} + \frac{{{\partial^2}}}{{\partial {z^2}}}} \right) \) operators, ρ d is the dry air density, K ζ is the molecular diffusivity of the quantity ζ, and S ζ represents its source/sink strength. This equation is instantaneous and applies to an infinitesimal volume of air. It states that the rate of change of the quantity (I) can be due to its atmospheric transport (II) to molecular diffusion (III) or to its production by a source/absorption by a sink into the infinitesimal volume (IV). It can be applied to any scalar or vector quantity provided source terms are defined accordingly. In particular, if ζ is 1, Eq. 1.3 is the continuity equation, if ζ is air enthalpy, it is the enthalpy conservation equation, and if ζ is the mixing ratio of an atmospheric component (water vapor, carbon dioxide, etc.), it is the scalar conservation equation. If the quantity is a component of the velocity vector in one given direction, Eq. 1.3 expresses the conservation of the momentum component in this direction. The three equations describing the momentum conservation in the three directions constitute the Navier Stokes equations.

Application of these equations to the surface boundary layer requires application of the Reynolds decomposition rules: the variables \( \zeta, \,\,{\rho_{\text{d}}},\vec{u} \), and S ζ should each be decomposed into a mean and a fluctuating part according to Eq. 1.2, followed by application of the averaging operator, and appropriate rearrangement and simplification. This procedure will be applied to each equation below.

1.3.1 Dry Air Mass Conservation (Continuity) Equation

By replacing ζ by 1 in Eq. 1.3, one obtains

$$ \frac{{\partial {\rho_{\text{d}}}}}{{\partial t}} + \vec{\nabla }(\vec{u}{\rho_{\text{d}}}) = 0 $$
(1.4)

as there is neither a source nor sink of dry air in the atmosphere. Application of the time- averaging operator gives immediately:

$$ \frac{{\overline {\partial \rho d} }}{{\partial t}} + \vec{\nabla }(\overline {\vec{u}{\rho_{\text{d}}}} ) = 0 $$
(1.5)

1.3.2 Momentum Conservation Equation

By replacing ζ in Eq. 1.3 with the component of wind velocity in one given direction, u i, one obtains the momentum conservation equation in this direction:

$$ \frac{{\partial {\rho_{\text{d}}}{u_{\text{i}}}}}{{\partial t}} + \vec{\nabla }(\vec{u}{\rho_{\text{d}}}\,{u_{\text{i}}}) = {S_{\text{i}}} $$
(1.6)

In Eq. 1.6, the source/sink terms correspond to momentum source/sink, namely to forces. Forces that can act on air parcels in the atmospheric boundary layer are drag, pressure gradient, Coriolis forces, viscous forces, or buoyancy. The first three forces are considered negligible for a flat, horizontally homogeneous surface boundary layer above the roughness elements (i.e. not including vegetation) (Businger 1982; Foken 2008; Stull 1988). Buoyancy appears only in the equation for vertical momentum. The horizontal component of momentum parallel to the mean wind is dominant in the surface boundary layer and thus the buoyancy term is not considered. In a Cartesian coordinate system (x, y, z) where x corresponds to the horizontal, parallel to the average wind velocity, y to the horizontal, perpendicular to the average velocity, and z to the vertical; u, v, w are the x, y, and z components of velocity, respectively, and this equation is written as

$$ \frac{{\partial {\rho_{\text{d}}}u}}{{\partial t}} + \frac{{\partial {\rho_{\text{d}}}{u^2}}}{{\partial x}} + \frac{{\partial {\rho_{\text{d}}}vu}}{{\partial y}} + \frac{{\partial {\rho_{\text{d}}}wu}}{{\partial z}} = 0 $$
(1.7)

Application of the Reynolds decomposition to Eq. 1.7 and use of the following simplifications (Businger 1982; Stull 1988):

$$ \begin{aligned}[b] & I\;\left| {p^\prime /\bar{p}} \right| \ll \left| {{{\rho ^\prime }_{\text{d}}}/\overline {{\rho_{\text{d}}}} } \right| \\[3pt] & \mathit{II}\;\left| {p^\prime /\bar{p}} \right| \ll \left| {\theta ^\prime /\bar{\theta }} \right|, \\[3pt] & \mathit{III}\;\left| {{{\rho ^\prime }_{\text{d}}}/\overline {{\rho_{\text{d}}}} } \right| \ll 1 \\[3pt] & \mathit{IV}\;\left| {\theta ^\prime /\bar{\theta }} \right| \ll 1 \end{aligned} $$
(1.8)

where p is the pressure and θ the air temperature, leads to

$$ \frac{{\overline {\partial u} }}{{\partial t}} + \bar{u}\frac{{\partial \bar{u}}}{{\partial x}} + \bar{v}\frac{{\partial \bar{u}}}{{\partial y}} + \bar{w}\frac{{\partial \bar{u}}}{{\partial z}} + \frac{{\partial \overline {{{u^\prime }^2}} }}{{\partial x}} + \frac{{\partial \overline {v^\prime u^\prime } }}{{\partial y}} + \frac{{\partial \overline {w^\prime u^\prime } }}{{\partial z}} = 0 $$
(1.9)

Equation 1.8, III corresponds to the Boussinesq-approximation (Boussinesq 1877), which neglects density fluctuations except in the buoyancy (gravitation) term, because the acceleration of gravity is relatively large in comparison with the other accelerations in the momentum equation. By choosing a coordinate system such that \( \bar{v} \) and \( \bar{w} \) are zero and assuming horizontal homogeneity (horizontal gradients nullify) and steady state conditions (time derivative nullifies) we obtain finally

$$ \frac{{\partial \overline {w^\prime u^\prime } }}{{\partial z}} = 0 $$
(1.10)

Where \( \overline {w^\prime u^\prime } \) is the eddy covariance term. Equation 1.10 suggests that, under the preceding assumptions, this flux is constant with height and that it is representative of the vertical flux of momentum through a horizontal plane above the surface roughness elements. This approach is called the eddy covariance method.

Neglecting the pressure gradient, molecular/viscous transport, gravity, and Coriolis terms to derive Eq. 1.10 does not have significant impact on the eddy covariance method over flat, homogeneous surfaces. These conditions are however rare in ecosystems located in a patchy landscape or undulating topography. Steady-state conditions are also rare in the surface layer because of diurnal variations in atmospheric stability. It is then necessary to measure the change in storage term using an array of sensors (Sect. 2.5) or to assume quasi-steady conditions. Methods to estimate errors caused by neglecting the storage term are included in the data quality procedures discussed in Sect. 4.3.

1.3.3 Scalar Conservation Equation

By replacing ζ in Eq. 1.3 by χ s, the mixing ratio of one atmospheric component, one obtains

$$ \frac{{\partial {\rho_{\text{d}}}{\chi_{\text{s}}}}}{{\partial t}} + \vec{\nabla }(\vec{u}{\rho_{\text{d}}}\,{\chi_{\text{S}}}) = {S_{\text{s}}} $$
(1.11)

Through application of the Reynolds decomposition and the continuity Eq. 1.5, Leuning (2003) showed that Eq. 1.11 can be written as

$$ \overline {\rho d} \frac{{\overline {\partial {\chi_{\text{S}}}} }}{{\partial t}} + \overline {{\rho_{\text{d}}}\vec{u}} \,\,\vec{\nabla }\left( {\overline {{\chi_{\text{S}}}} } \right) + \vec{\nabla }\left[ {\overline {\rho d}\ \overline {\vec{u}^\prime {{\chi ^\prime }_{\text{S}}}} } \right] = \overline {{S_{\text{s}}}} $$
(1.12)

This equation states that the source term \( \overline {{S_{\text{s}}}} \) is given by the sum of the rate of change of the mixing ratio χ s, advection due to spatial gradients in χ s, and to divergences in the eddy fluxes.

Expanding this in terms of spatial derivatives and assuming constant dry air density give the one point conservation equation of a scalar:

$$ \overline {\rho d} \frac{{\overline {\partial {\chi_{\text{s}}}} }}{{\partial t}} + \overline {{\rho_{\text{d}}}u} \frac{{\partial \overline {{\chi_{\text{s}}}} }}{{\partial x}} + \overline {{\rho_{\text{d}}}v} \frac{{\partial \overline {{\chi_{\text{s}}}} }}{{\partial y}} + \overline {{\rho_{\text{d}}}w} \frac{{\partial \overline {{\chi_{\text{s}}}} }}{{\partial z}} + \frac{{\partial \overline {{\rho_{\text{d}}}} \overline {u^\prime {{\chi ^\prime }_{\text{s}}}} }}{{\partial x}} + \frac{{\partial \overline {{\rho_{\text{d}}}} \overline {v^\prime {{\chi ^\prime }_{\text{s}}}} }}{{\partial y}} + \frac{{\partial \overline {{\rho_{\text{d}}}} \overline {w^\prime {{\chi ^\prime }_{\text{s}}}} }}{{\partial z}} = {\bar{S}_{\text{s}}} $$
(1.13)

Considering that \( \bar{v} \) and \( \bar{w} \) are zero, due to axis choice (Sect. 3.2.4) and assuming horizontal homogeneity (horizontal gradients nullify) and steady state conditions (time derivative nullifies) we get, similar to Eq. 1.10:

$$ \frac{{\partial \overline {{\rho_{\text{d}}}} \overline {w^\prime {{\chi ^\prime }_{\text{s}}}} }}{{\partial z}} = {\bar{S}_{\text{s}}} $$
(1.14)

expressing that the vertical gradient of eddy covariance is equal to the tracer source/sink term in the volume element. In the case of passive tracers (water vapor, CO2), this term is zero. In the case of active tracers (ozone, VOCs, NOx,…), \( {\bar{S}_{\text{s}}} \) corresponds to the rate of chemical production/destruction of the component in the volume element.

1.3.4 Enthalpy Equation

By replacing ζ by c P Θ, the air enthalpy, one obtains

$$ \frac{{\partial \rho {c_{\text{P}}}\theta }}{{\partial t}} + \overrightarrow \nabla (\vec{u}\rho {c_{\text{P}}}\theta ) = {S_{{{\theta }}}} $$
(1.15)

where c P is the specific heat of the air and \( \rho \) is moist air density. The same development as before leads to

$$ \frac{{\overline {\partial \theta } }}{{\partial t}} + \bar{u}\frac{{\partial \bar{\theta }}}{{\partial x}} + \bar{v}\frac{{\partial \bar{\theta }}}{{\partial y}} + \bar{w}\frac{{\partial \bar{\theta }}}{{\partial z}} + \frac{{\partial \overline {u^\prime \theta ^\prime } }}{{\partial x}} + \frac{{\partial \overline {v^\prime \theta ^\prime } }}{{\partial y}} + \frac{{\partial \overline {w^\prime \theta ^\prime } }}{{\partial z}} = \frac{1}{{\bar{\rho }{c_{\text{P}}}}}\left[ {\frac{{\partial R}}{{\partial z}}} \right] $$
(1.16)

and

$$ \frac{{\partial \overline {w^\prime \theta ^\prime } }}{{\partial z}} = \frac{1}{{\bar{\rho }{c_{\text{P}}}}}\left[ {\frac{{\partial R}}{{\partial z}}} \right] $$
(1.17)

Where \( \frac{{\partial R}}{{\partial z}} \) is the vertical radiative flux divergence, which is close to zero in clear surface layers (no fog, rain, smoke, etc.).

1.4 Integrated Relations

Eddy covariance measurements can be used as a tool to estimate fluxes exchanged by ecosystems. To this end, preceding equations may be integrated both horizontally over the area of interest, A (2 × 2 L) and vertically, from soil to the measurement height h m (Fig. 1.2).

Fig. 1.2
figure 2_1

Schematic image of integration of Eq. 1.15 on a control volume in homogeneous terrain (Finnigan et~al. 2003)

Full size image

1.4.1 Dry Air Budget Equation

Integrating (1.5) on the control volume and assuming horizontal homogeneity gives:

$$ \int_0^{{{h_{\text{m}}}}} {\frac{{\overline {\partial {\rho_{\text{d}}}} }}{{\partial t}}dz + \bar{w}\overline {{\rho_{\text{d}}}} } {|_{{{h_{\text{m}}}}}} + \overline {w^\prime {{\rho ^\prime }_{\text{d}}}} {|_{{{h_{\text{m}}}}}} = 0 $$
(1.18)

where assumptions of zero flux of dry air at the ground and no net sources or sinks of dry air in the layer of air below \( {h_{\text{m}}} \) are made. Slight imbalances between molar fluxes of CO2 and O2 during photosynthesis or respiration or fluxes of nitrogen or volatile organic compounds are extremely small and do not invalidate Eq. 1.18.

1.4.2 Scalar Budget Equation (Generalized Eddy Covariance Method)

Integrating (1.13) in the control volume gives

$$ {\fontsize{7.5}{9.5}\selectfont{\begin{aligned}[b] & \frac{1}{{4{L^2}}}\int_{{ - L}}^L {\int_{{ - L}}^L {\int_0^{{{h_m}}} {\!\left[\! {\underbrace{{\overline {{\rho_{\text{d}}}} \frac{{\partial \overline {{\chi_{\text{s}}}} }}{{\partial t}}}}_I + \underbrace{{\overline {{\rho_{\text{d}}}u} \frac{{\partial \overline {{\chi_{\text{s}}}} }}{{\partial x}} + \overline {{\rho_{\text{d}}}v} \frac{{\partial \overline {{\chi_{\text{s}}}} }}{{\partial y}} + \overline {{\rho_{\text{d}}}w} \frac{{\partial \overline {{\chi_{\text{s}}}} }}{{\partial z}}}}_{{II}} + \underbrace{{\frac{{\partial \overline {{\rho_{\text{d}}}} \overline {u^\prime {{\chi ^\prime }_{\text{s}}}} }}{{\partial x}} + \frac{{\partial \overline {{\rho_{\text{d}}}} \overline {v^\prime {{\chi ^\prime }_{\text{s}}}} }}{{\partial y}}}}_{{III}} + \underbrace{{\frac{{\partial \overline {{\rho_{\text{d}}}} \overline {w^\prime {{\chi ^\prime }_{\text{s}}}} }}{{\partial z}}}}_{{IV}}} \!\right]\mathit{dz}\,\mathit{dx}\,\mathit{dy}} } } \\ & \quad = \frac{1}{{4\rho {L^2}}}\int_{{ - L}}^L {} \int_{{ - L}}^L {} \int_0^{{{h_{\text{m}}}}} {\underbrace{{\overline {{S_{\text{s}}}} \,\mathit{dz}\;\mathit{dx}\;\mathit{dy}}}_V} \raisetag{17pt}\end{aligned}}} $$
(1.19)

Equation 1.19 represents the complete budget equation of the component s. It shows that the component produced by the source or absorbed by the sink (V) may be either stored in the control volume (I), or transported by advection (II), or by turbulence (III and IV). In these conditions, the source/sink term represents both the sources/sinks inside the air volume and those at the lower limit of the volume (soil, litter).

This equation may be simplified in several ways using different hypotheses. The most common simplification, thoroughly discussed by Finnigan et~al. (2003), supposes that the measurement system is placed in a horizontally homogeneous equilibrium layer where all horizontal gradients in Eq. 1.19 are negligible and the mixing ratios and turbulent fluxes measured on the tower are assumed representative of the whole volume. In these conditions, horizontal integration is unnecessary and a simplified one-dimensional mass balance can then be deduced as

$$ \underbrace{{\int_0^{{{h_{\text{m}}}}} {{{\overline \rho }_{\text{d}}}\overline {\frac{{\partial {\chi_{\text{s}}}}}{{\partial t}}} dz} }}_I\underbrace{{ + \int_0^{{{h_{\text{m}}}}} {\overline {{\rho_{\text{d}}}w} \,\overline {\frac{{\partial {\chi_{\text{s}}}}}{{\partial z}}} } \,dz}}_{\mathit{II}} + \underbrace{{{{\left. {\overline {{\rho_{\text{d}}}} \overline {w^\prime {{\chi ^\prime }_{\text{s}}}} } \right|}_{{{h_{\text{m}}}}}}}}_{\mathit{IV}} = \underbrace{{{F_{\text{s}}}}}_V\,\,\, $$
(1.20)

where \( {\left. {\overline {w^\prime {{\chi ^\prime }_{\text{s}}}} } \right|_{{{h_{\text{m}}}}}} \) represents the vertical turbulent flux at the top of the control volume and \( {F_{\text{s}}} \) the averaged source/sink strength in the whole control volume, that is, the net ecosystem exchange for the component s. Term II represents the vertical advection at the top of the control volume that results from dry air density change with time in the air layer below h m. By application of the dry air conservation Eq. 1.18, this term may be rewritten as

$$ \int_0^{{{h_{\text{m}}}}} {\overline {{\rho_{\text{d}}}w} \overline {\frac{{\partial {\chi_{\text{s}}}}}{{\partial z}}} } \,dz = - \int_0^{{{h_{\text{m}}}}} {\left[ {\int\limits_0^z {\overline {\frac{{\partial {\rho_{\text{d}}}}}{{\partial t}}} dz^\prime } } \right]\overline {\frac{{\partial {\chi_{\text{s}}}}}{{\partial z}}} } \,dz $$
(1.21)

and after integration by parts as

$$ \int_0^{{{h_{\text{m}}}}} {\overline {{\rho_{\text{d}}}w} \,\overline {\frac{{\partial {\chi_{\text{s}}}}}{{\partial z}}} } \,dz = \int_0^{{{h_{\text{m}}}}} {\left[ {\overline {{\chi_{\text{s}}}} (z) - \overline {{\chi_{\text{s}}}} (h)} \right]\overline {\frac{{\partial {\rho_{\text{d}}}}}{{\partial t}}} } dz $$
(1.22)

Equation 1.20 may thus be rewritten as

$$ \int_0^{{{h_{\text{m}}}}} {{{\overline \rho }_{\text{d}}}\overline {\frac{{\partial {\chi_{\text{s}}}}}{{\partial t}}} dz} + \int_0^{{{h_{\text{m}}}}} {\left[ {\overline {{\chi_{\text{s}}}} (z) - \overline {{\chi_{\text{s}}}} (h)} \right]\overline {\frac{{\partial {\rho_{\text{d}}}}}{{\partial t}}} } dz + {\left. {\overline {{\rho_{\text{d}}}} \,\overline {w^\prime {{\chi ^\prime }_{\text{s}}}} } \right|_{{{h_{\text{m}}}}}} = {F_{\text{s}}} $$
(1.23)

However, most often, term II is negligible so that Eq. 1.20 may be written more simply as

$$ \underbrace{{\int_0^{{{h_{\text{m}}}}} {{{\overline \rho }_{\text{d}}}\overline {\frac{{\partial {\chi_{\text{s}}}}}{{\partial t}}} dz} }}_I + \underbrace{{{{\left. {\overline {{\rho_{\text{d}}}} \,\overline {w^\prime {{\chi ^\prime }_{\text{s}}}} } \right|}_{{{h_{\text{m}}}}}}}}_{{IV}} = \underbrace{{{F_{\text{s}}}}}_V\,\, $$
(1.24a)

This equation is at the basis of the generalized eddy covariance method: it suggests indeed that the flux of a scalar exchanged by an ecosystem (F s, term V) can be estimated as the sum of the vertical eddy covariance \( \left. {\overline {w^\prime {{\chi ^\prime }_{\text{s}}}} } \right| \) at height h m (F ECs , term IV) and of the change of storage of the scalar between the soil and this height (F STOs , term I), namely:

$$ {F_{\text{s}}} = F_{\text{s}}^{\text{EC}} + F_{\text{s}}^{\text{STO}} $$
(1.24b)

The above hypotheses are known to work fairly well in daytime conditions when turbulence is fully developed, but they appear to be too restrictive to describe completely nighttime conditions. It is then necessary to include the horizontal and vertical advection terms in the conservation equation, with the additional assumption that the vertical integral of \( \overline {{\rho_{\text{d}}}w} \,\partial {\overline \chi_{\text{s}}}/\partial z \) as measured on a single tower is representative of the whole volume. Equation 1.19 then becomes

$$ {\fontsize{8.3}{9.3}\selectfont{\begin{aligned}\underbrace{{\int_0^{{{h_{\text{m}}}}} {{{\bar{\rho }}_{\text{d}}}\frac{{\overline {\partial {\chi_{\text{s}}}} }}{{\partial t}}dz} }}_I + \underbrace{{\int_0^{{{h_{\text{m}}}}} {\left[ {\overline {{\rho_{\text{d}}}w} \frac{{\overline {\partial {\chi_{\text{s}}}} }}{{\partial z}}dz} \right]} }}_{\mathit{IIa}} + \underbrace{{\int_0^{{{h_{\text{m}}}}} {\left[ {\overline {{\rho_{\text{d}}}u} \frac{{\Delta {{\bar{\chi }}_{{{\text{s,x}}}}}}}{{\partial x}} + \overline {{\rho_{\text{d}}}v} \frac{{\Delta {{\bar{\chi }}_{{{\text{s,y}}}}}}}{{\partial y}}} \right]} dz}}_{\mathit{IIb}} + \underbrace{{\overline {{\rho_{\text{d}}}w^\prime {{\chi ^\prime }_{\text{s}}}} \left| {_{{{h_{\text{m}}}}}} \right.}}_{\mathit{IV}} {=} \underbrace{{{F_{\text{s}}}}}_V \end{aligned}}}$$
(1.25a)

in which \( \Delta {\overline \chi_{{{\text{s,}}x}}} = {\overline \chi_{{{\text{s,}}x{\text{ = L}}}}} - {\overline \chi_{{{\text{s,}}x{ = } - {\text{L}}}}} \) is the difference in mixing ratios at height z between the downwind (+L) and upwind (−L) vertical planes normal to the x-direction, with a similar definition for \( \Delta {\overline \chi_{{{\text{s,y}}}}} \) in the y-direction. Equation 1.25a may be rewritten as

$$ {F_{\text{s}}} = F_{\text{s}}^{\text{EC}} + F_{\text{s}}^{\text{VA}} + F_{\text{s}}^{\text{HA}} + F_{\text{s}}^{\text{STO}} $$
(1.25b)

where \( F_{\text{s}}^{\text{VA}} \) and \( F_{\text{s}}^{\text{HA}} \) represent vertical (Term IIa) and horizontal (Term IIb) advection of component s. One problem is that these terms cannot be measured on a single tower, and full use of this equation requires a three-dimensional array of instrumentation. The importance of the different terms of this equation will be discussed in Chap. 5.

1.5 Spectral Analysis

Thorough eddy covariance analysis, application of data quality criteria, or correct assessment of some correction factors require a spectral analysis of the (co)variances. The aim of this section is to give the necessary information about spectral analysis of a signal, atmospheric turbulence (co)spectra and the effects of measurement on these (co)spectra to allow the reader to perform these analyses. More details on spectral analysis can be found in the textbooks of Stull (1988), Kaimal and Finnigan (1994), or Foken (2008).

1.5.1 Spectral Analysis of Turbulence

Any turbulent flow may be thought of as a superposition of eddies over a wide range of sizes. As a result, the fluctuation with time of the signals (velocity components, temperature, scalar densities) measured by sensors placed in such flow vary over a wide range of frequencies. The relation between spatial and temporal scale can be established thanks to Taylor’s frozen turbulence hypothesis (Taylor 1938) which assumes that eddies do not change significantly in size when convected by the mean wind past a fixed observer. Spectral analysis uses signal frequency decomposition. It is performed by applying an integral transformation which converts a function of time into a function of frequency (f [Hz]):

$$ {\mathcal{F}_{\text{S}}}(f) = \frac{1}{{\sqrt {2} }}\int_{{ - \infty }}^{\infty } {{\chi_{{_{\text{S}}}}}(t){e^{{ift}}}dt} $$
(1.26)

F(f) is called the Fourier transform of the signal. Of special interest in eddy covariance are the power spectrum C ss of a signal \( {\chi_{{_{\text{S}}}}} \) and the cospectrum C ws of two signals w and \( {\chi_{{_{\text{S}}}}} \). The first one is defined as

$$ {C_{\text{ss}}}(f) = {\mathcal{F}_{\text{S}}}(f).\,{\mathcal{F}_{\text{S}}}^{*}(f) $$
(1.27)

and the second as the real part of the cross-spectrum is defined as

$$ {C_{\text{ws}}}(f) = {\mathcal{F}_{\text{w}}}(f) \cdot {\mathcal{F}_{\text{S}}}^{*}(f) $$
(1.28)

where \( {\mathcal{F}_{\text{S}}}^{*}(f) \) is the complex conjugate of \( {\mathcal{F}_{\text{w}}}(f) \). \( {C_{\text{ss}}}(f) \) and \( {C_{\text{ws}}}(f) \) are the spectral and cospectral density, respectively. The main interest of (co) spectra is that their integral over the whole frequency range equals the (co)variance of the signals:

$$ \begin{aligned}[b] \int_0^{\infty } {C_{\text{ss}}}(f)\mathit{df} & = \sigma_{\text{S}}^2 \\[4pt] \int_0^{\infty } {{C_{\text{ws}}}(f)} \mathit{df} & = \overline {w^\prime {{\chi ^\prime }_{\text{s}}}} \end{aligned} $$
(1.29)

so that (co) spectra may be thought of as a distribution of (co)variances into the different frequency bands of width df.

1.5.2 Spectral Analysis of Atmospheric Turbulence

In the frequency range of interest to micrometeorology, turbulence spectra can be divided into three major spectral regions: (1) at low frequencies (typically 10−4 Hz) is the energy containing range, where turbulent energy is produced; (2) at intermediate frequencies is the inertial subrange, where energy is neither produced nor dissipated but is transformed to smaller and smaller eddies due to an “energy cascade” process (see, e.g. Stull 1988); and (3) at higher frequencies is the dissipation range where turbulent energy is dissipated through viscosity. By considering similarity arguments, one can deduce that the shapes of suitably normalized atmospheric (co)spectra are repeatable and can be described by universal relations. Parameterizations of the momentum and sensible heat cospectra proposed by Kaimal et~al. (1972) are given by

$$ - \frac{{f{C_{\text{uw}}}(f)}}{{u_{{*}}^2}} = \frac{{12n}}{{{{(1 + 9.6n)}^{{\frac{7}{3}}}}}} \vspace*{6pt}$$
(1.30a)
$$ \begin{aligned}[b]- \frac{{f{C_{{{{w\theta }}}}}(f)}}{{{u_{{*}}}\,{\theta_{*}}}} & = \frac{{11n}}{{{{(1 + 13.3n)}^{{\frac{7}{4}}}}}}\quad {\text{for}}\quad n \leqslant 1\\ - \frac{{f{C_{{{{w\theta }}}}}(f)}}{{{u_{*}}\,{\theta_{*}}}} &= \frac{{4n}}{{{{(1 + 3.8n)}^{{\frac{7}{4}}}}}}\quad {\text{for}}\quad n \geqslant 1 \vspace*{4pt}\end{aligned} $$
(1.30b)

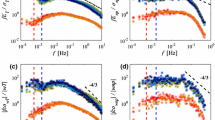
where n is a dimensionless frequency defined as: \( n = f({h_{\text{m}}} - d)/\overline u \) and d is the zero-plane displacement height. The \( \overline {u^\prime w^\prime } \) and \( \overline {w^\prime \theta ^\prime } \) covariances are normalized by \( u_{*}^2 \) and \( {u_{*}}{\theta_{*}} \), respectively, where \( {u_{*}} \)is the friction velocity and \( {\theta_{*}} \) is the dynamic temperature. An illustration of Eq. 1.30 is given in Fig. 1.3 (black curve).

Fig. 1.3
figure 3_1

Typical atmospheric cospectrum (black curve) with effects of high pass filtering (a, gray curve) and low pass filtering (b, gray curve)

Full size image

1.5.3 Sensor Filtering

Eddy covariance systems, like any sensor, act as frequency filters in dampening high and low frequencies. The reasons for this may be diverse and will be discussed in detail in Sect. 4.1.3. In this chapter, we limit ourselves to the description of the impact of low or high frequency filtering on the (co)spectra shape and on the resulting error that affects fluxes. The evolution of this impact with measurement height and wind velocity will also be discussed.

To represent high or low frequency dampening by a measurement system, signal theory generally use sigmoïdal transfer functions which are equal to 1 in the frequency range where the signal is not attenuated and that decays to zero in the range where signal is attenuated. The shapes of these functions vary according to the processes that are responsible of the dampening (Sect. 4.1.3).

As an example, Fig. 1.3 depict the impact of filtering on a typical cospectrum, Fig. 1.3a showing the effect of a low pass filtering and Fig. 1.3b the effect of a high pass filtering.

The relative error on the fluxes due to frequency losses, \( \frac{{{\delta_{\text{S}}}}}{{F_{\text{S}}^{\text{EC}}}} \), may be computed according to:

$$ \frac{{{\delta_{\text{S}}}}}{{F_{\text{S}}^{\text{EC}}}} = 1 - \frac{{\smallint_0^{\infty }{C_{\text{ws}}}(f){T_{\text{ws}}}(f)\mathit{df}}}{{\smallint_0^{\infty }{C_{\text{ws}}}(f)\mathit{df}}} $$
(1.31)

where C ws(f) is the ideal cospectral density and T ws(f) is the apparatus transfer function. The ratio in the integrals on the right hand side of Eq. 1.31 is represented in Fig. 1.3 by the ratio of areas below the gray and black curves. Figure 1.3a shows clearly that low pass filtering causes a loss of covariance and always induces a systematic error. Figure 1.3b suggests the same thing for high pass filtering. However, it could be deceptive as the low frequency spectral range (energy containing range) is not so well defined as it could also depend on mesoscale atmospheric movements. In some conditions, it is possible to observe cospectral densities of different signs at low and high frequencies. In these conditions, the impact of the low pass filtering is not necessarily systematic.

1.5.4 Impacts of Measurement Height and Wind Velocity

The preceding observations allow predicting the impact of measurement height and of wind velocity on errors due to frequency losses, which is synthesized in Fig. 1.4.

Fig. 1.4
figure 4_1

(a) Undamped (full line) and low pass filtered (dotted line) cospectra; (b) Undamped (full line) and high pass filtered (dotted line) cospectra

Full size image

Equations 1.30 describe universal cospectra as a function of the nondimensional frequency \( n = \frac{{f({h_{\text{m}}} - d)}}{{\overline u }} \). This implies that the decrease in \( {h_{\text{m}}} - d \) shifts the cospectrum toward higher frequencies (Fig. 1.4). However, as the apparatus transfer function does not depend on measurement height, systems placed at lower heights would be more sensitive to high-frequency losses (Fig. 1.4a) while systems placed at higher heights would be more sensitive to low-frequency losses (Fig. 1.4b). The first ones would require set ups able to capture fluctuations at higher frequencies while the second would need longer averaging times (the main cause of low-frequency losses). Further details about frequency losses and their correction are presented in Sect. 4.1.3.