1 Introduction

A number of multiple criteria decision making (MCDM) approaches have been developed and applied to diverse fields, such as engineering, management, economics, and so on. Among those approaches, TOPSIS (technique for order performance by similarity to ideal solution), first developed by Hwang and Yoon [1], is widely adopted by practitioners and researchers. The primary concept of the TOPSIS approach is that the most preferred alternative should not only have the shortest distance from the positive ideal solution (PIS), but also have the farthest distance from the negative ideal solution (NIS) [1, 2]. The applications of TOPSIS have some advantages, including (a) a simple, rationally comprehensible concept, (b) good computational efficiency, and (c) being able to measure the relative performance of each alternative in a simple mathematical form [3].

In 1965, Zadeh [4] first introduced the theory of fuzzy sets. Later on, many researchers have been working on the process of dealing with fuzzy decision making problems by applying fuzzy sets theory. Zadeh’s fuzzy sets only assign a single membership value between zero and one to each element. However, the non-membership degree of an element to a fuzzy set may not always be just equal to one minus the membership degree. In 1993, Gau and Buehrer [5] pointed out that this single value could not attest to its accuracy and proposed the concept of vague sets. Bustince and Burillo [6], however, pointed out that the notion of vague sets coincides with that of intuitionistic fuzzy sets (IFSs) proposed by Atanassov [7] almost 10 years earlier. IFSs are represented by two characteristic functions expressing the degrees of membership and non-membership of elements of the universal set to the IFS. IFSs can cope with the presence of vagueness and hesitancy originating from imprecise knowledge or information. In the last two decades, there have been many studies on the theory and application of IFSs, including logic programming, medical diagnosis, fuzzy topology, decision making, pattern recognition, and so on. Different from other studies, in this work, the criteria weights are obtained by conducting Shannon’s entropy concept; after that, a fuzzy TOPSIS method is employed to order the alternatives. The proposed model can deal with uncertain problems and its calculation is not difficult, so that it can provide an efficient way to help the decision maker (DM) in making decisions.

2 Preliminaries

2.1 Intuitionistic Fuzzy Sets

Definition 1.

[7]. An IFS A in the universe of discourse X is defined with the form

$$A = \left \{\left \langle x,{\mu}_{A}(x),\ {\nu}_{A}(x)\right \rangle \vert x \in X\right \},$$

where

$${\mu}_{A} : X \rightarrow [0,\,1],\ {\nu}_{A} : X \rightarrow [0,\,1]$$

with the condition

$$0 \leq {\mu}_{A}(x) + {\nu}_{A}(x) \leq 1,\ \forall x \in X.$$

The numbers μ A (x) and ν A (x) denote the membership and non-membership degrees of x to A, respectively.

Obviously, each ordinary fuzzy set may be written as

$$\left \{\left \langle x,{\mu}_{A}(x),\ 1 - {\mu}_{A}(x)\right \rangle \vert x \in X\right \}.$$

That is to say, fuzzy sets may be reviewed as the particular cases of IFSs.

Note that A is a crisp set if and only if for ∀x ∈ X, either μ A (x) = 0, ν A (x) = 1 or μ A (x) = 1, ν A (x) = 0.

For each IFS, A in X, we will call

$${\pi}_{A}(x) = 1 - {\mu}_{A}(x) - {\nu}_{A}(x)$$

the intuitionistic index of x in A. It is a measure of hesitancy degree of x to A [7]. It is obvious that 0 ≤ π A (x) ≤ 1 for each x ∈ X. Figure 2.1 illustrates the three degrees (membership, non-membership, and hesitancy).

Fig. 1
figure 1

Membership, non-membership, and hesitancy degrees

Full size image

For convenience of notation, IFSs(X) is denoted as the set of all IFSs in X.

Definition 2.

[8]. For every A ∈ IFSs(X), the IFS λA for any positive real number λ is defined as follows:

$$\lambda A = \left \{\acute{\mathrm{a}}x,1 - {(1 - {\mu}_{A}(x))}^{\lambda},{({\nu}_{A}(x))}^{\lambda}\tilde{\mathrm{n}}\vert x \in X\right \}.$$
(1)

2.2 Entropy of IFS

In 1948, Shannon [9] proposed the entropy function, H(p 1, p 2, ⋯ , p n ) = − ∑ i = 1 n p i log(p i ), as a measure of uncertainty in a discrete distribution based on the Boltzmann entropy of classical statistical mechanics, where p i (i = 1, 2, …, n) are the probabilities of random variable according to a probability mass function P. Later, De Luca and Termini [10] defined a non-probabilistic entropy formula of a fuzzy set based on Shannon’s function on a finite universal set X = {x 1, x 2, …, x n }. as follows:

$${E}_{\mathrm{LT}}(A) = -k{\sum \limits}_{i=1}^{n}\left [{\mu}_{A}({x}_{i})\ \ln \ {\mu}_{A}({x}_{i}) + (1 - {\mu}_{A}({x}_{i}))\ \ln (1 - {\mu}_{A}({x}_{i}))\right ],$$
(2)

where k > 0.

Szmidt and Kacprzyk [11] extended De Luca and Termini’s axioms to present four definitions with regard to the entropy measure on IFSs(X) as follows:

EI1::

E(A) = 0 iff A is a crisp set;

EI2::

E(A) = 1 iff μ A (x i ) = ν A (x i ), ∀x i ∈ X;

EI3::

E(A) ≤ E(B) if A is less fuzzy than B, i.e., μ A (x i ) ≤ μ B (x i ) and ν A (x i ) ≥ ν B (x i ) for μ B (x i ) ≤ ν B (x i ), ∀x i ∈ X;

or

μ A (x i ) ≥ μ B (x i ) and ν A (x i ) ≤ ν B (x i ) for μ B (x i ) ≥ ν B (x i ), ∀x i ∈ X;

EI4::

E(A) = E(A c), where A c is the complement of A.

Recently, Vlachos et al. [12] presented Eq. 2.3 as the measure of intuitionistic fuzzy entropy which was proved to satisfy the four axiomatic requirements mentioned above.

$$\begin{array}{rcl} & & {E}_{\mathrm{LT}}^{\mathrm{IFS}}(A) =\, - \frac{1} {n\,\ln 2}{\sum \limits}_{i=1}^{n}\left [{\mu}_{A}({x}_{i})\,\ln {\mu}_{A}({x}_{i}) + {\nu}_{A}({x}_{i})\,\ln {\nu}_{A}({x}_{i})\right. \\ & & \qquad \qquad \quad \left.-(1 - {\pi}_{A}({x}_{i}))\,\ln (1 - {\pi}_{A}({x}_{i})) - {\pi}_{A}({x}_{i})\,\ln 2\right ]. \end{array}$$
(3)

It is noted that E LT IFS(A) is composed of the hesitancy degree and the fuzziness degree of the IFS A.

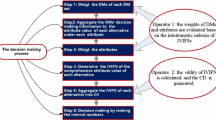
3 Proposed Fuzzy TOPSIS Group Decision Making Model

The procedures of calculation for this proposed model can be described as follows:

Construct an intuitionistic fuzzy decision matrix based on opinions of DMs.

An MCDM problem can be concisely expressed in matrix format as

$$D = \begin{array}{c}\qquad \begin{array}{llll} {C}_{1}&{C}_{2}&\cdots &{C}_{n} \end{array}\\ \begin{array}{c} {A}_{1} \\ {A}_{2} \\ \vdots \\ {A}_{m} \end{array} \left[ \begin{array}{llll} {x}_{11} &{x}_{12} &\cdots &{x}_{1n} \\ {x}_{21} &{x}_{22} &\cdots &{x}_{2n}\\ \vdots &\vdots &\vdots &\vdots \\ {x}_{m1}&{x}_{m2}&\cdots &{x}_{mn}\\ \end{array} \right]\\ W = {({w}_{1},{w}_{2},\ldots ,{w}_{n})}^{T} \end{array}$$
(4)

Let A = A 1, A 2, …, A m be a set of alternatives which consists of m non-inferior decision-making alternatives. Each alternative is assessed on n criteria, and the set of all criteria is denoted C = C 1, C 2, …, C n . Let W = (w 1, w 2, …, w n )T be the weighting vector of criteria, where w j ≥ 0 and ∑ j = 1 n w j = 1.

In this study, the characteristics of the alternatives A i are represented by the IFS as:

$${A}_{i} = \left \{\langle {C}_{j},{\mu}_{{A}_{i}}({C}_{j}),\ {\nu}_{{A}_{i}}({C}_{j})\rangle \vert {C}_{j} \in C\right \},\ i= 1,2,\ldots ,m,$$
(5)

where \({\mu}_{{A}_{i}}({C}_{j})\) and \({\nu}_{{A}_{i}}({C}_{j})\) indicate the degrees that the alternative A i satisfies and does not satisfy the criterion C j , respectively, and \({\mu}_{{A}_{i}}({C}_{j}) \in [0,\,1],\ {\nu}_{{A}_{i}}({C}_{j}) \in [0,\,1],\ {\mu}_{{A}_{i}}({C}_{j}) + {\nu}_{{A}_{i}}({C}_{j}) \in [0,\,1]\). The intuitionistic index \({\pi}_{{A}_{i}}({C}_{j}) =\) \(1 - {\mu}_{{A}_{i}}({C}_{j}) - {\nu}_{{A}_{i}}({C}_{j})\) has the feature that the larger \({\pi}_{{A}_{i}}({C}_{j})\) the greater the hesitancy of the DM about the alternative A i with respect to the criterion C j .

For a group decision making (GDM) problem, let E = {e 1, e 2, …, e l } be the set of DMs, and λ = (λ1, λ2, …, λ l )T be the weighting vector of DMs, where λ k ≥ 0, k = 1, 2, …, l and ∑ k lλ k = 1. Let \(\tilde{{D}}^{k} = {[\tilde{{x}}_{\mathit{ij}}^{k}]}_{m\times n}\) be an intuitionistic fuzzy decision matrix of each DM, where i = 1, 2, …, m; j = 1, 2, …, n. In the process of GDM, all the individual decision opinions need to be aggregated into a group opinion to conduct the collective decision matrix \(\tilde{D} = {[\tilde{{x}}_{\mathit{ij}}]}_{m\times n}\). In order to do this, an IFWA (intuitionistic fuzzy weighted averaging) operator [13] is used. Here,

$$\begin{array}{rcl} \tilde{{x}}_{\mathit{ij}}& =&{\mathit{IFWA}}_{\lambda}(\tilde{{x}}_{\mathit{ij}}^{1},\tilde{{x}}_{ij}^{2},\ldots ,\tilde{{x}}_{ij}^{l}) = {\lambda}_{1}\tilde{{x}}_{ij}^{1} \oplus {\lambda}_{2}\tilde{{x}}_{\mathit{ij}}^{2} \oplus \cdots \oplus {\lambda}_{1}\tilde{{x}}_{\mathit{ij}}^{l} \\ & =& \left \langle 1 -{\prod \nolimits}_{k=1}^{l}{(1 - {\mu}_{ij}^{k})}^{{\lambda}_{k}},{\prod \nolimits}_{k=1}^{l}{({\nu}_{ij}^{k})}^{{\lambda}_{k}}\right \rangle \end{array}$$
(6)

Determine the criteria weights using the entropy-based method.

The well-known entropy method [1, 2] can obtain the objective weights, called entropy weights. The smaller entropy value reveals that the evaluated values of all alternative A i (i = 1, 2, …, m) with respect to a criterion are less similar. Consequently, for the decision matrix \(\tilde{D} = {[\tilde{{x}}_{ij}]}_{m\times n}\) in an intuitionistic fuzzy environment, the expected information content emitted from each criterion C j can be measured by the entropy value, denoted as E LT IFS(C j ), as

$$\begin{array}{rcl}{E}_{\mathrm{LT}}^{\mathrm{IFS}}({C}_{j}) =& -& \frac{1} {m\,\ln 2}{\sum}_{i=1}^{m}\left [{\mu}_{\mathit{ij}}({C}_{j})\,\ln {\mu}_{\mathit{ij}}({C}_{j}) + {\nu}_{ij}({C}_{j})\,\ln {\nu}_{ij}({C}_{j})\right. \\ & -& \left.(1 - {\pi}_{\mathit{ij}}({C}_{j}))\,\ln (1 - {\pi}_{\mathit{ij}}({C}_{j})) - {\pi}_{\mathit{ij}}({C}_{j})\,\ln 2\right ]. \end{array}$$
(7)

where j = 1, 2, …, n and 1 ∕ (m ln 2) is a constant to ensure 0 ≤ E LT IFS(C j ) ≤ 1.

Therefore, the degree of divergence (d j ) of the average intrinsic information provided by the corresponding performance ratings on criterion C j can be defined as

$${d}_{j} = 1 - {E}_{\mathrm{LT}}^{\mathrm{IFS}}({C}_{j}),\ j= 1,2,\ldots ,\ n.$$
(8)

illustrated as Fig. 2.2. The value of d j represents the inherent contrast intensity of criterion C j , and thus the entropy weight of the jth criterion is

$${w}_{j} = {d}_{j}/{\sum}_{j=1}^{n}{d}_{j}.$$
(9)

It should be noted that w j is a crisp weight.

Fig. 2
figure 2

The divergence degree of information on each criterion

Full size image

Construct the weighted intuitionistic fuzzy decision matrix.

A weighted intuitionistic fuzzy decision matrix \(\tilde{Z}\) can be obtained by aggregating the weighting vector W and the intuitionistic fuzzy decision matrix \(\tilde{D}\) as:

$$\tilde{Z} = W \otimes \tilde{D} = W \otimes {\left [\tilde{{x}}_{ij}\right ]}_{m\times n} ={\left [\hat{{x}}_{ij}\right ]}_{m\times n}.$$
(10)

where

$$\begin{array}{rcl} & & W ={\left ({w}_{1},{w}_{2},\ldots ,{w}_{j},\ldots ,{w}_{n}\right )}^{T}; \\ & & \hat{{x}}_{ij} = \left \langle \hat{{\mu}}_{ij},\hat{{\nu}}_{ij}\right \rangle = \left \langle 1 - {(1 - {\mu}_{ij})}^{{w}_{j}},\,{\nu}_{ij}^{{w}_{j}}\right \rangle ,\ {w}_{j} > \end{array}$$
(0.)

Determine the intuitionistic fuzzy positive-ideal solution (IFPIS, A +) and intuitionistic fuzzy negative-ideal solution (IFNIS, A −).

In general, the evaluation criteria can be categorized into two kinds, benefit and cost. Let G be a collection of benefit criteria and B be a collection of cost criteria. According to IFS theory and the principle of classical TOPSIS method, IFPIS and IFNIS can be defined as:

$$\begin{array}{ll}{A}^{+}=&\left\{\left\langle{C}_{j},\left(({\max}_{i}\hat{{\mu}}_{\mathit{ij}}({C}_{j})\vert j\in G),({\min}_{i} \hat{{\mu}}_{\mathit{ij}}({C}_{j})\vert j\in B)\right)\right.\right.,\\ &\left.\left.\left.\left(({\min}_{i}\hat{{\nu}}_{\mathit{ij}}({C}_{j})\vert j\in G),({\max}_{i}\hat{{\nu}}_{\mathit{ij}}({C}_{j})\vert j\in B)\right)\right\rangle\right\vert i\in m\right\}.\\ \end{array}$$
(11a)
$$\begin{array}{ll}{A}^{-} = &\left\{\left\langle {C}_{j},\left(({\min}_{i}\hat{{\mu}}_{\mathit{ij}}({C}_{j})\vert j \in G),({\max}_{i}\hat{{\mu}}_{\mathit{ij}}({C}_{j})\vert j \in B)\right)\right.\right.,\\ &\left.\left.\left.\left(({\max}_{i} \hat{{\nu}}_{ij}({C}_{j})\vert j \in G),({\min}_{i}\hat{{\nu}}_{ij}({C}_{j})\vert j \in B)\right)\right\rangle \right\vert i \in m\right\}.\\ \end{array}$$
(11b)

Calculate the distance measures of each alternative A i from IFPIS and IFNIS.

We use the measure of intuitionistic Euclidean distance (refer to Szmidt and Kacprzyk [14]) to help determine the ranking of all alternatives. 2.1111

$$\begin{array}{l} {d}_{\mathrm{IFS}}({A}_{i},{A}^{+})\\ =\sqrt{{\sum\limits}_{j=1}^{n}\left[{\left(\hat{{\mu}}_{{A}_{i}}({C}_{j}) -\hat{{\mu}}_{{A}^{+}}({C}_{j})\right)}^{2} + {\left(\hat{{\nu}}_{{A}_{i}}({C}_{j}) -\hat{{\nu}}_{{A}^{+}}({C}_{j})\right)}^{2} +{\left(\hat{{\pi}}_{{A}_{i}}({C}_{j}) -\hat{{\pi}}_{{A}^{+}}({C}_{j})\right)}^{2}\right]}\\ \end{array}$$
(12a)
$$\begin{array}{l} {d}_{\mathrm{IFS}}({A}_{i},{A}^{-})\\ =\sqrt{{\sum\limits}_{j=1}^{n}\left[{\left(\hat{{\mu}}_{{A}_{i}}({C}_{j}) -\hat{{\mu}}_{{A}^{-}}({C}_{j})\right)}^{2} + {\left(\hat{{\nu}}_{{A}_{i}}({C}_{j}) +\hat{{\nu}}_{{A}^{-}}({C}_{j})\right)}^{2} +{\left(\hat{{\pi}}_{{A}_{i}}({C}_{j}) -\hat{{\pi}}_{{A}^{-}}({C}_{j})\right)}^{2}\right]}\\ \end{array}$$
(12b)

Calculate the relative closeness coefficient (CC) of each alternative and rank the preference order of all alternatives.

The relative closeness coefficient (CC) of each alternative with respect to the intuitionistic fuzzy ideal solutions is calculated as:

$${\mathit{CC}}_{i} = {d}_{\mathrm{IFS}}({A}_{i},{A}^{-})\left /\right. \left ({d}_{\mathrm{IFS}}({A}_{i},{A}^{+})+{d}_{\mathrm{IFS}}({A}_{i},{A}^{-})\right ),$$
(13)

where 0 ≤ CC i ≤ 1, i = 1, 2, . . . , m.

The larger value of CC indicates that an alternative is closer to IFPIS and farther from IFNIS simultaneously. Therefore, the ranking order of all the alternatives can be determined according to the descending order of CC values. The most preferred alternative is the one with the highest CC value.

4 Illustrative Example

An example is provided [15] in this section in order to demonstrate the calculation process of the proposed approach. An investment company wants to invest an amount of money. There are five possible companies \({A}_{i}\,(i = 1,2,\ldots ,5)\) in which to invest: (1) A 1 is a car company; (2) A 2 is a food company; (3) A 3 is a computer company; (4) A 4 is an arms company; and (5) A 5 is a TV company. An expert group is formed of three experts e k (k = 1, 2, 3) with the weighting vector λ = (0. 4, 0. 3, 0. 3)T. Each possible company will be evaluated across three criteria with regard to the: (1) economic benefit (C 1); (2) social benefit (C 2); and (3) environmental pollution (C 3), where C 1 and C 2 are benefit criteria, and C 3 is a cost criterion.

The proposed fuzzy TOPSIS GDM model is applied to solve this problem, and the computational procedure is described in a step-by-step way, as below:

The ratings for five possible companies with respect to the three criteria are represented by IFSs, and the three experts construct the intuitionistic fuzzy decision matrices \(\tilde{{D}}^{k}(k = 1,2,3)\), as listed in Tables 2.1–2.3. The three individual decision matrices are then fused into a collective intuitionistic fuzzy decision matrix \(\tilde{D}\) in Table 2.4.

Table 2.1 Intuitionistic fuzzy decision matrix \(\tilde{{D}}^{1}\)
Full size table
Table 2.2 Intuitionistic fuzzy decision matrix \(\tilde{{D}}^{2}\)
Full size table
Table 2.3 Intuitionistic fuzzy decision matrix \(\tilde{{D}}^{3}\)
Full size table
Table 2.4 Intuitionistic fuzzy decision matrix \(\tilde{D}\)
Full size table

Determine the criteria weights. Using Eq. 2.7, the entropy values for criteria C 1, C 2 and C 3, respectively, are: 0.4477, 0.4985, and 0.9679. The degree of divergence d j on each criterion ‘ C j (j = 1, 2, 3) may be obtained by Eq. 2.8 as 0.5523, 0.5015, and 0.0321, respectively. Therefore, the criteria weighting vector can be expressed as W = (0. 509, 0. 462, 0. 030)T by applying Eq. 2.9.

After determining the criteria weighting vector, using Eq. 2.10, the weighted intuitionistic fuzzy decision matrix \(\tilde{Z}\) is then obtained as Table 2.5.

Table 2.5 Weighted intuitionistic fuzzy decision matrix \(\tilde{Z}\)
Full size table

In this case, criteria C 1 and C 2 are benefit criteria, while C 3 is a cost criterion. Using Eq. 2.11a and b, each alternative’s IFPIS (A +) and IFNIS (A −) with respect to the criteria can be determined as

  • \({A}^{+} = \left (\acute{\mathrm{a}}0.6749,0.0000\tilde{\mathrm{n}}\,\acute{\mathrm{a}}0.6104,0.0000\tilde{\mathrm{n}}\,\acute{\mathrm{a}}0.0098,0.9843\tilde{\mathrm{n}}\right )\)

  • \({A}^{-} = \left (\acute{\mathrm{a}}0.5706,0.4178\tilde{\mathrm{n}}\,\acute{\mathrm{a}}0.5032,0.4162\tilde{\mathrm{n}}\,\acute{\mathrm{a}}0.0206,0.9736\tilde{\mathrm{n}}\right )\)

Calculate the distance between alternatives and intuitionistic fuzzy ideal solutions (IFPIS and IFNIS) using Eq. 12a and b.

Using Eq. 2.13, the relative closeness coefficient (CC) can be obtained.

The distance, relative closeness coefficient, and corresponding ranking of five possible companies are tabulated in Table 2.6 Therefore, we can see that the order of ranking among the five alternatives is A 2 ≻ A 4 ≻ A 1 ≻ A 3 ≻ A 5, where “ ≻ ” indicates the relation “preferred to”. Therefore, the best choice would be A 2 (food company). From the above processes, we can conclude that the proposed approach is suitable for dealing with fuzzy MCDM problems in GDM by using IFSs.

Table 2.6 The distance measure, relative closeness coefficient and ranking of the five alternatives
Full size table

5 Conclusion

In this work, we propose an entropy-based multiple criteria GDM model, in which the characteristics of the alternatives are represented by IFSs. In information theory, the entropy is related to the average information quantity of a source. Based on this principle, the optimal criteria weights can be obtained by the proposed entropy-based model. The main difference between this method and the classical TOPSIS is the introduction of objective entropy weight in an intuitionistic fuzzy environment with the former. Although the example provided here is for selecting an optimal investment company, the proposed approach can be applied to many different fields. However, this proposed model considers using only objective criteria weights. To overcome this limitation, future work will examine situations in which the DMs can provide and modify their preferences with regard to the criteria weights incorporated in the proposed model.