Accurate Frequency Estimation Method Based on Basis Approach and Empirical Wavelet Transform

Abstract

Due to proliferating harmonic pollution in the power system, analysis and monitoring of harmonic variation in real-time have become important. In this paper, a novel approach for estimation of fundamental frequency in power system is discussed. In this method, the fundamental frequency component of the signal is extracted using Empirical Wavelet Transform. The extracted component is then projected onto fourier basis, where the frequency is estimated to a resolution of 0.001 Hz. The proposed approach gives an accurate frequency estimate compared with some existing methods.

1 Introduction

The real-time measurement of frequency is now important for many applications in the power system. Several methods have been proposed and adopted to compute frequency for the power system applications. The Fast Fourier Transform is the most widely used method for frequency estimation. Due to leakage effect, picket fence effect, and aliasing effect, it cannot produce a better result [1]. Further extensions and enhancements are done on this method by utilizing the original FFT with different windowing and interpolation to produce an accurate estimate [2]. For zero crossing technique, the signal is considered to be pure sinusoidal and the signal frequency is estimated from the time between two zero crossing. However, in reality the measured signals are available in distorted form. The paper [3] explains about the estimation of harmonic amplitudes and phases using several variants of recursive least square (RLS) algorithms. When extended complex kalman filter is used for estimation, the accuracy is reached around the nominal frequency due to the shrinkage of Taylor series expansion of nonlinear terms [4]. In prony method [5], using fourier technique algorithm, the distorted voltage signal is filtered and filter coefficients are calculated assuming constant frequency. However, these filter coefficients are not exact due to frequency deviation. Then a complex prony analysis was proposed where the frequency is estimated by approximating the cosine-filtered and sine-filtered signals simultaneously [6]. In the paper [7], using an optimization method, frequency is estimated by comparing the filtered voltage with a mathematical approach. Other approaches to compute frequency are by using recursive DFT and phasor rotating method [8]. Artificial neural networks are also one of the methods adopted for real-time frequency and harmonic evaluation [9]. Harmonics were also estimated using linear least squares method and by singular value decomposition (SVD) [10].

In this paper, a new approach for frequency estimation is discussed. The paper is divided into five sections including the introduction. Section 2 discusses the Empirical Wavelet Transform and linear algebra concept of basis approach used for the proposed method and Sect. 3 explains the proposed algorithm. Section 4 discusses the results and inferences obtained from the proposed method and the conclusions are given in Sect. 5.

2 Background

2.1 Empirical Wavelet Transform

In Empirical Wavelet Transform [11], a bank of N wavelet filters, one low pass and $N - 1$ bandpass filters are made by adapting from the processed signal. A similar approach is used in the fourier method, by building bandpass filters. For the adaption process, the location of information in the spectrum is identified with frequency, $\omega { \in }[0,\Pi ]$. This is used as filter support.

First, the fourier transformed signal is partitioned into N segments. The boundary limits for each segment is denoted using $\omega_{n}$. Each partition is denoted as $\wedge_{n} = [\omega_{n - 1} ,\,\omega_{n} ],\,\bigcup\nolimits_{n = 1}^{N} \wedge_{n}$. Around each $\omega_{n}$, a small area of width $2\tau_{n}$ is defined. The empirical wavelets are defined on each of the $\wedge_{n}$. It is a bandpass filter constructed using Littlewood-Paley and Mayer’s wavelets. The subbands are extracted using this filtering operations.

Each partition in the spectrum is considered as modes which contain a central frequency with certain support. Since 0 and $\Pi$ are used as the limits to the spectrum, the number of boundary limits required will be $N - 1$. Therefore the partition boundaries, $\omega_{n}$, comprise of 0, selected maxima, and $\Pi$. The expression for scaling function $\hat{\phi }_{n} (\omega )$ is defined as

$$ \hat{\phi }_{n} (\omega ) = \left\{ {\begin{array}{*{20}l} {1\quad \quad {\text{if}}\quad \left| \omega \right| \le \omega_{n} - \tau_{n} } \hfill \\ {\cos \left[ {\frac{\pi }{2}\beta \left( {\left| \omega \right| - \omega_{n} + \tau_{n} } \right)} \right]} \hfill \\ {\quad \quad \;{\text{if}}\quad \omega_{n} - \tau_{n} \le \left| \omega \right| \le \omega_{n} + \tau_{n} } \hfill \\ {0\quad \quad {\text{otherwise}}} \hfill \\ \end{array} } \right. $$

(1)

The expression for empirical wavelet function $\hat{\psi }_{n} (\omega )$ is defined as

$$ \hat{\psi }_{n} (\omega ) = \left\{ {\begin{array}{*{20}l} {1\quad \quad {\text{if}}\quad \quad \omega_{n} + \tau_{n} \le \left| \omega \right| \le \omega_{n + 1} - \tau_{n + 1} } \hfill \\ {\cos \left[ {\frac{\pi }{2}\beta \left( {\frac{1}{{2\tau_{n + 1} }}\left( {\left| \omega \right| - \omega_{n + 1} + \tau_{n + 1} } \right)} \right)} \right]} \hfill \\ {\quad \quad \;{\text{if}}\quad \quad \omega_{n + 1} - \tau_{n + 1} \le \left| \omega \right| \le \omega_{n + 1} + \tau_{n + 1} } \hfill \\ {\sin \left[ {\frac{\pi }{2}\beta \left( {\frac{1}{{2\tau_{n} }}\left( {\left| \omega \right| - \omega_{n} + \tau_{n} } \right)} \right)} \right]} \hfill \\ {\quad \quad \;{\text{if}}\quad \quad \omega_{n} - \tau_{n} \le \left| \omega \right| \le \omega_{n} + \tau_{n} } \hfill \\ {0\quad \quad \quad {\text{otherwise}}} \hfill \\ \end{array} } \right. $$

(2)

The function $\beta (x)$ is an arbitrary function, the expressions can be referred in [11]. The width around each $\omega_{n}$ is decided using $\tau_{n}$ and it is defined as $\omega_{n} :\tau_{n} = \gamma \omega_{n} ,\,0 < \gamma < 1,\,{\forall }\,n > 0$. Now for function f, the detail coefficients is obtained by taking the inverse of convolution operation between f and $\psi_{n}$ (wavelet function).

$$ \begin{array}{*{20}l} {W_{f}^{\varepsilon } (n,t) = ((\hat{f}(\omega ))\overline{{\hat{\psi }_{n} (\omega ))^{ - 1} }} } \hfill \\ \end{array} $$

The approximate coefficients are obtained by taking the inverse of convolution operation between f and $\phi_{n}$ (scaling function).

$$ W_{f}^{\varepsilon } (0,t) = ((\hat{f}(\omega ))\overline{{\hat{\phi }_{1} (\omega ))^{ - 1} }} $$

(3)

The empirical mode function, denoted by f _k , is given as

$$ f_{0} (t) = W_{f}^{\varepsilon } (0,t) * \phi_{1} (t) $$

(4)

$$ f_{k} (t) = W_{f}^{\varepsilon } (k,t) * \phi_{k} (t) $$

(5)

2.2 Concept of Basis

Any N point signal can be considered as a point in $C^{N}$ (C denotes the complex space) and the operation of taking its FFT can be considered as a mapping from $C^{N} \to C^{N}$. There are infinite number of choices for a probable basis set in $C^{N}$ space [12]. Construction of fourier basis in $C^{N}$ space requires N orthogonal

vectors of the form $e^{{\frac{j2\pi kn}{N}}}$, $k \in {\mathbb{Z}}$. Consider the signal $e^{j\theta }$, $\theta = \frac{2\pi nk}{N}$, and $n = \left\{ {0,1, \ldots .\,N - 1} \right\}$, we can observe that, irrespective of value of k, $\theta$ is varied from $\left[ {0,2\pi } \right)$. We need to take only the samples from the signal corresponding to one period which will constitute the N tuple in $C^{N}$ space, and n is such that it covers one period. The matrix shown (the Twiddle Matrix) has N Fourier basis arranged column wise.

3 Signal Model and Proposed Method

Consider a continuous-time signal, $x\left( t \right)$ with amplitude, frequency, and phase denoted as A, f, and $\theta$, respectively. The signal $x\left( t \right) = A.\cos \left( {2\pi ft + \theta } \right)$ can be discretized as

$$ x\left[ n \right] = A.\cos \left( {2\pi \frac{f}{{f_{0} }}\frac{n}{{N_{0} }} + \theta } \right) = A.\cos \left( {2\pi f.n\Delta t + \theta } \right) $$

(6)

where $f_{0}$ is the nominal fundamental frequency, $N_{0}$ is the number of samples per cycle at $f_{0}$, and $\Delta t$ is the sampling period. In the proposed method, a synthetic signal is created and then discretized. Using EWT, the signal is decomposed into various modes. From these modes, fundamental frequency component is extracted. To get the frequency with high resolution, the extracted fundamental frequency component is projected on to a basis matrix. Figure 1 gives the flowchart of the proposed method.

Fig. 1

Flowchart of proposed method of frequency estimation

4 Results and Discussions

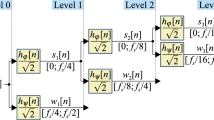
In this section, the performance of the proposed algorithm is discussed. To demonstrate the effectiveness of this method an input signal is synthesized with fundamental frequency of 50.218 Hz. It contains 20 % third harmonic component and 10 % fifth harmonic component. The synthesized signal was sampled at the rate of 1024 samples/cycle. As a prefiltering process, the harmonic contents present in the signal are removed or fundamental frequency component is extracted by using EWT. The Fig. 2 gives the processing stages of signal. Generally in a power system, the third and fifth harmonic components causes the main impact. When signal is decomposed using EWT, the first mode always gives a decaying DC component. The second mode gives the fundamental frequency component and rest of the other modes gives the harmonics.

Fig. 2

Processing stages of signal

When FFT of this second component is computed, it estimates the frequency as 51 Hz. Since the given input signal is generated at 50.218 Hz the difference in estimated frequency arose due to spectral leakage phenomena. The Fig. 3 gives the frequency spectrum of the extracted component and the effect of spectral leakage is visible.

Fig. 3

FFT of the extracted fundamental frequency component

Now to estimate it most accurately the method proposed in Sect. 2.2 is used. The power system signal has to be maintained within a permissible range of 48–52 Hz. Otherwise, it could result in the grid collapsing. So the extracted fundamental frequency component is projected on to a basis matrix, created for a resolution of 0.001 between the range of 48–52 Hz. By using this approach, estimated frequency is 50.218, which is same as the given input frequency. Figure 4 gives the EWT decomposition of three modes.

Fig. 4

Signal decomposition using EWT when the mode given is 3

From Fig. 5, we can infer that when the number of mode increases, the fundamental frequency component and harmonics get splitted into several modes. By the split of these components, information about fundamental frequency will be less.

Fig. 5

Signal decomposition using EWT when the mode given is 4

The basis approach is applied for different frequencies and modes, the results are shown in Table 1. From Table 1, we infer that mainly the second mode of the input signal after decomposing gives the accurate frequency estimate the same as the given input frequency of the synthesized signal. The other splitted component also estimates the frequency near to the given input frequency, but it does not give the resolution of 0.001 Hz as expected. Therefore, for accurate estimation, the number of modes in EWT can be fixed as three or four.

Table 1 Frequency estimation using basis approach for different frequencies and modes

Also, the proposed method is compared with many conventional frequency estimation algorithms such as FFT, zero crossing technique, prony method, recursive DFT, and phasor rotation method. Table 2 shows the estimated frequencies obtained from these methods.

Table 2 Comparison with other frequency estimation methods

When sliding window recursive DFT with dyadic downsampling is applied for mode decomposition to find out the fundamental frequency component. The basis approach estimation gives frequency estimate of 50.2300 Hz. From this, it can be inferred that EWT decomposition gives more information about fundamental frequency component when compared to sliding window recursive DFT with dyadic downsampling decomposition method.

5 Conclusion

The paper proposes a new fundamental frequency estimation approach using the concept of basis. The proposed method use EWT to find the fundamental frequency component present in the signal. The frequency is estimated to a resolution of 0.001 Hz by projecting the fundamental frequency component to a basis matrix. This method is compared with many other conventional methods.