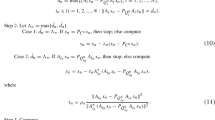Split Feasibility and Fixed Point Problems

Abstract

In this survey article, we present an introduction of split feasibility problems, multisets split feasibility problems and fixed point problems. The split feasibility problems and multisets split feasibility problems are described. Several solution methods, namely, CQ methods, relaxed CQ method, modified CQ method, modified relaxed CQ method, improved relaxed CQ method are presented for these two problems. Mann-type iterative methods are given for finding the common solution of a split feasibility problem and a fixed point problem. Some methods and results are illustrated by examples.

1 Introduction

Let $C$ and $Q$ be nonempty closed convex sets in $\mathbb {R}^{N}$ and $\mathbb {R}^{M}$, respectively, and $A$ be a given $M\times N$ real matrix. The split feasibility problem (in short, SFP) is to find $x^{*}$ such that

$$\begin{aligned} x^{*} \in C \quad \text {and} \quad Ax^{*} \in Q. \end{aligned}$$

(1)

It was introduced by Censor and Elfving [14] for modeling inverse problems, which arise from phase retrievals and in medical image reconstruction [5]. Recently, it is found that SFP can also be used to model the intensity modulated radiation therapy [13, 15, 16, 20]. It has also several applications in various fields of science and technology.

If $C$ and $Q$ are nonempty closed convex subsets of real Hilbert spaces $\fancyscript{H}_{1}$ and $\fancyscript{H}_{2}$, respectively, and $A \in B(\fancyscript{H}_{1},\fancyscript{H}_{2})$, where $B(\fancyscript{H}_{1},\fancyscript{H}_{2})$ denotes the space of all bounded linear operators from $\fancyscript{H}_{1}$ to $\fancyscript{H}_{2}$, then the SFP is to find a point $x^{*}$ such that

$$\begin{aligned} x^{*} \in C \quad \text {and} \quad Ax^{*} \in Q. \end{aligned}$$

(2)

A special case of the SFP (2) is the following convexly constrained linear inverse problem (in short, CCLIP) [29] of finding $x^{*}$ such that

$$\begin{aligned} x^{*} \in C \quad \text {and} \quad Ax^{*} = b. \end{aligned}$$

(3)

It has extensively been investigated in the literature by using the projected Landweber iterative method [42]. However, SFP has received much less attention so far, due to the complexity resulted from the set $Q$.

The original algorithm introduced in [14] involves the computation of the inverse $A^{-1}$ (assuming the existence of the inverse of $A$) and thus does not become popular. A more popular algorithm that solves SFP seems to be the $CQ$ algorithm of Byrne [5, 6], which is found to be a gradient-projection method in convex minimization (it is also a special case of the proximal forward-backward splitting method [19, 21]).

Throughout the chapter, we denote by $\Gamma$ the solution set of the SFP, that is,

$$ \Gamma = \{ x \in C : Ax \in Q \} = C \cap A^{-1}Q.$$

We also assume that the SFP is consistence, that is, the solution set $\Gamma$ is nonempty, closed and convex.

For each $j = 1,2,\ldots ,J$, let $K_{j}$, be a nonempty closed convex subset of a $M$-dimensional Euclidean space $\mathbb {R}^{M}$ with $\cap _{j=1}^{J} K_{j} \ne \emptyset$. The convex feasibility problem (in short, CFP) is to find an element of $\cap _{j=1}^{J} K_{j}$. Solving the SFP is equivalent to find a member of the intersection of two sets $Q$ and $A(C) = \{ Ac : c \in C \}$ or of the intersection of two sets $A^{-1}(Q)$ and $C$, so the split feasibility problem can be viewed as a particular case of the CFP.

During the last decade, SFP has been extended and generalized in many directions. Several iterative methods have been proposed and analyzed; See, for example, references given in the bibliography.

1.1 Multiple-Sets Split Feasibility Problem

The multiple-sets split feasibility problem (in short, MSSFP) is to find a point closest to a family of closed convex sets in one space such that its image under a linear transformation will be closest to another family of closed convex sets in the image space. It can be a model for many inverse problems where constraints are imposed on the solutions in the domain of a linear operator as well as in the operator’s range. It generalizes the convex feasibility problems and split feasibility problems. Formally, given nonempty closed convex sets $C_{i} \subseteq \mathbb {R}^{N}$, $i= 1,2,\ldots ,t$, and the nonempty closed convex sets $Q_{j} \subseteq \mathbb {R}^{M}$, $j = 1,2,\ldots ,r$, in the $N$ and $M$ dimensional Euclidean spaces, respectively, the multiple-sets split feasibility problem (in short, MSSFP) is to

$$\begin{aligned} \text {find } x^{*} \in C:= \bigcap _{i = 1}^{t}C_{i} \quad \text {such that} \quad Ax^{*} \in Q :=\bigcap _{j =1}^{r} Q_{j}, \end{aligned}$$

(4)

where $A$ is given $M \times N$ real matrix. This can serve as a model for many inverse problems where constraints are imposed on the solutions in the domain of a linear operators as well as in the operator’s range. The multiple-sets split feasibility problem extends the well-known convex feasibility problem, which is obtained from (4) when there are no matrix $A$ and the set $Q_{j}$ present at all.

The multiple split feasibility problems [15] arise in the field of intensity-modulated radiation therapy (in short, IMRT) when one attempts to describe physical dose constraints and equivalent uniform does (EUD) within a single model. The intensity-modulated radiation therapy is described in Sect. 1.1.1. For further details, see Censor et al. [13].

1.1.1 Intensity-Modulated Radiation Therapy

Intensity-modulated radiation therapy (in short, IMRT) [13] is an advanced mode of high-precision radiotherapy, that used computer-controlled linear accelerators to deliver precise radiation doses to specific areas within the tumor. IMRT allows for the radiation doses to confirm more precisely to the three-dimensional (3D) shape of the tumor by modulating-or controlling the intensity of the radiation beam in multiple small volumes. IMRT also allows higher radiation doses to be focused to regions within the tumor while minimizing the dose to surrounding normal critical structures. Treatment is carefully planned by using 3-D computed tomograpy (CT) or magnetic resonance (MRI) images of the patient in conjuction with computarized dose calculations to determine the dose intensity pattern that will best conform to the tumor shape. Typically, combinations of multiple intensity-modulated field coming from different beam directions produce a custom tailored radiation dose that maximizes tumor dose while also minimizing the dose to adjacent normal tissues. Because the ratio of normal tissue dose to tumor dose is reduced to a minimum with the IMRT approach higher and more effective radiation doses can safely delivered to tumor with fewer side effects compared with conventional radiotherapy techniques. IMRT also has the potential to reduce treatment toxicity, even when doses are not increased. Radiation therapy, including IMRT stops cancer cells from dividing and growing, thus slowing or stopping tumour growth. In many cases, radiation therapy is capable of killing all of the cancer cells, thus shrinking or eliminating tumors.

1.1.2 The Multiple-Sets Split Feasibility Problem in Intensity-Modulated Radiation Therapy

Let us first define the notations:

$\mathbb {R}^{J}$ : The radiation intensity space, the $J$-dimensional Euclidean space.

$\mathbb {R}^{I}$ : The dose space, the $I$-dimensional Euclidean space.

$x$ = $(x_{j})_{j=1}^{J} \in \mathbb {R}^{J}$ : vector of beamlet intensity.

$h$ = $(h_{i})_{i= 1}^{I} \in \mathbb {R}^{I}$ : vector of doses absorbed in all voxels.

$d_{ij}$ : doses absorbed in the voxel $i$ due to radiation of unit intensity from the $j{\text {th}}$

beamlet.

$S_{t}$ : Set of all voxels indices in the structure $t$.

$N_{t}$ : Number of voxel in the structure $S_{t}$.

We divide the entire volume of patient into $I$ voxels, enumerated by $i = 1,2, \ldots ,I$. Assume that $T+Q$ anatomical structures have been outlined including planning target volumes (PTVs) and organ at risk (OAR). Let us count all PTVs and OARs sequentially by $S_{t}$, $t = 1,2,\ldots , T, T+1,\ldots ,T+Q$, where the first $T$ structure represents the planning target volume and the next $Q$ structure represents the organ at risk.

Let us assume that the radiation is delivered independently from each of the $J$ beamlet, which are arranged in certain geometry and indexed by $j = 1,2,\ldots ,J$. The intensities $x_{j}$ of the beamlets are arranged in a $J$-dimensional vector $x = (x_{j})_{j = 1}^{J} \in \mathbb {R}^{J}$ in the $J$ dimensional Euclidean space $\mathbb {R}^{J}$- the radiation intensity space.

The quantities $d_{ij}\ge 0$, which represent the dose absorbed in voxel $i$ due to radiation of unit intensity from the $j{\text {th}}$ beamlet are calculable by any forward program. Let $h_{i}$ denote the total dose absorbed in the voxel $i$ and let $h = (h_{i})_{i = 1}^{I}$ be the vector of doses absorbed in all voxels. We call the space $\mathbb {R}^{I}$-the dose space. we can calculate $h_{i}$ as

$$\begin{aligned} h_{i} = \sum _{j = 1}^{J}d_{ij}x_{j}. \end{aligned}$$

(5)

The dose influence matrix $D = (d_{ij})$ is the $I\times J$ matrix whose elements are the $d_{ij}'s$ mentioned above. Thus, (5) can be written as the vector equation

$$\begin{aligned} h = Dx. \end{aligned}$$

(6)

The constraint are formulated in two different Euclidean vector space. The delivery constraints are formulated in the Euclidean vector space of radiation intensity vector (that is, vector whose component are radiation intensities). The equivalent uniform dose (in short, EUD) constraints are formulated in the Euclidean vector space of dose vectors (that is, vectors whose components are dose in each voxel).

Now, let us assume that $M$ constraints in the dose space and $N$ constraints in the intensity space. Let $H_{m}$ be the set of dose vectors that fulfil the $m{\text {th}}$ dose constraints and, let $X_{n}$ be the set of beamlet intensity vectors that fulfil the $n{\text {th}}$ intensity constraint. Each of the constraint sets $H_{m}$ and $X_{n}$ can be one of the specific $H$ and $X$ sets, respectively, described below.

In the dose space, a typical constraint is that given critical structure $S_{t}$, the dose should not exceed an upper bound $u_{t}$. The corresponding set $H_{{\text {max}},t}$ is

$$\begin{aligned} H _{\mathrm{{max}},t} = \{ h \in \mathbb {R}^{I} \mid h_{i} \le u_{t},\quad \text {for all } i\in S_{t} \}. \end{aligned}$$

(7)

Similarly, in the target volumes (in short, TVs), the dose should not fall below a lower bound $l_{t}$. The set $H_{\mathrm{{min}},t}$ of dose vectors that fulfil this constraint is

$$\begin{aligned} H_{\mathrm{{min}},t} = \{ h \in \mathbb {R}^{I} \mid l_{t} \le h_{i} \quad \text {for all } i \in S_{t} \}. \end{aligned}$$

(8)

To handle the equivalent uniform dose EUD constraint for each structure $S_{t}$, we define a real-valued function $E_{t} = \mathbb {R}^{I} \rightarrow \mathbb {R}$, called the EUD function, is defined by

$$\begin{aligned} E_{t}(h) = \left( \frac{1}{N_{t}}\sum _{i \in S_{t}}(h_{i})^{\alpha _{t}} \right) ^{1/\alpha _{t}}. \end{aligned}$$

(9)

where $N_{t}$ is the number of voxels in the structure $S_{t}$.

The parameter $\alpha _{t}$ is a tissue-specific number which is negative for target volumes TVs and positive for organ at risk OAR. For $\alpha _{t} = 1$,

$$\begin{aligned} E_{t}(h) = \frac{1}{N_{t}}\sum _{i \in S_{t}}(h_{i}), \end{aligned}$$

(10)

that is, it is the mean dose of the organ for which it is calculated.

On the other hand, letting $\alpha _{t} \rightarrow \infty$ makes the equivalent uniform dose EUD function approach the maximal value, $\text {max}\{h_{i}\mid i \in S_{t}\}$.

For each planning target volume PTVs structure $S_{t}$, $t = 1,2,\ldots ,T$, the parameter $\alpha _{t}$ is chosen negative and the equivalent uniform dose EUD constraint is described by the set

$$\begin{aligned} H_{\mathrm{EUD}, t} = \{ h \in \mathbb {R}^{I} \mid E^{\mathrm{{min}}} \le E_{t}(h) \}, \end{aligned}$$

(11)

where $E^\mathrm{min}$ is given, for each planning target volumes PTVs structure, by the treatment planner. For each organ at risk OAR, $S_{\mu }$, $\mu = T+1, T+2, \ldots ,T+Q$, the parameter is chosen $\alpha _{t} \ge 1$ and the equivalent uniform dose EUD constraint can be described by the set

$$\begin{aligned} H_{\mathrm{EUD}, t} = \{ h \in \mathbb {R}^{I} \mid E_{t}(h) \le E^{\mathrm{{max}}} \}, \end{aligned}$$

(12)

where $E^{\mathrm{{max}}}$ is given, for each organ at risk OAR, by the treatment planner. Due to the non-negativity of dose, $h \ge 0$ the equivalent uniform dose EUD function is convex for all $\alpha _{t} \ge 1$ and concave for all $\alpha _{t} < 1$. Therefore, the constraint sets $H_{\mathrm{{EUD}}, t}$ are always convex sets in the dose vector space, since they are level sets of the convex functions $E_{t}(h)$ for organ at risk OAR (with $\alpha _{t} \ge 1$), or of the convex functions $-E_{t}(h)$ for the targets (with $\alpha _{t} < 0$).

In the radiation intensity space, the most prominent constraint is the non-negativity of the intensities, described by the set.

$$\begin{aligned} X_{+} = \{ x \in \mathbb {R}^{J} \mid \quad x_{j}\ge 0 \quad \forall j=1,2,\ldots ,J \}. \end{aligned}$$

(13)

Thus, our unified model for physical dose and equivalent uniform dose EUD constraints takes the form of multiple-sets split feasibility problem, where some constraints (the non-negativity of radiation intensities) are defined in the radiation intensity space $\mathbb {R}^{J}$ and other constraints (upper and lower bounds on dose and the equivalent uniform dose EUD constraints) are defined in the dose space $\mathbb {R}^{I}$, and the two spaces are related by a (known) linear transformation $D$ (the dose matrix).

The unified problem can be formulated as follows:

$$\begin{aligned} \text {find } x^{*}\in X_{+} \bigcap \left( \bigcap _{i = 1}^{N}X_{n}\right) \text { such that } h^{*} = Dx^{*} \text { and } h^{*}\in \left( \bigcap _{m= 1}^{M}H_{m}\right) . \end{aligned}$$

(14)

2 Preliminaries

This section provides the basic definitions and results, which will be used in the sequel.

Throughout the chapter, we adopt the following terminology and notations.

Let $\fancyscript{H}$ be a real Hilbert space whose norm and inner product are denoted by $\Vert \cdot \Vert$ and $\langle .,.\rangle$, respectively. Let $C$ be a nonempty subset of $\fancyscript{H}$. The set of fixed points of a mapping $T : C \rightarrow C$ is denoted by Fix($T$). Let $\{x_{n}\}$ be a sequence in $\fancyscript{H}$ and $x \in \fancyscript{H}$. We use $x_{n} \rightarrow x$ and $x_{n} \rightharpoonup x$ to denote the strong and weak convergence of the sequence $\{x_{n}\}$ to $x$, respectively. We also use $\omega _{w}(x_{n})$ to denote the weak $\omega$-limit sets of the sequence $\{x_{n}\}$, namely,

$$\omega _{w}(x_{n}) := \{x \in \fancyscript{H} : x_{n_{i}} \rightharpoonup x \text { for some subsequence } \{x_{n_{i}}\} \text { of } \{x_{n} \} \}.$$

The following result provides the weak convergence of a bounded sequence.

Proposition 1

[65, Proposition 2.6] Let $C$ be a nonempty closed convex subset of a real Hilbert space $\fancyscript{H}$ and $\{x_{n}\}$ be a bounded sequence such that the following conditions hold:

• (i) Every weak limit point of $\{x_{n}\}$ lies in $C$;

• (ii) $\displaystyle \lim _{n \rightarrow \infty }\Vert x_{n}-x\Vert$ exists for every $x \in C$.

Then, the sequence $\{x_{n}\}$ converges weakly to a point in $C$.

Lemma 1

[59] Let $\{x_{n}\}$ and $\{y_{n}\}$ be bounded sequences in a real Hilbert space $\fancyscript{H}$ and $\{\alpha _{n}\}$ be a sequence in $[0,1]$ with $0 < \displaystyle \liminf _{n \rightarrow \infty } \alpha _{n} \le \displaystyle \limsup _{n \rightarrow \infty }\alpha _{n} < 1$. Suppose that $x_{n+1} = (1 - \alpha _{n})y_{n}+ \alpha _{n}x_{n}$ for all $n \ge 0$, and $\displaystyle \limsup _{n \rightarrow \infty }(\Vert y_{n+1}-y_{n}\Vert -\Vert x_{n+1} - x_{n}\Vert ) \le 0$. Then, $\displaystyle \lim _{n \rightarrow \infty }\Vert y_{n}-x_{n}\Vert = 0$.

Lemma 2

[33] Let $\fancyscript{H}$ be a real Hilbert space. Then, for all $x,y \in \fancyscript{H}$ and $\lambda \in [0,1]$,

$$\Vert \lambda x+ (1-\lambda )y\Vert ^{2} = \lambda \Vert x\Vert ^{2} + (1-\lambda )\Vert y\Vert ^{2} -\lambda (1-\lambda )\Vert x-y\Vert ^{2}.$$

Definition 1

A mapping $T :\fancyscript{H} \rightarrow \fancyscript{H}$ is said to be

• (a) Lipschitz continuous if there exists a constant $L > 0$ such that

  $$\begin{aligned} \Vert Tx-Ty \Vert \le L\Vert x-y\Vert , \quad \text {for all } x,y \in \fancyscript{H}; \end{aligned}$$

  (15)

• (b) contraction if there exists a constant $\alpha \in (0,1)$ such that

  $$\begin{aligned} \Vert Tx - Ty \Vert \le \alpha \Vert x-y\Vert , \quad \text {for all } x,y \in \fancyscript{H}; \end{aligned}$$

  (16)

  If $\alpha =1$, then $T$ is said to be nonexpansive;

• (c) firmly nonexpansive if $2T-I$ is nonexpansive, or equivalently,

  $$\begin{aligned} \langle x-y, Tx-Ty \rangle \ge \Vert Tx-Ty \Vert ^{2},\quad \text {for all } x,y \in \fancyscript{H}. \end{aligned}$$

  (17)

  Alternatively, $T$ is firmly nonexpansive if and only if $T$ can be expressed as

  $$T = \frac{1}{2}(I+S),$$

  where $S : \fancyscript{H} \rightarrow \fancyscript{H}$ is nonexpansive;

• (d) averaged mapping if it can be written as the average of the identity mapping $I$ and a nonexpansive mapping, that is,

  $$\begin{aligned} T = (1-\alpha ) I + \alpha S, \end{aligned}$$

  (18)

  where $\alpha \in (0,1)$ and $S : \fancyscript{H} \rightarrow \fancyscript{H}$ is nonexpansive. More precisely, when Eq. (18) holds, we say that $T$ is $\alpha$-averaged.

The Cauchy-Schwartz inequality implies that every firmly nonexpansive mapping is nonexpansive but converse need not be true.

Proposition 2

Let $S,T,V:\fancyscript{H} \rightarrow \fancyscript{H}$ be given mappings.

• (a) If $T = (1-\alpha ) S + \alpha V$ for some $\alpha \in (0,1)$, $S$ is averaged and $V$ is nonexpansive, then $T$ is averaged.

• (b) $T$ is firmly nonexpansive if and only if the complement $I-T$ is firmly nonexpansive.

• (c) If $T = (1-\alpha )S + \alpha V$ for some $\alpha \in (0,1)$, $S$ is firmly nonexpansive and $V$ is nonexpansive, then $T$ is averaged.

• (d) The composite of finitely many averaged mappings is averaged. That is, if each of the mappings $\{T_{i}\}_{i = 1}^{N}$ is averaged, then so is the composite $T_{1}o\dots oT_{N}$. In particular, if $T_{1}$ is $\alpha _{1}$-averaged and $T_{2}$ is $\alpha _{2}$-averaged, where $\alpha _{1},\alpha _{2} \in (0,1)$, then the composite $T_{1} \circ T_{2}$ is $\alpha$-averaged, where $\alpha = \alpha _{1}+\alpha _{2}-\alpha _{1}\alpha _{2}$.

• (e) If the mappings $\{T_{i}\}_{i = 1}^{N}$ are averaged and have a common fixed point, then

  $$\bigcap _{i = 1}^{N} Fix (T_{i}) = Fix (T_{1} \circ \cdots \circ T_{N}).$$

  The notion Fix($T$) denotes the set of all fixed points of the mapping $T$, that is, $Fix(T) = \{x \in \fancyscript{H}: Tx = x \}$.

Definition 2

Let $T$ be a nonlinear operator whose domain $D(T) \subseteq \fancyscript{H}$, and range is $R(T)\subseteq \fancyscript{H}$. The operator $T$ is said to be

• (a) monotone if

  $$\begin{aligned} \langle x-y, Tx - Ty \rangle \ge 0,\quad \text {for all } x,y \in D(T). \end{aligned}$$

  (19)

• (b) strongly monotone (or $\beta$ -strongly monotone) if there exists a constant $\beta > 0$ such that

  $$\begin{aligned} \langle x-y, Tx - Ty \rangle \ge \beta \Vert x-y\Vert ^{2},\quad \text {for all } x,y \in D(T). \end{aligned}$$

  (20)

• (c) inverse strongly monotone (or $\nu$ -inverse strongly monotone) ($\nu$-ism) if there exists a constant $\nu > 0$ such that

  $$\begin{aligned} \langle x-y, Tx-Ty \rangle \ge \nu \Vert Tx - Ty \Vert ^{2},\quad \text {for all } x,y \in D(T). \end{aligned}$$

  (21)

It can be easily seen that if $T$ is nonexpansive, then $I-T$ is monotone.

It is well-known that if the function $f : \fancyscript{H} \rightarrow \mathbb {R}$ is Lipschitz continuous, then its gradient $\nabla f$ is $\frac{1}{L}$-ism.

Lemma 3

Let $f : \fancyscript{H} \rightarrow \mathbb {R}$ be a Lipschitz continuous function with Lipschtiz constant $L > 0$. Then, the gradient operator $\nabla f : \fancyscript{H} \rightarrow \fancyscript{H}$ is $\frac{1}{L}$-ism, that is,

$$\begin{aligned} \langle \nabla f(x)-\nabla f(y),x-y\rangle \ge \frac{1}{L}\Vert \nabla f(x)-\nabla f(y)\Vert ^{2},\quad \mathrm{{for}}\,\mathrm{{all}} x,y \in \fancyscript{H}. \end{aligned}$$

(22)

Proposition 3

Let $T : \fancyscript{H} \rightarrow \fancyscript{H}$ be a mapping.

• (a) $T$ is nonexpansive if and only if the complement $I-T$ is $\frac{1}{2}$-ism.

• (b) If $T$ is $\nu$-ism, then for $\gamma > 0$, $\gamma T$ is $\frac{\nu }{\gamma }$-ism.

• (c) $T$ is averaged if and only if the complement $I-T$ is $\nu$-ism for some $\nu > \frac{1}{2}$. Indeed, for $\alpha \in (0,1)$, $T$ is $\alpha$-averaged if and only if $I-T$ is $\frac{1}{2\alpha }$-ism.

2.1 Metric Projection

Let $C$ be a nonempty subset of a normed space $X$ and $x \in X$. An element $y_{0} \in C$ is said to be a best approximation of $x$ if

$$\Vert x-y_{0}\Vert = d (x,C),$$

where $d(x,C) = \displaystyle \inf _{y \in C}\Vert x-y\Vert$. The number $d(x,C)$ is called the distance from x to C. The (possibly empty) set of all best approximations from $x$ to $C$ is denoted by

$$ P_{C}(x) = \{y \in C : \Vert x-y\Vert = d(x,C)\}.$$

This defines a mapping $P_{C}$ from $X$ into $2^{C}$ and it is called the metric projection onto $C$. The metric projection mapping is also known as the nearest point projection, proximity mapping or best approximation operator.

Theorem 1

Let $C$ be a nonempty closed convex subset of a Hilbert space $\fancyscript{H}$. Then, for each $x \in \fancyscript{H}$, there exists a unique $y \in C$ such that

$$\Vert x-y\Vert = \displaystyle \inf _{z \in C}\Vert x-z\Vert .$$

The above theorem says that $P_{C}(.)$ is a single-valued projection mapping from $\fancyscript{H}$ onto $C$.

Some important properties of projections are gathered in the following proposition.

Proposition 4

Let $C$ be a nonempty closed convex subset of a real Hilbert space $\fancyscript{H}$. Then,

• (a) $P_{C}$ is idempotent, that is, $P_{C}(P_{C}(x)) = P_{C}(x)$, for all $x \in \fancyscript{H}$;

• (b) $P_{C}$ is firmly nonexpansive, that is, $\langle x-y, P_{C}(x)-P_{C}(y)\rangle \ge \Vert P_{C}(x)-P_{C}(y)\Vert ^{2}$, for all $x, y \in \fancyscript{H}$;

• (c) $P_{C}$ is nonexpansive, that is, $\Vert P_{C}(x)-P_{C}(y)\Vert \le \Vert x- y\Vert$, for all $x,y \in \fancyscript{H}$;

• (d) $P_{C}$ is monotone, that is, $\langle P_{C}(x)-P_{C}(y),x-y\rangle \ge 0$, for all $x, y \in \fancyscript{H}$.

2.2 Projection Gradient Method

Let $C$ be a nonempty closed convex subset of a Hilbert space $\fancyscript{H}$ and $f : C \rightarrow \mathbb {R}$ be a function. Consider the constrained minimization problem:

$$\begin{aligned} \min _{x \in C} f(x). \end{aligned}$$

(23)

Assume that the minimization problem (23) is consistent.

If $f : C \rightarrow \mathbb {R}$ is Fréchet differentiable convex function, then it is well known (see, for example, [2, 39]) that the minimization problem (23) is equivalent to the following variational inequality problem:

$$\begin{aligned} \text {Find } x^{*} \in C \quad \text { such that } \quad \langle \nabla f(x^{*}),y-x^{*}\rangle \ge 0, \quad \text {for all } y \in C, \end{aligned}$$

(24)

where $\nabla f : \fancyscript{H} \rightarrow \fancyscript{H}$ is the gradient of $f$. The following is the general form of the variational inequality problem:

$$ {\text {VIP}(F,C)} \qquad \text {Find } x^{*} \in C \quad \text {such that} \quad \langle F(x^{*}),y-x^{*}\rangle \ge 0, \quad \text {for all } y \in C,$$

where $F : C \rightarrow \fancyscript{H}$ be a nonlinear mapping. For further details and applications of variational inequalities, we refer to [2, 30, 39] and the references therein. The following result provides the equivalence between a variational inequality problem and a fixed point problem.

Proposition 5

Let $C$ be a nonempty closed convex subset of a real Hilbert space $\fancyscript{H}$ and $F : C \rightarrow \fancyscript{H}$ be an operator. Then, $x^{*} \in C$ is a solution of the VIP$(F,C)$ if and only if for any $\gamma > 0$, $x^{*}$ is a fixed point of the mapping $P_{C}(I-\gamma F): C \rightarrow C$, that is,

$$\begin{aligned} x^{*} = P_{C}(x^{*}-\gamma F(x^{*})), \end{aligned}$$

(25)

where $P_{C}(x^{*}-\gamma F(x^{*}))$ denotes the projection of $(x^{*}-\gamma F(x^{*}))$ onto $C$, and $I$ is the identity mapping.

In view of the above proposition and discussion, we have the following proposition.

Proposition 6

Let $C$ be a nonempty closed convex subset of a real Hilbert space $\fancyscript{H}$ and $F : C \rightarrow \fancyscript{H}$ be a convex and Fréchet differential function. Then, the following statement are equivalent:

• (a) $x^{*} \in C$ is a solution of the minimization problem (23);

• (b) $x^{*} \in C$ solves $VIP(F,C)$ (24);

• (c) $x^{*} \in C$ is a solution of the fixed point Eq. (25).

From the above equivalence, we have the following projection gradient method.

Theorem 2

(Projection Gradient Method) Let $C$ be a nonempty closed convex subset of a real Hilbert space $\fancyscript{H}$ and $F : C \rightarrow \fancyscript{H}$ be a Lipschitz continuous and strongly monotone mapping with constants $L > 0$ and $\beta > 0$, respectively. Let $\gamma > 0$ be a constant such that $\gamma < \frac{2\beta }{L^{2}}$. Then,

• (i) $P_{C}(I-\gamma F): C\rightarrow C$ is a contraction mapping and there exists a solution $x^{*} \in C$ of the VIP$(F,C)$.

• (ii) The sequence $\{x_{n}\}$ generated by the following iterative, process:

  $$x_{n+1} = P_{C}(I-\gamma F)x_{n}, \quad \mathrm{for}\, \mathrm{all} \; n\in \mathbb {N},$$

  converges strongly to a solution $x^{*}$ of the $VIP(F,C)$.

In view of Proposition 6 and Theorem 2, we have the following method for finding an approximate solution of a convex and differentiable minimization problem.

Theorem 3

Let $C$ be a nonempty closed convex subset of a real Hilbert space $\fancyscript{H}$ and $f : C \rightarrow \mathbb {R}$ be a convex and Fréchet differentiable function such that the gradient $\nabla f$ is Lipschitz continuous and strongly monotone mapping with constants $L > 0$ and $\beta > 0$, respectively. Let $\{\gamma _{n}\}$ be a sequence of strictly positive real numbers such that

$$\begin{aligned} 0 < \displaystyle \liminf _{n \rightarrow \infty } \gamma _{n}\le \displaystyle \limsup _{n \rightarrow \infty }\gamma _{n} < \frac{2\beta }{L^{2}}. \end{aligned}$$

(26)

Then, the sequence $\{x_{n}\}$ generated by the following projection gradient method

$$\begin{aligned} x_{n+1} = P_{C}(I-\gamma _{n} \nabla f)x_{n}, \quad \mathrm{{for}}\,\mathrm{{all}}\; n\in \mathbb {N}, \end{aligned}$$

(27)

converges strongly to a unique solution of the minimization problem (23).

The sequence $\{x_{n}\}$ generated by the Eq. (27) converges weakly to the unique solution of the minimization problem (23) even when $\nabla f$ is not necessary strongly monotone.

We present an example to illustrate projection gradient method.

Example 1

Let $C = [0,1]$ be a closed convex set in $\mathbb {R}$, $f(x) = x^{2}$ and $\gamma _{n}=1/5$ for all $n$. Then, all the conditions of the Theorem 3 are satisfied and the sequence generated by the Eq. (27) converges to $0$ with initial guess $x_{1} = 0.01$. We have the following table of iterates:

From Table 1, it is clear that the solution $x =0$ is obtained after 11th iteration. We performed the iterative scheme in Matlab R2010 (Fig. 1).

Table 1 Convergence of $\{x_{n}\}$ in Example 1

Fig. 1

Convergence of $\{x_{n}\}$ in Example 1

2.3 Mann’s Iterative Method

Let $C$ be a nonempty closed convex subset of a real Hilbert space $\fancyscript{H}$ and $T : C \rightarrow C$ be a mapping. The well-known Mann’s iterative algorithm is the following.

Algorithm 1

(Mann’s Iterative Algorithm) For arbitrary $x_{0} \in \fancyscript{H}$, generate a sequence $\{x_{n}\}$ by the recursion:

$$\begin{aligned} x_{n+1}=(1-\alpha _{n})x_{n}+\alpha _{n}T x_{n}, \quad n\ge 0, \end{aligned}$$

(28)

where $\{\alpha _{n}\}$ is (usually) assumed to be a sequence in $[0,1]$.

Theorem 4

Let $C$ be a nonempty closed convex subset of a real Hilbert space $\fancyscript{H}$ and $T : C\rightarrow C$ be a nonexpansive mapping with a fixed point. Assume that $\{\alpha _{n}\}$ is a sequence in $[0,1]$ such that

$$\begin{aligned} \sum _{n=1}^{\infty }\alpha _{n}(1-\alpha _{n})=\infty . \end{aligned}$$

(29)

Then, the sequence $\{x_{n}\}$ generated by Mann’s Algorithm 1 converges weakly to a fixed point of $T$.

Xu [65] studied the weak convergence of the sequence generated by the Mann’s Algorithm 1 to a fixed point of an $\alpha$-averaged mapping.

Theorem 5

[65, Theorem 3.5] Let $\fancyscript{H}$ be a real Hilbert space and $T : \fancyscript{H} \rightarrow \fancyscript{H}$ be an $\alpha$-averaged mapping with a fixed point. Assume that $\{\alpha _{n}\}$ is a sequence in [0,1/$\alpha$] such that

$$\begin{aligned} \sum _{n=1}^{\infty }\alpha _{n}\left( \frac{1}{\alpha }-\alpha _{n}\right) =\infty . \end{aligned}$$

(30)

Then, the sequence $\{x_{n}\}$ generated by Mann’s Algorithm 1 converges weakly to a fixed point of $T$.

We illustrates Mann’s Algorithm 1 with the help of the following examples:

Example 2

Let $T : [0,1] \rightarrow [0,1]$ be a mapping defined by

$$T x = \frac{x^{2}}{4}-\frac{x}{2}+\frac{1}{4}, \quad \text {for all } x \in [0,1].$$

Then, $T$ is nonexpansive. Let $\{\alpha _{n}\}=\{\frac{1}{n+1}\}$. Then, all the conditions of Theorem 4 are satisfied and the sequence $\{x_{n}\}$ generated by Mann’s Algorithm 1 converges to a fixed point of $T$, that is, to $x = 0.1716$. We take the initial guest $x_{1} =.01$ and perform the Mann’s Algorithm 1 by using Matlab R2010. We obtain the iterates in Table 2.

Table 2 Convergence of $\{x_{n}\}$ in Example 2

Fig. 2

Convergence of $\{x_{n}\}$ in Example 2

From Table 2, it is clear that the sequence generated by the Mann’s Algorithm 1 converges to $x = 0.1716$ which is obtained after 19th iteration (Fig. 2).

Example 3

Let $T : [0,1] \rightarrow [0,1]$ be defined by

$$T x = \frac{9}{10}x + \frac{1}{10} Sx,\quad \text {for all } x \in [0,1].$$

where $S x = \frac{x^{2}}{4}-\frac{x}{2}+\frac{1}{4}$ is a nonexpansive map and $\{\alpha _{n}\} =10-\{\frac{1}{n}\}$. Then, $T$ is a $\frac{1}{10}$-averaged mapping and all the conditions of Theorem 5 are satisfied. Hence, the sequence $\{x_{n}\}$ generated by Mann’s Algorithm 1 converges to a fixed point of $T$, that is, to $0.1716$ with initial guess $x_{1} =0.01$.

Table 3 Convergence of $\{x_{n}\}$ in Example 3

From Table 3, it is clear that the fixed point $x =0.1716$ is obtained after 9th iteration. We performed the iterative scheme in Matlab R2010 (Fig. 3).

Fig. 3

Convergence of $\{x_{n}\}$ in Example 3

3 CQ-Methods for Split Feasibility Problems

In the pioneer paper [14], Censor and Elfving introduced the concept of a split feasibility problem (SFP) and used multidistance method to obtain the iterative algorithms for solving this problem. Their algorithms as well as others obtained later involves matrix inverses at each step. Byrne [5, 6] proposed a new iterative method called CQ-method that involves only the orthogonal projections onto $C$ and $Q$ and does not need to compute the matrix inverses, where $C$ and $Q$ are nonempty closed convex subsets of $\mathbb {R}^{N}$ and $\mathbb {R}^{M}$, respectively. It is one of the main advantages of this method compare to other methods. The CQ algorithm is as follows:

$$ x_{n+1} = P_{C} \left( x_{n}-\gamma A^{\top }(I-P_{Q})A x_{n} \right) , \quad n = 0,1, \ldots ,$$

where $\gamma \in \left( 0,2/L \right)$, $A$ is a $M \times N$ matrix, $A^{\top }$ denotes the transpose of the matrix $A$, $L$ is the largest eigenvalue of the matrix $A^{\top }A$, and $P_{C}$ and $P_{Q}$ denote the orthogonal projections onto $C$ and $Q$, respectively. Byrne also studied the convergence of the CQ algorithm for arbitrary nonzero matrix $A$. Inspired by the work of Byrne [5, 6], Yang [68] proposed a modification of the CQ algorithm, called relaxed CQ algorithm in which he replaced $P_{C}$ and $P_{Q}$ by $P_{C_{n}}$ and $P_{Q_{n}}$, respectively, where ${C_{n}}$ and ${Q_{n}}$ are half-spaces. One common advantage of the CQ algorithm and relaxed CQ algorithm is that the computation of the matrix inverses is not necessary. However, a fixed step-size related to the largest eigenvalue of the matrix $A^{\top }A$ is used. Computing the largest eigenvalue may be hard and conservative estimate of the step-size usually results in slow convergence. So, Qu and Xiu [53] modified the CQ algorithm and relaxed CQ algorithm by adopting Armijo-like searches. The modified algorithm need not compute the matrix inverses and the largest eigenvalue of the matrix $A^{\top }A$, and make a sufficient decrease of the objective function at each iteration. Zhao et al. [75] proposed a modified CQ algorithm by computing step-size adaptively and perform an additional projection step onto some simple closed convex set $X \subseteq \mathbb {R}^{N}$ in each iteration. Since all the algorithms have been introduced in finite-dimensional setting, Xu [65] proposed the relaxed CQ algorithm in infinite-dimensional setting, and also proved the weak convergence of the proposed algorithm. In 2011, Li [45] developed some improved relaxed CQ methods with the optimal step-length to solve the split feasibility problem based on the modified relaxed CQ algorithm [53].

In this section, we present different kinds of CQ algorithms, namely, CQ algorithm, relaxed CQ algorithm, modified CQ algorithm, modified relaxed CQ algorithm, modified projection type CQ algorithm, modified projection type relaxed CQ algorithm and improved relaxed CQ algorithm. We present the convergence results for these algorithms. We also present an example to illustrate CQ algorithm and its convergence result.

3.1 CQ Algorithm

Let $C$ and $Q$ be nonempty closed convex sets in $\mathbb {R}^{N}$ and $\mathbb {R}^{M}$, respectively, and $A$ be an $M \times N$ real matrix with its transpose matrix $A^{\top }$. Let $\gamma > 0$ and assume that $x^{*}\in \Gamma$. Then, $Ax^{*} \in Q$ which implies the equation $(I-P_{Q})Ax^{*} =0$ which in turns implies the equation $\gamma A^{\top }(I-P_{Q})Ax^{*}=0$, hence the fixed point equation $(I-\gamma A^{\top }(I-P_{Q})A)x^{*}=x^{*}$. Requiring that $x^{*} \in C$, Xu [65] considered the fixed point equation:

$$\begin{aligned} P_{C}(I-\gamma A^{\top }(I-P_{Q})A)x^{*}=x^{*}. \end{aligned}$$

(31)

and also observed that solutions of the fixed point Eq. (31) are exactly solutions of SFP.

Proposition 7

[65, Proposition 3.2] Given $x^{*}\in \mathbb {R}^{N}$. Then, $x^{*}$ solves the SFP if and only if $x^{*}$ solves the fixed point Eq. (31).

Byrne [5, 6] introduced the following CQ algorithm:

Algorithm 2

Let $x_{0} \in \mathbb {R}^{N}$ be an initial guess. Generate a sequence $\{x_{n}\}$ by

$$\begin{aligned} x_{n+1} = P_{C} \left( x_{n}-\gamma A^{\top }(I-P_{Q})A x_{n} \right) , \quad n = 0,1,2, \ldots , \end{aligned}$$

(32)

where $\gamma \in \left( 0,2/L \right)$ and $L$ is the largest eigenvalue of the matrix $A^{\top }A$.

It can be easily seen that the CQ algorithm does not require the computation of the inverse of any matrix. We need only to compute the projection onto the closed convex sets $C$ and $Q$, respectively.

Byrne [5] studied the convergence of the above method and established the following convergence result.

Theorem 6

[5, Theorem 2.1] Assume that the SFP is consistent. Then, the sequence $\{x_{n}\}$ generated by the CQ Algorithm 2 converges to a solution of the SFP.

Remark 1

The particular cases of the CQ algorithm are the Landweber and projected Landweber methods [42]. These algorithms are discussed in detail in the book by Bertero and Boccacci [8], primarily in the context of image restoration within infinite-dimensional spaces of functions (see also Landweber [41]). With $C = \mathbb {R}^{N}$ and $Q = \{b\}$, the CQ algorithm becomes the Landweber iterative method for solving the linear equations $Ax = b$.

The following example illustrates the CQ Algorithm 2 and its convergence result.

Example 4

Let $C = Q = [-1,1]$ and $A(x)=2x$. Then, $A$ is a bounded linear operator with norm $2$. Let $\gamma = 2/5$. Then, all the conditions of Theorem 6 are satisfied.

We perform the computation of the CQ Algorithm 2 by taking the initial guess $x_{1} = 0.01$ and by using Matlab R2010. We obtain the iterates in Table 4.

Table 4 Convergence of $\{x_{n}\}$ in Example 4

From Table 4, it is clear that the sequence generated by the CQ Algorithm 2 converges to 0.5 after 16th iteration (Fig. 4).

Fig. 4

Convergence of $\{x_{n}\}$ in Example 4

Xu [65] extended Algorithm 2 in the setting of real Hilbert spaces to find the minimum-norm solution of the SFP with the help of regularization parameter. He considered $x_{\min }$ to be the minimum-norm solution of the SFP if $x_{\min } \in \Gamma$ has the property

$$\Vert x_{\min }\Vert = \min \{\Vert x^{*}\Vert :x^{*}\in \Gamma \}.$$

3.2 Relaxed CQ Algorithm

Let $C$ and $Q$ be nonempty closed convex sets in $\mathbb {R}^{N}$ and $\mathbb {R}^{M}$ respectively, and $A$ be an $M \times N$ real matrix with its transpose matrix $A^{\top }$. Let $P_{C_{n}}$ and $P_{Q_{n}}$ denote the orthogonal projections onto the half-spaces $C_{n}$ and $Q_{n}$, respectively. In some cases it is impossible or need too much time to compute the orthogonal projections [7, 32, 34]. Therefore, if this is the case, the efficiency of the projection type methods will be seriously affected, as would the CQ algorithm. Inexact technology plays an important role in designing efficient, easily implemented algorithms for the optimization problem, variational inequality problem and so on. The relaxed projection method may be viewed as one of the inexact methods. Fukushima [32] proposed a relaxed projection algorithm for solving variational inequalities and the theoretical analysis. The numerical experiment shows the efficiency of his method.

Inspired by the work of Fukushima [32], Yang [68] proposed the relaxed CQ algorithm. In order to describe relaxed CQ algorithm, he made some assumptions on $C$ and $Q$, which are as follow:

• The solution set of the split feasibility problem is nonempty.

$$\begin{aligned} C=\{x\in \mathbb {R}^{N}: c(x)\le 0 \} \quad \text {and} \quad Q=\{y\in \mathbb {R}^{M}: q(y)\le 0\}. \end{aligned}$$

(33)

where $c$ and $q$ are the convex functionals on $\mathbb {R}^{N}$ and $\mathbb {R}^{M}$, respectively.

The subgradients $\partial {c}(x)$ and $\partial {q}(y)$ of $c$ and $q$ at $x$ and $y$, respectively, are defined as follows:

$$\partial {c}(x)=\{z \in \mathbb {R}^{N} : c(u) \ge c(x) + \langle u-x,z \rangle ,~\forall u\in \mathbb {R}^{N}\} \ne \emptyset , \quad \text {for all } x\in C,$$

and

$$\partial {q}(y) = \{w \in \mathbb {R}^{M}: q(v) \ge q(y) + \langle v-y,w \rangle ,~\forall v\in \mathbb {R}^{M}\} \ne \emptyset , \quad \text {for all } y\in Q.$$

Note that the differentiability of $c(x)$ or $q(y)$ is not assumed. Therefore, both $C$ and $Q$ are general enough. For example, suppose any system of inequalities $c_{i}(x) \le 0$, $i \in J$, where $c_{i}(x)$ are convex and $J$ is an arbitrary index set, may be regarded as equivalent to the single inequality $c(x) \le 0$ with $c(x) = \sup \{c_{i}(x) : i \in J\}$. One may easily get an element of $\partial {c}(x)$ by the expression of $\partial {c}(x)$ provided all $c_{i}(x)$ are differentiable.

With these assumptions, Yang [68] proposed the following relaxed CQ algorithm.

Algorithm 3

Let $x_{0}$ be arbitrary. For $n = 0,1,2,\dots$, calculate

$$\begin{aligned} x_{n+1} = P_{C_{n}} \left( x_{n}-\gamma A^{\top }(I-P_{Q_{n}})A x_{n} \right) , \end{aligned}$$

(34)

where $\{C_{n}\}$ and $\{Q_{n}\}$ are the sequences of closed convex sets defined as follows:

$$\begin{aligned} C_{n} = \{ x \in \mathbb {R}^{N} : c(x_{n}) + \langle \xi _{n},x-x_{n} \rangle \le 0\}, \end{aligned}$$

(35)

where $\xi _{n} \in \partial {c}(x_{n})$, and

$$\begin{aligned} Q_{n} = \{y \in \mathbb {R}^{M} : q(A(x_{n})) + \langle \eta _{n},y-A(x_{n}) \rangle \le 0\}, \end{aligned}$$

(36)

where $\eta _{n} \in \partial {q}(A(x_{n}))$.

It can be easily seen that $C\subset C_{n}$ and $Q \subset Q_{n}$ for all $n$. Due to special form of $C_{n}$ and $Q_{n}$, the orthogonal projections onto $C_{n}$ and $Q_{n}$ may be directly calculated [32]. Thus, the proposed algorithm can be easily implemented.

Yang [68] proved the following convergence result for Algorithm 3.

Theorem 7

[68, Theorem 1] Let $\{x_{n}\}$ be the sequence generated by the Algorithm 3. Then, $\{x_{n}\}$ converges to a solution of the SFP.

Xu [65] further studied the relaxed CQ algorithm in the setting of Hilbert spaces. He proposed the generalized form of the Algorithm 3 in the setting of Hilbert spaces and studied the weak convergence of the sequence generated by the proposed method.

3.3 Modified CQ Algorithm and Modified Relaxed CQ Algorithm

In CQ method and relaxed CQ method, we use a fixed step-size related to the largest eigenvalue of the matrix $A^{\top }A$, which sometimes affects convergence of the algorithms. Therefore, several modifications of these methods are proposed during the recent years. This section deals with such modified CQ method and relaxed CQ method.

By adopting Armijo-like searches, which are popular in iterative algorithms for solving nonlinear programming problems, variational inequality problems and so on [30, 67], Qu and Xiu [53] presented modification of CQ algorithm and relaxed CQ algorithm. In these modifications, it is not needed to compute the matrix inverses and the largest eigenvalue of the matrix $A^{\top }A$, and make a sufficient decrease of the objective functions at each iteration.

Let $C$, $Q$ and $A$ be the same as in Sect. 3.1. Qu and Xiu [53] proposed the following modified CQ algorithm:

Algorithm 4

Given constants $\beta > 0$, $\sigma \in (0,1)$, $\gamma \in (0,1)$. Let $x_{0}$ be arbitrary. For $n=0,1, 2, \ldots$, calculate

$$ x_{n+1} =P_{C} \left( x_{n} -\alpha _{n}A^{\top }(I-P_{Q})Ax_{n} \right) , $$

where $\alpha _{n}=\beta \gamma ^{m_{n}}$ and $m_{n}$ is the smallest nonnegative integer $m$ such that

$$f(P_{C}(x_{n}-\beta \gamma ^{m}A^{\top }(I-P_{Q})Ax_{n})) \le $$

$$f(x_{n})- \sigma \left\langle A^{\top }(I-P_{Q})Ax_{n}, x_{n} - P_{C} \left( x_{n} - \beta \gamma ^{m}A^{\top }(I-P_{Q}) Ax_{n} \right) \right\rangle ,$$

where $f(x) : = \frac{1}{2} \Vert Ax - P_{Q} Ax \Vert ^{2}$.

Algorithm 4 is in fact a special case of the standard gradient projection method with the Armijo-like search rule for solving convexly constrained optimization.

Qu and Xiu [53] established the following convergence of the modified CQ Algorithm 4.

Theorem 8

[53, Theorem 3.1] Let $\{x_{n}\}$ be a sequence generated by the Algorithm 4. Then the following conclusions hold:

• (a) $\{x_{n}\}$ is bounded if and only if the solution set $S$ of minimization problem:

  $$\min _{x\in C} f(x) := \frac{1}{2}\Vert Ax-P_{Q}Ax\Vert ^{2},$$

  is nonempty. In this case, $\{x_{n}\}$ must converge to an element of $S$.

• (b) $\{x_{n}\}$ is bounded and $\displaystyle \lim _{n\rightarrow \infty }f(x_{n})=0$ if and only if the SFP is solvable. In such a case, $\{x_{n}\}$ must converge to a solution of the SFP.

Remark 2

Algorithm 4 is more applicable and it is easy to compute as compared to CQ Algorithm 2 proposed by Byrne [5], as it need not determine or estimate the largest eigenvalue of the matrix $A^{\top }A$. The step-size $\alpha _{n}$ is judiciously chosen so that the function value $f(x_{n+1})$ has a sufficient decrease. It can also be identified the existence of solution to the concerned problem by the iterative sequence.

Qu and Xiu [53] studied relaxed CQ algorithm proposed in Sect. 3.2 and proposed a modified relaxed CQ algorithm. Let $C$, $Q$, $A$, $C_{n}$ and $Q_{n}$ be the same as in Sect. 3.2.

For every $n$, let $F_{n} : \mathbb {R}^{N} \rightarrow \mathbb {R}^{N}$ be function defined as

$$F_{n}(x) = A^{\top }(I-P_{Q_{n}})Ax, \quad \text {for all } x \in \mathbb {R}^{N}.$$

Modified relaxed CQ algorithm is the following:

Algorithm 5

Let $x_{0}$ be arbitrary and $\gamma > 0$, $l\in (0,1)$, $\mu \in (0,1)$ be given. For $n=0,1,2,\ldots$, let

$$\overline{x}_{n}= P_{C_{n}} \left( x_{n}-\alpha _{n}F_{n}(x_{n}) \right) ,$$

where $\alpha _{n} =\gamma l^{m_{n}}$ and $m_{n}$ is the smallest nonnegative integer $m$ such that

$$\begin{aligned} \Vert F_{n}(\overline{x}_{n})-F_{n}(x_{n})\Vert \le \mu \frac{\Vert \overline{x}_{n}-x_{n}\Vert }{\alpha _{n}}. \end{aligned}$$

(37)

Set

$$x_{n+1}=P_{C_{n}}(x_{n}-\alpha _{n}F_{n}(\overline{x}_{n})),$$

where $C_{n}$, $Q_{n}$ are the sequences of closed convex sets defined as in (35) and (36).

Qu and Xiu [53] established the following convergence theorem.

Theorem 9

[53, Theorem 4.1] Let $\{x_{n}\}$ be a sequence generated by Algorithm 5. If the solution set of SFP is nonempty, then $\{x_{n}\}$ converges to a solution of SFP.

Inspired by Tseng’s modified forward-backward splitting method for finding a zero of the sum of two maximal monotone mappings [60], Zhao et al. [75] proposed a modification of CQ algorithm, which computes the step-size adaptively, and performs an additional projection step onto some simple closed convex set $X \subseteq \mathbb {R}^{N}$ in each iteration. Let $C$, $Q$ and $A$ be the same as in Sect. 3.1.

Algorithm 6

[75] Let $x_{0}$ be arbitrary, $\sigma _{0}> 0$, $\beta \in (0,1)$, $\theta \in (0,1)$, $\rho \in (0,1)$. For $n = 0,1,2,\dots$ compute

$$\begin{aligned} \bar{x}_{n}= P_{C}(x_{n}-\gamma _{n}F(x_{n})), \end{aligned}$$

(38)

where $F = A^{\top }(I-P_{Q})A$, $\gamma _{n}$ is chosen to be the largest $\gamma \in \{\sigma _{n},\sigma _{n}\beta ,\sigma _{n}\beta ^{2},\ldots \}$ satisfying

$$\begin{aligned} \gamma \Vert F(\bar{x}_{n})-F(x_{n})\Vert \le \theta \Vert \bar{x}_{n}-x_{n}\Vert . \end{aligned}$$

(39)

Let

$$\begin{aligned} x_{n+1}=P_{X} \left( \bar{x}_{n}-\gamma _{n}(F(\bar{x}_{n})-F(x_{n})) \right) . \end{aligned}$$

(40)

If

$$\begin{aligned} \gamma _{n}\Vert F(x_{n+1})-F(x_{n})\Vert \le \rho \Vert x_{n+1}-x_{n}\Vert , \end{aligned}$$

(41)

then set $\sigma _{n}=\sigma _{0}$; otherwise, set $\sigma _{n}=\gamma _{n}$.

This algorithm involves projection onto a nonempty closed convex set $X$ rather than onto the set $C$, which can be advantageous when $X$ has a simpler structure than $C$. The set $X$ can be chosen variously. It can be chosen to be a simple bounded subset of $\mathbb {R}^{N}$ that contains at least one solution of split feasibility problem, it can also be directly chosen as $X=\mathbb {R}^{N}$. In fact, it can be more generally chosen to be a dynamically changing set $X_{n}$, provided $\bigcap _{n=0}^{\infty } X_{n}$ contains a solution of the split feasibility problem. This does not affect the convergent result. The last step is used to reduce the inner iterations for searching the step-size $\gamma _{n}$.

For such algorithm, we usually take

$$\frac{1}{2}\Vert x_{n}-P_{C}(x_{n})\Vert ^{2}+\frac{1}{2}\Vert Ax_{n}-P_{Q}(Ax_{n})\Vert ^{2}< 0$$

or

$$\frac{1}{2}\Vert (I-P_{Q})Ax_{n}\Vert ^{2}< \varepsilon $$

as the termination criterion, where $\varepsilon > 0$ is chosen to be sufficiently small.

Zhao et al. [75] established the following convergence result for the Algorithm 6.

Theorem 10

[75, Theorem 2.1] Let $\{x_{n}\}$ be a sequence generated by Algorithm 6, $X$ be a nonempty closed convex set in $\mathbb {R}^{N}$ with a simple structure. If $X \cap \Gamma$ is nonempty, then $\{x_{n}\}$ converges to a solution of SFP.

Remark 3

This modified $CQ$ algorithm differs from the extragradient-type method [38, 40, 53], whose second equation is

$$x_{n+1}=P_{C}(x_{n}-\gamma _{n}F(\overline{x}_{n})).$$

It also differs from the modified projection-type method [54, 57], whose second equation is

$$x_{n+1}=x_{n}-\gamma _{n}(x_{n}-\overline{x}_{n}+\alpha _{n}(F(\overline{x}_{n})-F(x_{n})).$$

In Algorithm 6, the orthogonal projections $P_{C}$ and $P_{Q}$ had been calculated many times even in one iteration step, so they should be assumed to be easily calculated. However, sometimes it is difficult or even impossible to compute them. In order to overcome such situation turn to relaxed or inexact methods [31, 32, 34, 53, 68], which are more efficient and easily implemented. Zhao et al. [75] introduced relaxed modified CQ algorithm for split feasibility problem. Let $C$, $Q$, $A$, $C_{n}$ and $Q_{n}$ be the same as in the Sect. 3.2:

Algorithm 7

[75, Algorithm 3.1] Let $x_{0}$ be arbitrary, $\sigma _{0} > 0$, $\beta \in (0,1)$, $\theta \in (0,1)$, $\rho \in (0,1)$ for $n=0,1,2,\ldots$, compute

$$\begin{aligned} \bar{x}_{n} = P_{C_{n}} \left( x_{n}-\gamma _{n}F_{n}(x_{n}) \right) , \end{aligned}$$

(42)

where $F_{n}(x) = A^{\top } (I - P_{Q_{n}}) Ax_{n}$ and $\gamma _{n}$ is chosen to be the largest $\gamma \in \{\sigma _{k},\sigma _{k}\beta ,\sigma _{k} \beta ^{2} \dots \}$ satisfying

$$\begin{aligned} \gamma \Vert F_{n}(\bar{x}_{n})-F_{n}(x_{n})\Vert \le \theta \Vert \bar{x}_{n}-x_{n} \Vert . \end{aligned}$$

(43)

Let

$$\begin{aligned} x_{n+1} = P_{X} \left( \bar{x}_{n} - \gamma _{n}(F_{n}(\bar{x}_{n})-F_{n}(x_{n})) \right) . \end{aligned}$$

(44)

If

$$\begin{aligned} \gamma _{n}\Vert F_{n}(x_{n+1})-F_{n}(x_{n})\Vert \le \rho \Vert x_{n+1}-x_{n}\Vert , \end{aligned}$$

(45)

then set $\sigma _{n} = \sigma _{0}$; otherwise, set $\sigma _{n}=\gamma _{n}$, where $\{C_{n}\}$ and $\{Q_{n}\}$ are the sequences of closed convex sets defined as in (35) and (36), respectively.

Since projections onto half-spaces can be directly calculated, the relaxed algorithm is more practical and easily implemented than Algorithm 6 [31, 32, 34, 53, 68]. Here, we may take

$$\frac{1}{2}\Vert x_{n}-P_{C_{n}}(x_{n})\Vert ^{2}+\frac{1}{2}\Vert Ax_{n}-P_{Q_{n}}(Ax_{n})\Vert ^{2} < \epsilon ,$$

or

$$\frac{1}{2}\Vert (I-P_{Q_{n}})Ax_{n}\Vert ^{2} < \epsilon $$

as the termination criterion.

We have the following convergence result for the Algorithm 7.

Theorem 11

[75, Theorem 3.1] Let $\{x_{n}\}$ be a sequence generated by Algorithm 7, $X$ be a nonempty closed convex set in $\mathbb {R}^{N}$ with a simple structure. if $X \cap \Gamma$ is nonempty, then $\{x_{n}\}$ converges to a solution of SFP.

Remark 4

In Algorithm 7, the set $X$ can be chosen to be any closed subset of $\mathbb {R}^{N}$ with a simple structure, provided it contains a solution of split feasibility problem. Dynamically changing it does not affect the convergence. For example, set $X_{n}= C_{n}$, then we get the following double-projection method:

$$ \bar{x}_{n} = P_{C_{n}} \left( x_{n}-\gamma _{n}F_{n}(x_{n}) \right) ,$$

$$x_{n+1} = P_{C_{n}} \left( \bar{x}_{n}-\gamma _{n}(F_{n}(\bar{x}_{n})-F_{n}(x_{n})) \right) ,$$

for $n = 0,1,2,\ldots$. This method differs from the modified relaxed CQ algorithm in [53]. Their method is in fact an extragradient method, with the second equation written as

$$x_{n+1} = P_{C_{n}} \left( x_{n}-\gamma _{n}F_{n}(\bar{x}_{n}) \right) . $$

3.4 Improved Relaxed CQ Methods

Li [45] proposed the following two improved relaxed CQ methods and shown how to determine the optimal step length. The detailed procedure of the new methods is presented as follows:

Let $C$, $Q$, $A$, $C_{n}$ and $Q_{n}$ be the same as in the Sect. 3.2 and $F_{n}$ be the same as defined in Sect. 3.3:

Algorithm 8

Initialization: choose $\mu \in (0,1)$, $\epsilon > 0$, $x_{0}\in \mathbb {R}^{N}$ and $n=0$.

Step 1. Prediction: Choose an $\alpha _{n}> 0$ such that

$$\begin{aligned} \bar{x}_{n} = P_{C_{n}} \left( x_{n}-\alpha _{n}F_{n}(x_{n}) \right) \end{aligned}$$

(46)

and

$$\begin{aligned} \alpha _{n}\Vert F_{n}(x_{n})-F_{n}(\bar{x}_{n})\Vert \le \mu \Vert x_{n}- \bar{x}_{n}\Vert \end{aligned}$$

(47)

Step 2. Stopping Criterion : compute

$$e_{n}(x_{n},\alpha _{n})=x_{n}-\bar{x}_{n}.$$

If $\Vert e_{n}(x_{n},\alpha _{n})\Vert \le \epsilon$, terminate the iteration with the approximate solution $x_{n}$. Otherwise, go to step 3.

Step 3. Correction: The new iterate $x_{n+1}$ is updated by

$$\begin{aligned} x_{n+1}=x^{*}_{n}=P_{C_{n}}(x_{n}-\beta _{n}\alpha _{n}F_{n}(\bar{x}_{n})), \end{aligned}$$

(48)

where

$$\begin{aligned} \beta _{n}=\delta _{n}\beta _{n}^{*}, \quad \beta ^{*}_{n} = \frac{\langle x_{n}-\bar{x}_{n},d_{n}(x_{n},\bar{x}_{n},\alpha _{n}) \rangle }{\Vert d_{n}(x_{n},\bar{x}_{n},\alpha _{n})\Vert ^{2}},\quad \delta _{n}\in [\delta _{L},\delta _{V}]\subseteq (0,2), \end{aligned}$$

(49)

and

$$\begin{aligned} d_{n}(x{_n},\bar{x}_{n},\alpha _{n})= x_{n}-\bar{x}_{n}-\alpha _{n}(F_{n}(x_{n})-F_{n}(\bar{x}_{n})). \end{aligned}$$

(50)

Set $n := n+1$ and go to step $1$.

Algorithm 9

: Initialization: Choose $\mu \in (0,1)$, $\epsilon > 0$, $x_{0}\in \mathbb {R^{N}}$ and $n = 0$.

Step 1. Prediction: Choose an $\alpha _{n}> 0$ such that

$$\begin{aligned} \bar{x}_{n} = P_{C_{n}}(x_{n}-\alpha _{n}F_{n}(x_{n})) \end{aligned}$$

(51)

and

$$\begin{aligned} \alpha _{n}\Vert F_{n}(x_{n})-F_{n}(\bar{x}_{n})\Vert \le \mu \Vert x_{n}-\bar{x}_{n}\Vert . \end{aligned}$$

(52)

Step 2. Stopping Criteria : Compute

$$e_{n}(x_{n},\alpha _{n})= x_{n}-\overline{x}_{n}.$$

If $\Vert e_{n}(x_{n},\alpha _{n})\Vert \le \epsilon$, terminate the iteration with the approximate solution $x_{n}$. Otherwise go to step 3.

Step 3. Correction: The corrector $x_{n}^{*}$ is given by the following equation

$$\begin{aligned} x_{n}^{*} = P_{C_{n}}(x_{n}-\beta _{n}\alpha _{n}F_{n}(\bar{x}_{n})), \end{aligned}$$

(53)

where

$$\begin{aligned} \beta _{n}= \gamma _{n}\beta ^{*}_{n}, \quad \beta _{n}^{*}= \frac{\langle x_{n}-\bar{x}_{n},d_{n}(x_{n},\bar{x}_{n},\alpha _{n}) \rangle }{\Vert d_{n}(x_{n},\bar{x}_{n},\alpha _{n})\Vert ^{2}}, \quad \delta _{n}\in [\delta _{L},\delta _{U}]\subseteq (0,2), \end{aligned}$$

(54)

and

$$\begin{aligned} d_{n}(x_{n},\bar{x}_{n},\alpha _{n})= x_{n}-\bar{x}_{n}-\alpha _{n}(F_{n}(x_{n})-F_{n}(\bar{x}_{n})). \end{aligned}$$

(55)

Step 4. Extension: The new iterate $x_{n+1}$ is updated by

$$\begin{aligned} x_{n+1}=P_{C_{n}}(x_{n}-\rho _{n}(x_{n}-x^{*}_{n})), \end{aligned}$$

(56)

where

$$\begin{aligned} \rho _{n}=\gamma _{n\rho ^{*}_{n}} ,\quad \rho _{n}^{*}=\frac{\Vert x_{n}-x^{*}_{n}\Vert ^{2} +\beta _{n}\alpha _{n}\langle x^{*}_{n}-\bar{x}_{n},F_{n}(\bar{x}_{n}) \rangle }{\Vert x_{n}-x^{*}_{n}\Vert ^{2}}, \quad \gamma _{n}\in [\gamma _{L},\gamma _{U}]\subseteq (0,2).\nonumber \\ \end{aligned}$$

(57)

Set $n := n+1$ and go to step $1$.

Remark 5

In the prediction step, if the selected $\alpha _{n}$ satisfies $0< \alpha _{n}\le \mu /L$ ($L$ is the largest eigenvalue of the matrix $A^{\top }A$), from [45, Lemma 2.3], we have

$$\begin{aligned} \alpha _{n}\Vert F_{n}(x_{n})-F_{n}(\bar{x}_{n})\Vert \le \alpha _{n}L\Vert x_{n}-\bar{x}_{n}\Vert \le \mu \Vert x_{n}-\bar{x}_{n}\Vert , \end{aligned}$$

(58)

and thus condition (47) or (52) is satisfied. Without loss of generality, we can assume that $\inf \{\alpha _{n}\}=\alpha _{\min }> 0$. Since we do not know the value of $L>0$ but it exist, in practice, a self-adaptive scheme is adopted to find such a suitable $\alpha _{n}> 0$. For given $x_{n}$ and a trial $\alpha _{n}> 0$, along with the value of $F_{n}(x_{n})$, we set the trial $\overline{x}_{n}$ as follows:

$$\bar{x}_{n} = P_{C_{n}}(x_{n}-\alpha _{n}F_{n}(x_{n})).$$

Then calculate

$$ r_{n}:=\frac{\alpha _{n}\Vert F_{n}(x_{n})-F_{n}(\bar{x}_{n})\Vert }{\Vert x_{n}-\bar{x}_{n}\Vert },$$

if $r_{n}\le \mu$, the trial $\bar{x}_{n}$ is accepted as predictor; otherwise, reduce $\alpha _{n}$ by $\alpha _{n}:= .9\mu \alpha _{n}^{*} \min (1,1/r_{n})$ to get a new smaller trial $\alpha _{n}$ and repeat this procedure. In the case that the predictor has been accepted, a good initial trial $\alpha _{n+1}$ for the next iteration is prepared by the following strategy:

$$\begin{aligned} \alpha _{n+1}= {\left\{ \begin{array}{ll} \frac{0.9}{r_{n}}\alpha _{n} &{}\text {if}~ r_{n} \le \nu , \\ \alpha _{n} &{}\text {otherwise,} \end{array}\right. } \end{aligned}$$

(59)

(usually $\nu \in [0.4,0.5]$).

Condition (47) or (52) ensure that $\alpha _{n}\Vert F_{n}(x_{n})-F_{n}(\bar{x}_{n})\Vert$ is smaller than $\Vert x_{n}-\bar{x}_{n}\Vert$, however, too small $\alpha _{n}\Vert F_{n}(x_{n})-F_{n}(\bar{x}_{n})\Vert$ leads to slow convergence. The proposed adjusting strategy (59) is intended to avoid such a case as indicated in [35, 36]. Actually it is very important to balance the quantity of $\alpha _{n}\Vert F_{n}(x_{n})-F_{n}(\bar{x}_{n})\Vert$ and $\Vert x_{n}-\bar{x}_{n}\Vert$ in practical computation. Note that there are at least two times to utilize the value of function in the prediction step: one is $F_{n}(x_{n})$, and the other is $F_{n}(\bar{x}_{n})$ for testing whether the condition (47) or (52) holds. When $\alpha _{n}$ is selected well enough, $\bar{x}_{n}$ will be accepted after only one trial and in this case, the prediction step exactly utilizing the value of concerned function twice in one iteration.

It follow from [45, Relation (3.16)] and [45, Relation (3.27)] that for Algorithm 8, there exists a constant $\tau _{1} > 0$ such that

$$\begin{aligned} \Vert x_{n+1} - x^{*}\Vert ^{2} \le \Vert x_{n} - x^{*}\Vert ^{2}-\tau _{1}\cdot \Vert x_{n}-\bar{x}_{n}\Vert ^{2}. \end{aligned}$$

(60)

From [45, Relation (3.38)], for Algorithm 9, there exist a constant $\tau _{2} > 0$ such that

$$\begin{aligned} \Vert x_{n+1}-x^{*}\Vert ^{2} \le \Vert x_{n}-x^{*}\Vert ^{2} - \tau _{2}\cdot \{\Vert x_{n}-\bar{x}_{n}\Vert ^{2}+\Vert x_{n}-x^{*}_{n}\Vert ^{2}\}. \end{aligned}$$

(61)

Finally, we have the following convergence result of the proposed methods.

Theorem 12

[45] Let $\{x_{n}\}$ be a sequence generated by the proposed methods (Algorithms 8 and 9), $\{\alpha _{n}\}$ be a positive sequence and $\inf {\{\alpha _{n}\}} = \alpha _{\min }> 0$. If the solution set of the SFP is nonempty, then $\{x_{n}\}$ converges to a solution of the SFP.

4 Extragradient Methods for Common Solution of Split Feasibility and Fixed Point Problems

Korplevich [40] introduced the so-called extragradient method for finding a solution of a saddle point problem. She/He proved that the sequences generated by this algorithm converge to a saddle point. Motivated by the idea of an extragradient method,

Ceng et al. [10] introduced and analyzed an extragradient method with regularization for finding a common element of the solution set $\Gamma$ of the split feasibility problem (SFP) and the set Fix($S$) of the fixed points of a nonexpansive mapping $S$ in the setting of Hilbert spaces. Combining the regularization method and extragradient method due to Nadezhkina and Takahashi [50], they proposed an iterative algorithm for finding an element of Fix($S$) $\cap \Gamma$. They proved that the sequences generated by the proposed method converges weakly to an element $z \in$ Fix($S$) $\cap \Gamma$.

On the other hand, Ceng et al. [11] introduced relaxed extragradient method for finding a common element of the solution set $\Gamma$ of the SFP and the set Fix($S$) of fixed points of a nonexpansive mapping $S$ in the setting of Hilbert spaces. They combined Mann’s iterative method and extragradient method to propose relaxed extragradient method. The weak convergence of the sequences generated by the proposed method is also studied. The relaxed extragradient method with regularization is studied by Deepho and Kumam [26]. They considered the set $S$ of fixed points of a asymptotically quasi-nonexpansive and Lipschtiz continuous mapping in the setting of Hilbert spaces. They obtained the weak convergence result for their method.

Recently, Ceng et al. [12] proposed three different kinds of iterative methods for computing the common element of the solution set $\Gamma$ of the split feasibility problem (SFP) and the set Fix($S$) of the fixed points of a nonexpansive mapping in the setting of Hilbert spaces. By combining Mann’s iterative method and the extragradient method, they first proposed Mann-type extragradient-like algorithm for finding an element of the set Fix($S$) $\cap \Gamma$. Moreover, they derived the weak convergence of the proposed algorithm under appropriate conditions. Second, they combined Mann’s iterative method and the viscosity approximation method to introduce Mann-type viscosity algorithm for finding an element of the Fix($S$) $\cap \Gamma$. The strong convergence of the sequences generated by the proposed algorithm to an element of the set Fix($S$) $\cap \Gamma$ under mild conditions is also proved. Finally, by combining Mann’s iterative method and the relaxed $CQ$ methods, they introduced Mann-type relaxed $CQ$ algorithm for finding an element of the set Fix($S$) $\cap \Gamma$. They also established a weak convergence result for the sequences generated by the proposed Mann type relaxed $CQ$ algorithm under appropriate assumptions.

Very recently, Li et al. [44] and Zhu et al. [76] developed iterative methods for finding the common solutions of a SFP and a fixed point problem.

In this section, we discuss extragradient method with regularization, relaxed extragradient method and relaxed extragradient method with regularization. We also mention the convergence results for these methods. Two examples are presented to illustrate these methods. We present Mann-type extragradient-like algorithm, Mann-type viscosity algorithm, and Mann-type relaxed $CQ$ algorithm for computing an element of the set Fix($S$) $\cap \Gamma$. The weak convergence results for these methods are presented. Some methods are illustrated by some examples.

4.1 An Extragradient Method

Throughout this section, we assume that $\Gamma \cap$ Fix($S$) $\ne \emptyset$.

We present the following extragradient method with regularization for finding a common element of the solution set $\Gamma$ of the split feasibility problem and the set Fix($S$) of the fixed points of a nonexpansive mapping $S$. We also mention the weak convergence of this method.

Theorem 13

[10, Theorem 3.1] Let $C$ be a nonempty closed convex subset of a real Hilbert space $\fancyscript{H}_{1}$ and $S:C\rightarrow C$ be a nonexpansive mapping such that Fix($S$) $\cap \Gamma \ne \emptyset$. Let $\{x_{n}\}$ and $\{y_{n}\}$ be the sequences in $C$ generated by the following extragradient algorithm:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{0}=x\in C \quad \mathrm{chosen}\,\,\mathrm{arbitrarily},\\ y_{n}=P_{C}(I-\lambda _{n}\nabla f_{\alpha _{n}})x_{n},\\ x_{n+1}=\beta _{n}x_{n} + (1-\beta _{n})SP_{C}(x_{n}-\lambda _{n}\nabla f_{\alpha _{n}}(y_{n})),\quad \mathrm{for}\,\,\mathrm{all}\,n \ge 0, \end{array}\right. } \end{aligned}$$

(62)

where $\nabla f_{\alpha _{n}} = \alpha _{n}I+ A^{*}(I-P_{Q})A$, $\sum _{n=0}^{\infty } a_{n} < \infty$, $\{\lambda _{n}\} \subset [a , b]$ for some $a, b \in \left( 0,\frac{1}{\Vert A\Vert ^{2}}\right)$ and $\{\beta _{n}\} \subset [c,d]$ for some $c, d \in (0,1)$. Then, both the sequences $\{x_{n}\}$ and $\{y_{n}\}$ converge weakly to an element $\bar{x} \in$ Fix($S$) $\cap \Gamma$.

Furthermore, by utilizing [50, Theorem 3.1], we can immediately obtain the following weak convergence result.

Theorem 14

[10, Theorem 3.2] Let $\fancyscript{H}_{1}, C$ and $S$ be the same as in Theorem 13. Let $\{x_{n}\}$ and $\{y_{n}\}$ be the sequences in $C$ generated by the following Nadezhkina and Takahashi extragradient algorithm:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{0} = x\in C \quad \mathrm {chosen}\, \mathrm{arbitrarily,}\\ y_{n} = P_{C}(I-\lambda _{n}\nabla f)x_{n},\\ x_{n+1}=\beta _{n}x_{n}+ (1-\beta _{n})SP_{C}(x_{n}-\lambda _{n}\nabla f(y_{n})), \quad \mathrm{{for}}\,\mathrm{{all}} \, n \ge 0,\\ \end{array}\right. } \end{aligned}$$

(63)

where $\nabla f = A^{*}(I-P_{Q})A$, $\{\lambda _{n}\} \subset [a, b]$ for some $a, b \in \left( 0,\frac{1}{\Vert A\Vert ^{2}}\right)$ and $\{\beta _{n}\} \subset [c, d]$ for some $c, d \in (0,1)$. Then, both the sequences $\{x_{n}\}$ and $\{y_{n}\}$ converge weakly to an element $\bar{x} \in$ Fix($S$) $\cap \Gamma$.

By utilizing Theorem 13, we obtain the following results.

Corollary 1

[10, Corollary 3.2] Let $C = \fancyscript{H}_{1}$ be a Hilbert space and $S :\fancyscript{H}_{1}\rightarrow \fancyscript{H}_{1}$ be a nonexpansive mapping such that $\text{ Fix }(S) \cap (\nabla f)^{-1}0 \ne \emptyset$. Let $\{x_{n}\}$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{0} = x \in C \quad \mathrm {chosen} \, \mathrm{arbitrarily},\\ x_{n+1} = \beta _{n}x_{n}+(1-\beta _{n})S(x_{n}-\lambda _{n}\nabla _{n} f_{\alpha _{n}} (I-\lambda _{n}\nabla f_{\alpha _{n}})x_{n}), \quad \mathrm{{for}}\,\mathrm{{all}} \, n\ge 0,\\ \end{array}\right. } \end{aligned}$$

(64)

where $\Sigma _{n=0}^{\infty } a_{n} < \infty$, $\{ \lambda _{n}\} \subset [a,b]$ for some $a, b \in \left( 0,\frac{1}{\Vert A\Vert ^{2}}\right)$ and $\{\beta _{n}\} \subset [c,d]$ for some $c, d \in (0,1)$. Then, the sequence $\{x_{n}\}$ converges weakly to $\bar{x} \in Fix($S$)\cap (\nabla f)^{-1}$.

For the definition of maximal monotone operator and resolvent operator, see Chap. 6.

Corollary 2

[10, Corollary 3.3] Let $C = \fancyscript{H}_{1}$ be a Hilbert space and $B : \fancyscript{H}_{1}\rightarrow 2^{\fancyscript{H}_{1}}$ be a maximal monotone mapping such that $B^{-1}0 \cap (\nabla f)^{-1}0 \ne \emptyset$. Let $j^{B}_{r}$ be the resolvent of $B$ for each $r > 0$. Let $\{x_{n}\}$ be a sequence generated by

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{0} = x \in C \quad \mathrm {chosen \, arbitrarily},\\ x_{n+1} = \beta _{n}x_{n} + (1-\beta _{n})j^{B}_{r}(x_{n}-\lambda _{n}\nabla f_{\alpha _{n}} (I-\lambda _{n}\nabla f_{\alpha _{n}})x_{n}),\quad \forall \, n\ge 0, \end{array}\right. } \end{aligned}$$

(65)

where $\Sigma _{n=0}^{\infty } a_{n} < \infty$, $\{ \lambda _{n}\} \subset [a,b]$ for some $a, b \in \left( 0,\frac{1}{\Vert A\Vert ^{2}}\right)$ and $\{\beta _{n}\} \subset [c,d]$ for some $c, d \in (0,1)$. Then, the sequence $\{x_{n}\}$ converges weakly to $\bar{x} \in B^{-1}0 \cap (\nabla f)^{-1}$.

Example 5

Let $C = Q = [0,1]$ and $S: C \rightarrow C$ be defined as

$$ S x = \frac{x(x+1)}{4}, \quad \text {for all } x \in C.$$

Then, $S$ is a nonexpansive mapping and $0 \in$ Fix($S$). Let $A x = x$ be a bounded linear operator. Let $\alpha _{n} = \frac{1}{n^{2}}$, $\beta _{n}= \frac{1}{2n}$ and $\lambda _{n}=\frac{1}{2(n+1)}$. All the conditions of Theorem 13 are satisfied. The sequences $\{x_{n}\}$ and $\{y_{n}\}$ generated by the scheme (62) starting with $x_{1} = 0.1$. Then, we observe that these sequences converge to an element $0 \in$ Fix($S$) $\cap \Gamma$ (Figs. 5 and 6).

Fig. 5

Convergence of $\{y_{n}\}$ in Example 5

We did the computation in Matlab R2010 and got the solution $0$ after 8th iterates (Figs. 5 and 6, Table 5).

Fig. 6

Convergence of $\{x_{n}\}$ in Example 5

4.2 Relaxed Extragredient Methods

In this section, we present a relaxed extragradiend method and study the weak convergence of the sequences generated by this method. We also present a relaxed extragradiend method with regularization for finding a common element of the solution set $\Gamma$ of the SFP and the set Fix($S$) of fixed points of a asymptotically quasi-nonexpansive and Lipschtiz continuous mapping in the setting of Hilbert spaces. The weak convergence of the sequences generated by this method is also presented.

Table 5 Convergence of $\{x_{n}\}$ and $\{y_{n}\}$ in Example 5

Theorem 15

[11, Theorem 3.2] Let $C$ be a nonempty closed and convex subset of a Hilbert space $\fancyscript{H}_{1}$ and $S:C\rightarrow C$ be a nonexpansive mapping such that $\text {Fix(S)} \cap \Gamma \ne \emptyset$. Assume that $0< \lambda < \frac{2}{\Vert A\Vert ^{2}}$, and let $\{x_{n}\}$ and $\{y_{n}\}$ be the sequences in $C$ generated by the following Mann-type extragradient-like algorithm:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{0} = x\in C \quad \mathrm {chosen \, arbitrarily},\\ y_{n} = (1-\beta _{n})x_{n}+\beta _{n}P_{C}(x_{n}-\lambda \nabla f_{\alpha _{n}}(x_{n})),\\ x_{n+1} = \gamma _{n}x_{n}+(1-\gamma _{n})SP_{C}(y_{n}-\lambda \nabla f_{\alpha _{n}}(y_{n})), \quad \mathrm{{for}}\, \mathrm{all} \, n\ge 0, \end{array}\right. } \end{aligned}$$

(66)

where $\nabla f_{\alpha _{n}} = \nabla f + \alpha _{n} I = A^{*} (I-P_{Q})A + \alpha _{n} I$ and the sequences of parameters $\{\alpha _{n}\}$, $\{\beta _{n}\}$, $\{\gamma _{n}\}$ satisfy the following conditions:

• (i) $\sum _{n=0}^{\infty } \alpha _{n} < \infty$;

• (ii) $\{\beta _{n}\} \subset [0,1]$ and $0 < \displaystyle \liminf _{n\rightarrow \infty }\beta _{n} \le \displaystyle \limsup _{n\rightarrow \infty }\beta _{n} < 1$;

• (iii) $\{\gamma _{n}\} \subset [0,1]$ and $0 < \displaystyle \liminf _{n\rightarrow \infty }\gamma _{n} \le \displaystyle \limsup _{n\rightarrow \infty }\gamma _{n} < 1$.

Then, both the sequences $\{x_{n}\}$ and $\{y_{n}\}$ converge weakly to an element $z\in$ Fix($S$) $\cap \Gamma$.

The following relaxed extragradiend method with regularization for finding a common element of the solution set $\Gamma$ of the SFP and the set Fix($S$) of fixed points of a asymptotically quasi-nonexpansive and Lipschtiz continuous mapping in the setting of Hilbert spaces is proposed and studied by Deepho and Kumam [26]. They also studied the weak convergence of the sequences generated by this method.

Theorem 16

[26, Theorem 3.2] Let $C$ be a nonempty closed and convex subset of a Hilbert space $\fancyscript{H}_{1}$ and $S:C\rightarrow C$ be a uniformly $L$-Lipschitz continuous and asymptotically quasi-nonexpansive mapping such that $\text {Fix(S)} \cap \Gamma \ne \emptyset$. Assume that $\{ k_{n} \} \in [0,\infty )$ for all $n \in \mathbb {N}$ such that $\sum _{n=1}^{\infty } (k_{n} - 1) < \infty$. Let $\{x_{n}\}$ and $\{y_{n}\}$ be the sequences in $C$ generated by the following algorithm:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{0} = x\in C \quad chosen\,\,arbitrarily,\\ y_{n} = P_{C}(I-\lambda _{n} \nabla f_{\alpha _{n}}(x_{n})),\\ x_{n+1} = \beta _{n} x_{n} + (1-\beta _{n}) S^{n}(y_{n}), \quad for\,\,all\,\,n\ge 0, \end{array}\right. } \end{aligned}$$

(67)

where $\nabla f_{\alpha _{n}} = \nabla f + \alpha _{n} I = A^{*} (I-P_{Q})A + \alpha _{n} I$, $S^{n}= \underbrace{S\circ S \circ \dots \circ S}_\mathrm{n \,times}$. The sequences of parameters $\{\alpha _{n}\}$, $\{\beta _{n}\}$, $\{\lambda _{n}\}$ satisfy the following conditions:

• (i) $\sum _{n=1}^{\infty } \alpha _{n} < \infty$;

• (ii) $\{\lambda _{n}\} \subset [a,b]$ for some $a,b \in \left( 0, \frac{1}{\Vert A \Vert ^{2}} \right)$ and $\sum _{i=1}^{\infty } | \lambda _{n+1} - \lambda _{n} | < \infty$;

• (iii) $\{\beta _{n}\} \subset [c,d]$ for some $c,d \in (0,1)$.

Then, both the sequences $\{x_{n}\}$ and $\{y_{n}\}$ converge weakly to an element $z\in$ Fix($S$) $\cap \Gamma$.

5 Mann-Type Iterative Methods for Common Solution of Split Feasibility and Fixed Point Problems

In this section, we present three different kinds of Mann-type iterative methods for finding a common element of the solution set $\Gamma$ of the split feasibility problem and the set $\text{ Fix }(S)$ of fixed points of a nonexpansive mapping $S$ in the setting of infinite dimensional Hilbert spaces.

By combining Mann’s iterative method and the extragradient method, we first propose Mann-type extragradient-like algorithm for finding an element of the set ${\text{ Fix }(S) \cap \Gamma }$; moreover, we drive the weak convergence of the proposed algorithm under appropriate conditions. Second, we combine Mann’s iterative method and the viscosity approximation method to introduce Mann-type viscosity algorithm for finding an element of the $\text{ Fix }(S) \cap \Gamma$; moreover, we derive the strong convergence of the sequences generated by the proposed algorithm to an element of the set $\text{ Fix }(S) \cap \Gamma$ under mild conditions. Finally, by combining Mann’s iterative method and the relaxed $CQ$ methods, we introduce Mann type relaxed $CQ$ algorithm for finding an element of the set $\text{ Fix }(S) \cap \Gamma$. We also establish a weak convergence result for the sequences generated by the proposed Mann-type relaxed $CQ$ algorithm under appropriate assumptions.

5.1 Mann-Type Extragradient-Like Algorithm

Let $C$ and $Q$ be nonempty closed convex subset of Hilbert spaces $\fancyscript{H}_{1}$ and $\fancyscript{H}_{2}$, respectively, and $A \in B(\fancyscript{H}_{1}, \fancyscript{H}_{2})$. By combining Mann’s iterative method and the extragradient method, Ceng et al. [12] proposed the following Mann-type extragradient-like algorithm for finding an element of the set Fix($S$) $\cap \Gamma$ (Figs. 7 and 8):

Fig. 7

Convergence of $\{y_{n}\}$ in Example 6

The sequences $\{x_{n}\}$ and $\{y_{n}\}$ generated by the following iterative scheme:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{0} = x\in \fancyscript{H}_{1} \quad \mathrm {chosen \, arbitrarily},\\ y_{n} = (1-\beta _{n})x_{n} +\beta _{n}P_{C}(1-\lambda _{n}A^{*}(I-P_{Q})A)x_{n},\\ x_{n+1} = \alpha _{n}x_{n}+(1-\alpha _{n})SP_{C}(I-\lambda _{n}A^{*}(I-P_{Q})A)y_{n}, \quad \mathrm {for \, all } \, n\ge 0,\\ \end{array}\right. } \end{aligned}$$

(68)

where the sequences of parameters $\{\alpha _{n}\}$, $\{\beta _{n}\}$ and $\{\lambda _{n}\}$ satisfy some appropriate conditions.

The following result provides the weak convergence of the above scheme.

Theorem 17

[12, Theorem 3.2] Let $S: C \rightarrow C$ be a nonexpansive mapping such that Fix($S$) $\cap \Gamma \ne \emptyset$. Let $\{x_{n}\}$ and $\{y_{n}\}$ be the sequences by the Mann-type extragradient-like algorithm (68), where the sequences of parameters $\{\alpha _{n}\}$, $\{\beta _{n}\}$ and $\{\lambda _{n}\}$ satisfies the following conditions:

• (i) $\{\alpha _{n}\} \subset [0,1]$ and $0 < \displaystyle \liminf _{n\rightarrow \infty } \alpha _{n} \le \displaystyle \limsup _{n \rightarrow \infty }< 1$;

• (ii) $\{\beta _{n}\} \subset [0,1]$ and $\displaystyle \liminf _{n\rightarrow \infty }\beta _{n} > 0$;

• (iii) $\{\lambda _{n}\} \subset \left( 0,\frac{2}{\Vert A\Vert ^{2}}\right)$ and $0 < \displaystyle \liminf _{n\rightarrow \infty } \lambda _{n} \le \displaystyle \limsup _{n\rightarrow \infty }\lambda _{n} < \frac{2}{\Vert A\Vert ^{2}}$.

Then, both the sequences $\{x_{n}\}$ and $\{y_{n}\}$ converges weakly to an element $z \in$ Fix(S) $\bigcap \Gamma$, where

$$ z = \Vert \cdot \Vert - \lim _{n\rightarrow \infty }P_{Fix\mathrm{(}S\mathrm{)} \cap \Gamma } x_{n}.$$

We illustrate the above scheme and theorem by presenting the following example.

Example 6

Let $C = Q = [-1,1]$ be closed convex set in $\mathbb {R}$. Let $S: C \rightarrow C$ be a mapping defined by

$$ S x = \frac{(x+1)^{2}}{4}, \quad \text {for all } x \in C.$$

Then, clearly $S$ is a nonexpansive map and $1 \in$ Fix($S$) $\cap \Gamma$. Let $A x = x$ be a bounded linear operator. If we choose $\alpha _{n} = \frac{1}{20}-\frac{1}{n}$ and $\beta _{n} = 1-\frac{1}{2n}$, then all the conditions of Theorem 17 are satisfied. We choose the initial point $x_{1} = 2$ and perform the iterative scheme in Matlab R2010. We obtain the solution after 6th iteration (Figs. 7 and 8, Table 6).

5.2 Mann-Type Viscosity Algorithm

Ceng et al. [12] modified the Mann-type extragradient-like algorithm, proposed in the last section, to obtain the strong convergence of the sequences. This modification is of viscosity approximation nature [9, 22, 48].

Theorem 18

[12, Theorem 4.1] Let $f:C \rightarrow C$ be a $\rho$-contraction with $\rho \in [0,1)$ and $S:C\rightarrow C$ be a nonexpansive mapping such that $\text{ Fix }(S) \cap \Gamma \ne \emptyset$. Let $\{x_{n}\}$ and $\{y_{n}\}$ be the sequences generated by the following Mann-type viscosity algorithm:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{0} = x_{1}\in \fancyscript{H}_{1} \quad \mathrm {chosen \, arbitrarily},\\ y_{n} = P_{C}(I-\lambda _{n}A^{*}(I-P_{Q})A)x_{n},\\ z_{n} = P_{C}(I-\lambda _{n}A^{*}(I-P_{Q})A)y_{n},\\ x_{n+1} = \theta _{n}f(y_{n})+\mu _{n}x_{n}+\nu _{n}z_{n}+\delta _{n}Sz_{n},\, \forall \, n\ge 0,\\ \end{array}\right. } \end{aligned}$$

(69)

where the sequences of parameters $\{\theta _{n}\}$, $\{\mu _{n}\}$, $\{\nu _{n}\}$, $\{\delta _{n}\} \subset [0,1]$ and $\{\lambda _{n}\} \subset \left( 0,\frac{2}{\Vert A\Vert ^{2}}\right)$ satisfy the following conditions:

• (i) $\theta _{n}+\mu _{n} + \nu _{n}+\delta _{n} = 1$;

• (ii) $\displaystyle \lim _{n\rightarrow \infty } \theta _{n}=0$ and $\Sigma _{n=0}^{\infty }\theta _{n} =\infty$;

• (iii) $\displaystyle \liminf _{n\rightarrow \infty } \delta _{n} > 0$;

• (iv) $\displaystyle \lim _{n\rightarrow \infty }\left( \frac{\nu _{n+1}}{1- \mu _{n+1}}-\frac{\nu _{n}}{1-\mu _{n}}\right) = 0$;

• (v) $0 < \displaystyle \liminf _{n\rightarrow \infty }\lambda _{n}\le \displaystyle \limsup _{n\rightarrow \infty }\lambda _{n} < \frac{2}{\Vert A\Vert ^{2}}$ and $\displaystyle \lim _{n\rightarrow \infty }(\lambda _{n}-\lambda _{n+1})=0$.

Then, both the sequences $\{x_{n}\}$ and $\{y_{n}\}$ converge strongly to $x^{*}\in \text{ Fix }(S) \cap \Gamma$ which is also a unique solution of the variational inequality (VI):

$$\langle (I-f)x^{*},x-x^{*}\rangle \ge 0, \quad \text {for all } x \in \text{ Fix }(S) \cap \Gamma .$$

In other words, $x^{*}$ is a unique fixed point of the contraction $P_{\text{ Fix }(S) \cap \Gamma }f,x^{*}= (P_{\text{ Fix }(S) \cap \Gamma } f)x^{*}$.

Fig. 8

Convergence of $\{x_{n}\}$ in Example 6

Table 6 Convergence of $\{ x_{n} \}$ and $\{ y_{n} \}$ in Example 6

5.3 Mann-Type Relaxed CQ Algorithm

As pointed out earlier, the CQ algorithm (Algorithm 2) involves two projections $P_{C}$ and $P_{Q}$ and hence might hard to be implemented in the case where one of them fails to have closed-form expression. Thus, in [65] it was shown that if $C$ and $Q$ are level sets of convex functions, then the projections onto half-spaces are just needed to make the $CQ$ algorithm implementable in this case. Inspired by relaxed $CQ$ algorithm, Ceng et al. [12] proposed the following Mann-type relaxed $CQ$ algorithm via projections onto half-spaces.

Define the closed convex sets $C$ and $Q$ as the level sets:

$$\begin{aligned} C = \{ x \in \fancyscript{H}_{1} : c(x) \le 0 \} \quad \text {and} \quad Q = \{ x \in \fancyscript{H}_{2} : q(x) \le 0 \}, \end{aligned}$$

(70)

where $c : \fancyscript{H}_{1} \rightarrow \mathbb {R}$ and $q : \fancyscript{H}_{2} \rightarrow \mathbb {R}$ are convex functions. We assume that $c$ and $q$ are subdifferentiable on $C$ and $Q$, respectively, namely, the subdifferentials

$$ \partial c(x) = \{ z \in \fancyscript{H}_{1} : c(u) \ge c(x) + \langle u-x, z \rangle ,~ \forall u \in \fancyscript{H}_{1} \} \ne \emptyset $$

for all $x \in C$, and

$$ \partial q(x) = \{ w \in \fancyscript{H}_{2} : q(v) \ge q(y) + \langle v-y, w \rangle ,~ \forall v \in \fancyscript{H}_{1} \} \ne \emptyset $$

for all $y \in Q$. We also assume that $c$ and $q$ are bounded on the bounded sets. Note that this condition is automatically satisfied when the Hilbert spaces are finite dimensional. This assumption guarantees that if $\{ x_{n} \}$ is a bounded sequence in $\fancyscript{H}_{1}$ (respectively, $\fancyscript{H}_{2}$) and $\{ x_{n}^{*} \}$ is another sequence in $\fancyscript{H}_{1}$ (respectively, $\fancyscript{H}_{2}$) such that $x_{n}^{*} \in \partial c(x_{n})$ (respectively, $x_{n}^{*} \in \partial q(x_{n})$) for each $n \ge 0$, then $\{ x_{n}^{*} \}$ is bounded.

Let $S:\fancyscript{H}_{1} \rightarrow \fancyscript{H}_{1}$ be a nonexpansive mapping. Assume that the sequences of parameters $\{\alpha _{n}\}$, $\{\beta _{n}\}$ and $\{\lambda _{n}\}$ satisfy the following conditions:

• (i) $\{\alpha _{n}\} \subset [0,1]$ and $0 < \displaystyle \liminf _{n\rightarrow \infty } \alpha _{n} \le \displaystyle \limsup _{n \rightarrow \infty } \alpha _{n} < 1$;

• (ii) $\{\beta _{n}\} \subset [0,1]$ and $\displaystyle \liminf _{n\rightarrow \infty }\beta _{n} > 0$;

• (iii) $\{ \lambda _{n}\}\subset \left( 0,\frac{2}{\Vert A\Vert ^{2}}\right)$ and $0 < \displaystyle \liminf _{n\rightarrow \infty } \le \displaystyle \limsup _{n\rightarrow \infty } \lambda _{n} < \frac{2}{\Vert A\Vert ^{2}}.$

Let $\{x_{n}\}$ and $\{y_{n}\}$ be the sequence defined by the following Mann-type relaxed $CQ$ algorithm:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{0} = x \in \fancyscript{H}_{1} \quad \mathrm {chosen \, arbitrarily},\\ y_{n} = (1-\beta _{n})x_{n}+\beta _{n}P_{C_{n}}(I- \lambda _{n}A^{*}(I-P_{Q_{n}})A)x_{n},\\ x_{n+1} = \alpha _{n}x_{n}+(1-\alpha _{n})SP_{C_{n}}(I-\lambda _{n}A^{*}(I-P_{Q_{n}})A)y_{n}, \quad \mathrm {for \, all} \, n\ge 0, \end{array}\right. } \end{aligned}$$

(71)

where $\{C_{n}\}$ and $\{Q_{n}\}$ are the sequences of closed convex sets defined as follows:

$$\begin{aligned} C_{n} = \{ x \in \fancyscript{H}_{1} : c(x_{n}) + \langle \xi _{n}, x-x_{n} \rangle \le 0 \}, \end{aligned}$$

(72)

where $\xi _{n} \in \partial c(x_{n})$, and

$$\begin{aligned} Q_{n} = \{ y \in \fancyscript{H}_{2} : q(Ax_{n}) + \langle \eta _{n}, y-A x_{n} \rangle \le 0 \}, \end{aligned}$$

(73)

where $\eta _{n} \in \partial q(Ax_{n})$.

It can be easily seen that $C \subset C_{n}$ and $Q \subset Q_{n}$ for all $n \ge 0$. Also, note that $C_{n}$ and $Q_{n}$ are half-spaces; thus, the projections $P_{C_{n}}$ and $P_{Q_{n}}$ have closed-form expressions.

Ceng et al. [12] established the following weak convergence theorem for the sequences generated by the scheme (71).

Theorem 19

[12, Theorem 5.1] Suppose that Fix(S) $\cap \Gamma \ne \emptyset$. Then, the sequences $\{x_{n}\}$ and $\{y_{n}\}$ generated by the algorithm (71) converge weakly to an element $z \in \text{ Fix }(S) \cap \Gamma$, where

$$ z = \Vert \cdot \Vert - \lim _{n \rightarrow \infty } P_{\text{ Fix }(S) \bigcap \Gamma } x_{n}.$$

6 Solution Methods for Multiple-Sets Split Feasibility Problems

For each $i = 1,2,\ldots ,t$ and each $j =1,2,\ldots ,r$, let $C_{i} \subseteq \fancyscript{H}_{1}$ and $Q_{j} \subseteq \fancyscript{H}_{2}$ be nonempty closed convex set in Hilbert spaces $\fancyscript{H}_{1}$ and $\fancyscript{H}_{2}$, respectively. Let $A \in B(\fancyscript{H}_{1}, \fancyscript{H}_{2})$. The convex feasibility problem (CFP) is to find a vector $x^{*}$ such that

$$\begin{aligned} x^{*} \in \bigcap _{i=1}^{t} C_{i}. \end{aligned}$$

(74)

During the last decade, it received a lot of attention due to its applications in approximation theory, image recovery and signal processing, optimal control, biomedical engineering, communications, and geophysics, see, for example, [7, 17, 58] and the references therein.

Consider the multiple-sets split feasibility problem (MSSFP) of finding a vector $x^{*}$ satisfying

$$\begin{aligned} x^{*} \in C := \bigcap _{i=1}^{t} C_{i} \quad \text { such that } \quad A x^{*} \in Q := \bigcap _{j=1}^{r} Q_{j}. \end{aligned}$$

(75)

As we have seen in the first section that this problem can be a unified model of several practical inverse problems, namely, image reconstruction, signal processing, an inverse problem of intensity-modulated radiation therapy, etc. Of course, when $i=j=1$, MSSFP reduces to SFP.

The MSSFP (75) can be viewed as a special case of the CFP (74). In fact, (75) can be rewritten as

$$\begin{aligned} x^{*} \in \bigcap _{i=1}^{t+r} C_{i}, \quad \text {where } C_{t+j} := \{ x \in \fancyscript{H}_{1} : A^{-1} x \in Q_{j} \}, \quad 1 \le j \le r. \end{aligned}$$

(76)

However, the methodologies for studying the MSSFP (75) are different from those for the CFP (74) in order to avoid usage of the inverse $A^{-1}$. In other words, the methods for solving CFP (74) may not be applied to solve the MSSFP (75) without involving the inverse $A^{-1}$. The CQ Algorithm 2 is such an example where only the operator $A$ (not the inverse $A^{-1}$) is relevant.

In view of Proposition 7, one can see that MSSFP (75) is equivalent to a common fixed point problem of finitely many nonexpansive mappings. Indeed, decompose MSSFP (75) into $N$ subproblems ($1 \le i \le t$):

$$\begin{aligned} x^{*}_{i} \in C_{i} \quad \text { such that } \quad A x^{*}_{i} \in Q := \bigcap _{j=1}^{r} Q_{j}. \end{aligned}$$

(77)

For each $i = 1,2, \ldots ,t$, define a mapping $T_{i}$ by

$$\begin{aligned} T_{i}(x) = P_{C_{i}} \left( I - \gamma _{i} \nabla f \right) x = P_{C_{i}} \left( I - \gamma _{i} \sum _{j=1}^{r} \beta _{j} A^{*} (I - P_{Q_{j}}) A \right) x_{i}, \end{aligned}$$

(78)

where $f$ is defined by

$$\begin{aligned} f(x) = \frac{1}{2} \sum _{j=1}^{r} \beta _{j} \Vert A x - P_{Q_{j}} A x \Vert ^{2}, \end{aligned}$$

(79)

with $\beta _{j} > 0$ for all $j = 1,2, \ldots ,t$. Note that the gradient $\nabla f$ of $f$ is

$$\begin{aligned} \nabla f(x) = \sum _{j=1}^{r} \beta _{j} A^{*} \left( I - P_{Q_{j}} \right) A x, \end{aligned}$$

(80)

which is $L$-Lipschitz continuous with constant $L = \sum _{j=1}^{r} \beta _{j} \Vert A \Vert ^{2}$. If $\gamma _{i} \in (0, 2/L)$, then $T_{i}$ is nonexpansive. Hence, fixed point algorithm for nonexpansive mappings can be applied to MSSFP (75)

Now we present the optimization method to solve MSSFP (75).

If $x^{*}$ solves the MSSFP (75), then

• (i) the distance from $x^{*}$ to each $C_{i}$ is zero, and

• (ii) the distance from $A x^{*}$ to each $Q_{j}$ is also zero.

This motivate us to consider the proximity function

$$\begin{aligned} p(x) := \frac{1}{2} \sum _{i = 1}^{t} \alpha _{i} \Vert x-P_{C_{i}}(x)\Vert ^{2} + \frac{1}{2} \sum _{j = 1}^{r} \beta _{j} \Vert Ax - P_{Q_{j}}(Ax)\Vert ^{2}, \end{aligned}$$

(81)

where $\alpha _{i} > 0$ for all $i$, $\beta _{j} > 0$ for all $j$. Then the proximity function is convex and differentiable with gradient

$$\begin{aligned} \nabla p(x) = \sum _{i = 1}^{t} \alpha _{i} \left( I-P_{C_{i}}\right) (x) + \sum _{j = 1}^{r} \beta _{j} A^{*} \left( I-P_{Q_{j}} \right) A x, \end{aligned}$$

(82)

where $^{*}$ is the adjoint of $A$.

Proposition 8

[69] $x^{*}$ is a solution of MSSFP (75) if and only if $p(x^{*}) = 0$.

Since the gradient $\nabla p(x)$ is $L^{\prime }$-Lipschtiz continuous with constant

$$\begin{aligned} L^{\prime } = \sum _{i=1}^{t} \alpha _{i} + \sum _{j=1}^{r} \beta _{j} \Vert A \Vert ^{2}, \end{aligned}$$

(83)

one can use the project gradient method to solve the

$$\begin{aligned} \min _{x \in \Omega }\, p(x), \end{aligned}$$

(84)

where $\Omega$ is a closed convex subset of $\fancyscript{H}_{1}$ whose intersection with the solution set of MSSFP (75) is nonempty, and get a solution of the so-called constrained multiple-sets split feasibility problem [15]:

$$\begin{aligned} \text {Find } x^{*} \in \Omega \quad \text {such that } \quad x^{*} \text { solves } (84). \end{aligned}$$

(85)

In view of the above discussion, Censor et al. [15] proposed the following project gradient algorithm to find the solution of MSSFP (75) in the setting of finite-dimensional Hilbert spaces.

Algorithm 10

(Projection Gradient Algorithm) For any arbitrary $x_{0} \in \fancyscript{H}_{1}$, generates a sequence $\{ x_{n} \}$ by

$$\begin{aligned} \begin{array}{lll} x_{n+1} &{} = &{} P_{\Omega } \left( x_{n} - \gamma \nabla p(x_{n}) \right) \\ &{} = &{} P_{\Omega } \left( x_{n} - \gamma \left( \sum _{i=1}^{t} \alpha _{i} (I- P_{C_{i}})(x_{n}) + \Sigma _{j=1}^{r} \beta _{j} A^{*} (I- P_{Q_{j}}) Ax_{n} \right) \right) , \quad n \ge 0, \end{array} \end{aligned}$$

(86)

where $\gamma {\in ( 0, 2/L^{\prime })}$.

Censor et al. [15] established the convergence of the Algorithm 10. The following theorem is a version of their theorem in infinite dimensional Hilbert spaces established by Xu [64].

Theorem 20

Let MSSFP (75) be consistent and a minimizer of the function $p$ over $\Omega$ be inconsistent. Assume that $0 < \gamma < 2/ L^{\prime }$, where $L^{\prime }$ is given by (83). The sequence $\{x_{n}\}$ generated by Algorithm 10 converges weakly to a point $z$ which is a solution of MSSFP (75).

In this direction, several methods and results were obtained during the last decade. In [69], Yao et al. reviewed and presented some recent results on iterative approaches to MSSFP (75).

Zhao et al. [75] proposed the following modified projection algorithm for MSSFP (75) in finite dimensional Euclidean spaces.

Given closed convex sets $C_{i} \subseteq \mathbb {R}^{N}$, $i = 1,2,\ldots ,t$, and closed convex sets $Q_{j} \subseteq \mathbb {R}^{M}$, $j =1,2,\ldots ,r$, in the $N$ and $M$ dimensional Euclidean spaces, respectively, and $A$ an $M \times N$ real matrix. Let $\Omega$ be a closed convex subset of $\mathbb {R}^{N}$ whose intersection with the solution set of MSSFP (75) is nonempty,

Algorithm 11

For any arbitrary $x_{0} \in \mathbb {R}^{N}$, $\sigma _{0} > 0$, $\beta \in (0,1)$, $\theta \in (0,1)$, $\rho \in (0,1)$. For $n = 0,1,2,\ldots$, compute

$$\begin{aligned} \bar{x}_{n} = P_{\Omega }(x_{n}-\gamma _{n}\nabla p(x_{n})), \end{aligned}$$

(87)

where $\gamma _{n}$ is chosen to be the largest $\gamma \in \{ \sigma _{n},\sigma _{n}\beta ,\sigma _{n}\beta ^{2}, \dots \}$ satisfying

$$\begin{aligned} \gamma \Vert \nabla p(\bar{x}_{n})-\nabla p(x_{n})\Vert \le \theta \Vert \bar{x}_{n}-x_{n}\Vert . \end{aligned}$$

(88)

Let

$$\begin{aligned} x_{n+1} = P_{X}(\bar{x}_{n}-\gamma _{n}(\nabla p(\bar{x}_{n})-\nabla p (x_{n}))). \end{aligned}$$

(89)

If

$$\begin{aligned} \gamma _{n}\Vert \nabla p(x_{n+1})-\nabla p (x_{n})\Vert \le \rho \Vert x_{n+1}-x_{n}\Vert , \end{aligned}$$

(90)

then set $\sigma _{n}= \sigma _{0}$; otherwise, set $\sigma _{n}= \gamma _{n}$, where $p(x)$ is proximity function as defined by (81).

We can take $p(x_{n}) < \epsilon$ or $\Vert \nabla p(x_{n})\Vert < \epsilon$ as the stopping criteria in this algorithm.

We have the following result on the convergence of the sequence generated by Algorithm 11.

Theorem 21

[75, Theorem 4.1] Let $X$ be a nonempty closed convex set in $\mathbb {R}^{N}$ with a simple structure and $\{x_{n}\}$ be a sequence generated by Algorithm 11. If the set $X$ contains at least one solution of the constrained multiple-sets split feasibility problem, then $\{x_{n}\}$ converges to a solution of the constrained multiple-sets split feasibility problem.

A relaxed scheme of Algorithm 11 is also presented in [75].

Censor et al. [16] proposed a perturbed projection algorithm for multiple-sets split feasibility problem by applying the orthogonal projections onto a sequence of supersets of the original sets of the problem. Their work is based on the results of Santo and Scheimberg [55].