Abstract
Recent efficient constructions of zero-knowledge Succinct Non-interactive Arguments of Knowledge (zk-SNARKs), require a setup phase in which a common-reference string (CRS) with a certain structure is generated. This CRS is sometimes referred to as the public parameters of the system, and is used for constructing and verifying proofs. A drawback of these constructions is that whomever runs the setup phase subsequently possesses trapdoor information enabling them to produce fraudulent pseudoproofs.
Building on a work of Ben-Sasson, Chiesa, Green, Tromer and Virza [BCG+15], we construct a multi-party protocol for generating the CRS of the Pinocchio zk-SNARK [PHGR16], such that as long as at least one participating party is not malicious, no party can later construct fraudulent proofs except with negligible probability. The protocol also provides a strong zero-knowledge guarantee even in the case that all participants are malicious.
This method has been used in practice to generate the required CRS for the Zcash cryptocurrency blockchain.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
The recently deployed Zcash cryptocurrency supports shielded (private) transactions where sender, receiver and amount are not revealed; and yet, an outside observer can still distinguish between a valid and non-valid transaction. The “cryptographic engine” that enables these shielded transactions is a zero-knowledge Succinct Non-interactive Argument of Knowledge (zk-SNARK); currently, Zcash uses the Pinocchio zk-SNARK [PHGR16], or more precisely, the variant of it described in [BCTV14] as implemented in libsnark [lib].
A potential weakness of Zcash, is that if anybody obtained the trapdoor information corresponding to the Common Reference String (CRS) used for constructing and verifying the SNARKs, they could forge unlimited amounts of the currency, potentially without anyone detecting they are doing so.
Motivated by this, Zcash generated the required CRS in an elaborate “ceremony” [Wil] to reduce the chance of this happening. The purpose of this technical report is to give a detailed description of the multi-party protocol that was used in the ceremony.
Our Results: Ben-Sasson, Chiesa, Green, Tromer and Virza [BCG+15] presented a generic method for computing CRSs of zk-SNARKs in a multi-party protocol, with the property that only if all players collude together they can reconstruct the trapdoor, or, more generally, deduce any other useful information beyond the resultant CRS.
Based on [BCG+15], we devise an arguably simpler method for generating the CRS of the Pinocchio zk-SNARK [PHGR16] with a similar security guarantee: Namely, given that the CRS generated by the protocol is later used to verify proofs; a party controlling all but one of the players will not be able to construct fraudulent proofs except with negligible probability. See full version for details.
Moreover, we show that even if a malicious party controls all players, statistical zero-knowledge holds when constructing proofs according to the resultant parameters. Interestingly, this means the protocol is useful also when run by one player; as the transcript will provide proof to the prover that sending her proof will not leak additional informationFootnote 1.
This property has been recently called subversion Zero-Knowledge [BFS16]. As opposed to the soundness guarantee, zero-knowledge only requires the random oracle model; and in particular, no knowledge assumptions in contrast to some recent works on subversion-ZK [Fuc17, ABLZ17]. On the other hand, our proof only obtains statistical-ZK with polynomially small error (with simulator polynomial running time depending on the desired polynomial error), as opposed to the mentioned recent works that can obtain negligible error (again, using knowledge assumptions). See full version for details.
Comparison to [BCG+15]: Our protocol is not significantly different from that of [BCG+15] for duplex-pairing groups, described in Sect. 5 of that paper. The main purpose here is to give full details for the case of the Pinocchio CRS. Nonetheless, some advantages of this writeup compared to [BCG+15] are:
-
1.
Eliminating the need for NIZK proofs for the relation \(R_{aux}\) described in Sect. 5 there; this is since in Sect. 3.1 we do not commit directly to secret values s, but only to “random s-pairs”.
-
2.
Reducing the memory per player and simplifying the protocol description, by not using [BCG+15]’s generic “sampling to evaluation” procedure, but rather, explicitly presenting the protocol for our use case. In particular, individual players only need to store the messages of the player preceding them, and not the whole transcript as in a straightforward implementation of [BCG+15]. This simplified approach was later generalized [BGM17] for circuits with a certain layered structure.
-
3.
Reducing transcript verification complexity, by taking advantage of bi-linearity of pairings and randomized checking (see Corollary 1). In particular, the number of pairing operations to verify the transcript is constant, while in [BCG+15] it grows linearly with the size of the circuit for which we are constructing SNARK parameters.
-
4.
Giving a full proof of both soundness and subversion zero-knowledge. In [BCG+15] the soundness proof is only sketched, and the subversion zero-knowledge property is not described (though it holds for their protocol).
Organization of Paper: Section 2 introduces some terminology and auxiliary methods that will be used in the protocol. Section 3 describe the protocol in detail. The full version of the paper describes the security proof of the protocol.
2 Definitions, Notation and Auxiliary Methods
Terminology: We always assume we are working with a field \({\mathbb F}_r\) for prime r chosen according to a desired security parameter (more details on this in full version). We assume together with \({\mathbb F}_r\) we have generated groups \({\mathbb {G}_{1}, \mathbb {G}_{2}, \mathbb {G}_{t}}\), all cyclic of order r; where we write \({\mathbb {G}_{1}}\) and \({\mathbb {G}_{2}}\) in additive notation and \({\mathbb G}_t\) in multiplicative notation. Furthermore, we have access to generators \(g_1\in {\mathbb {G}_{1}},g_2\in {\mathbb {G}_{2}}\), and an efficiently computable pairing  , i.e., a non-trivial map such that for any \(a,b\in {\mathbb F}_r \)
, i.e., a non-trivial map such that for any \(a,b\in {\mathbb F}_r \)
for a fixed generator \(g_T\in {\mathbb G}_t \). We use the notations \(g:=(g_1,g_2)\) and  .
.
We think of the field size r as a parameter against which we measure efficiency. In particular, we say a circuit \(A\) is efficient if its size is polynomial in \(\log r\). More precisely, when we refer in the security analysis to an efficient adversary or efficient algorithm, we mean it is a (non-uniform) sequence of circuits indexed by r, of size \(\mathrm{{poly}}\log r\). When we say “with probability p”, we mean “with probability at least p”.
We assume we have at our disposal a function \(\mathsf {COMMIT}\) taking as input strings of arbitrary length; that, intuitively speaking, behaves like a commitment scheme. That is, it is infeasible to deduce \(\mathsf {COMMIT}\) ’s input from seeing its output, and it is infeasible to find two inputs that \(\mathsf {COMMIT}\) maps to the same output. In our implementation we use the BLAKE-2 hash function as \(\mathsf {COMMIT}\). For the actual security proof, we need to assume that \(\mathsf {COMMIT}\) ’s outputs are chosen by a random oracle.
Symmetric Definitions: In the following sections we introduce several methods that receive as parameters elements of both \({\mathbb {G}_{1}}\) and \({\mathbb {G}_{2}}\). We assume implicitly that whenever such a definition is made, we also have the symmetric definition where the roles are reversed between what parameters come from \({\mathbb {G}_{1}}\) and \({\mathbb {G}_{2}}\). For example, if we define a method receiving as input a vector of \({\mathbb {G}_{1}}\) elements and a pair of \({\mathbb {G}_{2}}\) elements. We assume thereafter that we also have the symmetric method receiving as input a vector of \({\mathbb {G}_{2}}\) elements and a pair of \({\mathbb {G}_{1}}\) elements.
2.1 Comparing Ratios of Pairs Using Pairings
Definition 2.1
Given \(s\in {\mathbb F}_r ^*\), an s-pair is a pair (p, q) such that \(p, q \in \mathbb {G}_{1} \setminus \{0\}\), or \(p,q\in \mathbb {G}_{2} \setminus \{0\}\); and \(s\cdot p=q\). When not clear from the context whether p, q are in \(\mathbb {G}_{1}\) or \(\mathbb {G}_{2}\), we use the terms \(\mathbb {G}_{1}\)-s-pair and \(\mathbb {G}_{2}\)-s-pair.
A recurring theme in the protocol will be to check that two pairs of elements in \({\mathbb {G}_{1}}\) and \({\mathbb {G}_{2}}\) respectively, “have the same ratio”, i.e., are s-pairs for the same \(s\in {\mathbb F}_r ^* \).

-
1.
If one of the elements p, q, f, H is zero; return \(\mathsf {rej}\).
-
2.
Return \(\mathsf {acc}\) if \(e(p,H)=e(q,f)\); return \(\mathsf {rej}\) otherwise.
Claim
Given \(p,q\in {\mathbb {G}_{1}}\) and \(f,H\in {\mathbb {G}_{2}}\), \(\mathsf {SameRatio}((p,q),(f,H)) =\mathsf {acc} \) if and only if there exists \(s\in {\mathbb F}_r ^* \) such that (p, q) is a \(\mathbb {G}_{1}\)-s-pair and (f, H) is a \(\mathbb {G}_{2}\)-s-pair.
Proof
Suppose that \(s\cdot p=q\) and \(s^{\prime }\cdot f=H\). Write \(p=a\cdot g_1, f=b\cdot g_2\) for some \(a,b\in {\mathbb F}_r \). Note that if one of \(\left\{ a,b,s,s^{\prime }\right\} \) is 0, we return \(\mathsf {rej}\) in the first step.
Otherwise, we have
and
and thus \(\mathsf {SameRatio}((p,q),(f,H)) =1\) if and only if \(s=s^{\prime }\) (\(mod\; r\)).
Let \(V=((p_i,q_i))_{i\in [d]} \), be a vector of pairs in \({\mathbb {G}_{1}}\). We say V is an s-vector in \({\mathbb {G}_{1}}\) if for each \(i\in [d]\), \((p_i,q_i)\) is a \(\mathbb {G}_{1}\)-s-pair, or is equal to (0, 0). We make the analogous definition for \({\mathbb {G}_{2}}\), and similarly to above, sometimes omit the group name when it is clear from the context what group the elements are in, simply using the term s-vector. In our protocol we often want to check if a long vector \(((p_i,q_i))_{i \in [d]}\) is an s-vector for some \(s\in {\mathbb F}_r ^* \). The next claim enables us to do so with just one pairing.
Claim
Suppose that \(((p_i,q_i))_{i \in [d]}\) is a vector of elements in \({\mathbb {G}_{1} \setminus \{0\}}\) that is not an s-vector. Choose random \(c_1,\ldots ,c_d \in {\mathbb F}_r \) and define
Then, with probability at least \(1-2/r\), both \((p,q)\ne (0,0)\) and (p, q) is not an \(s\)-pair.
Proof
Write \(p_i=a_i \cdot g_1\) for \(a_i\in {\mathbb F}_r \), and \(q_i= s_i\cdot p_i\) for some \(s_i\in {\mathbb F}_r \). Thus, we have \(p=a\cdot g_1\) for \(a\triangleq {\sum _{i\in [d]}c_i a_i}\) and \(q=b\cdot g_1\) for \( b\triangleq {\sum _{i\in [d]}\alpha _i a_i s_i}\). Let us assume \(a\ne 0\). This happens with probability \(1-1/r\). Write [d] as a disjoint union \(S\cup T\) where S is the set of indices of the s-pairs. That is \(S\triangleq \left\{ i\in [d]|s_i=s\right\} \). We have
Thus, \(b/a=s\) if and only if the fraction in the right hand side is zero. As the numerator is a random combination of non-zero elements, this happens with probability 1 / r.
We conclude that with probability at least \(1-2/r\), (p, q) is not an \(s\)-pair.
Claim 2.1 implies the correctness of \(\mathsf {sameRatio}(V,(f,H))\) that given an \(s\)-pair (f, H) in \({\mathbb {G}_{2}}\), checks whether V is an s-vector in \({\mathbb {G}_{1}}\).

-
1.
If there exists a pair of the form (0, a) or (a, 0) for some \(a\ne 0\) in V; return \(\mathsf {rej}\).
-
2.
“Put aside” all elements of the form (0, 0), and from now on assume all pairs in V are in \({\mathbb {G}_{1} \setminus \{0\}}\). (If all pairs are of the form (0, 0) then return \(\mathsf {acc}\)).
-
3.
Choose random \(c_1,\ldots ,c_d\in {\mathbb F}_r \).
-
4.
Define \(p\triangleq \sum _{i\in [d]} c_i\cdot p_i\), and \(q\triangleq \sum _{i\in [d]}c_i\cdot q_i\).
-
5.
If \(p=q=0\), return \(\mathsf {acc}\).
-
6.
Otherwise, return \(\mathsf {SameRatio}((p,q),(f,H))\).
Corollary 1
Suppose \(\mathsf {rp}_{s}\) in a \(\mathbb {G}_{2}\)-s-pair, and V is a vector of pairs of \({\mathbb {G}_{1}}\) elements. If V is an s-vector, \(\mathsf {sameRatio}(V,\mathsf {rp}_{s})\) accepts with probability one. If V is not an s-vector, \(\mathsf {sameRatio}(V,\mathsf {rp}_{s})\) accepts with probability at most 2/r.
Let V be a vector of \({\mathbb {G}_{1}}\)-elements and \(\mathsf {rp}_{s}\) be a pair of \({\mathbb {G}_{2}}\)-elements. We also use a method \(\mathsf {sameRatioSeq}(V,\mathsf {rp}_{s})\) that given an \(s\)-pair \(\mathsf {rp}_{s}\), checks that each two consecutive elements of V are an \(s\)-pair. It does so by calling \(\mathsf {sameRatio}(V',\mathsf {rp}_{s})\) with \(V'= ((V_0,V_1),(V_1,V_2),\ldots ,(V_{d-1},V_d))\).
2.2 Schnorr NIZKs for Knowledge of Discrete Log
We review and define notation for using the well-known Schnorr protocol [Sch89]. Given an \(s\)-pair \(\mathsf {rp}_{s} =(f,H=s\cdot f)\), and a string h, we define the (randomized) string \(\mathrm {NIZK}(\mathsf {rp}_{s},h)\) that can be interpreted as a proof that the generator of the string knows s.

-
1.
Choose random \(a\in {\mathbb F}_r ^* \) and let \(R:=a\cdot f\).
-
2.
Let \(c:=\mathsf {COMMIT}(R\circ h) \) and interpret c as an element of \({\mathbb F}_r \), e.g. by taking it’s first \(\log r\) bits.
-
3.
Let \(u:=a+cs\).
-
4.
Define \(\mathrm {NIZK}(\mathsf {rp}_{s},h) :=(R,u)\).
Let us denote by \(\pi \) a string that is supposedly of the form \(\mathrm {NIZK}(\mathsf {rp}_{s},h) \), for some string h.
 is a boolean predicate that verifies that \(\pi \) is indeed of this form for the same given h.
is a boolean predicate that verifies that \(\pi \) is indeed of this form for the same given h.

-
1.
Let R, u be as in the description above.
-
2.
Compute \(c:=\mathsf {COMMIT}(R\circ h) \).
-
3.
Return \(\mathsf {acc}\) when \(u\cdot f=R+ c\cdot H\); and \(\mathsf {rej}\) otherwise.
2.3 The Random-Coefficient Subprotocol
A large part of the protocol will consist of invocations of the random-coefficient subprotocol. In this subprotocol, we multiply a vector of \({\mathbb {G}_{1}}\) elements coordinate-wise by the same scalar \(\alpha \in {\mathbb F}_r ^* \). \(\alpha \) here is a product of secret elements \(\left\{ \alpha _i\right\} _{i\in [n]}\), that we refer to later as comitted elements. By this we mean, that before the subprotocol is invoked, for each \(i\in [n] \), \(P_i\) has broadcasted a  , denoted
, denoted  , that is accessible to the protocol verifier. (This will become clearer in the context of Sect. 3).
, that is accessible to the protocol verifier. (This will become clearer in the context of Sect. 3).

Common Input: vector \(V\in {\mathbb {G}_{1}^d}\).
Individual Inputs: element \(\alpha _i \in {\mathbb F}_r ^*\) for each \(i\in [n] \).
Output: vector \(\alpha \cdot V \in {\mathbb {G}_{1}^d}\), where \(\alpha =\prod _{i=1}^n\alpha _{i}\).
-
1.
\(P_1\) computes broadcasts \(V_{1}:=\alpha _{1}\cdot V\).
-
2.
For \(i=2,\ldots ,n\), \(P_i\) broadcasts \(V_{i}:=\alpha _{i}\cdot V_{i-1}\).
-
3.
Players output \(V_{n}\) (which should equal \(\alpha \cdot V\)).
Before discussing the transcript verification we define one more useful notation. For vectors \(S,T\in {\mathbb {G}_{1}^d}\) and a  returns \(\mathsf {sameRatio}(V,\mathsf {rp}_{\alpha })\), where \(V_i:=(S_i,T_i)\). The transcript verification procedure receives as input \(V,V_1,\ldots ,V_n\), and for each \(i\in [n] \), the
returns \(\mathsf {sameRatio}(V,\mathsf {rp}_{\alpha })\), where \(V_i:=(S_i,T_i)\). The transcript verification procedure receives as input \(V,V_1,\ldots ,V_n\), and for each \(i\in [n] \), the  .
.

Input: V, protocol transcript \(V_1,\ldots ,V_n\in {\mathbb {G}_{1}^d}\), for each \(i\in [n] \) a  .
.
Output: \(\mathsf {acc}\) or \(\mathsf {rej}\).
-
1.
Run \(\mathsf {sameRatio}((V,V_1),\mathsf {rp}_{\alpha _{1}}) \).
-
2.
For \(i=2,\ldots ,n\), run \(\mathsf {sameRatio}((V_{i-1},V_{i}),\mathsf {rp}_{\alpha _{i}}) \).
-
3.
Return \(\mathsf {acc}\) if all invocations returned \(\mathsf {acc}\); and return \(\mathsf {rej}\) otherwise.
From the correctness of the \(\mathsf {sameRatio}(,)\) method (Corollary 1) we have that
Claim
If the players follow the protocol correctly, the output is \(\alpha \cdot V\), and transcript verification outputs \(\mathsf {acc}\) with probability one. Otherwise, transcript verification outputs \(\mathsf {acc}\) with probability at most 2/r.
3 Protocol Description
The Participants: The protocol is conducted by n players, a coordinator, and a protocol verifier. In the implementation the role of the coordinator and protocol verifier can be played by the same server. We find it useful to separate these roles, though, as the actions of the protocol verifier may be executed only after the protocol has terminated, if one wishes to reduce the time the players have to be engaged. Moreover, any party wishing to check the validity of the transcript and generated parameters can do so solely with access to the protocol transcript. On the other hand, this has the disadvantage that non-valid messages will be detected only in hindsight, and the whole process will have to be restarted if one wishes to generate valid SNARK parameters.
Similarly, the role of the coordinator is not strictly necessary if one assumes a blackboard model where each player sees all messages broadcasted. (In our actual implementation the coordinator passes messages between the players). Our security analysis holds when all messages are seen by all players. However, even in such a blackboard model there is an advantage of having of a coordinator role: At the beginning of Round 3 a heavy computation needs to performed (Subsect. 3.3) that in theory could be performed by the first player before he sends his message for that round. However, as this heavy computation does not require access to any secrets of the players, having the coordinator perform it can save much time, if the coordinator is run on a strong server, and the players have weaker machines.
The protocol consists of four “round-robin” rounds, where for each \(i\in [n] \), player \(P_i\) can send his message after receiving the message of \(P_{i-1}\). \(P_1\) can send his message after receiving an“initializer message” from the coordinator, which is empty in some of the rounds. An exception of this is the first round, where all players may send their message to the coordinator in parallel. However, security is not harmed if a player sees other players’ messages before sending his in that round. Round 2 is divided into several parts for clarity, however the messages of a player \(P_i\) in all parts of that round can be sent in parallel. Similarly, Round 3 and 4 consist of several one round round-robin subprotocols; however, the messages of a player \(P_i\) in all these subprotocols can be sent in parallel.
3.1 Round 1: Commitments
For each \(i\in [n] \), \(P_i\) does the following.
-
1.
Generate a set of uniform elements in \({\mathbb F}_r ^*\)
$$\begin{aligned} \mathsf {secrets} _i:=\left\{ \tau _i,\rho _{A,i},\rho _{B,i},\alpha _{A,i},\alpha _{B,i},\alpha _{C,i},\beta _i,\gamma _i\right\} . \end{aligned}$$Omitting the index i for readability from now on, let
$$\begin{aligned} \mathsf {elements}_{i} :=\{\tau , \rho _{A}, \rho _{B}, \alpha _{A}, \alpha _{B}, \alpha _{C}, \beta , \gamma , \rho _{A}\alpha _{A}, \rho _{B} \alpha _{B}, \end{aligned}$$$$\begin{aligned} \rho _{A}\rho _{B}, \rho _{A}\rho _{B}\alpha _{C}, \beta \gamma \} \end{aligned}$$ -
2.
Now \(P_i\) generates the set of group elementsFootnote 2
$$\begin{aligned} \mathsf {e}_{i} :=(\tau ,\rho _A, \rho _A \rho _B, \rho _A\alpha _A, \rho _A\rho _B\alpha _B, \rho _A\rho _B\alpha _C, \gamma ,\beta \gamma )\cdot g. \end{aligned}$$ -
3.
\(P_i\) computes \(h_i:=\mathsf {COMMIT}(\mathsf {e}_{i}) \) and broadcasts \(h_i\).
3.2 Round 2
Part 1: Revealing commitments: For each \(i\in [n] \)
-
1.
\(P_i\) broadcasts \(\mathsf {e}_{i}\).
-
2.
The protocol verifier checks that indeed \(h_i=\mathsf {COMMIT}(\mathsf {e}_{i}) \).
Committed Elements: From the end of Round 2, part 1 of the protocol, we refer to the elements of \(\mathsf {elements}_{i}\) for some \(i\in [n] \) as committed elements. The reason is that by this stage of the protocol, for each \(s\in \mathsf {elements}_{i} \), \(P_i\) has sent an \(s\)-pair in both \({\mathbb {G}_{1}}\) and \({\mathbb {G}_{2}}\), effectively committing him to the value of s. For each such element s, we refer to the \(s\)-pair in \({\mathbb {G}_{1}}\) by \(\mathsf {rp}_{s}\) and the \(s\)-pair in \({\mathbb {G}_{2}}\) by \(\mathsf {rp_{s}^2}\). We list the corresponding elements and \(s\)-pairs, omitting the i subscript for readability:
-
\(\tau \): \((\mathsf {rp}_{\tau }^{1},\mathsf {rp_{\tau }^2}) = (g,\tau \cdot g)\).
-
\(\rho _A\): \((\mathsf {rp}_{\rho _A}^{1},\mathsf {rp_{\rho _A}^2}) = (g,\rho _A\cdot g)\).
-
\(\rho _B\): \((\mathsf {rp}_{\rho _B}^{1},\mathsf {rp_{\rho _B}^2}) = (g,\rho _B\cdot g)\).
-
\(\alpha _A\): \((\mathsf {rp}_{\alpha _A}^{1},\mathsf {rp_{\alpha _A}^2}) = (\rho _A\cdot g,\rho _A\alpha _A\cdot g)\).
-
\(\alpha _B\): \((\mathsf {rp}_{\alpha _B}^{1},\mathsf {rp_{\alpha _B}^2}) = (\rho _A\rho _B\cdot g,\rho _A\rho _B \alpha _B\cdot g)\).
-
\(\alpha _C\): \((\mathsf {rp}_{\alpha _C}^{1},\mathsf {rp_{\alpha _C}^2}) = (\rho _A\rho _B\cdot g,\rho _A\rho _B \alpha _C\cdot g)\).
-
\(\beta \): \((\mathsf {rp}_{\beta }^{1},\mathsf {rp_{\beta }^2}) = ( \gamma \cdot g,\beta \gamma \cdot g)\).
-
\(\gamma \): \((\mathsf {rp}_{\gamma }^{1},\mathsf {rp_{\gamma }^2}) = ( g, \gamma \cdot g)\).
-
\(\rho _A\alpha _A\): \((\mathsf {rp}_{\rho _A\alpha _A}^{1},\mathsf {rp_{\rho _A\alpha _A}^2}) = ( g,\rho _A\alpha _A \cdot g)\).
-
\(\rho _B\alpha _B\): \((\mathsf {rp}_{\rho _B\alpha _B}^{1},\mathsf {rp_{\rho _B\alpha _B}^2}) = ( \rho _A\cdot g,\rho _A\rho _B\alpha _B \cdot g)\).
-
\(\rho _A\rho _B\): \((\mathsf {rp}_{\rho _A\rho _B}^{1},\mathsf {rp_{\rho _A\rho _B}^2}) = ( g,\rho _A\rho _B \cdot g)\).
-
\(\rho _A\rho _B\alpha _C\): \((\mathsf {rp}_{\rho _A\rho _B\alpha _C}^{1},\mathsf {rp_{\rho _A\rho _B\alpha _C}^2}) = ( g,\rho _A\rho _B\alpha _C \cdot g)\).
-
\(\beta \gamma \): \((\mathsf {rp}_{\beta \gamma }^{1},\mathsf {rp_{\beta \gamma }^2}) = ( g,\beta \gamma \cdot g)\).
Of course, we need to check that \(P_i\) has committed to the same element \(s\in {\mathbb F}_r ^*\) by \(\mathsf {rp}_{s}\) and \(\mathsf {rp_{s}^2}\). This is done by the protocol verifier in the next stage.
Part 2: Checking Commitment Consistency Between both Groups: For each \(i\in [n] \), and \(s\in \mathsf {elements}_{i} \), the protocol verifier runs \(\mathsf {SameRatio}(\mathsf {rp}_{s},\mathsf {rp_{s}^2})\), and outputs \(\mathsf {rej}\) if any invocation returned \(\mathsf {rej}\).
Part 3: Proving and Verifying Knowledge of Discrete Logs: Let \(h:=\mathsf {COMMIT}(h_1\circ \ldots \circ h_n) \) be the hash of the transcript of Round 1. \(P_1\) computes and broadcasts h.
For each \(i\in [n] \)
-
1.
For \(s\in \mathsf {secrets} _{i}\), let \(h_{i,s}:=h\circ \mathsf {rp}_{s}^{1} \). Note that both \(P_i\) and the protocol verifier, seeing the transcript up to this point, can efficiently compute the elements \(\left\{ h_{i,s}\right\} \).
-
2.
For each \(s\in \mathsf {secrets} _{i}\), \(P_i\) broadcasts \(\pi _{i,s}:=\mathrm {NIZK}(\mathsf {rp}_{s}^{1},h_{i,s}) \).
-
3.
The protocol verifier checks for each \(s\in \mathsf {secrets} _{i}\) that
 .
.
Part 4: The Random Powers Subprotocol: The purpose of the subprotocol is to output the vector

where \(\tau :=\tau _1\cdots \tau _n\). Recall that \(\tau _1,\ldots ,\tau _n\) are committed values from Round 1.
For a vector \(V\in {\mathbb {G}_{1}^{d+1}}\), and \(a\in {\mathbb F}_r \), we use below the notation \(\mathsf {powerMult}(V,a) \in {\mathbb {G}_{1}^{d+1}}\), defined as
for \(i\in \left\{ 0,\ldots ,d\right\} \). We use the analogous notation for a vector \(V\in {\mathbb {G}_{2}^{d+1}}\).
Phase 1: Computing Power Vectors
-
1.
\(P_1\) does the following.
-
(a)
Computes
 and
and 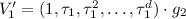 .
. -
(b)
Broadcasts \((V_1,V'_1)\).
-
(a)
-
2.
For \(i=2,\ldots ,n\), \(P_i\) does the following:
-
(a)
Compute
 .
. -
(b)
Broadcasts \((V_i,V'_i)\).
-
(a)
Phase 2: Checking Power Vectors are Valid: The protocol verifier performs the following checksFootnote 3 on the broadcasted data from Phase 1:
-
1.
Check that
$$\begin{aligned} \mathsf {sameRatioSeq}(V_1,\mathsf {rp_{\tau _1}^2}), \end{aligned}$$and
$$\begin{aligned} \mathsf {sameRatioSeq}(V'_1,(V_{1,0},V_{1,1})) \end{aligned}$$ -
2.
For each \(i\in [n]\setminus \left\{ 1\right\} \) check that
$$\begin{aligned} \mathsf {sameRatioSeq}(V_i,(V'_{i,0},V'_{i,1})), \end{aligned}$$$$\begin{aligned} \mathsf {sameRatioSeq}(V'_i,(V_{i,0},V_{i,1})), \end{aligned}$$and
$$\begin{aligned} \mathsf {SameRatio}((V_{i-1,1},V_{i,1}),\mathsf {rp_{\tau _i}^2}) \end{aligned}$$
The protocol verifier rejects the transcript if one of the checks failed; otherwise, the coordinator defines \((PK_H\triangleq V_n,PK_H'\triangleq V'_n)\) is taken as the subprotocol output.
Phase 3: Checking we didn’t Land in the Zeros of Z: The zero-knowledge property of the SNARK requires we weren’t unlucky and \(\tau \) landed in the zeroes of \(Z(X):=X^d-1\).
-
Protocol verifier and all players check that \(Z(\tau )\cdot g_1 = (\tau ^d-1)\cdot g_1 = V_{n,d}-V_{n,0}\ne 0\). If the check fails the protocol is aborted and restarted.
3.3 Coordinator After Round 2: Computing Lagrange Basis Using FFT, and Preparing the Vectors \(\mathbf {A}\), \(\mathbf {B}\) and \(\mathbf {C}\)
To avoid a quadratic proving time the polynomials in the QAP must be evaluated in a Lagrange basis. There seems to be no way of directly computing a Lagrange basis at \(\tau \) in a 1-round MPC in a similar way we did for the standard basis in the Random-Powers subprotocol. Thus we will do ‘FFT in the coefficient’ to compute the Lagrange basis on the output of the random-powers subprotocol. Details and definitions follow. Let \(\omega \in {\mathbb F}_r \) be a primitive root of unity of order \(d=2^{\ell }\), in code d is typically the first power of two larger or equal to the circuit size.
For \(i=1,\ldots ,d\), we define \(L_{i}\) to be the i’th Lagrange polynomial over the points \(\left\{ \omega ^i\right\} _{i\in [d]}\). That is, \(L_{i}\) is the unique polynomial of degree smaller than d, such that \(L_{i} (\omega ^i)=1\) and \(L_{i} (\omega ^j)=0\), for \(j\in [d]\setminus \left\{ i\right\} \).
Claim
For \(i\in [d]\) we have
for \(c_d:=\frac{1}{d}\).
Proof
Substituting \(X=\omega ^{i'}\) for \(i'\ne i\) we have a sum over all roots of unity of order d which is 0. Substituting \(X=\omega ^i\) we have a sum of d ones divided by d which is one.
For \(\tau \in {\mathbb F}_r ^* \), denote by we denote by \(\mathrm {LAG}_{\tau } \in {\mathbb {G}_{1}^{d}}\times {\mathbb {G}_{2}^{d}}\) the vector
The purpose of the FFT-protocol is to compute \(\mathrm {LAG}_{\tau }\) from \(\mathrm {POWERS}_{\tau }\). Let us focus for simplicity how to compute the first half containing the \({\mathbb {G}_{1}}\) elements. Computing the second half is completely analogous. We define the polynomial \(P(Y)(=P_{\tau } (Y))\) by
It is easy to check that
Claim
For \(i\in [d]\)
and thus
Thus our task reduces to computing the vector  (and then reordering accordingly). We describe an algorithm to compute the vector \((P(\omega ^i))_{i\in [d]}\) using the vector \((1,\tau ,\tau ^{2},\ldots ,\tau ^{d})\) as input and only linear combination gates. This suffices as these linear combinations can be simulated by scalar multiplication and addition in \({\mathbb {G}_{1}}\), when operating on \(\mathrm {POWERS}_{\tau }\). We proceed to review standard FFT tricks that will be used.
(and then reordering accordingly). We describe an algorithm to compute the vector \((P(\omega ^i))_{i\in [d]}\) using the vector \((1,\tau ,\tau ^{2},\ldots ,\tau ^{d})\) as input and only linear combination gates. This suffices as these linear combinations can be simulated by scalar multiplication and addition in \({\mathbb {G}_{1}}\), when operating on \(\mathrm {POWERS}_{\tau }\). We proceed to review standard FFT tricks that will be used.
For a polynomial \(P(Y)=\sum _{i=0}^{<d}a_i\cdot Y^i\) of degree smaller than d, where d is even, we define the polynomials
and
It is easy to see that
In particular, for \(i\in [d]\)
For \(j=0,\ldots ,\ell -1\) denote \(\omega _j\triangleq \omega ^{2^j}\). Note further that \(\left\{ \omega ^{2i}\right\} _{{i\in [d]}}\) is a subgroup if size d/2 generated by \(\omega _1\). More generally, for \(j=1,\ldots ,\ell -1\) \(\left\{ \omega _{j-1}^{2i}\right\} _{i\in [d]}\) is a subgroup of size \(2^{d-j}\) generated by \(\omega _j\). The above discussion suggests the following (well-known FFT) recursive algorithm.
FFT
input: Polynomial P, given as list of coefficients, element \(\omega \in {\mathbb F}_r \) generating a group of size \(d=2^{\ell }\).
output: The vector \(V=(P(\omega ^i))_{i\in [d]} \).
-
1.
If \(d=2\) compute V directly.
-
2.
Otherwise,
-
(a)
Call the method recursively twice; first with \(P_{\mathrm {EVEN}}\) and \(\omega ^2\) to obtain output \(E:=(P_{\mathrm {EVEN}} (\omega ^{2i}))_{i\in [d/2]} \), and then with \(P_{\mathrm {ODD}}\) and \(\omega ^2\) to obtain the vector \(O:=(P_{\mathrm {ODD}} (\omega ^{2i}))_{i\in [d/2]} \).
-
(b)
Compute the vector V using E, O and the equality mentioned above. More specifically, each element \(V_i\) of V is computed as
$$\begin{aligned} V_i = P(\omega ^i)= P_{\mathrm {EVEN}} (\omega ^{2i})+\omega ^i\cdot P_{\mathrm {ODD}} (\omega ^{2i}) = E_i + \omega ^i\cdot O_i, \end{aligned}$$(where we subtract d/2 from indices of E and O when they are larger than d/2).
-
(a)
In summary, we obtain \(\mathrm {LAG}_{\tau }\) by applying the FFT and the polynomial P described above, with coefficients \(1,\tau ,\ldots ,\tau ^{d-1}\) and an \(\omega \) of order d - which should be the same \(\omega \) used in the QAP construction. After getting the result from the FFT, we reverse the order of the vector and multiply each element by the scalar 1/d.
Preparing the vectors \(\mathbf {A}\),\(\mathbf {B}\) and \(\mathbf {C}\): We need to compute the vectors  ,
,  ,
,  , and
, and  . We remark that [BCTV14] use the same notation for vectors of polynomials, while we are looking at the vector of these polynomials evaluated at \(\tau \).
. We remark that [BCTV14] use the same notation for vectors of polynomials, while we are looking at the vector of these polynomials evaluated at \(\tau \).
Note thatFootnote 4 \(A_{m+1}=B_{m+1}=C_{m+1}:=Z[\tau ]\cdot g_1 = (\tau ^d-1)\cdot g_1\). After the FFT, we have obtained \(\mathrm {LAG}_{\tau }\), so each such element is a linear combination of elements of \(\mathrm {LAG}_{\tau }\); except \(Z(\tau )\cdot g\), that can be computed using the elements \(\tau ^d\cdot g\) in \(\mathrm {POWERS}_{\tau }\).
3.4 Round 3
After the random-powers subprotocol and the FFT, the MPC consists of a few invocations of the random-coefficient subprotocol. These invocations add a total of two rounds to the MPC, as sometimes and random-coefficient subprotocol will need the output of a previous random-coefficient subprotocol as input.
Part 1: Broadcasting Result of FFT: The coordinator broadcasts the vectors \(\mathbf {A},\mathbf {B},\mathbf {C},\mathbf {B_2} \).
Part 2: Random Coefficient Subprotocol Invocations: We apply the random-coefficient subprotocol numerous times to obtain the different key elements. For an element \(\alpha _i\in \mathsf {elements}_{i} \), we abuse notation here and denote \(\alpha :=\alpha _1\cdots \alpha _n\) (as opposed to ommitting the index i and writing \(\alpha \) for \(\alpha _i\) which we did when describing Round 1).
-
1.
\(PK_A = \mathrm {RCPC}(\mathbf {A},\rho _A) \).
-
2.
\(PK_B = \mathrm {RCPC}(\mathbf {B_2},\rho _B) \).
-
3.
\(PK_C = \mathrm {RCPC}(\mathbf {C},\rho _A\rho _B) \).
-
4.
\(PK'_A= \mathrm {RCPC}(\mathbf {A},\rho _A\alpha _A) \)
-
5.
\(PK'_B = \mathrm {RCPC}(\mathbf {B},\rho _B\alpha _B) \).
-
6.
\(PK'_C =\mathrm {RCPC}(\mathbf {C},\rho _A\rho _B\alpha _C) \)
-
7.
\(temp_B = \mathrm {RCPC}(\mathbf {B},\rho _B) \)
-
8.
\(VK_Z= \mathrm {RCPC}(g_2\cdot Z(\tau ),\rho _A\rho _B) \). We use that \(g_2\cdot Z(\tau ) = g_2\cdot (\tau ^d-1)\) can be computed from \(PK'_H\) that was computed in Round 2, part 2, as described in Sect. 3.2.
-
9.
\(VK_A = \mathrm {RCPC}(g_2,\alpha _A) \).
-
10.
\(VK_B = \mathrm {RCPC}(g_1,\alpha _B) \).
-
11.
\(VK_C = \mathrm {RCPC}(g_2,\alpha _C) \).
3.5 Round 4: Computing Key Elements Involving \(\beta \), Especially \(PK_K\)
Each player (or just the coordinator) computes \(V:=PK_A + temp_B + PK_C\). The players compute
-
1.
\(PK_K = \mathrm {RCPC}(V,\beta ) \)
-
2.
\(VK_\gamma = \mathrm {RCPC}(g_2,\gamma ) \)
-
3.
\(VK^1_{\beta \gamma } = \mathrm {RCPC}(g_1,\beta \gamma ) \).
-
4.
\(VK^2_{\beta \gamma } = \mathrm {RCPC}(g_2,\beta \gamma ) \).
Finally, the protocol verifier will run \(\mathrm {\mathsf {verify}RCPC}(,)\) on the input and transcript of each subprotocol executed in Round 3 or 4; and output \(\mathsf {acc}\) if and only if all invocations of \(\mathrm {\mathsf {verify}RCPC}(,)\) returned \(\mathsf {acc}\).
The proof of security for the protocol is given in the appendix.
Notes
- 1.
Thanks to Eran Tromer for pointing this out, and more generally the connection to subversion zero-knowledge. We note that if one wishes to run the protocol with one player, transcript verification can stay the same, but the player should be altered to take advantage of field rather than group operations when possible for better efficiency.
- 2.
In the actual code a more complex set of elements is used that can be efficiently derived from \(\mathsf {elements}_{i}\), as described in the full version. The reason we use the more complex set is that it potentially provides more security as it contains less information about \(\mathsf {secrets} _i\). However, the proof works as well with this definition of \(\mathsf {e}_{i} \) and it provides a significantly simpler presentation. We explain in the full version the slight modification for protocol and proof for using the more complex element set.
- 3.
The checks below could be simplified if we had also used
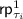 . We do not use it as in the actual code, as explained in the full version, we do not have a
. We do not use it as in the actual code, as explained in the full version, we do not have a  .
. - 4.
A technicality is that in the protocol description in [BCTV14] \(Z(\tau )\cdot g_2\) is appended with index \(m+2\) in \(\mathbf {B_2} \), and \(Z(\tau )\cdot g_1\) is appended in index \(m+3\) in C. However in the actual libsnark code, they are appended in index \(m+1\), and the prover algorithm is slightly modified to take this into account. But for the security proof we assume later on as in [BCTV14] that \(A_{m+1}=C_{m+3} =Z(\tau )\cdot g_1\), \(B_{m+2} = Z(\tau )\cdot g_2\), \(A_{m+2},A_{m+3},B_{m+1},B_{m+3},C_{m+1},C_{m+2}=0\).
References
Abdolmaleki, B., Baghery, K., Lipmaa, H., Zając, M.: A subversion-resistant SNARK. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10626, pp. 3–33. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_1
Ben-Sasson, E., Chiesa, A., Green, M., Tromer, E., Virza, M.: Secure sampling of public parameters for succinct zero knowledge proofs. In: 2015 IEEE Symposium on Security and Privacy, SP 2015, San Jose, CA, USA, 17–21 May 2015, pp. 287–304 (2015)
Ben-Sasson, E., Chiesa, A., Tromer, E., Virza, M.: Succinct non-interactive zero knowledge for a von neumann architecture. In: Proceedings of the 23rd USENIX Security Symposium, San Diego, CA, USA, 20–22 Aug 2014, pp. 781–796 (2014)
Bellare, M., Fuchsbauer, G., Scafuro, A.: Nizks with an untrusted CRS: security in the face of parameter subversion. IACR Cryptology ePrint Archive 2016:372 (2016)
Bowe, S., Gabizon, A., Miers, I.: Scalable multi-party computation for zk-SNARK parameters in the random beacon model (2017)
Campanelli, M., Gennaro, R., Goldfeder, S., Nizzardo, L.: Zero-knowledge contingent payments revisited: attacks and payments for services. In: ACM Communications (2017)
Fuchsbauer, G.: Subversion-zero-knowledge SNARKs. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10769, pp. 315–347. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_11
https://github.com/scipr-lab/libsnark, https://github.com/zcash/libsnark
Parno, B., Howell, J., Gentry, C., Raykova, M.: Pinocchio: nearly practical verifiable computation. Commun. ACM 59(2), 103–112 (2016)
Schnorr, C.P.: Efficient identification and signatures for smart cards. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 239–252. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_22
Wilcox, Z.: https://z.cash/blog/the-design-of-the-ceremony.html
Acknowledgements
We thank Eli Ben-Sasson, Alessandro Chiesa, Jens Groth, Daira Hopwood, Hovav Shacham, Eran Tromer, Madars Virza, Nathan Wilcox and Zooko Wilcox for helpful discussions. We thank Daira Hopwood for pointing out some technical inaccuracies. We thank Eran Tromer for bringing to our attention the work of [CGGN17], and the relevance of our protocol to that work, and the connection to subversion zero-knowledge in general. We thank the anonymous reviewers of the 5th Workshop on Bitcoin and Blockchain Research for their comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Financial Cryptography Association
About this paper
Cite this paper
Bowe, S., Gabizon, A., Green, M.D. (2019). A Multi-party Protocol for Constructing the Public Parameters of the Pinocchio zk-SNARK. In: Zohar, A., et al. Financial Cryptography and Data Security. FC 2018. Lecture Notes in Computer Science(), vol 10958. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-58820-8_5
Download citation
DOI: https://doi.org/10.1007/978-3-662-58820-8_5
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-58819-2
Online ISBN: 978-3-662-58820-8
eBook Packages: Computer ScienceComputer Science (R0)





 .
. and
and 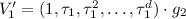 .
. .
.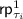 . We do not use it as in the actual code, as explained in the full version, we do not have a
. We do not use it as in the actual code, as explained in the full version, we do not have a  .
.