Abstract
Taking an algebraic perspective on the basic structures of Rough Concept Analysis as the starting point, in this paper we introduce some varieties of lattices expanded with normal modal operators which can be regarded as the natural rough algebra counterparts of certain subclasses of rough formal contexts, and introduce proper display calculi for the logics associated with these varieties which are sound, complete, conservative and with uniform cut elimination and subformula property. These calculi modularly extend the multi-type calculi for rough algebras to a ‘nondistributive’ (i.e. general lattice-based) setting.
The research of the fourth author is supported by the NWO Vidi grant 016.138.314, the NWO Aspasia grant 015.008.054, and a Delft Technology Fellowship awarded in 2013.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- Rough set theory
- Formal Concept Analysis
- Modal logic
- Lattice-based logics
- Algebras for rough sets
- Proper display calculi
1 Introduction
This paper continues a line of investigation started in [10] and aimed at introducing sequent calculi for the logics of varieties of ‘rough algebras’, introduced and discussed in [1, 20]. The ‘rough algebras’ considered in the present paper are nondistributive (i.e. general lattice-based) generalizations of those of [20, 21]; specifically, they are varieties of lattices expanded with normal modal operators, natural examples of which arise in connection with (certain subclasses of) rough formal contexts, introduced by Kent in [15] as the basic notion of Rough Concept Analysis (RCA), a synthesis of Rough Set Theory [19] and Formal Concept Analysis [8]. The core idea of Kent’s approach is to use a given indiscernibility relation E on the objects of a formal context (A, X, I) to generate E-definable approximations R and S of the relation I such that \(S\subseteq I\subseteq R\). The starting point of our approach is that R and S can be used to generate tuples of adjoint normal modal operators \(\langle S\rangle \dashv [S]\) and \(\langle R\rangle \dashv [R]\). We identify conditions under which [S] and \(\langle R\rangle \) are interior operators and [R] and \(\langle S\rangle \) are closure operators. This provides the basic algebraic framework, which we axiomatically extend so as to define ‘nondistributive’ counterparts of the varieties introduced in [21], whenever possible.
From an algebraic perspective, it is interesting to observe that, unlike \(\langle S\rangle \) and [S], the modal operators \(\langle R\rangle \) and [R] play the reverse roles they usually have in rough set theory: namely, [R], being an inflationary map, plays naturally the role of the closure operator providing the upper lax approximation of a given formal concept, and similarly \(\langle R\rangle \), being a deflationary map, plays the role of the interior operator, providing the lower lax approximation of a given formal concept.
From a proof-theoretic perspective, these properties make it possible to extend the multi-type approach (thanks to which, a modular family of analytic calculi was introduced in [10] for the logics of ‘rough algebras’) to varieties of ‘rough algebras’ on a ‘nondistributive’ propositional base. In particular, the calculi defined in Sect. 6 are all proper display calculi (cf. [24]), the cut elimination and subformula property of which can be straightforwardly verified by appealing to the meta-theorem of [5].Footnote 1 An interesting departure from the calculi of [10] concerns the counterparts of the IA3 condition, which in the present paper comes in two variants: the lower (strict), and the upper (lax). The inequality corresponding to the lower variant of IA3, which was analytic in the presence of distributivity, is not analytic inductive in the absence of distributivity (cf. [7, Definition 55]). However, the inequality corresponding to the upper variant of IA3 is analytic inductive, and hence can be captured by an analytic structural rule.
This paper contains the first algebraic and proof-theoretic contribution to a line of research aimed at integrating Rough Set Theory and Formal Concept Analysis, and at building the necessary logical machinery to support formal reasoning about categorization decisions under the assumption that categories and concepts can be vague. Future directions concern enriching this basic framework so as to formally account for the fact that the dynamics of categories also affect their becoming vaguer or sharper.
2 Preliminaries
The purpose of this section, which is based on [3, Appendix] and [2] and [18, Sects. 2.3 and 2.4], is to briefly recall the basic notions of the theory of enriched formal contexts (cf. Definition 2) while introducing the notation which will be used throughout the paper. For any relation \(T\subseteq U\times V\), and any \(U'\subseteq U\) and \(V'\subseteq V\), let
It can be easily verified that \(U'\subseteq T^{(0)}[V']\) iff \(V'\subseteq T^{(1)}[U']\), that \(V_1\subseteq V_2\subseteq V\) (resp. \(U_1\subseteq U_2\subseteq U\)) implies that \(T^{(0)}[V_2]\subseteq T^{(0)}[V_1]\) (resp. \(T^{(1)}[U_2]\subseteq T^{(1)}[U_1]\)), and \(S\subseteq T\subseteq U\times V\) implies that \(S^{(0)}[V']\subseteq T^{(0)}[V']\) and \(S^{(1)}[U']\subseteq T^{(1)}[U']\) for all \(V'\subseteq V\) and \(U'\subseteq U\).
Formal contexts, or polarities, are structures \(\mathbb {P} = (A, X, I)\) such that A and X are sets, and \(I\subseteq A\times X\) is a binary relation. Intuitively, formal contexts can be understood as abstract representations of databases [8], so that A represents a collection of objects, X as a collection of features, and for any object a and feature x, the tuple (a, x) belongs to I exactly when object a has feature x. In what follows, we use a, b (resp. x, y) for elements of A (resp. X), and B (resp. Y) for subsets of A (resp. of X).
As is well known, for every formal context \(\mathbb {P} = (A, X, I)\), the pair of maps
\((\cdot )^\uparrow : \mathcal {P}(A)\rightarrow \mathcal {P}(X)\quad \text { and } \quad (\cdot )^\downarrow : \mathcal {P}(X)\rightarrow \mathcal {P}(A),\)
respectively defined by the assignments \(B^\uparrow : = I^{(1)}[B]\) and \(Y^\downarrow : = I^{(0)}[Y]\), form a Galois connection and hence induce the closure operators \((\cdot )^{\uparrow \downarrow }\) and \((\cdot )^{\downarrow \uparrow }\) on \(\mathcal {P}(A)\) and on \(\mathcal {P}(X)\) respectively.Footnote 2 Moreover, the fixed points of these closure operators form complete sub-\(\cap \)-semilattices of \(\mathcal {P}(A)\) and \(\mathcal {P}(X)\) respectively, and hence are complete lattices which are dually isomorphic to each other via the restrictions of the maps \((\cdot )^{\uparrow }\) and \((\cdot )^{\downarrow }\). This motivates the following.
Definition 1
For every formal context \(\mathbb {P} = (A, X, I)\), a formal concept of \(\mathbb {P}\) is a pair \(c = (B, Y)\) such that \(B\subseteq A\), \(Y\subseteq X\), and \(B^{\uparrow } = Y\) and \(Y^{\downarrow } = B\). The set B is the extension of c, which we will sometimes denote \([\![{c}]\!]\), and Y is the intension of c, sometimes denoted \((\![{c}]\!)\). Let \(L(\mathbb {P})\) denote the set of the formal concepts of \(\mathbb {P}\). Then the concept lattice of \(\mathbb {P}\) is the complete lattice

where for every \(\mathcal {X}\subseteq L(\mathbb {P})\),
Then clearly, \(\top ^{\mathbb {P}^+}: = \wedge \varnothing = (A, A^{\uparrow })\) and \(\bot ^{\mathbb {P}^+}: = \vee \varnothing = (X^{\downarrow }, X)\), and the partial order underlying this lattice structure is defined as follows: for any \(c, d\in L(\mathbb {P})\),
Theorem 1
(Birkhoff’s theorem, main theorem of FCA). Any complete lattice \(\mathbb {L}\) is isomorphic to the concept lattice \(\mathbb {P}^+\) of some formal context \(\mathbb {P}\).
Definition 2
An enriched formal context is a tuple \(\mathbb {F} = (\mathbb {P}, R_\Box , R_\Diamond )\) such that \(\mathbb {P} = (A, X, I)\) is a formal context, and \(R_\Box \subseteq A\times X\) and \(R_\Diamond \subseteq X\times A\) are I-compatible relations, that is, \(R_{\Box }^{(0)}[x]\) (resp. \(R_{\Diamond }^{(0)}[a]\)) and \(R_{\Box }^{(1)}[a]\) (resp. \(R_{\Diamond }^{(1)}[x]\)) are Galois-stable for all \(x\in X\) and \(a\in A\). The complex algebra of \(\mathbb {F}\) is
where \(\mathbb {P}^+\) is the concept lattice of \(\mathbb {P}\), and \([R_\Box ]\) and \(\langle R_\Diamond \rangle \) are unary operations on \(\mathbb {P}^+\) defined as follows: for every \(c \in \mathbb {P}^+\),
Since \(R_{\Box }\) and \( R_{\Diamond }\) are I-compatible, \([R_\Box ],\langle R_{\Diamond }\rangle , [R_\Diamond ^{-1}],\langle R_{\Box }^{-1}\rangle : \mathbb {P}^+\rightarrow \mathbb {P}^+\) are well-defined.
Lemma 1
(cf. [18, Lemma 3]). For any enriched formal context \(\mathbb {F} = (\mathbb {P}, R_{\Box }, R_{\Diamond })\), the algebra \(\mathbb {F}^+ = (\mathbb {P}^+, [R_{\Box }], \langle R_{\Diamond }\rangle )\) is a complete lattice expanded with normal modal operators such that \([R_\Box ]\) is completely meet-preserving and \(\langle R_\Diamond \rangle \) is completely join-preserving.
Definition 3
For any formal context \(\mathbb {P}= (A,X,I)\) and any I-compatible relations \(R, T\subseteq A\times X\), the composition \(R\, ;T\subseteq A \times X\) is defined as follows: for any \(a\in A\) and \(x \in X\),
3 Motivation: Kent’s Rough Concept Analysis
Below, we report on the basic definitions and constructions in Rough Concept Analysis [15], cast in the notational conventions of Sect. 2.
Rough formal contexts (abbreviated as Rfc) are tuples \(\mathbb {G} = (\mathbb {P}, E)\) such that \(\mathbb {P} = (A, X, I)\) is a polarity (cf. Sect. 2), and \(E\subseteq A\times A\) is an equivalence relation (the indiscernibility relation between objects). For every \(a\in A\) we let \((a)_E: = \{b\in A\mid aEb\}\). The relation E induces two relations \(R, S\subseteq A\times I\) approximating I, defined as follows: for every \(a\in A\) and \(x\in X\),
By definition, R, S are E-definable (i.e. \(R^{(0)}[x] = \cup _{aRx}(a)_E\) and \(S^{(0)}[x]= \cup _{aSx}(a)_E\) for any \(x\in X\)), and E being reflexive immediately implies that
Lemma 2
For any Rfc \(\mathbb {G} = (\mathbb {P}, E)\), if R and S are defined as in (1), then
Intuitively, we can think of R as the lax version of I determined by E, and S as its strict version determined by E. Following the methodology introduced in [4] and applied in [2, 3] to introduce a polarity-based semantics for the modal logics of formal concepts, under the assumption that R and S are I-compatible (cf. Definition 2), the relations R and S can be used to define normal modal operators \([R], \langle R\rangle , [S], \langle S\rangle \) on \(\mathbb {P}^+\) defined as follows: for any \(c\in \mathbb {P}^+\),


That is, the members of [R]c are exactly those objects that satisfy (possibly by proxy of some object equivalent to them) all features in the description of c, while the members of [S]c are exactly those objects that not only satisfy all features in the description of c, but that ‘force’ all their equivalents to also satisfy them. The assumption that \(S\subseteq I\) implies that \([\![{[S] c}]\!] = S^{(0)}[(\![{c}]\!)] \subseteq I^{(0)}[(\![{c}]\!)]= [\![{c}]\!]\), hence [S]c is a sub-concept of c. The assumption that \(I \subseteq R\) implies that \([\![{c}]\!] = I^{(0)}[(\![{c}]\!)]\subseteq R^{(0)}[(\![{c}]\!)] = [\![{[R] c}]\!]\), hence [R]c is a super-concept of c. Moreover, for any \(c\in \mathbb {P}^+\),


That is, \(\langle R\rangle c\) is the concept described by those features shared not only by each member of c but also by their equivalents, while \(\langle S\rangle c\) is the concept described by the common features of those members of c which ‘force’ each of their equivalents to share them. The assumption that \(I\subseteq R\) implies that \((\![{c}]\!) = I^{(1)}[[\![{c}]\!]]\subseteq R^{(1)}[[\![{c}]\!]] = (\![{\langle R\rangle c}]\!)\), and hence \(\langle R\rangle c\) is a sub-concept of c. The assumption that \(S\subseteq I\) implies that \((\![{\langle S\rangle c}]\!) = S^{(1)}[[\![{c}]\!]] \subseteq I^{(1)}[[\![{c}]\!]] = (\![{c}]\!) \), and hence \(\langle S\rangle c\) is a super-concept of c. Summing up the discussion above, we have verified that the conditions \(I\subseteq R\) and \(S\subseteq I\) imply that the following sequents of the modal logic of formal concepts are valid on Kent’s basic structures:
where \(\Box _s\) is interpreted as [S], \(\Box _{\ell }\) as [R], \(\Diamond _s\) as \(\langle S\rangle \) and \(\Diamond _{\ell }\) as \(\langle R\rangle \). Translated algebraically, these conditions say that \(\Box _s\) and \(\Diamond _{\ell }\) are deflationary, as interior operators are, \(\Diamond _s\) and \(\Box _{\ell }\) are inflationary, as closure operators are. Hence, it is natural to ask under which conditions they (i.e. their semantic interpretations) are indeed closure/interior operators. The next definition and lemma provide answers to this question.
Definition 4
An Rfc \(\mathbb {G} = (\mathbb {P}, E)\) is amenable if E, R and S (defined as in (1)) are I-compatible.Footnote 3
Lemma 3
For any amenable Rfc \(\mathbb {G} = (\mathbb {P}, E)\), if and R and S are defined as in (1), then
Proof
Let \(x\in X\). To show that \(R^{(0)}[I^{(1)}[R^{(0)}[x]]]\subseteq R^{(0)}[x]\), let \(a\in R^{(0)}[I^{(1)}[R^{(0)}[x]]]\). By adjunction, this is equivalent to \(I^{(1)}[R^{(0)}[x]]\subseteq R^{(1)}[a]\), which implies that \( I^{(0)}[R^{(1)}[a]]\subseteq I^{(0)}[I^{(1)}[R^{(0)}[x]]] = R^{(0)}[x]\), the last equality holding since R is I-compatible by assumption. Moreover, \(I\subseteq R\) (cf. Lemma 2) implies that \(I^{(1)}[a]\subseteq R^{(1)}[a]\), which implies that \( I^{(0)}[R^{(1)}[a]]\subseteq I^{(0)}[I^{(1)}[a]] \subseteq (a)_E\), the last inclusion holding since E is I-compatible by assumption. Hence, \(I^{(0)}[R^{(1)}[a]]\subseteq R^{(0)}[x]\cap (a)_E\). Suppose for contradiction that \(a\notin R^{(0)}[x]\). By the E-definability of R, this is equivalent to \(R^{(0)}[x]\cap (a)_E = \varnothing \). Hence \(I^{(0)}[R^{(1)}[a]] = \varnothing \), from which it follows that \(R^{(1)}[a] = I^{(1)}[I^{(0)}[R^{(1)}[a]]] = I^{(1)}[\varnothing ] = X\). Hence, \(x\in R^{(1)}[a]\), i.e. \(a\in R^{(0)}[x]\), against the assumption that \(a\notin R^{(0)}[x]\).
Let \(x\in X\). To show that \(S^{(0)}[x]\subseteq S^{(0)}[I^{(1)}[S^{(0)}[x]]]\), assume that \(a\in S^{(0)}[x]\). Since S is E-definable by construction, this is equivalent to \((a)_E\subseteq S^{(0)}[x]\). To show that \(a\in S^{(0)}[I^{(1)}[S^{(0)}[x]]]\), we need to show that bIy for any \(b\in (a)_E\) and any \(y\in I^{(1)}[S^{(0)}[x]]\). Let \(y\in I^{(1)}[S^{(0)}[x]]\). Hence, by definition, \(b'Iy\) for every \(b'\in S^{(0)}[x]\). Since \((a)_E\subseteq S^{(0)}[x]\), this implies that bIy for any \(b\in (a)_E\), as required.
By the general theory developed in [4] and applied to enriched formal contexts in [18, Proposition 5], properties (8) guarantee that the following sequents of the modal logic of formal concepts are also valid on amenable Rfc’s:
Finally, again by [18, Proposition 5], the fact that by construction \(\Box _s\) and \(\Diamond _s\) (resp. \(\Box _{\ell }\) and \(\Diamond _{\ell }\)) are interpreted by operations defined in terms of the same relation guarantees the validity of the following sequents on amenable Rfc’s:
Axioms (7), (9) and (10) constitute the starting point and motivation for the proof-theoretic investigation of the logics associated to varieties of algebraic structures which can be understood as abstractions of amenable Rfc’s. We define these varieties in the next section.
4 Kent Algebras
In the present section, we introduce basic Kent algebras (and the variety of abstract Kent algebras (aKa) to which they naturally belong), as algebraic generalizations of amenable Rfc’s, and then introduce some subvarieties of aKas in the style of [20, 21].
Definition 5
A basic Kent algebra is a structure \(\mathbb {A} = (\mathbb {L}, \Box _s, \Diamond _s, \Box _{\ell }, \Diamond _{\ell })\) such that \(\mathbb {L}\) is a complete lattice, and \(\Box _s, \Diamond _s, \Box _{\ell }, \Diamond _{\ell }\) are unary operations on \(\mathbb {L}\) such that for all \(a, b\in \mathbb {L}\),
and for any \(a\in \mathbb {L}\),
We let \({\mathsf {KA}}^{+}\) denote the class of basic Kent algebras.
From (11) it follows that, in basic Kent algebras, \(\Box _s\) and \(\Box _{\ell }\) are completely meet-preserving, \(\Diamond _s\) and \(\Diamond _{\ell }\) are completely join-preserving. For any amenable Rfc \(\mathbb {G} = (\mathbb {P}, E)\), if R and S are defined as in (1), then
where \(\mathbb {P}^+\) is the concept lattice of the formal context \(\mathbb {P}\) and \([S], \langle S\rangle , [R], \langle R\rangle \) are defined as in (3)–(6). The following proposition is an immediate consequence of [18, Proposition 5], using Lemmas 2 and 3, and the fact that [R] and \(\langle R\rangle \) (resp. [S] and \(\langle S\rangle \)) are defined using the same relation.
Proposition 1
If \(\mathbb {G} = (\mathbb {P}, E)\) is an amenable Rfc, then \(\mathbb {G}^+\) is a basic Kent algebra.
The natural variety containing basic Kent algebras is defined as follows.
Definition 6
An abstract Kent algebra (aKa) is a structure \(\mathbb {A} = (\mathbb {L}, \Box _s, \Diamond _s, \Box _{\ell }, \Diamond _{\ell })\) such that \(\mathbb {L}\) is a lattice, and \(\Box _s, \Diamond _s, \Box _{\ell }, \Diamond _{\ell }\) are unary operations on \(\mathbb {L}\) validating (11), (12) and (13). We let \({\mathsf {KA}}\) denote the class of abstract Kent algebras.
From (11) it follows that, in aKas, \(\Box _s\) and \(\Box _{\ell }\) are finitely meet-preserving, \(\Diamond _s\) and \(\Diamond _{\ell }\) are finitely join-preserving.
Lemma 4
For any aKa \(\mathbb {A} = (\mathbb {L}, \Box _s, \Diamond _s, \Box _{\ell }, \Diamond _{\ell })\) and every \(a\in \mathbb {L}\),
Proof
The inequalities in (15) are straightforward consequences of (11). The inequalities in (14) and (16) follow from (12) and (15), using the transitivity of the order. The inequalities in (17) follow from those in (13) using (11).
Conditions (17) define the‘Kent algebra’ counterparts of topological quasi Boolean algebras 5 (tqBa5) [21]. In the next definition, we introduce ‘Kent algebra’ counterparts of some other varieties considered in [21] (omitting those the axiomatization of which involves negation and those that cannot be captured by multi-type analytic rules in the present setting), and also varieties characterized by interaction axioms between lax and strict connectives which follow the pattern of the 5-axioms in rough algebras.
Definition 7
An aKa \(\mathbb {A}\) as above is an aKa5’ if for any \(a\in \mathbb {L}\),
is a K-IA3\(_s\) if for any \(a, b\in \mathbb {L}\),
and is a K-IA3\(_{\ell }\) if for any \(a, b\in \mathbb {L}\),
Notice that the axioms above do not need to be analytic inductive in order for the resulting logic to be (multi-type) properly displayable: interestingly, the third and fourth inequality in (18) are not analytic inductive (cf. [7, Definition 55]), but are equivalent to analytic inductive inequalities in the multi-type language of the heterogeneous algebras discussed in the next section. This is an illustration of the technical advantage of moving to the multi-type setting (see also [10, Introduction, Sect. 4], where it is discussed how the multi-type approach was key in overcoming the difficulties encountered by the authors of [17] in introducing an analytic calculus for IA3).
5 Multi-type Presentation of Kent Algebras
Similarly to what holds for rough algebras (cf. [10, Sect. 3]), since the modal operations of any aKa \(\mathbb {A} = (\mathbb {L}, \Box _s, \Diamond _s, \Box _{\ell }, \Diamond _{\ell })\) are either interior operators or closure operators, each of them factorizes into a pair of adjoint normal modal operators which are retractions or co-retractions, as illustrated in the following table:

where \(\mathrm {S}_I:= \Box _s[\mathbb {L}]\), \(\mathrm {S}_C:= \Diamond _s[\mathbb {L}]\), \(\mathrm {L}_C:= \Box _{\ell }[\mathbb {L}]\), and \(\mathrm {L}_I:= \Diamond _s[\mathbb {L}]\), and such that for all \(\alpha \in \mathrm {S}_I\), \(\delta \in \mathrm {S}_C\), \(a\in \mathbb {L}\), \(\pi \in \mathrm {L}_I\), \(\sigma \in \mathrm {L}_C\),

Again similarly to what observed in [10], the lattice structure of \(\mathbb {L}\) can be exported to each of the sets \(\mathrm {S}_I, \mathrm {S}_C, \mathrm {L}_C\) and \(\mathrm {L}_I\) via the corresponding pair of modal operators as follows.
Definition 8
For any aKa \(\mathbb {A}\), the strict interior kernel \(\mathsf {S}_{\mathsf{I}}= (\mathrm {S}_I, \cup _I, \cap _I, \mathrm {t}_I, \mathrm {f}_I)\) and the strict closure kernel \(\mathsf {S}_{\mathsf{C}} = (\mathrm {S}_C, \cup _C, \cap _C, \mathrm {t}_C, \mathrm {f}_C)\) are such that, for all \(\alpha , \beta \in S_I\), and all \(\delta , \gamma \in S_C\),

The lax interior kernel \(\mathsf {L}_{\mathsf{I}}= (\mathrm {L}_I, \sqcup _I, \sqcap _I, 1_\mathbb {I}, 0_\mathbb {I})\) and the lax closure kernel \(\mathsf {L_C} = (\mathrm {L}_C, \sqcup _C, \sqcap _C, 1_\mathbb {C}, 0_\mathbb {C})\) are such that, for all \(\pi , \xi \in L_I\), and all \(\sigma , \tau \in L_C\),

Similarly to what observed in [10], it is easy to verify that the algebras defined above are lattices, and the operations indicated with a circle (either black or white) are lattice homomorphisms (i.e. are both normal box-type and normal diamond-type operators). The construction above justifies the following definition of class of heterogeneous algebras equivalent to aKas:
Definition 9
A heterogeneous aKa (haKa) is a tuple

such that:
-
H1 \(\mathbb {L}, \mathsf {S}_{\mathsf{I}},\mathsf {S}_{\mathsf{C}}, \mathsf {L}_{\mathsf{I}},\mathsf {L_C}\) are bounded lattices;
-
H2 \(\circ _I\,: \mathsf {S}_{\mathsf{I}}\hookrightarrow \mathbb {L}\), \(\circ _C\,: \mathsf {S}_{\mathsf{C}}\hookrightarrow \mathbb {L}\), \({\bullet _I}\,: \mathbb {L}\twoheadrightarrow \mathsf {L}_{\mathsf{I}}\), \({\bullet _C}\,: \mathbb {L}\twoheadrightarrow \mathsf {L_C}\) are lattice homomorphisms;
-
H3
 ;
; -
H4
 Footnote 4
Footnote 4
The haKas corresponding to the varieties of Definition 7 are defined as follows:

Notice that the inequalities defining haKa5’ are all analytic inductive. A heterogeneous algebra \(\mathbb {H}\) is perfect if every lattice in the signature of \(\mathbb {H}\) is perfect (cf. [4, Definition 1.8]), and every homomorphism (resp. hemimorphism) in the signature of \(\mathbb {H}\) is a complete homomorphism (resp. hemimorphism).
Similarly to what discussed in [10, Sect. 3], one can readily show that the classes of haKas defined above correspond to the varieties defined in Sect. 4. That is, for any aKa \(\mathbb {A}\) one can define its corresponding haKa \(\mathbb {A}^+\) using the factorizations described at the beginning of the present section and Definition 8, and conversely, given a haKa \(\mathbb {H}\), one can define its corresponding aKa \(\mathbb {H}_+\) by endowing its first domain \(\mathbb {L}\) with modal operations defined by taking the appropriate compositions of pairs of heterogeneous maps of \(\mathbb {H}\). Then, for every \(\mathbb {K}\in \{\)aKa, aKa5’, K-IA3\(_s\), K-IA3\(_\ell \}\), letting \(\mathbb {HK}\) denote its corresponding class of heterogeneous algebras, the following holds:
Proposition 2
-
1.
If \(\mathbb {A} \in \mathbb {K}\), then \(\mathbb {A}^+\in \mathbb {HK}\).
-
2.
If \(\mathbb {H}\in \mathbb {HK}\), then \(\mathbb {H}_+\in \mathbb {K}\).
-
3.
\( \mathbb {A} \cong (\mathbb {A}^+)_+ \quad \text {and}\quad \mathbb {H} \cong (\mathbb {H}_+)^+\).
-
4.
The isomorphisms of the previous item restrict to perfect members of \(\mathbb {K}\) and \(\mathbb {HK}\).
-
5.
If \(\mathbb {A} \in \mathbb {K}\), then \(\mathbb {A}^\delta \cong ((\mathbb {A}^+)^\delta )_+\) and if \(\mathbb {H} \in \mathbb {HK}\), then \(\mathbb {H}^\delta \cong ((\mathbb {H}_+)^\delta )^+\).
6 Multi-type Calculi for the Logics of Kent Algebras
In the present section, we introduce the multi-type calculi associated with each class of algebras \(\mathsf {K}\in \{aKa, aKa5', K\text {-}IA3_{\ell }\}\). The language of these logics matches the language of haKas, and is built up from structural and operational (i.e. logical) connectives. Each structural connective is denoted by decorating its corresponding logical connective with \(\hat{ {a}}\) (resp. \(\check{ {a}}\) or \(\tilde{ {a}}\)). In what follows, we will adopt the convention that unary connectives bind more strongly than binary ones.

-
Interpretation of structural connectives as their logical counterpartsFootnote 5
-
1.
structural and operational pure \(\mathsf {L}\)-type connectives:

-
2.
structural and operational pure \(\mathsf {S}_{\mathsf{I}}\)-type and \(\mathsf {S}_{\mathsf{C}}\)-type connectives:

-
3.
structural and operational pure \(\mathsf {L}_{\mathsf{I}}\)-type and \(\mathsf {L_C}\)-type connectives:
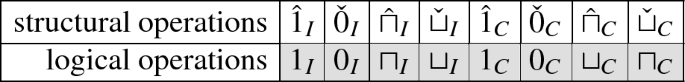
-
4.
structural and operational multi-type strict connectives:

-
5.
structural and operational multi-type lax connectives:

In what follows, we will use x, y, z as structural variables of arbitrary types, a, b, c as term variables of arbitrary types.
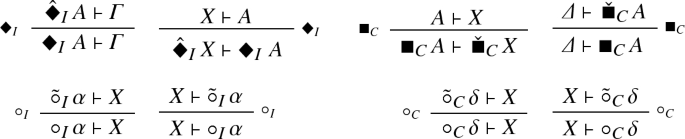
The calculus \(\mathrm {D.AKA}\) consists of the following axiom and rules.
-
Identity and Cut:

-
Multi-type display rules (we omit the display rules capturing the adjunctions \(\Diamond _I\, \dashv {\bullet _I}\, \dashv \Box _I\, \) and \(\Diamond _I\, \dashv {\bullet _I}\, \dashv \Box _I\, \)):

-
Multi-type structural rules for strict-kernel operators:

-
Multi-type structural rules for lax-kernel operators:

-
Multi-type structural rules for the correspondence between kernels:

-
Logical rules for multi-type connectives related to strict kernels:
-
Logical rules for lattice connectives:

-
Logical rules for lattice connectives:

The proper display calculi for the subvarieties of \(\mathrm {aKa}\) discussed in Sect. 4 are obtained by adding the following rules:

These calculi enjoy the properties of soundness, completeness, conservativity, cut elimination and subformula property the verification of which is standard and follows from the general theory of proper display calculi (cf. [6, 11,12,13,14, 16, 23]). These verifications are discussed in the appendix.
Notes
- 1.
In [22], sequent calculi for non-distributive versions of the logics associated with varieties of ‘rough algebras’ are introduced, which are sound and complete but without cut elimination.
- 2.
When \(B=\{a\}\) (resp. \(Y=\{x\}\)) we write \(a^{\uparrow \downarrow }\) for \(\{a\}^{\uparrow \downarrow }\) (resp. \(x^{\downarrow \uparrow }\) for \(\{x\}^{\downarrow \uparrow }\)).
- 3.
The assumption that E is I-compatible does not follow from R and S being I-compatible. Let \(\mathbb {G} = (\mathbb {P}, Id_A)\) for any polarity \(\mathbb {P}\) such that not all singleton sets of objects are Galois-stable. Hence \(E = Id_A\) is not I-compatible. However, if \(E = Id_A\), then \(R = S = I\) are I-compatible.
- 4.
Condition H3 implies that \(\blacksquare _I\,: \mathbb {L}\twoheadrightarrow \mathsf {S}_{\mathsf{I}}\) and \(\Box _I\,: \mathsf {L}_{\mathsf{I}} \hookrightarrow \mathbb {L}\) are \(\wedge \)-hemimorphisms and
 and \(\Diamond _C\,: \mathsf {L_C} \hookrightarrow \mathbb {L}\) are \(\vee \)-hemimorphisms; condition H4 implies that the black connectives are surjective and the white ones are injective.
and \(\Diamond _C\,: \mathsf {L_C} \hookrightarrow \mathbb {L}\) are \(\vee \)-hemimorphisms; condition H4 implies that the black connectives are surjective and the white ones are injective. - 5.
The connectives which appear in a grey cell in the synoptic tables will only be included in the present language at the structural level.
References
Banerjee, M., Chakraborty, M.K.: Rough sets through algebraic logic. Fundamenta Informaticae 28(3, 4), 211–221 (1996)
Conradie, W., Frittella, S., Palmigiano, A., Piazzai, M., Tzimoulis, A., Wijnberg, N.M.: Categories: how I learned to stop worrying and love two sorts. In: Väänänen, J., Hirvonen, Å., de Queiroz, R. (eds.) WoLLIC 2016. LNCS, vol. 9803, pp. 145–164. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-52921-8_10
Conradie, W., Frittella, S., Palmigiano, A., Piazzai, M., Tzimoulis, A., Wijnberg, N.M.: Toward an epistemic-logical theory of categorization. In: Proceedings of the TARK 2017. EPTCS, vol. 251, pp. 167–186 (2017)
Conradie, W., Palmigiano, A.: Algorithmic correspondence and canonicity for non-distributive logics. Annals of Pure and Applied Logic ArXiv:1603.08515
Frittella, S., Greco, G., Kurz, A., Palmigiano, A., Sikimić, V.: Multi-type sequent calculi. In: Indrzejczak, A., et al. (eds.) Proceedings of the Trends in Logic XIII, pp. 81–93 (2014)
Frittella, S., Greco, G., Palmigiano, A., Yang, F.: A multi-type calculus for inquisitive logic. In: Väänänen, J., Hirvonen, Å., de Queiroz, R. (eds.) WoLLIC 2016. LNCS, vol. 9803, pp. 215–233. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-52921-8_14
Greco, G., Ma, M., Palmigiano, A., Tzimoulis, A., Zhao, Z.: Unified correspondence as a proof-theoretic tool. J. Logic Comput. 28(7), 1367–1442 (2018)
Ganter, B., Wille, R.: Formal Concept Analysis: Mathematical Foundations. Springer, Heidelberg (1999). https://doi.org/10.1007/978-3-642-59830-2
Greco, G., Kurz, A., Palmigiano, A.: Dynamic epistemic logic displayed. In: Grossi, D., Roy, O., Huang, H. (eds.) LORI 2013. LNCS, vol. 8196, pp. 135–148. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40948-6_11
Greco, G., Liang, F., Manoorkar, K., Palmigiano, A.: Proper multi-type display calculi for rough algebras. arXiv preprint 1808.07278
Greco, G., Liang, F., Moshier, M.A., Palmigiano, A.: Multi-type display calculus for semi De Morgan logic. In: Kennedy, J., de Queiroz, R.J.G.B. (eds.) WoLLIC 2017. LNCS, vol. 10388, pp. 199–215. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-55386-2_14
Greco, G., Liang, F., Palmigiano, A., Rivieccio, U.: Bilattice logic properly displayed. Fuzzy Sets Syst. (2018). https://doi.org/10.1016/j.fss.2018.05.007
Greco, G., Palmigiano, A.: Linear logic properly displayed. arXiv preprint: 1611.04184
Greco, G., Palmigiano, A.: Lattice logic properly displayed. In: Kennedy, J., de Queiroz, R.J.G.B. (eds.) WoLLIC 2017. LNCS, vol. 10388, pp. 153–169. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-55386-2_11
Kent, R.E.: Rough concept analysis: a synthesis of rough sets and formal concept analysis. Fundamenta Informaticae 27(2, 3), 169–181 (1996)
Liang, F.: Multi-type algebraic proof theory. Ph.D. thesis, TU Delft (2018)
Ma, M., Chakraborty, M.K., Lin, Z.: Sequent calculi for varieties of topological quasi-Boolean algebras. In: Nguyen, H.S., Ha, Q.-T., Li, T., Przybyła-Kasperek, M. (eds.) IJCRS 2018. LNCS (LNAI), vol. 11103, pp. 309–322. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-99368-3_24
Manoorkar, K., Nazari, S., Palmigiano, A., Tzimoulis, A., Wijnberg, N.M.: Rough concepts (2018, Submitted)
Pawlak, Z.: Rough set theory and its applications to data analysis. Cybern. Syst. 29(7), 661–688 (1998)
Saha, A., Sen, J., Chakraborty, M.K.: Algebraic structures in the vicinity of pre-rough algebra and their logics. Inf. Sci. 282, 296–320 (2014)
Saha, A., Sen, J., Chakraborty, M.K.: Algebraic structures in the vicinity of pre-rough algebra and their logics II. Inf. Sci. 333, 44–60 (2016)
Sen, J., Chakraborty, M.K.: A study of interconnections between rough and 3-valued Łukasiewicz logics. Fundamenta Informaticae 51(3), 311–324 (2002)
Tzimoulis, A.: Algebraic and proof-theoretic foundations of the logics for social behaviour. Ph.D. thesis, TUDelft (2018)
Wansing, H.: Sequent systems for modal logics. In: Gabbay, D.M., Guenthner, F. (eds.) Handbook of Philosophical Logic, vol. 8, pp. 61–145. Springer, Dordrecht (2002). https://doi.org/10.1007/978-94-010-0387-2_2
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Properties
A Properties
Throughout this section, we let \(\mathsf {K}\in \{aKa, aKa5', K\text {-}IA3_{\ell }\}\), and \(\mathsf {HK}\) the class of heterogeneous algebras corresponding to \(\mathsf {K}\). Further, we let \(\text {D.K}\) denote the multi-type calculus for the logic \(\text {H.K}\) canonically associated with \(\mathsf {K}\).
1.1 A.1 Soundness for Perfect \(\mathsf {HK}\) Algebras
The verification of the soundness of the rules of \(\text {D.K} \) w.r.t. the semantics of perfect elements of \(\mathsf {HK}\) (see Definition 9) is analogous to that of many other multi-type calculi (cf. [6, 11,12,13,14, 16, 23]). Here we only discuss the soundness of the rule \(k\text {-}ia3_{\ell }\). By definition, the following quasi-inequality is valid on every K-IA3\(_{\ell }\):
This quasi-inequality equivalently translates into the multi-type language as follows:
By adjunction, the quasi-inequality above can be equivalently rewritten as follows:
which, thanks to a well known property of adjoint maps, simplifies as:
Hence, the quasi-inequality above is equivalent to the following inequality:
The inequality above is analytic inductive (cf. [7, Definition 55]), and hence running ALBA on this inequality produces:

The last quasi-inequality above is the semantic translation of the rule \(k\text {-}ia3_{\ell }\):

which we then proved to be sound on every perfect heterogeneous K-IA3\(_{\ell }\), by the soundness of the ALBA steps. Likewise, the defining condition of K-IA3\(_{\ell }\) translates into the inequality

which, however, is not analytic inductive, and hence it cannot be transformed into an analytic rule via ALBA.
1.2 A.2 Completeness
Let \(A^\tau \vdash B^\tau \) be the translation of any sequent \(A\vdash B\) in the language of \(\text {H.K}\) into the language of \(\text {D.K}\) induced by the correspondence between \(\mathsf {K}\) and \(\mathsf {HK}\) described in Sect. 5.
Proposition 3
For every \(\text {H.K}\)-derivable sequent \(A {\ \vdash \ }B\), the sequent \(A^{\tau } {\ \vdash \ }B^{\tau }\) is derivable in \(\text {D.K}\).
Below we provide the multi-type translations of the single-type sequents corresponding to inequalities (11). All of them are derivable in D.AKA by logical introduction rules, display rules, and the rules \(\,\check{\Box }\, \,\tilde{{\bullet }}\, \) and  .
.

Below we provide the multi-type translations of the single-type sequents corresponding to inequalities (12) and (13), respectively. All of them are derivable in D.AKA by logical introduction rules and display rules.

Below we provide the multi-type translation of the single-type sequents corresponding to inequalities (18). All of them are derivable in D.AKA5’.

Below we provide the multi-type translations of the single-type rules corresponding to quasi-inequality (20), respectively.

Below, we derive (20). Firstly, \(A \wedge \Box _C\, {\bullet _C}\, B {\ \vdash \ }\Diamond _I\, {\bullet _I}\, A \vee B\) is derivable via \(k\text {-}ia3_\ell \) by means of the following derivation \(\mathcal {D}\):

Assuming \(\Diamond _I\, {\bullet _I}\, A {\ \vdash \ }\Diamond _I\, {\bullet _I}\, B\) and \(\Box _C\, {\bullet _C}\, A {\ \vdash \ }\Box _C\, {\bullet _C}\, B\), we derive \(A{\ \vdash \ }B\) via cut as follows:

1.3 A.3 Conservativity
To argue that \(\text {D.K}\) is conservative w.r.t. \(\text {H.K}\), we follow the standard proof strategy discussed in [7, 9]. We need to show that, for all formulas A and B in the language of \(\text {H.K}\), if \(A^\tau \vdash B^\tau \) is a \(\text {D.K}\)-derivable sequent, then \(A \vdash B\) is derivable in \(\text {H.K}\). This claim can be proved using the following facts: (a) The rules of \(\text {D.K}\) are sound w.r.t. perfect members of \(\mathsf {HK}\) (cf. Sect. A.1); (b) \(\text {H.K}\) is complete w.r.t. the class of perfect algebras in \(\mathsf {K}\); (c) A perfect element of \(\mathsf {K}\) is equivalently presented as a perfect member of \(\mathsf {HK}\) so that the semantic consequence relations arising from each type of structures preserve and reflect the translation. Let A, B be as above. If \(A^\tau \vdash B^\tau \) is \(\text {D.K}\)-derivable, then by (a), \(\models _{\mathbb {HK}} A^\tau \vdash B^\tau \). By (c), this implies that \(\models _{\mathsf {K}} A\vdash B\), where \(\models _{\mathsf {K}}\) denotes the semantic consequence relation arising from the perfect members of class \(\mathsf {K}\). By (b), this implies that \(A\vdash B\) is derivable in \(\text {H.K}\), as required.
1.4 A.4 Cut Elimination and Subformula Property
Cut elimination and subformula property for each \(\text {D.K}\) are obtained by verifying the assumptions of [5, Theorem 4.1]. All of them except \(\mathrm {C}'_8\) are readily satisfied by inspecting the rules. Condition \(\mathrm {C}'_8\) requires to check that reduction steps can be performed for every application of cut in which both cut-formulas are principal, which either remove the original cut altogether or replace it by one or more cuts on formulas of strictly lower complexity. In what follows, we only show \(\mathrm {C}'_8\) for some heterogeneous connectives.


The remaining cases are analogous.
Rights and permissions
Copyright information
© 2019 Springer-Verlag GmbH Germany, part of Springer Nature
About this paper
Cite this paper
Greco, G., Jipsen, P., Manoorkar, K., Palmigiano, A., Tzimoulis, A. (2019). Logics for Rough Concept Analysis. In: Khan, M., Manuel, A. (eds) Logic and Its Applications. ICLA 2019. Lecture Notes in Computer Science(), vol 11600. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-58771-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-662-58771-3_14
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-58770-6
Online ISBN: 978-3-662-58771-3
eBook Packages: Computer ScienceComputer Science (R0)





 ;
;


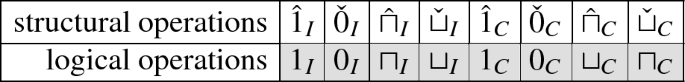










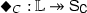 and
and