Abstract
We propose a formal model of Bitcoin transactions, which is sufficiently abstract to enable formal reasoning, and at the same time is concrete enough to serve as an alternative documentation to Bitcoin. We use our model to formally prove some well-formedness properties of the Bitcoin blockchain, for instance that each transaction can only be spent once. We release an open-source tool through which programmers can write transactions in our abstract model, and compile them into standard Bitcoin transactions.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
In recent years we have observed a growing interest around cryptocurrencies. Bitcoin [13], the first decentralized cryptocurrency, was introduced in 2009, and through the years it has consolidated its position as the most popular one. Bitcoin and other cryptocurrencies have pushed forward the concept of decentralization, providing means for reliable interactions between mutually distrusting parties on an open network.
The nodes of the Bitcoin network maintain a public and immutable data structure, called blockchain. The blockchain stores the historical record of all transfers of bitcoins, which are referred to as transactions. When a node updates the blockchain, the other nodes verify if the appended transactions are valid, e.g. by checking if the conditions specified in scripts are satisfied. Scripts are programmable boolean functions: in their standard (and mostly used) form they verify a digital signature against a public key. Since the blockchain is immutable, tampering with a stored transaction would result in the invalidation of all the subsequent ones. Updating the state of the blockchain, i.e. appending new transactions, requires solving a moderately difficult cryptographic puzzle. In case of conflicting updates, the chain that required the largest computational effort is considered the valid one. Hence, the immutability and the consistency of the blockchain is bounded by the total computational power of honest nodes. An adversary with enough resources can append invalid transactions, e.g. with incorrect digital signatures, or rewrite a part of the blockchain, e.g. to perform a double-spending attack. The attack consists in paying someone by publishing a transaction on the blockchain, and then removing it (making the funds unspent).
Besides the intended monetary application, the Bitcoin blockchain can be seen as a way to consistently maintain the state of a system over a peer-to-peer network, without the need of a trusted authority. If the system is a currency, its state is the amount of funds in each account. This concept can be generalised to the case where the system is a smart contract [15], namely an executable computer protocol which can also handle transfers of currency. The idea of exploiting the Bitcoin blockchain to build smart contracts has recently been explored by several works. Lotteries [2, 5, 6, 11], gambling games [10], contingent payments [4], covenants [12, 14], and other kinds of fair computations [1, 9] are some examples of the capabilities of Bitcoin as a platform for smart contracts.
Smart contracts often rely on features of Bitcoin that go beyond the standard transfers of currency. For instance, while the vast majority of Bitcoin transactions uses scripts only to verify signatures, smart contracts like the above-mentioned ones exploit more complex scripts, e.g. to determine the winner of a lottery, or to check if a secret has been revealed. Smart contracts may also exploit other (infrequently used) features of Bitcoin, e.g. various signature modifiers, and temporal constraints on transactions.
As a matter of fact, using these advanced features to design a new smart contract is not a trivial matter, for two reasons. First, while the overall behaviour of Bitcoin is clear, the details of many of its crucial aspects are poorly documented. To understand the details of how a mechanism actually works, one has to explore various web pages (often inaccurate, or inconsistent, or overly technical), and eventually resort to the source code of the Bitcoin clientFootnote 1 to have the correct answer. Second, the description of advanced features is often too concrete to be effectively used in the design and analysis of a smart contract (indeed, in many cases the only available description coincides with the implementation).
Contributions. We propose a formal model of Bitcoin transactions. This model is abstract enough to allow for formal reasoning on the behaviour of Bitcoin transactions. For instance, we use our model to formally prove some properties of the Bitcoin blockchain, e.g. that transactions cannot be spent twice (Theorem 1), and that the overall value contained in the blockchains (excluding the coinbase transactions) is decreasing (Theorem 2).
Our model formally specifies some poorly documented features of Bitcoin, e.g. transaction signatures and signature modifiers (Definition 4), output scripts (Definitions 1 and 7), multi-signature verification (Definition 6), Segregated Witnesses (Definitions 2 and 9), paving the way towards automatic verification.
We make available an open-source toolFootnote 2 which translates transactions specified in our model to standard Bitcoin transactions.
Structure of the Paper. Section. 2 briefly recaps Bitcoin transactions, which we formalise in Sect. 3. Besides transactions, we also provide an high-level model of the blockchain, and we study its basic properties. In Sect. 4 we illustrate, through a basic case study, the impact of the Segregated Witness feature on the expressiveness of Bitcoin smart contracts. In Sect. 5 we show how to translate transactions from our model to standard Bitcoin transactions. We discuss the differences between our model and the actual Bitcoin in Sect. 6.
2 Bitcoin Transactions in a Nutshell
We now give a minimalistic introduction to the behaviour of Bitcoin transactions (see [7] for a general survey on the other aspects of Bitcoin).
Users interact with Bitcoin through addresses, which they can freely generate. Transactions describe transfers of bitcoins ( ) between addresses. The log of all transactions is recorded on a public, immutable and decentralised data structure called blockchain. To explain how the blockchain works, consider the transactions
) between addresses. The log of all transactions is recorded on a public, immutable and decentralised data structure called blockchain. To explain how the blockchain works, consider the transactions  and
and  displayed in Fig. 1. The transaction
displayed in Fig. 1. The transaction  contains
contains  , which can be redeemed by putting on the blockchain a transaction (e.g.,
, which can be redeemed by putting on the blockchain a transaction (e.g.,  ), whose
), whose  field is a reference to
field is a reference to  . To redeem
. To redeem  , the witness of the redeeming transaction (the value in its
, the witness of the redeeming transaction (the value in its  field) must make the output script of
field) must make the output script of  (the first element of the pair in the
(the first element of the pair in the  field) evaluate to true. When this happens, the value of
field) evaluate to true. When this happens, the value of  is transferred to the new transaction, and
is transferred to the new transaction, and  is no longer redeemable.
is no longer redeemable.
In the example displayed before, the output script of  evaluates to true when receiving a digital signature on the redeeming transaction
evaluates to true when receiving a digital signature on the redeeming transaction  , with a given key pair \(k_{}\). We denote with \(\mathsf{versig}_{k_{}}({x_{}})\) the verification of the signature \(x_{}\) on the redeeming transaction: of course, since the signature must be included in the witness of the redeeming transaction, it will consider all the parts of that transaction except its
, with a given key pair \(k_{}\). We denote with \(\mathsf{versig}_{k_{}}({x_{}})\) the verification of the signature \(x_{}\) on the redeeming transaction: of course, since the signature must be included in the witness of the redeeming transaction, it will consider all the parts of that transaction except its  field. We assume that \(\sigma \) is the signature of
field. We assume that \(\sigma \) is the signature of  .
.
Now, assume that the blockchain contains  , not yet redeemed, and someone tries to append
, not yet redeemed, and someone tries to append  . To validate this operation, the nodes of the Bitcoin network check that \(v_{1} \le v_{0}\), and then they evaluate the output script of
. To validate this operation, the nodes of the Bitcoin network check that \(v_{1} \le v_{0}\), and then they evaluate the output script of  , by instantiating its formal parameter \(x_{}\) to the signature \(\sigma \) in the witness of
, by instantiating its formal parameter \(x_{}\) to the signature \(\sigma \) in the witness of  . The function \(\mathsf{versig}_{k_{}}({\sigma })\) verifies that \(\sigma \) is actually the signature of
. The function \(\mathsf{versig}_{k_{}}({\sigma })\) verifies that \(\sigma \) is actually the signature of  : therefore, the output script succeeds, and
: therefore, the output script succeeds, and  redeems
redeems  . Subsequently, a new transaction can redeem
. Subsequently, a new transaction can redeem  by satisfying its output script \(\lambda y_{}{.}e\) (not specified in the figure).
by satisfying its output script \(\lambda y_{}{.}e\) (not specified in the figure).
Bitcoin transactions may be more general than the ones illustrated by the previous example. First, there can be multiple inputs and outputs. Each output has an associated output script and value, and can be redeemed independently from the others. Consequently,  fields must specify which output they are redeeming. A transaction with multiple inputs associates a witness to each of them. The sum of the values of all the inputs must be greater or equal to the sum of the values of all the outputs, otherwise the transaction is considered invalid. In its general form, the output script is a program in a (non Turing-complete) scripting language, featuring a limited set of logic, arithmetic, and cryptographic operators. Finally, a transaction can specify time constraints (absolute, or relative to its input transactions) about when it can appear on the blockchain.
fields must specify which output they are redeeming. A transaction with multiple inputs associates a witness to each of them. The sum of the values of all the inputs must be greater or equal to the sum of the values of all the outputs, otherwise the transaction is considered invalid. In its general form, the output script is a program in a (non Turing-complete) scripting language, featuring a limited set of logic, arithmetic, and cryptographic operators. Finally, a transaction can specify time constraints (absolute, or relative to its input transactions) about when it can appear on the blockchain.
3 A Formal Model of Bitcoin Transactions
In this section we introduce a formal model of Bitcoin transactions. We start in Sect. 3.1 by defining the scripts that can be used in transaction outputs. Then, in Sect. 3.2 we formalise transactions, and in Sect. 3.3 we define a signature scheme for them. Sections 3.4 and 3.5 give semantics, respectively, to scripts and transactions. In Sect. 3.6 we model the Bitcoin blockchain, and in particular we define the crucial notion of consistency, which corresponds to the one enforced by the Bitcoin consensus protocol. We then state a few results about consistent blockchains (their proofs are in Appendix A).
We start by introducing some auxiliary notation. We assume several sets, ranged over by meta-variables as shown in the left column of Table 1. We use the bold notation to denote finite sequences of elements. We denote with  the i-th element of a sequence
the i-th element of a sequence  , i.e.
, i.e.  if
if  , and with
, and with  the subsequence of
the subsequence of  starting from the i-th element and ending to the j-th element. We denote with
starting from the i-th element and ending to the j-th element. We denote with  the number of elements of \({{\varvec{x}}}\), and with \([]\) the empty sequence. We denote with \(f: A \rightharpoonup B\) a partial function f from A to B, with \({\text {dom}} {f}\) the domain of f, i.e. the subset of A where f is defined, and with \({\text {ran}} {f}\) the range of f, i.e.
the number of elements of \({{\varvec{x}}}\), and with \([]\) the empty sequence. We denote with \(f: A \rightharpoonup B\) a partial function f from A to B, with \({\text {dom}} {f}\) the domain of f, i.e. the subset of A where f is defined, and with \({\text {ran}} {f}\) the range of f, i.e.  . We use \(\bot \) to represent an “undefined” element; in particular, when the element is a partial function, \(\bot \) denotes the function with empty domain. For a pair (x, y), we define \( fst {(x,y)} = x\) and \( snd {(x,y)} = y\).
. We use \(\bot \) to represent an “undefined” element; in particular, when the element is a partial function, \(\bot \) denotes the function with empty domain. For a pair (x, y), we define \( fst {(x,y)} = x\) and \( snd {(x,y)} = y\).
3.1 Scripts
Each output in a Bitcoin transaction contains a script, which is used to establish when the output can be redeemed by another transaction. Intuitively, a script is a first-order function (written in a non Turing-equivalent language), which is applied to the witness provided by the redeeming transaction. The output can be redeemed only if such function application evaluates to true.
In our model, we abstract from the actual stack-based scripting language implemented in BitcoinFootnote 3, by using instead a minimalistic language of expressions.
Definition 1 (Scripts)
We define the set Exp of script expressions (ranged over by \(e, e', \dots \)) as follows:

We denote with Script the set of terms of the form \(\lambda \mathbf {z}{.}e\) such that all the variables in \(e\) occur in \({{\varvec{z}}}\).
Besides some basic arithmetic and logical operators, script expressions include a few operators inspired from the actual Bitcoin scripting language. The expression  denotes the size, in bytes, of the evaluation of \(e\). The expression \(\mathsf{H}(e)\) evaluates to the hash of \(e\). The expression
denotes the size, in bytes, of the evaluation of \(e\). The expression \(\mathsf{H}(e)\) evaluates to the hash of \(e\). The expression  takes as arguments a sequence of m script expressions, representing signatures of the enclosing transactions, and a sequence of n public keys. Intuitively, it evaluates to true whenever the provided signatures are verified by using m out of the n provided keys. The expressions
takes as arguments a sequence of m script expressions, representing signatures of the enclosing transactions, and a sequence of n public keys. Intuitively, it evaluates to true whenever the provided signatures are verified by using m out of the n provided keys. The expressions  and
and  define temporal constraints (see Sect. 3.4). They evaluate as \(e\) if the constraints are satisfied, otherwise they fail.
define temporal constraints (see Sect. 3.4). They evaluate as \(e\) if the constraints are satisfied, otherwise they fail.
Notation 1
We use the following syntactic sugar for expressions: (i) \( false \) to denote \(1~\textsf {=}~0\) (ii) \( true \) to denote \(1~\textsf {=}~1\) (iii) \(e\wedge e'\) to denote \(\mathsf {if}~{e}~\mathsf {then}~{e'}~\mathsf {else}~{ false }\) (iv) \(e\vee e'\) to denote \(\mathsf {if}~{e}~\mathsf {then}~{ true }~\mathsf {else}~{e'}\) (v) \(\mathsf{not}~{e}\) to denote \(\mathsf {if}~{e}~\mathsf {then}~{ false }~\mathsf {else}~{ true }\).
3.2 Transactions
The following definition formalises Bitcoin transactions.
Definition 2 (Transactions)
We inductively define the set \(\textsf {Tx} \) of transactions as follows. A transaction  is a tuple
is a tuple  , where:
, where:
-

-
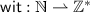 , where
, where 
-

-

-
 , where
, where 
where, for all  ,
,  and
and  .
.
We denote with  the value of field
the value of field  of
of  , for
, for  .
.
We say that  is initial when
is initial when  and
and  .
.
The fields  and
and  represent, respectively, the inputs and the outputs of a transaction. There is an input for each
represent, respectively, the inputs and the outputs of a transaction. There is an input for each  , and an output for each
, and an output for each  . When
. When  , it means that the i-th input of
, it means that the i-th input of  wants to redeem the j-th output of
wants to redeem the j-th output of  . The side condition
. The side condition  ensures that inputs are pairwise distinct. The side condition
ensures that inputs are pairwise distinct. The side condition  is related to the Segregated Witness (SegWit) featureFootnote 4, and it requires that the witness of the input transaction is left unspecified. The output
is related to the Segregated Witness (SegWit) featureFootnote 4, and it requires that the witness of the input transaction is left unspecified. The output  is a pair
is a pair  , meaning that \(v_{}\) Satoshis (
, meaning that \(v_{}\) Satoshis ( Satoshis) can be redeemed by whoever can provide a witness which satisfies \(\lambda {{\varvec{z}}}{.}e\). Such witness is defined by
Satoshis) can be redeemed by whoever can provide a witness which satisfies \(\lambda {{\varvec{z}}}{.}e\). Such witness is defined by  . The fields
. The fields  and
and  specify a constraint on when
specify a constraint on when  can be put on the blockchain: the first in absolute terms, whereas the second is relative to the transaction in the input
can be put on the blockchain: the first in absolute terms, whereas the second is relative to the transaction in the input  . More specifically,
. More specifically,  means that
means that  can appear on the blockchain only after time \(t_{}\). If
can appear on the blockchain only after time \(t_{}\). If  , then
, then  can appear only after time \(t_{}\) since the transaction in
can appear only after time \(t_{}\) since the transaction in  appeared.
appeared.
To improve readability, we use the following conventions: (i) if  has exactly one input, we denote it by
has exactly one input, we denote it by  (omitting the index, which we assume to be 1); We act similarly for
(omitting the index, which we assume to be 1); We act similarly for  ,
,  , and
, and  ; (ii) if
; (ii) if  , we omit it (similarly for
, we omit it (similarly for  when it is \(\bot \)); (iii) we denote with
when it is \(\bot \)); (iii) we denote with  and
and  , respectively, the first and the second element of the pair
, respectively, the first and the second element of the pair  .
.
3.3 Transaction Signatures
We extend to transactions the signing and verification functions of the signature schemes, denoted respectively as  and
and  . For simplicity, although we will always use
. For simplicity, although we will always use  for key pairs, we implicitly assume that
for key pairs, we implicitly assume that  only uses the private part
only uses the private part  , while
, while  only uses the public part \(k_{p}\).
only uses the public part \(k_{p}\).
In Bitcoin, transaction signatures never apply to the whole transaction: users can specify which parts of a transaction are signed (with the exception of the  field, which is never signed). However, not all possible combinations of transaction parts are possible; the legit ones are listed in Definition 4. In order to specify which parts of a transaction are signed, we first introduce the auxiliary notion of transaction substitution.
field, which is never signed). However, not all possible combinations of transaction parts are possible; the legit ones are listed in Definition 4. In order to specify which parts of a transaction are signed, we first introduce the auxiliary notion of transaction substitution.
Definition 3 (Transaction substitutions)
A transaction substitution  is a function from \(\textsf {Tx} \) to \(\textsf {Tx} \). For a transaction field
is a function from \(\textsf {Tx} \) to \(\textsf {Tx} \). For a transaction field  , we denote with
, we denote with  the substitution which replaces the value of
the substitution which replaces the value of  with d. For
with d. For  and \(i \in \mathbb {N}\), we denote with
and \(i \in \mathbb {N}\), we denote with  the substitution which replaces
the substitution which replaces  with d. Further, for
with d. Further, for  , we denote with
, we denote with  the substitution which replaces
the substitution which replaces  with d, for all
with d, for all  .
.
Definition 4 (Signature modifiers)
We define signature modifiers \(\mu _{i}\) (with \(i \in \mathbb {N}\)) in Fig. 2. We associate to each modifier a substitution, and we denote with  the result of applying it to the transaction
the result of applying it to the transaction  .
.
Each modifier is represented by a pair of symbols, describing, respectively, the set of inputs and of outputs being signed (\(\textit{a}\) = all, \(\textit{s}\) = single, \(\textit{n}\) = none), and an index \(i \in \mathbb {N}\). The index has different meanings, depending on the modifier. Regarding the first symbol of the modifier, if it is \(\textit{a}\), then i is the index of the witness where the signature will be included, so to ensure that a signature computed for being included in the witness at index i can not be used in any witness with index \(j \ne i\) (see Example 4). If the first symbol of the modifier is \(\textit{s}\), then only the i-th input is signed, while all the other inputs are removed from the transaction. With respect to the second symbol of the modifier, if it is \(\textit{s}\), then i is the index of the signed output; otherwise, i has no effect on the outputs to be signed. Note that a single index is used for both inputs and outputs: in any case, the index refers to the witness where the signature will be included.
Definition 5 (Transaction signatures)
We define the transaction signature (under modifier \(\mu _{}\) and index i) and verification functions as follows:

Hereafter, we use \(\sigma , \sigma ', \dots \) to range over transaction signatures.
Note that a signature  does not contain the index i. Consequently, the verification function requires i to be passed as parameter, i.e. we write
does not contain the index i. Consequently, the verification function requires i to be passed as parameter, i.e. we write  . The parameter i will be instantiated by the script verification function (see Definition 8). Besides the modified transaction
. The parameter i will be instantiated by the script verification function (see Definition 8). Besides the modified transaction  , the signature also applies to the modifier \(\mu _{}\). In this way, signing a single-input transaction
, the signature also applies to the modifier \(\mu _{}\). In this way, signing a single-input transaction  with modifier \({\textit{a}\textit{a}}_1\) and with modifier \({\textit{s}\textit{a}}_1\) results in two different signatures, even though
with modifier \({\textit{a}\textit{a}}_1\) and with modifier \({\textit{s}\textit{a}}_1\) results in two different signatures, even though  .
.
Notation 2
Note that  can meaningfully appear within
can meaningfully appear within  , since such signature does not depend on the
, since such signature does not depend on the  field of transactions (as all signature modifiers overwrite all the witnesses). When a signature of
field of transactions (as all signature modifiers overwrite all the witnesses). When a signature of  appears within
appears within  , as a shorthand we denote it with
, as a shorthand we denote it with  (so, neglecting the enclosing transaction
(so, neglecting the enclosing transaction  and the index i), or just
and the index i), or just  .
.
We now extend the signature verification  to the case where, instead of providing a single key
to the case where, instead of providing a single key  and a single signature \(\sigma \), one has many keys and signatures, i.e.
and a single signature \(\sigma \), one has many keys and signatures, i.e.  . Intuitively, if
. Intuitively, if  and
and  , the function
, the function  implements a m-of-n multi-signature scheme, i.e. it evaluates to true if all the m signatures match (some of) the keys in
implements a m-of-n multi-signature scheme, i.e. it evaluates to true if all the m signatures match (some of) the keys in  . The actual definition is a bit more complex, to be coherent with the one implemented in Bitcoin.
. The actual definition is a bit more complex, to be coherent with the one implemented in Bitcoin.
Definition 6 (Multi-signature verification)
Let \({\varvec{k}}\) and \(\varvec{\sigma }\) be sequences of (public) keys and signatures such that  , and let \(i \in \mathbb {N}\). For all \(m, n \in \mathbb {N}\), we define the function:
, and let \(i \in \mathbb {N}\). For all \(m, n \in \mathbb {N}\), we define the function:

Then, we define  .
.
Our formalisation of multi-signature verification (Definition 6) follows closely the implementation of Bitcoin, whose stack-based scripting language imposes that the sequence \(\varvec{\sigma }\) is read in reverse order. Accordingly, the function  tries to verify the last signature in \(\varvec{\sigma }\) with the last key in \({{\varvec{k}}}\). If they match, the function
tries to verify the last signature in \(\varvec{\sigma }\) with the last key in \({{\varvec{k}}}\). If they match, the function  proceeds to verify the previous signature in the sequence, otherwise it tries to verify the signature with the previous key.
proceeds to verify the previous signature in the sequence, otherwise it tries to verify the signature with the previous key.
Example 1 (2-of-3 multi-signature)
Let  , and let \(\varvec{\sigma } = \sigma _p \sigma _q\) be such that
, and let \(\varvec{\sigma } = \sigma _p \sigma _q\) be such that  , and false otherwise. We have that:
, and false otherwise. We have that:

Note that, if we let \(\mathbf {\sigma '} = \sigma _q \sigma _p\), the resulting evaluation will be:

3.4 Semantics of Scripts
Definition 7 gives the semantics of script expressions. This semantics will be used in Sect. 3.5 to define when a transaction can redeem another one. We use an environment \(\rho : \mathsf Var\rightharpoonup \mathbb {Z}\) which associates a denotation to each variable occurring in it. Further, we use a transaction  and an index \(i \in \mathbb {N}\) to indicate the witness redeeming the script, both used to evaluate the timelock expressions. We use the denotation \(\bot \) to represent “failure” of the evaluation. This is the case e.g. of timelock expressions, when the temporal constraint is not satisfied. All the semantic operators used in Definition 7 are strict, i.e. they evaluate to \(\bot \) if some of their operands is \(\bot \).
and an index \(i \in \mathbb {N}\) to indicate the witness redeeming the script, both used to evaluate the timelock expressions. We use the denotation \(\bot \) to represent “failure” of the evaluation. This is the case e.g. of timelock expressions, when the temporal constraint is not satisfied. All the semantic operators used in Definition 7 are strict, i.e. they evaluate to \(\bot \) if some of their operands is \(\bot \).
Definition 7 (Expression evaluation)
Let \(\rho : \mathsf Var\rightharpoonup \mathbb {Z}\), let  and \(i \in \mathbb {N}\). We define the function
and \(i \in \mathbb {N}\). We define the function  in Fig. 3, where we use the following operators on denotations:
in Fig. 3, where we use the following operators on denotations:

Definition 8 (Script verification)
We say that the input i of  verifies
verifies  (in symbols:
(in symbols:  ) when
) when  ,
,  , and:
, and:

Example 2
Let  be a hash function, let
be a hash function, let  be such that
be such that  , and let
, and let  be such that
be such that  , with
, with  . We prove that:
. We prove that:

To do this, let  . We have that:
. We have that:

3.5 Semantics of Transactions
Definition 9 describes when the j-th input of a transaction  (put on the blockchain at time \(t'_{}\)) can redeem v Satoshis from the i-th output of the transaction
(put on the blockchain at time \(t'_{}\)) can redeem v Satoshis from the i-th output of the transaction  (put on the blockchain at time \(t_{}\)). We denote this by \((\).
(put on the blockchain at time \(t_{}\)). We denote this by \((\).
Definition 9 (Output redeeming)
We write  iff all the following conditions hold:
iff all the following conditions hold:
-
(a)

-
(b)

-
(c)

-
(d)

-
(e)

We write  when for no \(v_{}\) it holds that
when for no \(v_{}\) it holds that  .
.
Item (a) links the j-th input of  to the i-th output of
to the i-th output of  . Note that, since we are modelling SegWit, the witness in the transaction
. Note that, since we are modelling SegWit, the witness in the transaction  is left unspecified: this is why we set to \(\bot \) also the witness of
is left unspecified: this is why we set to \(\bot \) also the witness of  . Item (b) requires that the j-th witness of
. Item (b) requires that the j-th witness of  verifies the i-th output script of
verifies the i-th output script of  . Item (c) just defines \(v_{}\) as the value in the i-th output of
. Item (c) just defines \(v_{}\) as the value in the i-th output of  . Items (d) and (e) check the absolute and relative timelocks, respectively. The first constraint states that
. Items (d) and (e) check the absolute and relative timelocks, respectively. The first constraint states that  cannot appear on the blockchain before
cannot appear on the blockchain before  ; the second one states that
; the second one states that  cannot appear until at least
cannot appear until at least  time units have elapsed since
time units have elapsed since  was put on the blockchain.
was put on the blockchain.
Example 3
With the transactions in Fig. 4, we have  . Indeed, for item (a) we have that
. Indeed, for item (a) we have that  ; for item (b),
; for item (b),  ; for item (c),
; for item (c),  . The other two items trivially hold, as there are no time constraints. We also have
. The other two items trivially hold, as there are no time constraints. We also have  . To show that, we have to check also items (d) and (e). For item (d), we have that
. To show that, we have to check also items (d) and (e). For item (d), we have that  . For item (e), we have that
. For item (e), we have that  . \(\square \)
. \(\square \)
Example 4
Consider the transactions in Fig. 5. The signature in  is computed as follows:
is computed as follows:

We prove that, when verifying  , item (b) of Definition 9 holds, i.e.
, item (b) of Definition 9 holds, i.e.  . To this purpose, let
. To this purpose, let  , where
, where  . We have that:
. We have that:

We now show that w is not valid for the other witness, i.e.  , where
, where  . Let
. Let  . Item (b) of Definition 9 does not hold:
. Item (b) of Definition 9 does not hold:

In the last equation, w is not a valid signature for  because it is computed on
because it is computed on  , and the two transactions differ on
, and the two transactions differ on  . \(\square \)
. \(\square \)
3.6 Blockchain and Consistency
In Definition 10 we model blockchains as sequences of timed transactions  , where \(t_{}\) represents the time when the transaction
, where \(t_{}\) represents the time when the transaction  has been added. Note that our definition is very permissive: for instance, it allows a blockchain to contain transactions which do not redeem any transactions, or double-spent transactions. We will rule out such inconsistent blockchains later on in Definition 13.
has been added. Note that our definition is very permissive: for instance, it allows a blockchain to contain transactions which do not redeem any transactions, or double-spent transactions. We will rule out such inconsistent blockchains later on in Definition 13.
Definition 10 (Blockchain)
A blockchain  is a sequence
is a sequence  , where
, where  is the only transaction with
is the only transaction with  , and \(t_{i} \le t_{j}\) for all \(1 \le i \le j \le n\).
, and \(t_{i} \le t_{j}\) for all \(1 \le i \le j \le n\).
We denote with  the set of transactions occurring in
the set of transactions occurring in  , and with
, and with  the time \(t_i\) of transaction
the time \(t_i\) of transaction  in
in  . Given a transaction
. Given a transaction  , we define
, we define  as the set of transactions
as the set of transactions  such that
such that  .
.
Definition 11 (Unspent output)
Let  be a blockchain. We say that the output j of transaction
be a blockchain. We say that the output j of transaction  is unspent in
is unspent in  whenever:
whenever:

Given a blockchain  , we define:
, we define:
-
 , the Unspent Transaction Output of
, the Unspent Transaction Output of  , as the set of pairs
, as the set of pairs  such that output j of
such that output j of  is unspent in
is unspent in  .
. -
 , the value of
, the value of  , as the sum of the values of all outputs in its \( UTXO _{}\).
, as the sum of the values of all outputs in its \( UTXO _{}\).
Example 5
Consider the transactions in Fig. 6, and let  . We have that
. We have that  and
and  , while the other outputs are unspent. Hence, the UTXO of
, while the other outputs are unspent. Hence, the UTXO of  is
is  . \(\square \)
. \(\square \)
The following definition establishes when  is a consistent update of
is a consistent update of  .
.
Definition 12 (Consistent update)
We write  iff either
iff either  ,
,  is initial and \(t=0\), or, given, for all
is initial and \(t=0\), or, given, for all  :
:

the following conditions hold:
-
(1)

-
(2)

-
(3)

-
(4)

Firstly, for each  we obtain the singleton
we obtain the singleton  from the blockchain, using
from the blockchain, using  , such that
, such that  . The update is inconsistent if
. The update is inconsistent if  is not a singleton for some i. Condition (1) requires that the redeemed outputs are currently unspent in
is not a singleton for some i. Condition (1) requires that the redeemed outputs are currently unspent in  . Condition (2) asks that each input of
. Condition (2) asks that each input of  redeems an output of a transaction in
redeems an output of a transaction in  . Condition (3) requires that the sum of the values of the outputs of
. Condition (3) requires that the sum of the values of the outputs of  is not greater than the total value it redeems. Finally, (4) requires that the time of
is not greater than the total value it redeems. Finally, (4) requires that the time of  is greater than or equal to the time of the last transaction in
is greater than or equal to the time of the last transaction in  .
.
Example 6
Consider again the transactions in Fig. 6, and let  . We prove that
. We prove that  . Let \(o_1 = 2\), \(o_2 = 3\), \(t'_{1} = t'_{2} = 0\), \(v_{1} = 5\), \(v_{2} = 7\). We now prove that the conditions of Definition 12 are satisfied. For condition (1), note that both
. Let \(o_1 = 2\), \(o_2 = 3\), \(t'_{1} = t'_{2} = 0\), \(v_{1} = 5\), \(v_{2} = 7\). We now prove that the conditions of Definition 12 are satisfied. For condition (1), note that both  and
and  are unspent, according to Definition 11. For condition (2), note that:
are unspent, according to Definition 11. For condition (2), note that:

hold, according to Definition 9. Finally, for condition (3), we have that:

Therefore,  is a consistent update of
is a consistent update of  . \(\square \)
. \(\square \)
Example 7 (Double spending)
Consider again the transactions in Fig. 6, and let  .
.
We prove that  is not a consistent update of
is not a consistent update of  . Although condition (2) of Definition 12 holds:
. Although condition (2) of Definition 12 holds:

we have that condition (1) is not satisfied. In fact, according to Definition 11,  is already spent in
is already spent in  because
because

holds and both  and
and  are in
are in  . Since
. Since  is trying to spend an output already spent, this transaction should not be appended to
is trying to spend an output already spent, this transaction should not be appended to  . \(\square \)
. \(\square \)
We now define when a blockchain is consistent. Intuitively, consistency holds when the blockchain has been constructed, started from the empty one, by appending consistent updates, only. The actual definition is given by induction.
Definition 13 (Consistency)
We say that a blockchain  is consistent if either
is consistent if either  , or
, or  with
with  consistent and
consistent and  .
.
Note that the empty blockchain is consistent; the blockchain with a single transaction  is consistent iff
is consistent iff  is initial and
is initial and  . The transaction
. The transaction  models the first transaction in the genesis block (as discussed in Sect. 6, we are abstracting away the coinbase transactions, which forge new bitcoins).
models the first transaction in the genesis block (as discussed in Sect. 6, we are abstracting away the coinbase transactions, which forge new bitcoins).
We now establish some basic properties of consistent blockchains. Lemma 1 states that, in a consistent blockchain, the inputs of a transaction point backwards to the output of some transaction in the blockchain.
Lemma 1
If  is consistent, then:
is consistent, then:

The following theorem establishes that a transaction output cannot be redeemed twice in a consistent blockchain.
Theorem 1 (No double spending)
If  is consistent, then:
is consistent, then:

The following lemma states that there can be at most a single match of an arbitrary transaction within a consistent blockchain. This implies that the  field of an arbitrary transaction points at most to one transaction output within the blockchain.
field of an arbitrary transaction points at most to one transaction output within the blockchain.
Lemma 2
If  is consistent, then for all transactions
is consistent, then for all transactions  ,
,  contains at most one element.
contains at most one element.
Lemma 3 ensures that all the transactions on a consistent blockchain are pairwise distinct, even when neglecting their witnesses.
Lemma 3
If  is consistent, then:
is consistent, then:

The following theorem states that the overall value of a blockchain decreases as the blockchain grows. This is because our model does not keep track of the coinbase transactions, which in Bitcoin allow miners to collect transaction fees (the difference between inputs and outputs of a transaction), and block rewards.
Theorem 2 (Non-increasing value)
Let  be a consistent blockchain, and let
be a consistent blockchain, and let  be a non-empty prefix of
be a non-empty prefix of  . Then,
. Then,  .
.
Note that the scripting language and its semantics are immaterial in all the statements above. Actually, proving these results never involves checking condition (b) of Definition 9. Of course, the choice of the scripting language affects the expressiveness of the smart contracts built upon Bitcoin.
4 Example: Static Chains of Transactions
We now formally specify in our model a simple smart contractFootnote 5, which illustrates the impact of SegWit on the expressiveness of Bitcoin contracts.
A participant  wants to send an indirect payment of
wants to send an indirect payment of  to
to  , routing it through
, routing it through  . To authorize the payment,
. To authorize the payment,  wants to keep a fee of
wants to keep a fee of  . However,
. However,  is afraid that
is afraid that  will keep all the money for himself, so she exploits the following contract. She creates a chain of transactions, as shown in Fig. 7. The transaction
will keep all the money for himself, so she exploits the following contract. She creates a chain of transactions, as shown in Fig. 7. The transaction  transfers
transfers  from
from  to
to  (but it is not signed by
(but it is not signed by  , yet), while
, yet), while  transfers
transfers  from
from  to
to  . We assume that
. We assume that  is a transaction output redeemable by
is a transaction output redeemable by  through her key
through her key  , and that
, and that  is the key of
is the key of  .
.
The protocol of  is the following:
is the following:  starts by asking
starts by asking  for his signature on
for his signature on  , ensuring that
, ensuring that  will be paid. After receiving and verifying the signature,
will be paid. After receiving and verifying the signature,  puts
puts  on the blockchain, adding her signature on the
on the blockchain, adding her signature on the  field. Then, she also appends
field. Then, she also appends  , replacing the
, replacing the  field with her signature and
field with her signature and  ’s one. Since
’s one. Since  takes care of publishing the transactions, the behaviour of
takes care of publishing the transactions, the behaviour of  consists just in sending his signature on
consists just in sending his signature on  .
.
Remarkably, this contract relies on the SegWit feature: indeed, without SegWit it no longer works. We can disable SegWit by changing our model as follows:
-
in Definition 2, we no longer require that

-
in Definition 9, we replace item (a) with the condition:

-
in Definition 10, we let
 if
if  occurs in
occurs in  , empty otherwise.
, empty otherwise.
To see why disabling SegWit breaks the contract, assume that the transaction  is unspent on the blockchain, when participant
is unspent on the blockchain, when participant  attempts to append also
attempts to append also  . To be a consistent update, by item (2) of Definition 12 we must have (for some \(t_{1} \le t_{2}\)):
. To be a consistent update, by item (2) of Definition 12 we must have (for some \(t_{1} \le t_{2}\)):

For this, all the conditions in Definition 9 must hold. However, since we have disabled SegWit, for item (a) we no longer check that:

but instead we need to check the condition:

where the transactions  correspond to the non-SegWit versions of
correspond to the non-SegWit versions of  , i.e. their
, i.e. their  fields point to their actual parents, according to the new Definition 2.
fields point to their actual parents, according to the new Definition 2.
Hence, condition (2) checks the equality between  (the transaction in the input of
(the transaction in the input of  ) and
) and  (the transaction
(the transaction  ). Note that all the fields of the second transaction—but the
). Note that all the fields of the second transaction—but the  field—are equal to those of the first transaction. Instead, the witness of
field—are equal to those of the first transaction. Instead, the witness of  is
is  , while the one of
, while the one of  contains the signature of
contains the signature of  . This difference in the
. This difference in the  field is ignored with the SegWit semantics, while it is discriminating for the older version of Bitcoin.
field is ignored with the SegWit semantics, while it is discriminating for the older version of Bitcoin.
A naïve attempt to amend the contract would be to set the input field of  to
to  . However, this would invalidate the signature of
. However, this would invalidate the signature of  on
on  .
.
5 Compiling to Standard Bitcoin Transactions
We now sketch how to compile the transactions of our abstract model into concrete Bitcoin transactions. In particular, we aim at producing standard Bitcoin transactions, which respect further constraints on their fieldsFootnote 6. This is crucial, because non-standard transactions are mostly discarded by the Bitcoin network.
Our compiler produces output scripts of the following kinds, which are all allowed in standard transactions:
- Pay to Public Key Hash (P2PKH):
-
takes as parameters a public key and a signature, and checks that (i) the hash of the public key matches the hash hardcoded in the script; (ii) the signature is verified against the public key.
- Pay to Script Hash (P2SH):
-
contains only a hash (say, \(h_{}^{}\)). The actual script
 —which is not required to be standard—is contained instead in the
—which is not required to be standard—is contained instead in the  field of the redeeming transaction, alongside with the actual parameters \({{\varvec{k}}}\). The evaluation succeeds if
field of the redeeming transaction, alongside with the actual parameters \({{\varvec{k}}}\). The evaluation succeeds if  and
and  evaluates to \( true \). The only constraint imposed by P2SH is on the size of the script, which is limited to the size of a stack element (520 bytes).
evaluates to \( true \). The only constraint imposed by P2SH is on the size of the script, which is limited to the size of a stack element (520 bytes). - OP_RETURN:
-
allows to put up to 80 bytes of data in an output script, making the output unredeemable.
We compile the scripts of the form  to P2PKH, and those of the form \(\lambda . k_{}\) to OP_RETURN. All other scripts are compiled to P2SH when they comply with the size constraint, otherwise compilation fails. In this way, our compiler always produces standard transactions.
to P2PKH, and those of the form \(\lambda . k_{}\) to OP_RETURN. All other scripts are compiled to P2SH when they comply with the size constraint, otherwise compilation fails. In this way, our compiler always produces standard transactions.
Our compiler exploits the alternative stack as temporary storage of the variable values. In this way we cope with the stack-based nature of the Bitcoin scripting language. For instance, for the script \(\lambda x_{}. \mathsf{H}(x_{}) = \mathsf{H}(x_{}+1)\), the variable \(x_{}\) is pushed on the alternative stack beforehand, then duplicated and copied in the main stack before each operation involving x.
6 Conclusions
We have proposed a formal model for Bitcoin transactions. Our model abstractly describes their essential aspects, at the same time enabling formal reasoning, and providing a formal specification to some of Bitcoin’s less documented features.
An alternative model of transactions in blockchain systems has been proposed in [8]. Roughly, blockchains are represented as directed acyclic graphs, where edges denote transfers of assets. This model is quite abstract, so that it can be instantiated to different blockchains (e.g., Bitcoin, Ethereum, and Hyperledger Fabric). Differently from ours, the model in [8] does not capture some peculiar features of Bitcoin, like e.g. transaction signatures and signature modifiers, output scripts, multi-signature verification, and Segregated Witnesses.
Our work provides the theoretical foundations to model Bitcoin smart contracts, reducing the gap between cryptography and programming languages communities. A formal description of smart contracts enables their automated verification and analysis, which are of crucial importance in a context where design flaws may result in loss of money. For instance, our model has been exploited in [3] to present a comprehensive survey of Bitcoin smart contracts.
Differences Between Our Model and Bitcoin. There are some differences between our model and the actual Bitcoin, which we outline below.
In Definition 2, we stipulate that the  field of a transaction points to another transaction. Instead, in Bitcoin the
field of a transaction points to another transaction. Instead, in Bitcoin the  field contains the identifier of the input transaction. More specifically, this identifier is defined as
field contains the identifier of the input transaction. More specifically, this identifier is defined as  , where: (i)
, where: (i)  since the activation of the SegWit feature; (ii) \(\mu _{}= \bot \), beforehand. Consequently, the condition
since the activation of the SegWit feature; (ii) \(\mu _{}= \bot \), beforehand. Consequently, the condition  item (a) of Definition 9 would be translated in Bitcoin as:
item (a) of Definition 9 would be translated in Bitcoin as:  , where
, where  . Intuitively, the
. Intuitively, the  field specifies the transaction (and the output index) to redeem. Since the activation of SegWit, the computation of the transaction identifier does not take in account the
field specifies the transaction (and the output index) to redeem. Since the activation of SegWit, the computation of the transaction identifier does not take in account the  field.
field.
The scripting language in Definition 1 is a bit more expressive than Bitcoin’s. For instance, the script  is admissible in our model, while it is not in Bitcoin. Indeed, the Bitcoin scripting language only admits the comparison (via the OP_LESSTHANOREQUAL opcode) on 32-bit integers, while two arbitrary values can only be tested for equality (via the OP_EQUAL opcode). Similar restrictions apply to arithmetic operations. It is straightforward to adapt our model to apply the same restrictions on Bitcoin scripts. Indeed, our compiler already implements a simple type system which rules away scripts not admissible in Bitcoin.
is admissible in our model, while it is not in Bitcoin. Indeed, the Bitcoin scripting language only admits the comparison (via the OP_LESSTHANOREQUAL opcode) on 32-bit integers, while two arbitrary values can only be tested for equality (via the OP_EQUAL opcode). Similar restrictions apply to arithmetic operations. It is straightforward to adapt our model to apply the same restrictions on Bitcoin scripts. Indeed, our compiler already implements a simple type system which rules away scripts not admissible in Bitcoin.
Definition 10 models blockchains as sequences of transactions, while in Bitcoin they are sequences of blocks of transactions. In this way, we are abstracting both from the cryptographic puzzle that miners have to solve to append new blocks to the blockchain, and from the coinbase transactions, which (like our initial transaction) do not redeem other transactions, and mint new bitcoins (the block rewards). Coinbase transactions are also used in Bitcoin to collect transaction fees, which are just discarded in our model. Extending our model with coinbase transactions would falsify Theorem 2, since the overall value in the blockchain would no longer be decreasing. Definition 10 requires the timestamp of each transaction to increase monotonically. Instead, in Bitcoin a timestamp is valid if it is greater than the median timestamp of previous 11 blocks.
In Definitions 2 and 9, the  and
and  fields specify the time when a transaction can be appended to the blockchain. In Bitcoin transactions, besides the time we can also use the block height, i.e. the distance between any given block and the genesis block. Setting the block height to h implies that the transaction can be mined from the block h onward.
fields specify the time when a transaction can be appended to the blockchain. In Bitcoin transactions, besides the time we can also use the block height, i.e. the distance between any given block and the genesis block. Setting the block height to h implies that the transaction can be mined from the block h onward.
Notes
- 1.
- 2.
- 3.
- 4.
This feature, specified in the BIP 141 and activated on August 24th 2017, implies that witnesses are not used in the computation of transaction hashes.
- 5.
- 6.
References
Andrychowicz, M., Dziembowski, S., Malinowski, D., Mazurek, Ł.: Fair two-party computations via Bitcoin deposits. In: Böhme, R., Brenner, M., Moore, T., Smith, M. (eds.) FC 2014. LNCS, vol. 8438, pp. 105–121. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44774-1_8
Andrychowicz, M., Dziembowski, S., Malinowski, D., Mazurek, L.: Secure multiparty computations on Bitcoin. In: IEEE Symposium on Security and Privacy, pp. 443–458 (2014)
Atzei, N., Bartoletti, M., Cimoli, T., Lande, S., Zunino, R.: SoK: unraveling Bitcoin smart contracts. In: Bauer, L., Küsters, R. (eds.) POST 2018. LNCS, vol. 10804, pp. 217–242. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89722-6_9
Banasik, W., Dziembowski, S., Malinowski, D.: Efficient zero-knowledge contingent payments in cryptocurrencies without scripts. In: Askoxylakis, I., Ioannidis, S., Katsikas, S., Meadows, C. (eds.) ESORICS 2016. LNCS, vol. 9879, pp. 261–280. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45741-3_14
Bartoletti, M., Zunino, R.: Constant-deposit multiparty lotteries on Bitcoin. In: Brenner, M., et al. (eds.) FC 2017. LNCS, vol. 10323, pp. 231–247. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70278-0_15
Bentov, I., Kumaresan, R.: How to use Bitcoin to design fair protocols. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 421–439. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_24
Bonneau, J., Miller, A., Clark, J., Narayanan, A., Kroll, J.A., Felten, E.W.: SoK: research perspectives and challenges for Bitcoin and cryptocurrencies. In: IEEE S & P, pp. 104–121 (2015)
Cachin, C., Caro, A.D., Moreno-Sanchez, P., Tackmann, B., Vukolić, M.: The transaction graph for modeling blockchain semantics. Cryptology ePrint Archive, Report 2017/1070 (2017). https://eprint.iacr.org/2017/1070
Kumaresan, R., Bentov, I.: How to use Bitcoin to incentivize correct computations. In: ACM CCS, pp. 30–41 (2014)
Kumaresan, R., Moran, T., Bentov, I.: How to use Bitcoin to play decentralized poker. In: ACM CCS, pp. 195–206 (2015)
Miller, A., Bentov, I.: Zero-collateral lotteries in Bitcoin and Ethereum. In: EuroS&P Workshops, pp. 4–13 (2017)
Möser, M., Eyal, I., Gün Sirer, E.: Bitcoin covenants. In: Clark, J., Meiklejohn, S., Ryan, P.Y.A., Wallach, D., Brenner, M., Rohloff, K. (eds.) FC 2016. LNCS, vol. 9604, pp. 126–141. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53357-4_9
Nakamoto, S.: Bitcoin: a peer-to-peer electronic cash system (2008). https://bitcoin.org/bitcoin.pdf
O’Connor, R., Piekarska, M.: Enhancing bitcoin transactions with covenants. In: Brenner, M., et al. (eds.) FC 2017. LNCS, vol. 10323, pp. 191–198. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70278-0_12
Szabo, N.: Formalizing and securing relationships on public networks. First Monday 2(9) (1997). http://firstmonday.org/htbin/cgiwrap/bin/ojs/index.php/fm/article/view/548
Acknowledgments
The authors thank the anonymous reviewers of Financial Cryptography 2018 and A. S. Podda for their insightful comments. This work is partially supported by Aut. Reg. Sardinia project P.I.A. 2013 “NOMAD”. Stefano Lande gratefully acknowledges Sardinia Regional Government for the financial support of his PhD scholarship (P.O.R. Sardegna F.S.E. Operational Programme of the Aut. Reg. Sardinia, European Social Fund 2014–2020).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Proofs
A Proofs
Proof of Lemma 1
By Definition 13,  is a consistent update of
is a consistent update of  . The thesis follows from condition (2) of Definition 12. \(\square \)
. The thesis follows from condition (2) of Definition 12. \(\square \)
Proof of Theorem 1
Let  be consistent. By contradiction, assume that there exist \(i < j\) and \(i',j'\) such that
be consistent. By contradiction, assume that there exist \(i < j\) and \(i',j'\) such that  . By consistency, there exist \(h,h'\) such that
. By consistency, there exist \(h,h'\) such that  . Since
. Since  , then by item (2) of Definition 12 it must be
, then by item (2) of Definition 12 it must be  . Hence, by Definition 11 it follows that
. Hence, by Definition 11 it follows that  is already spent in
is already spent in  . Since
. Since  , by item (1) of Definition 12,
, by item (1) of Definition 12,  must be unspent—contradiction. \(\square \)
must be unspent—contradiction. \(\square \)
Proof of Lemma 2
Let  be consistent. By contradiction, assume that
be consistent. By contradiction, assume that  , with
, with  (and so,
(and so,  ). By Definition 10 it must be
). By Definition 10 it must be  , hence in particular
, hence in particular  . There are two cases. If
. There are two cases. If  , then by Definition 10
, then by Definition 10  is not a blockchain, since \(i \ne j\). Hence,
is not a blockchain, since \(i \ne j\). Hence,  . By Theorem 1, this cannot happen because
. By Theorem 1, this cannot happen because  is consistent—contradiction. \(\square \)
is consistent—contradiction. \(\square \)
Proof of Lemma 3
Straightforward from Lemma 2, taking  . \(\square \)
. \(\square \)
Proof of Theorem 2
Let  . By contradiction, there exists some \(i<n\) such that, given
. By contradiction, there exists some \(i<n\) such that, given  :
:

Let \(U_i\) and \(U_{i+1}\) be the UTXOs of  and of
and of  , respectively, and let \(U = U_i \cap U_{i+1}\). Since \( val {(U_i)} < val {(U_{i+1})}\), then it must be \( val {(U_i \setminus U)} < val {(U_{i+1} \setminus U)}\). The set \(U_i \setminus U\) contains the outputs redeemed by
, respectively, and let \(U = U_i \cap U_{i+1}\). Since \( val {(U_i)} < val {(U_{i+1})}\), then it must be \( val {(U_i \setminus U)} < val {(U_{i+1} \setminus U)}\). The set \(U_i \setminus U\) contains the outputs redeemed by  , while the set \(U_{i+1} \setminus U\) contains exactly the outputs in
, while the set \(U_{i+1} \setminus U\) contains exactly the outputs in  . Since
. Since  is consistent, then
is consistent, then  . Then, by Definition 12, for each
. Then, by Definition 12, for each  , there exists a unique \(j \le i\) such that, given
, there exists a unique \(j \le i\) such that, given  and
and  :
:

Then, by item (3) of Definition 12:

while we assumed \( val {(U_i \setminus U)} < val {(U_{i+1} \setminus U)}\)—contradiction. \(\square \)
Rights and permissions
Copyright information
© 2018 International Financial Cryptography Association
About this paper
Cite this paper
Atzei, N., Bartoletti, M., Lande, S., Zunino, R. (2018). A Formal Model of Bitcoin Transactions. In: Meiklejohn, S., Sako, K. (eds) Financial Cryptography and Data Security. FC 2018. Lecture Notes in Computer Science(), vol 10957. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-58387-6_29
Download citation
DOI: https://doi.org/10.1007/978-3-662-58387-6_29
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-58386-9
Online ISBN: 978-3-662-58387-6
eBook Packages: Computer ScienceComputer Science (R0)







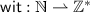 , where
, where 


 , where
, where 








 for the transaction within the
for the transaction within the  field (e.g., we just write
field (e.g., we just write  within
within  ). Also, we use dates in time constraints.
). Also, we use dates in time constraints.
 is
is  , while the second is
, while the second is  .
. , the Unspent Transaction Output of
, the Unspent Transaction Output of  , as the set of pairs
, as the set of pairs  such that output j of
such that output j of  is unspent in
is unspent in  .
. , the value of
, the value of  , as the sum of the values of all outputs in its
, as the sum of the values of all outputs in its 







 if
if  occurs in
occurs in  , empty otherwise.
, empty otherwise. —which is not required to be standard—is contained instead in the
—which is not required to be standard—is contained instead in the  field of the redeeming transaction, alongside with the actual parameters
field of the redeeming transaction, alongside with the actual parameters  and
and  evaluates to
evaluates to