Abstract
The two main challenges in deploying real world secure poker protocols lie in enforcing the distribution of rewards and dealing with misbehaving/aborting parties. Using recent advances in cryptocurrencies and blockchain techniques, Kumaresan et al. (CCS 2015) and Bentov et al. (ASIACRYPT 2017) were able to solve those problems for the general case of secure multiparty computation. However, in the specific case of secure poker, they leave major open problems in terms of efficiency and security. This work tackles these problems by presenting the first full-fledged simulation-based security definition for secure poker and the first fully-simulatable secure poker protocol that provably realizes such a security definition. Our protocol provably enforces rewards distribution and penalties for misbehaving parties, while achieving efficiency comparable to previous tailor-made poker protocols, which do not have formal security proofs and rewards/penalties enforcement. Moreover, our protocol achieves reduced on-chain storage requirements for the penalties and rewards enforcement mechanism.
B. David and M. Larangeira—This work was supported by the Input Output Cryptocurrency Collaborative Research Chair, which has received funding from Input Output HK.
R. Dowsley—This project has received funding from the European research Council (ERC) under the European Unions’s Horizon 2020 research and innovation programme (grant agreement No. 669255).
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Shamir, Rivest and Adleman, soon after their seminal work on the RSA cryptosystem, started exploring new ideas on cryptography inspired by everyday activities such as playing games. In particular, they started investigating how to play poker remotely [26], a problem related to very interesting questions in the distributed setting. For example, securely shuffling with remote parties requires every player to participate in the procedure; otherwise, security may not be assured at all for the participants.
Mental Poker, Cryptography and the Gambling Market: Since its origins the research on mental poker and card games worked as a drive for the research in cryptography. The original work of Shamir et al. inspired a number of follow-ups, starting in the eighties with the works on the feasibility of playing mental games, e.g. [11]. The first protocols for mental poker faced several limitations due to poor efficiency, which was improved in the following decades several by a number of works, e.g. [3, 9, 25, 28, 29, 32, 33].
In economic terms, online poker has been a strong industry since the “Poker Boom” of the 2000s, as described in prestigious economic venues [15]. Much of the strong interest in online gambling has its advent due to the appearance of online casinos. Despite legal restrictions imposed by new US legislation, players resort to websites based in other countries. For example, a Financial Times report [1] describes how UK firms filled the vacuum left by the US counterparts in the estimated 40 billion dollars global market of international online gambling (with one of the major online casino reporting 22 millions users and revenue of 2.5 billions dollars).
The current model of online gambling is based on trusted casinos, which are responsible for generating the randomness used to shuffle the cards and for enforcing the proper execution of the game. In contrast, a real world poker game requires almost no trust among the players, or between players and third parties like casinos. In the current model, a malicious casino or an insider attacker working for a casino can greatly influence the outcome of the game by manipulating the randomness used for shuffling or by leaking additional information to the players. And such cases have already happened (see Section “Integrity and Fairness” of [30] for more details). This state of affairs represents a clear disadvantage from online poker in comparison with a game played face-to-face. Techniques from mental poker can be used to overcome this problem and securely play poker online without the need of trusted casinos.
Challenges Preventing Deployment: Two central problems preventing deployment of secure poker protocols that were not addressed in the literature until very recently are protecting against aborts and ensuring that winners get their rewards. The first problem consists in players who leave the game prematurely (i.e. abort the protocol execution) causing the protocol to freeze. Castellà-Roca et al. [9] investigated this scenario and proposed a protocol that we show to be flawed (details in the full version of this paper [12]). The second problem of ensuring that a player actually gets a reward if it wins has only been tackled very recently after the advent of cryptocurrencies and blockchain technologies. Kumaresan et al. [20] addressed the problem with the help of Bitcoin and blockchains following the approach of [2, 6]. They concurrently also dealt with the abort problem in a far more satisfactory way by imposing financial penalties on the aborting parties and using the collected money to compensate the remaining players.
Basically, the protocol of Kumaresan et al. [20] uses an unfair multiparty computation protocol along with many simple smart contracts and Bitcoin deposits to ensure that the rewards are distributed to players whenever the relevant conditions are fulfilled, and to enforce financial penalties on aborting/misbehaving parties. Using this strategy, a specific poker protocol was also designed, although with inefficiencies (for a more detailed discussion see [7, Sect. 6]). A significant improvement was obtained by Bentov et al. [7] by leveraging the power of stateful contracts to greatly improve the efficiency, solving some of the bottlenecks in the previous protocol. While the protocol in [20] requires \(O(n^2)\) rounds of interaction with the cryptocurrency network and an amount of collateral linear in the number of messages exchanged during the protocol, the protocol of Bentov et al. [7] requires O(1) rounds of interaction with the cryptocurrency network and an amount of collateral equal to the compensation the players would receive. The central idea for improving the performance and decreasing the amount of collateral is to use a single stateful contract that keeps all the deposits and executes the unfair protocol off-chain. After the initial deposits, this contract is only involved in two situations: for the cash distribution, or if a problem happens.
Lack of Strong Security Proofs: Even though efficient solutions are known for different components of card games, most have not been formally proven secure in a strong security model. In fact, it has been observed in [25] that the protocols of [32, 33] are broken and we describe in the full version of this work [12] new concrete flaws that we have identified in the protocols proposed in [9] and [3]. Out of the few protocols that have been suggested, it seems that only [20] and its follow-up work [7] present a more detailed security proof in a strong, simulation-based security model. However, in [7] only the general solution based on enhanced trapdoor permutations has a full security proof (but incurs high computational and communication costs due to its generality). Bentov et al. [7, Sect. 7] argue that, instead of the general protocol, the tailor-made protocol of Wei and Wang [28, 29] can be used as a building block and coupled with their techniques for dealing with aborts and cash distribution in order to obtain more efficient poker protocols. However they do not present a proof for this claim, and not even define the security properties that such tailor-made poker protocol would have to satisfy in order for the overall solution to be secure. In fact, the security models used in [28, 29] are not formally defined and seem to be rather weak (judging by the informal descriptions given in these works).
General Requirements for Useful Poker Protocol: The current state of the art is unsatisfactory as there is no solution that meets all the following criteria necessary in a deployment in a real world scenario in which money is at stake: (1) Efficiency: performance that is comparable to tailor-made poker protocols; (2) Security: a simulation-based, formal proof of security; (3) Penalties: avoiding aborts/misbehavior or penalizing the misbehaving players; (4) Rewards: securely distributing the rewards to the players.
The works that are closer to achieve these criteria are [20] and [7], which made fundamental progress towards providing viable solutions to satisfy conditions (3) and (4). Nevertheless, none of their solutions meet simultaneously conditions (1) and (2). The solutions in [20] as well as the general solution in [7] do not meet condition (1), while the solution in [7] using tailor-made protocol improves on condition (1) but does not address (2) as it lacks a security proof.
1.1 Our Contribution
We present our protocol, Kaleidoscope, named after the homonymous poker themed movie from the sixties [18]. Given the earlier discussion, our main goal in this work is to design a poker protocol that concurrently meets all four criteria above. In designing our solution we face two main challenges: 1. constructing an efficient off-chain protocol without sacrificing provable security guarantees as in previous tailor-made poker protocols, 2. reducing the amount of data stored in the blockchain, which is a highly constrained resource. In summary, our contributions are: (1) First full-fledged simulation-based security definition for poker (check full version [12]); (2) First fully-simulatable poker protocol (Sect. 3), which provably realizes our security definition; (3) Improved concrete computational and communication complexities for off-chain card operations (around 10 times better than previous works) and reduced on-chain storage requirements for the penalties and rewards enforcement mechanism (estimated in Sect. 4).
As our goal is to provide a strong security guarantee, we first specify a poker functionality that encompasses the whole game execution, penalizes aborting parties and guarantees the distribution of the rewards. Such modeling of the whole poker game as an ideal functionality is, to the best of our knowledge, novel. Then we design a tailor-made protocol that provably realizes such functionality in a simulation-based security model. Our protocol is designed with both off-chain and on-chain efficiency in mind. We focus on the case where players act honestly and the on-chain protocol execution is used as a last resort to recover from malicious actions. In this context, we meet criteria (1) and (2) by designing an off-chain protocol that is highly efficient while providing compact witnesses to be posted to the blockchain for claiming rewards or enforcing penalties. Our protocol represents cards as ciphertexts of a threshold version of the well known El Gamal cryptosystem as proposed by Barnett and Smart [3] but significantly differs from their work in the techniques we employ for distributed key generation and card shuffling. Namely, we use a technique for distributed key generation of threshold El Gamal public keys that addresses the security issue we found in the protocol of [3] (described in the full version of this work [12]) without sacrificing efficiency. Moreover, we significantly improve the efficiency of the card shuffling procedure by leveraging recent advances in zero-knowledge proofs for correctness of shuffles [4]. This initial protocol itself is unfair, meaning that an adversarial abort can cause the execution to fail without consequences. In order to meet criteria (3) and (4), we build on top of the ideas in [20] and [7], financially penalizing an adversary and rewarding honest players through a stateful smart contract. We optimize their general rewards/penalties mechanism for the specific case of poker and define concrete compact witnesses of correct behavior, resulting in a smaller on-chain footprint.
1.2 Overview and Intuition of Our Protocol
Next we present a more detailed overview of our protocol. Due to the fact that it is not reasonable to assume that the majority of the players are honest in a poker game, the secure poker protocol will not be able to guarantee fairness. Instead, we follow the approach of imposing a financial penalty on the party that interrupts the correct execution of the protocol, and use this money to compensate the honest parties. A stateful contract is used to enforce these properties. As it is highly desirable to decrease the burden on the blockchain as much as possible (thus improving the efficiency and decreasing the impact on other users), the execution of the protocol is performed mostly off-chain and the parties only go back on-chain for the cash distribution or if some problem happens. When the protocol goes back on-chain, the parties need to present witnesses to the stateful contract to validate the state of the game. It is important to decrease the size of these witnesses that need to be stored by the players, as well as the verification costs for the stateful contract. In this regard, a key characteristic of poker is that the future execution is independent from the past when conditioned on a few variables that keep track of the current status. Hence, if all participants sign these variables at a checkpoint, then this constitutes a witness witness that can be delivered to the stateful contract in order to prove the state of the game at this particular point. Therefore, at the checkpoints, the players can delete all other previous witnesses, saving space for the players and verification efforts for the stateful contract. The general overview of the protocol is:
-
1.
Initially the parties lock into the stateful contract functionality an amount of money equal to the sum of the collateral and the money that they will use for the bets. A few initialization procedures are also executed during this stage.
-
2.
The players run our novel unfair tailor-made poker protocol off-chain. During this stage, an aborting adversary can cause the off-chain protocol to fail, so the players need to record a few witnesses that must be sent to the stateful contract in the case of problems that require its intervention. All messages are signed by the senders, and at some checkpoints a few variables that summarize the status of the game are signed by all players, constituting a compact witness of correct execution.
-
3.
If the protocol finishes correctly off-chain, then the final payout amounts will have been signed by all players, and so the parties only come back on-chain for the cash distribution that is performed by the stateful contract.
-
4.
If some problem happens and a player requests the intervention of the stateful contract, each party that does not want to get penalized handles their respective recorded witnesses to the stateful contract, which is then able to verify the latest status of the protocol execution and continue the execution (on-chain) under its mediation. During the mediated execution, it penalizes any participant that does not follow the protocol rules or abort.
Note that on Step 2, the adopted technique is used in order to decrease the size of the witnesses that the players need to store after the checkpoint as well as to reduce the amount of on-chain verification that needs to be performed in case of intervention (thus reducing the burden on the blockchain, which affects all cryptocurrency’s users). The safe deposit d that each of the n participants lock into the contract should be enough to pay the compensation amount q for all the other parties, i.e., \(d \ge q(n-1)\). Obviously, the monetary compensation q should be related to the maximum possible bet amount m at each hand; otherwise the corrupted parties would have an incentive to abort the protocol if they notice that one hand will end up badly for them.
2 Preliminaries
We now define some building blocks used in our protocols. For details about the Decision Diffie Hellman problem and digital signatures check the full version [12].
Security Model, Adversarial Model and Setup Assumptions: We prove our protocol secure in the real/ideal simulation paradigm with sequential composition. This is an intuitive paradigm that provides strong security guarantees for the protocols that are proven secure according to it. For more details, check the full version of this work [12]. We consider malicious adversaries that may deviate from the protocol in arbitrary ways. Moreover we consider the static case, where the adversary is only allowed to corrupt parties before protocol execution starts and parties remain corrupted (or not) throughout the execution. Our protocol uses the Random Oracle Model (ROM) [5] and assumes the existence of a stateful contract functionality \(\mathcal {F}_{\mathsf {SC}}\) (that is described in Sect. 3 and can be implemented using blockchain techniques).
Non-interactice Zero-Knowledge Proofs: We will need a NIZK of knowledge of a value \(\alpha \in \mathbb {Z}_p\) such that \(x = g^\alpha \) and \(y = h^\alpha \) given \(g,x,h,y\). For this we use the Fiat-Shamir transformation on the protocol of Chaum and Pedersen [10], which we denote by \(\mathsf {DLEQ}(g,x,h,y)\). We will also need a simpler NIZK of knowledge of a value \(\alpha \in \mathbb {Z}_p\) such that \(x = g^\alpha \) given \(g,x\). For this we use the Fiat-Shamir transformation on the protocol of Schnorr [24], which we denote by \(\mathsf {DLOG}(g,x)\). We give a full description of these NIZKs in the full version [12].
A central component of our protocol is a zero-knowledge proof that an ordered set of ElGamal ciphertexts has been obtained by re-randomizing each ciphertext and permuting the resulting ciphertexts in a previous ordered set (an operation called a Shuffle). Formally, we want to prove knowledge of a permutation \(\pi \in \varSigma _{N}\) and randomness \(\mathbf {r}=(r_1,\ldots ,r_N)\) such that for the vectors of ciphertexts \(\mathbf {c}=(c_1,\ldots ,c_N)\) and \(\mathbf {c}'=(c_1^{\prime },\ldots ,c_N^{\prime })\) we have \(c_i^{\prime } = \mathsf {TEG}.\mathsf {ReRand}(c_{\pi (i)},r_i)\). An efficient zero-knowledge argument for correctness of this kind of shuffle has been proposed in [4] and it can be turned into the required zero-knowledge proof through the Fiat-Shamir heuristic [17, 22]. We denote this NIZK by \(\mathsf {ZKSH}(\pi ,\mathbf {r},\mathbf {c},\mathbf {c}')\) and refer interested readers to [4] for details on its construction and proof. Further discussion of this NIZK’s efficiency and distributed generation of setup parameters is presented in the full version [12].
(n, n)-Threshold ElGamal Cryptosystem: A cryptosystem with (t, n)-threshold allow a group of n parties to jointly generate a public key that is then used to encrypt plaintext messages in such a way that they can only be recovered from the ciphertexts if at least t parties cooperate [13]. In our card deck generation procedure we employ a (n, n)-threshold version of the ElGamal cryptosystem [16] based on the constructions of [14, 21] with a verifiable decryption protocol similar to the Verifiable Threshold Masking Functions (VTMF) of [3]. The final goal is to encode card information as Threshold ElGamal ciphertexts as in the VTMF based construction of [3]. However, we employ different techniques for distributed key generation in order to address the security issues we have identified in [3]. Moreover, we do not require the verifiable masking and verifiable re-masking (rerandomization) operations because the verification that these ciphertexts are correctly re-randomized is handled by the zero-knowledge proofs of correctness of a shuffle [4] presented in the next section. We do use the fact that this scheme is additively homomorphic (and rerandomizable) and a verifiable decryption procedure, where it is possible to verify that each user is providing a valid decryption share. We now present the (n, n)-Threshold ElGamal cryptosystem with verifiable decryption \(\mathsf {TEG}\) and refer interested readers to [3, 14, 21] for a full discussion:
-
Key Generation \(\mathsf {TEG}.\mathsf {Gen}(1^{\lambda })\) : Each party \(\mathcal {P}_i\) generates a random secret-key share \(\mathsf {TEG}.sk_i {\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}}\mathbb {Z}_p\) and broadcasts \(h_i=g^{\mathsf {TEG}.sk_i}\) along with a proof \(\mathsf {DLOG}(g,h_i)\)Footnote 1. Once all n parties have broadcast their public key share \(h_i\), each party \(\mathcal {P}_i\) verifies the accompanying proofs \(\mathsf {DLOG}(g,h_j)\) (aborting if invalid) and then saves all \(h_j\), for \(i \ne j\), reconstructing the public key by computing \(\mathsf {TEG}.pk= h=\prod _{i=1}^{n} h_i = g^{\sum _{i=1}^{n} \mathsf {TEG}.sk_i}\).
-
Encryption \(\mathsf {TEG}.\mathsf {Enc}_{\mathsf {TEG}.pk}(m,r)\) : The encryption of a message \(m \in \mathbb {G}\) under a public-key \(\mathsf {TEG}.pk\) with randomness \(r \in \mathbb {Z}_p\) is carried out as a regular ElGamal encryption. Namely, a ciphertext \(c=(c_1=g^{r},c_2=h^{r} m)\) is generated.
-
Re-Randomization \(\mathsf {TEG}.\mathsf {ReRand}(c,r^{\prime })\) : For fresh randomness \(r^{\prime }\), a ciphertext \(c=(c_1,c_2)\) is re-randomized by computing \(c^{\prime } = (g^{r^{\prime }} c_1,h^{r^{\prime }} c_2)\).
-
Verifiable Decryption \(\mathsf {TEG}.\mathsf {Dec}_{\mathsf {TEG}.sk_1,\ldots ,\mathsf {TEG}.sk_n}(c)\): Parse \(c=(c_1,c_2)\). Each party \(\mathcal {P}_i\) broadcast a decryption share \(d_i=c_1^{\mathsf {TEG}.sk_i}\) and a proof \(\mathsf {DLEQ}(g,h_i,c_1, d_i)\) showing that they have correctly used their secret-key share \(\mathsf {TEG}.sk_i\). Once all n parties have broadcast their decryption share \(d_i\), each party \(\mathcal {P}_i\) checks that the \(\mathsf {DLEQ}(g,h_j,c_1,d_j)\) proofs are correct for all \(i \ne j\) (aborting otherwise) and retrieves the message by computing
$$ \frac{c_2}{\prod _{i=1}^{n} d_i} = \frac{c_2}{c_1^{\sum _{i=1}^{n} \mathsf {TEG}.sk_i}} = \frac{m \cdot \mathsf {TEG}.pk^{r}}{g^{r \sum _{i=1}^{n} \mathsf {TEG}.sk_i}} = \frac{m {\left( g^{\sum _{i=1}^{n} \mathsf {TEG}.sk_i}\right) }^{r}}{g^{r \sum _{i=1}^{n} \mathsf {TEG}.sk_i}}=m.$$
Smart Contracts: The concept of smart contracts was introduced by Szabo [27] and recently popularized by the Ethereum plaftorm [8, 31], which implements smart contracts based on blockchain techniques. Basically, smart contracts allow a user to specify much richer conditions for transactions to be approved over a cryptocurrency scheme, mimicking contracts in real life. Besides ensuring that an amount of money is paid to a certain party who manages to fulfill a given static set of conditions, smart contracts can also maintain an evolving state that is taken into consideration when evaluating conditions for contract fulfillment.
In Ethereum, smart contracts can be written using Solidity, a Turing complete programming language specially designed for this purpose. In order to avoid denial-of-service attacks, the amount of computation involved in verifying fulfillment of a contract is bounded by how much a user is willing to pay have the contract checked. This payment is made by means of an auxiliary cryptocurrency called gas, which is given to the miners who verify a contract. Basically, more complex contracts require larger amounts of gas to be verified so that the miners receive compensation for computationally heavy contract verification.
The use of Ethereum based stateful contracts for rewards/penalties enforcement in secure multiparty computation protocols was first proposed in [7]. Their approach consists in having parties provide a deposit of a certain number of coins before protocol execution, later receiving a refund in case they behave honestly. Our protocol follows the same approach and consists mainly of operations over a cyclic group (where the Discrete Logarithm and DDH assumptions are believed to be hard). It has been estimated in [23] that a modular exponentiation over such a group (computed as a scalar multiplication over an elliptic curve) costs 40000 gas (0.075 US Dollars) while [7] estimated the DLEQ NIZK [10] to cost 1287858 gas (0.30 US Dollars) assuming an exponentiation cost of 300000 gas. Such estimates provide good evidence that our protocol could be implemented in a smart contract platform such as Ethereum at a reasonable price.
3 Poker Protocol
For an overview of the poker game and the game formalization using the ideal functionality \(\mathcal {F}_{\mathsf {poker}}\), check the full version of this work [12].
Our protocol represents cards as ciphertexts of a threshold ElGamal cryptosystem, similarly to the scheme of [3], but employs different techniques for distributed key generation in order to address the security issues we have identified in [3] and a highly improved procedure for shuffling cards based on recent advances in zero-knowledge proofs of shuffle correctness [4]. In order to generate the representation of a shuffled deck, the parties first run a distributed key generation algorithm to obtain a public-key (while each holds a share of the secret-key). Next, they start a shuffling procedure that involves rerandomizing and the randomly permuting ciphertexts that encrypt the numbers assigned to each card (1 to 52), which is executed by all parties in a round-robin manner. The parties also provide to each other proofs that the shuffling was correctly executed, meaning that the resulting ciphertexts are indeed rerandomized and permuted version of ciphertexts provided by the previous party, which prevents adversaries from injecting ciphertexts representing arbitrary cards. When cards are intended to be revealed publicly, each party broadcasts a decryption share of the ciphertext representing the card along with a zero-knowledge proof showing its correctness. If a covered card is to be given to one specific party, each of the other parties sends their decryption shares and proofs directly to that party through a private channel. The main efficiency improvement in our protocol is obtained by employing an a compact zero-knowledge proof of a shuffle introduced in [4] (made non-interactive by the Fiat-Shamir transform), instead of the cut-and-choose technique employed by [3]. This proof is compatible with ElGamal ciphertexts and achieves the same security level of the one in [3] with only a fraction of the computational and communication complexities.
The main new feature of our protocols is a mechanism for detecting and (financially) punishing cheaters without requiring the whole protocol to the executed on chain. This mechanism requires that the parties first deposit of a number of coins for “collateral”, i.e. they lose these coins if they are detected as cheaters or abort. The protocol execution has a series of checkpoints where parties cooperate to generate a witness that the execution was correct up to that point. The witness is a signature by all parties agreeing on the current state of the execution. If at any point a protocol malfunction occurs (a party either does not receive a message or receives a invalid message), the party who detected it posts a complaint to the blockchain along with the last checkpoint witness and the protocol messages generated after the checkpoint. All the other are required to do the same or face punishment otherwise. This procedure verifies the current state of the protocol and then the execution continues in the blockchain until the next checkpoint. Any misbehavior or abort in this on-chain execution is punished financially. After the protocol execution reaches the next checkpoint and the parties obtain the corresponding witnesses, the protocol is again executed off-chain.
Smart Contract Functionality \(\mathcal {F}_{\mathsf {SC}}\) : Our poker protocol \(\pi _{\mathsf {Poker}}\) makes use of a stateful contract functionality \(\mathcal {F}_{\mathsf {SC}}\), described in Fig. 1, that models blockchain transactions used to keep collateral deposits and enforce punishment of players who misbehave, as well as ensuring that winners get their rewards. It is important to emphasize that the \(\mathcal {F}_{\mathsf {SC}}\) functionality can be easily implemented via smart contracts over a blockchain. More formally, using a public available ledger. Moreover, our construction (for protocol \(\pi _{\mathsf {Poker}}\)) requires only simple operations, i.e., verification of signatures and discrete logarithm operations over cyclic groups. The regular operation of our protocol is performed entirely off-chain, without intervention of the contract. However in the event that any problem happen or in the case that any participant in the game claim problems in the execution, any player can publish their agreed status of the game in the chain, via short witnesses (to be detailed in the protocol description).
Protocol \(\pi _{\mathsf {Poker}}\): The protocol is executed by n players \((\mathcal {P}_1, \ldots , \mathcal {P}_n\)) interacting with the stateful contract functionality \(\mathcal {F}_{\mathsf {SC}}\), and is parametrized by the small sb and big bb blind bets amount, the initial stake t, the maximum bet m per hand, the security deposit d and a timeout limit \(\tau \). In addition to the stateful contract functionality \(\mathcal {F}_{\mathsf {SC}}\), the other setup assumption is the random oracle model. We assume that the parties agree on a generator \(g\) of a group \(\mathbb {G}\) of order p for the (n, n)-Threshold ElGamal cryptosystem \(\mathsf {TEG}\) and also on a  secure digital signature scheme \(\mathsf {SIG}\). Moreover, a nonce unique to each protocol execution and protocol round (e.g. a hash of the public protocol transcript up to the current round) is implicitly attached to every signed message to avoid replay attacks. The protocol proceeds in phases as described below:
secure digital signature scheme \(\mathsf {SIG}\). Moreover, a nonce unique to each protocol execution and protocol round (e.g. a hash of the public protocol transcript up to the current round) is implicitly attached to every signed message to avoid replay attacks. The protocol proceeds in phases as described below:
-
Recovery Triggers: Whenever a signature or NIZK proof is received, its validity is tested. If the test fails, the party proceeds to the recovery phase. The same happens if a party does not receive an expected message until a timeout limit \(\tau \). These triggers will be omitted henceforth.
-
Players Check-in: For \(i=1,\ldots ,n\), player \(\mathcal {P}_i\) proceeds as follows:
-
1.
generates the keys of the signature scheme \((\mathsf {SIG}.vk_i,\mathsf {SIG}.sk_i) {\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}}\mathsf {SIG}.\mathsf {Gen}(1^{\lambda })\).
-
2.
generates \(\mathsf {TEG}\)’s key shares by sampling \(\mathsf {TEG}.sk_i {\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}}\mathbb {Z}_p\), setting \(h_i=g^{\mathsf {TEG}.sk_i}\) and generating a proof \(\mathsf {DLOG}(g,h_i)\).
-
3.
sends \((\textsc {checkin},\mathsf {coins}(d+t),\mathsf {SIG}.vk_i, h_i,\mathsf {DLOG}(g,h_i))\) to \(\mathcal {F}_{\mathsf {SC}}\) and waits until getting from \(\mathcal {F}_{\mathsf {SC}}\) the check-in confirmation \((\textsc {checkedin},\mathcal {P}_j,\mathsf {SIG}.vk_j, h_j, \mathsf {DLOG}(g,h_j))\) of each player and the parties’ order \((\mathcal {P}_1, \ldots , \mathcal {P}_n)\) that is used henceforth in the protocol. If not received until the timeout limit \(\tau \), contact \(\mathcal {F}_{\mathsf {SC}}\) to dropout and reclaim the deposited coins.
-
4.
verifies each \(\mathsf {DLOG}(g,h_j)\) for \(j \ne i\), reconstructs the initial public key \(\mathsf {TEG}.pk= \prod _{j=1}^{n} h_j\), record all \(h_j\), and initializes a vector \(\mathsf {balance}=(t,\ldots , t)\), a vector \(\mathsf {bets}=(0,\ldots , 0)\), a counter \(psb=1\) and a counter \(pbb=2\).
-
1.
-
Hand Execution - Shuffle: As the first step in executing a hand, the parties generate a randomly shuffled deck of closed cards \(\mathsf {c}_{1},\ldots ,\mathsf {c}_{52}\). For \(i=1,\ldots ,n\), \(\mathcal {P}_i\) proceeds as follows (w.l.o.g. we assume all parties are active, the adaptation to the other cases is the straightforward one):
-
1.
If \(\mathcal {P}_i=\mathcal {P}_1\), it sets \(\mathbf {c}^{0}=(\mathsf {c}^{0}_1,\ldots ,\mathsf {c}^{0}_{52})\) where \(\mathsf {c}^{0}_j=\mathsf {TEG}.\mathsf {Enc}_{\mathsf {TEG}.pk}(j,1)\). Otherwise, \(\mathcal {P}_i\) considers the cards \(\mathbf {c}^{i-1}=( \mathsf {c}^{i-1}_{1},\ldots , \mathsf {c}^{i-1}_{52})\) received from \(\mathcal {P}_{i-1}\). Notice that these initial ciphertexts just encrypt the number of each card (in increasing order) under deterministic randomness 1, allowing \(\mathcal {P}_2\) to locally compute the initial set of ciphertexts for verification.
-
2.
\(\mathcal {P}_i\) samples uniformly at random a permutation \(\pi \in \varSigma _{52}\) and \(\mathbf {r}=(r_1,\ldots ,r_{52})\) where \(r_j {\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}}\mathbb {Z}_p\), and sets \(\mathsf {c}_j^{i}=\mathsf {TEG}.\mathsf {ReRand}_{\mathsf {TEG}.pk}(\mathsf {c}_{\pi (j)}^{i-1},r_j)\), obtaining a new set \(\mathbf {c}^{i}=(\mathsf {c}_{1}^{i},\ldots ,\mathsf {c}_{52}^{i})\). Notice that this new set of ciphertexts representing cards simply contains rerandomized versions of the previous ciphertexts in a random order.
-
3.
\(\mathcal {P}_i\) generates a zero-knowledge proof of correctness of shuffle \(\mathsf {ZKSH}(\pi ,\mathbf {r},\mathbf {c}^{i-1},\mathbf {c}^{i})\) and broadcasts it with the shuffled deck \(\mathbf {c}^{i}\). All other parties verify this zero-knowledge proof.
-
1.
After all parties have participated in the shuffling procedure, the shuffled deck for the current hand is set to be \(\mathcal {D}=\mathbf {c}^{n}\). All parties sign it by computing \(\sigma ^{i}_{\mathcal {D}}=\mathsf {SIG}.\mathsf {Sign}_{\mathsf {SIG}.sk}(\mathtt {DECK-READY},\mathcal {D})\), broadcasts \(\sigma ^{i}_{\mathcal {D}}\) and verifies all signatures. Checkpoint Witness: The previous checkpoint witness concatenated with the deck \(\mathcal {D}\) and corresponding signatures \(\sigma ^{i}_{\mathcal {D}}\).
-
Hand Execution - Small and Big Blinds: After the shuffle is done, all parties wait for the small blind, i.e. for \(\mathcal {P}_{psb}\) to broadcast a signature \(\sigma ^{psb}_{sb}=\mathsf {SIG}.\mathsf {Sign}_{\mathsf {SIG}.sk_{psb}}(\mathtt {SB})\) as well as signatures on vectors \(\mathsf {balance}\) and \(\mathsf {bets}\), where \(\mathsf {balance}[psb]\) is decreased by sb coins, \(\mathsf {bets}[psb]\) is increased by sb coins, while all other coordinates remain the same. Upon receiving the signatures, each party \(\mathcal {P}_i\) broadcasts a signature \(\sigma ^{i}_{sb}=\mathsf {SIG}.\mathsf {Sign}_{\mathsf {SIG}.sk_i}(\mathtt {SB})\) as well as signatures on \(\mathsf {balance}\) and \(\mathsf {bets}\). All signatures are verified. Proceed analogously for the big blind. Checkpoint Witness: The previous checkpoint witness with the updated \(\mathsf {balance}\) and \(\mathsf {bets}\) (and signatures on them) concatenated with all signatures \(\sigma ^{i}_{sb}\) and \(\sigma ^{i}_{bb}\).
-
Hand Execution - Drawing Cards and Private Cards Distribution: Two private cards \(\mathsf {pc}_{i,1},\mathsf {pc}_{i,2}\) for each active party \(\mathcal {P}_i\) as well as the community cards \(\mathsf {cc}_1, \mathsf {cc}_2, \mathsf {cc}_3, \mathsf {cc}_4, \mathsf {cc}_5\) are drawn from \(\mathcal {D}\) according to the rules of poker. For \(i=1,\ldots ,n\) , \(\mathcal {P}_i\) proceeds as follows to open cards \(\mathsf {pc}_{j,1},\mathsf {pc}_{j,2}\) towards \(\mathcal {P}_j\) for \(j=1,\ldots ,n\) and to obtain its own private cards (here all parties act in parallel):
-
1.
\(\mathcal {P}_i\) computes its decryption shares for \(\mathsf {pc}_{j,1},\mathsf {pc}_{j,2}\) by parsing \(\mathsf {pc}_{j,k}\) as \((c_{j,k,1},c_{j,k,2})\) and computing \(d_{j,k,i}=c_{j,k,1}^{\mathsf {TEG}.sk_i}\) and a NIZK \(\mathsf {DLEQ}(g,h_i,c_{j,k,1},d_{j,k,i})\) for \(k \in \{1,2\}\). \(\mathcal {P}_i\) sends the decryption shares \(d_{j,1,i},d_{j,2,i}\) along with their corresponding proofs to \(\mathcal {P}_j\) through a private channel.
-
2.
Once it has received all \(d_{i,1,j},d_{i,2,j}\) and corresponding DLEQ proofs from the other parties, \(\mathcal {P}_i\) checks that the proofs are valid. Finally, \(\mathcal {P}_i\) learns its private cards by computing \(\mathsf {pc}^{\prime }_{i,k}=\frac{c_{i,k,2}}{\prod _{i=1}^{n} d_{i,k,j}}\) for \(k \in \{1,2\}\).
-
3.
\(\mathcal {P}_i\) broadcasts \(\sigma ^{i}_{pc}=\mathsf {SIG}.\mathsf {Sign}_{\mathsf {SIG}.sk_i}(\mathtt {PRIVATE-CARDS})\) after retrieving its private cards. Remember the signature implicitly includes a nonce unique to this protocol execution and specific round. Once signatures \(\sigma ^{j}_{pc}\) from all parties have been received, verify them.
-
1.
Checkpoint Witness: The previous checkpoint witness, except for the signatures \(\sigma ^{i}_{sb}\) and \(\sigma ^{i}_{bb}\), concatenated with all \(\sigma ^{i}_{pc}\).
-
Hand Execution - Main Flow: After cards are drawn and private cards are distributed, all parties proceed to the main flow of playing a hand, where a number of community cards will be opened and a number of betting rounds will be played, both according to the community card opening and betting round procedures. All parties continue the main flow by proceeding as follows:
-
Execute a betting round starting with the closest active successor of \(\mathcal {P}_{pbb}\).
-
Execute a community card opening procedure for flop cards \(\mathsf {cc}_1, \mathsf {cc}_2, \mathsf {cc}_3\).
-
Execute a betting round starting with the closest active successor of \(\mathcal {P}_{psb-1}\).
-
Execute a community card opening procedure for turn card \(\mathsf {cc}_4\).
-
Execute a betting round starting with the closest active successor of \(\mathcal {P}_{psb-1}\).
-
Execute a community card opening procedure for river card \(\mathsf {cc}_5\).
-
Execute a betting round starting with the closest active successor of \(\mathcal {P}_{psb-1}\).
-
Proceed to showdown starting with the last player who increased the bet in the last round, if there is one; otherwise, the closest active successor of \(\mathcal {P}_{psb-1}\).
-
-
Community Card Opening: In the steps of \(\pi _{\mathsf {Poker}}\) where a community card \(\mathsf {cc}\in \{\mathsf {cc}_1, \mathsf {cc}_2, \mathsf {cc}_3, \mathsf {cc}_4, \mathsf {cc}_5\}\) has to be opened, party \(\mathcal {P}_i\), for \(i=1,\ldots ,n\), proceeds as follows:
-
1.
\(\mathcal {P}_i\) parses \(\mathsf {cc}=(cc_{1},cc_{2})\) and broadcasts its decryption shares \(d_{i}=cc_{1}^{\mathsf {TEG}.sk_i}\) along with a NIZK \(\mathsf {DLEQ}(g,h_i,cc_{1},d_{i})\).
-
2.
After all decryption shares \(d_{j}\) and corresponding DLEQ NIZKs are received from all parties, \(\mathcal {P}_i\) verifies if all NIZKs are valid. \(\mathcal {P}_i\) opens \(\mathsf {cc}\) by computing \(\frac{cc_{2}}{\prod _{i=1}^{n} d_{j}}\).
-
3.
After opening \(\mathsf {cc}\), \(\mathcal {P}_i\) broadcasts \(\sigma ^{i}_{\mathsf {cc}}=\mathsf {SIG}.\mathsf {Sign}_{\mathsf {SIG}.sk}(\mathtt {COMMUNITY-OPEN},\mathsf {cc})\) in order to communicate it has successfully opened \(\mathsf {cc}\). Once all signatures \(\sigma ^{j}_{\mathsf {cc}}\) from other parties have been received, \(\mathcal {P}_i\) verifies that they are all valid.
-
1.
Checkpoint Witness: The previous one together with all signatures \(\sigma ^{i}_{\mathsf {cc}}\).
-
Betting Round: In the steps of \(\pi _{\mathsf {Poker}}\) that require a betting round starting from party \(\mathcal {P}_s\), each party \(\mathcal {P}_i\) communicates its betting action
 (as defined in \(\mathcal {F}_{\mathsf {poker}}\)) in a round robin manner starting from \(\mathcal {P}_s\) and following the order \((\mathcal {P}_1, \ldots , \mathcal {P}_n)\) received from \(\mathcal {F}_{\mathsf {SC}}\), proceeding as follows until the conditions specified in \(\mathcal {F}_{\mathsf {poker}}\) for finishing the betting round are met:
(as defined in \(\mathcal {F}_{\mathsf {poker}}\)) in a round robin manner starting from \(\mathcal {P}_s\) and following the order \((\mathcal {P}_1, \ldots , \mathcal {P}_n)\) received from \(\mathcal {F}_{\mathsf {SC}}\), proceeding as follows until the conditions specified in \(\mathcal {F}_{\mathsf {poker}}\) for finishing the betting round are met:-
When it is \(\mathcal {P}_i\)’s turn to state its bet, \(\mathcal {P}_i\) updates vectors \(\mathsf {bets}\) and \(\mathsf {balance}\) according to its action \(\textsc {action}_i\), i.e. it increases (resp. decreases) \(\mathsf {bets}[i]\) (resp. \(\mathsf {balance}[i]\)) by the amount of coins required by \(\textsc {action}_i\) as defined in \(\mathcal {F}_{\mathsf {poker}}\). \(\mathcal {P}_i\) generates a signature \(\sigma ^{i}_{bet}=\mathsf {SIG}.\mathsf {Sign}_{\mathsf {SIG}.sk_i}(\textsc {action}_i,\mathsf {bets}[i],\mathsf {balance}[i])\) and broadcasts \((\textsc {action}_i,\mathsf {bets}[i],\mathsf {balance}[i],\sigma ^{i}_{bet})\).
-
Upon receiving \((\textsc {action}_j,\mathsf {bets}[j],\mathsf {balance}[j],\sigma ^{j}_{bet})\) from party \(\mathcal {P}_j\) for \(j \ne i\), \(\mathcal {P}_i\) checks the validity of \(\sigma ^{j}_{bet}\). Next, \(\mathcal {P}_i\) verifies that \(\mathsf {bets}[j]\) and \(\mathsf {balance}[j]\) are consistent with \(\textsc {action}_j\) according to the rules defined in \(\mathcal {F}_{\mathsf {poker}}\). If not, \(\mathcal {P}_i\) proceeds to the recovery phase. If both checks succeed, \(\mathcal {P}_i\) updates its local copy of \(\mathsf {bets}\) and \(\mathsf {balance}\) with the new values of \(\mathsf {bets}[j]\) and \(\mathsf {balance}[j]\), and proceeds in the betting round.
-
When the conditions for ending the betting round specified in \(\mathcal {F}_{\mathsf {poker}}\) are met, each party \(\mathcal {P}_i\) broadcasts a signature \(\sigma ^{i}_{betstate}=\mathsf {SIG}.\mathsf {Sign}_{\mathsf {SIG}.sk_i}(\mathsf {bets},\mathsf {balance})\) on its local copy of vectors \(\mathsf {bets}\) and \(\mathsf {balance}\). \(\mathcal {P}_i\) waits until all signatures \(\sigma ^{j}_{betstate}\) are received from every other party \(\mathcal {P}_j\) for \(j \ne i\) and verifies that they are valid signatures on their local vectors \(\mathsf {bets}\) and \(\mathsf {balance}\) (verifying that all parties agree on the final \(\mathsf {bets}\) and \(\mathsf {balance}\)). Checkpoint Witness: The previous checkpoint witness with the updated vectors \(\mathsf {bets}\) and \(\mathsf {balance}\), along with all signatures \(\sigma ^{i}_{betstate}\) on the updated vectors.
-
Showdown: The parties proceed in a round-robin way. If a party \(\mathcal {P}_i\) wishes to open its private cards \(\mathsf {pc}_{i,1},\mathsf {pc}_{i,2}\) during showdown, \(\mathcal {P}_i\) broadcasts the decryption shares \(d_{i,1,j},d_{i,2,j}\) along with their corresponding DLEQ proofs, for \(j=1,\ldots ,n\). For every party \(\mathcal {P}_i\) who opens its private cards during showdown, the other parties \(\mathcal {P}_j\) decrypt \(\mathsf {pc}_{i,1},\mathsf {pc}_{i,2}\) by following the same procedure used for reconstructing their own private cards. If decryption fails, \(\mathcal {P}_j\) proceed to the recovery phase. If a party \(\mathcal {P}_i\) wishes to muck during showdown, it broadcasts a signature \(\sigma ^{i}_{muck}=\mathsf {SIG}.\mathsf {Sign}_{\mathsf {SIG}.sk_i}(\mathtt {MUCK})\), the other parties verify the signature. Once all parties have either opened or mucked, the parties proceed to the pot distribution.
-
Pot Distribution: Each party \(\mathcal {P}_i\) uses the opened cards, chronological order of folded/mucked hands and current vectors \(\mathsf {balance}\) and \(\mathsf {bets}\) to locally compute the updated \(\mathsf {balance}\) for all parties according to the rules of poker. It also zeros out \(\mathsf {bets}\). \(\mathcal {P}_i\) broadcast signatures on \(\mathsf {balance}\) and \(\mathsf {bets}\). Upon receiving these values from each party \(\mathcal {P}_j\), \(\mathcal {P}_i\) verifies that it is a valid signature on its own local updated vectors \(\mathsf {balance}\) and \(\mathsf {bets}\). A party \(\mathcal {P}_i\) who wishes to continue playing broadcasts a signature \(\sigma ^{i}_{cont}=\mathsf {SIG}.\mathsf {Sign}_{\mathsf {SIG}.sk_i}(\mathtt {CONTINUE})\). A party \(\mathcal {P}_i\) who no longer wishes to play or who has \(\mathsf {balance}[i]=0\) broadcasts a signature \(\sigma ^{i}_{chko}=\mathsf {SIG}.\mathsf {Sign}_{\mathsf {SIG}.sk_j}(\mathtt {CHECKOUT})\). Each party \(\mathcal {P}_i\) checks that all other parties’ signatures are valid. For all parties \(\mathcal {P}_j\) who choose to check-out, mark party \(\mathcal {P}_j\) as inactive. After determining which parties remain active and which check out, each party \(\mathcal {P}_i\) constructs a vector \(\mathsf {active}\) such that \(\mathsf {active}[j]=1\) if party \(\mathcal {P}_j\) is active in the next hand or \(\mathsf {active}[j]=0\) if \(\mathcal {P}_j\) is checking out. \(\mathcal {P}_i\) broadcasts a signature \(\sigma ^{i}_{act}=\mathsf {SIG}.\mathsf {Sign}_{\mathsf {SIG}.sk_i}(\mathsf {active})\). \(\mathcal {P}_i\) checks that signatures \(\sigma ^{j}_{act}\) by all other parties \(\mathcal {P}_j\) are valid signatures on the same \(\mathsf {active}\) vector, otherwise it proceeds to the recovery phase. If there were check-outs, update the public key as \(\mathsf {TEG}.pk= \prod _{j=1 \text { s.t. j is active}}^{n} h_j\). Increment psb and pbb using the order among the active players. A signature on these values are also generated by each party and checked by the others. Checkpoint Witness: Vectors \(\mathsf {balance}\), \(\mathsf {bets}\) and \(\mathsf {active}\), counters psb and pbb, as well as all signatures on these values.
-
Player Check-out: If \(\mathcal {P}_i\) was marked as checking out in the pot distribution phase, it sends a message \((\textsc {checkout},\mathsf {active},\mathsf {balance},\sigma )\) to \(\mathcal {F}_{\mathsf {SC}}\), where \(\sigma \) contains all signatures on \(\mathsf {active}\) and \(\mathsf {balance}\), waits for confirmation from \(\mathcal {F}_{\mathsf {SC}}\) and stops execution.
-
Recovery Request: If a party \(\mathcal {P}_i\) enters the recovery phase at any step of a given phase, it sends a message \((\textsc {report},\mathcal {P}_i,\mathsf {Checkpoint}_i,\mathsf {CurrPhase}_i)\) to \(\mathcal {F}_{\mathsf {SC}}\), where \(\mathsf {Checkpoint}_i\) is the checkpoint witness from the previous phase and \(\mathsf {CurrPhase}_i\) is the transcript of the current phase so far (i.e. only the messages that received and sent by \(\mathcal {P}_i\) after the last checkpoint).
-
Responding to a Recovery Request: Upon receiving a message \((\textsc {request}, \mathcal {P}_i, \mathsf {Checkpoint}_i,\mathsf {CurrPhase}_i)\) from \(\mathcal {F}_{\mathsf {SC}}\) containing the checkpoint witness and current phase transcript included in the \(\textsc {report}\) message of \(\mathcal {P}_i\), every other party \(\mathcal {P}_j\) sends a message \((\textsc {response},\mathcal {P}_j,\mathsf {Checkpoint}_j,\mathsf {CurrPhase}_j)\) to \(\mathcal {F}_{\mathsf {SC}}\) containing their own most recent checkpoint witness and transcript of the current phase if they are different from the ones already submitted by other parties. Otherwise, it simply acknowledges the one that is equal. Once all parties have responded to the recovery request, all parties have learned each other checkpoint witnesses and the transcripts of the current phase. For \(i=1,\ldots ,n\), party \(\mathcal {P}_i\) proceeds as follows:
-
Upon receiving the message
 from \(\mathcal {F}_{\mathsf {SC}}\), \(\mathcal {P}_i\) computes its message \(\mathsf {msg}_{\mathsf {phase},\mathsf {round}}\) for the round specified by \(\mathsf {round}\) of the phase specified by \(\mathsf {phase}\) and sends
from \(\mathcal {F}_{\mathsf {SC}}\), \(\mathcal {P}_i\) computes its message \(\mathsf {msg}_{\mathsf {phase},\mathsf {round}}\) for the round specified by \(\mathsf {round}\) of the phase specified by \(\mathsf {phase}\) and sends 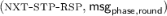 to \(\mathcal {F}_{\mathsf {SC}}\) following the protocol.
to \(\mathcal {F}_{\mathsf {SC}}\) following the protocol. -
Upon receiving \((\textsc {recovered},\mathsf {phase},\mathsf {Checkpoint})\) from \(\mathcal {F}_{\mathsf {SC}}\), \(\mathcal {P}_i\) records the checkpoint witness of the phase specified by \(\mathsf {phase}\) and returns to the regular execution of next phase as described in the protocol by communicating directly to the other parties.
-
The security of Protocol \(\pi _{\mathsf {Poker}}\) is captured in the following theorem whose proof is presented in the full version of this work [12] due to space limitations.
Theorem 1
Assuming that the DDH problem is hard and that the digital signature scheme \(\mathsf {SIG}\) is  secure, protocol \(\pi _{\mathsf {Poker}}\) securely computes \(\mathcal {F}_{\mathsf {poker}}\) in the \(\mathcal {F}_{\mathsf {SC}}\)-hybrid, random oracle model in the presence of malicious static adversaries.
secure, protocol \(\pi _{\mathsf {Poker}}\) securely computes \(\mathcal {F}_{\mathsf {poker}}\) in the \(\mathcal {F}_{\mathsf {SC}}\)-hybrid, random oracle model in the presence of malicious static adversaries.
4 Concrete Complexity Analysis
In this section we analyze the concrete communication and computational complexities of \(\pi _{\mathsf {Poker}}\). We estimate (off-chain) communication and computational complexities for the case where no user cheats (thus never triggering the recovery phase). The exact cost of performing recovery will depend on the exact point of the protocol where the recovery request happened, since the players are required to post their protocol messages generated in each round after the latest checkpoint witness. Nevertheless, we discuss why our on-chain space complexity is generally low given that we explicitly define compact witnesses for intermediate step of the protocol (even inside poker rounds). On the other hand, previous works in [20] and [7] only mention (but not define) intermediate witnesses for each round of the poker game. Moreover, we exclude the cost of generating and sending the messages between the parties and \(\mathcal {F}_{\mathsf {SC}}\), since these messages are basically transactions being posted in the blockchain and their size and generation cost may vary depending on the concrete implementation.
Estimating Complexity: We estimate computational complexity in terms of the number of exponentiations that each party has to perform in each phase of the protocol. On the other hand, we estimate communication complexity in terms of the total number of group (i.e. \(\mathbb {G}\)) elements and ring (i.e. \(\mathbb {Z}_p\)) elements transferred by all parties in each phase of the protocol. Most of the messages exchanged in the protocol are broadcast to all partiesFootnote 2. However, during private cards distribution, decryption shares for each card are sent directly to its owner through a private channel. We denote messages transmitted through private channels by [private] and messages broadcast through public channels by [broadcast]. Messages that are not explicitly marked are assumed to be broadcast by public channels. Both the Betting Round and Showdown phases have complexities that fully depend on the behavior of each player in the game of poker and other conditions such as the stake of the game. For example, a user can choose to keep raising his bet in a Betting Round and users can choose whether to show their cards or muck in Showdown. Those choices are perfectly honest and permitted in the game but they result in different final complexities for these phases of \(\pi _{\mathsf {Poker}}\). In the case of the Betting Round phase, we estimate the complexity for the case where all players speak once, which can be easily used to compute the complexity in cases where each player speaks multiple times. In the case of the Showdown phase, we estimate the complexity for the worst case (in terms of complexity), where all players choose to show their cards.
Instantiating the Building Blocks: In this analysis we instantiate ZKSH (NIZK of correctness of a shuffle) with parameters \(k=4\) and \(l=13\), which results in 208 exponentiations for the prover and 208 exponentiations for the verifier, with a proof size of 44 elements of \(\mathbb {G}\) and 65 elements of \(\mathbb {Z}_p\). Notice that this estimation is actually an upper bound for concrete communication complexity, since it pertains to the interactive version of ZKSH, which is significantly improved in terms of concrete communication complexity after applying the Fiat-Shamir heuristic. We instantiate the signature scheme \(\mathsf {SIG}\) with the ECDSA scheme [19], where a public key consists of a elliptic curve point (that we count as an element of \(\mathbb {G}\)) and a signature consists of two scalars (we count as elements of \(\mathbb {Z}_p\)). The ECDSA scheme requires one elliptic curve point multiplication by a scalar for generating a key pair, one for signing and two for signature verification (without optimizations), which we count as group exponentiations since \(\pi _{\mathsf {Poker}}\) is written in terms of groups with multiplicative notation. The concrete communication and computational complexities of are presented in Table 1.
On-Chain Space Complexity: Considering that players act honestly throughout the protocol, information is only stored in the blockchain when a player wishes to redeem its rewards. In this case, the player must post a witness showing that all players agree that the protocol was correctly executed. This witness consists of a simple digital signature. In case a malicious player does cheat and an honest player triggers the recovery mechanism, players are required to post to the blockchain their latest checkpoint witness (if they disagree with the witnesses posted by other players) and the protocol messages generated after that witness. Notice that this checkpoint witness is also a simple digital signature and that the bulk of the data posted on the blockchain actually depends on which phase of the protocol is currently being executed. For example, if recovery is triggered during the Main Flow phase of Hand Execution, only the latest checkpoint witness and short messages required in that phase would have to be posted to the blockchain, excluding the long messages previously sent in the Shuffle and Drawing Cards phase. On the other hand, previous protocols in [20] and [7] only mention that intermediate witnesses could be generated after a full round of poker, incurring in a much higher overhead in terms of blockchain storage when recovery happens. Moreover, such witnesses are not explicitly defined in [20] and [7].
Comparison with Previous Protocols: While we present estimated computational and communication complexities for each phase of a complete poker game, previous works only focus on individual card operations [3, 9, 25, 28, 29, 32, 33], making it hard to provide direct comparisons to our results. In order to provide a meaningful comparison, we will focus on the card shuffling phase, which is the main bottleneck of poker protocols. Considering a deck of 52 cards (necessary for a poker game) and a security parameter \(k=40\) for the cut-and-choose step (which is the lowest security parameter used for this kind of technique in modern cryptography), the protocol of [29] (used as a building block in [7]) requires 2120n exponentiations per player in the Shuffle phase where there are n players. With the same parameters, the Shuffle phase of the protocol proposed in [3] requires \(6240(n-1)+8320\) exponentiations, where n is the number of players. On the other hand, our protocol only requires \(209n+104\) exponentiations per player as detailed in Table 1, resulting in improvements of an order of (at least) 10 times.
5 Conclusion
We introduced the first specific purpose protocol for secure poker with payment distribution and penalty enforcement with fully-simulatable security. In order to argue about our protocol’s security, we introduced the first formal simulation based security notions for such protocols, overlooked by previous works. Moreover, we identified concrete flaws in previously proposed protocols [3, 9], showcasing the need for formal security definitions and proofs. Our work improves on previous heuristic approaches for constructing poker protocols and provides a more efficient alternative to general results that provide payment distribution and penalty enforcement for general MPC protocols, where generality comes at the cost of efficiency.
Notes
- 1.
This zero-knowledge proof of the knowledge of the exponent solves the issue in [3] that was pointed out in the introduction.
- 2.
We remark that, in our scenario, broadcasts can achieved by having parties communicate directly with each other due to the low number of parties (typically \(n \le 10\)).
References
Ahmed, M.: How UK beat the odds to win at online gambling (2017). https://www.ft.com/content/044a3d9e-7d1a-11e7-9108-edda0bcbc928. Accessed 29 Aug 2017
Andrychowicz, M., Dziembowski, S., Malinowski, D., Mazurek, L.: Secure multiparty computations on bitcoin. In: 2014 IEEE Symposium on Security and Privacy, pp. 443–458. IEEE Computer Society Press, May 2014
Barnett, A., Smart, N.P.: Mental poker revisited. In: Paterson, K.G. (ed.) Cryptography and Coding 2003. LNCS, vol. 2898, pp. 370–383. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-40974-8_29
Bayer, S., Groth, J.: Efficient zero-knowledge argument for correctness of a shuffle. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 263–280. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_17
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: Ashby, V. (ed.) ACM CCS 1993, pp. 62–73. ACM Press, November 1993
Bentov, I., Kumaresan, R.: How to use bitcoin to design fair protocols. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 421–439. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_24
Bentov, I., Kumaresan, R., Miller, A.: Instantaneous decentralized poker. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10625, pp. 410–440. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70697-9_15
Buterin, V.: White paper (2013). https://github.com/ethereum/wiki/wiki/White-Paper. Accessed 5 Dec 2017
Castellà-Roca, J., Sebé, F., Domingo-Ferrer, J.: Dropout-tolerant TTP-free mental poker. In: Katsikas, S., López, J., Pernul, G. (eds.) TrustBus 2005. LNCS, vol. 3592, pp. 30–40. Springer, Heidelberg (2005). https://doi.org/10.1007/11537878_4
Chaum, D., Pedersen, T.P.: Wallet databases with observers. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 89–105. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_7
Crépeau, C.: A zero-knowledge Poker protocol that achieves confidentiality of the players’ strategy or how to achieve an electronic Poker face. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 239–247. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_18
David, B., Dowsley, R., Larangeira, M.: Kaleidoscope: an efficient poker protocol with payment distribution and penalty enforcement. Cryptology ePrint Archive, Report 2017/899 (2017). https://eprint.iacr.org/2017/899
Desmedt, Y.: Society and group oriented cryptography: a new concept. In: Pomerance, C. (ed.) CRYPTO 1987. LNCS, vol. 293, pp. 120–127. Springer, Heidelberg (1988). https://doi.org/10.1007/3-540-48184-2_8
Desmedt, Y., Frankel, Y.: Threshold cryptosystems. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 307–315. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_28
The Economist: A Big Deal (2007). http://www.economist.com/node/10281315#print. Accessed 24 Aug 2017
ElGamal, T.: A public key cryptosystem and a signature scheme based on discrete logarithms. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 10–18. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_2
Fiat, A., Shamir, A.: How To prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
IMDb: Kaleidoscope (2017). http://www.imdb.com/title/tt0060581/. Accessed 12 Sept 2017
Johnson, D., Menezes, A., Vanstone, S.: The elliptic curve digital signature algorithm (ECDSA). Int. J. Inf. Secur. 1(1), 36–63 (2001)
Kumaresan, R., Moran, T., Bentov, I.: How to use bitcoin to play decentralized poker. In: Ray, I., Li, N., Kruegel, C. (eds.) ACM CCS 2015, pp. 195–206. ACM Press, October 2015
Pedersen, T.P.: A threshold cryptosystem without a trusted party. In: Davies, D.W. (ed.) EUROCRYPT 1991. LNCS, vol. 547, pp. 522–526. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-46416-6_47
Pointcheval, D., Stern, J.: Security proofs for signature schemes. In: Maurer, U. (ed.) EUROCRYPT 1996. LNCS, vol. 1070, pp. 387–398. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68339-9_33
Reitwiessner, C.: EIP 196 (2017). https://github.com/ethereum/EIPs/blob/master/EIPS/eip-196.md. Accessed 13 Dec 2017
Schnorr, C.P.: Efficient signature generation by smart cards. J. Cryptol. 4(3), 161–174 (1991)
Sebe, F., Domingo-Ferrer, J., Castella-Roca, J.: On the security of a repaired mental poker protocol. In: Third International Conference on Information Technology: New Generations, pp. 664–668 (2006)
Shamir, A., Rivest, R.L., Adleman, L.M.: Mental poker. In: Klarner, D.A. (ed.) The Mathematical Gardner, pp. 37–43. Springer, Heidelberg (1981). https://doi.org/10.1007/978-1-4684-6686-7_5
Szabo, N.: Smart contracts: building blocks for digital markets (1996). http://www.fon.hum.uva.nl/rob/Courses/InformationInSpeech/CDROM/Literature/LOTwinterschool2006/szabo.best.vwh.net/smart_contracts_2.html. Accessed 5 Dec 2017
Wei, T.J.: Secure and practical constant round mental poker. Inf. Sci. 273, 352–386 (2014)
Wei, T.J., Wang, L.C.: A fast mental poker protocol. J. Math. Cryptol. 6(1), 39–68 (2012)
Wikipedia: Online Poker (2017). https://en.wikipedia.org/wiki/Online_poker. Accessed 29 Aug 2017
Wood, G.: Ethereum: a secure decentralized transaction ledger (2014). http://gavwood.com/paper.pdf. Accessed 5 Dec 2017
Zhao, W., Varadharajan, V.: Efficient TTP-free mental poker protocols. In: ITCC 2005 - Volume II, vol. 1, pp. 745–750, April 2005
Zhao, W., Varadharajan, V., Mu, Y.: A secure mental poker protocol over the internet. In: ACSW Frontiers 2003, pp. 105–109. Australian Computer Society Inc., Darlinghurst (2003)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Financial Cryptography Association
About this paper
Cite this paper
David, B., Dowsley, R., Larangeira, M. (2018). Kaleidoscope: An Efficient Poker Protocol with Payment Distribution and Penalty Enforcement. In: Meiklejohn, S., Sako, K. (eds) Financial Cryptography and Data Security. FC 2018. Lecture Notes in Computer Science(), vol 10957. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-58387-6_27
Download citation
DOI: https://doi.org/10.1007/978-3-662-58387-6_27
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-58386-9
Online ISBN: 978-3-662-58387-6
eBook Packages: Computer ScienceComputer Science (R0)






 (as defined in
(as defined in  from
from 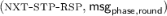 to
to