1 Introduction

E-cash was first proposed by Chaum [8] in 1983, but did not see mainstream interest and deployment until the advent of Bitcoin [26] in 2009. With a market cap of over 300 trillion US dollars by December 2017, Bitcoin has given an unprecedented demonstration that the time was ripe for digital currencies.

On the flip side, Bitcoin’s dramatic expansion has provoked serious questions about the currency’s long-term sustainability. Bitcoin miners produce proofs of work (PoW) to add blocks to the blockchain, the public ledger of all transactions. For each block added, there is a reward of newly minted coins. One concern is that proofs of work deplete large amounts of natural resources: by some estimates from December 2017, the Bitcoin network consumed over 30 terawatt-hours per year, which exceeds Denmark’s energy consumption. Moreover, most mining is currently done by specialized ASICs, which have no use beyond Bitcoin mining.

A related concern is the emergence of a “mining oligarchy” controlled by a handful of powerful entities. One of the original ideas behind basing Bitcoin mining on computing power was that anyone could participate in the network by dedicating their spare CPU cycles, incurring little cost as they would be repurposing idle time of already-existing personal computers. However, modern Bitcoin mining dynamics have become starkly different [31]: the network’s mining clout is overwhelmingly concentrated in large-scale mining farms using special-purpose hardware for Bitcoin mining, often in collaboration with electricity producers. As a result, mining with one’s spare CPU cycles today would result in net loss due to electricity costs. This phenomenon undermines the stability and security intended by the original decentralized design.

In light of these issues, there has been increasing interest in cryptocurrencies based on alternatives to proofs of work. The most explored alternative is proofs of stake (PoStake), in which a miner’s probability of successfully creating a block increases with the amount of currency he holds, rather than the amount of computation he performs. This concept has several incarnations, from ad-hoc implementations in existing cryptocurrencies [9, 22] to designs with rigorous security proofs in various models [10, 11, 21, 23]. While these are innovative proposals, the early constructions have variously suffered from attacks that arise due to the inexpensive nature of mining. On the other hand, the more recent proposals are fairly complex, usually running some kind of Byzantine agreement protocol among a sufficiently large subset of stakeholders, and thus diverge substantially from the simplicity of the original Nakamoto design. Such schemes also typically fail in case of low participation (i.e., if stakeholders are not mostly online).

In this paper, we propose SpaceMint, a cryptocurrency that uses proofs of space (PoSpace) [4, 14, 30] to address the aforementioned issues that occur in Bitcoin and alternative proposals such as PoSpace-based currencies. To mine blocks in SpaceMint, miners invest disk space rather than computing power, and dedicating more disk space yields a proportionally higher expectation of successfully mining a block. SpaceMint has several advantages compared to a PoW-based blockchain like Bitcoin, summarized below.

  • Ecological: Once the dedicated space for mining is initialized, the cost of mining is marginal: a few disk accesses with minimal computation.

  • Economical: Unused disk space is readily available on many personal computers today, and the marginal cost of dedicating it to SpaceMint mining would be small (by the previous point).Footnote 1 We thus expect that space will be dedicated towards mining even if the reward is much smaller than the cost of buying disk space for mining. In contrast, in PoW-based blockchains rational miners will stop mining if the reward does not cover the energy cost.

  • Egalitarian: Bitcoin mining is done almost entirely on application-specific integrated circuits (ASIC) and by large “mining farms,” to the point that small-scale participation (e.g., based on general-purpose hardware) is impossible. We believe SpaceMint to be less susceptible to specialized hardware than Bitcoin, as discussed in Sect. 5. Another cause of centralization of mining power in Bitcoin is mining pools. This paper does not address that problem directly, but an elegant and simple idea [25] to discourage mining pools in PoW-based blockchains – namely, having the mining process require the secret key to redeem the block reward – can be straightforwardly adapted for SpaceMint.Footnote 2

1.1 Challenges and Our Contributions

In order to “replace” PoW by PoSpace to achieve consensus on the blockchain, the following problems must be addressed.

  • Interactivity: PoSpace, as originally defined [14], is an interactive protocol. Although the same is true for the original definition of PoW [13], there the interaction was very simple (i.e., a two-message, public-coin protocol). PoSpace requires more interaction, thus it is more challenging to adapt PoSpace to the blockchain setting.

  • Determine the winner: In a PoW-based blockchain like Bitcoin, the probability of a miner being the first to find an eligible next block increases with its hashing power. The Bitcoin protocol prescribes that once an eligible next block is announced, all miners should append that block to the blockchain and continue mining on the new longest chain. Generating a PoSpace, on the other hand, is deliberately computationally cheap. We thus need some way to determine which of many different proofs “wins”. Moreover, the probability of any miner winning should be proportional to the space it dedicates, and we want a miner to learn if he is a likely winner without any interaction.

  • “Nothing-at-stake” problems: When replacing PoW by proofs that are computationally easy to generate (such as PoStake or PoSpace), a series of problems arise known as nothing-at-stake problems [16].Footnote 3 The computation-intensive nature of Bitcoin mining is a key property that, informally, ensures that all miners are incentivized to concentrate their mining efforts on a single chain, which leads to consensus. When mining is computationally cheap however, miners can intuitively (1) mine on multiple chains simultaneously, not just the one the protocol specifies, and (2) try creating many different blocks with a single proof (of space or of stake) by altering the block contents slightly (e.g., by using different transaction sets) before choosing the most favorable one to announce. The latter behavior is known as “(block) grinding”. Those issues are undesirable as

    1. 1.

      they slow down consensus;

    2. 2.

      they potentially allocate a greater reward to cheating miners

    3. 3.

      they potentially enable double-spending attacks by an adversary controlling much less than 50% of the space.

  • Challenge grinding: Yet another issue arises when the content of past blocks can influence which blocks are added to the blockchain in future. Then it may be possible for a miner to generate a long sequence of blocks whose earlier blocks might have proofs of low quality, but are generated in a biased way (by “grinding” through all the possible proofs) so that the miner can create high quality proofs later in the sequence. The problem arises when the overall sequence is of higher quality than would be expected from the miner’s disk space size, due to the disproportionately high quality of later blocks. Challenge grinding may be considered a nothing-at-stake problem, but we state it separately as, unlike the other nothing-at-stake problems, we have not encountered it in other contexts.

To tackle the interactivity problem, SpaceMint uses the Fiat-Shamir paradigm (a standard technique to replace a public-coin challenge with a hash of the previous message, already used to adapt PoW for Bitcoin); additionally, we leverage the blockchain itself to record messages of the PoSpace protocol (concretely, we use a special type of transaction to record the commitment to its space a prover needs to send to the verifier in the initialization phase of the PoSpace).

To determine the winner, we define a quality function, which assigns a quality value to a PoSpace proof. This function can be computed by the miner locally, and is designed such that the probability of a miner having the highest-quality proof in the network is proportional to the space it dedicates.

The nothing-at-stake problems are more challenging to solve. To tackle these, we introduce several new ideas and leverage existing approaches. To disincentivize miners from extending multiple chains we ensure such behavior is detected and penalize it. To prevent block grinding, SpaceMint ensures that the PoSpace is “unique”, i.e., a miner can generate exactly one valid proof for every given challenge, and this challenge itself is uniquely determined by the proofs that were used to mine a previous block. This is done by basically running two chains in parallel, a “proof chain” that contains the proofs, and a “signature chain” that contains the transactions.

Finally, to address challenge grinding, SpaceMint prescribes that past blocks influence the quality of short sequences of future blocks, thus exponentially driving down the probability that a miner could generate a sequence of blocks of disproportionately high quality by exploiting the relationship between past and future blocks.

The idea of making the challenge for a block a deterministic function of a unique credential of the resource that “won” a previous block – in combination with having a quality function by which miners can locally decide if they are likely winners – has been used in subsequent blockchain proposals like Algorand [23] or the Chia Network [3].

We also implement and evaluate the modified PoSpace to demonstrate the effectiveness of our scheme. Even for space larger than 1 TB, we show that (1) miners need less than a second to check if they are likely to “win” and therefore should generate a candidate next block, (2) block generation takes less than 30 s, and (3) verifying the validity of a block takes a fraction of a second. Moreover, these numbers grow logarithmically with larger space.

Finally, we provide a game-theoretic analysis of SpaceMint modeled as an extensive game. To do this, we formally specify a stylized model of SpaceMint mining and show that adhering to the protocol is a sequential equilibrium for rational miners in this game (i.e., deviating from the protocol does not pay off). Our analysis works in a simplified model that serves to rule out certain classes of attacks (i.e., profitable deviations based on a simplistic set of possible actions), but does not capture all possible attack vectors by real miners.Footnote 4 To our knowledge, this is the first analysis of a cryptocurrency mining as an extensive game with the corresponding game-theoretic equilibrium concepts; though the model is simplistic, we hope that this framework for rigorously ruling out certain classes of attacks will serve as a useful base upon which to build more nuanced game-theoretic models to rule out larger classes of attacks, in this and other similar cryptocurrencies.

1.2 Related Work

We have already discussed proofs of stake above. Here, we briefly mention other related proposals. A more detailed discussion can be found in the full version [27].

Proof of storage/retrievability [6, 7, 12, 18, 19, and many more] are proof systems where a verifier sends a file to a prover and later requests a proof that the prover really stored the file. Proving storage of a (random) file does show that one dedicated space, but the verifier must send the entire file first. In contrast, PoSpace requires verifier computation and communication to be polylogarithmic in the prover’s storage size.

Proof of secure erasure (PoSE), one-time computable functions [5, 15, 20, 29] are proof systems where a prover convinces the verifier that is has access to some space. Additionally one can require that the proof implies that the space also was erased [20, 29], or some function can only be computed in forward direction [15]. Those protocols have only one phase, and thus cannot be used as a PoSpace, i.e., to efficiently prove space usage over time.

Permacoin [24] is a cryptocurrency proposal that uses proofs of retrievability with a novel variant of PoW. While solutions to Bitcoin’s PoW puzzles carry no intrinsic value, Permacoin makes proof-of-work mining serve a useful purpose: miners are incentivized to store useful data and thus the network serves as a data archive. Permacoin is however still fundamentally a PoW-based scheme. In contrast, in SpaceMint the dedicated storage does not store anything useful, but we completely avoid PoW and the associated perpetual computation.

Burstcoin [1] is the only cryptocurrency we are aware of in which disk space is the primary mining resource. However, Burstcoin’s design allows time/memory trade-offs: i.e., a miner doing a little extra computation can mine at the same rate as an honest miner, while using just a small fraction (e.g., 10%) of the space. Moreover, Burstcoin requires a constant (albeit small) fraction (0.024%) of dedicated disk space to be read every time a block is mined, while SpaceMint requires only a logarithmic fraction. Finally, verification in Burstcoin is problematic: miners must hash over 8 million blocks to verify another miner’s claim. The details on this attacks can be found in Appendix B of the full version [27].

Chia Network [3] is a very recent proposal of a blockchain based on PoSpace in combination with proofs of sequential work. In a nutshell, the better the quality of the PoSpace, the faster the block can be “finalized” by a proof of sequential work, and this proof tuple then can be used to create a block. By using proofs of sequential work on top of PoSpace, Chia is even more similar to Bitcoin than SpaceMint in several respects: for example, it requires no synchronization/clocks (except, as in Bitcoin, time-stamped blocks for the occasional re-calculation of the mining difficulty), while retaining the efficiency of a pure PoSpace-based currency. The PoSpace that was developed for Chia [4] is based on ideas completely different from the PoSpace [14] we use. It has worse asymptotic security guarantees, but unlike [14], it has a non-interactive initialization phase and extremely short and efficient proofs.

Outline

  • Cryptocurrency from proofs of space: In (Sects. 2 and 3) we modify PoSpace [14] for the blockchain setting and present SpaceMint, a cryptocurrency based purely on proofs of space.

  • Addressing the “nothing-at-stake” problems: After describing attacks that arise from nothing-at-stake problems and challenge grinding, we describe how our design uses novel approaches to overcome them (Sect. 4). Our solutions extend to other blockchain designs based on easy-to-generate proofs.

  • Evaluation of proof of space: We evaluate our modified PoSpace in terms of time to initialize the space, to generate and verify blocks, and block size (Sect. 5).

  • Game theory of SpaceMint: We model SpaceMint as an extensive game, and show that adhering to the protocol is an \(\varepsilon \)-sequential Nash equilibrium (Sect. 6).

2 Proof of Space in SpaceMint

A PoSpace [14] is a two-phase protocol between a prover \(\mathcal{P}\) and a verifier \(\mathcal{V}\). After an initialization phase, \(\mathcal{P}\) stores some data \(S_\gamma \) of size N, and \(\mathcal{V}\) stores a short commitment \(\gamma \) to \(S_\gamma \). Then, in the execution phase, \(\mathcal{V}\) sends a challenge c to \(\mathcal{P}\), who returns a short answer a after reading a small fraction of \(S_\gamma \).

The PoSpace from [14, 30] are specified a family of “hard-to-pebble” directed acyclic graphs of increasing size. The prover picks a graph \(G=(V,E)\) from this family depending on the amount of space it wants to dedicate. \(\mathcal{P}\) then stores a label \(l_i\) for each node \(i\in V\), which is computed as

$$\begin{aligned} l_i:=\mathsf {hash}(\mu ,i,l_{{p_1}},\ldots ,l_{{p_t}}), \end{aligned}$$
(1)

where \(p_1, \ldots , p_t\) are the parents of node i and \(\mathsf {hash}\) is a hash function (sampled by \(\mathcal{V}\)). In [14] two graph families are suggested, one for which any successful cheating prover must either use \(\varOmega (|V|/\log (|V|))\) space between the initialization and execution phase, or use \(\varOmega (|V|/\log (|V|))\) space during execution. The other graph family enforces either \(\Theta (|V|)\) space between the phases (i.e., the same as the honest prover, up to a constant), or \(\Theta (|V|)\) time during execution.

Formally, [14] specifies a PoSpace by a tuple of algorithms \(\{\mathsf{Init},\mathsf{Chal},\mathsf{Ans},\mathsf{Vrfy}\}\), which specify a two-phase protocol between a verifier \(\mathcal{V}\) and a prover \(\mathcal{P}\). \(\mathsf{Init}\) is used to initialize the space, \(\mathsf{Chal}\) generates a challenge, \(\mathsf{Ans}\) computes the response to a challenge and \(\mathsf{Vrfy}\) verifies the response. The initialization phase consists of running Algorithm 1,Footnote 5 where \(\mathcal{P}\) commits to its space, followed by Algorithm 2, where \(\mathcal{P}\) proves that the commitment is computed “mostly correct”. In the execution phase, given by Algorithm 3, \(\mathcal{V}\) simply opens some of the committed labels to prove it has stored them.

The algorithms we give here are already made partially non-interactive for our blockchain application – in the actual PoSpace the challenges in Algorithms 2 and 3, as well as \(\mu \) in Algorithm 1 are sampled by \(\mathcal{V}\) and sent to \(\mathcal{P}\).

figure a
figure b
figure c

3 SpaceMint Protocol

3.1 Mining

The mining process consists of two phases: initialization and mining.

Initialization. When a miner first joins the SpaceMint network and wants to contribute N bits of space to the mining effort, it first generates a public/secret key pair (pk, sk) and runs Algorithm 1 as \(\mathcal{P}\), with nonce \(\mu \) set to pk, to generate

$$\begin{aligned} (\gamma ,S_\gamma ):=\mathsf{Init}(pk,N). \end{aligned}$$

The miner stores \((S_\gamma ,sk)\) and announces its space commitment \((pk,\gamma )\) via a special transaction. We require miners to commit \((pk, \gamma )\) to prevent a type of grinding attack: the problem is that the PoSpace we use [14] have the property that by making minor changes one can turn \((pk,\gamma )\) into many other space commitments that re-use most of the space.

Once this transaction is in the blockchain, the miner can start mining.

Mining. Similar to Bitcoin, SpaceMint incentivizes mining (adding new blocks) through block rewards (freshly minted coins per block) and transaction fees. Once initialized, each miner attempts to add a block to the blockchain every time period. For time period i, a miner proceeds as follows:

  1. 1.

    Retrieve the hash value of the last block in the best chain so far, and a challenge c (we discuss how c is derived in Sect. 3.4), which serves as a short seed from which we derive two long random strings \(\$_p,\$_v\).

  2. 2.

    Compute challenges \((c_1,\ldots ,c_{k_{p}}):=\mathsf{Chal}(n,k_{p},\$_p)\) for use in Algorithm 3.

  3. 3.

    Compute the proof of space \(a=\{a_1,\ldots ,a_{k_p}\}\) using Algorithm 3.

  4. 4.

    Compute the quality \(\mathsf{Quality}(pk,\gamma ,c,a)\) of the proof (details of the quality function are given in Sect. 3.5).

  5. 5.

    If the quality is high enough, so that there is a realistic chance of being the best answer in period i, compute the proof of correct commitment \(b=\{b_1,\ldots ,b_{k_v}\}\) using Algorithm 2; then create a block and send it to the network in an attempt to add it to the chain. This block contains the proofs a and b computed above and a set of transactions; the exact specification is in given Sect. 3.2 below.

Remark 1

(Postponing Algorithm 2). Note that unlike in the interactive PoSpace where one runs Algorithms 1 and 2 during initialization, we only require miners to execute Algorithm 2 if they want to add a block. This is done for efficiency reasons. For one thing, this way, the proof b (which is significantly larger than a or \(\gamma \)) must only be recorded in the blockchain once the corresponding space has actually been used to mine a block. Another more subtle advantage is that now the challenge for Algorithm 2 changes with every block; thus a cheating miner (who computed some of the labels incorrectly) will only know if he was caught cheating at the same time when he generates a potentially winning proof a (and if b does not pass, he cannot use a). This allow us to tolerate a much larger soundness error in Algorithm 2, which means we can choose a smaller \(k_v\) (concretely, it’s ok if he passes the proof with large probability p, as long as this requires using at least a p times the space an honest miner would use).

Fig. 1.
figure 1

Our blockchain consists of a proof chain that prevents grinding, and a signature chain that binds the transactions to the proof chain.

Full size image

3.2 Blockchain Format

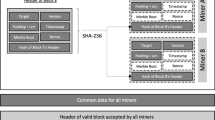
A blockchain in SpaceMint is a sequence of blocks \(\beta _0,\beta _1,\ldots \) which serve as a public ledger of all transactions. Each block \(\beta _i=(\phi _i,\sigma _i,\tau _i)\) consists of three parts, called “sub-blocks”, which contain the index i that specifies the position of the block in the blockchain. The structures of sub-blocks are as follows:

  • The hash sub-block \(\phi _i\) contains

    • the current block index i,

    • the miner’s signature \(\zeta _\phi \) on \(\phi _{i-1}\), the \((i-1)\)th hash sub-block, and

    • a “space proof” containing the miner’s pk.

  • The transaction sub-block \(\tau _i\) contains

    • the current block index i and

    • a list of transactions (Sect. 3.3).

  • The signature sub-block \(\sigma _i\) contains

    • the current block index i,

    • the miner’s signature \(\zeta _\tau \) on \(\tau _i\), the ith transaction sub-block, and

    • the miner’s signature \(\zeta _\sigma \) on \(\sigma _{i-1}\), the \((i-1)\)th signature sub-block.

The links between blocks in a blockchain are illustrated in Fig. 1. We will refer to the hash sub-blocks as the proof chain, and the signature sub-blocks with the transactions as the signature chain. While the signature and transaction sub-blocks are all linked, the hash sub-blocks are only linked to each other and not to any signature or transaction sub-blocks.

This design may seem to prevent any kind of consensus, as now we can have arbitrary many signature chains containing different transactions consistent with the same proof chain. The key observation is that once an honest miner adds the ith block (honest in the sense that he will only sign one block and keep its secret key secret), the transactions corresponding to this proof chain up to block i cannot be changed any more even by an adversary who controls all secret keys from miners that added the first \(i-1\) blocks.

3.3 Transactions in SpaceMint

There are three types of transactions in SpaceMint: (1) payments, (2) space commitments, and (3) penalties. Every transaction is signed by the user generating the transaction, and sent to the miners to be added to the blockchain. Here, we specify the three types of transactions.

Payments. Coins in SpaceMint are held and transferred by parties identified by public keys. A payment transaction transfers coins from m benefactors to n beneficiaries and has the form

$$ctx = (\mathsf{payment}, txId , {{\varvec{in}}},{{\varvec{out}}}).$$

  • \( txId \): A unique, arbitrary transaction identifier. That is, no two transactions in a blockchain can have the same identifier.

  • \({\varvec{in}}\): A list of input coins to the transaction. Specifically, \({\varvec{in}}=(in_1,\dots ,in_n)\), a list of n benefactors, each being a triple: \(in_j=( txId _j,k_j,sig_j)\), where:

    • \( txId _j\) is the identifier of a past transaction,

    • \(k_j\) is an index that specifies a beneficiary \(pk_{k_j}\) of the transaction \( txId _j\),

    • \(sig_j\) is a signature of \(( txId , txId _j,k_j,{\varvec{out}})\), which verifies under key \(pk_{k_j}\) proving ownership of the the \(k_j\)th beneficiary of transaction \( txId _j\) and binding the coin to the beneficiaries.

  • \({\varvec{out}}\): A list of beneficiaries and the amount they receive. Specifically, \({\varvec{out}}=(out_1,\dots ,out_m)\) with \(out_i=(pk_i,v_i)\), where:

    • \(pk_i\) specifies a beneficiary, and

    • \(v_i\) is the number of coins that \(pk_i\) is to be paid.

For a transaction to be valid, we require that (1) all signatures in \({\varvec{in}}\) verify correctly; (2) no benefactor is referenced by more than one subsequent transaction in the blockchain (to prevent double-spending); (3) the sum of the input values to the transaction is at least the sum of the amounts paid to beneficiaries.

Space Commitments. A space-commitment transaction

$$ctx = (\mathsf{commit}, txId ,(pk,\gamma )) $$

consists of pk, a public key, and \(\gamma \) which was computed as \((\gamma ,S_\gamma ):=\mathsf{Init}(pk,N)\). Thus, ctx is a space commitment to a space of size N.

Penalties. A penalty transaction

$$ctx = (\mathsf{penalty}, txId ,pk, \textit{prf}\,) $$

consists of pk, the public key of the transaction creator, and \(\textit{prf}\), a proof of penalty-worthy behavior by another miner. These transactions serve to penalize miners that engage in malicious behavior. The primary usage of penalties in SpaceMint is to disincentivize mining on multiple chains (e.g., the proof would contain two blocks of the same index signed by the same miner), but penalty transactions can be used to discourage other types of (detectable) behavior in blockchain-based currencies.

3.4 Where the Challenge Comes From

In Bitcoin, the PoW challenge for block i is simply the hash of block \(i-1\). For SpaceMint, using block \(i-1\) for the challenge can slow down consensus: If there are many different chains, miners can get different challenges for different chains. A rational miner would thus compute answers for many different chains (since it is easy to do), and if one of them is very good, try to add a block to the corresponding chain, even if this chain is not the best chain seen so far. If all miners behave rationally, this will considerably slow down consensus, as bad chains get extended with blocks of quality similar to the current best chain, and it will take longer for lower-quality chains to die off.

Instead, we derive the challenge for block i from the hash of block \(i-\varDelta \), for a reasonably large \(\varDelta \): the probability of multiple chains surviving for more than \(\varDelta \) blocks decreases exponentially as \(\varDelta \) increases. Moreover, in contrast to Bitcoin, we only hash the block from the proof chain, but not the signature chain (Fig. 1): this serves to prevent block-grinding attacks, since there is nothing to grind on (the proof chain is fixed regardless of the set of transactions in the block). Finally, we will use the same challenge not just for one, but for \(\delta \) consecutive blocks. This is done to prevent challenge-grinding attacks, as we explain in Sect. 4.

3.5 Quality of Proofs and Chains

Quality of a Proof. The block to be added to the chain at each time step is decided by a quality measure on the PoSpace proof included in each proposed block. For a set of valid proofs \(\pi _1\!=\!(pk_1,\gamma _1,c_1,a_1),\,\ldots ,\,\pi _m\!=\!(pk_m,\gamma _m,c_m,a_m)\), we require \(\mathsf{Quality}(\pi _i)\) to be such that the probability that \(\pi _i\) has the best quality among \(\pi _1,\ldots ,\pi _m\) corresponds to the ith miner’s fraction of the total space in the network. The probability is over the choice of the random oracle \(\mathsf {hash}\), which we use to hash answer a. We require:

$$ \mathop {\Pr }\limits _{\mathsf {hash}}\big [\forall j\ne i\,:\, \mathsf{Quality}(\pi _i)> \mathsf{Quality}(\pi _j)\big ]=\frac{N_{\gamma _i}}{\sum _{j=1}^mN_{\gamma _j}}, $$

where \(N_{\gamma _i}\) is the space committed to by \(\gamma _i\).

Let \(D_N\) be a distribution that samples N values in [0, 1] at random and outputs the largest of them:

$$\begin{aligned} D_N\sim \max \big \{ r_1,\ldots ,r_N: r_i\leftarrow [0,1],i\in [N] \big \}. \end{aligned}$$
(2)

Let \(D_N(\tau )\) denote a sample from \(D_N\) with sampling randomness \(\tau \). For valid proofs we now define

$$\begin{aligned} \mathsf{Quality}(pk,\gamma ,c,a) := D_{N_\gamma }(\mathsf {hash}(a)). \end{aligned}$$
(3)

The \(\mathsf{Quality}\) of an invalid proof is set to 0.

It remains to show how to efficiently sample from the distribution \(D_N\) for a given N. Recall that if \(F_X\) denotes the cumulative distribution function (CDF) of some random variable X over [0, 1]. If the inverse \(F_X^{-1}\) exists, then \(F_X^{-1}(U)\) for U uniform over [0, 1] is distributed as X. The random variable X sampled according to distribution \(D_N\) has CDF \(F_X(z)=\Pr [X\le z] = z^N\), since this is the probability that all N values \(r_i\) considered in (2) are below z. Therefore, if we want to sample from \(D_N\), we can simply sample \(F_X^{-1}(U)\) for U uniform over [0, 1], which is \(U^{1/N}\). In (3) we want to sample \(D_{N_{\gamma _i}}\) using randomness \(\mathsf {hash}(a_i)\). To do so, we normalize the \(\mathsf {hash}\) outputs in \(\{0,1\}^{L}\) to a value in [0, 1], and get

$$ D_{N_{\gamma _i}}(\mathsf {hash}(a_i)) := \big ( \mathsf {hash}(a_i)/2^{L} \big )^{1/N} \; . $$

Quality of a Chain. In order to decide which of two given proof-chain branches is the “better” one, we also need to define the quality of a proof chain \((\phi _0,\ldots ,\phi _i)\), which we denote by \(\mathsf{QualityPC}(\phi _0,\ldots ,\phi _i)\). Each hash sub-block \(\phi _j\) contains a proof \((pk_j,\gamma _j,c_j,a_j)\), and the quality of the block is \(v_j=D_{N_j}(\mathsf {hash}(a_j))\). For any quality \(v\in [0,1]\), we define

the space required to obtain a proof with quality better than v on a random challenge with probability . This quantity captures the amount of space required to generate a proof of this quality.

In order to prevent challenge-grinding attacks, it is desirable for the chain quality to depend multiplicatively on constituent block qualities (described in more detail in Sect. 4), and moreover it is useful to weight the contribution of the jth block for a chain of length i by a discount factor \(\varLambda ^{i-j}\). From these motivations we derive the following quality function. Note that we have used a sum of logarithms, rather than a product, to achieve the multiplicativity.

$$\begin{aligned} \mathsf{QualityPC}(\phi _0,\ldots ,\phi _i)= \textstyle \sum _{j=1}^i \log (\mathscr {N}(v_j))\cdot \varLambda ^{i-j}. \end{aligned}$$
(4)

4 Nothing-at-Stake Problems and Solutions

In this section we discuss the “nothing-at-stake” issues, which were already mentioned in the introduction. We describe them here in more detail, and outline how SpaceMint defends against them.

Recall that the difficulty arises due to the ease of computing multiple candidate blocks: in a PoSpace (or PoStake) based currency, a miner can compute many proofs (either extending different chains, or computing different proofs for the same chain) at little extra cost. Deviating from the protocol like this can be rational for a miner as it might lead to higher expected rewards. PoW-based blockchains also suffer from such “selfish mining” attacks [17], and basing the blockchain on efficiently computable proofs like PoSpace or PoStake can further aggravate this problem. Such behavior can significantly slow down consensus as well as push the scheme to follow energy expenditure trends similar to PoW-based schemes, which arise whenever there is an advantage to be gained by doing extra computation.

An even more serious issue is double-spending attacks, which become possible if a miner can create a sufficiently long chain in private which has better quality than the honestly mined chain. In all known blockchain proposals, a miner controlling more than half of the mining resources (hashing power, stake or space) can do this. But it is considered problematic if a blockchain is susceptible to double spending by adversaries with significantly less than half of the network resources.

I. Grinding Blocks. The problem: In Nakamoto-style blockchains, the challenge for the proof computed by the miners (like PoW in Bitcoin or PoSpace in SpaceMint) is somehow derived from previous blocks. If it is computationally easy to generate proofs, a miner can try out many different blocks (for example by including different transactions) until it finds an advantageous one that will allow him to generate good proofs for future blocks. This is an issue for selfish-mining and double-spending attacks.

The solution: We decouple proofs from transactions as shown in Fig. 1. This eliminates the problem of block grinding, as now challenges depend only on the proof chain. Moreover, our PoSpace are “unique” in that a prover can generate at most one valid proof per challenge. Hence, the only degree of freedom that a miner has in influencing future challenges is to either publish its proof (so it might end up in the chain), or to withhold it.

II. Mining on Multiple Chains. The problem: In Bitcoin, rational miners will always work towards extending the longest known chain. However, when mining is computationally easy, it can be rational to mine on all (or at least many) known chains in parallel, to “hedge one’s bets” across all chains that might eventually become part of the public ledger. Again, this is an issue for selfish-mining and double-spending attacks.

The solution: To address this problem in the context of selfish-mining attacks (we discuss double-spending later), we derive the challenge for block i from block \(i-\varDelta \) for some parameter \(\varDelta \) (Sect. 3.4). Let us consider two cases, depending on whether mining is done on two or more chains that forked more or less than \(\varDelta \) blocks in the past.

Case 1: chains forked less than \(\varDelta \) ago. In this case, the miner will get the same challenge for both chains. SpaceMint uses penalties (Sect. 3.3) to disincentivize miners from extending multiple chains in this case; without the penalties, a rational miner with a good-quality PoSpace proof could announce blocks on multiple chains to maximize his chances of winning. Concretely, suppose a miner \(pk'\) attempts to mine concurrently on two chains whose most recent blocks are \(\beta _j\) and \(\beta _j'\), by announcing \(\beta _{j+1}\) and \(\beta _{j+1}'\) (which have the same quality and were mined using the same space). Then anyone who observes this can generate a transaction \((\mathsf{penalty}, txId, pk, \{pk',\beta _{j+1}, \beta _{j+1}'\})\) to penalize \(pk'\). This transaction can be added to a chain extending \(\beta _{j+1}\) (or \(\beta _{j+1}'\)), and its meaning is that half of the reward (block reward and transaction fees) that should go to the miner who announced \(\beta _{j+1}\), is now going to pk (the “accuser”) instead, and the other half of the reward is destroyed, i.e., cannot be redeemed by any party. We destroy half of the reward so the penalty hurts even if the cheating miner can be reasonably sure to be able to accuse itself. For this to work, mining rewards can only be transferred by a miner some time after the block was added, so that there is enough time for other miners to claim the penalty.Footnote 6

Case 2: chains forked more than \(\varDelta \) ago. In this case the miner receives different challenges for different chains, leading to proofs of different quality for the two chains. In this case, even with our penalty scheme in place, a rational miner can still get an advantage by deviating: instead of only trying to extending the highest-quality chain, it also generates proofs for the lesser chain. As the challenges differ, so will the two proofs, and if the proof on the lesser chain has very high quality, the rational miner would publish it, hoping that this chain will become the best chain and survive.

We address this problem by arguing that it is extremely unlikely (the probability is exponentially small in \(\varDelta \)) that this case occurs, as a weaker branch of the chain would have to “survive” for \(\varDelta \) blocks despite a strong incentive (via our punishment scheme) for miners to only extend the chain of highest quality.

III. Grinding Challenges. The problem: Challenge grinding is a type of attack that can be used for double-spending, by generating a long chain in private that is of higher quality than what would result when using one’s resources honestly. It arises from the fact that an adversary can split its space into m smaller chunks. As discussed in Sect. 3.5, the quality of a block is purposely designed such that splitting a fixed amount of space into smaller chunks and choosing the highest-quality block among them does not affect the expected quality of the block generated. However, a miner can examine all possible chains of some given length, and then pick the chain that gives it the most favorable challenges for future blocks.

Concretely, consider our setting, where the challenge for block i is determined by block \(i-\varDelta \). An adversary can generate a sequence of length \(2\varDelta \) where the first half of the blocks is chosen to provide the most favorable challenges for the later half of the sequence.Footnote 7 Note that the first half of this sequence would be of even poorer quality than the expected quality from honest mining given the adversary’s total amount of space; however, the benefit gained in the second half of the sequence can outweigh this loss in quality in the first half. The adversary can then release this high-quality chain (all at once) in an attempt to overtake the current best chain.

Note that in this attack the adversary explores multiple chains in parallel, which we have addressed already using a penalizing scheme. But penalizing does not protect against double-spending attacks in which the adversary never actually published two proofs for the same slot. And even he would, a double-spending attack can be profitable even if one loses some mining rewards due to the penalizing scheme.

The solution: As mentioned in Sect. 3.5, the problem with this attack is exacerbated if the metric for determining the quality of a chain is a sum or any other linear function. Thus, to prevent this attack, (1) we define the quality of a chain as the product of the amounts of space needed for the proofs in it, rather than their sum; and (2) we use the same block to derive challenges for \(\delta \) future blocks (i.e., use \(\mathsf {hash}(\beta _i, nonce)\) for \(nonce \in [1, \delta ]\) as challenges for time \(i+\varDelta \) through \(i+\varDelta +\delta \)).

Intuitively, (1) makes it harder for the adversary to find a good chain of length \(2\varDelta \), as worse blocks are weighted more; and (2) is helpful because it means that a challenge-grinding adversary would have to choose “early” blocks to optimize their chances over sequences of \(\delta \) future challenges rather than just a single future challenge, thus making it exponentially harder (in \(\delta \)) to find a “good” challenge that will yield \(\delta \) high-quality blocks at once. Another way to see this is that by the Chernoff bound, the average of \(\delta \) independent random variables deviates less from its expectation as \(\delta \) grows. So for large \(\delta \), even the ability to select between multiple challenges (each giving a sample of the average of \(\delta \) i.i.d. variables) is not very useful to find one where this value deviates by a lot from its expectation. A more detailed discussion of this attack and our defense is given in the full version [27].

5 Evaluation

To evaluate SpaceMint, we focused on space initialization time, proof size, and time for proof generation and verification. We implemented a prototype in Go using SHA3 in 256-bit mode as the hash function and the graphs from [28], which forces cheating provers to store \(\varOmega (N/\log (N))\) bits to efficiently generate proofs. We used a desktop computer equipped with an Intel i5-4690K Haswell CPU and 8 GB of memory, and an off-the-shelf 2 TB hard disk drive with 64 MB cache.

Figure 2a shows initialization time for spaces from 8 KB to 1.3 TB, which involves computing hashes of the nodes and a Merkle tree over them and is only done once. For 1.3 TB this takes approximately 41 h, which prevents re-using the same space for different commitments.

Fig. 2.
figure 2

Results of evaluation

Full size image

A proof consists of the Merkle inclusion proof for a set of node labels. The number of nodes to be opened is \(\lambda \cdot \log (n)+1\) (as \(k_v= \lambda \cdot \log (n)\) in Algorithm 2 and \(k_p\ll k_v\) in Algorithm 3), where \(\lambda \) is a statistical security parameter. Every node has at most two parents, and each opening of a node is \(\log (n)\cdot 32\) bytes. The overall proof size is thus at most \(3\cdot \lambda \cdot \log ^2(n)\cdot 32\) bytes. (Opening fewer than \(\lambda \log (n)\) nodes was not shown to be secure, but we are not aware of concrete attacks even for opening \(\lambda \) nodes; we believe that the number required for security lies somewhere in between, closer to opening \(\lambda \) nodes.) Fig. 2b shows the proof size for opening \(\lambda \log (n)\) or only \(\lambda \) nodes, for \(\lambda =30\).

Assuming a miner is storing the space correctly, she only needs to open a small \(k_p\) number of nodes in the Merkle tree to check the quality of her solution (Sect. 3.1). As it takes <1 ms to read a hash from the disk, this takes just a fraction of a second. In the rare event that the answer is of very good quality, she generates the full proof, which takes less than 30 s. Since a miner must open \(k_p\) nodes in every time slot, we want \(k_p\) to be small. In practice \(k_p=1\) seems secure; for safety, we set it to a small constant. Proofs in SpaceMint are substantially bigger than in Bitcoin and require more than one hash evaluation to verify. However, for an active currency, the transactions contained in a block will largely dominate block size and verification time. Figure 2c shows that while it takes seconds to generate the proof, it only takes a fraction of a second to verify it.

In terms of power consumption of the network, currently, the Bitcoin miners consume more than 32 TWh of energy annually, or around 220 GJ/min. Our prototype was evaluated on a full CPU, but a cost-conscious miner would mine on a more energy-efficient device, such as a Raspberry Pi [2], which consumes less than 10 W of power. Furthermore, we could set the quality threshold such that only a small number of miners, e.g., 1,000 miners, have a realistic chance of winning (i.e., have to generate a full proof). In such a scenario, the estimated energy consumption of a SpaceMint network per block would be

$$10W \cdot M \cdot 0.01s + 10W \cdot 1000 \cdot 20s = (200,000 + 0.1M)J/\text {block},$$

where M is the number of miners in the network. In such scenario, even with a billion miners in the network and with a block being added every minute, SpaceMint network would use less than 1% of the power of the current Bitcoin network.

Impact of Storage Medium. Almost all modern Bitcoin mining is done by clusters of application-specific integrated circuits (ASICs), which can compute hashes for a tiny fraction of the hardware and energy cost of a general-purpose processor. We believe that SpaceMint mining would not be as susceptible to advantages from specialized hardware as Bitcoin, and that regular hard disk drives are well-suited to serve as SpaceMint mining equipment. Let us consider existing categories of storage devices. Although hard disks are expensive compared to other storage devices, most notably tapes, devices like tapes are not adequate for mining as we require frequent random accesses to answer the PoSpace challenges. Solid state drives do allow for (fast) random accesses, but are more expensive than hard disks and do not provide any benefit since the rate of lookups required for mining is very low. Notably, SpaceMint mining hinges on doing a few random lookups every minute. The required frequency is so low that speed is a non-issue: cheap, slow random access is what SpaceMint miners are after.

6 Game Theory of SpaceMint

The miners in a cryptocurrency are strategic agents who seek to maximize the reward that they get for mining blocks. As such, it is a crucial property of a cryptocurrency that “following the rules” is an equilibrium strategy: i.e., it is important that the protocol is designed so that miners are never in a situation where deviating from the protocol is more profitable than behaving honestly.

To establish by a rigorous analysis that no deviations are beneficial is a natural theoretical goal. In game theory, such analyses are done in the context of a model specifying the “actions” that players can take during the course of a game in which each player’s goal is to maximize her own utility. In our context, utility corresponds to profit from mining rewards. It is assumed that “actions” describe all behavior that players may exhibit: in our context, this means that the notion of “following the protocol,” as well as any possible deviations from the protocol, are assumed to be expressible by an action or sequence of actions.

To our knowledge, this paper presents the first rigorous equilibrium analysis in which cryptocurrency mining is modeled as an extensive game, the canonical game-theoretic notion for games that take place over time. Our analysis works in a simplified model that serves to rule out certain classes of attacks (i.e., profitable deviations by modeled actions). In our stylized game, play occurs over a series of discrete time steps, in each of which a block is added to the blockchain. At each time step, each player (miner) must choose a strategy, specified by: (1) which blocks to extend (if any), and (2) which extended blocks to publish (if any).

Our analysis herein is intended as a basic framework to model mining in blockchain-based cryptocurrencies as an extended game, and does not claim to comprise an exhaustive modeling of all possible attack vectors. In particular, our stylized model does not capture some important aspects, most notably block withholding, which is used in “selfish mining.” Nevertheless, we believe that our simple modeling framework for cryptocurrency as an extended game can serve as a useful base upon which to build more nuanced game-theoretic models.

Due to space constraints, we defer to the full version [27] the details of the modeling of mining as an extensive game and the proof of equilibrium. Here, we give just an informal statement of our main equilibrium theorem.

Theorem 1

It is a sequential equilibrium of the SpaceMint game (defined in [27, Sect. 7]) for all computationally bounded players to adhere to the mining protocol, provided that no player holds more than 50% of all space.

Showing that adhering to the protocol is an equilibrium of such a game means that rational miners are not incentivized to deviate from the protocol when playing the game: from this, it follows that rational miners will reach consensus on a single chain, as they would not be able to get an advantage by using a “cheating” strategy.