On the Price of Stability of Undirected Multicast Games

Abstract

In multicast network design games, a set of agents choose paths from their source locations to a common sink with the goal of minimizing their individual costs, where the cost of an edge is divided equally among the agents using it. Since the work of Anshelevich et al. (FOCS 2004) that introduced network design games, the main open problem in this field has been the price of stability (PoS) of multicast games. For the special case of broadcast games (every vertex is a terminal, i.e., has an agent), a series of works has culminated in a constant upper bound on the PoS (Bilò et al., FOCS 2013). However, no significantly sub-logarithmic bound is known for multicast games. In this paper, we make progress toward resolving this question by showing a constant upper bound on the PoS of multicast games for quasi-bipartite graphs. These are graphs where all edges are between two terminals (as in broadcast games) or between a terminal and a nonterminal, but there is no edge between nonterminals. This represents a natural class of intermediate generality between broadcast and multicast games. In addition to the result itself, our techniques overcome some of the fundamental difficulties of analyzing the PoS of general multicast games, and are a promising step toward resolving this major open problem.

Rupert Freeman thanks NSF IIS-1527434 and ARO W911NF-12-1-0550 for support.

Samuel Haney and Debmalya Panigrahi were supported in part by NSF Awards CCF-1527084 and CCF-1535972l.

1 Introduction

In cost sharing network design games, we are given a graph/network $G = (V,E)$ with edge costs and a set of users (agents/players) who want to send traffic from their respective source vertices to sink vertices. Every agent must choose a path along which to route traffic, and the cost of every edge is shared equally among all agents having the edge in their chosen path, i.e., using the edge to route traffic. This creates a congestion game since the players benefit from other players choosing the same resources. A Nash equilibrium is attained in this game when no agent has incentive to unilaterally deviate from her current routing path. The social cost of such a game is the sum of costs of edges being used in at least one routing path, and efficiency of the game is measured by the ratio of the social cost in an equilibrium state to that in an optimal state. (The optimal state is defined as one where the social cost is minimized, but the agents need not be in equilibrium.) The maximum value of this ratio (i.e., for the most expensive equilibrium state) is called the price of anarchy of the game, while the minimum value (i.e., for the least expensive equilibrium state) is called its price of stability. It is well known that even for the most restricted settings, the price of anarchy can be $\varOmega (n)$ for n agents. Therefore, the main question of research interest has been to bound the price of stability (PoS) of this class of congestion games.

Anshelevich et al. [2] introduced network design games and obtained a bound of $O(\log n)$ on the PoS in directed networks with arbitrary source-sink pairs. While this is tight for directed networks, they left determining tighter bounds on the PoS in undirected networks as an open question. Subsequent work has focused on the case of all agents sharing a common sink (called multicast games) and its restricted subclass where every vertex has an agent residing at it (called broadcast games). These problems are natural analogs of the Steiner tree and minimum spanning tree (MST) problems in a game-theoretic setting. For broadcast games, Fiat et al. [13] improved the PoS bound to $O(\log \log n)$, which was subsequently improved to $O(\log \log \log n)$ by Lee and Ligett [15], and ultimately to O(1) by Bilò et al. [5]. For multicast games, however, progress has been much slower, and the only improvement over the $O(\log n)$ result of Anshelevich et al. is a bound of $O(\log n / \log \log n)$ due to Li [16]. In contrast, the best known lower bounds on the PoS of both broadcast and multicast games are small constants [4]. As a result, determining the PoS of multicast games has become a compelling open question in the area of network games.

In this paper, we achieve progress toward answering this question. In the multicast setting, a vertex is said to be a terminal if it has an agent on it, else it is called a nonterminal. Note that in the broadcast problem, there are no nonterminals and all the edges are between terminal vertices. In this paper, we consider multicast games in quasi-bipartite graphs: all edges are either between two terminals, or between a nonterminal and a terminal. (That is, there is no edge with both nonterminal endpoints.) This is a natural setting of intermediate generality between broadcast and multicast games. Moreover, quasi-bipartite graphs have been widely studied for the Steiner tree problem (see, e.g., [6, 7, 17, 18]) and has provided insights for the problem on general graphs. Our main result is an O(1) bound on the PoS of multicast games in quasi-bipartite graphs.

Theorem 1

The price of stability of multicast games in quasi-bipartite graphs is a constant.

In addition to the result itself, our techniques overcome some of the fundamental difficulties of analyzing the PoS of general multicast games, and therefore represent a promising step toward resolving this important open problem. To illustrate this point, we outline the salient features of our analysis below.

The previous PoS bounds for multicast games [2, 16] are based on analyzing a potential function $\phi _e$ defined on each edge e as its cost scaled by the harmonic of the number of agents using the edge, i.e., $\phi _e = cost(e) \cdot (1+1/2+1/3+\cdots +1/j)$ where j is the number of terminals using e. The overall potential is $\phi = \sum _e \phi _e$. When an agent changes her routing path (called a move), this potential exactly tracks the change in her shared cost. If the move is an improving one, then the shared cost of the agent decreases and so too does the potential. As a consequence, for an arbitrary sequence of improving moves starting with the optimal Steiner tree, the potential decreases in each move until a Nash Equilibrium (NE) is reached. This immediately yields a PoS bound of $H(n) = O(\log n)$ [2]. To see this, note that the potential of any configuration is bounded below by its cost, and above by its cost times H(n). Then, letting $S_{NE}$ be the Nash equilibrium reached, and $T^*$ be the optimal routing tree, we have

$$\begin{aligned} c(S_{NE}) \le \phi (S_{NE}) \le \phi (T^*) \le H(n)c(T^*). \end{aligned}$$

This bound was later improved to $O(\log n/\log \log n)$ by Li [16] with a similar but more careful accounting argument.

The previous PoS bounds for broadcast games [5, 13, 15] use a different strategy. As in the case of multicast games, these results analyze a game dynamics that starts with an optimal solution (MST) and ends in an NE. However, the sequence of moves is carefully constructed — the moves are not arbitrary improving moves. At a high level, the sequence follows the same pattern in all the previous results for broadcast games:

• 1. Perform a critical move: Allow some terminal v to switch its path to introduce a single new edge into the solution, that is not in the optimal routing tree and is adjacent to v. This edge is associated with v and denoted $e_v$. Any edge introduced by the algorithm in any move other than a critical move uses only edges in the current routing tree, and edges in the optimal routing tree. Therefore, we only need to account for edges added by critical moves.

• 2. Perform a sequence of moves to ensure that the routing tree is homogenous. That is, the difference in costs of a pair of terminals is bounded by a function of the length of the path between them on the optimal routing tree. For example, suppose two terminals w and $w'$ differ in cost by more than the length of the path between them in the optimal routing tree. Then the terminal with larger cost has an improving move that uses this path, and then the other terminal’s path to the root. Such a move introduces only edges in the optimal routing tree.

• 3. Absorb a set of terminals around v in the shortest path metric defined on the optimal tree: terminals w replace their current strategy with the path in the optimal routing tree to v, and then v’s path to the root. If w had an associated edge $e_w$, introduced via a previous critical move, it is removed from the solution in this step.

The absorbing step allows us to account for the cost of edges added via critical moves, by arguing that vertices associated with critical edges of similar length must be well-separated on the optimal routing tree. If edges $e_u$ and $e_v$ are not far apart, the second edge to be added would be removed from the solution via the absorbing step.

Homogeneity facilitates absorption: Suppose v has performed a critical move adding edge $e_v$, and let w be some other terminal. While v pays $c(e_v)$ to use edge $e_v$, w would only pay $c(e_v)/2$ to use $e_v$, since it would split the cost with v. That is, if w bought a path to v and then used v’s path to the root, it would save at least $c(e_v)/2$ over v’s current cost. If the current costs paid by v and w are not too different, and the distance between v and w not too large, then such a move is improving for w.

The previous results differ in how well they can homogenize: the tighter the bound on the difference in costs of a pair of terminals as a function of the length of the path between them in the optimal routing tree, the larger the radius in the absorb step. In turn, a larger radius of absorption establishes a larger separation between edges with similar cost, which yields a tighter bound on the PoS.

This homogenization-absorption framework has not previously been extended to multicast games. The main difficulty is that there can be nonterminals that are in the routing tree at equilibrium but are not in the optimal tree. No edge incident on these vertices is in the optimal tree metric, and therefore these vertices cannot be included in the homogenization process. So, any critical edge incident on such a vertex cannot be charged via absorption. This creates the following basic problem: what metric can we use for the homogenization-absorption framework that will satisfy the following two properties?

• 1. The metric is feasible – the sum of all edge costs in (a spanning tree of) the metric is bounded by the cost of the optimal routing tree. These edges can therefore be added or removed at will, without need to perform another set of moves to pay for them (in contrast to critical edges). This allows us to homogenize using these edges.

• 2. The metric either includes all vertices (as is the case with the optimal tree metric for broadcast games), or if there are vertices not included in the metric, critical edges adjacent to these vertices can be accounted for separately, outside the homogenization-absorption framework.

We create such a metric for quasi-bipartite graphs, allowing us to extend the homogenization-absorption framework to multicast games. Our metric is based on a dynamic tree containing all the terminals and a dynamic set of nonterminals. We show that under certain conditions, we can include the shortest edge incident on a nonterminal vertex, even if it is not in the optimal routing tree, in this dynamic tree. These edges are added and removed throughout the course of the algorithm. Our new metric is now defined by shortest path distances on this dynamic tree: the optimal routing tree extended with these special edges. We ensure homogeneity not on the optimal routing tree, but on this dynamic metric. Likewise, absorption happens on this new metric. We define the metric in such a way that the following hold:

• 1. The metric is feasible. That is, the total cost of all edges in the dynamic tree is within a constant factor of the cost of the optimal tree.

• 2. Consider some critical edge $e_v$ such that the corresponding vertex v is not in the metric. That is, it was not possible to add the shortest edge adjacent to v to the dynamic tree while keeping it feasible. Therefore, v is at infinite distance from every other vertex in this metric, ruling out homogenization. Then, $e_v$ can be accounted for separately, outside the homogenization-absorption framework.

For the remaining edges $e_v$ such that v is in the metric, we account for them by using the homogenization-absorption framework. Our main technical contribution is in creating this feasible dynamic metric, going beyond the use of static optimal metrics in broadcast games. While the proof of feasibility currently relies on the quasi-bipartiteness of the underlying graph, we believe that this new idea of a feasible dynamic metric is a promising ingredient for multicast games in general graphs.

In the rest of the paper, we present the algorithm in detail, and provide an outline of its analysis. Details of the analysis are deferred to the full version of the paper due to space constraints.

1.1 Related Work

Recall that the upper bounds for PoS are a (large) constant and $O\left( \frac{\log n}{\log \log n}\right)$ for broadcast and multicast games, respectively. The corresponding best known lower bounds are 1.818 and 1.862 respectively by Bilò et al. [4], leaving a significant gap, even for broadcast games. Moreover, Lee and Ligett [15] show that obtaining superconstant lower bounds, even for multicast games where they might exist, is beyond current techniques. While this lends credence to the belief that the PoS of multicast games is O(1), Kawase and Makino [14] have shown that the potential function approach of Anshelevich et al. [2] cannot yield a constant bound on the PoS, even for broadcast games. In fact, Bilò et al. [5] used a different approach for broadcast games, as do we for multicast games on quasi-bipartite graphs.

Various special cases of network design games have also been considered. For small instances ($n=2, 3, 4$), both upper [10] and lower [3] bounds have been studied. [10] show upper bounds of 1.65 and 4/3 for two and three players respectively. For weighted players, Anshelevich et al. [2] showed that pure Nash equilibria exist for $n=2$, but the possibility of a corresponding result for $n\ge 3$ was refuted by Chen and Roughgarden [9], who also provided a logarithmic upper bound on the PoS. An almost matching lower bound was later given by Albers [1]. Recently, Fanelli et al. [12], showed that the PoS of network design games on undirected rings is 3/2.

Network design games have also been studied for specific dynamics. In particular, starting with an empty graph, suppose agents arrive online and choose their best response paths. After all arrivals, agents make improving moves until an NE is reached. The worst-case inefficiency of this process was determined to be poly-logarithmic by Charikar et al. [8], who also posed the question of bounding the inefficiency if the arrivals and moves are arbitrarily interleaved. This question remains open. Upper and lower bounds for the strong PoA of undirected network design games have also been investigated [1, 11]. They show that the price of anarchy in this setting is $\varTheta (\log n)$.

2 Preliminaries

Let $G = (V,E)$ be an undirected edge-weighted graph and let c(e) denote the cost of edge e. Let $U \subseteq V$ be a set of terminals and $r \in U$. In an instance of a network design game, each terminal u is associated with a player, or agent, that must select a path from u to r. We consider instances in which G is quasi-bipartite, that is no edge e has two nonterminal end points.

A solution, or state, is a set of paths connecting each player to the root. Let $\mathcal {S}$ be the set of all possible solutions. For a solution S, a terminal u, and some subset $E'$ of the edges in the graph, let $c_u^{E'}(S) = \sum _{e \in E'} c(e)/n_e(S)$ be the cost paid by u for using edges in $E'$, where $n_e(S)$ is the number of players using edge e in state S. Let $p_u(S)$ be the set of edges used by u to connect to the root in S and let $c_u(S) = c_u^{p_u(S)}(S)$ be the total cost paid by u to use those edges. For a nonterminal v, if every terminal u with $v \in p_u(S)$ uses the same path from v to the root then define $p_v(S)$ to be this path from v to r, and $c_v(S) = c_u^{p_v(S)}(S)$. Additionally, we will sometimes refer to the cost a vertex v pays, even if v is a nonterminal. By this we mean $c_v(S)$. For any vertex $v \in S$, let $e_v$ be the edge in $p_v(S)$ with v as an endpoint.

Let $\varPhi : \mathcal {S} \rightarrow \mathbb {R}_+$ be the potential function introduced by Rosenthal [19], defined by

$$\begin{aligned} \varPhi (S) = \sum _{e \in E} c(e) H_{n_e(S)} = c(e) \left( 1+\frac{1}{2}+\cdots +\frac{1}{n_e(S)}\right) . \end{aligned}$$

Let $u \in U$ and suppose S and $S'$ are states for which $p_v(S) = p_v(S')$ for all players $v \not = u$. Then $\varPhi (S')-\varPhi (S) = c_u(S')-c_u(S)$. In particular, if a single player changes their path to a path of lower cost, the potential decreases.

The goal of each player is to find a path of minimum cost. A solution where no player can benefit by unilaterally changing their path is called a Nash Equilibrium. Let $T^*$ be a solution that minimizes the total cost paid. Note that $T^*$ is a minimum Steiner tree for G. The price of stability (PoS) is the ratio between the minimum cost of a Nash equilibrium and the cost of $T^*$.

Let $p_{T^*}(u,v)$ be the path in $T^*$ between u and v. Let $v_1,\dots ,v_n$ be the vertices of $T^*$ in the order they appear in a depth first search of $T^*$. Let MC, the “main cycle”, be the concatenation of $p_{T^*}(v_1,v_2), p_{T^*}(v_2,v_3),\dots , p_{T^*}(v_{n-1},v_n), p_{T^*}(v_n,v_1)$. Note that each edge in $T^*$ appears exactly twice in MC. The following property will be helpful:

Fact 2

Any x to y path in MC completely contains $p_{T^*}(x,y)$.

Define the class of edge e, class(e), as $\alpha$ if $256^{\alpha } \le c(e) < 256^{\alpha +1}$. Without loss of generality, we assume that $c(e) \ge 1$ for all $e \in E$, so the minimum possible edge class is 0. For simplicity, define $\lfloor c(e) \rfloor = 256^{class(e)}$, a lower bound for c(e), and $\lceil c(e) \rceil = 256^{class(e)+1}$, an upper bound for c(e).

For each nonterminal v, let $\sigma _v$ be the minimum cost edge adjacent to v in G. Let $t_v$ be the terminal adjacent to $\sigma _v$. Let $T^+$ be the extended optimal metric: $T^* \cup \{\sigma _v\}_{v \in V}$. We maintain a dynamic set of nonterminals $\mathcal {Z}_S = \left\{ w \notin T^*: c(\sigma _w) \le \lfloor c(e_w) \rfloor /64 \right\}$. That is, $\mathcal {Z}_S$ are those nonterminals w in solution S whose first edge $e_w$ has cost within a constant factor of the cost of $\sigma _w$ For any $w \in S$, if $\sigma _w$ is added to S while $w \in \mathcal {Z}_S$, then we show that we will be able to pay for $\sigma _w$ if it remains in the final solution. In the algorithm, we denote the current state by $S_{curr}$. For ease of notation, we define $\mathcal {Z}= \mathcal {Z}_{S_{curr}}$.

The remaining definitions are modifications of key definitions from [5]. The interval around vertex $v \in T^*$ with budget y, $I_{v,y}$, is the concatenation of its right and left intervals, $I^+_{v,y}$ and $I^-_{v,y}$, where $I^+_{v,y}$ is the maximal contiguous interval in MC with v a left endpoint such that

$$\begin{aligned} 2\sum _{\alpha \ge 0} 256^{\alpha +1} H^2_{n_{I^+, \alpha }} \le y, \end{aligned}$$

where $n_{I^+, \alpha }$ is the number of edges of class $\alpha$ in $I_{v,y}^+$ (repeated edges are counted every time they appear). We define $I^-_{v,y}$ similarly.

The neighborhood of v in state S, $N_S(v)$ is an interval around v as well as certain $w\not \in T^*$ with $t_w$ in the interval. Formally,

$$\begin{aligned} N_S(v) = {\left\{ \begin{array}{ll} I_{v,\frac{\lfloor c(e_v) \rfloor }{56}} \cup \left\{ w \in \mathcal {Z}_S \bigg | t_w \in I_{v,\frac{\lfloor c(e_v) \rfloor }{56}} \text { and } c(\sigma _w) \le \frac{\lfloor c(e_v) \rfloor }{64} \right\} &{}\text {if } v\in T^*, \\ I_{t_v,\frac{\lfloor c(e_v) \rfloor }{56}} \cup \left\{ w \in \mathcal {Z}_S \bigg | t_w \in I_{t_v,\frac{\lfloor c(e_v) \rfloor }{56}} \text { and } c(\sigma _w) \le \frac{\lfloor c(e_v) \rfloor }{64} \right\} &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$

$N^+_S(v)$ and $N^-_S(v)$ are the right and left intervals of the neighborhood respectively (that is, the portions of $N_S(v)$ to the right and left of v or $t_v$ respectively). We denote $N_{S_{curr}}(v)$ as N(v). Roughly speaking, we are going to charge the cost of edges in the final solution not in $T^*$ to the interval portions of non-overlapping right neighborhoods. A path $X = p_{T^*}(x,y)$ is homogenous if

$$\begin{aligned} |c_x(S) - c_y(S)| \le 4 \sum _{\alpha \ge 0} 256^{\alpha +1} H_{n_{X,\alpha }}^2. \end{aligned}$$

If $X = p_{T^*}(x,y) \subseteq N(v) \cap T^*$ is a homogenous path then

$$\begin{aligned} |c_x(S) - c_y(S)| \le 4 \sum _{\alpha \ge 0} 256^{\alpha +1} H^2_{n_{X, \alpha }} \le 8 \sum _{\alpha \ge 0} 256^{\alpha +1} H^2_{n_{N^+(v), \alpha }} \le \lfloor c(e) \rfloor / 14. \end{aligned}$$

N(v) is homogenous if the following holds: For all $x,y \in N(v)$ with $x,y \ne u_v$, a special vertex to be defined later, such that the path in $T^+$ from x to y does not contain v, $|c_x(S_{curr}) - c_y(S_{curr})| \le \frac{23\lfloor c(e_v) \rfloor }{112}$. Homogenous neighborhoods allow us to bound the difference in cost between any two vertices in N(v) which will be useful when arguing that players have improving strategy changes.

3 Algorithm

The initial state of the algorithm is the minimum cost tree $T^*$ connecting all the terminals to the root. The algorithm carefully schedules a series of potential-reducing moves. (Recall the potential function $\varPhi (S) = \sum _{e \in E} c(e) H_{n_e(S)}$ introduced in Sect. 2). Since there are finitely many states possible, such a series of moves must always be finite. Since any improving move reduces potential, we must be at a Nash equilibrium if there is no potential reducing move. These moves are scheduled such that if any edge outside of $T^*$ is introduced, it is subsequently accounted for by charging to some part of $T^*$. In particular, we will show that at any point in the process, and therefore in the equilibrium state at the end, the total cost of these edges is bounded by $O(1) \cdot c(T^*)$.

Fig. 1.

Types of critical improving moves. Dotted edges represent the new edges being added.

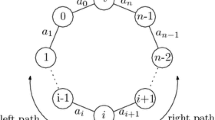
The algorithm is a series of loops, which we run repeatedly until we reach a Nash equilibrium. Each loop begins with a terminal, a, performing either a safe improving move, or a critical improving move. In both cases, a switches strategy to follow a new path to the root. Let S be the state before the start of the loop. A safe improving move is one which results in some state $S' \subseteq T^*\cup S$, i.e., the new path of a contains edges currently in S and edges in the optimal tree $T^*$. A safe improving move requires no additional accounting on our part. A critical improving move on the other hand introduces one or two new edges that must be accounted for (see Fig. 1). We will show later that in any non-equilibrium state, a safe or critical improving move always exists (see Lemma 3).

The algorithm will use a sequence of (potential-reducing) moves to account for the new edges introduced by a critical move. At a high level, each of these edges is accounted for in the following way. Let $e_v$ be the edge in question, and v be the first vertex using $e_v$ on its path to the root.

• 1. In some neighborhood around v, perform a sequence of moves to ensure that for every pair of vertices (excluding v and at most one other special vertex), the difference in shared costs of these vertices is not too large. (Recall that the while nonterminals do not pay anything, the shared cost of a nonterminal u is defined to be $c_u(S)$, the cost that a terminal using u pays on its subpath from u to the root). This sequence of moves must be potential-reducing, and cannot add any edges outside of $T^*\cup S$ to the solution.

• 2. For every vertex y in the neighborhood around v, v has an alternative path to the root consisting of the path in $T^+$ to y, and y’s path to the root. (Recall from Sect. 2 that $T^+$ is the optimal tree, $T^*$, augmented with minimum cost edges incident on nonterminals $\{\sigma _w : w \text { is a nonterminal}\}$).

  • (a) If a y exists for which this alternative path is improving for v, then v can switch to this new path and $e_v$ will be removed from the solution.

  • (b) If every path is not improving for v, then we show that every vertex in the neighborhood of v has an improving move that uses $e_v$.

These steps ensure that we either remove $e_v$ from the solution, or else for any vertex y in the neighborhood we remove edge $e_y \not \in T^*$ from the solution. We elaborate on the steps above, referencing the subroutines described in Algorithm 2 – Homogenize, Absorb, and MakeTree:

Step 1: This is accomplished in two ways. For any path in $T^*$, the Homogenize subroutine ensures that a path in $T^*$ is homogenous. Recall that this gives a bound (relative to the cost of $e_v$) on the difference in shared costs of the endpoints of the path. Additionally, for any pair of adjacent vertices, if the difference in the shared costs is more than the cost of the edge between them, then one vertex must have an improving move through this edge. This move adds no edges outside of $T^*$. The second way of bounding differences in shared cost is much weaker, but we will use it only a small number of times. Overall, the path between any two vertices in the neighborhood will comprise homogenous segments connected by edges whose cost is bounded by the second method above. Adding up the cost bounds for these segments gives us the total bound.

Step 2(a): The purpose of this step is to establish that either the shared cost of v is not much larger than the shared cost of every other vertex in its neighborhood, or that we can otherwise remove $e_v$ from the solution. If the shared cost of v is much larger than some other vertex in the neighborhood, then it is also much larger than the shared cost of an adjacent vertex (call it q) in $T^+$. This is because every pair of vertices in the neighborhood have a similar shared cost (by Step 1). Then, v has a lower cost path to the root consisting of the (v, q) edge, combined with q’s current path to the root. Such a move would remove $e_v$ from the solution.

Step 2(b): If we reach this step, we need to account for the cost of $e_v$ by making every other vertex in the neighborhood give up its first edge, if that edge is not in $T^+$. This ensures that at the end, the edges in the solution that are not in $T^+$ will be very far apart. This is accomplished via the Absorb function: v is currently paying the entire cost of $e_v$, while any vertex that would switch to using v’s path to the root would only pay at most half the cost of $e_v$. Furthermore, if vertices close to v in $T^+$ switch first, vertices farther from v (who must pay a higher cost to buy a path to v) will reap the benefits of more sharing, and therefore a further reduction in shared cost. This is formalized in the definition of Absorb.

There are some other details which we mention here before moving on to a more formal description of the algorithm:

• If v is a nonterminal, let $u_v$ be the terminal that added v as part the critical move. We avoid including $u_v$ in any path provided to the Homogenize subroutine. This is because Homogenize switches the strategies of terminals to follow the strategy of some terminal on input path. If terminals were switched to follow $u_v$’s path, this would increase the sharing on $e_v$, when it is required at the beginning of Step (2b) that only one terminal is using $e_v$. When v is a terminal, then $u_v$ is undefined and this problem does not exist. We define two versions of a loop of the algorithm, defined as MainLoop in Algorithm 1, to account for this difference.

• We have only described how to account for a single edge, but sometimes a critical move adds two new edges that must be accounted for. Suppose $e_a$ and $e_b$ are the new edges added by a (a is a terminal and b is a nonterminal). Then we run MainLoop $(e_b)$ first, and then MainLoop $(e_a)$. The first loop does not increase sharing on $e_a$, so the second loop is still valid.

• We assume the existence of a function $\textsc {MakeTree}$. This function takes as input a set of strategies. Its output is a new set of strategies such that (1) the new set of strategies has lower potential than the old set, (2) the edge set of the new strategies is a subset of the old edge set, and (3) the edge set of the new strategies is a tree. In particular, MakeTree $(S_{curr} \setminus \{p_{u_v}(S_{curr}),p_v(S_{curr})\})$, used on line 9 does not increase sharing on $e_v$, since v and $u_v$ are the only two vertices using $e_v$ on their path to the root. MakeTree $(S_{curr} \setminus \{p_{u_v}(S_{curr}),p_v(S_{curr})\})$ will also not increase sharing on $e_{u_v}$ if this edge has just been added (and therefore $u_v$ is the only vertex using the edge). We will not go into more detail about this function, since an identical function was used in both [5, 13].

• We assume that all edges in E with $c(e) > c(T^*)$ have been removed from the graph. This is without loss of generality: if the final state $S_f$ is a Nash equilibrium, then $S_f$ is still an equilibrium after reintroducing e with $c(e) > c(T^*)$. This is because any vertex with an improving move that adds such an edge e also has a path to the root (in $T^*$) with total cost less than c(e).

We walk through the peusdocode next: We execute the MainLoop function given in Algorithm 1 either once or twice, once for each edge not in $T^*\cup S$ that is added by a critical move. If two edges have been added, we execute in the order MainLoop $(e_b)$ then MainLoop $(e_a)$ (where a is the terminal and b the nonterminal). We define two versions of MainLoop $(e_v)$, one when v is a terminal, and one when v is a nonterminal, appearing on lines 17 and 1 respectively. When v is a nonterminal, we denote the terminal which added $e_v$ to the solution as part of the initial improving move as $u_v$. For brevity, we define $u_v$ as “empty” when v is a terminal. Thus if v is a terminal, define $N(v) \setminus \{u_v\} = N(v)$.

The while loops at lines 2 and 18 terminate with N(v) being homogenous. For any violated if statement within the while loop, we perform a move that reduces potential, and does not increase sharing on $e_v$, or on $e_{u_v}$ if it was added along with $e_v$ as part of $u_v$’s critical move. If none of these if conditions hold, N(v) is homogenous. Therefore, this while loop eventually terminates in a homogenous state.

We next ensure that the cost that v pays is similar to the cost every other vertex in N(v) pays. If these costs are not close, we can show that the condition at line 11/24 will be true, and $e_v$ will be deleted from the solution.

If $e_v$ is still present at this point, we finally call the Absorb function. We use the precondition of the Absorb function to show that the switches made by all the vertices in N(v) are improving, and therefore reduce potential.

Note that although we do not make this explicit, if at any point $S_{curr}$ contains edges that are not part of $p_u(S_{curr})$ for any terminal u, these edges are deleted immediately. This ensures that any nonterminal in $S_{curr}$ is always used as part of some terminal’s path to r.

Outline of Analysis. We first show that all parts of the algorithm reduce potential, guaranteeing that the algorithm terminates (by the definition of the potential function, the minimum decrease in potential is bounded away from 0). Most steps in the algorithm involve single terminals making improving moves, and therefore these steps reduce potential. There are two parts of the algorithm for which it is not immediately obvious that potential is reduced: the Homogenize function and the Absorb function. The lemma below states that Homogenize reduces potential, and we give its proof in the full paper.

Lemma 1

Suppose there is a path $X = p_{T^*}(x,y) \in N(v)$ which is not homogenous. Let $(x = x_1,x_2,\dots ,x_k,x_{k+1} = y)$ be the sequence of vertices in X. Then there exists a prefix of X, $(x_1,\dots ,x_i)$, such that the sequence of moves in which each $x_j,$ $j \in \{ 1, \ldots , i \},$ switches its strategy to $p_{T^*}(x_j,x_{i+1}) \cup p_{x_{i+1}}(S)$ reduces potential.

Proof that the precondition for the Absorb function is satisfied (homogeneity is required here) is deferred to the full version. If it is satisfied, we can show that the Absorb function reduces potential.

Lemma 2

If $c_q(S_{curr}) \ge c_v(S_{curr}) - \frac{2 \cdot \lfloor c(e_v) \rfloor }{7}$ for all $q \ne u_v \in N(v)$, then every strategy change in Absorb reduces potential.

Lemmas 1 and 2 imply that the entire main loop is potential reducing. Since the minimum decrease in potential is bounded away from zero, and the potential is always at least zero, the algorithm necessarily terminates. However, termination alone does not guarantee that the final state is a Nash equilibrium. Since we have restricted the set of moves that the algorithm can perform, we must show that whenever an improving move is available to some terminal, there is also an improving move that is either a safe or critical move (proof in full version).

Lemma 3

The final state reached by the algorithm, $S_f$, is a Nash equilibrium.

Finally, we show our main result, i.e., that $c(S_f) = O(c(T^*))$. To establish the theorem, it is sufficient to show that $c(S_f \setminus T^*) = O(c(T^*))$. We devise a charging scheme that distributes the cost of edges in $S_f \setminus T^*$ among edges in $T^*$. Each $e \in S_f \setminus T^*$ must be an $e_v$ edge for some vertex v. Furthermore, these $e_v$ edges were not later removed as the result of an absorbing process initiated from another $e_{v'}$. At a high level, this allows us to distribute the cost of each $e_v$ to the edges in the neighborhood $N(v) \cap T^*$, since the Absorb(v) function removes many other $e_{v'}$ edges where $v' \in N(v)$ from the solution.

We first consider a set of edges that we will not charge to their neighborhood. Define $E_\sigma = \left\{ e_v \in S_f | v \text { is a nonterminal, } \frac{\lfloor c(e_v) \rfloor }{64} \le c(\sigma _v) \right\}$. We bound the cost of $E_\sigma$ by the cost of edges in $S_f \setminus E_\sigma$ (proof in full version).

Lemma 4

$c(E_\sigma ) = O(c(S_f \setminus E_\sigma ))$.

Our goal now is to find a set of edges $e_v$ such that the right neighborhoods associated with edges of the same class are not overlapping. In the absence of nonterminals, this is simple: For every edge in $S_f \setminus T^*$, the right neighborhoods of vertices corresponding to edges of the same class being overlapping implies that each edge is contained in the other’s neighborhood. Therefore, we argue that the second edge to arrive would have deleted the first through the Absorb function, which gives a contradiction. With nonterminals, the same property does not hold. When edge $e_v$ is added for some nonterminal v, $e_{u_v}$ will not be deleted from the solution, even if $u_v$ falls in v’s neighborhood. The presence of $\sigma _v$ for which no MainLoop $(\sigma _v)$ was run (added, e.g., in line 35) further complicates things. To show that no right neighborhoods overlap, we will therefore remove some edges from $S_f \setminus (T^*\cup E_{\sigma })$.

For nonterminal v, if v is adjacent to at least two edges in $S_f \setminus (T^*\cup E_{\sigma })$ and $\sigma _v$ is one such edge, remove $\sigma _v$ and charge it to one of the remaining edges adjacent to v. Next, for any pair of edges $e_u$ and $e_v$ in $S_f \setminus (T^*\cup E_{\sigma })$ such that u was the terminal which added $e_v$, we delete the smaller of $e_u$ and $e_v$ and charge it to the remaining edge. We are left with a set of edges which we denote $E^*$, each of which has been charged by at most two edges that were removed (and each edge removed is charged to some edge in $E^*$).

Our argument will charge to each edge in $T^*$ at most one edge in $E^*$ of each class. To make the argument simpler, it is desirable to charge those $\sigma _v$’s for which MainLoop $(\sigma _v)$ was never run to higher classes than their actual classes. To this end, we increase the cost of each such $\sigma _v$ to $c(e_{\sigma _v})$, the cost of the first edge on v’s path in the state just before $\sigma _v$ was added.

Lemma 5

For edges $e_u,e_v \in E^*$, if $class(e_v) = class(e_u)$, then $N^+(v)$ and $N^+(u)$ are disjoint.

Given Lemma 5, the scheme from [5] for distributing the cost of each $e_v$ to its neighborhood can be applied directly. This leads to Theorem 1. For the details of this analysis, the reader is referred to the full version of the paper.