Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The problem of finding equilibria in non-cooperative games is a central problem in game theory. Nash’s seminal theorem proved that every finite normal-form game has at least one Nash equilibrium [17], and this raises the natural question of whether we can find one efficiently. After several years of extensive research, it was shown that finding a Nash equilibrium is PPAD-complete [6] even for two-player bimatrix games [2], which is considered to be strong evidence that there is no polynomial-time algorithm for this problem.

Approximate Equilibria. The fact that computing an exact Nash equilibrium of a bimatrix game is unlikely to be tractable, has led to the study of approximate Nash equilibria. There are two natural notions of approximate equilibrium, both of which will be studied in this paper. An \(\epsilon \) -approximate Nash equilibrium (\(\epsilon \)-NE) is a pair of strategies in which neither player can increase their expected payoff by more than \(\epsilon \) by unilaterally deviating from their assigned strategy. An \(\epsilon \) -well-supported Nash equilibrium (\(\epsilon \)-WSNE) is a pair of strategies in which both players only place probability on strategies whose payoff is within \(\epsilon \) of the best response payoff. Every \(\epsilon \)-WSNE is an \(\epsilon \)-NE but the converse does not hold, so a WSNE is a more restrictive notion.

Approximate Nash equilibria are the more well studied of the two concepts. A line of work has studied the best guarantee that can be achieved in polynomial time [1, 5, 7]. The best algorithm known so far is the gradient descent method of Tsaknakis and Spirakis [19] that finds a 0.3393-NE in polynomial time, and examples upon which the algorithm finds no better than a 0.3385-NE have been found [11]. On the other hand, progress on computing approximate-well-supported Nash equilibria has been less forthcoming. The first correct algorithm was provided by Kontogiannis and Spirakis [15] (which shall henceforth be referred to as the KS algorithm), who gave a polynomial time algorithm for finding a \(\frac{2}{3}\)-WSNE. This was later slightly improved by Fearnley et al. [9] (whose algorithm we shall refer to as the FGSS-algorithm), who gave a new polynomial-time algorithm that extends the KS algorithm and finds a 0.6608-WSNE; prior to this work, this was the best known approximation guarantee for WSNEs. For the special case of symmetric games, there is a polynomial-time algorithm for finding a \(\frac{1}{2}\)-WSNE [4].

Previously, it was considered a strong possibility that there is a PTAS for this problem (either for finding an \(\epsilon \)-NE or \(\epsilon \)-WSNE, since their complexity is polynomially related). A very recent result of Rubinstein [18] sheds serious doubt on this possibility. \(\textsc {EndOfTheLine}\) is the canonical problem that defines the complexity class \(\mathtt {PPAD}\). The “Exponential Time Hypothesis” (ETH) for \(\textsc {EndOfTheLine}\) says that any algorithm that solves an \(\textsc {EndOfTheLine}\) instance with n-bit circuits, requires \(2^{\tilde{ \varOmega }(n)}\) time. Rubinstein’s result says that, subject to the ETH for \(\textsc {EndOfTheLine}\), there exists a constant, but so far undetermined, \(\epsilon ^*\), such that for \(\epsilon < \epsilon ^*\), every algorithm for finding an \(\epsilon \)-NE takes quasi-polynomial time, so the quasi-PTAS of Lipton et al. [16] is optimal.

Communication Complexity. Approximate Nash equilibria can also be studied from the communication complexity point of view, which captures the amount of communication the players need to find a good approximate Nash equilibrium. It models a natural scenario where the two players each know their own payoff matrix, but do not know their opponent’s payoff matrix. The players must then follow a communication protocol that eventually produces strategies for both players. The goal is to design a protocol that produces a sufficiently good \(\epsilon \)-NE or \(\epsilon \)-WSNE while also minimizing the amount of communication between the two players.

Communication complexity of equilibria in games has been studied in previous works [3, 14]. The recent paper of Goldberg and Pastink [12] initiated the study of communication complexity in the bimatrix game setting. There they showed \(\varTheta (n^2)\) communication is required to find an exact Nash equilibrium of an \(n \times n\) bimatrix game. Since these games have \(\varTheta (n^2)\) payoffs in total, this implies that there is no communication-efficient protocol for finding exact Nash equilibria in bimatrix games. For approximate equilibria, they showed that one can find a \(\frac{3}{4}\)-NE without any communication, and that in the no-communication setting, finding a \(\frac{1}{2}\)-NE is impossible. Motivated by these positive and negative results, they focused on the most interesting setting, which allows only a polylogarithmic (in n) number of bits to be exchanged between the players. They showed that one can compute 0.438-NE and 0.732-WSNE in this context.

Query Complexity. The payoff query model is motivated by practical applications of game theory. It is often the case that we know that there is a game to be solved, but we do not know what the payoffs are, and in order to discover the payoffs, we would have to play the game. This may be costly, so it is natural to ask whether we can find an equilibrium while minimizing the number of experiments that we must perform.

Payoff queries model this situation. In the payoff query model we are told the structure of the game, i.e., the strategy space, but we are not told the payoffs. We can then make payoff queries, where we propose a pure strategy profile, and we are told the payoff of each player under that strategy profile. Our task is to compute an equilibrium of the game while minimizing the number of payoff queries that we make.

The study of query complexity in bimatrix games was initiated by Fearnley et al. [10], who gave a deterministic algorithm for finding a \(\frac{1}{2}\)-NE using \(2n - 1\) payoff queries. A subsequent paper of Fearnley and Savani [8] showed a number of further results. Firstly, they showed an \(\varOmega (n^2)\) lower bound on the query complexity of finding an \(\epsilon \)-NE with \(\epsilon < \frac{1}{2}\), which combined with the result above, gives a complete view of the deterministic query complexity of approximate Nash equilibria in bimatrix games. They then give a randomized algorithm that finds a \((\frac{3 - \sqrt{5}}{2} + \epsilon )\)-NE using \(O(\frac{n \cdot \log n}{\epsilon ^2})\) queries, and a randomized algorithm that finds a \((\frac{2}{3} + \epsilon )\)-WSNE using \(O(\frac{n \cdot \log n}{\epsilon ^4})\) queries.

Our Contribution. In this paper we introduce a distributed technique that allows us to efficiently compute \(\epsilon \)-NE and \(\epsilon \)-WSNE using limited communication between the players.

Traditional methods for computing WSNEs have used an LP based approach that, when used on a bimatrix game (R, C), solves the zero-sum game \((R - C, C - R)\). The KS algorithm uses the fact that if there is no pure \(\frac{2}{3}\)-WSNE, then the solution to this zero-sum game is a \(\frac{2}{3}\)-WSNE. The slight improvement of the FGSS-algorithm [9] to 0.6608 was obtained by adding two further methods to the KS algorithm: if the KS algorithm does not produce a 0.6608-WSNE, then either there is a \(2 \times 2\) matching pennies sub-game that is 0.6608-WSNE or the strategies from the zero-sum game can be improved by shifting the probabilities of both players within their supports in order to produce a 0.6608-WSNE.

In this paper, we take a different approach. We first show that the bound of \(\frac{2}{3}\) can be matched using a pair of distributed LPs. Given a bimatrix game (R, C), we solve the two zero-sum games \((R, -R)\) and \((-C, C)\), and then give a simple procedure that we call the base algorithm, which uses the solutions to these games to produce a \(\frac{2}{3}\)-WSNE of (R, C). Goldberg and Pastink [12] also considered this pair of LPs, but their algorithm only produces a 0.732-WSNE. We then show that the base algorithm can be improved by applying the probability-shifting and matching-pennies ideas from the FGSS-algorithm. That is, if the base algorithm fails to find a 0.6528-WSNE, then a 0.6528-WSNE can be obtained either by shifting the probabilities of one of the two players, or by identifying a \(2 \times 2\) sub-game. This gives a polynomial-time algorithm that computes a 0.6528-WSNE, which provides the best known approximation guarantees for WSNEs.

It is worth pointing out that, while these techniques are thematically similar to the ones used by the FGSS-algorithm, the actual implementation is significantly different. The FGSS-algorithm attempts to improve the strategies by shifting probabilities within the supports of the strategies returned by the two player game, with the goal of reducing the other player’s payoff. In our algorithm, we shift probabilities away from bad strategies in order to improve that player’s payoff. This type of analysis is possible because the base algorithm produces a strategy profile in which one of the two players plays a pure strategy, which simplifies the analysis that we need to carry out. On the other hand, the KS-algorithm can produce strategies in which both players play many strategies, and so the analysis used for the FGSS-algorithm is necessarily more complicated.

Since our algorithm solves the two LPs separately, it can be used to improve upon the best known algorithms in the limited communication setting. This is because no communication is required for the row player to solve \((R, -R)\) and the column player to solve \((-C, C)\). The players can then carry out the rest of the algorithm using only poly-logarithmic communication. Hence, we obtain a randomized expected-polynomial-time algorithm that uses poly-logarithmic communication and finds a 0.6528-WSNE. Moreover, the base algorithm can be implemented as a communication efficient algorithm for finding a \((\frac{1}{2} + \epsilon )\)-WSNE in a win-lose bimatrix game, where all payoffs are either 0 or 1.

The algorithm can also be used to beat the best known bound in the query complexity setting. It has already been shown by Goldberg and Roth [13] that an \(\epsilon \)-NE of a zero-sum game can be found by a randomized algorithm that uses \(O(\frac{n \log n}{\epsilon ^2})\) payoff queries. Since the rest of the steps used by our algorithm can also be carried out using \(O(n \log n)\) payoff queries, this gives us a query efficient algorithm for finding a 0.6528-WSNE.

We also show that the base algorithm can be adapted to find a \(\frac{3 - \sqrt{5}}{2}\)-NE in a bimatrix game. Once again, this can be implemented in a communication efficient manner, and so we obtain an algorithm that computes a \((\frac{3 - \sqrt{5}}{2} + \epsilon )\)-NE (i.e., 0.382-NE) using only poly-logarithmic communication. For a summary of our contribution, see Table 1.

Table 1. Comparison of our approximation guarantees with the previous best-known guarantees.
Full size table

2 Preliminaries

Bimatrix Games. Throughout, we use [n] to denote the set of integers \(\{1, 2, \dots , n\}\). An \(n \times n\) bimatrix game is a pair (R, C) of two \(n \times n\) matrices: R gives payoffs for the row player and C gives the payoffs for the column player. We make the standard assumption that all payoffs lie in the range [0, 1]. For simplicity, as in [12], we assume that each payoff has constant bit-lengthFootnote 1. A win-lose bimatrix game has all payoffs in \(\{0, 1\}\).

Each player has n pure strategies. To play the game, both players simultaneously select a pure strategy: the row player selects a row \(i \in [n]\), and the column player selects a column \(j \in [n]\). The row player then receives payoff \(R_{i,j}\), and the column player receives payoff \(C_{i,j}\).

A mixed strategy is a probability distribution over [n]. We denote a mixed strategy for the row player as a vector \(\mathbf {x}\) of length n, such that \(\mathbf {x} _i\) is the probability that the row player assigns to pure strategy i. A mixed strategy of the column player is a vector \(\mathbf {y}\) of length n, with the same interpretation. Given a mixed strategy \(\mathbf {x}\) for either player, the support of \(\mathbf {x}\) is the set of pure strategies i with \(\mathbf {x} _i >0\). If \(\mathbf {x}\) and \(\mathbf {y}\) are mixed strategies for the row and the column player, respectively, then we call \((\mathbf {x}, \mathbf {y})\) a mixed strategy profile. The expected payoff for the row player under strategy profile \((\mathbf {x}, \mathbf {y})\) is given by \(\mathbf {x} ^T R \mathbf {y} \) and for the column player by \(\mathbf {x} ^T C \mathbf {y} \). We denote the support of a strategy \(\mathbf {x} \) as \(\mathrm {supp}(\mathbf {x})\), which gives the set of pure strategies i such that \(\mathbf {x} _i > 0\).

Nash Equilibria. Let \(\mathbf {y} \) be a mixed strategy for the column player. The set of pure best responses against \(\mathbf {y} \) for the row player is the set of pure strategies that maximize the payoff against \(\mathbf {y} \). More formally, a pure strategy \(i \in [n]\) is a best response against \(\mathbf {y} \) if, for all pure strategies \(i' \in [n]\) we have: \(\sum _{j \in [n]} \mathbf {y} _j \cdot R_{i, j} \ge \sum _{j \in [n]} \mathbf {y} _j \cdot R_{i', j}\). Column player best responses are defined analogously.

A mixed strategy profile \((\mathbf {x}, \mathbf {y})\) is a mixed Nash equilibrium if every pure strategy in \(\mathrm {supp}(\mathbf {x})\) is a best response against \(\mathbf {y} \), and every pure strategy in \(\mathrm {supp}(\mathbf {y})\) is a best response against \(\mathbf {x} \). Nash [17] showed that all bimatrix games have a mixed Nash equilibrium.

Approximate Equilibria. There are two commonly studied notions of approximate equilibrium, and we consider both of them in this paper. The first notion is of an \(\epsilon \) -approximate Nash equilibrium (\(\epsilon \)-NE), which weakens the requirement that a player’s expected payoff should be equal to their best response payoff. Formally, given a strategy profile \((\mathbf {x}, \mathbf {y})\), we define the regret suffered by the row player to be the difference between the best response payoff and actual payoff, i.e.,

$$\begin{aligned} \max _{i\in [n]} \big ((R\cdot y)_i\big ) - \mathbf {x} ^T \cdot R \cdot \mathbf {y}. \end{aligned}$$

Regret for the column player is defined analogously. We have that \((\mathbf {x}, \mathbf {y})\) is an \(\epsilon \)-NE if and only if both players have regret less than or equal to \(\epsilon \).

The other notion is of an \(\epsilon \)-approximate-well-supported equilibrium (\(\epsilon \)-WSNE), which weakens the requirement that players only place probability on best response strategies. Given a strategy profile \((\mathbf {x}, \mathbf {y})\) and a pure strategy \(j \in [n]\), we say that j is an \(\epsilon \)-best-response for the row player if

$$\begin{aligned} \max _{i \in [n]}\big ((R\cdot y)_i\big ) - (R\cdot y)_j \le \epsilon . \end{aligned}$$

An \(\epsilon \)-WSNE requires that both players only place probability on \(\epsilon \)-best-responses. In an \(\epsilon \)-WSNE both players place probability only on \(\epsilon \)-best-responses. Formally, the row player’s pure strategy regret under \((\mathbf {x}, \mathbf {y})\) is defined to be

$$\begin{aligned} \max _{i \in [n]}\big ((R\cdot y)_i\big ) - \min _{i \in \mathrm {supp}(\mathbf {x})}\big ((R\cdot y)_i\big ). \end{aligned}$$

Pure strategy regret for the column player is defined analogously. A strategy profile \((\mathbf {x}, \mathbf {y})\) is an \(\epsilon \)-WSNE if both players have pure strategy regret less than or equal to \(\epsilon \).

Communication Complexity. We consider the communication model for bimatrix games introduced by Goldberg and Pastink [12]. In this model, both players know the payoffs in their own payoff matrix, but do not know the payoffs in their opponent’s matrix. The players then follow an algorithm that uses a number of communication rounds, where in each round they exchange a single bit of information. Between each communication round, the players are permitted to perform arbitrary randomized computations (although it should be noted that, in this paper, the players will only perform polynomial-time computations) using their payoff matrix, and the bits that they have received so far. At the end of the algorithm, the row player outputs a mixed strategy \(\mathbf {x} \), and the column player outputs a mixed strategy \(\mathbf {y} \). The goal is to produce a strategy profile \((\mathbf {x}, \mathbf {y})\) that is an \(\epsilon \)-NE or \(\epsilon \)-WSNE for a sufficiently small \(\epsilon \) while limiting the number of communication rounds used by the algorithm. The algorithms given in this paper will use at most \(O(\log ^2 n)\) communication rounds. In order to achieve this, we use the following result of Goldberg and Pastink [12].

Lemma 1

[12].Given a mixed strategy \(\mathbf {x} \) for the row-player and an \(\epsilon > 0\), there is a randomized expected-polynomial-time algorithm that uses \(O(\frac{\log ^2 n}{\epsilon ^2})\)-communication to transmit a strategy \(\mathbf {x} _s\) to the column player where \(|\mathrm {supp}(\mathbf {x} _s)| \in O(\frac{\log n}{\epsilon ^2})\) and for every strategy \(i \in [n]\) we have:

$$\begin{aligned} | (\mathbf {x} ^T \cdot R)_i - (\mathbf {x} _s^T \cdot R)_i | \le \epsilon . \end{aligned}$$

The algorithm uses the well-known sampling technique of Lipton, Markakis, and Mehta to construct the strategy \(\mathbf {x} _s\), so for this reason we will call the strategy \(\mathbf {x} _s\) the sampled strategy from \(\mathbf {x} \). Since this strategy has a logarithmically sized support, it can be transmitted by sending \(O(\frac{\log n}{\epsilon ^2})\) strategy indexes, each of which can be represented using \(\log n\) bits. By symmetry, the algorithm can obviously also be used to transmit approximations of column player strategies to the row player.

Query Complexity. In the query complexity setting, the algorithm knows that the players will play an \(n \times n\) game (R, C), but it does not know any of the entries of R or C. These payoffs are obtained using payoff queries in which the algorithm proposes a pure strategy profile (i, j), and then it is told the value of \(R_{ij}\) and \(C_{ij}\). After each payoff query, the algorithm can make arbitrary computations (although, again, in this paper the algorithms that we consider take polynomial time) in order to decide the next pure strategy profile to query. After making a sequence of payoff queries, the algorithm then outputs a mixed strategy profile \((\mathbf {x}, \mathbf {y})\). Again, the goal is to ensure that this strategy profile is an \(\epsilon \)-NE or \(\epsilon \)-WSNE, while minimizing the number of queries made overall.

There are two results that we will use for this setting. Goldberg and Roth [13] have given a randomized algorithm that, with high probability, finds an \(\epsilon \)-NE of a zero-sum game using \(O(\frac{n \cdot \log n}{\epsilon ^2})\) payoff queries. Given a mixed strategy profile \((\mathbf {x}, \mathbf {y})\), an \(\epsilon \) -approximate payoff vector for the row player is a vector v such that, for all \(i \in [n]\) we have \(| v_i - (R \cdot \mathbf {y})_i | \le \epsilon \). Approximate payoff vectors for the column player are defined symmetrically. Fearnley and Savani [8] observed that there is a randomized algorithm that when given the strategy profile \((\mathbf {x}, \mathbf {y})\), finds approximate payoff vectors for both players using \(O(\frac{n \cdot \log n}{\epsilon ^2})\) payoff queries and that succeeds with high probability. We summarise these two results in the following lemma.

Lemma 2

[8, 13].Given an \(n \times n\) zero-sum bimatrix game, with probability at least \((1 - n^{-\frac{1}{8}})(1 - \frac{2}{n})^2\), we can compute an \(\epsilon \)-Nash equilibrium \((\mathbf {x}, \mathbf {y})\), and \(\epsilon \)-approximate payoff vectors for both players under \((\mathbf {x}, \mathbf {y})\), using \(O(\frac{n \cdot \log n}{\epsilon ^2})\) payoff queries.

3 The Base Algorithm

In this section, we introduce the base algorithm. This algorithm provides a simple way to find a \(\frac{2}{3}\)-WSNE. We present this algorithm separately for three reasons. Firstly, we believe that the algorithm is interesting in its own right, since it provides a relatively straightforward method for finding a \(\frac{2}{3}\)-WSNE that is quite different from the technique used in the KS-algorithm. Secondly, our algorithm for finding a 0.6528-WSNE will replace the final step of the algorithm with two more involved procedures, so it is worth understanding this algorithm before we describe how it can be improved. Finally, at the end of this section, we will show that this algorithm can be adapted to provide a communication efficient way to find a \((0.5 + \epsilon )\)-WSNE in win-lose games.

figure a

We argue that this algorithm is correct. For that, we must prove that the row i used in Step 4 actually exists.

Lemma 3

If Algorithm 1 reaches Step 4, then there exists a row i such that \(R_{i\mathfrak {j}^*} > 1/3\) and \(C_{i\mathfrak {j}^*} > 1/3\).

We now argue that the algorithm always produces a \(\frac{2}{3}\)-WSNE. There are three possible strategy profiles that can be returned by the algorithm, which we consider individually.

  • The algorithm returns in Step 2: Since \(v_c \le v_r\) by assumption, and since \(v_r \le \frac{2}{3}\), we have that \((R \cdot \mathbf {y} ^*)_i \le \frac{2}{3}\) for every row i, and \(((\hat{\mathbf {x}})^T \cdot C)_j \le \frac{2}{3}\) for every column j. So, both players can have pure strategy regret at most \(\frac{2}{3}\) in \((\hat{\mathbf {x}}, \mathbf {y} ^*)\), and thus this profile is a \(\frac{2}{3}\)-WSNE.

  • The algorithm returns in Step 3: Much like in the previous case, when the column player plays \(\mathbf {y} ^*\), the row player can have pure strategy regret at most \(\frac{2}{3}\). The requirement that \(C^T_j\mathbf {x} ^* \le \frac{2}{3}\) also ensures that the column player has pure strategy regret at most \(\frac{2}{3}\). Thus, we have that \((\mathbf {x} ^*, \mathbf {y} ^*)\) is a \(\frac{2}{3}\)-WSNE.

  • The algorithm returns in Step 4: Both players have payoff at least \(\frac{1}{3}\) under \((i, \mathfrak {j}^*)\) for the sole strategy in their respective supports. Hence, the maximum pure strategy regret that can be suffered by a player is \(1 - \frac{1}{3} = \frac{2}{3}\).

Observe that the zero-sum game solved in Step 1 can be solved via linear programming, and so the algorithm runs in polynomial time. Therefore, we have shown the following.

Theorem 1

Algorithm 1 always produces a \(\frac{2}{3}\)-WSNE in polynomial time.

Win-Lose Games. The base algorithm can be adapted to provide a communication efficient method for finding a \((0.5 + \epsilon )\)-WSNE in win-lose games. In brief, the algorithm can be modified to find a 0.5-WSNE in a win-lose game by making Steps 2 and 3 check against the threshold of 0.5. It can then be shown that if these steps fail, then there exists a pure Nash equilibrium in column \(\mathfrak {j}^* \). This can then be implemented as a communication efficient protocol using the algorithm from Lemma 1.

Theorem 2

For every win-lose game and \(\epsilon >0\), there is a randomized expected-polynomial-time algorithm that finds a \((0.5 + \epsilon )\)-WSNE with \(O\left( \frac{\log ^2 n}{\epsilon ^2}\right) \) communication.

4 An Algorithm for Finding a 0.6528-WSNE

In this section, we show how Algorithm 1 can be modified to produce a 0.6528-WSNE.

Outline. Our algorithm replaces Step 4 of Algorithm 1 with a more involved procedure. This procedure uses two techniques, that both find an \(\epsilon \)-WSNE with \(\epsilon < \frac{2}{3}\). Firstly, we attempt to turn \((\mathbf {x} ^*, \mathfrak {j}^*)\) into a WSNE by shifting probabilities. Observe that, since \(\mathfrak {j}^* \) is a best response, the column player has a pure strategy regret of 0 in \((\mathbf {x} ^*, \mathfrak {j}^*)\). On the other hand, we have no guarantees about the row player since \(\mathbf {x} ^*\) might place a small amount of probability strategies with payoff strictly less than \(\frac{1}{3}\). However, since \(\mathbf {x} ^*\) achieves a high expected payoff (due to Step 2,) it cannot place too much probability on these low payoff strategies. Thus, the idea is to shift the probability that \(\mathbf {x} ^*\) assigns to entries of \(\mathfrak {j}^* \) with payoff less than or equal to \(\frac{1}{3}\) to entries with payoff strictly greater than \(\frac{1}{3}\), and thus ensure that the row player’s pure strategy regret is below \(\frac{2}{3}\). Of course, this procedure will increase the pure strategy regret of the column player, but if it is also below \(\frac{2}{3}\) once all probability has been shifted, then we have found an \(\epsilon \)-WSNE with \(\epsilon < \frac{2}{3}\).

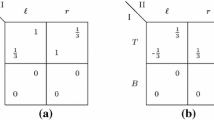
If shifting probabilities fails to find an \(\epsilon \)-WSNE with \(\epsilon < \frac{2}{3}\), then we show that the game contains a matching pennies sub-game. More precisely, we show that there exists a column \(\mathfrak {j}' \), and rows b and s such that the \(2 \times 2\) sub-game induced by \(\mathfrak {j}^* \), \(\mathfrak {j}' \), b, and s has the following form:

figure b

Thus, if both players play uniformly over their respective pair of strategies, then \(\mathfrak {j}^* \), \(\mathfrak {j}' \), b, and s with have payoff \(\approx 0.5\), and so this yields an \(\epsilon \)-WSNE with \(\epsilon < \frac{2}{3}\).

The Algorithm. We now formalize this approach, and show that it always finds an \(\epsilon \)-WSNE with \(\epsilon < \frac{2}{3}\). In order to quantify the precise \(\epsilon \) that we obtain, we parametrise the algorithm by a variable z, which we constrain to be in the range \(0 \le z < \frac{1}{24}\). With the exception of the matching pennies step, all other steps of the algorithm will return a \((\frac{2}{3} - z)\)-WSNE, while the matching pennies step will return a \((\frac{1}{2} + f(z))\)-WSNE for some increasing function f. Optimizing the trade off between \(\frac{2}{3} - z\) and \(\frac{1}{2} + f(z)\) then allows us to determine the quality of WSNE found by our algorithm.

The algorithm is displayed as Algorithm 2. Steps 1, 2, and 3 are versions of the corresponding steps from Algorithm 1, which have been adapted to produce a \((\frac{2}{3}-z)\)-WSNE. Step 4 implements the probability shifting procedure, while Step 5 finds a matching pennies sub-game.

Observe that the probabilities used in \(\mathbf {x}_\mathbf{mp} \) and \(\mathbf {y_\mathbf{mp}} \) are only well defined when \(z \le \frac{1}{24}\), because we have that \(\frac{1-15z}{2-39z} > 1\) whenever \(z > \frac{1}{24}\), which explains our required upper bound on z.

The Correctness of Step 5. This step of the algorithm relies on the existence of the rows b and s, which is shown in the following lemma.

Lemma 4

Suppose that the following conditions hold:

  1. 1.

    \(\mathbf {x} ^*\) has payoff at least \(\frac{2}{3} - z\) against \(\mathfrak {j}^* \).

  2. 2.

    \(\mathfrak {j}^* \) has payoff at least \(\frac{2}{3} - z\) against \(\mathbf {x} ^*\).

  3. 3.

    \(\mathbf {x} ^*\) has payoff at least \(\frac{2}{3} - z\) against \(\mathfrak {j}' \).

  4. 4.

    Neither \(\mathfrak {j}^* \) or \(\mathfrak {j}' \) contains a pure \((\frac{2}{3} - z)\)-WSNE (i, j) with \(i \in \mathrm {supp}(\mathbf {x} ^*)\).

Then, both of the following are true:

  • There exists a row \(b \in B \) such that \(R_{b\mathfrak {j}^*} > 1- \frac{18z}{1 + 3z}\) and \(C_{b\mathfrak {j}'} > 1- \frac{18z}{1 + 3z}\).

  • There exists a row \(s \in S \) such that \(C_{s\mathfrak {j}^*} > 1- \frac{27z}{1 + 3z}\) and \(R_{s\mathfrak {j}'} > 1- \frac{27z}{1 + 3z}\).

Observe that the preconditions are indeed true if the Algorithm reaches Step 5. The first and third conditions hold because, due to Step 2, we know that \(\mathbf {x} ^{*}\) is a min-max strategy that secures payoff at least \(v_r > \frac{2}{3} - z\). The second condition holds because Step 3 ensures that the column player’s best response payoff is at least \(\frac{2}{3} - z\). The fourth condition holds because Step 5 explicitly checks for these pure strategy profiles.

Quality of Approximation. We now analyse the quality of WSNE our algorithm produces. Steps 2, 3, 4, 5 each return a strategy profile. Observe that Steps 2 and 3 are the same as the respective steps in the base algorithm, but with the threshold changed from \(\frac{2}{3}\) to \(\frac{2}{3} - z\). Hence, we can use the same reasoning as we gave for the base algorithm to argue that these steps return \((\frac{2}{3} - z)\)-WSNE. We now consider the other two steps.

figure c

  • The algorithm returns in Step 4: By definition all rows \(r \in B \) satisfy \(R_{i\mathfrak {j}^*} \ge \frac{1}{3} + z\), so since \(\mathrm {supp}(\mathbf{x}_\mathbf{b}) \subseteq B \), the pure strategy regret of the row player can be at most \(1 - (\frac{1}{3} + z) =\frac{2}{3} - z\). For the same reason, since \((\mathbf{x}_\mathbf{b} ^T \cdot C)_{\mathfrak {j}^*} \ge \frac{1}{3} + z\) holds, the pure strategy regret of the column player can also be at \(\frac{2}{3} - z\). Thus, the profile \((\mathbf{x}_\mathbf{b}, \mathfrak {j}^*)\) is a \((\frac{2}{3} -z)\)-WSNE.

  • The algorithm returns in Step 5: Since \(R_{b\mathfrak {j}^*} > 1- \frac{18z}{1 + 3z}\), the payoff of b when the column player plays \(\mathbf {y_\mathbf{mp}} \) is at least:

    $$\begin{aligned} \frac{1 - 24z}{2 - 39z} \cdot \left( 1 - \frac{18z}{1 + 3z} \right) = \frac{1 - 39z + 360z^2}{2 - 33z - 117 z^2} \end{aligned}$$

    Similarly, since \(R_{s\mathfrak {j}'} > 1- \frac{27z}{1 + 3z}\), the payoff of s when the column player plays \(\mathbf {y_\mathbf{mp}} \) is at least:

    $$\begin{aligned} \frac{1 - 15z}{2 - 39z} \cdot \left( 1- \frac{27z}{1 + 3z} \right) = \frac{1 - 39z + 360z^2}{2 - 33z - 117 z^2} \end{aligned}$$

    In the same way, one can show that the payoffs of \(\mathfrak {j}^* \) and \(\mathfrak {j}' \) are also \(\frac{1 - 39z + 360z^2}{2 - 33z - 117 z^2}\) when the row player plays \(\mathbf {x}_\mathbf{mp} \). Thus, we have that \((\mathbf {x}_\mathbf{mp}, \mathbf {y_\mathbf{mp}})\) is a \((1 - \frac{1 - 39z + 360z^2}{2 - 33z - 117 z^2})\)-WSNE.

To find the optimal value for z, we need to find the largest value of z for which the following inequality holds.

$$\begin{aligned} 1 - \frac{1 - 39z + 360z^2}{2 - 33z - 117 z^2} \le \frac{2}{3} - z. \end{aligned}$$

Setting the inequality to an equality and rearranging gives us a cubic polynomial equation: \( 117 \, z^{3} + 432 \, z^{2} - 30 \, z + \frac{1}{3} = 0. \) Since the discriminant of this polynomial is positive, this polynomial has three real roots, which can be found via the trigonometric method. Only one of these roots lies in the range \(0 \le z < \frac{1}{24}\), which is the following:

$$\begin{aligned}&z = \frac{1}{117} \, \sqrt{3} \Bigg (\sqrt{2434} \sqrt{3} \cos \left( \frac{1}{3} \, \arctan \left( \frac{39}{240073} \, \sqrt{9749} \sqrt{3}\right) \right) \\&\qquad \qquad \qquad - 3 \, \sqrt{2434} \sin \left( \frac{1}{3} \, \arctan \left( \frac{39}{240073} \, \sqrt{9749} \sqrt{3}\right) \right) - 48 \, \sqrt{3}\Bigg ). \end{aligned}$$

Thus, we get \(z \approx 0.013906376\), and we have found an algorithm that always produces a 0.6528-WSNE. So we have the following theorem.

Theorem 3

There is a polynomial time algorithm that, given a bimatrix game, finds a 0.6528-WSNE.

Communication Complexity. We claim that our algorithm can be adapted for the limited communication setting by making the following modifications. After computing \(\mathbf {x}^*, \mathbf {y}^*, \hat{\mathbf {x}},\) and \(\hat{\mathbf {y}}\), we then use Lemma 1 to construct and communicate the sampled strategies \(\mathbf {x}^* _s, \mathbf {y}^* _s, \hat{\mathbf {x}}_s,\) and \(\hat{\mathbf {y}}_s\). These strategies are communicated between the two players using \(4 \cdot (\log n)^2\) bits of communication, and the players also exchange \(v_r = (\mathbf {x}^* _s)^T \cdot R\mathbf {y}^* _s\) and \(v_c = \hat{\mathbf {x}}_s^TC\hat{\mathbf {y}}_s\) using \(\log n\) rounds of communication. The algorithm then continues as before, except the sampled strategies are used in place of their non-sampled counterparts. Finally, in Steps 2 and 3, we test against the threshold \(\frac{2}{3} - z + \epsilon \) instead of \(\frac{2}{3} - z\).

Observe that, when sampled strategies are used, all steps of the algorithm can be carried out in at most \((\log n)^2\) communication. In particular, to implement Step 4, the column player can communicate \(\mathfrak {j}^* \) to the row player, and then the row player can communicate \(R_{i\mathfrak {j}^*}\) for all rows \(i \in \mathrm {supp}(\mathbf {x}^* _s)\) using \((\log n)^2\) bits of communication, which allows the column player to determine \(\mathfrak {j}' \). Once \(\mathfrak {j}' \) has been determined, there are only \(2 \cdot \log n\) payoffs in each matrix that are relevant to the algorithm (the payoffs in rows \(i \in \mathrm {supp}(\mathbf {x}^* _s)\) in columns \(\mathfrak {j}^* \) and \(\mathfrak {j}' \),) and so the two players can communicate all of these payoffs to each other, and then no further communication is necessary.

Theorem 4

For every \(\epsilon > 0\), there is a randomized expected-polynomial-time algorithm that uses \(O\left( \frac{\log ^2 n}{\epsilon ^2}\right) \) communication and finds a \((0.6528 + \epsilon )\)-WSNE.

Query Complexity. We now show that Algorithm 2 can be implemented in a payoff-query efficient manner. Let \(\epsilon > 0\) be a positive constant. We now outline the changes needed in the algorithm.

  • In Step 1 we use the algorithm of Lemma 2 to find \(\frac{\epsilon }{2}\)-NEs of \((R, -R)\), and \((C, -C)\). We denote the mixed strategies found as \((\mathbf {x} ^*_a, \mathbf {y} ^*_a)\) and \((\hat{\mathbf {x}}_a, \hat{\mathbf {y}}_a)\), respectively, and we use these strategies in place of their original counterparts throughout the rest of the algorithm. We also compute \(\frac{\epsilon }{2}\)-approximate payoff vectors for each of these strategies, and use them whenever we need to know the payoff of a particular strategy under one of these strategies. In particular, we set \(v_r\) to be the payoff of \(\mathbf {x} ^*_a\) according to the approximate payoff vector of \(\mathbf {y} ^*_a\), and we set \(v_c\) to be the payoff of \(\hat{\mathbf {y}}_a\) according to the approximate payoff vector for \(\hat{\mathbf {x}}_a\).

  • In Steps 2 and 3 we test against the threshold of \(\frac{2}{3} - z + \epsilon \) rather than \(\frac{2}{3} - z\).

  • In Step 4 we select \(j^*\) to be the column that is maximal in the approximate payoff vector against \(\mathbf {x} ^*_a\). We then spend n payoff queries to query every row in column \(j^*\), which allow us to proceed with the rest of this step as before.

  • In Step 5 we use the algorithm of Lemma 2 to find an approximate payoff vector v for the column player against \(\mathbf{x}_\mathbf{b} \). We then select \(\mathfrak {j}' \) to be a column that maximizes v, and then spend n payoff queries to query every row in \(\mathfrak {j}^* \), which allows us to proceed with the rest of this step as before.

Observe that the query complexity of the algorithm is \(O(\frac{n \cdot \log n}{\epsilon ^2})\), where the dominating term arises due to the use of the algorithm from Lemma 2 to approximate solutions to the zero-sum games.

Theorem 5

There is a randomized algorithm that, with high probability, finds a \((0.6528 + \epsilon )\)-WSNE using \(O(\frac{n \cdot \log n}{\epsilon ^2})\) payoff queries.