Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Petri nets [15] are a popular formalism for a high level modelling of distributed systems. Currently, there are more than 80 tools registered in the database of Petri net tools [8] and an annual model checking contest aiming at comparing the performance of the different tools has been running since 2011. In the last two editions of the contest, MCC’14 [10] and MCC’15 [11], our model checker TAPAAL [4] won a second place in the reachability category. In this paper, we report on the main verification techniques implemented in our tool and demonstrate their performance on the class of Petri nets from the latest edition of the model checking contest.

TAPAAL is a tool suite that apart from the verification engine for P/T nets supports also the modelling and analysis of a timed extension of the Petri net formalism called timed-arc Petri nets (for more details see [9]). The tool supports both continuous and discrete time verification and while the details about the continuous-time engine [5] and the discrete-time engine [1] were previously published, the untimed verification engine has not been presented yet.

We focus here solely on the TAPAAL verification techniques directly related to our participation in the model checking contest. The details about the other participating tools and a report on the competition results can be found in [11]. In what follows, we first describe an efficient heuristic search technique for explicit exploration of the Petri net state-space, then we discuss the adaptation of the state-equation approach to the case of cardinality queries and finally we demonstrate the applicability of the sequential and parallel structural reduction rules into the context of checking cardinality queries on weighted nets with inhibitor arcs.

TAPAAL is open-source and publicly available at www.tapaal.net. Citations to the related work connected to the techniques used in our tool are given at the respective sections of the paper. All experiments reported in this paper use the competition nets and queries from MCC’15 but the verification was rerun locally as we needed to compare the different options and techniques (the data for the different combinations of these parameters is not available at the MCC’15 web-page as we submitted there only the best working configuration of our tool).

2 Definitions

Let \(\mathbb {N}_0\) denote the set of natural numbers including zero. A Petri net (PN) with inhibitor arcs is a tuple \(N = (P, T, F, I)\) where

  • P is a finite, nonempty set of places,

  • T is a finite set of transitions such that \(P \cap T = \emptyset \),

  • \(F : (P \times T) \cup (T \times P) \rightarrow \mathbb {N}_0\) is the flow function, and

  • \(I \subseteq P \times T\) is the set of inhibitor arcs such that \((p,t) \in I\) implies \(F(p,t) = 0\).

Let \(N = (P, T, F, I)\) be a PN. A marking is a mapping \(M : P \rightarrow \mathbb {N}_0\) that assigns tokens to places. The set \(\mathcal {M}(N)\) denotes the infinite set of all markings on N. A marked PN is a pair \((N,M_0)\) where \(M_0 \in \mathcal {M}(N)\) is an initial marking.

The preset of a place/transition y is defined as \({}^{\bullet }y \overset{ def }{=} \{z \in P \cup T \mid F(z,y) > 0 \}\). Likewise, the postset is \(y^{\bullet } \overset{ def }{=} \{ z \in P \cup T \mid F(y,z) > 0 \}\). We denote the set of inhibitor places of a transition t as \(I(t) \overset{ def }{=} \{ p \in P \mid (p,t) \in I \}\) and transitions that a place p inhibits as \(I(p) \overset{ def }{=} \{ t \in T \mid (p,t) \in I \}\).

A transition \(t \in T\) is enabled in a marking M if for all \(p \in {}^{\bullet }t\) we have \(F(p,t) \le M(p)\) and \(M(p) = 0\) for all \(p \in I(t)\). A transition t enabled in a marking M can fire and produce a marking \(M'\) such that \(M'(p) = M(p) - F(p,t) + F(t,p)\) for all \(p \in P\), written as \(M \overset{t}{\rightarrow } M'\). This firing relation is in a natural way extended to a sequence of transitions \(w \in T^*\) so that \(M \overset{\epsilon }{\rightarrow } M\) and for \(w=tw'\) we write \(M \overset{w}{\rightarrow } M'\) if \(M \overset{t}{\rightarrow } M''\) and \(M'' \overset{w'}{\rightarrow } M'\). We also write \(M \rightarrow M'\) if \(M \overset{t}{\rightarrow } M'\) for some \(t \in T\). The reflexive and transitive closure of \(\rightarrow \) is denoted by \(\rightarrow ^*\). Finally, let \(\mathcal {R}(M) = \{ M' \mid M \rightarrow ^* M' \}\) be the set of markings reachable from M.

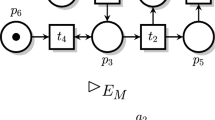
As usual, Petri net places are denoted by circles and can contain dots representing tokens, transitions are drawn as rectangles, input and output arcs are depicted as arrows labelled with their weights (if a label is missing we assume the default weight 1) and inhibitor arcs are denoted by circle-headed arrows.

After having introduced the standard syntax and semantics of Petri nets, we shall now define the reachability problem for cardinality queries, as the main MCC’15 competition category in the reachability analysis.

A cardinality formula is given by the abstract syntax

figure a

where \(\bowtie \ \in \{\le , <, =, \not =, >, \ge \}\), \(n \in \mathbb {N}_0\) and \(p \in P\).

The satisfaction relation \(M \models \varphi \) for a given marking is defined in the natural way such that \(M \models e_1 \bowtie e_2\) iff \( eval (M,e_1) \bowtie eval (M,e_2)\) where \( eval (M,e)\) is the evaluation of the arithmetical expression e into a number, assuming that \( eval (M,p) = M(p)\) for \(p \in P\) (in other words, a place p evaluates to the number of tokens currently present in it).

For a marked Petri net \((N,M_0)\), we write \((N,M_0) \models EF \,\varphi \) if there is a marking M such that \(M_0 \rightarrow ^* M\) and \(M \models \varphi \). As an example, the query \( EF \,p \ge 5 \wedge q \not =3\) asks whether we can reach a marking where the place p contains at least 5 tokens and the number of tokens in the place q is different from 3.

Note that the MCC’15 verification queries [11] also contain other types of reachability questions: (i) reachability fireability where we consider the atomic proposition \( fire (t)\) that is true in a given marking iff the transition t is fireable, (ii) reachability compute bounds where the expression \( bounds (X)\) for \(X \subseteq P\) is added as an atomic expression of e and it reports the maximum number of tokens in the places from X in any reachable marking and (iii) reachability deadlock where we ask if there is a reachable marking M such that there is no \(t \in T\) and no \(M'\) where \(M \overset{t}{\rightarrow } M'\).

We notice that fireability can be encoded as a cardinality query

$$\begin{aligned} fire (t) \equiv \bigwedge _{p \in {}^{\bullet }t} p \ge F(p,t)\ \wedge \ \bigwedge _{p \in I(t)} p = 0 \end{aligned}$$

and deadlock can be encoded as the cardinality query

$$\begin{aligned} deadlock \equiv \bigwedge _{t \in T} \lnot fire (t) \ . \end{aligned}$$

In TAPAAL, we indeed encode reachability fireability queries into the cardinality queries but we use a dedicated deadlock proposition in order to be able to apply structural reductions (see Sect. 5). The computation of bounds for a given set of places X is done by exploring the whole state-space while still being able to apply some structural reduction rules. Details are discussed in Sect. 5.

3 Explicit Search Algorithm with Heuristic Distance

We shall now describe the explicit search algorithm used in TAPAAL for answering reachability cardinality queries. The search is based on the standard search algorithm using passed/waiting sets (see e.g. [3]) as given in Algorithm 1 but with the important addition of exploring first the markings with the shortest distance to a given cardinality query \(\varphi \). The distance Distance \({(M, \varphi )}\) is computed in Algorithm 2 and it returns a nonnegative integer. If \(M \models \varphi \) then the distance function returns 0, otherwise the distance tries to estimate how far away is the marking M from satisfying the query \(\varphi \).

figure b

This is achieved by first estimating the distance between two integer values w.r.t. a given comparison operator \(\bowtie \), as defined by the \(\varDelta \) function in Algorithm 2. Intuitively, the function \(\varDelta (v_1,\bowtie ,v_2)\) returns the smallest number by which either \(v_1\) or \(v_2\) must be changed in order to make the predicate \(v_1 \bowtie v_2\) valid. The basic distance \(\varDelta \) is then extended to the logical connectives: for conjunction both conjuncts have to hold and hence we add the distances of the conjuncts together, and for disjunction where only one of the disjuncts needs to hold, we take the minimum. The negation is simply propagated down to the atomic predicates using De Morgan’s laws.

The heuristics operates very satisfactory in many scenarios as it relies on the assumption that similar markings are likely to be just a few firings away from each other. Nevertheless, in some scenarios the heuristic estimate may degrade the search performance.

We performed a number of experiments comparing the heuristic search strategy against breadth-first-search (BFS) and depth-first-search (DFS) on the competition nets and queries from MCC’15 [11]. We selected a number of hard border-line instances of problems where we still expected to get a reasonable number of conclusive answers for positive reachability queries, resulting in 1296 executions (432 executions for each search strategy). Out of those, we selected models and queries where at least one search strategy found a reachable marking satisfying the given cardinality query and where at least one search strategy took more than 3 s (in order to filter out the trivial instances). This resulted in 492 executions (164 for each search strategy) and the results are presented in Fig. 1.

figure c

The table shows that the heuristic search was the fastest one in 89 instances, which is more than the sum of cases where BFS or DFS won (75 instances in total). The heuristic strategy timed out in only 19 cases (where either BFS or DFS provided an answer) compared to the large number of runs where BFS and DFS did not find the answer. Finally, the heuristic strategy was in 17 cases the only one that found a marking satisfying the given cardinality query, whereas BFS provided a solo answer in 9 cases and DFS in only 2 cases.

In conclusion, if we use only a single-core for the verification, the heuristic search is preferable, however, in case of more available cores, it may be a good idea to run all three different search strategies independently.

4 State Equations for Cardinality Queries

In this section we present an adaptation of the technique based on integer programming (state-equations [12, 13]) which can be in some cases used to efficiently disprove reachability by over-approximating the state-space, hence avoiding the full state-space exploration. Let \(N = (P, T, F, I)\) be a PN and let \(M_0, M \in \mathcal {M}(N)\) be markings on N. If there is a sequence of transitions w such that \(M_0 \overset{w}{\rightarrow } M\) then a well-known fact (see e.g. [13]) says that there is a nonnegative solution to the following system of equations over the variables \(\{ x_t \mid t \in T \}\):

$$\begin{aligned} M_0(p) + \sum _{t \in T}{(F(t, p) - F(p, t)) \cdot x_t} = M(p) \ \ \ \ \text {for all}\, p \in P \ . \end{aligned}$$

Clearly, if we set \(x_t\) to be the number of times t was fired in the sequence w, then this gives us the requested solution. Conversely, if there is no solution to the state-equations then M is not reachable from \(M_0\). On the other hand, a solution to the state-equations does not in general imply that M is reachable from the marking \(M_0\).

Fig. 1.
figure 1

Heuristic, BFS and DFS search strategies (timeout at 5 min)

Full size image

Esparza and Melzer [7] proposed to use integer linear programming in order to solve the state-equations, ensuring that \(x_t \in \mathbb {N}_0\) for all \(t \in T\) and thus providing a more accurate approximation. We shall generalize this approach to cardinality queries which may require several calls to a linear program solver. A restriction is a function \(r: P \rightarrow \mathbb {N}_0\times (\mathbb {N}_0\cup \{\infty \})\) from places to right-open intervals representing the allowed number of tokens in each of the places (if \(r(p)=[0,\infty ]\) then there is no restriction on the number of tokens in p). Given two restrictions \(r_1\) and \(r_2\), we introduce the combined restriction \( combine (r_1,r_2)\) defined as \( combine (r_1,r_2)(p) = r_1(p) \cap r_2(p)\) where we assume here the standard interval intersection operator. We use the notation \(\langle p_1 \mapsto [a_1,b_1], \ldots p_n \mapsto [a_n,b_n] \rangle \) to represent a restriction r such that \(r(p_1)=[a_1,b_1]\), ..., \(r(p_n) = [a_n,b_n]\) and \(r(p)=[0,\infty ]\) for all \(p \in P \smallsetminus \{p_1, \ldots , p_n\}\). For example, \( combine (\langle p \mapsto [2,\infty ], q \mapsto [2,10] \rangle , \langle p \mapsto [0,7] \rangle ) = \langle p \mapsto [2,7], q \mapsto [2,10] \rangle \).

Let us now define the function \( constraints \) that for a given cardinality query \(\varphi \) returns a set of restrictions. For simplicity, we assume that the negation has already been pushed (using De Morgan rules) all the way to the atomic propositions where the negation can be replaced by the dual atomic propositions.

figure d

The actual use of state-equations in the setting of cardinality queries is now described in Algorithm 3.

figure e

Our implementation of the algorithm uses lpsolve [2] for the linear programming part and performs fast on most of the competition nets. We have selected two smallest instances of each scalable model from the known models used in MCC’15 in order to be able to make a full state-space search on most of these models for the purpose of our analysis. Then we ran the state-equation test for all cardinality queries, resulting in the total number of 1024 executions. If the over-approximation using state-equations succeeded (disproved reachability), we report this and terminate, otherwise we continue with the state-space search using the heuristic strategy with 5 min timeout. In 125 runs we did not get a conclusive answer and reached the timeout, in 405 runs the answer was negative (cardinality query was not reachable) and in the remaining 494 cases the query was reachable. Out of the 405 runs where the cardinality query was disproved, the state-equation technique succeeded in 118 cases (and hence the expensive state-space search was completely avoided). Moreover, it took on average only 0.15 s to perform the state-equation check, with only four tests exceeding 2 s. The most expensive over-approximation test was for the model PolyORBNT-S05J30 where it took 4.25 s.

The over-approximation using state-equations is a fast and efficient method to disprove the reachability of cardinality queries and it manages in almost 30 % of cases to provide a conclusive answer. In order to further increase the percentage of cases with conclusive answers, we plan to experiment with trap reduction [7] and other techniques in order to make the technique applicable to even more cardinality queries.

Fig. 2.
figure 2

Sequential rules for a cardinality formula \(\varphi \) and initial marking \(M_0\)

Full size image

5 Structural Reductions

We shall now present a set of structural reduction rules that allow us to reduce the net structure and decrease the size of the state-space, while preserving the answers to cardinality queries. The classical reduction rules for preserving liveness, safeness and boundedness were introduced in [13, 14]. We extend them to weighted nets with inhibitor arcs and specialize to the use for cardinality queries. The extension is not completely straightforward as a number of side conditions must be satisfied in order to preserve correctness—in fact TAPAAL was the only tool at MCC’15 that used structural reduction techniques. The rules are presented in Figs. 2 and 3 and they are relative to a given initial marking \(M_0\) and a cardinality query \(\varphi \), where \( places {(}\varphi )\) is the set of all places that occur in the query \(\varphi \).

Fig. 3.
figure 3

Parallel rules for a cardinality formula \(\varphi \) and initial marking \(M_0\)

Full size image

Theorem 1

Let \((N,M_0)\) be a marked Petri net and let \(\varphi \) be a cardinality query. Let \(N'\) be the net N after the application of some reduction rules from Figs. 2 and 3. Then \((N,M_0) \models EF \,\varphi \) if and only if \((N',M_0) \models EF \,\varphi \).

Proof

As cardinality queries are only concerned about the number of tokens in places, it is easy to see that the parallel transition rule in Fig. 3b is harmless as the transitions t and \(t'\) are enabled at the same time and they have the same firing effect, so we can easily remove one of them without affecting the reachable markings. Similarly, the parallel places rule in Fig. 3a ensures that the number of tokens in p and \(p'\) remain the same in any reachable marking (ensured by the assumption that p and \(p'\) contain the same number of tokens already in the initial marking). Now we can remove the place p, provided that p is not used in the cardinality query \(\varphi \) and either there are no inhibitor arcs connected to p or the places p and \(p'\) inhibit exactly the same set of transitions.

For a given net N, let \(N'\) be a net after one application of the sequential transition rule in Fig. 2a that removed the transition t. We shall first argue that if \((N,M_0) \models EF \,\varphi \), meaning that \(M_0 \overset{w}{\rightarrow } M\) for some sequence of transitions w such that \(M \models \varphi \), then also \((N',M_0) \models EF \,\varphi \). To show this, let \(w'\) be the transition sequence obtained from w by removing all occurrences of the transition t. Observe now that due to the fact that no inhibitor arcs are connected to p and \(p'\) (condition 5), we can execute from \(M_0\) in \(N'\) the sequence \(w'\) (\(M_0\) is a valid marking also in \(N'\) due to condition 4 requiring that the place we removed in \(N'\) has no tokens in \(M_0\)) and obtain a marking \(M'\) such that \(M'(\overline{p})=M(\overline{p})\) for all \(\overline{p} \in P \smallsetminus \{p,p'\}\) and \(M'(p'')=M(p)+M(p')\). As the query \(\varphi \) does not contain the places p and \(p'\) (condition 6), we can conclude that also \(M' \models \varphi \) and hence \((N',M_0) \models EF \,\varphi \). For the opposite direction, assume that \(M_0 \overset{w}{\rightarrow } M'\) in the net \(N'\) such that \(M' \models \varphi \). We shall now fire this transition sequence w in the original net N such that whenever the transition t that was removed in \(N'\) is enabled, we insert its firing into the sequence w as long as it is enabled. This will guarantee that all tokens from p are moved to \(p'\) due to the requirement that the single input and output arcs of t have weight 1 (conditions 2 and 3) and that t is not connected with any inhibitor arcs (condition 5). As p is not an input place for any other transition than t (condition 2), moving the tokens from p to \(p'\) does not influence the firing of other transitions in N. Similarly, the configuration of tokens in p and \(p'\) cannot influence the firing of other transitions in \(N'\) due to the absence of inhibitor arcs connected to p and \(p'\) (condition 5). Now, let M be the marking reached in N after firing the sequence of transitions described above. Clearly, \(M(\overline{p})=M'(\overline{p})\) for all \(\overline{p} \in P \smallsetminus \{p,p'\}\) and as \(\varphi \) is not referring to the places p and \(p'\) (condition 6), we get \(M \models \varphi \) implying that \((N,M_0) \models EF \,\varphi \).

The arguments for the rule in Fig. 2b, omitted due to space limitations, are analogous to the sequential transition removal rule discussed above.    \(\square \)

Note that the more places occur in the query \(\varphi \), the fewer reduction rules are in general applicable. The reachability of a deadlock can be expressed using a cardinality query but then all places connected to some transition will be mentioned in the query and hence the structural reduction rules will not be applicable. However, for deadlock we can reduce the net w.r.t. some trivial query that does not contain any places (e.g. \( EF \,2<1\)) and now \((N,M_0)\) is deadlock-free if and only if \((N',M_0)\) is deadlock-free.

Theorem 2

Let \((N,M_0)\) be a marked Petri net. Let \(N'\) be the net N after the application of some reduction rules from Figs. 2 and 3 for a query \(\varphi = 2 < 1\). Then \((N,M_0)\) has a deadlock if and only if \((N',M_0)\) has a deadlock.

Proof

The proof is very similar to the proof of Theorem 1 but some of the additional conditions like the requirement \(p \not = p'\) in the rule from Fig. 2a (condition 1) are important as removing the transition t in case of \(p=p'\) can create a new deadlock in \(N'\) that is not present in N.    \(\square \)

For the competition queries that ask to compute the maximum number of tokens in the net, we may only use reduction rules from Figs. 2b and 3b as the other two rules possibly decrease the maximum number of reachable tokens.

We have conducted experiments on the same nets as in Sect. 4 in order to see how many nets can be reduced and to what degree. The reductions were performed relative to a query that does not contain any places (as e.g. deadlock) in order to see the maximal possible reduction. If a query contains many places, the number of applications of the reduction rules may be possibly lower. The data show that out of the 261 nets, 118 of them were reducible, with an average reduction of 35 % of the net size (measured as the number of places plus the number of transitions). Some nets are reducible by only a few percent while others allow a reduction of up to 95 % (e.g. the house construction net). As reducing the size of a net can imply up to an exponential decrease in the size of the state-space, the effect of the reductions significantly contributes to the performance of our verification engine.

6 Tool Implementation

The verification engine for P/T nets, employing the techniques described in earlier sections, has been efficiently implemented in C++ and made publicly available as a part of the tool suite TAPAAL [4]. It includes a GUI for drawing the nets, graphical query creation dialog and advanced debugging (simulation) options. The tool allows us to import the MCC competition nets in PNML format as well as the cardinality and deadlock queries, and process them either individually or in a batch processing mode.

Regarding the implementation details, our experiments showed that the incidence matrix representation of a Petri net is preferred over the linked list representation as even though on larger nets the linked list representation preserves some space, it is remarkably slower [6] (likely due to the cache coherence issues). Finally, it is important to remark that for larger nets with several hundreds of places and transitions, an efficient implementation of the structural reduction rules is of great importance as a naive coding of the rules using up to four nested loops (like the rule in Fig. 3a) will use too much of the preprocessing time.

7 Conclusion

We described the most essential verification techniques used in the P/T net engine of TAPAAL. Each of the techniques has a significant performance effect, as documented by a number of experiments run on the nets and queries from MCC’15. We believe that it is the combination of these techniques and a relatively simple explicit search engine that contributed to the second place of our tool in the years 2014 and 2015. We are currently working on optimizing the performance of the successor generator, space optimizations and extending the reachability analysis to the full CTL model checking.