An Automaton Learning Approach to Solving Safety Games over Infinite Graphs

Abstract

We propose a method to construct finite-state reactive controllers for systems whose interactions with their adversarial environment are modeled by infinite-duration two-player games over (possibly) infinite graphs. The method targets safety games with infinitely many states or with such a large number of states that it would be impractical—if not impossible—for conventional synthesis techniques that work on the entire state space. We resort to constructing finite-state controllers for such systems through an automata learning approach, utilizing a symbolic representation of the underlying game that is based on finite automata. Throughout the learning process, the learner maintains an approximation of the winning region (represented as a finite automaton) and refines it using different types of counterexamples provided by the teacher until a satisfactory controller can be derived (if one exists). We present a symbolic representation of safety games (inspired by regular model checking), propose implementations of the learner and teacher, and evaluate their performance on examples motivated by robotic motion planning.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

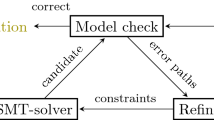
We propose an automata learning-based method to construct reactive controllers subject to safety specifications. We model the interaction between a controlled system and its possibly adversarial environment as a two-player game over a graph [16]. We consider games over infinite graphs. In this setting, the conventional techniques for reactive controller synthesis (e.g., fixed-point computations) are not applicable anymore. We resort to learning for constructing finite-state reactive controllers. The learning takes place in a setting akin to counterexample-guided inductive synthesis (CEGIS) [14] between a teacher, who has knowledge about the safety game in question, and a learner, whose objective is to identify a controller using information disclosed by the teacher in response to (incorrect) conjectures.

A natural context for our method is one in which the interaction between the controlled system and its environment is so complex that it can be represented only by graphs with infinitely many vertices (e.g., motion planning over unbounded grid worlds) or “practically infinitely many” states (i.e., the number of possible configurations is so large that the game becomes impractical for conventional techniques). Additionally, in situations in which a complete description of the game is not available in a format amenable to existing game solvers [6, 9], there may still exist human experts (or automated oracles, as in Sect. 4) who acts as teacher with their insight into how the controlled system should behave.

We focus on games with safety specifications, which already capture practically interesting properties (e.g., safety and bounded-horizon reachability). However, games over infinite graphs require special attention on the representation and manipulation of the underlying graph structure. Hence, one of our main contributions is a symbolic representation of safety games, called rational safety games, that follows the idea of regular model checking [7] in that it represents sets of vertices by regular languages and edges by so-called rational relations.

We develop an iterative framework for learning winning sets—equivalently controllers—in rational safety games and particular implementations of a teacher and learner. In each iteration, the learner conjectures a winning set, represented as a deterministic finite automaton. The teacher performs a number of checks and returns, based on whether the conjecture passes the checks, a counterexample. Following the ICE learning framework [10] and partially deviating from the classical learning frameworks for regular languages [1, 11], the counterexample may be one of the following four types: positive, negative, existential implication and universal implication counterexamples. Based on the response of the teacher, the learner updates his conjecture. If the conjecture passes all checks, the learning terminates with the desired controller. However, our technique is necessarily a semi-algorithm as reachability questions over rational relations are undecidable.

Even though the underlying game may be prohibitively large, a controller with a compact representation may realize the specifications. For example, depending on the given task specification in robotic motion planning, only a small subset of all possible interactions between a robot and its environment is often relevant. Based on this observation, our method possesses several desirable properties: (i) it usually identifies “small” solutions that are more likely to be interpretable by users; (ii) its runtime mainly depends on the size of the solution rather than the size of the underlying game; (iii) though the method is applicable generally, it performs particularly well when the resulting controller has a small representation; (iv) besides being applicable to infinite-state systems, the method performs well on finite-state problems by—unlike conventional techniques—avoiding potentially large intermediate artifacts. We demonstrate these properties empirically on a series of examples motivated by robotic motion planning.

Related Work. Games over infinite graphs have been studied, predominantly for games over pushdown graphs [15]. Also, a constraint-based approach to solving games over infinite graphs has recently been proposed [3]. Learning-based techniques for reachability games over infinite graphs were studied in [19]; in fact, our symbolic representation of safety games is a generalization of the representation proposed there. In the context of safety games, recent work [20] demonstrated the ability of learning-based approaches to extract small reactive controllers from a priori constructed controllers with a possibly large number of states. In this work, we by-pass this a priori construction of reactive controllers by learning a controller directly. Infinite (game) graphs occur often in the presence of data, and symbolic formalisms have been described for several domains, including examples such as interface automata with data [13] and modal specifications with data [2]. However, we are not aware of learning algorithms for these formalisms.

2 Rational Safety Games

We recap the basic notation and definitions used in the rest of the paper.

Safety Games.We consider safety games (i.e., infinite duration two-person games on graphs) [16]. A safety game is played on an arena $\mathfrak A = (V_0, V_1, E)$ consisting of two nonempty, disjoint sets $V_0, V_1$ of vertices (we denote their union by V) and a directed edge relation $E \subseteq V \times V$. In contrast to the classical (finite) setting, we allow $V_0$ and $V_1$ to be countable sets. As shorthand notation, we write the successors of a set $X \subseteq V$ of vertices as $E(X) = \{ y \mid \exists x \in X :(x, y) \in E \}$.

We consider safety games with initial vertices, which are defined as triples $\mathfrak G = (\mathfrak A, F, I)$ consisting of an arena $\mathfrak A = (V_0, V_1, E)$, a set $F \subseteq V$ of safe vertices, and a set $I \subseteq F$ of initial vertices. Such safety games are played by two players, named Player 0 and Player 1, who play the game by moving a token along the edges. Formally, a play is an infinite sequence $\pi = v_0 v_1 \ldots \in V^\omega$ that satisfies $v_0 \in I$ and $(v_i, v_{i+1}) \in E$ for all $i \in \mathbb N$. The set F defines the winning condition of the game in the sense that a play $v_0 v_1 \ldots$ is winning for Player 0 if $v_i \in F$ for all $i \in \mathbb N$—otherwise it is winning for Player 1.

A strategy for Player $\sigma$ $\in \{ 0, 1 \}$ is a mapping $f_\sigma :V^* V_\sigma \rightarrow V$, which prescribes how to continue playing. A strategy $f_\sigma$ is called winning if any play $v_0 v_1 \ldots$ that is played according to the strategy (i.e., that satisfies $v_{i+1} = f_\sigma (v_0 \ldots v_i)$ for all $i \in \mathbb N$ and $v_i \in V_\sigma$) is winning for Player $\sigma$. A winning strategy for Player 0 translates into a controller satisfying the given safety specifications. Hence, we restrict ourselves to compute winning strategies for Player 0. Computing a winning strategy for Player 0 usually reduces to finding a so-called winning set.

Definition 1

(Winning set). Let $\mathfrak G = (\mathfrak A, I, F)$ be a safety game over the arena $\mathfrak A = (V_0, V_1, E)$. A winning set is a set $W \subseteq V$ satisfying (1) $I \subseteq W$, (2) $W \subseteq F$, (3) $E(\{ v \}) \cap W \ne \emptyset$ for all $v \in W \cap V_0$ (existential closedness), and (4) $E(\{ v \}) \subseteq W$ for all $v \in W \cap V_1$ (universal closedness).

By computing a winning set, one immediately obtains a strategy for Player 0: starting in an initial vertex, Player 0 simply moves to a successor vertex inside W whenever it is his turn. A straightforward induction over the length of plays proves that every play that is played according to this strategy stays inside F, no matter how Player 1 plays, and, hence, is won by Player 0 (since $I \subseteq W \subseteq F$). A winning set is what we want to compute—or, more precisely, learn.

Algorithmically working with games over infinite arenas require symbolic representations. We follow the idea of regular model checking [7] and represent sets of vertices by regular languages and edges by so-called rational relations. Before we introduce our symbolic representation of safety games, however, we recap some basic concepts of automata theory.

Basics of Automata Theory. An alphabet $\varSigma$ is a nonempty, finite set, whose elements are called symbols. A word over the alphabet $\varSigma$ is a sequence $u = a_1 \ldots a_n$ of symbols $a_i \in \varSigma$ for $i \in \{1, \ldots , n\}$; the empty sequence is called empty word and denoted by $\varepsilon$. Given two words $u = a_1 \ldots a_m$ and $v = b_1 \ldots b_n$, the concatenation of u and v is the word $u \cdot v = uv = a_1 \ldots a_m b_1 \ldots b_n$. The set of all words over the alphabet $\varSigma$ is denoted by $\varSigma ^*$, and a subset $L \subseteq \varSigma ^*$ is called a language. The set of prefixes of a language $L \subseteq \varSigma ^*$ is the set $Pref (L) = \{ u \in \varSigma ^*\mid \exists v \in \varSigma ^*:uv \in L \}$.

A nondeterministic finite automaton (NFA) is a tuple $\mathcal A = (Q, \varSigma , q_0, \varDelta , F)$ consisting of a nonempty, finite set Q of states, an input alphabet $\varSigma$, an initial state $q_0 \in Q$, a transition relation $\varDelta \subseteq Q \times \varSigma \times Q$, and a set $F \subseteq Q$ of final states. A run of $\mathcal A$ on a word $u = a_1 \ldots a_n$ is a sequence of states $q_0, \ldots , q_n$ such that $(q_{i-1}, a_i, q_i) \in \varDelta$ for $i \in \{ 1, \ldots , n \}$. We denote this run by $\mathcal A :q_0 \xrightarrow {u} q_n$. An $NFA$ $\mathcal A$ accepts a word $u \in \varSigma ^*$ if $\mathcal A :q_0 \xrightarrow {u} q$ with $q \in F$. The set $L(\mathcal A) = \{u \in \varSigma ^*\mid \mathcal A :q_0 \xrightarrow {u} q, q \in F \}$ is called language of $\mathcal A$. A language L is regular if there exists an $NFA$ $\mathcal A$ with $L(\mathcal A) = L$. $NFA _\varSigma$ denotes the set of all $NFAs$ over $\varSigma$.

A deterministic finite automaton (DFA) is an NFA in which $(p, a, q) \in \varDelta$ and $(p, a, q') \in \varDelta$ imply $q = q'$. For DFAs, we replace the transition relation $\varDelta$ by a transition function $\delta :Q \times \varSigma \rightarrow Q$.

We define infinite arenas by resorting to transducers. A transducer is an NFA $\mathcal T = (Q, \hat{\varSigma }, q_0, \varDelta , F)$ over the alphabet $\hat{\varSigma } = (\varSigma \cup \{ \varepsilon \}) \times (\varGamma \cup \{ \varepsilon \})$—$\varSigma$ and $\varGamma$ are both alphabets—that processes pairs $(u, v) \in \varSigma ^*\times \varGamma ^*$ of words. The run of a transducer $\mathcal T$ on a pair (u, v) is a sequence $q_0, \ldots , q_n$ of states such that $(q_{i-1}, (a_i, b_i), q_i) \in \varDelta$ for all $i \in \{1, \ldots , n \}$, $u = a_1 \ldots a_n$, and $v = b_1 \ldots b_n$; note that u and v do not need to be of equal length since any $a_i$ or $b_i$ can be $\varepsilon$. A pair (u, v) is said to be accepted by $\mathcal T$ if there exists a run of $\mathcal T$ on (u, v) that starts in the initial state and ends in a final state. As an acceptor of pairs of words, a transducer $\mathcal T$ defines a relation, namely the relation consisting of exactly the pairs accepted by $\mathcal T$, which we denote by $R(\mathcal T)$. Finally, a relation $R \subseteq \varSigma ^*\times \varGamma ^*$ is called rational if there exists a transducer $\mathcal T$ with $R(\mathcal T) = R$. (This definition is simplified from that in [5] but sufficient for our purpose.) Note that transducers as defined above do not need to preserve the length of words.

Our learning framework relies on the two facts given in Lemma 1.

Lemma 1

Let $R \subseteq \varSigma ^*\times \varGamma ^*$ be a rational relation and $X \subseteq \varSigma ^*$ a regular set. Then, (1) the relation $R^{-1} = \{ (y, x) \mid (x, y) \in R \}$ is again rational, and a transducer defining this set can be constructed in linear time; and (2) the set $R(X) = \{ y \in \varGamma ^*\mid \exists x \in X :(x, y) \in R \}$, called the image of X under R, is again regular, and an NFA accepting this set can be constructed effectively.

Rational Safety Games. A rational safety game is a symbolic representation of a safety game in terms of regular languages and rational relations.

Definition 2

A rational arena over the alphabet $\varSigma$ is an arena $\mathfrak A_\varSigma = (V_0, V_1, E)$ where $V_0, V_1 \subseteq \varSigma ^*$ are regular languages and $E \subseteq V \times V$ is a rational relation.

Definition 3

A rational safety game over the alphabet $\varSigma$ is a safety game $\mathfrak G_\varSigma = (\mathfrak A_\varSigma , F, I)$ with a rational arena $\mathfrak A_\varSigma$ over $\varSigma$ and regular languages $F, I \subseteq \varSigma ^*$.

We assume regular languages to be given as $NFAs$ and rational relations as transducers. We use these notions interchangeably; for instance, we write a rational area $\mathfrak A_\varSigma = (V_0, V_1, E)$ as $\mathfrak A_\varSigma = (\mathcal A_{V_0}, \mathcal A_{V_1}, \mathcal T_E)$ given that $L(\mathcal A_{V_0}) = V_0$, $L(\mathcal A_{V_1}) = V_1$, and $R(\mathcal T_E) = E$.

Example 1

Consider an example motivated by motion planning (see Fig. 1a) in which a robot moves on an infinite, one-dimensional grid that is “bounded on the left”. It can move to an adjacent cell (provided that it has not reached left edge) or it stays still. The grid is partitioned into a safe (shaded in Fig. 1a) and an unsafe area. The safe area is parameterized by $k \in \mathbb N \setminus \{ 0 \}$ and consists of all positions greater than or equal to k. The robot starts inside the safe area.

Fig. 1.

Illustration of the safety game discussed in the introductory example.

The robot’s movement is governed by two adversarial players, called system and environment. The system can move the robot to the right or keep it at its current position, whereas the environment can move the robot to the left (if the edge has not been reached) or keep it at its current position. The players move the robot in alternation, and the system moves first. The system’s objective is to stay within the safe area, whereas the environment wants to move the robot out of it. Note that the system can win, irrespective of k, by always moving right.

A formalization as safety game is straightforward. Player 0 corresponds to the system and Player 1 corresponds to the environment. The arena $\mathfrak A = (V_0, V_1, E)$ consists of vertices $V_0 = \{ s \} \times \mathbb N$ and $V_1 = \{ e \} \times \mathbb N$—s, respectively e, indicates the player moving next—as well as the edge relation $E = \bigl \{ \bigl ((s, i), (e, i+1) \bigr ) \mid i \in \mathbb N \bigr \} \cup \bigl \{ \bigl ((e, i+1), (s, i) \bigr ) \mid i \in \mathbb N \bigr \}$. The safety game itself is the triple $\mathfrak G_k = (\mathfrak A, F, I)$ with $F = \{ s, e \} \times \{ i \in \mathbb N \mid i \ge k \}$ and $I = \{ s \} \times \{ i \in \mathbb N \mid i \ge k \}$. Figure 1b sketches the game $\mathfrak G_k$ for the case $k=2$.

We now turn $\mathfrak G_k$ into a rational safety game. To this end, we label each vertex uniquely with a finite word. In our example, we choose $\varSigma =\{s, e, \mathsf {l}\}$ and associate the vertex $(x, i) \in \{ s, e \} \times \mathbb N$ with the word $x\mathsf {l}^i$ where $\mathsf {l}^i$ is the encoding of i in unary. We represent the sets $V_0$ and $V_1$ by the following $NFAs$:

Moreover, we represent the edges by the following transducer:

Finally, the NFA

represents the set F; similarly, I is represented by a copy of $\mathcal A_F$ in which the transition labeled with e is omitted.

It is worth mentioning that rational arenas not only subsume finite arenas but also a rich class of infinite arenas, including such encoding computations of Turing machines. Hence, the problem of determining the winner of a rational safety game is undecidable, and any algorithm for computing a winning set can at best be a semi-algorithm (i.e., an algorithm that, on termination, gives the correct answer but does not guarantee to halt). The algorithm we design in this paper is of this kind and guarantees to learn a winning set if one exists. For ease of presentation, we always assume that a winning set exists.

3 The Learning Framework

Our learning framework is an extension of the ICE framework [10] for learning loop invariants from positive and negative data as well as implications. The learning takes place between a teacher, who has (explicit or implicit) knowledge about the rational safety game in question, and a learner, whose objective is to learn a DFA accepting a winning set, but who is agnostic to the game. We assume that the teacher announces the alphabet of the game before the actual learning starts.

The learning proceeds in a CEGIS-style loop [14]. In every iteration, the learner conjectures a DFA, call it $\mathcal C$, and the teacher checks whether $L(\mathcal C)$ is a winning set—this kind of query is often called equivalence or correctness query. Although the teacher does not know a winning set (the overall objective is to learn one after all), he can resort to Conditions (1)–(4) of Definition 1 in order to decide whether $L(\mathcal C)$ is a winning set. If $L(\mathcal C)$ satisfies Conditions (1)–(4), then the teacher replies “yes” and the learning ends. If this is not the case, the teacher returns a counterexample witnessing the violation of one of these conditions, and the learning continues with the next iteration. The definition below fixes the protocol between the teacher and the learner, and defines counterexamples.

Definition 4

(Teacher for rational safety games). Let $\mathfrak G_\varSigma = (\mathfrak A_\varSigma , F, I)$ be a rational safety game over the rational arena $\mathfrak A_\varSigma = (V_0, V_1, E)$. Confronted with a DFA $\mathcal C$, a teacher for $\mathfrak G_\varSigma$ replies as follows:

• 1. If $I \not \subseteq L(\mathcal C)$, then the teacher returns a positive counterexample $u \in I \setminus L(\mathcal C)$.

• 2. If $L(\mathcal C) \not \subseteq F$, then the teacher returns a negative counterexample $u \in L(\mathcal C) \setminus F$.

• 3. If there exists $u \in L(\mathcal C) \cap V_0$ such that $E(\{u\}) \cap L(\mathcal C) = \emptyset$, then the teacher picks such a word u and returns an existential implication counterexample $(u, \mathcal A) \in \varSigma ^*\times NFA _\varSigma$ where $L(\mathcal A) = E(\{u\})$.

• 4. If there exists $u \in L(\mathcal C) \cap V_1$ such that $E(\{u\}) \not \subseteq L(\mathcal C)$, then the teacher picks such a word u and returns a universal implication counterexample $(u, \mathcal A) \in \varSigma ^*\times NFA _\varSigma$ where $L(\mathcal A) = E(\{u\})$.

If $\mathcal C$ passes all four checks (in arbitrary order), the teacher replies “yes”.

It is easy to see that the language of a conjecture is indeed a winning set if the teacher replies “yes” (since it satisfies all conditions of Definition 1). The meaning of a positive counterexample is that any conjecture needs to accepts it but it was rejected. Similarly, a negative counterexample indicates that any conjecture has to reject it but it was accepted. An existential implication counterexample $(u, \mathcal A)$ means that any conjecture accepting u has to accept at least one $v \in L(\mathcal A)$, which was violated by the current conjecture. Finally, a universal implication counterexample $(u, \mathcal A)$ means that any conjecture accepting u needs to accept all $v \in L(\mathcal A)$. At this point, it is important to note that Definition 4 is sound (in particular, both types of implication counterexamples are well-defined due to Lemma 1 Part 2) and every counterexample is a finite object.

Example 2

We revisit Example 1 for $k = 2$ and describe how a winning set is learned. Suppose the learner conjectures the DFA $\mathcal C_0$ with $L(\mathcal C_0) = \emptyset$. As $\mathcal C_0$ fails Check 4 (it passes all other checks), the teacher returns a positive counterexample, say $u = s\mathsf {l}\mathsf {l}\in I$. Next, suppose the learner conjectures the DFA $\mathcal C_1$ with $L(\mathcal C_1) = \{ s \mathsf {l}^n \mid n \ge 2\}$, which passes all checks but Check 4 (as the players alternate but $L(\mathcal C_1)$ does not contain a vertex of the environment). The teacher replies with an existential implication counterexample, say $(s \mathsf {l}\mathsf {l}, \mathcal A)$ with $L(\mathcal A) = \{e \mathsf {l}\mathsf {l}, e \mathsf {l}\mathsf {l}\mathsf {l}\}$. In the next round, suppose the learner conjectures the DFA $\mathcal C_2$ with $L(\mathcal C_2) = \{ s \mathsf {l}^n \mid n \ge 2 \} \cup \{ e \mathsf {l}^m \mid m \ge 3 \}$. This conjecture passes all checks (i.e., $L(\mathcal C_2)$ is a winning set), the teacher replies “yes”, and the learning ends.

It is important to note that classical learning frameworks for regular languages that involve learning from positive and negative data only, such as Gold’s passive learning [11] or Angluin’s active learning [1], are insufficient in our setting. If the learner provides a conjecture $\mathcal C$ that violates Condition (3) or (4) of Definition 1, the teacher is stuck. For instance, if $\mathcal C$ does not satisfy Conditions (4), the teacher does not know whether to exclude u or to include $E(\{u\})$. Returning an implication counterexample resolves this problem by communicating exactly why the conjecture is incorrect and, hence, allows the learner to make progress.¹

4 A Generic Teacher

We now present a generic teacher that, taking a rational safety game as input, answers queries according to Definition 4. For the remainder of this section, fix a rational safety game $\mathfrak G_\varSigma = (\mathfrak A_\varSigma , \mathcal A_F, \mathcal A_I)$ over the rational arena $\mathfrak A_\varSigma = (\mathcal A_{V_0}, \mathcal A_{V_1}, \mathcal T_E)$, and let $\mathcal C$ be a DFA conjectured by the learner.

To answer a query, the teacher performs Checks 1 to 4 of Definition 4 as described below. If the conjecture passes all checks, the teacher returns “yes”; otherwise, he returns a corresponding counterexample, as described next.

Check 1 (initial vertices). The teacher computes an NFA $\mathcal B$ with $L(\mathcal B) = L(\mathcal A_I) \setminus L(\mathcal C)$. If $L(\mathcal B) \ne \emptyset$, he returns a positive counterexample $u \in L(\mathcal B)$.

Check 2 (safe vertices). The teacher computes an NFA $\mathcal B$ with $L(\mathcal B) = L(\mathcal C) \setminus L(\mathcal A_F)$. If $L(\mathcal B) \ne \emptyset$, he returns a negative counterexample $u \in L(\mathcal B)$.

Check 3 (existential closure). The teacher successively computes three NFAs:

• 1. An $NFA$ $\mathcal B_1$ with $L(\mathcal B_1) = R(\mathcal T_E)^{-1}(L(\mathcal C))$; the language $L(\mathcal B_1)$ contains all vertices that have a successor in $L(\mathcal C)$.

• 2. An $NFA$ $\mathcal B_2$ with $L(\mathcal B_2) = L(\mathcal A_{V_0}) \setminus L(\mathcal B_1)$; the language $L(\mathcal B_2)$ contains all vertices of Player 0 that have no successor in $L(\mathcal C)$.

• 3. An $NFA$ $\mathcal B_3$ with $L(\mathcal B_3) = L(\mathcal C) \cap L(\mathcal B_2)$; the language $L(\mathcal B_3)$ contains all vertices of Player 0 that belong to $L(\mathcal C)$ and have no successor in $L(\mathcal C)$.

Every $u \in L(\mathcal B_3)$ is a witness that $\mathcal C$ is not existentially closed. Hence, if $L(\mathcal B_3) \ne \emptyset$, the teacher picks an arbitrary $u \in L(\mathcal B_3)$ and returns the existential implication counterexample $(u, \mathcal A)$ where $L(\mathcal A) = R(\mathcal T_E)(\{u\})$.

Check 4 (universal closure). The teacher computes three NFAs:

• 1. An $NFA$ $\mathcal B_1$ with $L(\mathcal B_1) = \bigl ( L(\mathcal A_{V_0}) \cup L(\mathcal A_{V_1}) \bigr ) \setminus L(\mathcal C)$; the language $L(\mathcal B_1)$ contains all vertices not in $L(\mathcal C)$.

• 2. An $NFA$ $\mathcal B_2$ with $L(\mathcal B_2) = R(\mathcal T_E)^{-1}(L(\mathcal B_1))$; the language $L(\mathcal B_2)$ contains all vertices that have a successor not belonging to $L(\mathcal C)$.

• 3. An $NFA$ $\mathcal B_3$ with $L(\mathcal B_3) = L(\mathcal A_{V_1}) \cap L(\mathcal C) \cap L(\mathcal B_2)$; the language $L(\mathcal B_3)$ contains all vertices of Player 1 in $L(\mathcal C)$ with at least one successor not in $L(\mathcal C)$.

Every $u \in L(\mathcal B_3)$ is a witness that $\mathcal C$ is not universally closed. Hence, if $L(\mathcal B_3) \ne \emptyset$, the teacher picks an arbitrary $u \in L(\mathcal B_3)$ and returns the universal implication counterexample $(u, \mathcal A)$ where $L(\mathcal A) = R(\mathcal T_E)(\{u\})$.

All checks can be performed using standard methods of automata theory. In our implementation, the teacher performs the checks in the order 1 to 4.

5 A Learner for Rational Safety Games

We design our learner with two key features: (1) it always conjectures a DFA consistent with the counterexamples received so far, and (2) it always conjectures a minimal, consistent DFA (i.e., a DFA with the least number of states among all DFAs that are consistent with the received counterexamples). The first feature prevents the learner from making the same mistake twice, while the second facilitates convergence of the overall learning (provided that a winning set exists).

Our learner stores counterexamples in a so-called sample, which is a tuple $\mathcal S = ( Pos , Neg , Ex , Uni )$ consisting of a finite set $Pos \subset \varSigma ^*$ of positive words, a finite set $Neg \subset \varSigma ^*$ of negative words, a finite set $Ex \subset \varSigma ^*\times NFA _\varSigma$ of existential implications, and a finite set $Uni \subset \varSigma ^*\times NFA _\varSigma$ of universal implications. We encourage the reader to think of a sample as a finite approximation of the safety game learned thus far.

In every iteration, our learner constructs a minimal DFA consistent with the current sample $\mathcal S = ( Pos , Neg , Ex , Uni )$. A DFA $\mathcal B$ is called consistent with $\mathcal S$ if

• 1. $Pos \subseteq L(\mathcal B)$;

• 2. $Neg \cap L(\mathcal B) = \emptyset$;

• 3. $u \in L(\mathcal B)$ implies $L(\mathcal B) \cap L(\mathcal A) \ne \emptyset$ for each $(u, \mathcal A) \in Ex$; and

• 4. $u \in L(\mathcal B)$ implies $L(\mathcal A) \subseteq L(\mathcal B)$ for each $(u, \mathcal A) \in Uni$.

Constructing a DFA that is consistent with a sample is possible only if the sample does not contain contradictory information. Contradictions can arise in two ways: first, $Pos$ and $Neg$ are not disjoint; second, the (alternating) transitive closure of the implications in $Ex$ and $Uni$ contains a pair (u, v) with $u \in Pos$ and $v \in Neg$. This observation justifies the notion of contradiction-free samples: a sample $\mathcal S$ is called contradiction-free if a DFA that is consistent with $\mathcal S$ exists. If Player 0 wins from set I, a winning set exists and the counterexamples returned by the teacher always form contradiction-free samples.²

Once a minimal, consistent DFA is constructed, the learner conjectures it to the teacher. If the teacher replies “yes”, the learning terminates with a winning set. If the teacher returns a counterexample, the learner adds it to $\mathcal S$ and iterates. This procedure is sketched as Algorithm 1. Note that unravelling the game graph provides additional examples without the need to construct conjectures, but there is a trade-off between the number of iterations and the time needed to compute consistent DFAs. We leave an investigation of this trade-off for future work.

It is left to describe how the learner actually constructs a minimal DFA that is consistent with the current sample. However, this task, known as passive learning, is computationally hard (i.e., the corresponding decision problem is NP-complete) already in the absence of implications [11]. We approach this hurdle by translating the original problem into a sequence of satisfiability problems of formulas in propositional Boolean logic and use highly optimized constraint solvers as a practically effective means to solve the resulting formulas (note that a translation into a logical formulation is a popular and effective strategy). More precisely, our learner creates and solves propositional Boolean formulas $\varphi _n^\mathcal S$, for increasing values of $n \in \mathbb N$, $n \ge 1$, with the following two properties:

• 1. The formula $\varphi _n^\mathcal S$ is satisfiable if and only if there exists a DFA that has n states and is consistent with $\mathcal S$.

• 2. A model $\mathfrak M$ of (i.e., a satisfying assignment of the variables in) $\varphi _n^\mathcal S$ contains sufficient information to construct a DFA $\mathcal A_\mathfrak M$ that has n states and is consistent with $\mathcal S$.

If $\varphi _n^\mathcal S$ is satisfiable, then Property 2 enables us to construct a consistent DFA from a model. However, if the formula is unsatisfiable, then the parameter n has been chosen too small and the learner increments it. This procedure is summarized as Algorithm 2. We comment on its correctness later in this section. A proof can be found in the extended paper [22].

The key idea of the formula $\varphi _n^\mathcal S$ is to encode a DFA with n states by means of Boolean variables and to pose constraints on those variables. Our encoding relies on a simple observation: for every DFA there exists an isomorphic (hence, equivalent) DFA over the state set $Q = \{ 0, \ldots , n-1 \}$ with initial state $q_0 = 0$; moreover, given that Q and $q_0$ are fixed, any DFA with n states is uniquely determined by its transitions and final states. Therefore, we can fix the state set of the prospective DFA as $Q = \{ 0, \ldots , n-1 \}$ and the initial state as $q_0 = 0$; the alphabet $\varSigma$ is announced by the teacher.

Our encoding of transitions and final states follows an idea from [12, 21] (similar to the approach of Biermann and Feldman [4]). We introduce Boolean variables $d_{p, a, q}$ and $f_q$ where $p, q \in Q$ and $a \in \varSigma$, which have the following meaning: setting $d_{p, a, q}$ to $true$ means that the transition $\delta (p, a) = q$ exists in the prospective DFA, and setting $f_q$ to $true$ means that q is a final state.

To make sure that the variables $d_{p, a, q}$ encode a deterministic transition function, we impose two constraints:

$$\begin{aligned} \bigwedge _{p \in Q}~ \bigwedge _{a \in \varSigma }~ \bigwedge _{q, q' \in Q, q \ne q'}~ \lnot d_{p, a, q} \vee \lnot d_{p, a, q'} \end{aligned}$$

(1)

$$\begin{aligned} \bigwedge _{p \in Q}~ \bigwedge _{a \in \varSigma }~ \bigvee _{q \in Q}~ d_{p, a, q} \end{aligned}$$

(2)

Let $\varphi _n^\text {DFA}$ be the conjunction of Formulas (1) and (2). Given a model $\mathfrak M$ of $\varphi _n^\text {DFA}$ (we assume a model to be a map from the variables of a formula to the set $\{true, false\}$), deriving the encoded DFA is straightforward, as shown next.

Definition 5

(DFA $\mathcal A_\mathfrak M$ ). Given a model $\mathfrak M$ of $\varphi _n^\text {DFA}$, we define the DFA $\mathcal A_\mathfrak M = (Q, \varSigma , q_0, \delta , F)$ by (i) $\delta (p, a) = q$ for the unique $q \in Q$ with $\mathfrak M(d_{p, a, q}) = true$; and (ii) $F = \{ q \in Q \mid \mathfrak M(f_q) = true \}$. (Recall that we fixed $Q = \{0, \ldots , n-1 \}$ and $q_0 = 0$.)

To ensure that $\mathcal A_\mathfrak M$ is consistent with a sample $\mathcal S = ( Pos , Neg , Ex , Uni )$, we impose further constraints, corresponding to the requirements of consistent DFAs: (i) A formula $\varphi _n^ Pos$ asserting $Pos \subseteq L(\mathcal A_\mathfrak M)$. (ii) A formula $\varphi _n^ Neg$ asserting $Neg \cap L(\mathcal A_\mathfrak M) = \emptyset$. (iii) A formula $\varphi _n^ Ex$ asserting that $u \in L(\mathcal A_\mathfrak M)$ implies $L(\mathcal A_\mathfrak M) \cap L(\mathcal A) \ne \emptyset$ for each $(u, A) \in Ex$. (iv) A formula $\varphi _n^ Uni$ asserting that $u \in L(\mathcal A_\mathfrak M)$ implies $L(\mathcal A_\mathfrak M) \subseteq L(\mathcal A)$ for each $(u, A) \in Uni$. Then, $\varphi _n^\mathcal S := \varphi _n^\text {DFA} \wedge \varphi _n^ Pos \wedge \varphi _n^ Neg \wedge \varphi _n^ Ex \wedge \varphi _n^ Uni$. We here sketch formula $\varphi _n^ Uni$ and refer the reader to the extended paper [22] for a detailed presentation of the remaining formulas. A description of $\varphi _n^ Pos$ and $\varphi _n^ Neg$ can also be found in [21].

The Formula $\varvec{\varphi _n^ Uni }$ . We break the construction of $\varphi _n^ Uni$ down into smaller parts. Roughly, we construct a formula $\varphi _n^\iota$ that asserts $L(\mathcal A)\subseteq L(\mathcal A_\mathfrak M)$ if $u \in L(\mathcal A_\mathfrak M)$ for each universal implication $\iota = (u, \mathcal A) \in Uni$. The formulas $\varphi _n^ Uni$ is then the finite conjunction $\bigwedge _{\iota \in Uni } \varphi _n^\iota$. For the remainder, let us fix a universal implication $\iota \in Uni$, say $\iota = (u, A)$ with $A = (Q_\mathcal A, \varSigma , q_0^\mathcal A, \varDelta _\mathcal A, F_\mathcal A)$, and let $Ante ( Uni ) = \{ u \mid (u, \mathcal A) \in Uni \}$ be the set of all words occurring as antecedent of a universal implication.

As a preparatory step, we introduce auxiliary Boolean variables that track the runs of $\mathcal A_\mathfrak M$ on words of $Pref ( Ante ( Uni ))$ in order to detect when $\mathcal A_\mathfrak M$ accepts the antecedent of a universal implication. More precisely, we introduce variables $x_{u, q}$ where $u \in Pref ( Ante ( Uni ))$ and $q \in Q$, which have the meaning that $x_{u, q}$ is set to $true$ if $\mathcal A_\mathfrak M :q_0 \xrightarrow {u} q$ (i.e., $\mathcal A_\mathfrak M$ reaches state q on reading u):

$$\begin{aligned} x_{\varepsilon , q_0} \end{aligned}$$

(3)

$$\begin{aligned} \bigwedge _{u \in Pref ( Ante ( Uni ))}~ \bigwedge _{q \ne q' \in Q}~ \lnot x_{u, q} \vee \lnot x_{u,q'} \end{aligned}$$

(4)

$$\begin{aligned} \bigwedge _{ua \in Pref ( Ante ( Uni ))}~ \bigwedge _{p,q \in Q}~ (x_{u, p} \wedge d_{p, a, q}) \rightarrow x_{ua, q} \end{aligned}$$

(5)

Formula (3) asserts that $x_{\varepsilon , q_0}$ is set to $true$ since any run starts in the initial state $q_0$. Formula (4) enforces that for every $u \in Pref ( Ante ( Uni ))$ there exists at most one $q \in Q$ such that $x_{u, q}$ is set to $true$ (in fact, the conjunction of Formulas (2)–(5) implies that there exists a unique such state). Finally, Formula (5) prescribes how the run of $\mathcal A_\mathfrak M$ on a word $u \in Pref ( Ante ( Uni ))$ proceeds: if $\mathcal A_\mathfrak M$ reaches state p on reading u (i.e., $x_{u, p}$ is set to $true$) and there exists a transition from p to state q on reading the symbol $a \in \varSigma$ (i.e., $d_{p, a, q}$ is set to $true$), then $\mathcal A_\mathfrak M$ reaches state q on reading ua and $x_{ua}$ needs to be set to $true$.

We now define $\varphi _n^\iota$. The formula ranges, in addition to $d_{p, a, q}$, $f_q$, and $x_{u, q}$, over Boolean variables $y_{q, q'}^\iota$ where $q \in Q$ and $q' \in Q_\mathcal A$ and $y_{q, q'}^\iota$ track runs of $\mathcal A$ and $\mathcal A_\mathfrak M$. More precisely, if there exists a word $u \in \varSigma ^*$ with $\mathcal A_\mathfrak M :q_0 \xrightarrow {u} q$ and $\mathcal A :q_0^\mathcal A \xrightarrow {u} q'$, then $y_{q, q'}^\iota$ is set to $true$.

$$\begin{aligned} y_{q_0, q_0^\mathcal A}^\iota ~and \end{aligned}$$

(6)

$$\begin{aligned} \bigwedge _{p, q \in Q}~ \bigwedge _{(p', a, q') \in \varDelta _\mathcal A}~ (y_{p, p'}^\iota \wedge d_{p, a, q}) \rightarrow y_{q, q'}^\iota . \end{aligned}$$

(7)

Formula (6) enforces $y_{q_0, q_0^\mathcal A}^\iota$ to be set to $true$ because $\mathcal A_\mathfrak M :q_0 \xrightarrow {\varepsilon } q_0$ and $\mathcal A :q_0^\mathcal A \xrightarrow {\varepsilon } q_0^\mathcal A$. Formula (7) is similar to Formula (5) and describes how the runs of $\mathcal A_\mathfrak M$ and $\mathcal A$ proceed: if there exists a word v such that $\mathcal A_\mathfrak M :q_0 \xrightarrow {v} p$ and $\mathcal A :q_0^\mathcal A \xrightarrow {v} p'$ (i.e., $y_{p, p'}^\iota$ is set to $true$) and there are transitions $(p', a, q') \in \varDelta _\mathcal A$ and $\delta (p, a) = q$ in $\mathcal A_\mathfrak M$, then $\mathcal A_\mathfrak M :q_0 \xrightarrow {va} q$ and $\mathcal A :q_0^\mathcal A \xrightarrow {va} q'$, which requires $y_{q, q'}^\iota$ to be set to $true$.

Finally, the next constraint ensures that whenever $\mathcal A_\mathfrak M$ accepts u (i.e., the antecedent is $true$), then all words that lead to an accepting state in $\mathcal A$ also lead to an accepting state in $\mathcal A_\mathfrak M$ (i.e., the consequent is $true$):

$$\begin{aligned} \bigl ( \bigvee _{q \in Q}~ x_{u, q} \wedge f_q \bigr ) \rightarrow \bigl ( \bigwedge _{q \in Q}~ \bigwedge _{q' \in F_\mathcal A}~ y_{q, q'}^\iota \rightarrow f_q \bigr ) \end{aligned}$$

(8)

Let $\varphi _n^{ Ante ( Uni )}$ be the conjunction of Formulas (3), (4), and (5) as well as $\varphi _n^\iota$ the conjunction of Formulas (6), (7), and (8). Then, $\varphi _n^ Uni$ is the (finite) conjunction $\varphi _n^{ Ante ( Uni )} \wedge \bigwedge _{\iota \in Uni } \varphi _n^\iota$.

Correctness of the Learner. We now sketch the technical results necessary to prove the correctness of the learner—we refer the reader to the extended paper [22] for a detailed proof. First, we state that $\varphi _n^\mathcal S$ has the desired properties.

Lemma 2

Let $\mathcal S$ be a sample, $n \ge 1$, and $\varphi _n^\mathcal S$ be as defined above. Then, the following statements hold: (1) If $\mathfrak M \models \varphi _n^\mathcal S$, then $\mathcal A_\mathfrak M$ is a DFA with n states that is consistent with $\mathcal S$. (2) If there exists a DFA that has n states and is consistent with $\mathcal S$, then $\varphi _n^\mathcal S$ is satisfiable.

The next theorem states the correctness of Algorithm 2, which follows from Lemma 2 and the fact that n is increased by one until $\varphi _n^\mathcal S$ becomes satisfiable.

Theorem 1

Given a contradiction free-sample $\mathcal S$, Algorithm 2 returns a minimal DFA (in terms of the number of states) that is consistent with $\mathcal S$. If a minimal, consistent DFA has k states, then Algorithm 2 terminates after k iterations.

Finally, one can prove the correctness of our learner by using the facts that (a) the learner never conjectures a DFA twice as it always constructs minimal consistent DFAs, (b) conjectures grow in size, and (c) adding counterexamples to the sample does not rule out correct solutions.

Theorem 2

Given a teacher, Algorithm 1, equipped with Algorithm 2 to construct conjectures, terminates and returns a (minimal) DFA accepting a winning set if one exists.

6 Experiments

We implemented a Java prototype of our technique based on the Brics automaton library [17] and the Z3 [18] constraint solver.³ In addition to the learner of Sect. 5, we implemented a learner based on the popular RPNI algorithm [23], which is a polynomial time algorithm for learning DFAs from positive and negative words. For this learner, we modified the RPNI algorithm such that it constructs a consistent DFA from existential and universal implications in addition to positive and negative words (a detailed presentation can be found in the extended paper [22]). In contrast to Algorithm 2, this learner cannot guarantee to find smallest consistent DFAs and, hence, the resulting learner is a fast heuristic that is sound but in general not complete. Another limitation is that it can only handle implication counterexamples $(u, \mathcal A)$ where $L(\mathcal A)$ is finite. To accommodate this restriction, the arenas of the games used in the experiments are of finite out-degree (i.e., each vertex of an arena has a finite, but not necessarily bounded, number of outgoing edges). We refer to the learner of Sect. 5 as SAT learner and the RPNI-based learner as RPNI learner. As teacher, we implemented the generic teacher described in Sect. 4.

We conducted three series of experiments, all of which contain games that allow for small controllers. The first series serves to asses the performance of our techniques on games over infinite arenas. The second and third series compare our prototype to existing synthesis tools, namely GAVS+ [8] and TuLiP [24], on games over finite arenas. More precisely, in the second series, we consider motion planning problem in which an autonomous robot has to follow an entity through a fairly complex 2-dimensional grid-world, while the third series compares the scalability of different approaches on games of increasing size. We conducted all experiments on an Intel Core i7-4790K CPU running at 4.00 GHz with a memory limit of 16 GiB. We imposed a runtime limit of 300 s.

Games over Infinite Arenas. The first series of examples consists of the following games, which are predominantly taken from the area of motion planning.

• Diagonal game: A robot moves on a two-dimensional, infinite grid world. Player 0 controls the robot’s vertical movement, whereas Player 1 controls the horizontal movement. The players move in alternation, and, stating on the diagonal, Player 0 ’s objective is to stay inside a margin of two cells around the diagonal.

• Box game: A version of the diagonal game in which Player 0 ’s objective is to stay within a horizontal stripe of width three.

• Solitary box game: A version of the box game in which Player 0 is the only player and has control over both the horizontal and the vertical movement.

• Evasion game: Two robots, each controlled by one player, move in alternation on an infinite, two-dimensional grid. Player 0 ’s objective is to avoid a collision.

• Follow game: A version of the evasion game in which Player 0 ’s objective is to keep his robot within a distance of two cells to Player 1 ’s robot.

• Program-repair game: A finitely-branching version of the program-repair game described by Beyene et al. [3].

Table 1. Summary of results on games over infinite arenas.

Table 1 lists the overall runtimes (including the time taken by the teacher), the number of iterations, the number of states of the learned DFA, and the cardinality of each set of the final sample. As the table shows, the SAT learner computed the winning sets for all games, whereas the RPNI learner computed the winning sets for all but the Follow game. Since the RPNI learner does not compute minimal consistent DFAs, we expected that it is faster on average than the SAT learner, which turned out to be the case. However, the RPNI learner fails to solve the Follow game within the time limit.

It is worth noting that the teacher replied implication counterexamples in all but one experiment. This observation highlights that classical learning algorithms, which learn from positive and negative words only, are insufficient to learn winning sets (since the learning would be stuck at that point), and one indeed requires a richer learning framework.

Motion Planning. The motion planning example is designed to demonstrate the applicability of our techniques to motion planning problems in a fairly complex environment and compare it to mature tools. We considered an autonomous robot that has to follow some entity that is controlled by the environment through the (randomly generated) 2-dimensional $9 \times 9$ grid-world shown to the right (cells drawn black indicate obstacles that cannot be passed). More precisely, both the robot and the entity start at the same position and the robot’s objective is to maintain a Manhattan distance of at most 1 to the entity.

We modeled this game as rational safety game as well as for the tools TuLiP and GAVS+. The SAT learner solved the game in $7.8\,s$, the RPNI learner in $2.1\,s$, and TuLiP in $5.4\,s$. GAVS+ did not solve the game (it could only solve games on a $3 \times 3$ world).

Scalability. We compared the scalability of our prototype, GAVS+, TuLiP, as well as a simple fixed-point algorithm (using our automaton representation) on a slightly modified and finite version of the game of Example 1. In this modified game, the one-dimensional grid world consists of $m$ cells, of which all but the rightmost cell are safe. The movement of the robot is slight changed as well: the environment can move the robot to the right or stay; the system can move the robot to the left or stay, a move to the left, however, is only allowed on the first $\ell = \lfloor \frac{m}{2} \rfloor$ cells. As a result, any winning set is a subset of the cells smaller or equal than $\ell$. (In the case of TuLiP, we had to disallow Player 1 to stay for technical reasons; however, this does not change the described properties of the game.) Note that the number of states of the automata $\mathcal A_{V_0}$, $\mathcal A_{V_1}$, and $\mathcal A_F$ increase when $m$ increases as the automata need to count (in unary) to track the position of the robot. Moreover, note that this game is hard for algorithms based on fixed-point computations since a fixed point is reached no sooner than after at least $\ell$ steps.

Fig. 2.

Results of the scalability benchmark.

Figure 2 compares the runtimes of the various techniques for varying values of $m$ (the number of vertices of the resulting arena is roughly $2 m$). The RPNI learner performed best and solved games up to $m= 50\,000$ (about $100\,000$ vertices), while the SAT learner ranked second and solved game up to $m= 30\,000$. TuLiP, GAVS+, and the fixed-point algorithm, which all work with the complete, large arena (explicitly or symbolically), performed worse. The third-ranked algorithm TuLiP, for instance, solved games only up to $m= 10\,000$ and was one order of magnitude slower than the RPNI learner. Though designed for games over infinite arenas, these results demonstrate that our learning-based techniques perform well even on games over large finite arenas.

7 Conclusion

We developed an automata learning method to construct finite-state reactive controllers for systems whose interactions with their environment are modeled by infinite-state games. We focused on the practically interesting family of safety games, introduced a symbolic representation, developed specific implementations of learners and a teacher, and demonstrated the feasibility of the method on a set of problems motivated by robotic motion planning. Our experimental results promise applicability to a wide array of practically interesting problems.