A Symbolic Algorithm for Lazy Synthesis of Eager Strategies

Abstract

We present an algorithm for solving two-player safety games that combines a mixed forward/backward search strategy with a symbolic representation of the state space. By combining forward and backward exploration, our algorithm can synthesize strategies that are eager in the sense that they try to prevent progress towards the error states as soon as possible, whereas standard backwards algorithms often produce permissive solutions that only react when absolutely necessary. We provide experimental results for two new sets of benchmarks, as well as the benchmark set of the Reactive Synthesis Competition (SYNTCOMP) 2017. The results show that our algorithm in many cases produces more eager strategies than a standard backwards algorithm, and solves a number of benchmarks that are intractable for existing tools. Finally, we observe a connection between our algorithm and a recently proposed algorithm for the synthesis of controllers that are robust against disturbances, pointing to possible future applications.

1 Introduction

Automatic synthesis of digital circuits from logical specifications is one of the most ambitious and challenging problems in circuit design. The problem was first identified by Church [1]: given a requirement $\phi$ on the input-output behavior of a Boolean circuit, compute a circuit C that satisfies $\phi$. Since then, several approaches have been proposed to solve the problem [2, 3], which is usually viewed as a game between two players: the system player tries to satisfy the specification and the environment player tries to violate it. If the system player has a winning strategy for the game, then this strategy represents a circuit that is guaranteed to satisfy the specification. Recently, there has been much interest in approaches that leverage efficient data structures and automated reasoning methods to solve the synthesis problem in practice [4,5,6,7,8,9].

In this paper, we restrict our attention to safety specifications. In this setting, most of the successful implementations symbolically manipulate sets of states via their characteristic functions, represented as Binary Decision Diagrams (BDDs) [10]. The “standard” algorithm works backwards from the unsafe states and computes the set of all states from which the environment can force the system into these states. The negation of this set is the (maximal) winning region of the system, i.e., the set of all states from which the system can win the game. Depending on the specification, this algorithm may be suboptimal for two reasons: first, it may spend a lot of time on the exploration of states that are unreachable or could easily be avoided by the system player, and second, it may compute winning regions that include such states, possibly making the resulting strategy of controller more permissive and complicated than necessary. Additionally, for many applications it is preferable to generate strategies that avoid progress towards the error whenever possible, e.g., if the system should be tolerant to hardware faults or perturbations in the environment [11].

To keep the reachable state space small, some kind of forward search from the initial states is necessary. However, for forward search no efficient symbolic algorithm is known.

Contributions. In this work, we introduce a lazy synthesis algorithm that combines a forward search for candidate solutions with backward model checking of these candidates. All operations are such that they can be efficiently implemented with a fully symbolic representation of the state space and the space of candidate solutions. The combined forward/backward strategy allows us to find much smaller winning regions than the standard backward algorithm, and therefore produces less permissive solutions than the standard approach and solves certain classes of problems more efficiently.

We evaluate a prototype implementation of our algorithm on two sets of benchmarks, including the benchmark set of the Reactive Synthesis Competition (SYNTCOMP) 2017 [12]. We show that on many benchmarks our algorithm produces winning regions that are remarkably smaller: on the benchmark set from SYNTCOMP 2017, the biggest measured difference is by a factor of $10^{68}$. Moreover, it solves a number of instances that have not been solved by any participant in SYNTCOMP 2017.

Finally, we observe a relation between our algorithm and the approach of Dallal et al. [11] for systems with perturbations, and provide the first implementation of their algorithm as a variant of our algorithm. On the benchmarks above, we show that whenever a given benchmark admits controllers that give stability guarantees under perturbations, then our lazy algorithm will find a small winning region and can provide stability guarantees similar to those of Dallal et al. without any additional cost.

2 Preliminaries

Given a specification $\phi$, the reactive synthesis problem consists in finding a system that satisfies $\phi$ in an adversarial environment. The problem can be viewed as a game between two players, Player 0 (the system) and Player 1 (the environment), where Player 0 chooses controllable inputs and Player 1 chooses uncontrollable inputs to a given transition function. In this paper we consider synthesis problems for safety specifications: given a transition system that may raise a BAD flag when entering certain states, we check the existence of a function that reads the current state and the values of uncontrollable inputs, and provides valuations of the controllable inputs such that the BAD flag is not raised on any possible execution. We consider systems where the state space is defined by a set L of boolean state variables, also called latches. We write $\mathbb {B}$ for the set $\{0,1\}$. A state of the system is a valuation $q \in \mathbb {B}^L$ of the latches. We will represent sets of states by their characteristic functions of type $\mathbb {B}^L \rightarrow \mathbb {B}$, and similarly for sets of transitions etc.

Definition 1

A controllable transition system (or short: controllable system) TS is a 6-tuple $(L,X_u,X_c,$ $\mathcal {R}, BAD,q_0)$, where:

• L is a set of state variables for the latches

• $X_u$ is a set of uncontrollable input variables

• $X_c$ is a set of controllable input variables

• $\mathcal {R}:$ $\mathbb {B}^L \times \mathbb {B}^{X_u} \times \mathbb {B}^{X_c} \times \mathbb {B}^{L'} \rightarrow \mathbb {B}$ is the transition relation, where $L'=\{ l' ~|~ l \in L \}$ stands for the state variables after the transition

• $BAD: \mathbb {B}^L \rightarrow \mathbb {B}$ is the set of unsafe states

• $q_0$ is the initial state where all latches are initialized to 0.

We assume that the transition relation $\mathcal {R}$ of a controllable system is deterministic and total in its first three arguments, i.e., for every state $q \in \mathbb {B}^L$, uncontrollable input $u \in \mathbb {B}^{X_u}$ and controllable input $c \in \mathbb {B}^{X_c}$ there exists exactly one state $q' \in \mathbb {B}^{L'}$ such that $(q,u,c,q') \in \mathcal {R}$.

In our setting, characteristic functions are usually applied to a fixed vector of variables. Therefore, if $C: \mathbb {B}^L \rightarrow \mathbb {B}$ is a characteristic function, we write C as a short-hand for C(L). Characteristic functions of sets of states can also be applied to next-state variables $L'$, in that case we write $C'$ for $C(L')$.

Let $X=\{x_1,\ldots ,x_n\}$ be a set of boolean variables, and $Y \subseteq X\setminus \{x_i\}$ for some $x_i$. For boolean functions $F: \mathbb {B}^X \rightarrow \mathbb {B}$ and $f_{x_i}: \mathbb {B}^Y \rightarrow \mathbb {B}$, we denote by $F [x_i \leftarrow f_{x_i}]$ the boolean function that substitutes $x_i$ by $f_{x_i}$ in F.

Definition 2

Given a controllable system $TS=(L,X_u,X_c,\mathcal {R}, BAD,q_0)$, the synthesis problem consists in finding for every $x \in X_c$ a solution function $f_x: \mathbb {B}^L \times \mathbb {B}^{X_u} \rightarrow \mathbb {B}$ such that if we replace $\mathcal {R}$ by $\mathcal {R}[x \leftarrow f_x]_{x \in X_c}$, we obtain a safe system, i.e., no state in BAD is reachable.

If such a solution does not exist, we say the system is unrealizable.

To determine the possible behaviors of a controllable system, two forms of image computation can be used: (i) the image of a set of states C is the set of states that are reachable from C in one step, and the preimage are those states from which C is reachable in one step—in both cases ignoring who controls the input variables; (ii) the uncontrollable preimage of C is the set of states from which the environment can force the next transition to go into C, regardless of the choice of controllable variables. Formally, we define:

Definition 3

Given a controllable system $TS=(L,X_u,X_c,\mathcal {R}, BAD,q_0)$ and a set of states C, we have:

• $image(C) = \{q' \in \mathbb {B}^{L'} \mid \exists (q,u,c) \in \mathbb {B}^L \times \mathbb {B}^{X_u} \times \mathbb {B}^{X_c}: C(q) \wedge \mathcal {R}(q,u,c,q') \}$. We also write this set as $\exists L$ $\exists X_u$ $\exists X_{c}$ $(C \wedge \mathcal {R})$.

• $preimage(C) = \{q \in \mathbb {B}^L \mid \exists (u,c,q') \in \mathbb {B}^{X_u} \times \mathbb {B}^{X_c} \times \mathbb {B}^{L'}: C(q') \wedge \mathcal {R}(q,u,c,q')\}$. We also write this set as $\exists X_u$ $\exists X_{c}$ $\exists L'$ $(C' \wedge \mathcal {R})$.

• $UPRE(C) = \{ q \in \mathbb {B}^L \mid \exists u \in \mathbb {B}^{X_u}~\forall c \in \mathbb {B}^{X_c}~\exists q' \in \mathbb {B}^L: C(q') \wedge \mathcal {R}(q,u,c,q') \}$. We also write this set as $\exists X_u$ $\forall X_c$ $\exists L'$ $(C' \wedge \mathcal {R})$.

A direct correspondence of the uncontrollable preimage UPRE for forward computation does not exist: if the environment can force the next transition out of a given set of states, in general the states that we reach are not uniquely determined and depend on the choice of the system player.

Efficient symbolic computation. BDDs are a suitable data structure for the efficient representation and manipulation of boolean functions, including all operations needed for computation of image, preimage, and UPRE. Between these three, preimage can be computed most efficiently, while image and UPRE are more expensive—for image not all optimizations that are available for preimage can be used (see Sect. 5), and UPRE contains a quantifier alternation.

3 Existing Approaches

Before we introduce our new approach, we recapitulate three existing approaches and point out their benefits and drawbacks.

Backward fixpoint algorithm. Given a controllable transition system $TS=(L,X_u,X_c,\mathcal {R}, BAD,q_0)$ with BAD $\ne 0$, the standard backward BDD-based algorithm (see e.g. [10]) computes the set of states from which the environment can force the system into unsafe states in a fixed point computation that starts with the unsafe states themselves. To compute a winning region for Player 1, it computes the least fixed-point of UPRE on BAD :  $\mu C.~UPRE(BAD' \vee C')$.

Since safety games are determined, the complement of the computed set is the greatest winning region for Player 0, i.e., all states from which the system can win the game. Thus, this set also represents the most permissive winning strategy for the system player. We note two things regarding this approach:

• 1. To obtain a winning region, it computes the set of all states that cannot avoid moving into an error state, using the rather expensive UPRE operation.

• 2. The most permissive winning strategy will not avoid progress towards the error states unless we reach the border of the winning region.

A forward algorithm. [13, 14] A forward algorithm is presented by Cassez et al. [14] for the dual problem of solving reachability games, based on the work of Liu and Smolka [13]. The algorithm starts from the initial state and explores all states that are reachable in a forward manner. Whenever a state is visited, the algorithm checks whether it is losing; if it is, the algorithm revisits all reachable states that have a transition to this state and checks if they can avoid moving to a losing state. Although the algorithm is optimal in that it has linear time complexity in the state space, two issues should be taken into account:

• 1. The algorithm explicitly enumerates states and transitions, which is impractical even for moderate-size systems.

• 2. A fully symbolic implementation of the algorithm does not exist, and it would have to rely heavily on the expensive forward image computation.

Fig. 1.

High-level description of the lazy synthesis algorithm

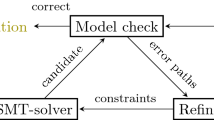
Lazy Synthesis. [15] Lazy Synthesis interleaves a backwards model checking algorithm that identifies possible error paths with the synthesis of candidate solutions. To this end, the error paths are encoded into a set of constraints, and an SMT solver produces a candidate solution that avoids all known errors. If new error paths are discovered, more constraints are added that exclude them. The procedure terminates once a correct candidate is found (see Fig. 1). The approach works in a more general setting than ours, for systems with multiple components and partial information. When applied to our setting and challenging benchmark problems, the following issues arise:

• 1. Even though the error paths are encoded as constraints, the representation is such that it explicitly branches over valuations of all input variables, for each step of the error paths. This is clearly impractical for systems that have more than a dozen input variables (which is frequently the case in the classes of problems we target).

• 2. In each iteration of the main loop a single deterministic candidate is checked. Therefore, many iterations may be needed to discover all error paths.

4 Symbolic Lazy Synthesis Algorithms

In the following, we present symbolic algorithms that are inspired by the lazy synthesis approach and overcome some of its weaknesses to make it suitable for challenging benchmark problems like those from the SYNTCOMP library. We show that in our setting, we can avoid the explicit enumeration of error paths. Furthermore, we can use non-deterministic candidate models that are restricted such that they avoid the known error paths. In this restriction, we prioritize the removal of transitions that are close to the initial state, which can help us avoid error paths that are not known yet.

Fig. 2.

High-level description of the symbolic lazy synthesis algorithm

4.1 The Basic Algorithm

To explain the algorithm, we need some additional definitions. Fix a controllable system $TS=(L,X_u,X_c,\mathcal {R}, BAD, q_0)$.

An error level $E_i$ is a set of states that are on a path from $q_0$ to BAD, and all states in $E_i$ are reachable from $q_0$ in i steps. Formally, $E_i$ is a subset of

$$ \{q_i \mid \exists (q_0,q_1,\ldots ,q_i,\ldots ,q_n), q_n \in BAD,\mathrm {~and~ }\exists (q_j,u,c,q_{j+1}) \in \mathcal {R}\mathrm {~for~}0 \le j < n\}. $$

We call $(E_0,...,E_n)$ a sequence of error levels if (i) each $E_i$ is an error level, (ii) each state in each $E_i$ has a transition to a state in $E_{i+1}$, and (iii) $E_n \subseteq BAD$. Note that the same state can appear in multiple error levels of a sequence, and $E_0$ contains only $q_0$.

Given a sequence of error levels $(E_0,...,E_n)$, an escape for a transition $(q,u,c,q')$ with $q \in E_i$ and $q' \in E_{i+1}$ is a transition $(q,u,c',q'')$ such that $q'' \not \in E_m$ $\forall m > i$. We say the transition $(q,u,c,q')$ matches the escape $(q,u,c',q'')$.

Given two error levels $E_i$ and $E_{i+1}$, we denote by $RT_i$ the following set of tuples, representing the “removable” transitions, i.e., all transitions from $E_i$ to $E_{i+1}$ that match an escape:

$$ RT_i=\{(q,u,q') \mid q \in E_i, q' \in E_{i+1} \text { and } \exists (q,u,c,q') \in \mathcal {R} \text { that has an escape} \}. $$

Overview. Figure 3 sketches the control flow of the algorithm. It starts by model checking the controllable system, without any restriction on the transition relation wrt. the controllable inputs. If unsafe states are reachable, the model checker returns a sequence of error levels. Iterating over all levels, we identify the transitions from the current level for which there exists an escape, and temporarily remove them from the transition relation. Based on the new restrictions on the transition relation, the algorithm then prunes the current error level by removing states that do not have transitions to the next level anymore. Whenever we prune at least one state, we move to the previous level to propagate back this information. If this eventually allows us to prune the first level, i.e., remove the initial state, then this error sequence has been invalidated and the new transition system (with deleted transitions) is sent to the model checker. Otherwise the system is unrealizable. In any following iteration, we accumulate information by merging the new error sequence with the ones we found before, and reset the transition relation before we analyze the error sequence for escapes.

Fig. 3.

Control flow of the algorithm

Detailed Description. In more detail, Algorithm 1 describes a symbolic lazy synthesis algorithm. The method takes as input a controllable system and checks if its transition relation can be fixed in a way that error states are avoided. Upon termination, the algorithm returns either unrealizable, i.e., the system can not be fixed, or a restricted transition relation that is safe and total. From such a transition relation, a (deterministic) solution for the synthesis problem can be extracted in the same way as for existing algorithms. Therefore, we restrict the description of our algorithm to the computation of the safe transition relation.

LazySynthesis: In Line 2, we initialize TR to the unrestricted transition relation $\mathcal {R}$ of the input system and E to the empty sequence, before we enter the main loop. Line 4 uses a model checker to check if the current TR is correct, and returns a sequence of error levels mcLvls if it is not. In more detail, function ModelCheck(TR) starts from the set of error states and uses the preimage function (see Definition 3) to iteratively compute a sequence of error levels.¹ It terminates if a level contains the initial state or if it reaches a fixed point. If the initial state was reached, the model checker uses the image function to remove from the error levels any state that is not reachable from the initial state.² Otherwise, in Line 6 we return the safe transition relation. If TR is not safe yet, Line 7 merges the new error levels with the error levels obtained in previous iterations by letting $E[i] \leftarrow E[i] \vee mcLvls[i]$ for every i. In Line 8 we call $PruneLevels(sys.\mathcal {R},E)$, which searches for a transition relation that avoids all error paths represented in E, as explained below. If pruning is not successful, in Lines 9–10 we return “Unrealizable”.

PruneLevels: In the first loop, we call ResolveLevel(E, i, TR) for increasing values of i (Line 4). Resolving a level is explained in detail below; roughly it means that we remove transitions that match an escape, and then remove states from this level that are not on an error path anymore. If ResolveLevel has removed states from the current level, indicated by the return value of isPrunable, we check whether we are at the topmost level—if this is the case, we have removed the initial state from the level, which means that we have shown that every path from the initial state along the error sequence can be avoided. If we are not at the topmost level, we decrement i before returning to the start of the loop, in order to propagate the information about removed states to the previous level(s). If isPrunable is false, we instead increment i and continue on the next level of the error sequence.

The first loop terminates either in Line 7, or if we reach the last level. In the latter case, we were not able to remove the initial state from E[0] with the local propagation of information during the main loop (that stops if we reach a level that cannot be pruned). To make sure that all information is completely propagated, afterwards we start another loop were we resolve all levels bottom-up, propagating the information about removed states all the way to the top. When we arrive at E[0], we can either remove the initial state now, or we conclude that the system is unrealizable.

ResolveLevel: Line 2 computes the set of transitions that have an escape: $\exists L'$ ( ( $\exists X_c$ TR $) \wedge \lnot E[i+1 : n]'$ ) is the set of all (q, u) for which there exists an escape $(q,u,c,q')$, and by conjoining $E[i] \wedge E[i+1]'$ we compute all tuples $(q,u,q')$ that represent transitions from E[i] to $E[i+1]$ matching an escape. Line 3 removes the corresponding transitions from the transition relation TR. Line 4 computes AvSet which represents the set of all states such that all their transitions within the error levels match an escape. After removing AVSet from the current level, we return.

Comparison. Compared to Lazy Synthesis (see Fig. 1), the main loop of our algorithm merges the Refine and Solve steps, and instead of computing one deterministic model per iteration, we collect restrictions on the non-deterministic transition relation TR. Keeping TR non-deterministic allows us to find and exclude more error paths per iteration.

Compared to the standard backward fixpoint approach (see Sect. 3), an important difference is that we explore the error paths in a forward analysis starting from the initial state, and avoid progress towards the error states as soon as possible. As a consequence, our algorithm can find solutions that visit only a small subset of the state space. If such solutions exist, our algorithm will find a solution faster and will detect a winning region that is much smaller than the maximal winning region detected by the standard algorithm.

4.2 Correctness of Algorithm 1

Theorem 1

(Soundness). Every transition relation returned by Algorithm 1 is safe, and total in the first two arguments.

Proof

The model checker guarantees that the returned transition relation TR is safe, i.e., unsafe states are not reachable. To see that TR is total in the first two arguments, i.e., $\forall q\ \forall u\ \exists c\ \exists q': (q,u,c,q') \in TR$, observe that this property holds for the initial TR, and is preserved by ResolveLevels: lines 2 and 3 ensure that a transition $(q,u,c,q') \in TR$ can only be deleted if $\exists c'~ \exists q''\ne q': (q,u,c',q'') \in TR$, i.e., if there exists another transition with the same state q and uncontrollable input u.

To prove completeness of the algorithm, we define formally what it means for an error level to be resolved.

Definition 4

(Resolved). Given a sequence of error levels $E=(E_0,...,E_n)$ and a transition relation TR, an error level $E_i$ with $i < n$ is resolved with respect to TR if the following conditions hold:

• $RT_i = \emptyset$

• $\forall q_i \in E_i \setminus BAD:\ \exists u\ \exists c\ \exists q_{i+1} \in E_{i+1}:\ (q_i,u,c,q_{i+1}) \in TR$

$E_i$ is unresolved otherwise, and $E_n$ is always resolved.

Informally, $E_i$ is resolved if all transitions from $E_i$ that match an escape have been removed from TR, and every state in $E_i$ can still reach $E_{i+1}$.

Theorem 2

(Completeness). If the algorithm returns “Unrealizable”, then the controllable system is unrealizable.

Fig. 4.

Error levels from iteration 1

Fig. 5.

solution for iteration 1

Proof

Observe that if a controllable system is unrealizable, then there exists an error sequence $E=(E_0=\{q_0\},E_1,...,E_n)$ where all levels are resolved and non-empty. Lines 2 and 3 of ResolveLevel guarantee that all transitions from $E_i$ to $E_{i+1}$ that match an escape will be deleted, so the only remaining transitions between $E_i$ and $E_{i+1}$ are those that have no escapes. Line 4 computes all states in $E_i$ that have no more transitions to $E_{i+1}$ and line 5 removes these states. Thus, after calling ResolveLevel, the current level will be resolved.

However, since ResolveLevel may remove states from $E_i$, the levels $E_j$ with $j<i$ could become unresolved. To see that this is not an issue note that before we output Unrealizable, we go through the second loop that resolves all levels from n to 0. After execution of this second loop all levels are resolved, and if $E_0$ still contains $q_0$, then the controllable system is indeed unrealizable, since from our sequence of error levels we can extract a subsequence of resolved and non-empty error levels.³

Theorem 3

(Termination). Algorithm 1 always terminates.

Proof

Termination is guaranteed due to the fact that there is a finite number of possible transition relations, and each call to PruneLevels either produces a TR that is different from all transition relations that we have seen before, or terminates with isUnrealizable.

4.3 Illustration of the Algorithm

Figure 4 shows error levels obtained from the model checker. The transitions are labeled with vectors of input bits, where the left bit is uncontrollable and the right bit controllable. The last level is a subset of BAD. After the first iteration of the algorithm, the transitions that are dashed in Figure 5 will be deleted. Note that another solution exists where instead we delete the two outgoing transitions from level $E_1$ to the error level Err. This solution can be obtained by a backward algorithm. However, our solution makes all states in $E_1$ unreachable and thus we detect smaller winning region.

In the second iteration, the model checker uses the restricted transition relation and computes a new sequence of error levels. This sequence is merged with the previous one and the resulting sequence will be resolved as before.

4.4 Example Problems

We want to highlight the potential benefit of our algorithm on two families of examples.

Fig. 6.

Example with small solution

Fig. 7.

Example that is solved fast

First, consider a controllable system where all paths from the initial state to the error states have to go through a bottleneck, e.g., a single state, as depicted in Fig. 6, and assume that Player 0 can force the system not to go beyond this bottleneck. In this case, our algorithm will have a winning region that only includes the states between the initial state and the bottleneck, whereas the standard algorithm may have a much bigger winning region (in the example including all the states in the fourth row). Moreover, the strategy produced by our algorithm will be very simple: if we reach the bottleneck, we force the system to stay there. In contrast, the strategy produced by the standard algorithm will in general be much more complicated, as it has to define the behavior for a much larger number of states.

Second, consider a controllable system where the shortest path between error and initial state is short, but Player 1 can only force the system to move towards the error on a long path. Moreover, assume that Player 0 can avoid entering this long path, for example by entering a separated part of the state space like depicted in Fig. 7. In this case, our algorithm will quickly find a simple solution: move to that separate part and stay there. In contrast, the standard algorithm will have to go through many iterations of the backwards fixpoint computation, until finally finding the point where moving into the losing region can be avoided.

5 Optimization

As presented, Algorithm 1 requires the construction of a data structure that represents the full transition relation $\mathcal {R}$, which causes a significant memory consumption. In practice, the size of a BDD that represents the full transition relation can be prohibitive even for moderate-size models.

As the transition relation is deterministic, it can alternatively be represented by a vector of functions, each of which updates one of the state variables. Such a partitioning of the transition relation is an additional computational effort, but it results in a more efficient representation that is necessary to handle large systems. In the following we describe optimizations based on such a representation.

Definition 5

A functional controllable system is a 6-tuple $TS_f =(L,X_u,$ $X_c,\mathbf {F}, BAD,q_0)$, where $\mathbf {F} = (f_1,...,f_{|L|})$ with $f_i: \mathbb {B}^L \times \mathbb {B}^{X_u} \times \mathbb {B}^{X_c} \rightarrow \mathbb {B}$ for all i, and all other components are as in Definition 1.

In a functional system with current state q and inputs u and c, the next-state value of the ith state variable $l_i$ is computed as $f_i(q,u,c)$. Thus, we can compute image and preimage of a set of states C in the following way:

• $image_f(C) = \exists L$ $\exists X_u$ $\exists X_c$ $(\bigwedge _{i=1}^{|L|} l_i' \equiv f_i \wedge C)$

• $preimage_f(C) = \exists L'$ $\exists X_u$ $\exists X_c$ $(\bigwedge _{i=1}^{|L|} l_i' \equiv f_i \wedge C')$

However, computing $\bigwedge _{i=1}^{|L|} l_i' \equiv f_i \wedge C'$ is still very expensive and might be as hard as computing the whole transition relation. To optimize the preimage computation, we instead directly substitute the state variables in the boolean function that represents C by the function that computes their new value:

$$ preimage_s(C) = \exists X_u~\exists X_c~C[l_i \leftarrow f_i]_{l_i \in L} $$

For the computation of image(C), substitution cannot be used. While alternatives exist (such as using the range function instead [16]), image computation remains much more expensive than preimage computation.

5.1 The Optimized Algorithm

The optimized algorithm takes as input a functional controllable system, and uses the following modified procedures:

OptimizedLazySynthesis: This procedure replaces LazySynthesis, with two differences, both in the model checker: the preimage is computed using $preimage_s$, and unreachable states are not removed, in order to avoid image computation. Thus, the error levels are over-approximated.

OptimizedResolveLevel: This procedure replaces ResolveLevel and computes RT and AvSet more efficiently. Note that for a given set of states C, the set $pretrans(C) = \{(q,u,c) \in \mathbb {B}^L \times \mathbb {B}^{X_u} \times \mathbb {B}^{X_c} \mid \mathbf {F}(q,u,c) \in C\}$ can efficiently be computed as $C[l_i \leftarrow f_i]_{l_i \in L}$. Based on this, we get the following:

RT: To compute the transitions that can be avoided, we compute the conjunction of the transitions from $E_i$ to $E_{i+1}$ as $pretrans(E[i+1]') \wedge E[i]$ with those transitions that have an escape: $\exists c$ $pretrans(\lnot E[i+1 : n]') \wedge E[i]$.

AvSet: The states that can avoid all transitions to the lower levels can now be computed as $\forall u$ [ $\exists c$ $pretrans(\lnot E[i+1 : n]') \wedge E[i]$ ].

Generalized Deletion of Transitions. In addition, we consider a variant of our algorithm that uses the following heuristic to speed up computation: whenever we find an escape $(q,u,c,q')$ with $q \in E_i$, then we not only remove all matching transitions that start in $E_i$, but matching transitions that start anywhere, and lead to a state $q'' \in E_j$ with $j>i$. Thus, we delete more transitions per iteration of the algorithm, all of which are known to lead to an error.

6 Experimental Evaluation

We implemented our algorithm in Python, using the BDD package CUDD [17]. We evaluate our prototype on a family of parameterized benchmarks based on the examples in Sect. 4.4, and on the benchmark set of SYNTCOMP 2017 [12]. We compare two versions of our algorithm (with and without generalized deletion as explained in Sect. 5.1) against a re-implementation of the standard backward approach, in order to have a fair comparison between algorithms that use the same BDD library and programming language. For the SYNTCOMP benchmarks, we additionally compare against the results of the participants in SYNTCOMP 2017. Our implementations of all algorithms include the most important general optimizations for this kind of algorithms, including a functional transition relation and automatic reordering of BDDs (see Jacobs et al. [10]).

6.1 Parameterized Benchmarks

On the parameterized versions of the examples from Sect. 4.4, we observe the expected behaviour:

• for the first example, the winning region found by our algorithm is always about half as big as the winning region for the standard algorithm. Even more notable is the size of the synthesized controller circuit: for example, our solution for an instance with $2^{18}$ states and 10 input variables has a size of just 9 AND-gates, whereas the solution obtained from the standard algorithm has 800 AND-gates.

• for the second example, we observe that for systems with 15–25 state variables, our algorithm solves the problem in constant time of 0.1s, whereas the solving time increases sharply for the standard algorithm: it uses 1.7s for a system with 15 latches, 92s for 20 latches, and 4194s for 25 latches.

6.2 SYNTCOMP Benchmarks

We compared our algorithm against the standard algorithm on the benchmark set that was used in the safety track of SYNTCOMP 2017, with a timeout of 5000 s on an Intel Xeon processor (E3-1271 v3, 3.6 GHz) and 32 GB RAM.

First, we observe that our algorithms often produce much smaller winning regions: out of the 76 realizable benchmarks that our algorithm without general deletion solved, we found a strictly smaller winning region than the standard backwards algorithm in 28 cases. In 14 cases, the winning region is smaller by a factor of $10^3$ or more, in 8 cases by a factor of $10^{20}$ or more, and in 4 cases by a factor of $10^{30}$ or more. The biggest difference in winning region size is a factor of $10^{68}$. A selection of results for such benchmarks is given in Table 1. Note that these results are for the algorithm without the generalized deletion heuristic; when using the algorithm with generalized deletion, our winning regions are somewhat bigger, but the tendency is the same. Regarding the size of synthesized circuits, the results are mixed: our solutions are often much smaller, but in several cases they are also of bigger or equal size.

Table 1. Comparison of Winning Region Size for Selected Benchmarks

Regarding solving time, out of the 234 benchmarks our algorithm without generalized deletion solved 99 before the timeout, and the version with the generalized deletion heuristic solved 116. While the standard algorithm solves a higher number of instances overall (163), for a number of examples the lazy algorithms are faster. In particular, both versions each solve 7 benchmarks that are not solved by the standard algorithm, as shown in Table 2.

Moreover, we compare against the participants of SYNTCOMP 2017: with a timeout of 3600 s, the best single-threaded solver in SYNTCOMP 2017 solved 155 problems, and the virtual best solver (VBS; i.e., a theoretical solver that on each benchmark performs as good as the best participating solver) would have solved 186 instances. If we include our two algorithms with a timeout of 3600 s, the VBS can additionally solve 7 out of the 48 instances that could not be solved by any of the participants of SYNTCOMP before. As our algorithms also solve some instances much faster than the existing algorithms, they would be worthwhile additions to a portfolio solver for SYNTCOMP.

Table 2. Benchmarks solved uniquely by the Lazy algorithm

7 Synthesis of Resilient Controllers

As mentioned in Sect. 1, our algorithm produces strategies that avoid progress towards the error states as early as possible, which could be useful for generating controllers that are tolerant to faults or perturbations. Dallal et al. [11] have modeled systems with perturbations, which are defined essentially as extraordinary transitions where Player 1 chooses values for both the uncontrollable and (a subset of) the controllable inputs. They introduced an algorithm that produces strategies with maximal resilience against such perturbations, defined as the number of perturbations under which the controller can still guarantee not to enter the winning region of Player 1.

The algorithm of Dallal et al. can be seen as a variant of our algorithm, except that it first uses the standard fixpoint algorithm to determine the winning region, and then uses a mixed forward/backward search to find a strategy that makes as little progress towards the losing region as possible. We have implemented this as a variant of our algorithm, providing to our knowledge its first implementation. An evaluation on the SYNTCOMP benchmarks provides interesting insights: only on 6 out of the 234 benchmarks the algorithm can give a guarantee of resilience against one or more perturbations. Moreover, when inspecting the behavior of our lazy algorithms on these benchmarks, we find that for all of them they provide a strictly smaller winning region than the standard algorithm. 5 of the 6 benchmarks appear in Table 1, with winning regions that are smaller by a factor of $10^9$ or more. In fact, for these benchmarks our algorithm can give a similar guarantee as the Dallal algorithm, without additional cost. The difference is that we measure the distance to the error states instead of the distance to the losing region (which is not known to us). This leads us to the conjecture that our algorithm performs particularly well on synthesis problems that allow resilient controllers, together with the observation that not many of these appear in the SYNTCOMP benchmark set that we have tested against.

8 Conclusions

We have introduced lazy synthesis algorithms with a novel combination of forward and backward exploration. Our experimental results show that our algorithms find much smaller winning regions in many cases. Moreover, they can solve a number of problems that are intractable for existing synthesis algorithms, both from our own examples and from the SYNTCOMP benchmark set.

In the future, we want to explore how lazy synthesis can be integrated into portfolio solvers and hybrid algorithms. Additionally, we want to further explore the applications of eager strategies in the synthesis of resilient controllers [11, 18,19,20] and connections to lazy algorithms for controllers of cyber-physical systems [21].