Photonic Neuromorphic Signal Processing and Computing

Abstract

There has been a recent explosion of interest in spiking neural networks (SNNs), which code information as spikes or events in time. Spike encoding is widely accepted as the information medium underlying the brain, but it has also inspired a new generation of neuromorphic hardware. Although electronics can match biological time scales and exceed them, they eventually reach a bandwidth fan-in trade-off. An alternative platform is photonics, which could process highly interactive information at speeds that electronics could never reach. Correspondingly, processing techniques inspired by biology could compensate for many of the shortcomings that bar digital photonic computing from feasibility, including high defect rates and signal control problems. We summarize properties of photonic spike processing and initial experiments with discrete components. A technique for mapping this paradigm to scalable, integrated laser devices is explored and simulated in small networks. This approach promises to wed the advantageous aspects of both photonic physics and unconventional computing systems. Further development could allow for fully scalable photonic networks that would open up a new domain of ultrafast, robust, and adaptive processing. Applications of this technology ranging from nanosecond response control systems to fast cognitive radio could potentially revitalize specialized photonic computing.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

8.1 Introduction

The brain, unlike the von Neumann processors found in conventional computers, is very power efficient, extremely effective at certain computing tasks, and highly adaptable to novel situations and environments. While these favorable properties are often largely credited to the unique connectionism of biological nervous systems, it is clear that the cellular dynamics of individual neurons also play an indispensable role in attaining these performance advantages. On the cellular level, neurons operate on information encoded as events or spikes, a type of signal with both analog and digital properties. Spike processing exploits the efficiency of analog signals while overcoming the problem of noise accumulation inherent in analog computation, which can be seen as a first step to attaining the astounding capabilities of bio-inspired processing [1]. Other physical and signal processing features at the single neuron level, including hybrid analog-digital signals, representational interleaving, co-location of memory and processing, unsupervised statistical learning, and distributed representations of information, have been implicated in various positive and conventionally impossible signal processing capabilities. Engineers have tried for nearly half a century to take inspiration from neuroscience by separating key properties that yield performance from simple idiosyncrasies of biology.

If some biological properties are distilled while others deemed irrelevant, then a bio-inspired engineered system could also incorporate nonbiological properties that may lead to computational domains that are potentially unexplored and/or practically useful. Many microelectronic platforms have attempted to emulate some advantages of neuron-like architectures while incorporating techniques in technology; however, the majority target rather than exceed biological time scales. What kind of signal processing would be possible with a bio-inspired visual front-end that operates ten million times faster than its biological counterpart? Unfortunately, microelectronic neural networks that are both fast and highly interconnected are subject to a fundamental bandwidth connection-density tradeoff, keeping their speed limited.

Photonic platforms offer an alternative approach to microelectronics. The high speeds, high bandwidth, and low cross-talk achievable in photonics are very well suited for an ultrafast spike-based information scheme with high interconnection densities. In addition, the high wall-plug efficiencies of photonic devices may allow such implementations to match or eclipse equivalent electronic systems in low energy usage. Because of these advantages, photonic spike processors could access a picosecond, low-power computational domain that is inaccessible by other technologies. Our work aims to synergistically integrate the underlying physics of photonics with bio-inspired spike-based processing. This novel processing domain of ultrafast cognitive computing could have numerous applications where quick, temporally precise and robust systems are necessary, including: adaptive control, learning, perception, motion control, sensory processing, autonomous robotics, and cognitive processing of the radio frequency spectrum.

In this chapter, we consider the system implications of wedding a neuron-inspired computational primitive with the unique device physics of photonic hardware. The result is a system that could emulate neuromorphic algorithms at rates millions of times faster than biology, while also overcoming both the scaling problems of digital optical computation and the noise accumulation problems of analog optical computation by taking inspiration from neuroscience. Our approach combines the picosecond processing and switching capabilities of both linear and nonlinear optical device technologies to integrate both analog and digital optical processing into a single hardware architecture capable of ultrafast computation without the need for conversion from optical signals to electrical currents. With this hybrid analog-digital processing primitive, it will be possible to implement processing algorithms of far greater complexity than is possible with existing optical technologies, and far higher bandwidth than is possible with existing electronic technologies.

The design and implementation of our devices is based upon a well-studied and paradigmatic example of a hybrid computational primitive: the spiking neuron. These simple computational elements integrate a small set of basic operations (delay, weighting, spatial summation, temporal integration, and thresholding) into a single device which is capable of performing a variety of computations depending on how its parameters are configured (e.g., delays, weights, integration time constant, threshold). The leaky-integrate-and-fire (LIF) neuron model is a mathematical model of the spiking dynamics which pervade animal nervous systems, well-established as the most widely used model of biological neurons in theoretical neuroscience for studying complex computation in nervous systems [2]. LIF neurons have recently attracted the attention of engineers and computer scientists for the following reasons:

• Algorithmic Expressiveness: They provide a powerful and efficient computational primitive from the standpoint of computational complexity and computability theory;

• Hardware Efficiency/Robustness: They are both robust and efficient processing elements. Complex algorithms can be implemented with less hardware;

• Utility in signal processing: There are known pulse processing algorithms for complex signal processing tasks (drawn from neuro-ethology). Pulse processing is already being used for implementing robust sensory processing algorithms in analog VLSI.

After comparing the fundamental physical traits of electronic and photonic platforms for implementation of neuromorphic architectures, this chapter will present a detailed cellular processing model (i.e. LIF) and describe the first emulation of this model in ultrafast fiber-optic hardware. Early experiments in photonic learning devices, critical for controlling the adaptation of neural networks, and prototypical demonstrations of simple bio-inspired circuits will be discussed. Recent research has sought to develop a scalable neuromorphic primitive based on the dynamics of semiconductor lasers which could eventually be integrated in very large lightwave neuromorphic systems on a photonic chip. This chapter will focus on the computational primitive, how it can be implemented in photonics, and how these devices interact with input and output signals; a detailed account of the structure and implementation of a network that can link many of these devices together is beyond the scope of this chapter.

8.2 Neuromorphic Processing in Electronics and Photonics

The harmonious marriage of a processing paradigm to the physical behaviors that bear it represents an important step in efficiency and performance over approaches that aim to abstract physics away entirely. Both thalamocortical structures observed in biology and emerging mathematical models of network information integration exhibit a natural separation of computation and communication. Computation rarely takes place in the axons of a neuron, but these communication pathways and their rich configurability are crucial for the informatic complexity of the network as a whole. Because of their favorable communication properties (i.e. low dispersion, high bandwidth, and low cross-talk), photonic spiking network processors could access a computationally rich and high bandwidth domain that is inaccessible by other technologies. This domain, which we call ultrafast cognitive computing, represents an unexplored processing paradigm that could have a wide range of applications in adaptive control, learning, perception, motion control, sensory processing (vision systems, auditory processors, and the olfactory system), autonomous robotics, and cognitive processing of the radio frequency spectrum.

Currently developing cortically-inspired microelectronic architectures including IBM’s neurosynaptic core [3, 4] and HP’s proposed memristive nanodevices [5, 6] use a dense mesh of wires called a crossbar array to achieve heightened network configurability and fan-in, which are less critical in conventional architectures. These architectures aim to target clock rates comparable to biological time scales rather than exceed them. At high-bandwidths, however, densely packed electronic wires cease to be effective for communication. Power use increases drastically, and signals quickly attenuate, disperse, or couple together unfavorably, especially on a crossbar array, which has a large area of closely packed signal wires. In contrast, photonic channels can support the high bandwidth components of spikes without an analogous speed, power, fan-in, and cross-talk trade-off.

Optical neural networks based on free space and fiber components have been explored for interconnection in the past, but undeveloped fiber-optic and photonic technologies in addition to scalability limitations of particular strategies (e.g. diffraction limit, analog noise accumulation) relegated these systems to small laboratory demonstrations [7–9]. Optical processing elements and lasers were not realistically available for use as fast computational primitives, so the ultrafast domain where optics fundamentally dominates microelectronics was never fully considered. Perhaps as culpable in the initial failure of optical neural networks was the sparsity of neurocomputational theories based on spike timing. The current states of photonic technology and computational neuroscience have matured enormously and are ripe for a new breed of photonic neuromorphic research.

8.3 Photonic Spike Processing

Optical communication has extensively utilized the high bandwidth of photonics, but, in general, approaches to optical computing have been hindered by scalability problems. We hypothesize that the primary barrier to exploiting the high bandwidth of photonic devices for computing lies in the model of computation being used, not solely in the performance, integration, or fabrication of the devices. Many years of research have been devoted to photonic implementation of traditional models of computation, yet neither analog nor digital approaches has proven scalable due primarily to challenges of cascadability and fabrication reliability. Analog photonic processing has found widespread application in high bandwidth filtering of microwave signals, but the accumulation of phase noise, in addition to amplitude noise, makes cascaded operations particularly difficult. Digital logic gates that suppress noise accumulation have also been realized in photonics, but photonic devices have not yet met the extremely high fabrication yield required for complex digital operations, a tolerance requirement that is greatly relaxed in systems capable of biomorphic adaptation. In addition, schemes that take advantage of the multiple available wavelengths require ubiquitous wavelength conversion, which can be costly, noisy, inefficient, and complicated.

The optical channel is highly expressive and correspondingly very sensitive to phase and frequency noise. Any proposal for a computational primitive must address the issue of practical cascadability, especially if multiple wavelength channels are intended to be used. Our proposed unconventional computing primitive addresses the traditional problem of noise accumulation by interleaving physical representations of information. Representational interleaving, in which a signal is repeatedly transformed between coding schemes (digital-analog) or physical variables (electronic-optical), can grant many advantages to computation and noise properties. For example, a logarithm transform can reduce a multiplication operation to a simpler addition operation. As discussed in Sect. 8.3.1, the spiking model found in biology naturally interleaves robust, discrete representations for communication signals with precise, continuous representations for computation variables in order to leverage the benefits of both types of coding. It is natural to deepen this distinction to include physical representational aspects, with the important result that optical noise does not accumulate. When a pulse is generated, it is transmitted and routed through a linear optical network with the help of its wavelength identifier. It is received only once into a fermionic degree of freedom, such as a deflection of carrier concentration in a photonic semiconductor or a current pulse in a photodiode. The soma tasks occur in a domain that is in some ways computationally richer (analog) and in other ways more physically robust (incoherent) to the type of phase and frequency noise that can doom optical computing architectures.

Another major hurdle faced by substantial photonic systems is relatively poor device yield. While difficult for digital circuits to build in redundancy overhead, neuromorphic systems are naturally reconfigurable and adaptive. Biological nervous systems adapt to shunt signals around faulty neurons without the need for external control. The structural fluidity of neural algorithms will itself provide an effective resistance against fabrication defects.

Fig. 8.1

Spiking neural networks encode information as events in time rather than bits. Because the time at which a spike occurs is analog while its amplitude is digital, the signals use a mixed-signal or hybrid encoding scheme

Fig. 8.2

Comparison of digital, analog, and hybrid systems in terms of robustness, expressiveness, power efficiency, and bandwidth limiter

8.3.1 Spiking Signals

On the cellular level, the brain encodes information as events or spikes in time [10], "hybrid signals" with both analog and digital properties as illustrated in Fig. 8.1. Spike processing has evolved in biological (nervous systems) and engineered (neuromorphic analog VLSI) systems using LIF neurons as processing primitives that encode data in the analog timing of spikes as inputs. Through its fine grained interleaving of analog and digital processing, it provides the means for achieving scalable high bandwidth photonic processing by overcoming both the analog noise accumulation problem [1] and the bandwidth inefficiency of digital processing. These unique properties of the spike processing model of computation enable a hybrid analog and digital approach that will allow photonics hardware to scale its processing complexity and efficiency. The foregoing discussion is summarized in Fig. 8.2 which compares digital, analog, and hybrid systems in terms of robustness, expressiveness, power efficiency, and the characteristic property that determines usable bandwidth. Spiking signals, which in addition to being inherently advantageous, carry information in a natural and accessible fashion that forms the very foundation of some of the astounding capabilities of systems studied in neuroscience.

8.3.2 Spike Processor: Computational Primitive

Like a gate in a digital computer, a spike processor serves as the baseline unit of larger interconnected networks that can perform more complex computations. There are five key computational properties to consider: (1) integration, the ability to sum and integrate both positive and negative weighted inputs over time; (2) thresholding, the ability to make a decision whether or not to send a spike; (3) reset, the ability to have a small refractory period during which no firing can occur immediately after a spike is released; (4) pulse generation, the ability to generate new pulses; and (5) adaptability, the ability to modify and regulate response properties on slow timescales based on statistical properties of environmental inputs and/or training.

These five properties all play important roles in the emulation of the widely accepted neurocomputational primitive, the LIF neuron. This model is more computationally powerful than either the rate or the earlier perceptron models [11], and can serve as the baseline unit for many modern cortical algorithms [12–14]. Although not every property is needed to do constrained useful computations, each one serves an important purpose to assure a high level of richness and robustness in the overall computational repertoire.

Integration is a temporal generalization of summation in older perceptron-based models. Spikes with varying amplitudes and delays arrive at the integrator, changing its state by an amount proportional to their input amplitudes. Excitatory inputs increase its state, while inhibitory inputs deplete it. The integrator is especially sensitive to spikes that are closely clustered in time or with high amplitudes, the basic functionality of temporal summation. Eventually, the state variable will decay to its equilibrium value without any inputs. Both the amplitude and timing play an important role for integration.

Thresholding determines whether the output of the integrator is above or below a predetermined threshold value, $T$. The neuron makes a decision based on the state of the integrator, firing if the integration state is above the threshold. Thresholding is the center of nonlinear decision making in a spiking system, which reduces the dimensionality of incoming information in a useful fashion and plays a critical role in cleaning up amplitude noise that would otherwise cause the breakdown of analog computation.

The reset condition resets the state of the integrator to a low, rest value immediately after a spike processor fires, causing a refractory period in which it is impossible or difficult to cause the neuron to fire again. It plays the same role in time as the thresholder does for amplitude, cleaning up timing jitter and preventing the temporal spreading of excitatory activity while putting a bandwidth cap on the output of a given spiking unit. It is additionally a necessary component for simulating the rate model of neural computation with spiking neurons.

Pulse generation refers to the ability for a system to spontaneously generate pulses. If pulses are not regenerated as they travel through systems, they will eventually be lost in noise. A system with this property can generate pulses without the need to trigger on input pulses whenever the integrator’s state variable reaches the threshold, $T$, which is crucial for simulating the rate model.

Table 8.1 Spiking neural automata properties

Table 8.2 Fabricating LIF neurons requires photonic elements

Adaptability is the network’s ability to change to better suit changing environmental and system conditions. Adaptation of network parameters typically occurs on time scales much slower than spiking dynamics and can be separated into either unsupervised learning, where alterations in overall signal statistics cause automatic adjustments, or supervised learning, where changes are guided based on the behavior of the system compared to a desired behavior presented by a teacher. Because of the extreme reconfigurability and fluidity of massively parallel neural networks, adaptation rules are necessary to stabilize the system’s structure and accomplish a desired task. Adaptation also corrects catastrophic system alterations by, for example, routing signals around a failed neuron to maintain overall process integrity.

The characteristics mentioned above are summarized in Table 8.1. In summary, (1) and (4) provide key properties of a system that is the basis of asynchronous communication, while (2) and (3) clean up amplitude and temporal noise, respectively, to allow for cascadability. Any processor designed to closely emulate LIF neurons should have all five properties.

In photonics, the challenge of creating a flexible, scalable, and efficient native hardware implementation of the spike processing model of computation lies in the design of the critical, programmable component devices of the LIF neuron. The ability of the LIF to perform matched filtering, dimensionality reduction, evidence accumulation, decision making, and communication of results requires analog, tunable component hardware elements as described in Table 8.2. These parts must perform adjustable operations and demonstrate configurable interconnectivity between large numbers of LIF neurons.

The weights and delays of the matched filter are applied at the interconnection of two LIF neurons and form a complicated junction that acts as the primary communications between the spiking elements. These interconnection controls are a key feature of the LIF and must be capable of rapid read and write reconfigurability and adjustability either through direct programming or through learning algorithms like spike timing dependent plasticity (STDP).

In the next section we review the LIF neuron model which is a mathematical model of the spiking neuron primitive.

8.4 Spiking Neuron Model

Our devices are based upon a well-studied and paradigmatic example of a hybrid computational primitive: the spiking neuron. Studies of morphology and physiology have pinpointed the LIF model as an effective spiking model to describe a variety of different biologically observed phenomena [2]. From the standpoint of computability and complexity theory, LIF neurons are powerful and efficient computational primitives that are capable of simulating both Turing machines and traditional sigmoidal neural networks [15]. These units perform a small set of basic operations (delaying, weighting, spatial summation, temporal integration, and thresholding) that are integrated into a single device capable of implementing a variety of processing tasks, including binary classification, adaptive feedback, and temporal logic.

Fig. 8.3

a Schematic and b operation of a leaky integrate-and-fire neuron. Weighted and delayed input signals are summed onto the soma, which integrates them together and makes a spike or no-spike decision. The resulting spike is sent to other neurons in the network

The basic biological structure of a LIF neuron is depicted in Fig. 8.3a. It consists of a dendritic tree that collects and sums inputs from other neurons, a soma that acts as a low pass filter and integrates the signals over time, and an axon that carries an action potential, or spike, when the integrated signal exceeds a threshold. Neurons are connected to each other via synapses, or extracellular gaps, across which chemical signals are transmitted. The axon, dendrite, and synapse all play an important role in the weighting and delaying of spike signals.

According to the standard LIF model, neurons are treated as an equivalent electrical circuit. The membrane potential $V_m(t)$, the voltage difference across their membrane, acts as the primary internal (activation) state variable. Ions that flow across the membrane experience a resistance $R=R_m$ and capacitance $C=C_m$ associated with the membrane. The soma is effectively a first-order low-pass filter, or a leaky integrator, with the integration time constant $\tau _m=R_mC_m$ that determines the exponential decay rate of the impulse response function. The leakage current through $R_m$ drives the membrane voltage $V_m(t)$ to 0, but an active membrane pumping current counteracts it and maintains a resting membrane voltage at a value of $V_m(t)=V_L$.

Figure 8.3b shows the standard LIF neuron model [15]. A neuron has: (1) $N$ inputs which represent induced currents through input synapses $\sigma _j(t)$, that are continuous time series consisting either of spikes or continuous analog values; (2) an internal activation state $V_m(t)$; and (3) a single output state $O(t)$. Each input is independently weighted¹ by $\omega _j$ and delayed by $\tau _j$ resulting in a time series that is spatially summed (summed pointwise). This aggregate input electrical current, $I_{\text {app}}(t)=\Sigma _{j=1}^{n}\omega _j\sigma _j(t-\tau _j)$. The result is then temporally integrated using an exponentially decaying impulse response function resulting in the activation state $V_m(t)=V_Le^{\frac{t-t_0}{\tau _m}}+\frac{1}{C_m}\int _0^{t-t_0}I_{\text {app}}(t-s)e^{\frac{s}{\tau _m}}ds$, where $t_0$ is the last time the neuron spiked. If $V_m(t)\ge V_{\text {thresh}}$, then the neuron outputs a spike, $O(t)=1$, and $V_m(t)$ is set to $V_{\text {reset}}$. After issuing a spike, there is a short period of time, the refractory period, during which it is difficult to issue another spike; that is, if $O(t)=1$ then $O(t-\varDelta t)=0$, $\varDelta t\le T_{\text {refract}}$. Consequently, the output of the neuron consists of a continuous time series comprised of spikes.

The parameters determining the behavior of the device are: the weights $\omega _j$, delays $\tau _j$, threshold $V_{\text {thresh}}$, resting potential $V_L$, refractory period $T_{\text {refract}}$, and the integration time constant $\tau _m$. There are three influences on $V_m(t)$: passive leakage of current, an active pumping current, and external inputs generating time-varying membrane conductance changes. These three influences are the three terms contributing to the differential equation describing $V_m(t)$ as

$$\begin{aligned}&\underbrace{\frac{dV_m(t)}{dt}}_{\text {Activation}}=\underbrace{\frac{V_L}{\tau _m}}_{\text {Active pumping}}-\underbrace{\frac{V_m(t)}{\tau _m}}_{\text {Leakage}}+\underbrace{\frac{1}{C_m}I_{app}(t)}_{\text {External input}};\end{aligned}$$

(8.1)

$$\begin{aligned}&\text {if}\,\, V_m(t)>V_{\text {thresh}}\; \text {then release a pulse and set } V_m(t)\rightarrow V_{\text {reset}}. \end{aligned}$$

(8.2)

8.5 Photonic Neuron Bench-Top Model

The first emulation of spiking LIF behavior in ultrafast optical components was a large fiber-based system that took up the area of an optical bench. Although this rudimentary photonic neuron was bulky, power hungry (2 W), and inefficient (1 %), it demonstrated a variety of important hybrid spike processing functions, including integration and thresholding [16–18]. Many of the same physical principles explored in these initial prototypes remain fundamental to more recently developed integrated models (Sect. 8.8).

The most striking resemblance between the physics of photonics and the neural computing paradigm is shown in a direct correspondence between the equations governing the intracellular potential of a LIF neuron (see 8.1a) and the gain dynamics of a semiconductor optical amplifier (SOA):

$$\begin{aligned} \underbrace{\frac{dN'(t)}{dt}}_{\text {Activation}}=\underbrace{\frac{N'_{rest}}{\tau _e}}_{\text {Active pumping}}-\underbrace{\frac{N'(t)}{\tau _e}}_{\text {Leakage}}+\underbrace{\frac{\varGamma a(\lambda )}{E_p}N'(t)P(t)}_{\text {External input}} \end{aligned}$$

(8.3)

where $N'(t)$ is the excited carrier concentration in the optically-coupled semiconductor junction, $\tau _e$ is the carrier lifetime, $P(t)$ is the incident optical power, and $\frac{\varGamma a(\lambda )}{E_p}$ is a wavelength-dependent light-matter coupling coefficient. The correspondence between the equations indicates that the natural physical behaviors of this standard electro-optical material can be made to emulate the primary analog portion of neural dynamics: summing and integration. Despite being dynamically isomorphic, these two equations operate on vastly different time scales; whereas the time constant $R_m C_m = \tau _m$ in biological neurons is around 10 ms, $\tau _e$ in SOAs typically falls within the range of 25–500 ps. It is thus possible to emulate a model of the neural integration function and perhaps tap into neuro-inspired processing techniques for applications at time scales millions to billions of times faster.

Fig. 8.4

Experimental setup for demonstrating simultaneous excitatory and inhibitory stimuli in the SOA through gain pumping and depletion by different wavelengths. Inputs have identical bit patterns, resulting in no net change in the probe power. Unbalanced inputs would result in positive and negative modulations of the SOA transmittance at probe wavelength

Electronic free carriers in the active region of the SOA are analogous to neuron state. Input spikes rapidly perturb the carrier concentration, which then decays back to its resting value. Optical inputs can perturb the SOA state either positively or negatively depending on their wavelength [19], which is represented in (8.3) by the gain parameter $a(\lambda )$. Wavelengths within the gain band of the SOA will deplete the carrier concentration while shorter wavelengths can pump it for the opposite effect. Figure 8.4 shows an experimental demonstration of simultaneous optical excitation and inhibition in an SOA integrator.

Fig. 8.5

Block diagram of a bench-top fiber based photonic neuron. $G$ variable attenuator. $T$ tunable delay line. $\lambda _1$ low power pulse train samples the carrier concentration of the SOA, which is depleted by input pulses

To extract information about the carrier concentration of the integrating SOA, a probe signal ($\lambda _1$ in Fig. 8.5) is modulated by its instant gain, which depends on the free carrier concentration. The stream of modulated pulses is sent to an optical thresholder, which makes the nonlinear spike or no-spike decision seen in biological spiking neurons. This represents the digital portion of the hybrid nature of the computation. Thresholding is performed by a nonlinear optical loop mirror (NOLM), which utilizes the nonlinear Kerr effect to induce an approximately sigmoid-like power transmission function [20]. Two NOLMs in succession were used in the experimental set-up shown in Fig. 8.5 to improve the sharpness of the thresholding characteristic.

Fig. 8.6

Thresholding capabilities of DREAM simulated in a commercial FDTD environment. Input pulse widths are 10 ps, threshold level is 350 pJ. The ideal thresholding characteristic is a Heaviside step function (red line)

Since both the SOA and the mode-locked laser are integratable devices, the ability to integrate the feedforward neuron depends crucially on shrinking the thresholder into a small footprint. A device has been recently been invented to better performs this task: the dual resonator enhanced asymmetric Mach-Zehnder interferometer (DREAM) [21, 22]. By tailoring the finesse of rings in each arm, the pulse width and peak power can be balanced to obtain an energy transfer response that very closely resembles the desired step function (Fig. 8.6). The DREAM could exceeed NOLM performance by four orders of magnitude in each of its key performance criteria: size, decision latency, and switching power. Decision latencies on the order of ten picoseconds are attainable using current material technologies [23].

Although this model successfully performs two qualitative features of biological computation integration and thresholding, it lacks a reset condition, the ability to generate optical pulses, and truly asynchronous behavior. Several modifications to this bench-top model, including a delayed output pulse fed back to reset the SOA, make it suitable for preliminary experiments in learning (Sect. 8.7) and simple lightwave neuromorphic circuits (Sect. 8.6). The original fiber-based photonic neuron is hardly scalable to networks of many neurons, but it identifies a new domain of ultrafast cognitive computing, which has informed the development of more advanced photonic neuron devices based on excitable laser dynamics, a model that is described in Sect. 8.8.

8.6 Lightwave Neuromorphic Circuits

Neuromorphic engineering provides a wide range of practical computing and signal processing tools by exploiting the biophysics of neuronal computation algorithms. Existing technologies include analog very-large-scale integration front-end sensor circuits that replicate the capabilities of the retina and the cochlea [24]. To meet the requirements of real-time signal processing, lightwave neuromorphic signal processing can be utilized to provide the high-speed and low-latency performance that is characteristic of photonic technology. We have demonstrated several small-scale lightwave neuromorphic circuits to mimic important neuronal behavior based on the bench-top model of the photonic neuron detailed in Sect. 8.5. Here, we present several prototypical lightwave neuromorphic circuits including: (1) simple auditory localization inspired by the barn owl [25], useful for light detection and ranging (LIDAR) localization; (2) the crayfish tail-flip escape response [18], which demonstrates accurate, picosecond pattern classification; and (3) principle and independent component analysis, which can adaptively separate mixed and/or corrupted signals based on statistical relationships between multiple sensors.

Fig. 8.7

a Schematic illustration of the auditory localization algorithm of the barn owl. b and c SOA carrier density when two signals are far apart (no spike) and when two signals are close (spike), respectively

8.6.1 Barn Owl Auditory Localization Algorithm

Figure 8.7 shows a simple diagram of auditory localization. Due to the difference in position of object 1 and object 2, there is a time difference between the signals arriving at the owl’s left sensor and right sensor, denoted as $\varDelta T_1=(t_{1a}-t_{1b})$ for object 1 and $\varDelta T_2=(t_{2a}-t_{2b})$ for object 2. Thus, the neuron can be configured to respond to a certain object location by adjusting the weight and delay of the neuron inputs. If the weighted and delayed signals are strong enough and arrive within the integration window, a given neuron spikes; otherwise no spike results and a different neuron corresponding to another location may fire. Figure 8.7 illustrates the corresponding SOA-based integrator response when the two weighted and delayed signals are relatively far apart. The stimulated signal cannot pass through the thresholder and therefore no spike is obtained. When the two inputs are close enough, the carrier density reaches the threshold and leads to a spike as depicted in Fig. 8.7. This algorithm could be used for front-end spatial filtering of RADAR waveform or LIDAR signals.

Figure 8.8 depicts the temporal sensitivity of the spike processor [17]. More specifically, Fig. 8.8 corresponds to the inputs consisting of a number of pulses (signals) with the same intensity but with different time interval, that is, in case I the input signals are close together (measured temporal resolution limited by the bandwidth of the photodetector) and in case II the input signals are further apart. After temporal integration at the SOA and thresholding at the optical thresholder, a spiking output is obtained as shown in Fig. 8.8. Due to the gain depletion property of the SOA, the spike output is inverted. No spike is observed when the input signals are close together (case I), while spike are observed when the input signals are further apart (case II).

Fig. 8.8

a Input to the photonic neuron: (1) case I input signals are close together; and (2) case II input signals are further apart. b Photonic neuron outputs (inverted): (1) case II no spike when signals are close; and (2) case II spike when signals are further apart

8.6.2 Crayfish Tail-Flip Escape Response

We have also demonstrated a device for signal feature recognition based on the escape response neuron model of a crayfish [26]. Crayfish escape from danger by means of a rapid escape response behavior. The corresponding neural circuit is configured to respond to appropriately sudden stimuli. Since this corresponds to a life-or-death decision for the crayfish, it must be executed quickly and accurately. A potential application of the escape response circuit based on lightwave neuromorphic signal processing could be for pilot ejection from military aircraft. Our device, which mimics the crayfish circuit using photonic technology, is sufficiently fast to be applied to defense applications in which critical decisions need to be made quickly while minimizing the probability of false alarm.

Fig. 8.9

a Schematic illustration of the crayfish tail-flip escape response. R receptors; SI sensory inputs; LG lateral giant. b Schematic illustration of the optical implementation of the escape response. w weight; t delay; EAM electro-absorption modulator; TH optical thresholder. Inset, measured recovery temporal profile of cross-absorption modulation in EAM

Figure 8.9 illustrates the (a) crayfish escape neuron model and (b) optical realization of the escape response for signal feature recognition. As shown in Fig. 8.9, signals from the receptors (R) are directed to the first stage of neurons—the sensory inputs (SI). Each of the SI is configured to respond to specific stimuli at the receptors. The SI integrate the stimuli and generate spikes when the inputs match the default feature. The spikes are then launched into the second stage of the neural circuit—the lateral giant (LG). The LG integrates the spikes from the first stage and one of the receptor signals. The neuron responds only when the signals are sufficiently close temporally and strong enough to induce a spike—an abrupt stimulus.

Our analog optical model shown in Fig. 8.9b exploits fast (subnanosecond) signal integration in electro-absorption modulators (EAM) and ultrafast (picosecond) optical thresholding in highly Ge-doped nonlinear loop mirrors (Ge-NOLM). The basic model consists of two cascaded integrators and one optical thresholder. The first integrator is configured to respond to a set of signals with specific features, while the second integrator further selects a subset of the signal from a set determined by a weighting and delay configuration and responds only when the input stimuli and the spike from the first integrator arrive within a very short time interval.

The inputs $a$, $b$, and $c$ are weighted and delayed such that the first EAM integrator (EAM 1) is configured to spike for inputs with specific features. A train of sampling pulses is launched together with the inputs to provide a pulsed source for the EAM to spike. The spiking behavior is based on cross-absorption modulation (XAM) [27] in an EAM. That is, when the integrated input power is large enough for XAM to occur, the sampling pulses within the integration window are passed through the EAM; otherwise they are absorbed. The spike output is then thresholded at the Ge-NOLM [20] such that the output spikes are of similar height, and the undesired weak spikes are removed. The thresholded output and part of input b are launched into the second integrator as the input control through path $\beta$ and $\alpha$, respectively. Sampling pulses are launched to the integrator through path $\xi$ as a spiking source. Through weighting and delaying of the inputs, spikes by the second integrator occur only for inputs with the desired features. The selection of the desired features can be reconfigured simply by adjusting the weights and delays of the inputs.

Fig. 8.10

Experimental results. a Optical inputs to EAM 1; b different spike patterns resulted from the first integrator; c thresheld output; d output spikes from EAM 2, recognizing pattern $abc$ and $ab-$; e output spike from EAM 2, recognizing pattern $abc$ only; f output from EAM 2, none of the input is recognized

The recognition circuit detects input patterns of $abc$ and $ab-$ having specific time intervals between the inputs as we configured. Figure 8.10 shows the experimental measurements of the signal feature recognizer. Figure 8.10a shows all eight combinations of the three inputs with specific weights and delays. We use “1” to represent the presence of input, while “0” means there is no input. Superimposed temporal profile of the input signal is shown in the inset of Fig. 8.10a. Sampling pulses with separation of $\sim$25 ps are used, as indicated by the arrows. The input signals are integrated, and the transmittance of the EAM 1 is represented by the spike pattern at the output (Fig. 8.10b). A Ge-NOLM is used to threshold the output of EAM 1 (Fig. 8.10c). The inset shows the superimposed temporal profile of the thresholded output.

When the output spikes from the first neuron arrive at the second integrator slightly after input $b$, i.e., within the integration interval, the second integrator will spike. By adjusting the time delay of the inputs to the EAM 2, the pattern recognizer identifies patterns $abc$ and $ab-$ (Fig. 8.10d) or just $abc$ (Fig. 8.10e). However, when the spikes from the first neuron arrive too late, i.e., exceed the integration time, the second integrator will not spike (Fig. 8.10f). These examples indicate that the signal feature recognizer is performing correctly and is reconfigurable through time delay adjustment.

8.7 Ultrafast Learning

Although biological neurons communicate using electro-chemical action potentials, they also possess a variety of slower, chemical regulatory processes that analyze the statistical properties of information flow. Such processes ensure network stability, maximize information efficiency, and adapt neurons to incoming signals from the environment [28, 29]. Learning as it occurs in biological neural networks can be divided into two primary categories: synaptic plasticity and intrinsic plasticity [30]. Synaptic plasticity controls the dynamics at the synapse between two communicating neurons and intrinsic plasticity controls the nonlinear transfer function of the neuron itself. Both play an important role in maximizing the mutual information between the input and output of each node and as a consequence, can perform principle component analysis (PCA) and independent component analysis (ICA) on incoming signals [31].

Our proposed photonic neural networks analogously use coherent light pulses to communicate and slower but higher density microelectronics to implement adaptive learning rules. Furthermore, successful implementation of PCA and ICA in our system will result in a robust, error-tolerant architecture that can blindly separate statistically independent unknown signals (including interference) received by antenna arrays.

8.7.1 Synaptic Time Dependent Plasticity

STDP is a highly parallel, linear gradient descent algorithm that tends to maximize the mutual information between the input and output of a given neuron. It operates independently on each connection and thus scales proportionally with the number of neurons times the average fan-in number. In the context of biological networks, it is an adaptive biochemical system that operates at the synapse—or gap—between communicating neurons. Its generality and simplicity allows it to be utilized for both supervised and unsupervised learning for a large variety of different learning tasks [32].

The rules governing STDP are as follows: suppose there are two neurons $i$, $j$, such that neuron $i$ (pre-synaptic) connects to neuron $j$ (post-synaptic) with weight $w_{ij}$. If neuron $i$ fires at $t_{\text {pre}}$ before $j$ fires at $t_{\text {post}}$, STDP strengthens the weight, $w_{ij}$, between them. If neuron $j$ fires before $i$, $w_{ij}$ weakens. Figure 8.11 illustrates the change in weight $w_{ij}$ as a function of the pre- and post-synaptic neuron relative spike timing difference $\varDelta T = t_{\text {post}} - t_\mathrm {pre}$. This plasticity curve asymmetric in $\varDelta T$ is not the only kind of learning rule. Hebbian learning is an example of a symmetric kind of plasticity; however, STDP is more difficult to implement at ultrafast time scales because of the sharp discontinuity at $\varDelta T = 0$. We therefore focus on STDP because it requires a photonic implementation whereas other learning rules could be implemented in slower electronic devices.

Fig. 8.11

The change in weight $w_{ij}$ for a given edge as a function of the pre- and post- spike timings

If a powerful signal travels through a network, the connections along which it travels tend to strengthen. As dictated by the STDP, since the pre-neuron $i$ will fire before the post-neuron $j$, the strength between them will increase. However, misfires of the post-neuron or spike blockage of the pre-neuron will tend to decrease the corresponding weight. As a general rule, STDP emphasizes connections between neurons if they are causally related in a decision tree.

Alternatively, one can view STDP in terms of mutual information. In a given network, a neuron $j$ can receive signals from thousands of other channels. Neurons, however, must compress that data into a single channel for their output. Since STDP strengthens the weight of causally related signals, it will attempt to minimize the difference between the information in the input and output channels of neuron $j$. It thereby maximizes the mutual information between input and output channels.

STDP is naturally suited for unsupervised learning and cluster analysis. After feeding the network ordered input, STDP will correlate neural signals to each other, organizing the network and designate different neurons to fire for different patterns or qualities. For supervised learning, forcing output units at the desired values allows STDP to correlate input and output patterns. Since STDP attempts to change the network connection strengths to reflect correlation between the input and output of each node, it will automatically correlate associated examples and mold the network for the given task.

In biological networks, STDP is implemented using bio-molecular protein transmitters and receivers. This technology is noisy but scalable. Unfortunately, photonic technology cannot match the scalability of biology. Because there are $N \cdot k$ connections for a network of $N$ neurons with mean indegree $k$, there is correspondingly a need for $N \cdot k$ STDP circuits to adjust each connection. This presents a scaling challege for photonic STDP because integrated photonic neural primitives themselves already approach the diffraction limit of light, and each may have many inputs.

8.7.2 Intrinsic Plasticity

Intrinsic Plasticity (IP) describes a set of adaptive algorithms that regulate the internal dynamics of neurons rather than the synapses connecting them [33]. IP operates within the neuron after STDP has applied the weights. Unlike STDP, it refers to a class of adaptations instead of a unified learning rule. Researchers posit that it tends to maximize the mutual information between a neuron’s input and output channels, like STDP [34]. Since IP controls spiking dynamics rather than connection strengths, it scales with the number of neurons, $N$ and does not present a significant architectural challenge. Photonic neurons exhibit changes in their dynamics with changes in the current injected into the semiconductor, providing this as a mechanism for photonic IP. The combination of IP algorithms with STDP encourages network stability and allows for a higher diversity of applications, including (ICA) [31].

8.7.3 Principal Component Analysis

PCA seeks to find the eigenvector(s) of a high-dimensional space of data along the direction of maximal variance. This assures that an orthogonal projection of the data into a desired subspace retains the maximum information from the original data set as possible. Spiking neurons can extract the principle components of incoming data using a combination of STDP, synaptic scaling (SS), and lateral inhibition. In this kind of circuit, signals are simply encoded as spike rates, where the amplitude of an incoming signal modulates the rate of fixed amplitude spikes. Spike-based rate coding is more robust against analog noise than direct analog modulation.

Fig. 8.12

An example of signal demixing with PCA. The top signal is mixed with an interfering signal in two channels, leading to the second two signals. Simulations with STDP and synaptic scaling show that a single neuron can extract the original signal from the mixed signals using PCA

Though neural weights are controlled by slow electronic integrators, a photonic STDP circuit (see Fig. 8.13a) is needed to distinguish pulse arrival times with picosecond resolution. The weight learning rule for STDP is given by a piecewise exponential curve in the spike relative arrival time domain (see Fig. 8.13b).

Synaptic scaling normalizes the sum of weights across all the inputs for a given neuron, preventing STDP from destabilizing the weights and introducing competition between weights. This normalization is implemented electronically. Lateral inhibition between neurons in the output layer decouples signals from each neuron, forcing them to avoid correlated outputs. This effect is required for extraction of principal components other than the first.

The PCA algorithm takes $N$ inputs encoded in spike rates along $N$ channels. Neurons output a projection of this data onto an initial vector (the weight vector) determined by the strength of the connections to that neuron. STDP is set to operate in a simple Hebbian learning scheme in which a positive change in weight depends multiplicatively on both the input and output firing rates. As each STDP circuit operates in parallel along each of the $N$ dimensions, the net effect is an adaptive adjustment of the weight vector towards the principle component eigenvector (see Fig. 8.12). Subsequent principle components can also be extracted by subtracting higher principle components from other neurons using lateral inhibition, forcing them to extract information from what remains.

8.7.4 Independent Component Analysis

Although PCA is useful for a variety of tasks, it cannot perform blind source separation if the signals are not mixed orthogonally. ICA, on the other hand, can separate multivariate data into its independent subcomponents for an arbitrary unknown mixing matrix. ICA operates effectively under the conditions that the numbers of inputs (or antennas) are at least as great as the number of original signals and the signals have non-Gaussian distributions. Spiking neurons can perform ICA with the addition of IP which can be implemented with photodetectors to measure activity and electronic circuits to implement adaptation.

The ICA algorithm operates similarly to the PCA algorithm with two modifications: (1) STDP can decrease the strength of the connection for inputs that initiate low outputs, and (2) IP can change the slope of the neuron’s transfer function based on the current activity of the neuron. The interaction of STDP with IP results in a learning scheme that favors highly kurtotic dimensions, allowing the extraction of non-orthogonal independent components [31]. Like in PCA, subsequent independent components can be extracted using lateral inhibition.

8.7.5 Photonic STDP

Artificial STDP has been explored in VLSI electronics [35], and more recently, has been proposed [36] and demonstrated [37] in memristive nanodevices. Some ongoing projects in microelectronics seek to develop hardware platforms based on this technology [3, 4]. The analog nature and resilience to noise of neuromorphic processing naturally complements the high variability and failure rates of nanodevices [6], enabling the possibility of densely connected adaptive spiking networks [38]. STDP was first explored in the optical domain by [39].

Fig. 8.13

a Photonic circuit diagram of STDP and b experimental function of output power vs. spike interval. Pre and post synaptic inputs cross phase modulate one another, with time constants determined by the SOA and EAM to give the characteristic STDP curve

Fig. 8.14

Adjustable parameters in both the EAM and SOA can dynamically change the properties of the STDP circuit

The optical STDP circuit is illustrated in Fig. 8.13. This implementation uses two slow integrators and optical summing to create an exponential-like response function. The resulting response is then incident on a photodetector, which regulates an electronic circuit to control the weight between two neurons. The response function shape can be dynamically adjusted with various control parameters (Fig. 8.14). This photonic STDP design can be integrated, but the exceptional need for up to $N \cdot k$ independent units limits the scalability of an overall system. Analogous STDP devices proposed in electronics such as memristors in nano-crossbar arrays [6] overcome this scaling challenge with extremely small nano-devices (on the order of nanometers). Novel implementations of STDP based on electronic-optical, photonic crystal [40], or plasmonic [41] technologies may become important to support scaling of complete adaptability. The requirement of every connection to adapt without supervision can also be relaxed, for example, by organizing the system as a liquid state machine (LSM) or in other reservoir architecture [42].

8.8 Excitable Laser Neuron

The fiber-based bench-top photonic neuron provided a starting basis for investigations into photonic implementations of spiking neuromorphic devices. The primary reason for moving beyond it is integrability. Photonic integration, much like electronic integration, enables much greater scalability, which is required to access a much more interesting and rich computational repertoire based on large groups of neurons. We have found that laser dynamics constrained to a dynamically excitable regime can also emulate the LIF model, in many ways more accurately and unambiguously than the initial bench-top device did [43, 44]. Experiments with a fiber-based prototype laser with a graphene SA have confirmed the ability of this laser model to achieve excitable dynamics [45, 46]. Additional advantages of integration include very low power operation, hardware cost reduction, and added robustness to environmental fluctuations. In this section, we reveal the analogy between the LIF model and a modified excitable laser model.

Fig. 8.15

A simple schematic of a SA laser. The device is composed of (i) a gain section, (ii) a saturable absorber, and (iii) mirrors for cavity feedback. In the LIF excitable model, inputs selectively perturb the gain optically or electrically

Our starting point is a set of dimensionless equations describing SA lasers that can generalize to a variety of different laser systems, including passively Q-switched microchip lasers [47], distributed BRAGG reflector lasers [48], and vertical cavity surface emitting lasers (VCSELs) [49]. The Yamada model describes the behavior of lasers with independent gain and saturable absorber (SA) sections with an approximately constant intensity profile across the cavity [50], as illustrated in Fig. 8.15. We assume that the SA has a very short relaxation time on the order of the cavity intensity, which can easily be achieved either through doping or special material properties. The dynamics now operate such that the gain is a slow variable while the intensity and loss are both fast. This three-dimensional dynamical system can be described with the following equations:

$$\begin{aligned} \dot{G(t)}&=\gamma _G\left[ A-G(t)-G(t)I(t)\right] \end{aligned}$$

(8.4)

$$\begin{aligned} \dot{Q(t)}&=\gamma _Q\left[ B-Q(t)-aQ(t)I(t)\right] \end{aligned}$$

(8.5)

$$\begin{aligned} \dot{I(t)}&=\gamma _I\left[ G(t)-Q(t)-1\right] I(t)+\epsilon f(G) \end{aligned}$$

(8.6)

where $G(t)$ models the gain, $Q(t)$ is the absorption, $I(t)$ is the laser intensity, $A$ is the bias current of the gain, $B$ is the level of absorption, $a$ describes the differential absorption relative to the differential gain, $\gamma _G$ is the relaxation rate of the gain, $\gamma _Q$ is the relaxation rate of the absorber, $\gamma _I$ is the inverse photon lifetime, and $\epsilon f(G)$ represents the small contributions to the intensity made by spontaneous emission (noise term) where $\epsilon$ is very small. Although conventionally $\gamma _I$ is set to $1$, we include the reverse photon lifetime $\gamma _I$ for clarity.

Fig. 8.16

Simulation results of an SA laser behaving as a LIF neuron. Arrows indicate excitatory pulses and inhibitory pulses that change the gain by some amount $\triangle G$. Enough excitatory input causes the system to enter fast dynamics in which a spike is generated, followed by the fast recover of the absorption $Q(t)$ and the slow recover of the gain $G(t)$. Variables were rescaled to fit within the desired range. Values used: $A = 4.3$; $B = 3.52$; $a = 1.8$; $\gamma _G= 0.05$; $\gamma _L, \gamma _I >> 0.05$

We further assume that inputs to the system cause perturbations to the gain $G(t)$ only. Pulses—from other excitable lasers, for example—will induce a change $\triangle G$ as illustrated by the arrows in Fig. 8.16 and analog inputs will modulate $G(t)$ continuously. This injection can be achieved either via optical pulses that selectively modulate the gain medium or through electrical current injection.

8.8.1 Before Pulse Formation

Since the loss $Q(t)$ and the intensity $I(t)$, are fast, they will quickly settle to their equilibrium values. On slower time scales, our system behaves as:

$$\begin{aligned} \dot{G(t)}&=\gamma _G\left[ A-G(t)-G(t)I(t)\right] +\theta (t)\end{aligned}$$

(8.7)

$$\begin{aligned} Q(t)&=Q_\mathrm{{eq}}\end{aligned}$$

(8.8)

$$\begin{aligned} I(t)&=I_\mathrm{{eq}} \end{aligned}$$

(8.9)

with $\theta (t)$ representing possible inputs, and the equilibrium values $Q_{eq}=B$ and $I_{eq}=\epsilon f(G)/\left[ \gamma _I \left( 1-G(t)+Q(t)\right) \right]$. Since $\epsilon$ is quite small, $I_\mathrm{{eq}}\approx 0$. With zero intensity in the cavity, the $G(t)$ and $Q(t)$ variables are dynamically decoupled. The result is that if inputs are incident on the gain, they will only perturb $G(t)$ unless $I(t)$ becomes sufficiently large to couple the dynamics together.

If $I(t)$ increases, the slow dynamics will break. $I(t)$ will become unstable when $G(t)-Q(t)-1>0$ because $\dot{I}(t)\approx \gamma _I\left[ G(t)-Q(t)-1\right] I(t)$. Given our perturbations to $G(t)$, we can define a threshold condition:

$$\begin{aligned} G_{\text {thresh}}=Q+1=B+1\;\text {(at equilibrium)} \end{aligned}$$

(8.10)

above which fast dynamics will take effect. This occurs after the third excitatory pulse in Fig. 8.16.

8.8.2 Pulse Generation

Perturbations that cause $G(t)>G_{\text {thresh}}$ will result in the release of a short pulse. Once $I(t)$ is lifted above the attractor ${I=0}$, $I(t)$ will increase exponentially. This results in the saturation of $Q(t)$ on a very fast time scale until $Q=0$, followed by the slightly slower depletion of the gain, $G(t)$. Once $G(t)-Q(t)-1<0$, that is, $G(t)<1$ following saturation, $I(t)$ will hit its peak intensity $I_{\text {max}}$, followed by a fast decay on the order of $1/\gamma _I$ in time. $I(t)$ will eventually reach $I\approx 0$ as it further depletes the gain to a final value $G_{\text {reset}}$, which—with a large enough intensity—is often close to the transparency level $G_{\text {reset}}\approx 0$.

A given pulse derives its energy from excited carriers in the cavity. The total energy of the pulse is $E_{pulse} = N h \nu$, where $N$ is the number of excited carriers that have been depleted and $h \nu$ is the energy of a single photon at the lasing frequency. Because the gain is proportional to the inversion population, $N$ must be proportional to the amount that the gain $G(t)$ has depleted during the formation of a pulse. Thus, if $G_{\text {fire}}$ is the gain that causes the release of a pulse, we can expect that an output pulse will take the approximate form:

$$\begin{aligned} P_{\text {out}}=E_{\text {pulse}}\cdot \delta (t-\tau _f)\end{aligned}$$

(8.11)

$$\begin{aligned} E_{pulse}\propto G_{\text {fire}}-G_{\text {reset}} \end{aligned}$$

(8.12)

where $\tau _f$ is the time at which a pulse is triggered to fire and $\delta (t)$ is a delta function. One of the properties of spike-encoded channels is that spike energies are encoded digitally. Spikes must have a constant amplitude every iteration, a characteristic property of the all-or-nothing response shared by biological neurons. We can normalize our output pulses if we set our system to operate close to threshold $G_{\text {thresh}}-G_{eq}\ll G_{\text {thresh}}$. Since the threshold is effectively lowered, the size of input perturbations $\triangle G$ must be scaled smaller. This implies $G_{ fire}\approx G_{\text {thresh}}$, which helps in suppressing variations in the output pulse amplitude by reducing the input perturbation to the system. This leads to a step-function like response, as illustrated in Fig. 8.17, which is the desired behavior.

Fig. 8.17

Neuron threshold functions. The red and blue curves are simulated, normalized transfer functions for a single input spike when the neuron is operated far from and close to the threshold, respectively. Setting $G_{\text {eq}}$ close to $G_{\text {thresh}}$ reduces the required perturbation $\triangle G$ to initiate a pulse and thereby minimizes the impact it has on the resulting output pulse, leading to the flatter one level region on the blue curve

After a pulse is released, $I(t)\rightarrow 0$ and $Q(t)$ will quickly recover to $Q_{eq}$. The fast dynamics will give way to slower dynamics, in which $G(t)$ will slowly creep from $G_{\text {reset}}$ to $G_{eq}$. The fast dynamics of $Q(t)$ assure that the threshold $G_{\text {thresh}}=1+Q(t)$ recovers quickly after a pulse is generated, preventing partial pulse release during the recovery period. In addition, the laser will experience a relative refractory period in which it is difficult—but not impossible—to fire another pulse.

8.8.3 LIF Analogy

If we assume the fast dynamics are nearly instantaneous, we can compress the behavior of our system into the following set of equations and conditions:

$$\begin{aligned} \frac{dG(t)}{dt}&=-\gamma _G(G(t)-A)+\theta (t);\end{aligned}$$

(8.13)

$$\begin{aligned}&\text {if}\; G(t) > G_{\text {thresh}}\; \text {then}\\&\text {release a pulse, and set}\; G(t)\rightarrow G_{\text {reset}}.\nonumber \end{aligned}$$

(8.14)

where $\theta (t)$ represent input perturbations. This behavior can be seen qualitatively in Fig. 8.16. The conditional statements account for the fast dynamics of the system that occur on times scales of order $1/\gamma _{I}$, and other various assumptions—including the fast $Q(t)$ variable and operation close to threshold—assure that $G_{\text {thresh}}$, $G_{\text {reset}}$ and the pulse amplitude $E_{\text {pulse}}$ remain constant. If we compare this to the LIF model, or (8.1):

$$\begin{aligned} C_m\frac{dV_m(t)}{dt}&=-\frac{1}{R_m}(V_m(t)-V_L)+I_{app}(t);\\&\text {if} V_m(t)>V_{\text {thresh}}\; \text {then}\\&\text {release a spike and set}\; V_m(t)\rightarrow V_{\text {reset}}. \end{aligned}$$

the analogy between the equations becomes clear. Setting the variables $\gamma _G=1/R_m C_m$, $A=V_L$, $\theta (t)= I_{app}(t)/R_m C_m$, and $G(t)=V_m(t)$ shows their algebraic equivalence. Thus, the gain of the laser $G(t)$ can be thought of as a virtual membrane voltage, the input current $A$ as a virtual leakage voltage, etc. There is a key difference, however—both dynamical systems operate on vastly different time scales. Whereas biological neurons have time constants $\tau _m=C_m R_m$ on order of milliseconds, carrier lifetimes of laser gain sections are typically in the $ns$ range and can go down to $ps$.

8.8.4 Excitable VCSELs

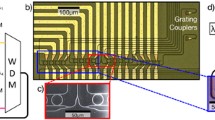
Although the excitable model is generalizable to a variety of different laser types, vertical cavity surface emitting lasers (VCSEL) are a particularly attractive candidate for our computational primitive as they occupy small footprints, can be fabricated in large arrays allowing for massive scalability, and use low powers [51]. An excitable VCSEL with an intra-cavity SA that operates using the same rate equation model described above has already been experimentally realized [52]. In addition, the technology is amenable to a variety of different interconnect schemes: VCSELs can send signals upward and form 3D interconnects [53], can emit downward into an interconnection layer via grating couplers [54] or connect monolithically through intra-cavity holographic gratings [55].

Fig. 8.18

A schematic diagram of an excitable VCSEL interfacing with a fiber leading to the network. In this configuration, inputs $\lambda _1, \lambda _2 \ldots \lambda _n$ selectively modulate the gain section. Various frequencies lie on different parts of the gain spectrum, leading to wavelength-dependent excitatory or inhibitory responses. The weights and delays are applied by amplifiers and delay lines within the fiber network. If excited, a pulse at wavelength $\lambda _0$ is emitted upward and transmitted other excitable lasers

A schematic of our VCSEL structure, which includes an intra-cavity SA, is illustrated in Fig. 8.18. To simulate the device, we use a typical two-section rate equation model such as the one described in [49]:

$$\begin{aligned} \frac{dN_{ph}}{dt}&=\varGamma _a g_a (n_a-n_{0a})N_{ph}+\varGamma _s g_s(n_s-n_{0s})N_{ph}\\&\quad -\,\frac{N_{ph}}{\tau _\mathrm{{ph}}}+V_a\beta B_r n^2_a \nonumber \end{aligned}$$

(8.15)

$$\begin{aligned} \frac{dn_a}{dt}&=-\varGamma _a g_a (n_a-n_{0a})\frac{(N_{ph}-\phi (t))}{V_a}-\frac{n_a}{\tau _a}+\frac{I_a}{e V_a}\end{aligned}$$

(8.16)

$$\begin{aligned} \frac{dn_s}{dt}&=-\varGamma _s g_s (n_s-n_{0s})\frac{N_{ph}}{V_s}-\frac{n_s}{\tau _s}+\frac{I_s}{eV_s} \end{aligned}$$

(8.17)

where $N_{ph}(t)$ is the total number of photons in the cavity, $n_a(t)$ is the number of carriers in the gain region, and $n_s(t)$ is the number of carriers in the absorber. Subscripts $a$ and $s$ identify the active and absorber regions, respectively. The remaining device parameters are summarized in Table 8.3. We add an additional input term $\phi (t)$ to account for optical inputs selectively coupled into the gain and an SA current injection term $I_s/e V_s$ to allow for an adjustable threshold.

These equations are analogous to the dimensionless set of (8.4) provided that the following coordinate transformations are made:

$$\begin{aligned} G(\tilde{t})&=\tau _{ph}\varGamma _a g_a (n_a(t)-n_{0a}), \, \, \, \, \, \, I(\tilde{t})=\frac{\tau _a \varGamma _a g_a}{V_a} N_{ph}(t) \\ Q(\tilde{t})&=\tau _{ph}\varGamma _s g_s (n_{0s}-n_s(t)), \, \, \, \, \, \, \tilde{t} = \frac{t}{\tau _{ph}} \end{aligned}$$

where differentiation is now with respect to $\tilde{t}$ rather than $t$. The dimensionless parameters are now

$$\begin{aligned} \gamma _G&=\frac{\tau _{ph}}{\tau _a}, \, \, \, \, \, \, A = \tau _a\tau _{ph}\varGamma _a g_a\left[ \frac{I_a}{e V_{a}}-\frac{n_{0a}}{\tau _a}\right] , \\ \gamma _Q&=\frac{\tau _{ph}}{\tau _s}, \, \, \, \, \, \, B = \tau _s\tau _{ph}\varGamma _s g_s\left[ \frac{n_{0s}}{\tau _s}-\frac{I_s}{e V_s}\right] , \\ \gamma _I&=1, \qquad \quad a = \frac{\tau _s\varGamma _s g_s V_a}{\tau _a \varGamma _a g_a V_s}, \\ \epsilon f(G)&=\tau _a\tau _{ph}\varGamma _{a} g_{a}\beta B_r\left[ \frac{G}{\tau _{ph}\varGamma _a g_a}+n_{0a}\right] ^2 \end{aligned}$$

For the simulation, we set the input currents to $I_a = 2$ mA and $I_s = 0$ mA for the gain and absorber regions, respectively. The output power is proportional to the photon number $N_{ph}$ inside the cavity via the following formula:

$$\begin{aligned} P_{\text {out}}(t) \approx \frac{\eta _c \varGamma _a}{\tau _p}\frac{hc}{\lambda } N_{ph}(t) \end{aligned}$$

(8.18)

in which $\eta _c$ is the output power coupling coefficient, $c$ the speed of light, and $hc/\lambda$ is the energy of a single photon at wavelength $\lambda$. We assume the structure is grown on a typical GaAs-based substrate and emits at a wavelength of $850$ nm.

Table 8.3 VCSEL-SA excitable laser parameters [49, 56–58]

Using the parameters described above, we simulated the device with optical injection into the gain as shown in Fig. 8.19. Input perturbations that cause gain depletion or enhancement—represented by positive and negative input pulses—modulate the carrier concentration inside the gain section. Enough excitation eventually causes the laser to enter fast dynamics and fire a pulse. This behavior matches the behavior of an LIF neuron described in Sect. 8.8.3.

Fig. 8.19

Simulation of an excitable, LIF excitable VCSEL with realistic parameters. Inputs (top) selectively modulate the carrier concentration in the gain section (middle). Enough excitation leads to the saturation of the absorber to transparency (bottom) and the release of a pulse, followed by a relative refractory period while the pump current recovers the carrier concentration back to its equilibrium value

Our simulation effectively shows that an excitable, LIF neuron is physically realizable in a VCSEL-SA cavity structure. The carrier lifetime of the gain is on the order of $1$ ns, which as we have shown in Sect. 8.8.3 is analogous to the $R_m C_m$ time constant of a biological neuron—typically on the order of $10$ ms. Thus, our device already exhibits speeds that are 10 million times faster than a biological equivalent. Lifetimes could go as short as $ps$, making the factor speed increase between biology and photonics up to a billion.

8.8.5 Other Spiking Photonic Devices

Since the early bench-top model of a spiking photonic neuron suggested an ultrafast cognitive computing domain, several other approaches have arisen to develop scalable, integrated photonic spike processing devices. One device designed and demonstrated by [59, 60] uses the nonlinear dynamics of polarization switching (PS) in a birefringent VCSEL to emulate the behavior of specialized kinds of neurons. Characteristic behaviors of the resonate-and-fire neural model [61] (as opposed to the above integrate-and-fire model) including tonic spiking, rebound spiking, and subthreshold oscillations have been observed. The state of the VCSEL depends on the lasing power of competetive orthogonally polarized modes, so the direction of input fluence (excitatory or inhibitory) is determined by the injected light polarization and wavelength.

Semiconductor ring lasers (SRL) have also been shown to exhibit dynamic excitability [62]. They are investigated for application as a computational primitive in [63]. Excitable bifurcations in SRLs can arise from weakly broken $\mathbb {Z}_2$ symmetry between counterpropagating normal modes of the ring resonator, where $\mathbb {Z}_2$ refers to the complex two-dimensional phase space that describes the SRL state. The direction of input fluence on SRL state is strongly modulated by the optical phase of the circulating and input fields due to this complex phase space characteristic of optical degrees of freedom. These neuron-like behaviors currently under investigation are so far all based on different constrained regimes of the dynamically rich laser equations. They differ primarily in their physical representation of somatic integration variables, spiking signals, and correspondingly the mechanism of influence of one on another.

8.9 Cortical Spike Algorithms: Small-Circuit Demos

This section describes implementation of biologically-inspired circuits with the excitable laser computational primitive. These circuits are rudimentary, but fundamental exemplars of three spike processing functions: multistable operation, synfire processing [64], and spatio-temporal pattern recognition [65].

We stipulate a mechanism for optical outputs of excitable lasers to selectively modulate the gain of others through both excitatory (gain enhancement) and inhibitory (gain depletion) pulses, as illustrated in Fig. 8.18. Selective coupling into the gain can be achieved by positioning the gain and saturable absorber regions to interact only with specific optical frequencies as experimentally demonstrated in [52]. Excitation and inhibition can be achieved via the gain section’s frequency dependent absorption spectrum—different frequencies can induce gain enhancement or depletion. This phenomenon been experimentally demonstrated in semiconductor optical amplifiers (SOAs) [19] and could generalize to laser gain sections if the cavity modes are accounted for. Alternatives to these proposed solutions include photodetectors with short electrical connections and injection into an extended gain region in which excited carriers are swept into the cavity via carrier transport mechanisms.

A network of excitable lasers connected via weights and delays—consistent with the model described in Sect. 8.4—can be described as a delayed differential equation (DDE) of the form: 

$$\begin{aligned} \frac{d}{dt} {\varvec{x}}(t) = f\!\!\left( {\varvec{x}}(t), {\varvec{x}}(t-\tau _1), {\varvec{x}}(t-\tau _2) \cdots {\varvec{x}}(t-\tau _n)\right) \end{aligned}$$

(8.19)

where the vector ${\varvec{x}}(t)$ contains all the state variable associated with the system. The output to our system is simply the output power, ${\varvec{P}}_{\mathbf{out}}(t)$,² while the input is a set of weighted and delayed outputs from the network, $\sigma (t) = \sum \nolimits _k W_k {\varvec{P}}_{\mathbf{out}}(t-\tau _k)$. We can construct weight and delay matrices $W, D$ such that the $W_{ij}$ element of $W$ represents the strength of the connection between excitable lasers $i,j$ and the $D_{ij}$ element of $D$ represents the delay between lasers $i,j$. If we recast (8.15) in a vector form, we can formulate our system in (8.19) given that the input function vector ${\varvec{\phi }} (t)$, is

$$\begin{aligned} {\varvec{\phi }} (t) = \varOmega \varvec{\varTheta }(t) \end{aligned}$$

(8.20)

where we create a sparse matrix $\varOmega$ containing information for both $W$ and $D$, and a vector $\varvec{\varTheta }(t)$ that contains all the past outputs from the system during unique delays $U = [\tau _1,\ \tau _2,\ \tau _3 \ \cdots \ \tau _n]$:

$$\begin{aligned} \varOmega = [W_0 \ W_1 \ W_2 \cdots W_n] \end{aligned}$$

(8.21)

$$\begin{aligned} \varvec{\varTheta }(t) = \left( \begin{array}{c} {\varvec{P}}_{\mathbf{out}}(t)\\ {\varvec{P}}_{\mathbf{out}}(t-\tau _1) \\ {\varvec{P}}_{\mathbf{out}}(t-\tau _2) \\ \vdots \\ {\varvec{P}}_{\mathbf{out}}(t-\tau _n) \end{array} \right) \end{aligned}$$

(8.22)

$W_k$ describes a sparse matrix of weights associated with the delay in element $k$ of the unique delay vector $U$. To simulate various system configurations, we used Runge-Kutta methods iteratively within a standard DDE solver in MATLAB. This formulation allows the simulation of arbitrary networks of excitable lasers which we used for several cortical-inspired spike processing circuits described below.

8.9.1 Multistable System

Multistability represents a crucial property of dynamical systems and arises out of the formation of hysteretic attractors. This phenomenon plays an important role in the formation of memory in processing systems. Here, we describe a network of two interconnected excitable lasers, each with two incoming connections and identical weights and delays, as illustrated in Fig. 8.20. The system is recursive rather than feedforward, which results in a settable dynamic memory element similar to a digital flip-flop.

Fig. 8.20

a Bistability schematic. In this configuration, two lasers are connected symmetrically to each other. b A simulation of a two laser system exhibiting bistability with connection delays of $1$ ns. The input perturbations to unit one are plotted, followed by the output powers of units 1 and 2 , which include scaled version of the carrier concentrations of their gain sections as the dotted blue lines. Excitatory pulses are represented by positive perturbations while inhibitory pulses are represented by negative perturbations. An excitatory input excites the first unit, causing a pulse to be passed back and forth between the nodes. A precisely timed inhibitory pulse terminates the sequence

Results for the two laser multistable system are shown in Fig. 8.20. The network is composed of two lasers, interconnected via optical connections with a delay of $1$ ns. An excitatory pulse travels to the first unit at $t = 5$ ns, initiating the system to settle to a new attractor. The units fire pulses repetitively at fixed intervals before being deactivated by a precisely timed inhibitory pulse at $t = 24$ ns. It is worth noting that the system is also capable of stabilizing to other states, including those with multiple pulses or different pulse intervals. It therefore acts as a kind of optical pattern buffer over longer time scales. Ultimately, this circuit represents a test of the network’s ability to handle recursive feedback. In addition, the stability of the system implies that a network is cascadable since a self-referent connection is isomorphic to an infinite chain of identical lasers with identical weights $W$ between every node. Because this system successfully maintains the stability of self-pulsations, processing networks of excitable VCSELs are theoretically capable of cascadibility and information retention during computations.

8.9.2 Synfire Chain

Synfire chains have been proposed by Abeles [66] as a model of cortical function. A synfire chain is essentially a feedforward network of neurons with many layers (or pools). Each neuron in one pool feeds many excitatory connections to neurons in the next pool, and each neuron in the receiving pool is excited by many neurons in the previous pool, so that a wave of activity can propagate from pool to pool in the chain. It has been postulated that such a wave corresponds to an elementary cognitive event [67].

Fig. 8.21

a Synfire schematic. In this configuration, two groups of lasers are connected symmetrically two each other. b Simulation of a four laser circuit forming synfire chains with connection delays of $14$ ns. The input perturbations to units 1, 2 are plotted over time, followed by the output powers of units 1–4 with the scaled carrier concentrations of their gain sections as the dotted blue lines. A characteristic spike pattern is repeatedly passed back and forth between the left and right set of nodes

Synfire chains are a rudimentary circuit for population encoding, which reduces the rate of jitter accumulation when sending, receiving, or storing a spatio-temporal bit pattern of spikes [64]. Population encoding occurs when multiple copies of a signal are transmitted along $W$ uncorrelated channels ($W$ for chain width). When these copies arrive and recombine in subsequent integrator units, statistically uncorrelated jitter and amplitude noise is averaged resulting in a noise factor that is less than the original by a factor of $W^{-1/2}$. One of the key features of a hybrid analog-digital system such as an SNN is that many analog nodes can process in a distributed and redundant way to reduce noise accumulation. Recruiting a higher number of neurons to accomplish the same computation is an effective and simple way of reducing spike error rates.

Figure 8.21a shows a demonstration of a simple four-laser synfire chain with feedback connections. The chain is simply a two unit expansion of each node in the multistability circuit from Fig. 8.20a. Like the multistability circuit, recursion allows the synfire chain to possess hysteric properties; however, the use of two lasers for each logical node provides processing redundancy and increases reliability. Once the spike pattern is input into the system as excitatory inputs injected simultaneously into the first two lasers, it is continuously passed back and forth between each set of two nodes. The spatio-temporal bit pattern persists after several iterations and is thereby stored in the network as depicted in Fig. 8.21b.

8.9.3 Spatio-Temporal Pattern Recognition Circuit

The concept of polychrony, proposed by Izhikevich [65] is defined as an event relationship that is precisely time-locked to firing patterns but not necessarily synchronous. Polychronization presents a minimal spiking network that consists of cortical spiking neurons with axonal delays and synaptic time dependent plasticity (STDP), an important learning rule for spike-encoded neurons. As a result of the interplay between the delays and STDP, spiking neurons spontaneously self-organize into groups and generate patterns of stereotypical polychronous activity.

One of the key properties of polychronization is the ability to perform delay logic to perform spatio-temporal pattern recognition. As shown in Fig. 8.22a, we construct a simple three unit pattern recognition circuit our of excitable lasers with carefully tuned delay lines, where each subsequent neuron in the chain requires stronger perturbations to fire. The resulting simulation is shown in Fig. 8.22b. Three excitatory inputs separated sequentially by $\varDelta t_1 = 5$ ns and $\varDelta t_2 = 10$ ns are incident on all three units. The third is configured only to fire if it receives an input pulse and pulses from the other two simultaneously. The system therefore only reacts to a specific spatio-temporal bit pattern.

Fig. 8.22

a Schematic of a three-laser circuit that can recognize specific spatio-temporal bit patterns. b A simulation of a spatio-temporal recognition circuit with $\triangle t_1 = 5$ ns and $\triangle t_2 = 10$ ns. The input perturbation to unit 1 is plotted, along with the output powers of units 1–3 with the scaled carrier concentrations of their gain sections as the dotted blue lines. The third neuron fires during the triplet spike pattern with time delays $\triangle t_1$ and $\triangle t_2$ between spikes

Although this circuit is simple, the ability to perform temporal logic implies that excitable, neuromorphic systems are capable of categorization and decision making. Two existing applications utilize temporal logic, including LIDAR sensitivity that is analogous to an owl’s echolocation system and the escape response of a crayfish [18, 25] as detailed in Sect. 8.6. Combined with learning algorithms such as STDP which has recently been demonstrated in optics [68], networks could potentially perform more complex tasks such as spike-pattern cluster analysis.

8.10 Summary and Concluding Remarks

In an effort to break the limitations inherent in traditional von Neumann architectures, some recent projects in computing have sought more effective signal processing techniques by leveraging the underlying physics of devices [3, 4, 6, 69–71]. Cognitive computing platforms inspired by biological neural networks could solve unconventional computing problems and outperform current technology in both power efficiency and complexity [72–74]. These novel systems rely on alternative sets of computational principles, including hybrid analog-digital signal representations, co-location of memory and processing, unsupervised learning, and distributed representations of information.

On the cellular level, the brain encodes information as events or spikes in time [10], a hybrid signal with both analog and digital properties. Studies of morphology and physiology have pinpointed the LIF model as an effective spiking model to describe a variety of different biologically observed phenomena [2]. From the standpoint of computability and complexity theory, LIF neurons are powerful computational primitives that are capable of simulating both Turing machines and traditional sigmoidal neural networks [15]. These units perform a small set of basic operations (delaying, weighting, spatial summation, temporal integration, and thresholding) that are integrated into a single device capable of implementing a variety of processing tasks, including binary classification, adaptive feedback, and temporal logic. Though purely analog processing is susceptible to noise accumulation, this is overcome by neurons because the amplitude of spikes carry no information. The digital spike can be thresheld and restored by each neuron, which can then be cascaded like electronic logic gates. Thus neurons exploit both the bandwidth efficiency of analog signal processing and the scalability of digital logic. Networks of connected neurons can perform a wide variety of very powerful computing systems.

Spike processing algorithms are well understood in a number of important biological sensory processing systems and are finding growing use in signal processing applications [15]. The combination of these physiological principles with engineering not only helps in studying biological neural circuits [75], but also opens up a wide range of applications in emulating biological circuits in silico. A photonic realization of spiking neuron dynamics harnesses the high-switching speeds, wide communication bandwidth of optics, and low cross-talk achievable in photonics, making them well suited for an ultrafast spike-based information scheme. Optical spike processing devices are a result of the cross-fertilization between spike processing in the fields of computational neuroscience and high speed processing in the nonlinear optical device physics. While the fastest timescale on which biological neurons operate is in the order of milliseconds, the photonic integrate-and-fire devices operate on picosecond width pulses, and have an integration time constant in the order of 100 ps, which is about eight orders of magnitude faster. Because of this, photonic spike processors can access a computational domain that is inaccessible by other technologies. This domain, which we describe as ultrafast cognitive computing, represents an unexplored processing paradigm that could have a wide range of applications in adaptive control, learning, perception, motion control, sensory processing, autonomous robotics, and cognitive processing of the radio frequency spectrum.

Recently, there has been a growing interest in photonic spike processing which has spawned a rich search for an appropriate computational primitive. In this context, we have demonstrated one of the first implementations of photonic spiking neurons capable of processing signals at terahertz rates [16, 17, 39]. Like its physiological counterpart, functions performed by photonic neurons are determined by the configuration of a set of parameters including the weights and delays of interconnections, the temporal integration time, and the spiking threshold. The first implementations of a photonic spiking neuron [16] achieves noise suppression and thresholding through a NOLM, generated pulses synchronously via a mode-locked laser, and utilized a SOA for integration. This model demonstrated temporal integration and spike thresholding, but too much excitation could lead to the release of multiple pulses, degrading spike-encoded information. In addition, spikes were not asynchronous, making the output of the system digital. Next, we demonstrated a fully functioning photonic neuron [17] which integrated both excitation and inhibition, but also suffered from the problems mentioned above. A newer asynchronous model was proposed recently by our group in [39] that generated spikes based on incoming spikes. Although the system could emit a pulse at analog times, because the system did not generate its own spikes through internal mechanisms, the spikes could eventually degrade into noise as non-spike inputs led to non-spike outputs.

These implementations are based on discrete photonic components and together with the reliance on nonlinear fibers and other similar technologies, have made these demonstrations bulky (on the order of meters), complex, and power-hungry (hundreds of watts). These platforms are simply unscalable beyond a few neurons and are best-suited for broadband signal processing applications that can be implemented with simple circuits. For example, we recently demonstrated several prototypical lightwave neuromorphic circuits including the simple auditory localization inspired by the barn owl [25], useful for light detection and ranging (LIDAR) localization, and the crayfish tail-flip escape response [18], which demonstrates accurate, picosecond pattern classification.

Integrated lasers, in contrast to first bench-top systems, are physically compact and are capable of using feedback rather than feedforward dynamics to radically enhance nonlinearity. Feedback allows for the emergence of more complex behaviors, including bistability, the formation of attractors, and excitability. The excitable models are a step in the right direction, given the similarities between lasers and biological phenomena and the stability of feedback systems.

Our latest photonic neuron model—excitable LIF laser neuron—avoids many previous issues by combining an excitable approach with some of the ideas of the feedforward model. The integration of a laser gain section—which is dynamically analogous to an SOA—and a saturable absorber, which is essentially a feedback version of the thresholder used in the fiber model, leads to many desirable properties and a close analogy with biology, including the formation of highly stereotyped and well-defined optical spikes. Furthermore, this device is capable of implementing cortical-inspired algorithms. We have shown that, unlike previous models, our device can effectively perform cognitive algorithms at ultrafast time scales. Networks of such devices are stable, robust to noise, and can recognize patterns.

One of the greatest strengths of neural systems is their natural amenability to learning. Learning based on experience is essential for a system to dynamically adapt to an unpredictable or changing environment, or one that is too complex to be characterized a priori. There are several different methods by which neurons can learn: unsupervised learning extract structure from an unknown signal environment for efficient encoding, dimensionality reduction, or clustering; supervised learning programs a system to perform a function defined in terms of its input-output pairs; and reinforcement learning optimizes a particular function based on performance criterion. In all these cases, the learning mechanism configures a set of system parameters, such as synaptic weights, based upon the activity of the system in response to its inputs, and as a consequence, the system changes. Synaptic plasticity is not only responsible for learning and information storage but also the formation and refinement of neuronal circuits during development. With photonic neurons, we focus on learning through a type of synaptic plasticity called STDP, whereby the strength on input connections is determined by the relative timing of pre-synaptic and post-synaptic spikes. The experimentally demonstrated optical STDP [68] is potentially useful for applications including coincidence detection, sequence learning, path learning, and directional selectivity in visual response. These demonstration forms the foundation for photonic neurons to learn about the environment like a biological brain.

All the components employed for optical STDP—including the Mach-Zehnder configuration, the EAM, and the SOA—can be fabricated with a small footprint in planar photonics. Integrating this together with LIF excitable neurons on a single chip could lead to systems that emulate a well-established paradigm for adaptive computing on a scalable platform. These compact, adaptive, unconventional processing systems would operate on unprecedented time scales. Large networks could potentially be constructed as LSMs for optical reservoir computing [76] to aid in the study of biology or open up new applications to high bandwidth signal processing, ultrafast control loops, ultralow latency classification functions, and ultrafast adaptive processing.